Теоремы теории вероятностей для егэ профиль презентация

Слайд 1

Обучение учащихся элементам теории вероятностей при подготовке к сдаче ГИА и ЕГЭ

Слайд 2

Классическое определение вероятности Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.

Слайд 3

Задачи на прямое использование классического определения вероятности На тарелке 16 пирожков: 7 с рыбой, 5 с вареньем и 4 с вишней. Юля наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней. Решение: m =4 – число пирожков с вишней (число благоприятных исходов) n= 16 – число всех пирожков (общее число равновозможных исходов)

Слайд 4

Задачи на прямое использование классического определения вероятности В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая. Решение: m =20-8-7=5 – число гимнасток из Китая (число благоприятных исходов) n=20 – число гимнасток, которые принимают участие в чемпионате (общее число равновозможных исходов)

Слайд 5

Задачи на прямое использование классического определения вероятности Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России? Решение: m =10-1=9 – число участников из России за исключением Руслана Орлова (число благоприятных исходов) n=2 6-1=25 – число бадминтонистов, участвующих в чемпионате за исключением Руслана Орлова (общее число равновозможных исходов)

Слайд 6

Задачи на прямое использование классического определения вероятности В классе учится 21 человек. Среди них две подруги: Аня и Нина. Класс случайным образом делят на 7 групп, по 3 человека в каждой. Найти вероятность того. что Аня и Нина окажутся в одной группе . Решение: Пусть Аня оказалась в некоторой группе, тогда m =21:7-1=2 – число вакантных мест в этой же группе (число благоприятных исходов) n=2 1-1=20 – число учащихся класса за исключением Ани (общее число равновозможных исходов)

Слайд 7

Задачи на прямое использование классического определения вероятности В классе учится 21 человек. Среди них две подруги: Аня и Нина. Класс случайным образом делят на 7 групп, по 3 человека в каждой. Найти вероятность того, что Аня и Нина окажутся в одной группе. 2 способ Вероятность того, что одна из подруг окажется в одной из групп равна Вероятность того, что вторая подруга окажется в этой же группе равна Поскольку все 7 групп равноправны, то вероятность попасть в одну группу равна

Слайд 8

Задачи на прямое использование классического определения вероятности В классе учится 21 человек. Среди них две подруги: Аня и Нина. Класс случайным образом делят на 7 групп, по 3 человека в каждой. Найти вероятность того, что Аня и Нина окажутся в одной группе. 3 способ Используем формулы комбинаторики:

Слайд 9

Задачи на прямое использование классического определения вероятности В классе учится 21 человек. Среди них две подруги: Аня и Нина. Класс случайным образом делят на 7 групп, по 3 человека в каждой. Найти вероятность того. что Аня и Нина окажутся в разных группах . Решение: События А – « подруги окажутся в одной группе » и В- « подруги окажутся в разных группах » являются противоположными. В этом случае P(A)=1-P(B) .

Слайд 10

Задачи на прямое использование классического определения вероятности В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых. Комбинации в выпадении очков на кубиках: 1 – 1 2 – 1 3 – 1 4 – 1 5 – 1 6 — 1 1 – 2 2 – 2 3 – 2 4 – 2 5 – 2 6 — 2 1 – 3 2 – 3 3 – 3 4 – 3 5 – 3 6 — 3 1 – 4 2 – 4 3 – 4 4 – 4 5 – 4 6 — 4 1 – 5 2 – 5 3 – 5 4 – 5 5 – 5 6 — 5 1 – 6 2 – 6 3 – 6 4 – 6 5 – 6 6 — 6 Жирным шрифтом выделены комбинации, в которых сумма очков равна 8.

Слайд 11

Задачи на прямое использование классического определения вероятности Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза . Обозначим «1» ту сторону монеты, которая отвечает за выигрыш жребия «Физиком», другую сторону монеты обозначим «0». Тогда Возможные комбинации жребия: 000 001 010 011 100 101 110 111 Жирным шрифтом выделены благоприятные комбинации.

Слайд 12

Задачи на прямое использование классического определения вероятности В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что решка выпадет ровно один раз. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что решка выпадет все три раза. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орёл выпадет ровно три раза.

Слайд 13

В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что решка выпадет ровно один раз Возможные исходы: О – О О – Р Р – Р Р – О Жирным шрифтом выделены благоприятные исходы

Слайд 14

В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что решка выпадет все три раза. Общее число исходов найдем по формуле Число благоприятных исходов

Слайд 15

В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орёл выпадет ровно три раза. Общее число исходов найдем по формуле Число благоприятных исходов: О-О-О-Р О-О-Р-О О-Р-О-О Р-О-О-О

Слайд 16

Задачи на прямое использование классического определения вероятности Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых. В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает. m=100 n=100+8=108 m=100 0 -5=9 9 5 n=100 0

Слайд 17

Основные понятия События А и В называются совместными , если они могут произойти оба в результате одного опыта. События А и В называются несовместными , если в результате испытания они никогда не могут наступить вместе

Слайд 18

Примеры совместных и несовместных событий Совместные события Два стрелка делают по одному выстрелу по мишени: событие А – попадание первого стрелка, событие В – попадание второго стрелка. Несовместные события Подбрасываем игральный кубик: событие А – выпадение 1, событие В – выпадение 5.

Слайд 19

Сумма событий Суммой А + В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий. Если из орудия произведены два выстрела: событие А — попадание при первом выстреле, событие В — попадание при втором выстреле, то событие А + В — попадание при первом выстреле, или при втором, или в обоих выстрелах.

Слайд 20

Теорема о сумме несовместных событий Пусть события A и В — несовместные, причем вероятности этих событий известны. Теорема. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий: Р (А + В) = Р (А) + Р (В).

Слайд 21

Использование теоремы о сумме несовместных событий На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем. Ответ: 0,35 Решение: Пусть событие А – достанется вопрос по теме «Вписанная окружность», событие В – достанется вопрос по теме «Параллелограмм», событие А+В – достанется вопрос по одной из этих тем. События А и В – несовместные, следовательно P(A + B) =P(A) + P(B). P(A + B) = 0 ,2+0,15=0, 35

Слайд 22

Теорема о сумме совместных событий Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления P(A+B) = P(A) + P(B) — P(AB) .

Слайд 23

Пример использования теоремы о сумме совместных событий В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,25. Вероятность того, что кофе закончится в обоих автоматах, равна 0,15. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах. Решение: Пусть А – кофе закончится в 1 автомате, В – кофе закончится во 2 автомате, А*В – кофе закончится в обоих автоматах, событие А+В – кофе закончится хотя бы в одном автомате, событие A+B – кофе останется в обоих автоматах. Тогда P(A)=P(B)=0, 25 , P(A*B)=0,1 5 События А и В – совместные, следовательно P(A+B)=0, 25 +0, 25 -0,1 5 =0, 35. Таким образом P(A + B) = 1-0, 35 =0, 6 5

Слайд 24

Произведение событий Произведением двух событий А и В называют событие А*В, состоящее в совместном появлении (совмещении) этих событий. Например, если А — деталь годная, В — деталь окрашенная, то А * В — деталь годна и окрашена. Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий. Например, если А, В, С — появление «герба» соответственно в первом, втором и третьем бросаниях монеты, то А * В * С — выпадение «герба» во всех трех испытаниях.

Слайд 25

Основные понятия Два события называют независимыми , если вероятность их совмещения равна произведению вероятностей этих событий; в противном случае события называют зависимыми . На практике о независимости событий заключают по смыслу задачи. Например, вероятности поражения цели каждым из двух орудий не зависят от того, поразило ли цель другое орудие, поэтому события «первое орудие поразило цель» и «второе орудие поразило цель» независимы.

Слайд 26

Теорема о произведении независимых событий Теорема. В случае независимых событий вероятность их произведения равна произведению вероятностей этих событий Р (А*В) = Р (А) * Р (В)

Слайд 27

Использование теоремы о произведении независимых событий Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза. Решение: Пусть событие А – выигрыш А. белыми фигурами , событие В – выигрыш А. черными фигурами, событие А*В – выигрыш А. разными фигурами. События А и В – независимые, следовательно P(A*B) =P(A)*P(B). P(A*B) = 0,52*0,3=0, 156

Слайд 28

Формула полной вероятности Пусть событие может произойти вместе с одним из независимых событий Обозначим через событие — «событие произошло вместе с . Тогда справедлива формула

Слайд 29

Пример решения задач с использованием теорем о вероятностях событий Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным. P ( A+B)=P(A)+P(B)= =0,03*0,45+0,01*0,55= =0,019

Слайд 30

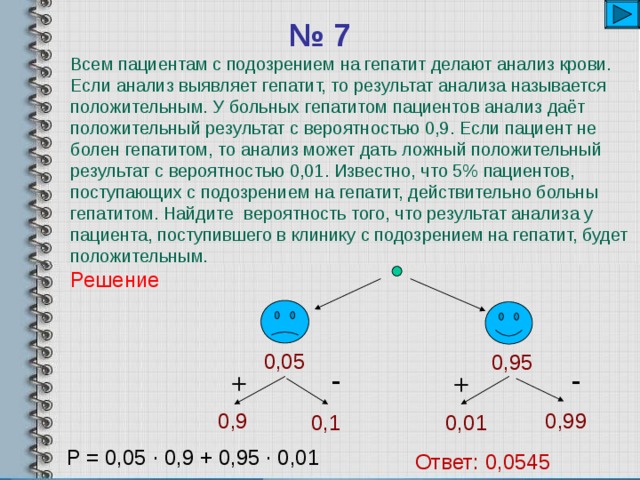
Пример решения задач с использованием теорем о вероятностях событий Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.

Слайд 31

Пример решения задач с использованием теорем о вероятностях событий A – пациент болен и анализ правильный, B – пациент здоров и анализ не правильный P(A)=0,05*0,9=0,045 P(B)=0,95*0,01=0,0095 События А и В – несовместные P(A+B)=0,045+0,0095= =0,0545 Пациент Болен гепатитом 5% Не болен гепатитом 100-5=95% Положительный результат 0,9 Ложный положительный результат 0,01

Слайд 32

Пример решения задач с использованием теорем о вероятностях событий Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 18 пассажиров, равна 0, 82 . Вероятность того, что окажется меньше 1 0 пассажиров, равна 0,5 1 . Найдите вероятность того, что число пассажиров будет от 1 0 до 1 7 . События A и B – несовместные, следовательно 0,82=0,51+x . Значит x=0,31

Слайд 33

Пример решения задач с использованием теорем о вероятностях событий В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах. Ответ: 0,6 Пусть А – событие «пятирублевые монеты в разных карманах» Наступление события А возможно лишь в трех случаях (три результата перекладывания монет): 5,10,10; 10,5,10 или 10,10,5. Эти события несовместные, вероятность их суммы равна сумме вероятностей этих событий:

Слайд 34

Пример решения задач с использованием теорем о вероятностях событий В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен. Решение: Пусть А – неисправен 1 автомат, В – неисправен 2 автомат, А*В – неисправны оба автомата, событие А*В – исправен хотя бы один автомат. Тогда P(A)=P(B)=0, 05 , События А и В – независимы P(A*B)=0, 05*0,05=0,0025 Таким образом P(A * B) = 1-0, 0025 =0, 997 5

Слайд 35

Статистическая вероятность Относительной частотой W(A) события А в данной серии испытаний называют отношение числа испытаний М , в которых событие А произошло, к числу N всех проведенных испытаний . При этом число М называют частотой события А Статистической вероятностью называют число, около которого колеблется относительная частота события при большом числе испытаний

Слайд 36

Пример решения задачи Вероятность того, что новый DVD-проигрыватель в течение года поступит в гарантийный ремонт, равна 0,045. В некотором городе из 1000 проданных DVD-проигрывателей в течение года в гарантийную мастерскую поступила 51 штука. На сколько отличается относительная частота события «гарантийный ремонт» от его вероятности в этом городе? Решение. A — событие «гарантийный ремонт» Частота события A равна М =51, число испытаний N =1000. Тогда относительная частота события «гарантийный ремонт» равна . Тогда

Слайд 37

Примеры решения задач с костями Задача. Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 9. Какова вероятность того, что для этого потребовалось два броска? Ответ округлите до сотых. Пусть А – событие «за два броска выпало более 9 очков» Наступление события А возможно лишь в трех случаях : выпало 10;11;12 очков. Пусть — выпало в сумме 10 очков. Это возможно только в трех случаях 4+6, 6+4, 5+5. Значит , Пусть — выпало в сумме 11 очков. Это возможно только в двух случаях 5+6, 6+5. Следовательно, Пусть — выпало в сумме 12 очков. Это возможно только в случае 6+6. Поэтому, Поскольку и события несовместные, вероятность их суммы равна сумме вероятностей этих событий :

Слайд 38

Испытание — бросание кубика. Выпадение восьми очков при двукратном бросании кубика возможно только при следующих результатах испытаний: 2+6, 6+2, 3+5, 5+3, 4+4. Тогда событию А — «выпало восемь очков и хотя бы раз 4» благоприятствует один исход ( m=1 ) , всего исходов пять ( n=5 ) . По определению вероятности получаем, что При двукратном бросании игральной кости в сумме выпало 8 очков. Какова вероятность того, что хотя бы раз выпало 4 очка?

Слайд 39

Игральную кость бросили два раза. Известно, что два очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 4». Испытание — двукратное бросание кубика. Возможные исходы испытания занесем в таблицу: (1 ;1) ( 3;1) ( 4;1) ( 5;1) ( 6;1) (1 ;3) ( 3;3) ( 4;3) ( 5;3) ( 6;3) (1 ;4) ( 3;4) ( 4;4) ( 5;4) ( 6;4) (1 ;5) ( 3;5) ( 4;5) ( 5;5) ( 5;6) (1 ;6) ( 3;6) ( 4;6) ( 5;6) ( 6;6) Здесь m=2, n=25, следовательно, по определению получаем

Слайд 40

Первый игральный кубик обычный, а на гранях второго кубика нет четных чисел, а нечетные числа 1,3 и 5 встречаются по два раза. В остальном кубики одинаковые. Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 3 и 5 очков. Какова вероятность того, что бросали первый кубик? Для удобства будем различать обозначения «троек» и «пятерок» на каждом из кубиков. Пусть на первом кубике это будут 3 и 5, а на втором — 3 , 3 , 5 , 5 . Тогда возможные наборы в двух испытаниях будут: ( 3 ,5) (5,3) ( 3 , 5 ) ( 5 , 3 ) ( 3 , 5 ) ( 5 , 3 ) ( 3 , 5 ) ( 5 , 3 ) ( 3 , 5 ) ( 5 , 3 ) Для события А — «бросали первый кубик» благоприятствуют только пары черного цвета ( m=2 ) , всего же видим десять пар ( n=10 ) Таким образом,

Слайд 41

Схема решения задач по теории вероятности Выяснить, в чем состоит рассматриваемое в задаче испытание. Обозначьте буквами события, рассматриваемые в условии задачи. С помощью введенных обозначений выразите событие, вероятность наступления которого необходимо найти. * Если требуется найти вероятность суммы событий , выясните, совместны или несовместны рассматриваемые события. * Если же требуется найти вероятность произведения событий , выясните, зависимы или независимы рассматриваемые события. Выберите соответствующую условию задачи формулу и вы­полните необходимые вычисления.

Слайд 42

Полезно почитать по теме https://self-edu.ru/books/dwn.php?filename=balak_scool https://www.mathedu.ru/text/lyutikas_fakultativnyy_kurs_po_teorii_veroyatnostey_1990/_tp.pdf

1. В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп:

1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?

Решение: Обозначим через А событие «команда России во второй группе». Тогда количество благоприятных событий m = 4 (четыре карточки с номером 2), а общее число равновозможных событий n = 16 (16 карточек).

Ответ: 0,25.

2. В чемпионате мира участвуют 15 команд. С помощью жребия их нужно разделить на пять групп по три команды в каждой. В ящике вперемешку лежат карточки с номерами групп:

1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда Италии окажется в третьей группе?

Решение: Обозначим через А событие «команда Италии в третьей группе». Тогда количество благоприятных событий m = 3 (три карточки с номером 3), а общее число равновозможных событий n = 15 (15 карточек).

Ответ: 0,2.

3. Конкурс исполнителей проводится в 4 дня. Всего заявлено 80 выступлений – по одному от каждой страны. В первый день 20 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?

Ответ: 0,25.

4. Научная конференция проводится в 5 дней. Всего запланировано 75 докладов – первые три дня по 17 докладов, остальные распределены поровну между четвёртым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность того, что доклад профессора М. окажется запланированным на последний день конференции?

Ответ: 0,16.

5. Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений – по одному от каждой страны. В первый день 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность того, что выступление представителя России состоится в третий день конкурса?

Ответ: 0,225.

6. На чемпионате по прыжкам в воду выступают 50 спортсменов, среди них 5 прыгунов из Испании и 3 прыгуна из Бразилии. Порядок выступлений определяется жребием. Найдите вероятность того, что сорок вторым будет выступать прыгун из Испании.

Ответ: 0,1.

7. В классе 21 шестиклассник, среди них два друга – Митя и Петя. Класс случайным образом делят на три группы, по 7 человек в каждой. Найдите вероятность того, что Митя и Петя окажутся в одной и той же группе.

Решение: В каждой группе 7 человек. Будем считать, что Митя уже занял место в одной группе. Обозначим через А событие «Петя оказался в той же группе». Для Пети останется n = 20 свободных мест, из них m = 6 мест.

Ответ: 0,3.

8. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России.

Решение: Общее число случаев (число участников, исключая самого Руслана Орлова) n = 26 – 1 = 25.

Число благоприятных случаев (число участников из России, исключая самого Руслана Орлова)

m = 10 – 1 = 9.

Ответ: 0,36.

9. Стрелок стреляет по мишени один раз. В случае промаха стрелок делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,6. Найдите вероятность того, что мишень будет поражена (одним из выстрелов).

Ответ: 0,84.

10. Две фабрики выпускают одинаковые стёкла для автомобильных фар. Первая фабрика выпускает 25% этих стёкол, вторая – 75%. Первая фабрика выпускает 4% бракованных стёкол, а вторая – 2%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Ответ: 0,025.

11. Два завода выпускают одинаковые автомобильные предохранители. Первый завод выпускает 40% предохранителей, второй – 60%. Первый завод выпускает 4% предохранителей, а второй – 3%. Найдите вероятность того, что случайно выбранный в магазине предохранитель окажется бракованным.

Ответ: 0,034.

12. На соревнования по метанию ядра приехали 5 спортсменов из Сербии, 7 из Хорватии и 3 из Норвегии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что двенадцатым будет выступать спортсмен из Норвегии

Решение: Общее число случаев (число всех спортсменов) n = 15. Число благоприятных случаев (число спортсменов из Норвегии) m = 3.

Ответ: 0,2.

13. Павел Иванович совершает прогулку из точки А по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Найдите вероятность того, что Павел Иванович попадёт в точку G.

A

C

G

H

F

B

D

E

К

Ответ: 0,125.

14. Вася, Петя, Коля и Лёша бросили жребий – кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя.

Решение: Обозначим через A событие «начинает игру Петя». Тогда количество благоприятствующих исходов m = 1, а общее число равновозможных исходов n (начинает игру Петя, начинает игру Вася, начинает игру Коля, начинает игру Лёша).

Ответ: 0,125.

15. Катя дважды бросает игральный кубик. В сумме у неё выпало 6 очков. Найдите вероятность того, что при одном из бросков выпало 5 очков.

Общее число случаев n = 5 ((1,5); (5,1); (2,4); (4,2); (3,3)). Число благоприятных случаев (комбинации (1,5); (5,1)) m = 2.

Ответ: 0,4.

Решение:

16. Люда дважды бросает игральный кубик. В сумме у неё выпало 9 очков. Найдите вероятность того, что при первом броске выпало 5 очков.

Решение: Общее число случаев n = 4 ((3,6); (4,5); (5,4); (6,3)). Число благоприятных случаев m = 1 (комбинация (5,4)).

Ответ: 0,25.

17. Таня и Нина играют в кости. Они бросают кость по одному разу. Выигрывает тот, кто выбросил больше очков. Если очков выпало поровну, то наступает ничья. В сумме выпало 6 очков. Найдите вероятность того, что Таня выиграла.

Решение: Общее число случаев n = 5 ((1,5); (2,4); (3,3); (4,2); (5,1)). Число благоприятных случаев m = 2 (комбинации (1,5); (2,4) или (4,2); (5,1)).

Ответ: 0,4.

18. Найдите вероятность того, что при бросании двух кубиков на каждом выпадет менее 4 очков.

Ответ: 0,25.

19. При двукратном бросании игрального кубика в сумме выпало 6 очков. Найдите вероятность того, что в первый раз выпало меньше 3 очков.

Решение: Общее число случаев n = 5 (комбинации (1,5); (5,1); (2,4); (4,2); (3,3)). Число благоприятных случаев (комбинации (1,5); (2,4)) m = 2.

Ответ: 0,4.

20. Перед началом футбольного матча судья бросает монету, чтобы определить, какая из команд будет первая владеть мячом. Команда «Меркурий» по очереди играет с командами «Марс», «Юпитер» и «Уран». Найдите вероятность того, что во всех матчах право владеть мячом выиграет команда «Меркурий».

Ответ: 0,125.

Ответ: 0,125.

2 способ решения:

21. Перед началом футбольного матча судья бросает монету, чтобы определить, какая из команд будет первая владеть мячом. Команда «Хуторянка» по очереди играет с командами «Радуга», «Дружба», «Заря» и «Воля». Найдите вероятность того, что команда «Хуторянка» будет первой владеть мячом только в первых двух играх.

Ответ: 0,0625.

22. Перед началом матча по водному поло судья устанавливает мяч в центр бассейна, и от каждой команды к мячу плывёт игрок, чтобы первым завладеть мячом. Вероятность выиграть мяч у игроков равны. Команда «Русалочка» по очереди играет с командами «Наяда», «Ундина» и «Ариэль». Найдите вероятность того, что во втором матче команда «Русалочка» выиграет мяч в начале игры, а в двух других проиграет

Ответ: 0,125.

23. В некоторой местности утро в июле может быть либо ясным, либо пасмурным. Наблюдения показали:

1) Если июльское утро ясное, то вероятность дождя в этот день 0,1.

2) Если июльское утро пасмурное, то вероятность дождя в течение дня равна 0,5.

3) Вероятность того, что утро в июле будет пасмурным, равна 0,2.

Найдите вероятность того, что в случайно взятый июльский день дождя не будет.

Ответ: 0,82.

24. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Решение: Первый способ. Обозначим через А событие «кофе закончится в первом автомате», через В событие «кофе закончится во втором автомате». Событие С «кофе закончится хотя бы в одном автомате» является их суммой С = А + В.

Ответ: 0,52.

Решение: Второй способ решения задачи 16.

25. В сборнике билетов по математике всего 20 билетов, в 7 из них встречается вопрос о производной. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не встретится вопрос о производной.

Решение: Общее число случаев (всего билетов)

n = 20. Число благоприятных случаев (количество билетов, в которых не встречается вопрос о производной) m = 20 – 7 = 13.

Ответ: 0,65.

26. В классе 7 мальчиков и 14 девочек. 1 сентября случайным образом определяют двух дежурных на 2 сентября, которые должны приготовить класс к занятиям. Найдите вероятность того, что будут дежурить два мальчика.

Ответ: 0,1.

27. Валя выбирает случайное трёхзначное число. Найдите вероятность того, что оно делится на 51.

Ответ: 0,1.

Формула классической вероятности

Вероятность – есть число, характеризующее возможность наступления события.

Сумма вероятностей всех элементарных событий случайного эксперимента равна 1.

Несовместные события. Формула сложения вероятностей

Определение. События называют несовместными, если они не могут происходить одновременно в одном и том же испытанию

Например, выигрыш, ничейный исход и проигрыш одного игрока в одной партии в шахматы – три несовместных события.

Теорема. Вероятность суммы двух несовместных событий A и B (появление хотя бы одного события) равна сумме вероятностей этих событий: P (A+B)=P(A) +P(B).

Теорема обобщается на любое число попарно несовместных событий

Совместные события. Формула сложения вероятностей (формула для вероятности суммы двух событий в общем случае (не обязательно несовместных))

Определение. События называют совместными, если они могут происходить одновременно. Например, при бросании двух монет выпадение решки на одной не исключает появление решки на другой монете.

Теорема. Вероятность суммы двух совместных событий A и B (появление хотя бы одного события) равна сумме их вероятностей без вероятности их совместного появления, то есть P (A+B)=P(A) +P(B) – P(AB).

Независимые события. Формула умножения вероятностей

Определение. Два случайных события называют независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события называют зависимыми.

Теорема. Вероятность произведения (совместного появления) двух независимых событий равна произведению вероятностей этих событий: P(AB) = P(A) · P(B).

Использованная литература:

• ЕГЭ-2014: Математика: самое полное издание типовых вариантов заданий/ авт.-сост. И.В.Ященко, И.Р. Высоцкий; под ред. А.Л.Семёнова, И.В.Ященко.- Москва: АСТ: Астрель, 2014.
• А.Г.Корянов , Н.В.Надежкина. Задача В10. ЕГЭ. Математика, 2014. Элементы теории вероятностей (интернет-ресурс http://alexlarin.net/ege/2014/b102014.html‎)
• ЕГЭ: 3000 задач с ответами по математике. Все задания группы В/А.Л.Семёнов, И.В.Ященко и др.; под ред. А.Л.Семёнова, И.В.Ященко. – М.: Издательство «Экзамен», 2014.
• Источник шаблона презентации : http://pedsovet.su/load/321-1-0-32889

1. Теория вероятностей в задачах ЕГЭ

2. Основные понятия

Событие- явление , которое происходит в результате
осуществления какого-либо определенного комплекса
условий. Осуществление комплекса условий называется
опытом или испытанием. Событие- результат испытания.
Случайным событием называется событие, которое
может произойти или не произойти в результате
некоторого испытания ( при бросании монеты может
выпасть орел , а может и не выпасть).
Достоверным событием называется событие, которое
обязательно произойдет в результате испытания
(извлечение белого шарика из ящика с белыми шарами).
Невозможным считается событие, которое не может
произойти в результате данного испытания( извлечение
черного шарика из ящика с белыми шарами).
О каждом таком событии можно сказать,что оно
произойдет с некоторой вероятностью

3.

Бросаем монетку. Орел или решка?
Бросить монетку – испытание
Орел или решка – два возможных исхода.
Вероятность выпадения орла – ½,
решки – ½.

4.

Бросаем игральную кость (кубик).
Выпадение одного очка – это один исход из шести
возможных.
Выпадение двух очков — один исход из шести
возможных.
Допустим, нам необходимо выпадение 2 очков,
такой исход в теории вероятностей называется
благоприятным.

5.

Вероятность выпадения тройки — 1/6.
Вероятность выпадения семерки – 0.
Вероятность выпадения четного числа – ½.
Вероятность выпадения числа, меньше пяти –
4/6 или 2/3

6.

Берем колоду из 36 карт.
Вероятность вытащить загаданную карту – 1/36.
Вероятность вытащить туза – 4/36 или 1/9
Вероятность вытащить карту масти бубен – 9/36
или ¼
Вероятность вытащить красную карту – 18/36
или ½.

7.

Вероятность события равна
отношению числа благоприятных
исходов к числу всех возможных
исходов.
b
Р ( А)
a
a– число всех исходов испытания
b– число исходов
благоприятствующих событию А
Вероятность не может
быть больше 1.

8. Методы решения

9. Непосредственные подсчеты

1.Метод логического перебора
(«решение напролом»)
– выписываются все
возможные исходы (а), выбираются
благоприятные (b) и находится
отношение p = b/a

10.

В случайном эксперименте монету
бросают два раза. Найдите вероятность
того, что орел выпадет ровно 1 раз.
Выпишем все возможные исходы:
ОО, ОР, РО, РР — 4
Благоприятные: ОР, РО – 2
Вероятность p= 2/4=0,5

11.

В случайном эксперименте монету
бросают три раза. Найдите вероятность
того, что решка не выпадет ни разу.
Выпишем все возможные исходы:
ООО, ООР, ОРО,РОО, ОРР, РОР,РРО, РРР — 8
Благоприятные: ООО – 1
Вероятность p= 1/8=0,125

12.

В случайном эксперименте монету бросают
четыре раза. Найдите вероятность того, что
решка выпадет два раза.
Выпишем все возможные исходы:
ОООР, ООРО,ОРОО,РООО,
РРОО, РОРО,РООР, ОРРО, ОРОР, ООРР,
ОРРР, РРРО, РОРР, РРОР,
ОООО, РРРР
— 16
Благоприятные: — 6
Вероятность p= 6/16=0,375

13. 2. Таблица вариантов

Составляется таблица, с
помощью которой находятся все
возможные исходы (а) и все
благоприятные исходы (b) и
вычисляется
вероятность p = b/a

14.

Игральную кость бросают два раза.
Найдите вероятность того, что сумма
выпавших очков будет равна 7.
1
1
2
3
2
3
4
5
6
Всего
исходов – 36
Благоприятных
исходов — 6
4
5
6
Вероятность
р = 6/36 = 1/6

15. 2. Полный граф

Условие задачи изображается в
виде графа (дерева), который
позволяет найти количество всех
возможных исходов, выбрать
благоприятные и вычислить
вероятность p = b/a

16.

Антон, Борис и Василий купили 3 билета на
1,2,3 места первого ряда. Сколькими
способами они могут занять имеющиеся
места?
А
Б
В
Б
А
В
А
Б
В
Ответ: 6
В
Б
В
А
Б
А

17.

Какова вероятность, что Антон займет первое
место?
Всего способов – 6
Благоприятные исходы – 2
Р = 2/6=1/3

18. Правила

Правила

19.

Два события называются
несовместными, если они не могут
появиться одновременно в одном и
том же испытании.
Вероятность появления хотя бы
одного из двух несовместных событий,
равна сумме вероятностей этих
событий.
р = р(A) +р(B)

20.

На экзамене по геометрии школьнику достается один вопрос
из списка экзаменационных вопросов. Вероятность того, что это
вопрос на тему «Вписанная окружность», равна 0,2.
Вероятность того, что это вопрос на тему «Параллелограмм»,
равна 0,15. Вопросов, относящихся одновременно к этим двум
темам, нет. Найдите вероятность того, что школьнику на
экзамене достанется вопрос по одной из этих тем.
События «вопрос о вписанной окружности»
и «вопрос о параллелограмме» несовместные, поэтому вероятность выбрать
один из них равна сумме вероятностей:
р = 0,2+0,15=0,35

21.

Вероятность того, что новый чайник прослужит
больше года равна 0,97. Вероятность того, что он
прослужит более двух лет , равна 0,89. Найдите
вероятность того, что чайник прослужит меньше двух
лет, но больше года.
События «чайник прослужит больше двух
лет» и « чайник прослужит больше года,
но менее двух лет» — несовместные. Сумма
этих событий равна событию «чайник
прослужит более года». Поэтому искомая
вероятность р = 0,97-0,89=0,08

22.

События называются совместными,
если они могут происходить
одновременно.
Вероятность появления хотя бы одного
события равна сумме их вероятностей
без вероятности их совместного
появления.
р = р(A) +р(B) – р(AB)

23.

В торговом центре два одинаковых кофейных автомата.
Вероятность того, что к концу дня в автомате закончится кофе
равна 0,3. Вероятность того, что кофе закончится в обоих
автоматах – 0,12. Найдите вероятность того, что к концу дня кофе
останется в обоих автоматах.
События « кофе останется в обоих
автоматах» и « кофе закончится хотя бы в
одном» — противоположные. Сумма их
вероятностей 1.
Найдем вероятность события « кофе
закончится хотя бы в одном автомате»
р=0,3+0,3-0,12 = 0,48.
Тогда вероятность события «кофе останется в
обоих автоматах» р = 1 – 0,48 = 0,52

24.

Два события называются
независимыми, если появление
одного из них не влияет на
вероятность появления другого.
Вероятность совместного появления
двух независимых событий равна
произведению вероятностей этих
событий.

25.

Стрелок попадает в цель с вероятностью 0,9.
Найдите вероятность того, что он попадет в цель
четыре выстрела подряд.
Попадание в цель при каждом
последующем выстреле – независимое
от предыдущего исхода событие
Вероятность
р = 0,9*0,9*0,9*0,9 = 0,6561

26.

Вероятность того, что батарейка бракованная, равна
0,02. Покупатель выбирает в магазине случайную
упаковку, в которой две такие батарейки. Найдите
вероятность того, что обе батарейки окажутся
исправными.
События «батарейка бракованная» и
«батарейка исправная» — противоположные,
поэтому вероятность события «батарейка
исправная»
р = 1-0,02 = 0,98.
События «1 батарейка исправная» и «2
батарейка исправная» — независимые,
поэтому вероятность того, что обе батарейки
исправны р = 0,98*0,98= 0,9604

27.

Помещение освещается фонарем с двумя лампами.
Вероятность перегорания одной лампы в течение года
равна 0,17. Найдите вероятность того, что в течение
года хотя бы одна лампа не перегорит.
Событие « хотя бы одна лампа не перегорит»
противоположно событию « обе лампы
перегорят» . Вероятность события «обе лампы
перегорят» равна произведению вероятностей
(т.к. события независимые)
р=0,17*0,17=0,0289
Тогда вероятность события « хотя бы одна
лампа не перегорит» равна: 1 – 0,0289 =
0,9711

28.

Зависимые события – наступление одного
из них изменяет вероятность
наступления другого.
Вероятность совместного появления двух
зависимых событий равна произведению
вероятности одного из них на условную
вероятность другого, вычисленную при
условии, что первое событие произошло.

29.

В урне 6 шаров – 2 белых и 4 черных. Без
возвращения выбираем два шара. Найдите
вероятность того, что оба шара белые.
Вероятность события «первый шар белый»
равна 2/6.
При условии что первый шар белый
вероятность события «второй шар белый» равна
1/5.
Вероятность события «оба шара белые» р =
2/6*1/5 = 1/15

30.

Полная
вероятность

31.

С первого станка поступает 40%, со второго – 30%
и с третьего – 30% всех деталей. Вероятность
изготовления бракованной детали равны для
каждого станка соответственно 0,01, 0,03, 0,05.
Найдите вероятность того, что наудачу взятая
деталь будет бракованной.

32.

3 станок
1 станок
0,4
0,3
2 станок
0,3
брак
0,01
брак
0,05
брак
0,03
Р = 0,4*0,01+0,3*0,03+0,3*0,05 = 0,028

33.

В волшебной стране бывает два
типа погоды: хорошая и
отличная, причем погода,
установившись утром, держится
неизменной весь день. Известно,
что с вероятностью 0,8 погода
завтра будет такой же , как и
сегодня. Сегодня 3 июня, погода
в волшебной стране хорошая.
Найдите вероятность того, что 6
июня в Волшебной стране будет
отличная погода.
Ответ: 0,392

34. Спасибо за внимание!

29.03.2017 г.

Классная работа

ЕГЭ

вероятность

задачи

теория

Тема урока:

Теория вероятностей

в задачах ЕГЭ

КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ

Вероятностью Р наступления случайного события А называется отношение , где N(A) – число всех благоприятных исходов, а N – число всех возможных исходов эксперимента

Основные теоремы

Суммой

событий А и В

называют

событие А + В ,

состоящее

в наступлении

хотя бы одного

из этих событий

Произведением

событий А и В

называют

событие А ∙ В ,

состоящее

в наступлении

обоих этих

событий

Р(А + В) = Р(А) + Р(В)

Р(А ∙ В) = Р(А) ∙ Р(В)

№ 1

Фабрика выпускает сумки. В среднем на 80 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.

Решение

N(A) = 80

N = 80 + 8 = 88

P(A) = 80:88

Ответ: 0,91

№ 2

На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Решение

События «вопрос о вписанной окружности» и

«вопрос о параллелограмме» — несовместные,

поэтому вероятность

выбрать один из них равна сумме вероятностей:

р = 0,2+0,15

Ответ: 0,35

№ 3

Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые четыре раза попал в мишени, а последний раз промахнулся. Результат округлите до сотых.

Решение

Попадание в цель при каждом последующем выстреле – независимое от предыдущего исхода событие.

Вероятность р = 0,6  0,6  0,6  0,6  0,4

Ответ: 0,05

№ 4

В торговом центре два одинаковых кофейных автомата. Вероятность того, что к концу дня в автомате закончится кофе равна 0,3. Вероятность того, что кофе закончится в обоих автоматах равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Решение

Со­бы­тие А – «кофе за­кон­чит­ся в пер­вом ав­то­ма­те»

Со­бы­тие В — «кофе за­кон­чит­ся во вто­ром ав­то­ма­те»

Тогда A·B – «кофе за­кон­чит­ся в обоих ав­то­ма­тах»

A + B — «кофе за­кон­чит­ся хотя бы в одном ав­то­ма­те» 

По усло­вию P(A) = P(B) = 0,3; P(A·B) = 0,12

Со­бы­тия A и B сов­мест­ные

  P (A + B) = P(A) + P(B) − P(A·B) = 0,3 + 0,3 − 0,12 = 0,48

События «кофе останется в обоих автоматах» и «кофе закончится хотя бы в одном» — противоположные.

Сле­до­ва­тель­но, ве­ро­ят­ность про­ти­во­по­лож­но­го со­бы­тия равна 1 − 0,48

Ответ: 0,52

№ 5

С первого станка поступает 40%, со второго – 30% и с третьего – 30% всех деталей. Вероятность изготовления бракованной детали равны для каждого станка соответственно 0,01; 0,03; 0,05. Найдите вероятность того, что наудачу взятая деталь будет бракованной.

Решение

1 станок

3 станок

0,4

0,3

2 станок

0,3

брак

брак

брак

0,05

0,01

0,03

Р = 0,4  0,01 + 0,3  0,03 + 0,3  0,05

Ответ: 0,028

№ 6

Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства – яйца высшей категории, а из второго хозяйства – 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

Решение

II

I

х

1 — х

В К

В К

0,8

0,2

0,4

0,6

0,4 ∙ Х + 0,2 ∙ (1 – Х) = 0,35

Ответ: 0,75

№ 7

Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.

Решение

0,05

0,95

—

—

+

+

0,9

0,99

0,1

0,01

Р = 0,05 ∙ 0,9 + 0,95 ∙ 0,01

Ответ: 0,0545

№ 8

Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 20 пассажиров, равна 0,94. Вероятность того, что окажется меньше 15 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 15 до 19.

Решение

Со­бы­тие A — «в ав­то­бу­се мень­ше 15 пас­са­жи­ров», Р(А) = 0,56

Со­бы­тие В — «в ав­то­бу­се от 15 до 19 пас­са­жи­ров» , Р(В) — ?

Со­бы­тие A + B — «в ав­то­бу­се мень­ше 20 пас­са­жи­ров»,

Р(А + В) = 0,94

Со­бы­тия A и В не­сов­мест­ные

  P(A + B) = P(A) + P(B); P(В) = 0,94 − 0,56

Ответ: 0,38

№ 9

В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,7 погода завтра будет такой же, как и сегодня. Сегодня 16 июня, погода в Волшебной стране хорошая. Найдите вероятность того, что 19 июня в Волшебной стране будет отличная погода.

Решение

Для погоды на 16, 17, 18 и 19 июня есть

4 варианта (х – хорошая, о – отличная погода).

Вероятность смены погоды равна 1 – 0,7 = 0,3. Найдем вероятности наступления такой погоды:

р(xхxo) = 0,7 · 0,7 · 0,3

р(хxoo) = 0,7 · 0,3 · 0,7

р(хoxo) = 0,3 · 0,3 · 0,3

р(хooo) = 0,3 · 0,7 · 0,7

Указанные события несовместные

р = 0,147 + 0,147 + 0,027 + 0,147  

Ответ: 0,468

№ 10

Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов – математика, русский язык и иностранный язык . Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов – математика, русский язык и обществознание . Вероятность того, что абитуриент получит не менее 70 баллов по математике , равна 0,6 , по русскому языку – 0,8 , по иностранному языку – 0,7 и по обществознанию – 0,5 . Найдите вероятность того, что абитуриент сможет поступить хотя бы на одну из двух упомянутых специальностей.

Подведем итоги

Синквейн   – это не простое стихотворение, а стихотворение, написанное по следующим правилам:

1 строка – одно существительное, выражающее главную тему синквейн

2 строка – два прилагательных, выражающих главную мысль

3 строка – три глагола, описывающие действия в рамках темы

4 строка – фраза, несущая определенный смысл

5 строка – заключение в форме существительного (ассоциация с первым словом)

Задание на дом

Выполнить задание

по карточке

1


Обучающая презентация по решению задач на теорию вероятности Подготовка к ГИА и ЕГЭ Учитель математики МАОУ « Лицей 62» Воеводина Ольга Анатольевна

2


Общая схема решения задач 1.Определить, в чем состоит случайный эксперимент и какие у него элементарные события (исходы). Убедиться, что они равновозможны. 2.Найти общее число элементарных событий N. 3.Определить, какие элементарные события благоприятствуют интересующему нас событию А, и найти их число N(А). 4. Найти вероятность события А по формуле P(A)=

3


Справочные материалы Элементарные события (элементарные исходы) – это простейшие события, которыми может окончиться случайный опыт. Сумма вероятностей всех элементарных событий опыта равна 1. Вероятность события А равна сумме вероятностей элементарных событий, благоприятствующих этому событию. Объединение событий — событие, состоящее из элементарных исходов, благоприятствующи х хотя бы одному из событий А и В.

4


Справочные материалы Пересечение событий- это событие, состоящее из элементарных исходов, благоприятствующих обоим событиям А и В. Несовместные события – события, которые не наступают в одном опыте. Противоположные события – те, которые состоят из тех и только тех элементарных исходов опыта, которые не входят в А и обозначаются Независимые события. События А и В называются независимыми, если

5


Вася, Петя, Коля, Леша бросили жребий – кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя. Решение. 1. Случайный эксперимент – бросание жребия. 2. Элементарное событие в этом эксперименте — участник, который выиграл жребий. Перечислим их: (Вася), (Петя), (Коля), (Леша). Общее число элементарных событий N=4. Жребий подразумевает, что элементарные события равновозможны. 3. Событию А={жребий выиграл Петя} благоприятствует только одно элементарное событие (Петя). Поэтому N(A)=1. 4. Тогда Р(А)=1/4=0,25 Ответ: 0,25.

6


Игральный кубик (кость) бросили один раз. Какова вероятность того, что выпало число очков, большее чем 4? Решение. 1.Случайный эксперимент – бросание кубика. 2. Элементарное событие – число на выпавшей грани. Граней всего 6, то есть N=6. 3.Событию А ={выпало больше чем 4} благоприятствуют два элементарных события: 5 и 6. 4.Поэтому N(A)=2. 5.Все элементарные события равновозможны, поэтому Р(А)=2/6=1/3. Ответ: 1/3.

7


В случайном эксперименте монету бросили три раза. Какова вероятность того, что орел выпал ровно два раза? Решение. 1.Орел обозначим буквой О, решку – буквой Р. Элементарные исходы – тройки, составленные из букв О и Р. 1.Выпишем их все: ООО, ООР, ОРО, ОРР, РОО, РОР, РРО, РРР 3. Всего исходов 8. Значит N=8. 4. Событию А={орел выпал ровно два раза}, благоприятствуют элементарные события ООР, ОРО, РОО, поэтому N(A)=3. 5. Тогда Р(А)=3/8=0,375 Ответ. 0,375

8


В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз. Решение. 1.Орел обозначим буквой О, решку – буквой Р. 2. Выпишем элементарные исходы: ОО, ОР, РО, РР. Значит N=4. 3. Событию А={выпал ровно один орел} Благоприятствуют элементарные события ОР и РО. Поэтому N(A)=2. 4. Тогда Р(А)=2/4=0,5. Ответ. 0,5

9


В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции, 5 – из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции. Решение. 1.Элементарный исход – спортсмен, который выступает последним. Последним может оказаться любой. Всего спортсменов 25, то есть N=25. 2.Событию А={последний из Швеции} благоприятствуют только девять исходов, поэтому N(A)=9, тогда Р(А)=9/25=0,36. Ответ. 0,36.

10


Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два раза промахнулся. Результат округлите до сотых. Решение. 1.Результат каждого следующего выстрела не зависит от предыдущих. Поэтому события «попал при первом выстреле», «попал при втором выстреле» и т.д. независимы. 2. Вероятность каждого попадания равна 0,8. Значит вероятность промаха равна 1-0,8=0,2. 3. По формуле умножения вероятностей независимых событий, получаем, что последовательность А={попал, попал, попал, промахнулся, промахнулся} имеет вероятность Р(А)=0,8*0,8*0,8*0,2*0,2=0,20480,02 Ответ. 0,02

11


Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,1. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо. Решение. 1.Событие А ={выбранная ручка пишет хорошо} 2.Тогда вероятность противоположного события: 3. Используем формулу вероятности противоположного события: Ответ. 0,9

12


На экзамене по геометрии школьнику достается один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему: «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем. Решение. 1.Определим события: А={вопрос на тему «Вписанная окружность} В={вопрос на тему «Параллелограмм»} 2. События А и В несовместны, так как по условию в списке нет вопросов, относящихся к этим двум темам одновременно.

13


На экзамене по геометрии школьнику достается один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему: «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем. 3. Событие С={вопрос по одной из этих двух тем} является их объединением: 4. Применим формулу сложения вероятностей несовместных событий: Р(С)=Р(А)+Р(В)=0,2+0,15=0,35 Ответ. 0,35

14


В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах. Решение. 1.Определим события: А={кофе закончится в первом автомате} В={кофе закончится во втором автомате} По условию задачи Р(А)=Р(В)=0,3 и 2. По формуле сложения вероятностей найдем вероятность события:

15


В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах. { кофе закончится хотя бы в одном из автоматов } =0,3+0,3-0,12=0,48 Следовательно, вероятность противоположного события «кофе останется в обоих автоматах» равна 1-0,48=0,52. Ответ. 0,52 =Р(А)+Р(В) –=

16


В магазине стоят два платежных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен. Решение. 1.Найдем вероятность противоположного события: ={оба автомата неисправны } 2. Для этого используем формулу умножения вероятностей независимых событий : 3.Значит вероятность события А={хотя бы один автомат исправен} равна: Р(А)=1 – 0,0025=0,9975. Ответ. 0,9975

17


В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1,1,1,1,2,2,2,2,3,3,3,3,4,4,4,4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе? Решение. 1.Элементарный исход – карточка, выбранная капитаном российской команды, значит N= Событию А={команда России во второй группе} благоприятствуют четыре карточки с номером «2», то есть N(А)=4. 3. Тогда Р(А)=4/16=0,25. Ответ. 0,25

18


Три друга А., Б., и В. летят на самолете. При регистрации им достались три кресла подряд, и друзья заняли их в случайном порядке. Найдите вероятность того, что А. сидит рядом с Б. Решение. 1.Перечислим число элементарных событий: АБВ, АВБ, БАВ, БВА, ВАБ, ВБА. N=6. Элементарные события равновозможны. 2.Событию А={А. сидит рядом с Б.} благоприятствуют четыре события, поэтому N(А)=4. 3. Тогда Р(А)=4/6=2/3. Ответ. 2/3

19


На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра окажется четной? Решение. 1. Общее число элементарных событий равно Все события равновозможны, Событию А={цифра окажется четной} благоприятствуют цифры 0, 2, 4, 6, 8, поэтому N(А)=5. 3. Тогда Р(А)=5/10=0,5. Ответ. 0,5

20


Учитель нарисовал на доске квадрат ABCD и предлагает учащемуся выбрать две вершины. Сколько элементарных событий в этом опыте? Решение. 1.Элементарное событие в этом эксперименте – учащийся выбрал две вершины. 2.Перечислим их: AB, AC, AD, BC, BD, CD. 3.Общее число элементарных событий равно 6, то есть N=6. Ответ. 6 А ВС D

21


Литература И.Р. Высоцкий, И.В. Ященко ЕГЭ Математика Задача В 10. Теория вероятностей

Урок-лекция по теме «теория вероятности»

Задание №4 из ЕГЭ 2016.

Профильный уровень.

1 Группа: задания на использование классической формулы вероятности.

• Первый уровень сложности.

• Задание 1. В фирме такси в наличии 60 легковых автомобилей; 27 из них чёрного цвета с жёлтыми надписями на боках, остальные — жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.

• Задание 2. Миша, Олег, Настя и Галя бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должна будет не Галя.

• Задание 3. В среднем из 1000 садовых насосов, поступивших в продажу, 7 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

• Задание 4. В сборнике билетов по химии всего 15 билетов, в 6 из них встречается вопрос по теме «Кислоты». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме «Кислоты».

• Задание 5. На чемпионате по прыжкам в воду выступают 45 спортсменов, среди них 4 прыгуна из Испании и 9 прыгунов из США. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что двадцать четвёртым будет выступать прыгун из США.

• Задание 6. Научная конференция проводится в 3 дня. Всего запланировано 40 докладов — в первый день 8 докладов, остальные распределены поровну между вторым и третьим днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?

• Второй уровень сложности.

• Задание 1. Перед началом первого тура чемпионата по теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 теннисистов, среди которых 9 участников из России, в том числе Тимофей Трубников. Найдите вероятность того, что в первом туре Тимофей Трубников будет играть с каким-либо теннисистом из России.

• Задание 2. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 22 спортсмена из России, в том числе Виктор Поляков. Найдите вероятность того, что в первом туре Виктор Поляков будет играть с каким-либо бадминтонистом из России.

• Задание 3. В классе 16 учащихся, среди них два друга — Олег и Михаил. Класс случайным образом разбивают на 4 равные группы. Найдите вероятность того, что Олег и Михаил окажутся в одной группе.

• Задание 4. В классе 33 учащихся, среди них два друга — Андрей и Михаил. Учащихся случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Андрей и Михаил окажутся в одной группе.

• Третий уровень сложности.

• Задание 1: На фабрике керамической посуды 20% произведенных тарелок имеют дефект. При контроле качества продукции выявляется 70% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых.

• Задание 2. На фабрике керамической посуды 30% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 60% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка имеет дефект. Ответ округлите до сотых.

• Задание 3: Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 30% этих стекол, вторая – 70%. Первая фабрика выпускает 3% бракованных стекол, а вторая – 4%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

2 Группа: нахождение вероятности противоположного события.

• Задание 1. Вероятность попасть в центр мишени с расстояния 20 м у профессионального стрелка равна 0,85. Найдите вероятность не попасть в центр мишени.

• Задание 2. При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет отличаться от заданного меньше, чем на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 66,99 мм или больше чем 67,01 мм.

3 Группа: Нахождение вероятности наступления хотя бы одного из несовместных событий. Формула сложения вероятностей.

• Задание 1. Найти вероятность того, что при бросании кубика выпадет 5 или 6 очков.

• Задание 2. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность вытянуть цветной шар.

• Задание 3. Стрелок стреляет по мишени, разделенной на 3 области. Вероятность попадания в первую область равна 0,45, во вторую – 0,35.Найти вероятность того, что стрелок при одном выстреле попадет либо в первую, либо во вторую область.

• Задание 4. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 18 пассажиров, равна 0,95. Вероятность того, что окажется меньше 12 пассажиров, равна 0,6. Найдите вероятность того, что число пассажиров будет от 12 до 17.

• Задание 5. Вероятность того, что новый электрический чайник прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

• Задание 6. Вероятность того, что на тестировании по биологии учащийся У. верно решит больше 9 задач, равна 0,61. Вероятность того, что У. верно решит больше 8 задач, равна 0,73. Найдите вероятность того, что У. верно решит ровно 9 задач.

4 Группа: Вероятность одновременного наступления независимых событий. Формула умножения вероятностей.

• Задание 1. Помещение освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.

• Задание 2. Помещение освещается фонарем с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.

• Задание 3. В магазине два продавца. Каждый из них занят с клиентом с вероятностью 0,4. Найдите вероятность того, что в случайный момент времени оба продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга).

• Задание 4. В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,2. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга).

• Задание 5: По отзывам покупателей, Михаил Михайлович оценил надежность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,81. Вероятность того, что этот товар доставят из магазина В, равна 0,93. Михаил Михайлович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.

• Задача 6: Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,6. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,4. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

5 Группа: Задачи на применение обеих формул.

• Задание 1: Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ дает положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,02. Известно, что 66% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.

• Задание 2. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из не пристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.

Задание 3:

В некоторой местности наблюдения показали:

1. Если июньское утро ясное, то вероятность дождя в этот день 0,1. 2. Если июньское утро пасмурное, то вероятность дождя в течение дня равна 0,4. 3. Вероятность того, что утро в июне будет пасмурным, равна 0,3.

Найдите вероятность того, что в случайно взятый июньский день дождя не будет.

Задание 4. При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,3, а при каждом последующем – 0,9. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,96?