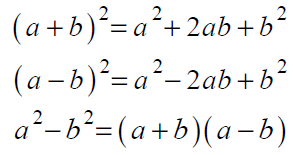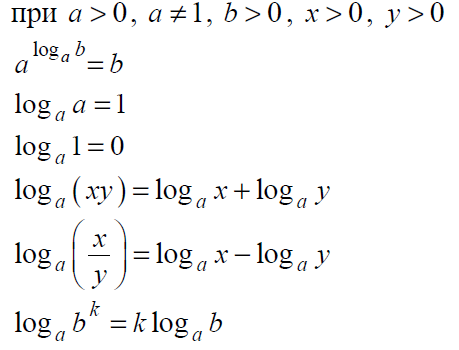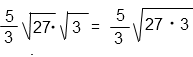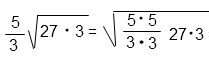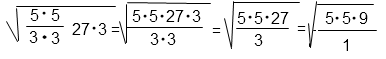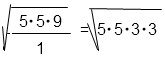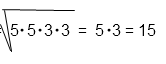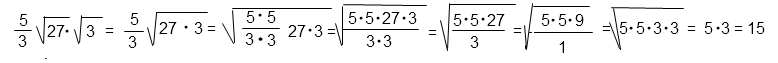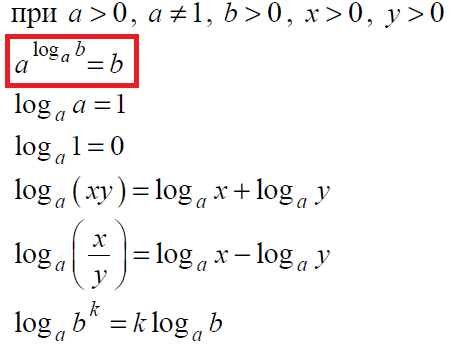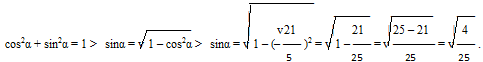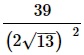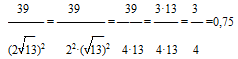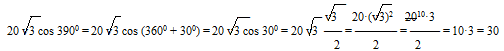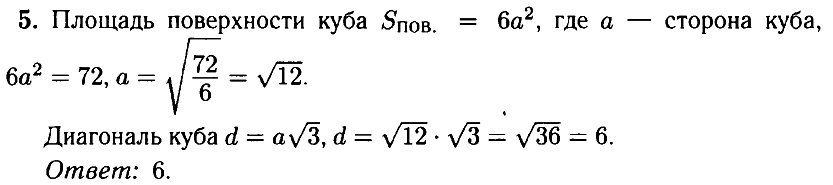Теория 5 номер егэ по математике - Помощь в подготовке к экзаменам и поступлению

В задании №5 варианта ЕГЭ вам встретятся всевозможные уравнения: квадратные и сводящиеся к квадратным, дробно-рациональные, иррациональные, степенные, показательные и логарифмические и даже тригонометрические. Видите, как много нужно знать, чтобы справиться с заданием! И еще ловушки и «подводные камни», которые ждут вас в самом неожиданном месте.

Вот список тем, которые стоит повторить:

Квадратные уравнения

Арифметический квадратный корень

Корни и степени

Показательная функция

Показательные уравнения

Логарифмическая функция

Логарифмические уравнения

Тригонометрический круг

Формулы приведения

Формулы тригонометрии

Простейшие тригонометрические уравнения 1

Уравнения, сводящиеся к квадратным

1. Решите уравнение $frac{6}{13}x^2=19frac{1}{2}$ . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Кажется, что уравнение очень простое. Но иногда здесь ошибаются даже отличники. А вот шестиклассник бы не ошибся.

С левой частью уравнения все понятно. Дробь $frac{6}{13}$ умножается на x^2. А в правой части — смешанное число $19frac{1}{2}.$ Его целая часть равна 19, а дробная часть равна $frac{1}{2}.$ Запишем это число в виде неправильной дроби:

$19frac{1}{2}= frac{19cdot 2+1}{2} = frac{39}{2}.$

Получим:

$frac{6}{13}x^2=frac{39}{2};$

$x^2=frac{39cdot 13}{2cdot 6}=frac{13cdot 3cdot 13}{2cdot 6}=frac{{13}^2}{4};$

$x=pm frac{13}{2};$

или

Выбираем меньший корень.

Ответ: -6,5.

2. Решите уравнение

Возведем в квадрат левую часть уравнения. Получим:

Ответ: -6.

Дробно-рациональные уравнения

3. Найдите корень уравнения

Перенесем единицу в левую часть уравнения. Представим 1 как $frac{4x-5}{4x-5}$ и приведем дроби к общему знаменателю:

$frac{5x-3}{4x-5}-frac{4x-5}{4x-5}=0;$

$frac{x+2}{4x-5}=0;$

x= - 2.

Ответ: -2.

Это довольно простой тип уравнений. Главное — внимательность.

Иррациональные уравнения

Так называются уравнения, содержащие знак корня — квадратного, кубического или n-ной степени.

4. Решите уравнение:

$sqrt{frac{6}{4{x}-54} } =frac{1}{7}.$

Выражение под корнем должно быть неотрицательно, а знаменатель дроби не равен нулю.

Значит, .

Возведём обе части уравнения в квадрат:

$frac{6}{4{x}-{ 54}} =frac{1}{49}.$

Решим пропорцию:

Условие при этом выполняется.

Ответ: 87.

5. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

А в этом уравнении есть ловушка. Решите его самостоятельно и после этого читайте дальше.

Выражение под корнем должно быть неотрицательно. И сам корень — величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:

$left{begin{matrix} 72-x=x^2\72-xgeq 0 hfill \xgeq 0 hfill end{matrix}right.$ .

Решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов:

$sqrt{72-x}=x Leftrightarrow left{begin{matrix} 72-x=x^2\72-x geq 0 \x geq 0 end{matrix}right. Leftrightarrow$

Мы получили, что x=8 . Это единственный корень уравнения.

Типичная ошибка в решении этого уравнения такая. Учащиеся честно пишут ОДЗ, помня, что выражение под корнем должно быть неотрицательно:

Возводят обе части уравнения в квадрат. Получают квадратное уравнение: Находят его корни: x=8 или x=-9. Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.

Теперь вы знаете, в чем дело. Конечно же, число -9 корнем этого уравнения быть не может.

Ответ: 8.

6. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Запишем решение как цепочку равносильных переходов:

Ответ: 9.

Показательные уравнения

При решении показательных уравнений мы пользуемся свойством монотонности показательной функции.

7. Решите уравнение $5^{x-7}=frac{1}{125}.$

Вспомним, что $125 = 5{}^{3}.$ Уравнение приобретает вид: $5{}^{x}{}^{-}{}^{7 }= 5{}^{-}{}^{3}.$ Функция y = 5^x монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

откуда x = 4.

Ответ: 4.

8. Решите уравнение ${left(frac{1}{49}right)}^{x-8}=7.$

Представим ${left(frac{1}{49}right)}^{ }$ как $7^{-2};$

${left(7^{-2}right)}^{x-8}=7;$

$7^{-2x+16}=7.$

Функция y = 7^x монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

x=7,5.

Ответ: 7,5.

9. Решите уравнение $left(frac{1}{9} right)^{{ x}-13} =3.$

Представим ${textstylefrac{1}{9}}$ в виде степени с основанием 3 и воспользуемся тем, что $left({ a}^{{ m}} right)^{{ n}} ={ a}^{{ mn}}.$

$left(3^{-2} right)^{{ x}-{ 13}} =3;$
$3^{-2{ x}+{ 26}} =3^{1} ;$

Ответ: 12,5.

Логарифмические уравнения

Решая логарифмические уравнения, мы также пользуемся монотонностью логарифмической функции: каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, значит, равны и сами числа.

И конечно, помним про область допустимых значений логарифма:

Логарифмы определены только для положительных чисел.

Основание логарифма должно быть положительно и не равно единице.

10. Решите уравнение:

${{log}_5 left(4+xright)=2 }.$

Область допустимых значений: . Значит,

Представим 2 в правой части уравнения как ${{log}_5 25 }$ , чтобы слева и справа в уравнении были логарифмы по основанию 5.

${{log}_5 left(4+xright)={{log}_5 25 } }.$

Функция $y = {{log}_5 x }$ монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом

4+x=25;
x=21.

Ответ: 21.

11. Решите уравнение: ${{log}_8 left(x^2+xright)={{log}_8 left(x^2-4right) } }.$

Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:

Ответ: -4.

12. Решите уравнение: $2^{{{log}_4 left(4x+5right) }}=9.$

Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:

${{log}_4 b }=frac{{{log}_2 b }}{{{log}_2 4 }}=frac{{{log}_2 b }}{2}.$

Записываем решение как цепочку равносильных переходов.

Ответ: 19.

13. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

${{log}_{x-5} 49=2 }.$

В этом уравнении тоже есть ловушка. Мы помним, что основание логарифма должно быть положительно и не равно единице.

Получим систему:

$small left{begin{matrix} left ( x-5 right )^2=49\x-50 \x-5 neq 1 end{matrix}right..$

Первое уравнение мы получили просто из определения логарифма.

Квадратное уравнение имеет два корня: x=12 и x=-2.

Очевидно, корень x=-2 является посторонним, поскольку основание логарифма должно быть положительным. Значит, единственный корень уравнения: x=12.

Ответ: 12.

Тригонометрические уравнения (Часть 1 ЕГЭ по математике)

Тригонометрические уравнения? В первой части вариантов ЕГЭ? — Да. Причем это задание не проще, чем задача 13 из второй части варианта Профильного ЕГЭ.

14. Найдите корень уравнения: $cos frac{pi (x+1)}{4}=frac{sqrt{2}}{2}.$ В ответе запишите наибольший отрицательный корень.

Типичная ошибка — решать это уравнение в уме. Мы не будем так делать! Несмотря на то, что это задание включено в первую части варианта ЕГЭ, оно является полноценным тригонометрическим уравнением, причем с отбором решений.

Сделаем замену $frac{pi left(x+1right)}{4}=t.$ Получим: $cos t=frac{sqrt{2}}{2}.$

Получаем решения: $t=pm frac{pi }{4}+2pi n, nin Z.$ Вернемся к переменной x.

$frac{pi (x+1)}{4}=pm frac{pi }{4}+2pi n, nin Z.$ Поделим обе части уравнения на и умножим на 4.

$left[ begin{array}{c}x=8n, nin Z \x=-2+8n end{array}right..$

Первой серии принадлежат решения

Вторая серия включает решения

Наибольший отрицательный корень — тот из отрицательных, который ближе всех к нулю. Это x = -2.

Ответ: -2.

15. Решите уравнение: $tg frac{pi left( x+1right)}{4}= -1.$ В ответе напишите наименьший положительный корень.

Решение:

Сделаем замену $frac{pi left(x+1right)}{4}=t.$ Получим: tgt=-1. Решения этого уравнения:

$t=-frac{pi }{4}+pi n, nin Z.$ Вернемся к переменной х:

$frac{pi left(x+1right)}{4}=-frac{pi }{4}+pi n, n in Z.$ Умножим обе части уравнения на 4 и разделим на .

Выпишем несколько решений уравнения и выберем наименьший положительный корень:

Наименьший положительный корень x = 2.

Ответ: 2.

Мы разобрали основные типы уравнений, встречающихся в задании №5 Профильного ЕГЭ по математике. Конечно, это не все, и видов уравнений в этой задаче существует намного больше. Именно поэтому мы рекомендуем начинать подготовку к ЕГЭ по математике не с задания 1, а с текстовых задач на проценты, движение и работу и основ теории вероятностей.
Успеха вам в подготовке к ЕГЭ!

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание №5. Простейшие уравнения. Профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник

: ЕГЭ по математике профиль

Задание 5 профильного уровня ЕГЭ, а также задач 4 и 7 базового уровня ЕГЭ представляет собой несложное показательное, логарифмическое, дробно-рациональное или иррациональное уравнение базового уровня, которое в одно-два действия сводится к линейному или квадратному уравнению, или тригонометрическое уравнение.

Если уравнение сводится к квадратному, то в условии задаётся дополнительное ограничение для отбора корня. В случае логарифмического или иррационального уравнения один из корней может быть отброшен как посторонний без дополнительного ограничения.

→ скачать конспект (простейшие уравнения)

Автор: Алькаева Л. Р.

Практический материал:

→ задание 5 из банка ФИПИ

→ задание 5 — тригонометрические уравнения

→ задание 5 — логарифмические уравнения

→ задание 5 — показательные уравнения

→ задание 5 — иррациональные уравнения

→ задание 5 — линейные, дробно-рациональные, квадратные уравнения

При решении уравнений встретятся ловушки и «подводные камни». Список тем, которые нужно повторить:

— Квадратные уравнения
— Арифметический квадратный корень
— Корни и степени
— Показательная функция
— Показательные уравнения
— Логарифмическая функция
— Логарифмические уравнения
— Тригонометрический круг
— Формулы приведения
— Формулы тригонометрии
— Простейшие тригонометрические уравнения

Связанные страницы:

Источник

Главная
Теория ЕГЭ
Математика — теория ЕГЭ
Задание 5 ЕГЭ 2021 по математике, теория

08.10.2018

Необходимая теория для успешного освоения и решения заданий №5 по математике профильного уровня на ЕГЭ в 2021 году.

Представлена вся теория и алгоритм решения различных заданий такого типа.

Тренировочные кимы ЕГЭ по математике
Практика — примеры для решения каждого типа заданий

Обсудить решение конкретных заданий вы можете в комментариях ниже.

Смотреть в PDF:

Или прямо сейчас: cкачать в pdf файле.

Сохранить ссылку:

Комментарии (0)
Добавить комментарий

Добавить комментарий

Комментарии без регистрации. Несодержательные сообщения удаляются.

Имя (обязательное)

E-Mail

Подписаться на уведомления о новых комментариях

Отправить

Источник

Значение выражений

[su_box title=”Описание задания” style=”soft” box_color=”#c1e8cc” title_color=”#0c0a0a”]

В задании №5 ЕГЭ по математике базового уровня нам необходимо вычислить значение выражения, пользуясь различными правилами: формулами сокращенного умножения, знаниями тригонометрии, свойствами логарифмов и другими. Данное задание требует более глубоких знаний и значительно сложнее первого задания, где достаточно было знать элементарные математические операции.

Тематика заданий: значение выражений

Бал: 1 из 20

Сложность задания: ♦♦♦

Примерное время выполнения: 5-7 мин.

[/su_box]

Теория к заданию №5

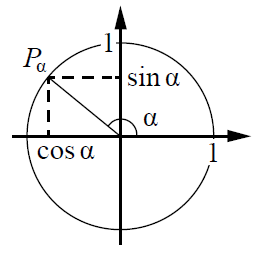
В данном задании, кроме операций со степенями, о которых мы говорили в прошлых заданиях, необходимо помнить формулы сокращенного умножения:

Кроме этого, очень часто встречаются задания на знания свойств логарифма:

Полезными будут представления о тригонометрической окружности, по которой можно определять знаки тригонометрических функций:

Разбор типовых вариантов заданий №5 ЕГЭ по математике базового уровня

Во всех заданиях необходимо найти значение выражения.

Вариант 5МБ1

Алгоритм выполнения

Представим угол 390° с учетом периодичности функции tg меньшим углом.
Найдем таблице значений тригонометрических функций (в справочных материалах) значение tg полученного угла.
Выполним умножение.

Решение:

Функция tg является периодической с периодом 180°, то есть каждый раз при увеличении или уменьшении угла на 180° значение tg повторяется.

То есть tg α = tg (α + 180°) = tg (α – 180°)

tg 390° = tg (390° – 180°) = tg 210° = tg (210° – 180°) = tg 30°

Найдем таблице значений тригонометрических функций (в справочных материалах) значение tg полученного угла.

tg 30° = √3/3

Подставим найденное значение в данное выражение.

20 · √3 · (√3/3) = (20 · √3 · √3)/3 = (20 · 3)/3 = 20

Решение в общем виде

Вычислим выражение, учитывая, что функция тангенс периодическая с периодом π радиан или 180°. Следовательно, угол 390° эквивалентен углу

и получаем выражение:

Ответ: 20.

Вариант 5МБ2

Алгоритм выполнения

Представим угол 420° с учетом периодичности функции tg меньшим углом.
Найдем таблице значений тригонометрических функций (в справочных материалах) значение tg полученного угла.
Выполним умножение.

Решение №1:

То есть

tg α = tg (α + 180°) = tg (α – 180°)

tg 390° = tg (420° – 180°) = tg 240° tg (240° – 180°) = tg 60°

Найдем таблице значений тригонометрических функций (в справочных материалах) значение tg полученного угла.

tg 60° = √3

Подставим найденное значение в данное выражение.

-50 · √3 · √3 = -50 · 3 = -150

Решение №2:

Заметим, что функция тангенс периодическая с периодом π радиан или 180°. Поэтому, тангенс угла 420° эквивалентен тангенсу угла в

получаем:

Ответ: -150.

Вариант 5МБ3

Алгоритм выполнения

Объединим подкоренные выражения под один корень.
Внесем под корень дробь.
Сократим дробь под корнем.
Представим произведение под корнем в виде произведения вторых степеней.
Вынесем из под корня множители.
Выполним умножение.

Решение:

Объединим подкоренные выражения под один корень. Имеем право так сделать использовав, свойство квадратного корня.

5/3 · √27 · √3 = 5/3 · √(27 · 3)

Внесем под корень дробь.

Корень квадратный, следовательно, чтобы внести дробь под знак корня нужно возвести ее в квадрат. То есть умножить сам на себя числитель и знаменатель.

(5/3)² = (5 · 5)/(3 · 3)

Сократим дробь под корнем на три дважды.

Представим произведение под корнем в виде произведения вторых степеней.

Вынесем из под корня множители и выполним умножение.

Решение в общем виде:

Ответ: 15.

Вариант 5МБ4

[su_note note_color=”#defae6″]

Найдите cos α, если sin α = 0,8 и 90° ‹ α ‹ 180°.

[/su_note]

Алгоритм выполнения

Запишем основное тригонометрическое тождество.
Подставим в основное тригонометрическое тождество все известные данные.
Решим полученное уравнение относительно cos α.
Выбрать корни, подходящие к условию задания.

Решение:

Запишем основное тригонометрическое тождество.

sin² α + cos² α = 1

Подставим в основное тригонометрическое тождество все известные данные.

0,8² + cos² α = 1

Решим полученное уравнение относительно cos α.

cos² α – неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.

cos² α = 1 – 0,8²

Чтобы найти вторую степень числа нужно число умножить само на себя.

0,8² = 0,8 · 0,8 = 0,64

cos² α = 1 – 0,8² 1 – 0,64 = 0,36

cos α = √0,36

cos α = 0,6 или -0,6

Условие 90° ‹ α ‹ 180° означает, что -1 ‹ соs α ‹ 0.

Следовательно данному условию удовлетворяет только один корень -0,6.

Ответ: -0,6.

Вариант 5МБ5

[su_note note_color=”#defae6″]

(2√13 −1)(2√13 +1).

[/su_note]

Алгоритм выполнения

В данном задании необходимо сразу заметить формулу сокращенного умножения – разность квадратов (последняя формула сокращенного умножения в теории выше).

Решение:

После этого, решение задания сводится к следующему:

(2√13 −1)(2√13 +1) = (2√13)² – 1² = 4 • 13 – 1 = 51

Ответ: 51.

Вариант 5МБ6

[su_note note_color=”#defae6″]

5^log₅6+1 .

[/su_note]

Алгоритм выполнения

Сначала вспомним свойства степеней и разложим выражение следующим образом:

5^log₅6 • 5¹

Затем вспомним определение и свойство логарифма – это вторая строчка из нашей теории:

Решение:

Получим:

6•5 = 30

Ответ: 30

Вариант 5МБ7

[su_note note_color=”#defae6″]

(√11-√3)(√11+√3)

[/su_note]

Алгоритм выполнения

Применяем формулу сокращенного умножения a²–b²=(a-b)(a+b).
Используем определение кв.корня: (√a)²=a.
Находим полученную разность целых чисел.

Решение:

Исходя из алгоритма, подставляем а=√11, а b=√3, тогда 11-3=8

Ответ: 8

Вариант 5МБ8

Алгоритм выполнения

Применяем тождество log_a(xy)=log_ax+log_ay.
Преобразовываем множители, стоящие под знаком логарифма, в степени.
Используем для выражения под знаком логарифма св-во степеней a^xb^x=(ab)^x.
Используем св-во логарифмов xlog_ab=log_ab^x.
Применяем тождество log_aa=1,.

Решение:

log₆27 + log₆8 = log₆27·8 = log₆3³·2³ = log₆(3·2)³ = log₆6³ = 3log₆6 = 3

Ответ:3

Вариант 5МБ9

Алгоритм выполнения

Вносим множитель √6 в скобки.
Выполняем умножение √24 и √6. Получим √144. Это число является полным квадратом: (√12)².
Перемножаем √6 и √6. Получаем (√6)².
Используя определение кв.корня (√а)²=а, находим, что (√12)²=12, а (√6)²=6.
Находим разность полученных целых чисел.

Решение:

Ответ: 6

Вариант 5МБ10

Найдите sinα, если

Алгоритм выполнения

Применим основное тригонометрическое тождество. В тождество подставим данное в условии числовое значение для косинуса.
Выполняем преобразование тождества, получаем числовой результат.
Определяем знак результата, исходя из величины угла α.

Решение:

Ответ: 0,4

Вариант 5МБ11

Алгоритм выполнения

Выполняем 1-ю по приоритетности операцию – возведение в степень (в знаменателе). Для этого используем св-во степеней (ab)²=a²·b². Далее для множителя (√13)² применяем формулу, определяющую понятие кв.корня: (√а)²=а.
Выполняем умножение в знаменателе.
Представляем число 39 в числителе как произведение 3·13.
Сокращаем дробь на 13.
Переводим полученную обыкновенную дробь в десятичную.

Решение:

Ответ: 0,75

Вариант 5МБ12

Алгоритм выполнения

Применяем к показателю степени 2log₃7 св-во логарифмов log_b^ya^x=(x/y)log_ba. Получим log₃7².
Применяем св-во логарифмов a^log_a^b=b. В результате знак логарифма исчезает, остается только выражение 7², которое было под знаком логарифма.
Возводим 7 в квадрат.

Решение:

2log₃7 log₃7²

3 = 3 = 7² = 49

Ответ:49

Вариант 5МБ13

Алгоритм выполнения

Используем св-во корней √(a·b)=√a·√b. Таким способом √63 разложим на множители √9 и √7.
Сгруппируем одинаковые множители √7. Получим (√7)².
Основываясь на определении кв.корня (√а)²=а, представляем √9=(√3)².
Возводим полученные числа в квадрат.
Находим итоговое произведение.

Решение:

Ответ: 21

Вариант 5МБ14

Алгоритм выполнения

Используем св-во степеней x^a+b=x^a·x^b. Получим 2 множителя, первый из которых равен 7, а второй представляет собой степень с основанием 7 и показателем, содержащим логарифм.
Для второго множителя применим св-во логарифмов a^loga^b=b.
Находим результирующее произведение.

Решение:

Ответ: 21

Вариант 5МБ15

Алгоритм выполнения

Для cos 390⁰ используем ф-лу приведения cos (360⁰+α)=cos α. Получим cos 30⁰=√3/2. Записываем получившееся выражение в виде дроби со знаменателем 2.
Вычисляем произведение √3·√3 путем возведения в степень. Для этого используем определение кв.корня: (√а)²=а.
Сокращаем 20 в числителе и 2 в знаменателе на 2.
Находим конечное произведение.

Решение:

Ответ: 30

Вариант 5МБ16

Алгоритм выполнения

Преобразовываем часть выражения, взятую в скобки. Для этого представляем 49 как 7². Затем используем св-во логарифмов log_ba^x=xlog_ba, а далее св-во log_aa=1. Получаем 2.
Применяем св-во логарифмов log_aa=1.

Решение:

log₂(log₇49) = log₂(log₇7²) = log₂(2log₇7) = log₂2 = 1

Ответ: 1

Даниил Романович | Просмотров: 13.5k

Источник

Задача 1

Найдите корень уравнения $9^{log_{81}(5x-2)}=30$.

Задача 2

Найдите корень уравнения $log_2(9-2x)=log_2(6+x)+3$.

Задача 3

Найдите корень уравнения $({1} / {81})^{7+x}=243$.

Задача 4

Найдите корень уравнения $3{2} / {7}x =46$.

Задача 5

Найдите корень уравнения $2^{2x-7}=4{,}5⋅9^{2x-7}$.

Задача 6

Найдите корень уравнения $3^{2+x}=0{,}6⋅5^{2+x}$.

Задача 7

Найдите корень уравнения $log_{216}{6^{2x-11}}=3$.

Задача 8

Найдите корень уравнения $log_{81}{3^{4x+7}}=5$.

Задача 9

Найдите корень уравнения $tg{πx}/{4} = 1$. В ответе напишите наименьший положительный корень.

Задача 10

Найдите корень уравнения $7^{log_{49}{(6x-6)}}=6$.

Задача 11

Найдите корень уравнения $5^{log_{25}{(3x-3)}}=3$.

Задача 12

Найдите корень уравнения $log_{4}{(2x-1)} =log_{4}{(x+3)} — 1$.

Задача 13

Найдите корень уравнения $log_{x-4}{36} = 2$.

Задача 14

Найдите корень уравнения ${2} / {3} x +1{2} / {7} = {5} / {21} x $.

Задача 15

Найдите корень уравнения $(2x+7)^3=-64$.

Задача 16

Найдите корень уравнения $log_{2}{(2x+15)} =log_{2}{3} — 1$.

Задача 17

Найдите корень уравнения $log_{7}{(11-x)} =log_{7}{3} + 1$.

Задача 18

Найдите корень уравнения ${7} / {13}x^2=2{2} / {13}$. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Задача 19

Найдите корень уравнения $√ {-23x-120}=-x$. Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Задача 20

Найдите корень уравнения $√ {{36} / {2x-15}}=3$.

Задачи из курса стереометрии впервые появляются в ЕГЭ по математике в задании 5. Вам будут предложены вопросы по вычислению геометрических параметров шара, куба, параллельного параллелепипеда, призмы, пирамиды, цилиндра, конуса, составных многогранников, а также комбинаций нескольких фигур. Составители тестов также внесли в КИМ этого номера отдельно условия, касающиеся вычисления объемов геометрических тел и площади их сторон.

Пятые номера, касающиеся куба, одни из самых простых. Вам будет предложено найти объем фигуры, если известна сумма S всех его граней, и наоборот. Часть вопросов касается диагоналей, сторон. Такие же условия вам возможно дадут в заданиях с призмами, пирамидами. Другая часть может звучать так: «Во сколько раз увеличится V куба, если все ребра тела увеличить в три раза?».

Сложными называют школьники No 5 по математике о составных многогранниках и комбинациях тел. К примеру, вам может попасться вариант экзаменационного билета с поиском V параллельного параллелепипеда, который описан вокруг цилиндра, где d=1 м.

Варианты на тему «Шар» — это обычно поиск объема тела, площади его поверхности, радиуса или диаметра. Есть и мини-задачи такого типа: «Объем первой сферы в 27 раз больше, чем у второй. Сравните S поверхностей. Во сколько раз первая фигура больше второй по этому показателю?». В задачах о конусе вам нужно будет вычислять его V, площадь, образующую, высоту, диаметр или радиус основания.

Источник

ЕГЭ по математике Профиль. Задание 5: Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».

ЕГЭ Профиль. Задание № 5

АЛГОРИТМ ВЫПОЛНЕНИЯ

Задание № 5 рассчитано на умение решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объёмов), использовать при выполнении знание свойств основных пространственных тел, применять планиметрические факты и методы.

Задание состоит из текстовой задачи и рисунка. Рассматриваются простые пространственные тела: куб, прямоугольный параллелепипед, правильная пирамида, правильная призма. Ответом является конечная десятичная дробь или целое число.

План выполнения:

Внимательно прочитайте задачу.
При необходимости выполните на черновике чертёж и дополнительные построения.
Сделайте на черновике необходимые вычисления.
Запишите полученное число в поле ответа КИМ и бланк ответов № 1.

Задачи на Прямоугольный параллепипед

Для решения подобных задач необходимо повторить свойства куба и прямоугольного параллелепипеда, формулы для вычисления площади поверхности, объёма этих тел.

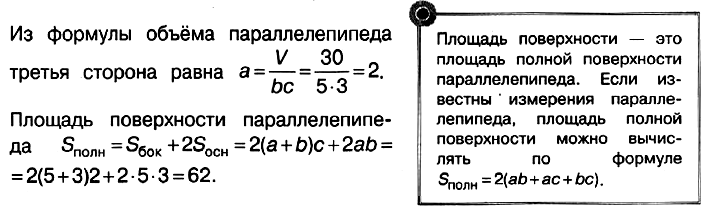
Задача № 5 (1). Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 5. Объём параллелепипеда равен 30. Найдите площадь его поверхности.

Решение:

Ответ: 62.

Задачи на Составные многогранники

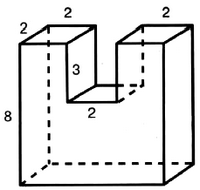
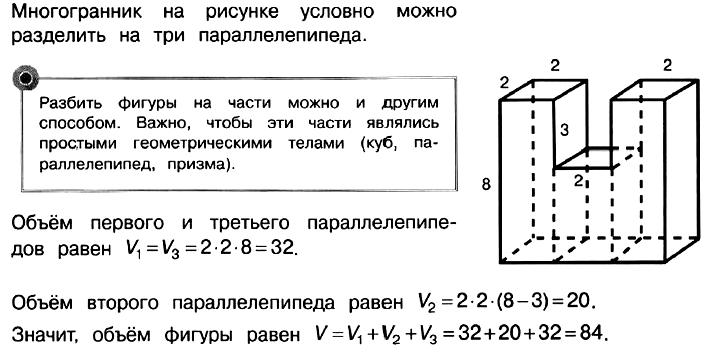
Задача № 5 (2). Найдите объём многогранника, изображённого на рисунке. Все двугранные углы многогранника прямые.

Решение:

Ответ: 84.

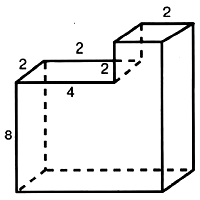
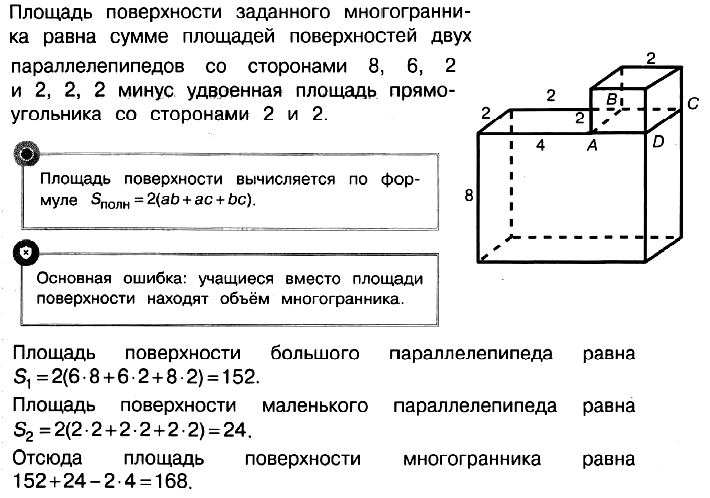
Задача № 5 (3). Найдите площадь поверхности многогранника, изображённого на рисунке. Все двугранные углы многогранника прямые.

Решение:

Ответ: 168.

Задачи на Призмы

Для решения задач этого типа необходимо повторить свойства призмы, формулы для вычисления площади поверхности и объёма призмы.

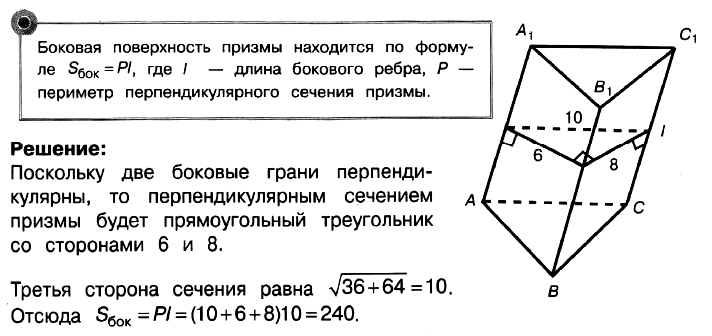
Задача № 5 (4). В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых рёбер на 6 и 8. Найдите площадь боковой поверхности этой призмы.

Решение:

Ответ: 240.

Задачи на Пирамиды

При подготовке нужно повторить основные свойства пирамиды, формулы для вычисления площади поверхности и объёма пирамиды.

Задача № 5 (5). Основание пирамиды — треугольник, у которого длины двух сторон равны 2 и 6, а угол между этими сторонами составляет 30°. Вычислите объём пирамиды, если её высота равна 3.

Решение:

Ответ: 3.

Задачи на Цилиндры

Для решения задач этого типа необходимо повторить формулы вычисления площади круга, длины окружности, площади поверхности цилиндра, объёма цилиндра.

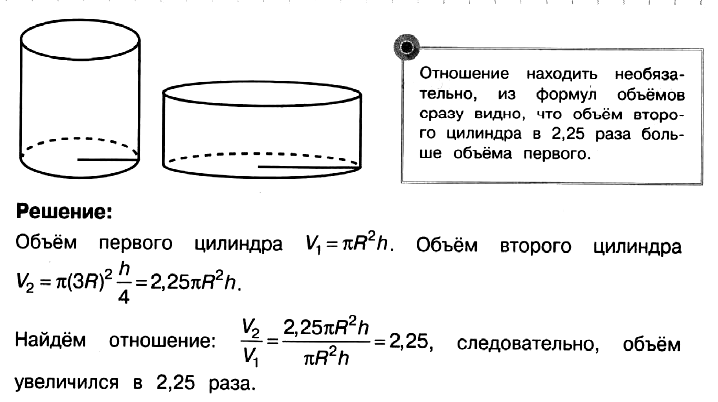
Задача № 5 (6). Радиус основания цилиндра увеличили в 3 раза, а его высоту уменьшили в 4 раза. Во сколько раз увеличится объём цилиндра?

Решение:

Ответ: 2,25.

Задачи на Конусы

При подготовке необходимо повторить свойства конуса, формулы для вычисления площади поверхности и объёма конуса, площади круга и длины окружности.

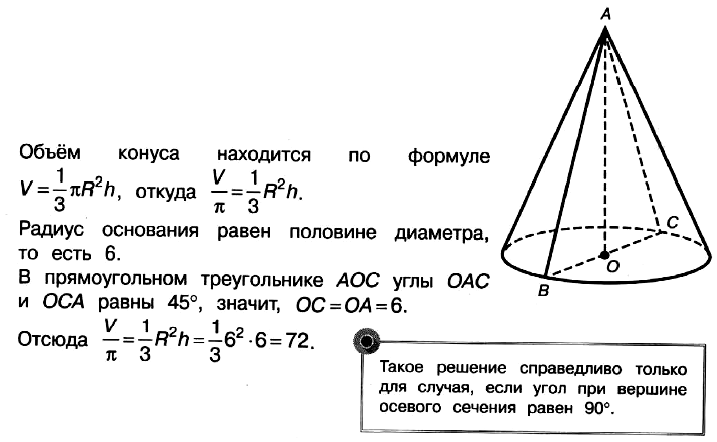
Задача № 5 (7). Диаметр основания конуса равен 12, угол при вершине осевого сечения равен 90°. Вычислите объём конуса, делённый на π.

Решение:

Ответ: 72.

Задачи на Шары

Для решения задач этого типа необходимо повторить формулы для вычисления площади круга, длины окружности, площади поверхности шара, объёма шара.

Задача № 5 (8). Площадь сечения шара плоскостью равна 36π см². Найдите радиус шара, если плоскость находится на расстоянии 8 см от центра шара.

Решение:

Ответ: 10.

Задачи на Комбинации многогранников
и тел вращения

Задача № 5 (9). В основании прямой призмы лежит прямоугольный треугольник с катетами 3 и 4. Боковые рёбра призмы равны 4/π. Найдите объём цилиндра, описанного около этой призмы.

Решение:

Ответ: 25.

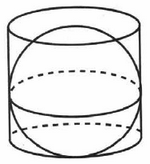
Задача № 5 (10). Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 15. Найдите площадь поверхности шара.

Решение:

Ответ: 10.

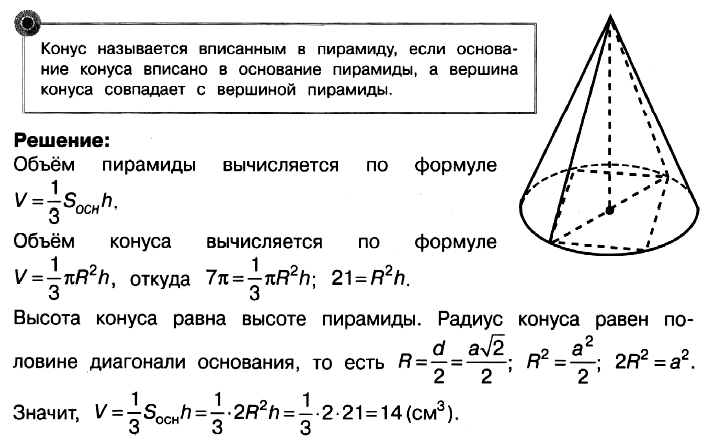
Задача № 5 (11). Объём конуса равен 7π см³. Найдите объём правильной четырёхугольной пирамиды, вписанной в конус.

Решение:

Ответ: 14.

Задача № 5 (12). Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 20. Найдите объём конуса.

Решение:

Ответ: 5.

Тренировочные задания с самопроверкой

№ 5.1. Площадь поверхности куба равна 72 (см. рис.). Найдите его диагональ.

Открыть ОТВЕТ

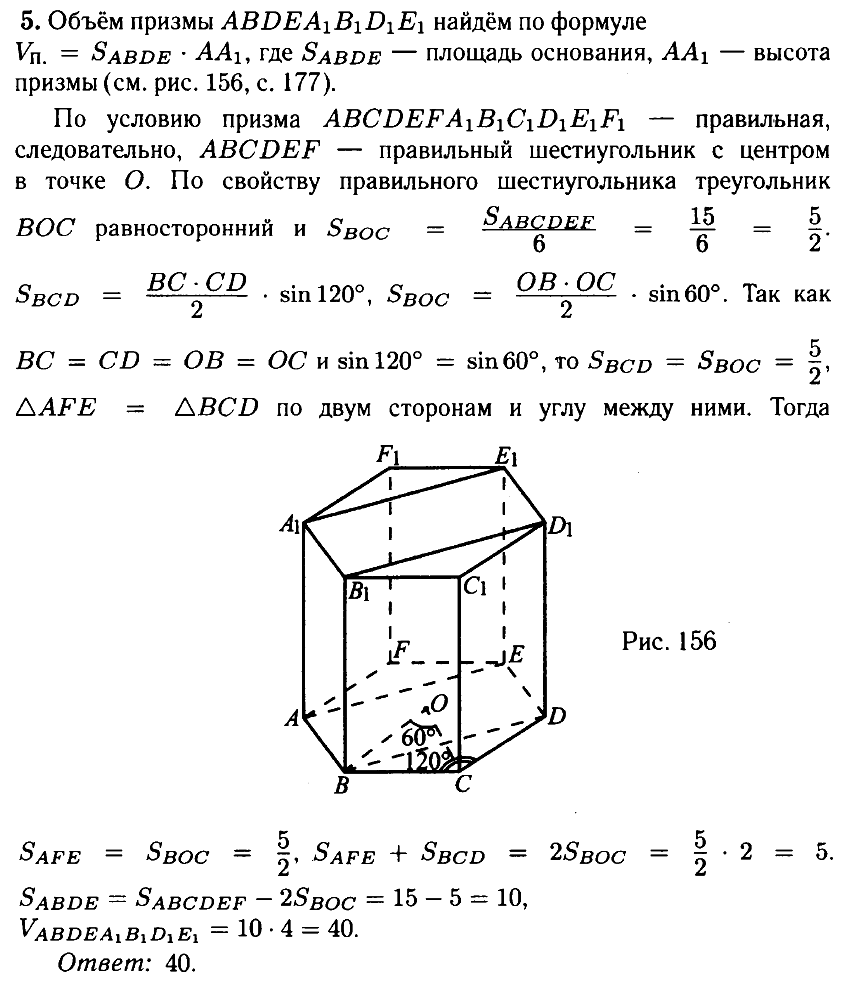
№ 5.2. Найдите объём многогранника, вершинами которого являются точки А, В, D, Е, А₁, В₁, D₁, E₁ правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁ (см. рис.). Площадь основания призмы равна 15, а боковое ребро равно 4.

Открыть ОТВЕТ

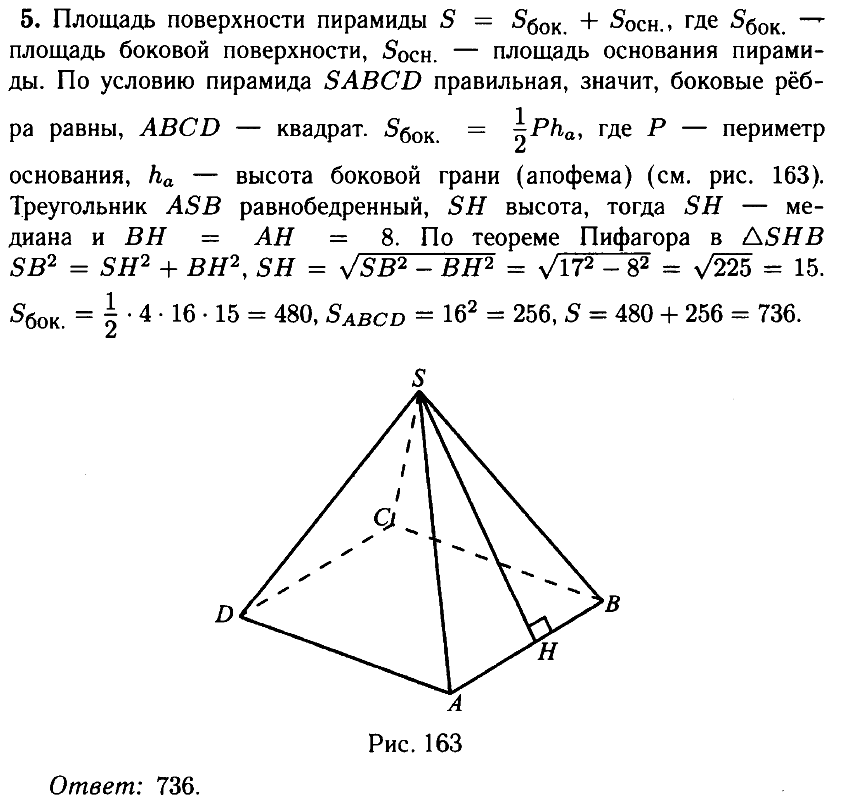
№ 5.3. Стороны основания правильной четырёхугольной пирамиды равны 16, боковые рёбра равны 17 (см. рис.). Найдите площадь поверхности этой пирамиды.

Открыть ОТВЕТ

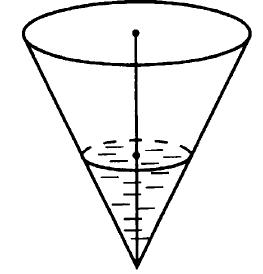
№ 5.4. В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты (см. рис.). Объём жидкости равен 60 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

Открыть ОТВЕТ

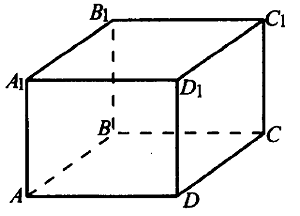
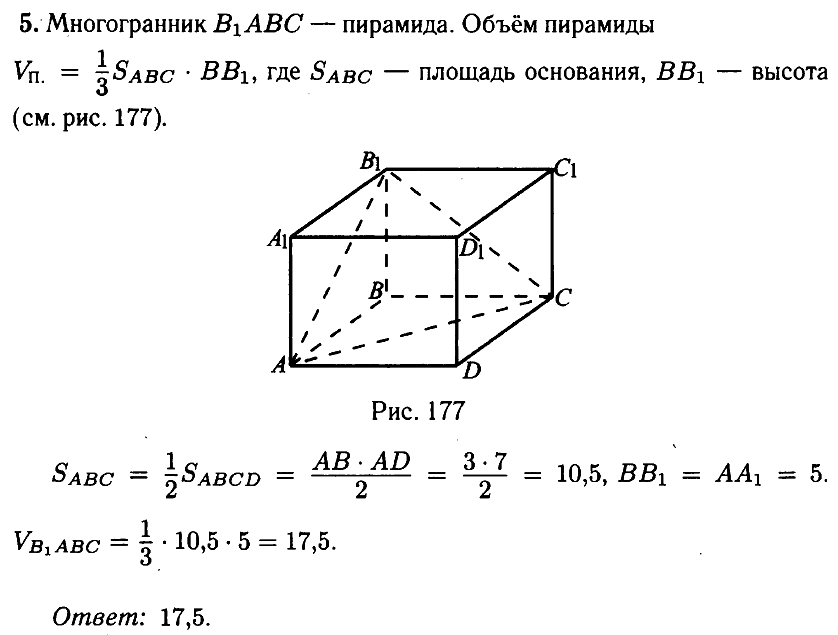
№ 5.5. Найдите объём многогранника, вершинами которого являются точки А, В, С, В прямоугольного параллелепипеда ABCDA₁B₁C₁D₁, у которого АВ = 3, AD = 7, АА₁ = 5 (см. рис.).

Открыть ОТВЕТ

Вы смотрели: ЕГЭ по математике Профиль. Задание 5: Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».

Источник

Единый государственный экзамен по математике базового уровня состоит из 20 заданий. В задании 5 проверяются навыки преобразования выражений. Школьник должен уметь преобразовывать числовые и буквенные алгебраические, логарифмические, показательные, тригонометрические и другие выражения. Здесь вы можете узнать, как решать задание 5 ЕГЭ по математике базового уровня, а также изучить примеры и способы решения на основе подробно разобранных заданий.

ЕГЭ база все задания (263)
ЕГЭ база задание 1 (5)
ЕГЭ база задание 2 (6)
ЕГЭ база задание 3 (45)
ЕГЭ база задание 4 (33)
ЕГЭ база задание 5 (2)
ЕГЭ база задание 6 (44)
ЕГЭ база задание 7 (1)
ЕГЭ база задание 8 (12)
ЕГЭ база задание 10 (22)
ЕГЭ база задание 12 (5)
ЕГЭ база задание 13 (20)
ЕГЭ база задание 15 (13)
ЕГЭ база задание 19 (23)
ЕГЭ база задание 20 (32)

Найдите значение алгебраического выражения

Найдите значение алгебраического выражения.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 5.

Найдите значение числового логарифмического выражения

Найдите значение числового логарифмического выражения.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 5.

Источник

Значение выражений

Теория к заданию №5

Разбор типовых вариантов заданий №5 ЕГЭ по математике базового уровня

Вариант 5МБ1

Алгоритм выполнения

Решение:

Решение в общем виде

Вариант 5МБ2

Алгоритм выполнения

Решение №1:

Решение №2:

Вариант 5МБ3

Алгоритм выполнения

Решение:

Вариант 5МБ4

Алгоритм выполнения

Решение:

Вариант 5МБ5

Алгоритм выполнения

Решение:

Вариант 5МБ6

Алгоритм выполнения

Решение:

Вариант 5МБ7

Алгоритм выполнения

Решение:

Вариант 5МБ8

Алгоритм выполнения

Решение:

Вариант 5МБ9

Алгоритм выполнения

Решение:

Вариант 5МБ10

Алгоритм выполнения

Решение:<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" loading="lazy" src="https://spadilo.ru/wp-content/uploads/2019/01/c-users-ksenya-desktop-korin-png-e1560417170386.png" alt width="483" height="62" />

Вариант 5МБ11

Алгоритм выполнения

Решение:<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" loading="lazy" src="https://spadilo.ru/wp-content/uploads/2019/01/c-users-ksenya-desktop-55-png-e1560417394213.png" alt width="238" height="59" />

Вариант 5МБ12

Алгоритм выполнения

Решение:

Вариант 5МБ13

Алгоритм выполнения

Решение:<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" loading="lazy" src="https://spadilo.ru/wp-content/uploads/2019/01/c-users-ksenya-desktop-k33-png-e1560417526909.png" alt width="221" height="28" />

Вариант 5МБ14

Алгоритм выполнения

Решение:

Вариант 5МБ15

Алгоритм выполнения

Решение:

Вариант 5МБ16

Алгоритм выполнения

Решение:

ЕГЭ Профиль. Задание № 5

АЛГОРИТМ ВЫПОЛНЕНИЯ

Задачи на Прямоугольный параллепипед

Задачи на Составные многогранники

Задачи на Призмы

Задачи на Пирамиды

Задачи на Цилиндры

Задачи на Конусы

Задачи на Шары

Задачи на Комбинации многогранников и тел вращения

Тренировочные задания с самопроверкой

Найдите значение алгебраического выражения

Найдите значение числового логарифмического выражения

Решение:

Решение:

Решение:

Задачи на Комбинации многогранников
и тел вращения