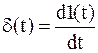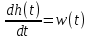Вопросы
к экзамену по ТАУ для з/о
-
Передаточная
функция замкнутой системы по входному
воздействию, временная
характеристика. -
Статическое
регулирование, характеристики и статизм
регулирования. -
Критерий
устойчивости Гурвица. Привести пример. -
Функциональная
схема
системы автоматического управления,
назначение элементов. -
Пример астатического
регулятора и его характеристики. -
Критерий
устойчивости Рауса. Привести пример. -
Общее представление
о прямом и обратном преобразованиях
Лапласа. -
Представление
передаточных функций системы в
операторной форме. -
Основное
условие устойчивости
систем автоматического управления.
Виды переходных
процессов в устойчивой и неустойчивой
системах. -
Статическое
и астатическое регулирование. Основное
их отличие. -
Алгебраические
критерии устойчивости и в чём заключается
их смысл (привести
пример). -
Понятие о
логарифмической амплитудно-частотной
характеристике звена или системы
(ЛАЧХ). -
Понятие
о логарифмической
фазочастотной характеристике
звена или системы (ЛФЧХ). -
Основные определения
и понятия о нелинейных системах. -
Усилительное
звено и его характеристики. -
Астатические
системы регулирования. Привести пример. -
Методика построения
логарифмических характеристик звена
или системы. -
Функциональная
схема системы автоматического управления,
и её основные элементы. -
Основные
типовые динамические звенья систем
регулирования. -
Классификация
и основные
функции систем автоматического
управления. -
Функциональная
схема и основные элементы автоматического
регулятора. -
Преобразование
Лапласа в применении к теории
автоматического регулирования. -
Безынерционное
звено и его характеристики -
Автоматический
регулятор, понятие, определение и
основные элементы. -
Инерционное
звено и его характеристики. -
Основные
способы включения звеньев в системах
управления. Привести схемы включения. -
Что
называют системой автоматического
регулирования (структурная схема и
элементы) -
Колебательное
звено и его характеристики. -
Методы
преобразования структурных схем систем
автоматического управления. Параллельное
соединение звеньев. -
Интегрирующее
звено и его характеристики. -
Последовательное
включение звеньев (одноконтурная
разомкнутая система). -
Логарифмический
критерий устойчивости САУ. -
Функциональная
схема автоматического регулятора и
назначение его элементов. -
Дифференцирующее
звено и его характеристики. -
Параллельное,
согласное включение звеньев системы.
Привести пример. -
Понятие
о системах управления и регулирования.
Чем отличается регулирование от
управления. -
Апериодическое
звено и его характеристики. -
Параллельное
встречное включение звеньев (обратная
связь). -
Структурная
схема автоматического регулирования
напряжения генератора постоянного
тока. -
Нахождение
Лапласова изображения для линейного
дифференциального уравнения. -
Общие
понятия об устойчивости систем
автоматического управления. Основное
условие устойчивости. -
Основные виды
нелинейностей в системах управления
и регулирования. -
Понятие о
функциональных элементах и динамических
звеньях системы регулирования. -
Запаздывающее
звено и его характеристики. -
Понятие
о фазовых портретах или годографах
систем управления. -
Основные показатели
качества процесса регулирования. -
Интегро-дифференцирующее
звено. -
Частотные
характеристики систем автоматического
управления. -
Структурная схема
САУ, которая осуществляет первую функцию
управления (пуск, торможение реверс). -
Структурная
схема САУ, которая осуществляет вторую
функцию
управления
(поддержание
регулируемой величины с высокой
точностью в статике и динамике). -
Структурная
схема САУ, которая осуществляет третью
функцию
управления
(Слежение
за вводимыми в систему сигналами). -
Структурная
схема САУ, которая осуществляет четвертую
функцию
управления
(Программное
автоматическое управление машинами и
механизмами). -
Структурная
схема САУ, которая осуществляет пятую
функцию
управления
(Управление,
обеспечивающее автоматический выбор
целесообразных режимов работы).
Соседние файлы в предмете Теория автоматического управления
- #
- #
- #
- #
- #
16.02.20172.18 Mб58Нелинейные САУ (можно взять этот вариант ответа).doc
- #
16.02.2017107.52 Кб32Нелинейные системы автоматического управления.doc
Описание
Вопросы к экзамену по курсу «Основы теории управления»
1.Принципы действия систем управления
2.Функциональные схемы и способы классификации систем управления
3.Описание воздействующих сигналов
4.Методика составления математических моделей динамических систем
5.Основные задачи теории автоматического управления
6.Передаточная функция системы управления
7.Уравнения и передаточные функции типовых динамических звеньев
8.Переходные и импульсные переходные (весовые) функции системы
9.Определение реакции системы на воздействие произвольного вида
10.Понятие о частотных характеристиках системы (АЧХ, АФЧХ, ФЧХ)
11.Частотные характеристики типовых динамических звеньев
12.Логарифмические частотные характеристики
13.Понятие о минимально-фазовых системах
14.Типовые передаточные функции соединений динамических звеньев
15.Преобразования, связанные с переносом в структурной схеме системы узлов
(разветвлений) и сумматоров
16.Многомерные линейные системы и способы их описания
17.Анализ управляемости и наблюдаемости систем управления (критерии и
примеры)
18.Понятие устойчивости САУ (необходимое условие устойчивости, два общих
критерия устойчивости систем управления)
19.Алгебраический критерий устойчивости Рауса-Гурвица
20.Критерий устойчивости Рауса-Гурвица для случая многомерной САУ
21.Анализ устойчивости линейных систем с помощью критерия А.В. Михайлова
22.Анализ устойчивости линейных систем с помощью критерия Найквиста
23.Использование логарифмических характеристик для исследования
устойчивости систем автоматического управления
24.Понятие о запасе устойчивости
25.Построения областей устойчивости (метод Д-разбиения)
26.Основные показатели (критерии) качества процесса управления
27.Миноранты и мажоранты переходных процессов
28.Оценка качества процесса регулирования с помощью диаграммы
Вышнеградского
29.Связь коэффициентов дифференциального уравнения и корней. Стандартные
коэффициенты характеристического уравнения
30.Интегральные оценки качества процесса управления
31.Частотные критерии качества регулирования (запас устойчивости,
показатель колебательности, степень затухания, полоса пропускания,
быстродействие)
32.Построение переходного процесса в системах управления по частотным
характеристикам (метод трапеций)
33.Оценка качества регулирования с помощью логарифмических характеристик
(с использованием номограмм Солодовникова и Честната-Майера
34.Понятие чувствительности системы автоматического управления
35.Постановка задачи синтеза линейных САУ и пути ее решения
36.Обеспечение требуемого качества процесса регулирования с помощью
корректирующих средств
37.Метод частотных логарифмических характеристик
38.Коррекция динамики системы управления с помощью интегрирующего
корректирующего устройства
39.Коррекция динамики системы управления с помощью форсирующего
корректирующего устройства
40.Коррекция динамики системы управления с помощью интегро-дифференцирующего корректирующего устройства
Характеристики вопросов/заданий
Список файлов
- ReadMe.txt 276 b
- Вопросы к экзамену по курсу Основы теории управления.doc 30,5 Kb
- Вопросы к экзамену по курсу Основы теории управления.docx 14,05 Kb
- Вопросы_1.jpg 1,06 Mb
- Вопросы_2.jpg 701,3 Kb
ReadMe
Файлы скачаны со студенческого портала для студенты «Baumanki.net»
Файлы представлены исключительно для ознакомления
Не забывайте, что Вы можете зарабатывать, выкладывая свои файлы на сайт
Оценивайте свой ВУЗ в различных голосованиях, в том числе в досье на преподавателей!
Вопросы_1
Распознанный текст из изображения:
Вопросы к экзамену по курсу «Основы теории управлении»
1. Принципы действия систем управления
2. Функциональные схемы и способы классификации систем управления
3. Описание воздействующих сигналов
4. Методика составления математических моделей динамических систем
5. Основные задачи теории автоматического управления
6. Передаточная функция системы управления
7. Уравнения и передаточные функции типовых динамических звеньев
8. Переходные и импульсные переходные (весовые) функции системы
9. Определение реакции системы на воздействие произвольного вида
10. Понятие о частотных характеристиках системы (АЧХ, АФЧХ, ФЧХ)
11. Частотные характеристики типовых динамических звеньев
12. Логарифмические частотные характеристики
13. Понятие о минимально-фазовых системах
14. Типовые передаточные функции соединений динамических звеньев
15. Преобразования, связанные с переносом в структурной схеме системы узлов
(разветвлений) и сумматоров
16. Многомерные линейные системы и способы их описания
17. Анализ управляемости и наблюдаемости систем управления (критерии и
примеры)
18. Понятие устойчивости САУ (необходимое условие устойчивости, два общих
критерия устойчивости систем управления)
19. Алгебраический критерий устойчивости Рауса-Гурвица
20. Критерий устойчивости Рауса-Гурвица для случая многомерной САУ
21. Анализ устойчивости линейных систем с помощью критерия А.В. Михайлова
22. Анализ устойчивости линейных систем с помощью критерия Найквиста
23. Использование логарифмических характеристик для исследования
устойчивости систем автоматического управления
24. Понятие о запасе устойчивости
25. Построения областей устойчивости (метод Д-разбиения)
26. Основные показатели (критерии) качества процесса управления
27. Миноранты и мажорапты переходных процессов
28. Оценка качества процесса регулирования с помощью диаграммы
Вышнеградского
Вопросы_2
Распознанный текст из изображения:
29. Связь коэффициентов дифференциального уравнения и корней. Стандартные
коэффициенты характеристического уравнения
30. Интегральные оценки качества процесса управления 31. Частотные критерии качества регулирования (запас устойчивости,
показатель колебательности, степень затухания, полоса пропускания,
быстродействие)
32. Построение переходного процесса в системах управления по частотным
характеристикам (метод трапеций)
33. Оценка качества регулирования с помощью логарифмических характеристик
(с использованием номограмм Солодовникова и Честната-Майера 34. Понятие чувствительности системы автоматического управления 35. Постановка задачи синтеза линейных САУ и пути ее решения 36. Обеспечение требуемого качества процесса регулирования с помощью
корректирующих средств
37. Метод частотных логарифмических характеристик 38. Коррекция динамики системы управления с помощью интегрирующего
корректирующего устройства
39. Коррекция динамики системы управления с помощью форсирующего
корректирующего устройства
40. Коррекция динамики системы управления с помощью интегродифференцирующего корректирующего устройства
Подборка по базе: Самые популярные вопросы о Чичикове из поэмы.docx, Примерные вопросы к дифференцированному зачету_Психология общени, Тестовые вопросы к разделу 5_ просмотр попытки.pdf, Тестовые вопросы к разделу 8_ просмотр попытки.pdf, Экзамен вопросы СП ОМ_англ_ok.docx, Ответы к экзамену.docx, 2.2 Вопросы к экзамену Смета+Финансы.docx, ВОПР К экзамену АСВТ.docx, РК-1 вопросы каз, русс 1 курс.docx, Экзаменационные вопросы для студентов лечебного факультетаКонтро
Вопросы к экзамену / зачету по дисциплине ТАУ
- Что является целью управления в системе автоматического регулирования?
Ответ: Основной задачей автоматического управления является поддержание определенного закона изменения одной или нескольких физических величин, характеризующих процессы, протекающие в ОУ, без непосредственного участия человека. Эти величины называются управляемыми величинами.
- Какая функция называется передаточной функцией системы? Ответ: Передаточная функция — один из способов математического описания динамической системы. Используется в основном в теории управления, связи и цифровой обработке сигналов. Представляет собой дифференциальный оператор, выражающий связь между входом и выходом линейной стационарной системы.
- Какое уравнение называется характеристическим уравнением системы?
Ответ: Характеристическое уравнение — алгебраическое уравнение вида определитель в этой формуле получается из определителя матрицы вычитанием величины x из диагональных элементов; он представляет собой многочлен относительно x и называется характеристическим многочленом
- Вычисление передаточной функции двух звеньев, соединенных последовательно.
Ответ: Передаточная функция последовательного соединения звеньев равна произведению передаточных функций отдельных звеньев.
- Вычисление передаточной функции двух звеньев, соединенных параллельно.
Ответ: Передаточная функция группы параллельно соединенных звеньев равна сумме отдельных звеньев.
- Вычисление передаточной функции двух звеньев, соединенных встречно-параллельно.
Ответ: Передаточная функция эквивалентного звена при встречно-параллельном соединении звеньев равна отношению передаточной функции звена прямой цепи к знаменателю, представляющему собой алгебраическую сумму единицы и произведения передаточных функций звена прямой цепи и звена обратной связи.
- Что такое переходная функция?
Ответ: Переходная функция, иногда называют переходный процесс — в теории управления реакция динамической системы на входное воздействие в виде функции Хэвисайда, при заданных начальных условиях. Также реакцию динамической системы на ступенчатое воздействие называют кривой разгона. - Временные характеристики звеньев.
Ответ: Временные характеристики — динамические свойства звеньев и систем определяются с помощью временных и частотных характеристик. Временные характеристики показывают изменение во времени выходного сигнала исследуемого звена или системы при подаче на их вход типового входного сигнала. - Какова взаимосвязь импульсной функции
и ступенчатой 1(t)?
Ответ: Единичная ступенчатая функция и единичная импульсная функция связаны соотношением
- Дельта-функция и ее свойства.
Ответ: Дельта-функция — обобщённая функция, которая позволяет записать точечное воздействие, а также пространственную плотность физических величин (масса, заряд, интенсивность источника тепла, сила и т.)
- Частотная передаточная функция: определение; ее представление через амплитуду и фазу.
Ответ: Частотно передаточная функция представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной.
- Вещественная и мнимая частотные характеристики; АФЧХ, логарифмические частотные характеристики. Их взаимосвязь.
Ответ: Вещественная частотная характеристика U(w) является четной функцией частоты w, а мнимая частотная характеристика V(w) – нечетной. Годограф передаточной функциипри
(обычно берут
) называется амплитудно-фазовой характеристикой (АФХ), а также амплитудно-фазовой частотной характеристикой (АФЧХ), или годографом Найквиста. АФЧХ строится на комплексной плоскости: по оси абсцисс откладывается вещественная часть
, а по оси ординат – мнимая часть
. Для каждой частоты на комплексной плоскости наносится точка. Полученные точки затем соединяются плавной кривой.
АФЧХ – график частотной передаточной функции на комплексной плоскости. Логарифмические частотные характеристики (ЛЧХ) — зависимость относительной амплитуды колебаний и фазового сдвига от частоты, построенная в логарифмических или полулогарифмических координатах.
- Взаимосвязь весовой функции, переходной характеристики и передаточной функции.
Ответ: Весовой функцией звена (системы) называется реакция системы при нулевых н.у. на единичное импульсное воздействие. Переходной функцией системы автоматического управления, ее звена, называют функцию, описывающую изменение выходной величины системы (ее звена), когда на ее вход подается единичное ступенчатое воздействие при нулевых начальных условиях. Импульсную переходную функцию w(t) также называют весовой функцией или функцией веса. Она является выходной координатой элемента или системы при подаче на вход единичного импульса (t). Связь между переходной функцией h(t) и импульсной переходной функцией w(t) выражается соотношением
- Если частотная передаточная функция задана в виде
W(j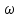
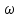
Ответ:
- Как задается звено первого порядка?
Ответ: Звено первого порядка обладает двумя параметрами: инерционностью T и коэффициентом усиления k = Y(t = ∞)/X. Чем больше производных учитывается в записи модели, тем со звеном большего порядка мы имеем дело, тем больше коэффициентов при производных следует определить. Передаточная функция звена первого порядка имеет вид: W = k/(Tp + 1),где «p» — символ дифференцирования, тождественно равный «d/dt». Символ «p» также называется алгебраизованным оператором дифференцирования.
- Как задается звено второго порядка?
Ответ: Звеном второго порядка называется звено, связь между выходной и входной величиной которого определяется линейным дифференциальным уравнением второго порядка вида.
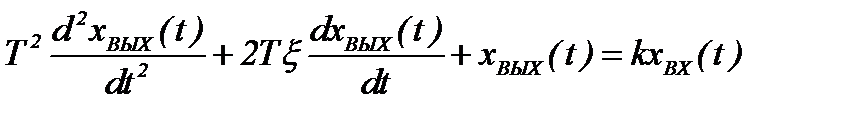
- Передаточные функции, временные и частотные характеристики безынерционного звена.
Ответ: Безынерционное звено является простейшим среди всех типовых звеньев. Оно передает сигнал со входа на выход мгновенно, без искажений его формы. В звене может происходить только усиление или ослабление мгновенных значений входной величины. Связь между мгновенными значениями входной величины x(t) и выходной величины y(t) описывается алгебраическим уравнением
Передаточные свойства звена определяются лишь одним параметром – передаточным коэффициентом k.
- Передаточные функции, временные и частотные характеристики интегрирующего звена.
Ответ: передаточная функция
Временные хар-ки где
Частотные хар-ки
- Передаточные функции, временные и частотные характеристики дифференцирующего звена.
Ответ: передаточная функция
Временные хар-ки
Частотные хар-ки
- Передаточные функции, временные и частотные характеристики форсирующего звена первого порядка.
Ответ: Передаточную функцию форсирующего звена принято записывать в стандартной форме W (p)=k (1+Tp), где k=k 1 – коэффициент усиления, а T=k 2 /k 1 – постоянная времени звена.
Временные хар-ки где
Частотные хар-ки
- Передаточные функции, временные и частотные характеристики апериодического звена первого порядка.
Ответ: передаточная функция
Временные хар-ки где 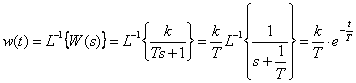
Частотные хар-ки
- Передаточные функции, временные и частотные характеристики колебательного звена.
Ответ: Передаточная функция
Временные хар-ки 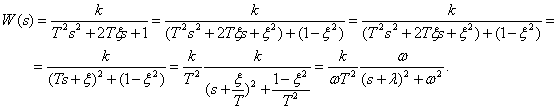
Частотная хар-ка
- Передаточные функции, временные и частотные характеристики консервативного звена и апериодического звена 2-го порядка.
Ответ: передаточная функция
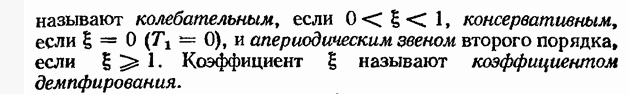
- Чему равна фаза для интегрирующего звена.
Ответ: Амплитудно-фазовая частотная характеристика интегрирующего звена совпадает с отрицательной мнимой полуосью.
- Какие значения может принимать коэффициент демпфирования?
Ответ: Коэффициент демпфирования — системный параметр, обозначаемый ζ (дзета), который может варьироваться от незатухающий (ζ = 0), недостаточно демпфированный (ζ < 1) через критически затухающий (ζ = 1) к чрезмерно демпфированный (ζ > 1).
- Где расположены корни характеристического полинома для устойчивой непрерывной САУ?
Ответ: Чтобы система была устойчива — необходимо, чтобы все корни характеристического полинома имели отрицательные вещественные части (располагались левее мнимой оси). Если хотя бы один корень характеристического полинома расположен на мнимой оси (а все остальные слева от нее), то такая система находится на границе устойчивости.
- Необходимый алгебраический критерий устойчивости линейных САУ.
Ответ: Необходимым и достаточным условием устойчивости линейной САУ является отрицательность вещественных частей всех корней ее характеристического уравнения. Последнее может быть получено из передаточной функции замкнутой системы, связывающей любые ее вход и выход, путем приравнивания к нулю знаменателя передаточной функции.
- В соответствии с критерием Гурвица, при выполнении каких условий система будет асимптотически устойчива?
Ответ: Если при движении в пространстве точки М и M неограниченно сближаются и разности их координат (yi y’ i) 0, то возмущенное движение постепенно возвращается к невозмущенному. Такое движение называется асимптотически устойчивым. Движение называется асимптотически устойчивым, если можно подобрать такое , что, если y0 y0 , то выполняется условие y y 0 при t .
29. В соответствии с критерием Михайлова, где начинается в устойчивой системе годограф Михайлова при 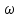
Ответ: Для устойчивых систем годограф Михайлова начинается при 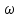
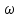
30. Какая точка является критической точкой при определении устойчивости с помощью критерия Найквиста?
Ответ: Точка (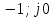
31. Какое условие должно выполняться для определения устойчивости замкнутой системы по критерию Найквиста?
Ответ: Для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф АФЧХ разомкнутой системы при изменении от 0 до 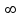
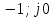
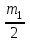
32. Как определяется частота среза 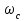
Ответ: частота среза – это частота, на которой кривая L(w) пересекает ось ω. Критическая частота – частота, на которой фазовая характеристика j (w) равна –180°.
33. Как определяется запас устойчивости по амплитуде и по фазе?
Ответ: Запас устойчивости по амплитуде (модулю) определяется величиной допустимого подъема ЛАЧХ, при котором система окажется на границе устойчивости. Запас устойчивости по фазе определяется величиной, на которую должно возрасти запаздывание по фазе в системе с частотой среза , чтобы система оказалась на границе устойчивости. Обычно рассчитывается в градусах.
Теория автоматического
управления
Билет №1
Объект управления, фазовые координаты, управляющие функции, уравнения
состояния объекта, управляющее устройство.Расширенное фазовое пространство
управляемой системы. Способы задания цели управления. Функционал задачи.
Замкнутые и разомкнутые системы управления. Программа управления, синтез
управления. Обратная связь по координатам и по возмущениям.
Билет №2Система
управления с обратной связью и её математическое описание с помощью линейной
системы дифференциальных уравнений. Звено системы управления и его описание с
помощью линейного дифференциального уравнения n-го порядка. Операторный подход
Хевисайда, операторная передаточная функция звена. Математическая формализация
подхода Хевисайда с помощью преобразования Лапласа.
Билет №3
Передаточная функция системы управления при различных видах соединения
звеньев: последовательном, параллельном, с обратной связью. Перенос точки съёма
сигнала и точки суммирования сигналов для получения более простой эквивалентной
схемы.
Билет №4
Свойства преобразования Лапласа (линейность, дифференцирование оригинала,
интегрирование оригинала, теорема запаздывания, теорема о свертке)
Билет №5
Весовая функция, переходная функция, амплитудно-фазовая характеристика.
Связь между весовой и переходной функциями. Связь между передаточной функцией и
амплитудно-фазовой характеристикой. Использование весовой функции для нахождения
отклика системы на произвольное внешнее воздействие.
Билет №6
Типовые звенья системы управления: идеальный усилитель, интегрирующее звено,
дифференцирующее звено, апериодическое звено. Построение для перечисленных
типовых звеньев передаточных, весовых, переходных функций и амплитудно-фазовых
характеристик.
Билет №7 Следящая
система. Передаточные функции для ошибки по задающему воздействию и по
возмущению. Исследование точности следящей системы. Различные подходы к синтезу
инвариантной системы: увеличение коэффициента усиления, введение положительной
обратной связи, введение корректирующих звеньев.
Билет №8
Исследование точности следящей системы на больших интервалах времени и в
предельном случае. Понятие о статической ошибке и устранение этой ошибки путём
введения в контур управления интегрирующих звеньев. Астатические системы.
Порядок астатизма.
Билет №9
Устойчивость системы управления
по начальным данным и её устойчивость по входу. Ограниченность входного и
выходного сигналов. Суждение об устойчивости системы по её весовой и
передаточной функциям.
Билет №10
Устойчивость системы управления. Связь устойчивости системы с расположением
корней характеристического полинома. Алгебраические и графические критерии
устойчивости (необходимое условие, критерий Рауса-Гурвица, критерий
Михайлова).
Билет №11
Устойчивость системы управления. Граница устойчивости в комплексной
плоскости корней полинома и граница устойчивости в плоскости параметров системы.
Метод Д-разбиения для нахождения областей устойчивости в плоскости
параметров
Билет №12
Графический метод исследования устойчивости замкнутой системы управления.
Суждение об устойчивости замкнутой системы по амплитудно-фазовой частотной
характеристике разомкнутой системы (критерий Найквиста). Использование
АФЧ-харакеристик для анализа устойчивости сложных систем при отсутствии их
точной математической модели.
Билет №13
Передаточная функция звена запаздывания. Устойчивость системы с обратной
связью при наличии запаздывания.
Билет №14 Структурная устойчивость систем
управления. Локальная обратная связь как один из способов изменения структуры
системы управления и устранения структурной неустойчивости.
Билет №15
Критерии наблюдаемости и управляемости систем управления
Билет №16
Робастная система управления, как система, сохраняющая свои основные
свойства при некотором изменении её параметров. Робастная устойчивость линейных
систем. Теорема Харитонова о робастной устойчивости полинома с независимыми
коэффициентами.
Билет №17
Синтез систем управления по желаемой передаточной функции. Условия
физической осуществимости и робастности. Метод синтеза регулятора по желаемой
передаточной функции.
Билет
№18 Оптимальное управление. Общая постановка задачи оптимального управления.
Задачи Лагранжа, Майера и Больца. Динамическое программирование. Принцип
оптимальности и уравнение Беллмана для поиска оптимального управления в форме
синтезирующей функции.
Билет
№19 Оптимальное управление. Общая постановка задачи оптимального управления.
Сопряжённые переменные, функция Гамильтона-Понтрягина, сопряжённая система,
условия трансверсальности. Принцип максимума Л.С. Понтрягина для задачи с
фиксированным левым и свободным правым концом.
Билет №20
Оптимальное управление.
Общая постановка задачи оптимального управления. Информационная матрица. Формула
для малых изменений функционала.
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5

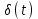 и ступенчатой 1(t)?
и ступенчатой 1(t)?