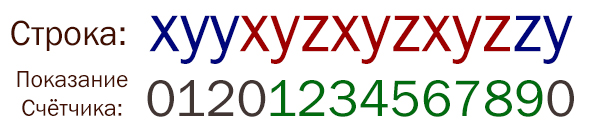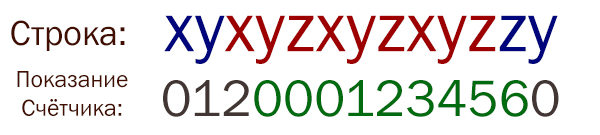Теория чисел егэ информатика - Помощь в подготовке к экзаменам и поступлению

Технология обработки информации в электронных таблицах

Ввод и редактирование данных в электронных таблицах, операции над данными

Программа Excel — одно из самых популярных средств управления электронными таблицами.

Каждый документ представляет собой набор таблиц — рабочую книгу, которая состоит из одного или многих рабочих листов. Каждый рабочий лист имеет название — это как бы отдельная электронная таблица. По умолчанию первый документ называется Книга1. При сохранении в файле документа это имя можно изменить.

Таблица состоит из столбцов и строк. Столбцы обозначаются латинскими буквами A, B, C, D и т. д. Если букв алфавита не хватает — используют двухбуквенные обозначения AA, AB, AC,…, IV. Максимальное число столбцов — 256. Строки нумеруются целыми числами. Максимальное число строк — 65535.

Ячейки располагаются на пересечении столбцов и строк. Номер (адрес) ячейки формируется из номера столбца и номера строки без пробела между ними. Например, A1, D24, M355. Одна из ячеек на рабочем листе всегда является текущей (активной). Она обведена широкой рамкой; в поле имени выводится ее номер, а в строке формул — ее содержимое. Именно с этой ячейкой производится работа — считывание или запись.

Заполнение таблиц данными

Ячейка может содержать три вида данных:

Текстовые данные — строка текста произвольной длины.
Числовые данные — отдельное число (в допустимом формате). Как числа рассматриваются данные, определяющие даты или денежные суммы.
Формулы — содержимое ячейки рассматривается как формула, если оно начинается со знака равенства «=». Ячейка, содержащая формулу, является вычисляемой, т. е. значение ее может зависеть от значений других ячеек таблицы. Формулы в ячейках не отображаются. Вместо формулы воспроизводится результат, полученный при ее вычислении. Чтобы увидеть формулу, хранящуюся в вычисляемой ячейке, нужно выделить эту ячейку (сделать текущей) и посмотреть в строку формул.

Возможна одновременная обработка нескольких ячеек (диапазона ячеек). Диапазон отображается на экране в инвертированном виде и обводится толстой рамкой. Бывают двумерные (строка, столбец) и трехмерные (строка, столбец, лист) диапазоны. Для обозначения диапазона используется разделитель « : ». Например, В:Е — диапазон столбцов от В до Е включительно, т. е. вертикальная полоса; 2:6 — диапазон строк со 2 по 6 включительно, т. е. горизонтальная полоса; B2:G12 — диапазон ячеек, левый верхний угол которого — ячейка В2, нижний правый угол — ячейка G12.

Данные вводятся в текущую ячейку и одновременно отображаются в строке формул. Вводимый текст автоматически выравнивается по левому краю, а числа — по правому. Необходимые данные можно вставить в электронную таблицу из других приложений с помощью команд группы Получить внешние данные вкладки Данные или обычным копированием с использованием буфера обмена Windows (здесь и далее приводятся команды для программы Excel из пакета MS Office 2007).

Редактирование введенных данных осуществляется следующим образом. Если в заполненную ячейку нужно ввести новые данные, то необходимо сделать ее текущей и начать вводить новые значения. Старое содержимое ячейки при этом утрачивается. Если же надо только откорректировать некоторые данные, то нужно, активизировав ячейку, нажать клавишу [F2] или выполнить двойной щелчок левой клавишей мыши по ячейке. При этом в ячейке появится текстовый курсор, и содержимое можно исправить. Также исправления можно ввести в строку формул активной ячейки.

В электронных таблицах реализована автоматизация ввода данных. Многие таблицы могут содержать в ячейках повторяющиеся данные. При заполнении таких таблиц Excel уже по первой букве «догадывается», что хочет ввести пользователь, и выводит подсвеченное значение в ячейку. Интеллектуальные способности программы можно развить и автоматизировать ввод не только повторяющихся данных, но и данных, поддающихся несложному закону изменения.

Чтобы размножить данные на несколько ячеек, нужно сделать активной первую ячейку диапазона и заполнить ее. Затем установить указатель мыши на маркер заполнения (правый нижний угол рамки текущей ячейки). Перетаскиванием маркера заполнения можно размножить содержимое текущей ячейки на несколько ячеек в столбце или строке. Если в первой ячейке были введены день недели или дата, то при перетаскивании вправо или вниз их значения будут увеличиваться на 1, а при перетаскивании влево или вверх — уменьшаться на 1. Если в ячейку было введено число или текст, то при перетаскивании маркера оно скопируется в другие ячейки. Для создания числового ряда при перетаскивании маркера заполнения следует удерживать нажатой клавишу [Ctrl]. По ходу перетаскивания содержимое последней ячейки отображается в небольшом всплывающем окне. Если для перетаскивания маркера использовать правую кнопку мыши, то при ее отпускании появится контекстное меню, позволяющее изменить способ заполнения диапазона.

Если требуется более сложный закон изменения последовательности значений, то после выбора первой ячейки и ввода в нее нужного значения надо выполнить команду Заполнить/Прогрессия из группы Редактирование вкладки Главная.

Автозаполнение ячеек данными можно также осуществить следующим образом. В первую ячейку надо ввести начальное значение ряда данных, а во вторую — следующее значение. Затем выделить эти две ячейки и перетащить маркер заполнения до конца нужного диапазона. Excel проанализирует данные двух исходных ячеек, определит, насколько отличаются их значения, и создаст такой же ряд. Если в исходную ячейку было введено смешанное значение, например текст и число, то автозаполнение копирует текстовую часть (если только это не месяц или день) и наращивает числовую часть, если число находится в начале или в конце значения (но не в середине).

Операции над данными

В Excel можно обрабатывать как одну ячейку, так и выделенный диапазон. Для отмены неверных действий можно пользоваться кнопками панели быстрого доступа.

Удаление. При нажатии клавиши [Del] произойдет очистка содержимого ячейки. Реальное удаление ячейки сопровождается изменением структуры таблицы. По команде Удалить ячейки из группы Ячейки вкладки Главная откроется диалоговое окно Удаление ячеек, в котором нужно выбрать направление смещения ячеек, занимающих освобождающееся место. Аналогичное окно открывается и при выборе команды Удалить из контекстного меню ячейки. Для удаления строки (столбца) надо выделить какую-либо ячейку в удаляемой строке (столбце) и выполнить команду Удалить строки с листа (Удалить столбцы с листа) из группы Ячейки вкладки Главная. Удалить строку или столбец целиком можно также выделив строку или столбец щелчком мыши по маркеру строки или столбца и выбрав команду Удалить из контекстного меню.

Копирование или перемещение. Эти операции можно осуществить разными способами:

Навести указатель мыши на границу текущей ячейки (диапазона) и перетащить при нажатой левой кнопке мыши на новое место. В результате произойдет перемещение ячейки (диапазона). Если при перетаскивании удерживать нажатой клавишу [Ctrl], то произойдет копирование ячейки. При перетаскивании появляется серая рамка, которая помогает правильно разместить блок на новом месте.
Выделить ячейку (диапазон), перейти на вкладку Главная и выполнить команду Копировать или Вырезать из группы Буфер обмена, а затем щелкнуть в нужном месте и выполнить команду Вставить .
Выполнить специальное перетаскивание нужного блока ячеек (нажата правая кнопка мыши). При отпускании кнопки мыши будет выведено контекстное меню, содержащее перечень допустимых операций: копирование, перемещение, копирование только значений или только форматов, копирование или перемещение со сдвигом остальных ячеек в нужную сторону.

Вставка. Для вставки в таблицу столбца щелкнуть на заголовке столбца, перед которым будет вставлен новый столбец, чтобы выделить его. Затем выполнить команду Вставить из контекстного меню выделенного столбца. Аналогично можно вставить строку, ячейку или блок ячеек.

Если нужно скопировать только часть информации, можно воспользоваться специальной вставкой. Команда Вставить/Специальная вставка из группы Буфер обмена откроет диалоговое окно, в котором можно указать, какую часть информации следует вставить из Буфера обмена (например, только значения без формул, по которым они получены; только форматы или только примечания).

Для вставки в таблицу рисунков или видеоклипов следует выбрать соответствующие параметры из группы Иллюстрации вкладки Вставка. Простой рисунок можно сделать и самому, воспользовавшись параметрами Фигуры и SmartArtt из группы Иллюстрации. При добавлении фигуры на лист, открывается дополнительная вкладка Средства рисования, параметры которой позволяют изменить размеры и стиль фигуры, задать дополнительные эффекты, упорядочить, сгруппировать несколько фигур, добавить надписи и т. д.

Отформатировать ячейку (выделенный диапазон ячеек) и ее содержимое можно с помощью параметров групп Шрифт, Выравнивание, Число и Стили вкладки Главная. Щелчок мышью на кнопке с изображением стрелки рядом с названием группы открывает диалоговое окно Формат ячеек. На вкладке Число этого окна можно выбрать формат представления чисел и задать различные параметры, зависящие от выбранного формата; на вкладке Выравнивание установить способ вертикального и горизонтального выравнивания данных в ячейке, задать перенос по словам, объединение ячеек, автоподбор их ширины и т. д.; с помощью команд вкладки Шрифт задать гарнитуру шрифта и его параметров; на вкладках Граница и Вид задать способ обрамления ячейки, выбрать цвет фона и узор заполнения; с помощью команд вкладки Защита защитить ячейку паролем.

Типы и формат данных. Работа с формулами. Абсолютная и относительная ссылки. Использование функций

В работе с электронными таблицами выделяют три основных типа данных: числа, текст и формулы. В зависимости от решаемой задачи применяются различные форматы представления данных. Чтобы задать формат данных, нужно выбрать соответствующий параметр из группы Число вкладки Главная или щелчком мыши на кнопке с изображением стрелки рядом с названием группы открыть диалоговое окно Формат ячеек, в котором на вкладке Число выбрать желаемый формат представления данных и настроить его параметры.

Числа в Excel отображаются в таких категориях форматов, как Числовой, Экспоненциальный, Финансовый, Денежный, Процентный и Дробный. Если необходимо ввести числа без привязки к каким-либо форматам, можно использовать формат Общий. При использовании числового формата можно задавать количество десятичных знаков с помощью кнопок Формат с разделителями, Увеличить разрядность, Уменьшить разрядность группы Число. Перевести число в процентный формат позволяет кнопка, а в денежный — кнопка.

Формат Дата и время позволяет хранить значения временных данных в удобном и привычном виде, например: 16.4; 16 апр; 16 Апрель 2009; апрель 2009; 16.04.09 1:30 РМ; 16.04.09 13:30 и т. д.

Текстом в Excel считается любая последовательность, состоящая из цифр, пробелов и нецифровых символов.

Формула должна начинаться со знака равенства и может включать в себя числа, имена ячеек, функции и знаки математических операций («+» — сложение; «–» — вычитание; «» — умножение; «/» — деление, «^» — возведение в степень).

Чтобы в формуле сделать ссылку на ячейку, нужно указать ее имя вручную или просто щелкнуть по ней мышью. При этом ячейка обводится цветной рамкой. Если содержимое ячейки, участвующей в формуле, изменится, то и значение формулы изменится.

Существуют следующие типы ссылок на адреса ячеек: относительные, абсолютные и смешанные. Различия между ними проявляются при копировании формулы из активной ячейки в другую ячейку.

Относительная ссылка указывает на ячейку, основываясь на ее положении относительно ячейки, в которой находится формула, например: «на две строки выше». Абсолютная ссылка использует для указания на ячейку ее фиксированное положение на листе, например: «ячейка находится в столбце А строки 2». Смешанная ссылка содержит относительную и абсолютную ссылки, например: «ячейка находится в столбце А и выше на две строки». Относительная ссылка на ячейку А1 записывается так: = А1.

Абсолютная ссылка на ячейку А1 имеет следующий вид: = $A$1.

Комбинируя абсолютные и относительные ссылки на ячейку А1, можно создать следующие смешанные ссылки: = $A1 = A$1.

Если символ «доллар» стоит перед буквой, то координата столбца абсолютная, а строки — относительная. Если же символ «доллар» стоит перед числом, то координата столбца относительная, а строки — абсолютная. С помощью клавиши [F4] можно быстро изменить тип ссылки по схеме: A1 → $A$1→ A$1 → $A1 → A1.

При перемещении или копировании формулы из активной ячейки относительные ссылки автоматически настраиваются, а абсолютные сохраняются. Например, если в ячейку С2 ввести формулу = А2 * В2 + $A$1, а затем перетащить маркер заполнения до ячейки С6, то в ячейках С3—С6 относительные ссылки А1 и В1 будут заменяться на А3, В3, А4, В4 и т. д., а ссылка $A$1 не изменится.

Формулы с текстовыми значениями

В большинстве случаев работа с текстовыми значениями происходит так же, как с числами. Например, если ячейка А1 содержит текст ABCDE и в ячейку А10 введена формула = А1, то в ячейке А10 также будет выведено ABCDE.

Для объединения текстовых значений используется текстовый оператор &. Например, если ячейка А1 содержит текст ABCDE, а ячейка А2 — текст WQRT, и в ячейку А3 введена формула = А1 & A2, то в ячейке А3 будет выведено ABCDEWQRT. Чтобы вставить пробел между двумя строками, нужно изменить формулу на следующую: = А1&» «&A2 && . Эта формула использует два текстовых оператора и текстовую константу — в данном случае пробел, заключенный в двойные кавычки.

С помощью оператора & можно объединять и числовые значения. Например, если ячейка А1 содержит числовое значение 123 и в ячейке А2 записано число 456, значением формулы =А1&А2 будет строка символов 123456. Эта строка выравнивается по левому краю, т. к. она является текстовым значением.

Кроме того, можно использовать оператор & для объединения текстовых и числовых значений. Например, если ячейка А1 содержит текст ABCDE, а ячейка А2 содержит числовое значение 123, то значением формулы = А1&А2 будет строка ABCDE123.

Если Excel не может вычислить результат формулы, то в ячейку выводится ошибочное значение, например: #Дел/0!, #ИМЯ?, #ЗНАЧ! и др.

Примеры решения задач

Пример 1. В ячейке С1 записана формула = 3 * $B1. Формулу скопировали в ячейку Е2. Какой вид приобретет формула в ячейке Е2?

Решение. В формуле используется смешанная ссылка на ячейку $B1: ссылка на столбец абсолютная, т. е. при копировании столбец не изменится; ссылка на строку относительная, т. е. при копировании номер строки настроится. В исходной формуле в качестве второго сомножителя выступают данные ячейки из той же строки, в которой находится и формула (из 1-й). Значит, и в скопированной формуле данные будут браться из той же строки (2-й).

Ответ: в ячейке Е2 будет записана формула = 3 * $B2.

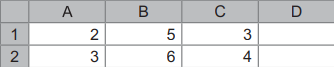
Пример 2. Дан фрагмент электронной таблицы:

В ячейку D2 введена формула А2 * В1 + $C$1. Какое значение появится в ячейке D2 после вычисления формулы?

Решение. Значение ячейки А2 — 3, В1 — 5, $C$1 — 3. Подставим значения в формулу: 3 · 5 + 3 = 18.

Ответ: 18.

Использование функций

Функция — это заранее определенная формула, которая оперирует с одним или несколькими значениями и возвращает одно или несколько значений.

Одно из самых распространенных действий — вычисление суммы значений в столбцах или строках. Excel предлагает функцию =СУММ (диапазон). Например, для суммирования значений в ячейках А1:А10 в ячейку А11 нужно ввести функцию =СУММ (А1:А10). Для облегчения доступа к этой функции в группе Редактирование вкладки Главная есть кнопка Сумма. Чтобы просуммировать значения в столбце (строке) надо выделить ячейку ниже суммируемых чисел (справа) и нажать кнопку Сумма.

Функция состоит из двух частей:

имя (СУММ, AVERAGE и др.) — описывает операцию, которую выполняет функция;
аргументы — задают значения или ячейки, используемые функцией.

Например, СУММ (А1:А6). Здесь СУММ — имя, а диапазон М А1:А6 — ее единственный аргумент.

Между именем функции и ее аргументами не должно быть пробелов. Некоторые функции не имеют аргументов, но круглые скобки все равно нужно ставить. Например: =А1 ПИ().

При использовании в функции нескольких аргументов нужно отделять их друг от друга « ; ». Например: функция =ПРОИЗВ(С1;С2;С5) перемножает числа в ячейках С1, С2 и С5.

В функции можно использовать до 30 аргументов, если при этом общая длина формулы не превосходит 1024 символа. Однако любой аргумент может быть диапазоном, содержащим произвольное число ячеек листа. Например, функция =СУММ (А1:А5; С2:С10; D3:D17) содержит всего три аргумента, но суммирует 29 ячеек. Указанные в ссылке ячейки в свою очередь могут содержать формулы, которые ссылаются на другие ячейки и диапазоны. Используя аргументы, можно легко создавать длинные цепочки формул для выполнения сложных операций.

Аргументы функций могут представлять собой выражения из комбинаций функций. Например: =СУММ (SIN (A1ПИ ( ) ); 2 * COS (A2ПИ ( ) ) ). Здесь функции SIN, COS и ПИ сначала вычисляются, а затем используются в качестве аргументов функции СУММ.

Функцию можно вводить на рабочий лист прямо с клавиатуры. Но удобнее воспользоваться командой Вставить функцию из группы Библиотека функций вкладки Формулы. Excel выведет окно диалога Мастер функций — шаг 1 из 2. В этом окне сначала надо выбрать категорию в одноименном списке, а затем в алфавитном списке Выберите функцию указать нужную функцию и нажать кнопку ОК. Excel выведет в ячейке и в строке формул знак равенства, имя функции и пару круглых скобок, а затем откроет второе окно диалога мастера функций. В нем содержатся поля для ввода аргументов выбранной функции. Если функция имеет переменное число аргументов, то это окно диалога увеличивается при вводе дополнительных аргументов. Справа от каждого поля аргумента отображается его текущее значение. После ввода всех аргументов надо нажать кнопку ОКК — и созданная функция появится в строке формул.

Также окно мастера функций можно вызвать щелчком на кнопке Вставить функцию в строке формул. Кроме того, если ввести знак равенства в ячейку, то поле Имя в строке формул заменится раскрывающимся списком, в котором перечислены 10 функций, использовавшихся последними, и пункт Другие функции, щелчок на котором откроет окно мастера функций. Еще один способ вызова мастера функций — в группе Редактирование вкладки Главная раскрыть список опций параметра Сумма и выбрать пункт Другие функции.

Всего в Excel более 300 встроенных функций. Вот некоторые из них.

Математические функции:

= СУММ (числа) — функция суммирует множество чисел.

= ABS (число) — возвращает абсолютное значение числа или формулы.

= ОКРУГЛ (число; количество_цифр) — округляет число, задаваемое ее аргументом, до указанного количества десятичных разрядов.

= КОРЕНЬ (число) — возвращает положительный квадратный корень из числа. Аргумент должен быть положительным числом.

= ПРОИЗВЕД (число1; число2;…) — перемножает все числа, задаваемые ее аргументами.

= LOG (число; основание) — возвращает логарифм положительного числа по заданному основанию. Если аргумент основание не задан, то Excel примет его равным 10.

= СТЕПЕНЬ (число; степень) — возводит число в заданную степень. Эта функция является эквивалентом оператора ^. Например, формулы =СТЕПЕНЬ(3;2) и =3^2 равносильны.

= SIN (число), = COS (число), = TAN (число) — возвращают синус, косинус, тангенс угла. Число — это угол в радианах.

Текстовые функции:

= ЗНАЧЕН (текст) — преобразование текста в число. Текст — это числа или даты, введенные в текстовом формате, т. е. заключенные в кавычки.

= ДЛСТР (текст) — возвращает количество символов в текстовой строке.

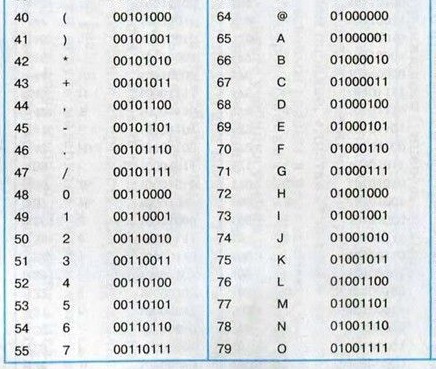
= СИМВОЛ (число) — возвращает символ, который соответствует заданному числовому коду ASCII.

= КОДСИМВ (текст) — возвращает код ASCII для первого символа аргумента.

Логические функции:

= ЕСЛИ (логическое_выражение; значение_если_истина; значение_если_ложь). В качестве аргументов этой функции можно использовать другие функции.

= И (логическое_значение1; логическое_значение2; …; логическое_значение30). Принимает значение ИСТИНА тогда и только тогда, когда все аргументы имеют значение ИСТИНА.

= ИЛИ(логическое_значение1; логическое_значение2; …; логическое_значение30). Принимает значение ИСТИНА, если хотя бы один аргумент имеет значение ИСТИНА.

= НЕ (логическое_значение). Принимает значение ИСТИНА, если аргумент имеет значение ЛОЖЬ, и наоборот.

Функции даты и времени:

= ДАТА (год; месяц; день) — возвращает десятичное значение даты, которое представляет собой количество дней между базовой и заданной датой.

= СЕГОДНЯ () — возвращает десятичное значение текущей даты.

= ВРЕМЯ (часы; минуты; секунды) — возвращает десятичное значение, которое представляет собой долю суток между полуночью и заданным временем. Аргумент секунды является необязательным: его можно опустить, но точку с запятой после аргумента минуты все равно надо поставить.

Статистические функции:

= СРЗНАЧ (число1; число2;…) — вычисляет среднее арифметическое значение. Функция игнорирует пустые, логические и текстовые ячейки.

= МАКС (число1; число2;…), = МИН (число1; число2;…) — возвращают наибольшее и наименьшее значения из набора данных.

= СУММЕСЛИ (диапазон; критерий; диапазон_суммирования) — каждая ячейка диапазона проверяется на соответствие критерию, прежде чем прибавляется к итогу.

= СЧЕТЕСЛИ (диапазон; критерий) — вычисляется количество ячеек, которые удовлетворяют заданному критерию.

Источник

На уроке рассматривается разбор 15 задания ЕГЭ по информатике, дается подробное объяснение того, как решать подобные задачи

Содержание:

Объяснение задания 15 ЕГЭ по информатике
- Элементы математической логики
- Математическая логика и теория множеств
- Задания с отрезками и ДЕЛ
- Задания с поразрядной конъюнкцией
Решение заданий 15 ЕГЭ по информатике
- Задания с множествами
- Задания с отрезками на числовой прямой
- Задания с ДЕЛ
- Задания с поразрядной конъюнкцией
- Задания на поиск наибольшего или наименьшего числа А

15-е задание: «Основные законы алгебры логики»

Уровень сложности

— повышенный,

Требуется использование специализированного программного обеспечения

— нет,

Максимальный балл

— 1,

Примерное время выполнения

— 5 минут.

Проверяемые элементы содержания: Знание основных понятий и законов математической логики

До ЕГЭ 2021 года — это было задание № 18 ЕГЭ

Типичные ошибки и рекомендации по их предотвращению:

«Важно понимать, что выражение должно быть тождественно истинно, т.е. истинно при любых допустимых значениях переменных x и у, а не только при некоторых наборах значений»

ФГБНУ «Федеральный институт педагогических измерений»

Элементы математической логики

Для выполнения задания рекомендуется повторить следующие темы:

Преобразование логических операций:

операцию импликация можно преобразовать в операции ИЛИ и НЕ:

A → B = ¬ A ∨ B
или
A → B = A + B

операцию эквивалентность можно преобразовать:

A ↔ B = A ⊕ B = A ∧ B ∨ A ∧ B
или
A ↔ B = A ⊕ B = A · B + A · B

операцию XOR (сложение по модулю 2) можно преобразовать так:

A ⊕ B = (¬A ∧ B) ∨ (A ∧ ¬B)
или
A ⊕ B = (A · B) + (A · B)

Законы алгебры логики:

кроме того, могут пригодиться базовые аксиомы и формулы:

Закон двойного отрицания:	¬¬ A = A
Закон исключения третьего:	A ∧ ¬ A = 0 или A · A = 0 A ∨ ¬ A = 1 или A + A = 1
Закон повторения (идемпотентности):	A ∧ A = A или A · A = A A ∨ A = A или A + A = A
Законы исключения логических констант:	A ∧ 0 = 0 A ∧ 1 = A A ∨ 0 = A A ∨ 1 = 1
Переместительный (коммутативный) закон:	A ∧ B = B ∧ A A ∨ B = B ∨ A
Сочетательный (ассоциативный) закон:	(A ∧ B) ∧ C = A ∧ (B ∧ C) (A ∨ B) ∨ С = A ∨ (B ∨ С)
Распределительный (дистрибутивный) закон:	(A ∧ B) ∨ C = (A ∨ C) ∧ (B ∨ C) (A ∨ B) ∧ С = (A ∧ С) ∨ (B ∧ С) и наоборот: (A ∨ B) ∧ (A ∨ C) = A ∨ (B ∧ C) (A ∧ B) ∨ (A ∧ C) = A ∧ (B ∨ C)
Закон общей инверсии (Законы де Моргана):	¬ (A ∧ B) = ¬ A ∨ ¬ B ¬ (A ∨ B) = ¬ A ∧ ¬ B
Закон исключения (склеивания):	(A ∧ B) ∨(¬A ∧ B) = B (A ∨ B) ∧(¬A ∨ B) = B
Упрощать выражения можно с помощью формул:
Закон поглощения:	A ∨ A ∧ B = A A ∧ (A ∨ B) = A A ∨ ¬A ∧ B = A ∨ B ¬A ∨ A ∧ B = ¬A ∨ B A ∧ (¬A ∨ B) = A ∧ B ¬A ∧ (A ∨ B) = ¬A ∧ B

Порядок выполнения логических операций:

выражения в скобках,
операции «НЕ»,
операции «И»,
операции «ИЛИ»,
операции «импликация»
операции «эквиваленция»

последовательность из операций импликации выполняется слева направо (при этом соблюдается принцип «операции с одинаковым приоритетом выполняются слева направо»):

A → B → C → D = ((A → B) → C) → D

Математическая логика и теория множеств

пересечение множеств соответствует логическому умножению, а объединение – логическому сложению;
пересечением двух множеств называется новое множество, состоящее из элементов, принадлежащих одновременно обеим множествам:

Пример:

объединением двух множеств называется новое множество, состоящее из элементов, принадлежащих отдельно каждому из множеств (без повторений);

Пример:

пустое множество ∅ – это множество, в котором не содержится ни одного элемента; пустому множеству в теории множеств соответствует 0;
универсальное множество U (на кругах Эйлера обозначается в виде прямоугольника) – это множество, содержащее все возможные элементы определенного типа (например, все вещественные числа):

универсальное множество соответствует логической единице: для любого множества целых чисел X справедливы равенства:

X ∨ U = U и X ∧ U = X

разностью двух множеств A и B называется новое множество, элементы которого принадлежат A, но не принадлежат B:

Пример разности множеств:

дополнение множества X – это разность между универсальным множеством U и множеством X (например, для целых чисел ¬ X – все целые числа, не входящие в X)

пусть требуется выбрать множество A так, чтобы выполнялось равенство A ∨ X = I; в этом случае множество A должно включать дополнение ¬ X, то есть A ≥¬ X (или A ⊇¬ X), то есть A_min = ¬ X
пусть требуется выбрать множество A так, чтобы выполнялось равенство ¬ A ∨ X = I, в этом случае множество ¬ A должно включать дополнение ¬ X, то есть ¬ A ⊇ ¬ X; отсюда A ⊆ X, то есть A_max = X

Для большей определенности стоит рассмотреть тему круги Эйлера

Задания с отрезками и ДЕЛ

Для решения заданий необходимо знать рассмотренную тему о множествах.

Для упрощения решений можно пользоваться следующими законами.

1. Если в задании формула тождественно истинна (равна 1), и
2. после упрощения A без отрицания
то используется закон:

A_min = ¬B

где B — известная часть выражения.

1. Если в задании формула тождественно истинна (равна 1), и
2. после упрощения A с отрицанием
то используется закон:

A_max = B

где B — известная часть выражения.

1. Если в задании формула тождественно ложна (равна 0), и
2. после упрощения A без отрицания
то используется закон:

A_max = ¬B

где B — известная часть выражения.

1. Если в задании формула тождественно ложна (равна 0), и
2. после упрощения A с отрицанием
то используется закон:

A_min = B

где B — известная часть выражения.

Задания с поразрядной конъюнкцией

В задании 15 ЕГЭ встречаются задачи, связанные с поразрядной конъюнкцией.
Например:

5 & 26

означает поразрядную конъюнкцию (логическое «И») между двоичными значениями двух чисел — 5 и 26. Выполняется так:

5  =   101₂ 
26 = 11010₂
0  = 00000₂

Задания, связанные с поразрядной конъюнкцией, решаются несколькими способами. Рассмотрим один из них.

Обозначим:

(x & K = 0) как Z_k

Для решения методом, предложенным А.В. Здвижковой, пригодится использование следующих свойств:

Z_k * Z_m = Z_{k or m}

Так, например, если в задании имеем:

(X & 5 = 0) ∧ (X & 26 = 0)

то сначала введем замену:

Z₅ ∧ Z₂₆

а затем, используя свойство 1, вычислим поразрядную дизъюнкцию двоичного значения чисел 26 и 5:

Z₅ ∧ Z₂₆ = Z_{26 or 5}
помним, что дизъюнкция - это операция логическое "ИЛИ" (сложение)
5  =   101₂ 
26 = 11010₂
31 = 11111₂

таким образом, получили:

Z₅ ∧ Z₂₆ = Z₃₁

Z_k + Z_m = Z_{k and m}

Так, например, если в задании имеем:

(X & 28 = 0) ∨ (X & 22 = 0)

то сначала введем замену:

Z₂₈ ∨ Z₂₂

а затем, используя свойство 2, вычислим поразрядную конъюнкцию двоичного значения чисел 28 и 22:

Z₂₈ ∨ Z₂₂ = Z_{28 and 22}
помним, что конъюнкция - это операция логическое "И" (умножение)
28 = 11100₂ 
22 = 10110₂
     10100₂ = 20₁₀

таким образом, получили:

Z₂₈ ∨ Z₂₂ = Z₂₀

Условие Z_k → Z_m истинно для любых натуральных значений x тогда и только тогда, когда все единичные биты двоичной записи числа M входят во множество единичных битов двоичной записи числа K.

На деле, это означает, что если имеем:

X & 29 = 0 → X & 5 = 0  Истинно или Ложно?

то сначала введем замену:

Z₂₉ → Z₅

а затем, используя свойство 3, определим истинность высказывания Z₂₉ → Z₅:

Z₂₉ → Z₅ = 1 (истине), тогда, когда:
29 = 11101₂
5  =   101₂  
единичные биты двоичного числа 5 входят в единичные биты двоичного числа 29 
(совпадают с ними)

таким образом, получили:

Z₂₉ → Z₅ = 1 (истинно)

(x & 125 = 5) то же самое, что и
Z₁₂₀ * ¬Z₄ * ¬Z₁ = 1 (истине)

Так, например, если в задании имеем:

X & 130 = 3

то сначала введем замену и, используя свойство 4, получим:

X & 130 = 3 то же самое, что и
Z₁₂₇ * ¬Z₂ * ¬Z₁

т.е. 3 = 2 + 1 :	

2 = 10
1 = 01
3 = 11

Решение заданий 15 ЕГЭ по информатике

Плейлист видеоразборов задания на YouTube:

Задание демонстрационного варианта 2022 года ФИПИ

Задания с множествами

Множества:

15_16:

Элементами множества А являются натуральные числа. Известно, что выражение

((x ∈ {1, 3, 5, 7, 9, 11}) → ¬(x ∈ {3, 6, 9, 12})) ∨ (x ∈ A)

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное значение суммы элементов множества A.

✍ Решение:

Введем обозначения:

P ≡ (x ∈ {1, 3, 5, 7, 9, 11}) ; 
Q ≡ (x ∈ {3, 6, 9, 12}) ; 
A ≡ (x ∈ A).

Выполним преобразования:

(P → ¬Q) ∨ A = 1
Избавимся от импликации:
¬P ∨ ¬Q ∨ A = 1

Разделим выражение на две части — известную часть и неизвестную. Чтобы неизвестная часть (А) была непременно истинной, необходимо, чтобы известная часть была ложна:

¬P ∨ ¬Q ∨ А = 1
    ⁰      ¹

То есть получаем:

¬P ∨ ¬Q = 0,
или 
¬P = 0  отсюда P = 1
¬Q = 0 отсюда Q = 1

Таким образом имеем пересечение (умножение) двух множеств Q и P. То есть необходимо выбрать элементы, которые встречаются в обоих множествах одновременно:

A = {3,9}

Сумма элементов:

3 + 9 = 12

Ответ: 12

Аналитическое решение:
📹 YouTube здесь

📹 Видеорешение на RuTube здесь

Множества:

15_17:

Элементами множества А являются натуральные числа. Известно, что выражение

(x ∈ {2, 4, 6, 8, 10, 12}) → (((x ∈ {3, 6, 9, 12, 15}) ∧ ¬(x ∈ A)) → 
→ ¬(x ∈ {2, 4, 6, 8, 10, 12}))

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное значение суммы элементов множества A.

Типовые задания для тренировки

✍ Решение:

Введем обозначения:

P≡(x ∈ {2, 4, 6, 8, 10, 12}) ; 
Q ≡ (x ∈ {3, 6, 9, 12, 15}) ; 
A ≡ (x ∈ A).

Выполним преобразования:

P → ((Q ∧ ¬A) → ¬P) = 
P → (¬(Q ∧ ¬А) ∨ ¬P) = 
¬P ∨ (¬(Q ∧ ¬А) ∨ ¬P) = 
¬P ∨ ¬Q ∨ А.

Разделим выражение на две части — известную часть и неизвестную. Чтобы неизвестная часть (А) была непременно истинной, необходимо, чтобы известная часть была ложна:

¬P ∨ ¬Q ∨ А = 1
    ⁰      ¹

То есть получаем:

¬P ∨ ¬Q = 0,
или 
¬P = 0  отсюда P = 1
¬Q = 0 отсюда Q = 1

Таким образом имеем пересечение (умножение) двух множеств Q и P. То есть необходимо выбрать элементы, которые встречаются в обоих множествах одновременно:

A = {6,12}

Сумма элементов:

6 + 12 = 18

Ответ: 18

Множества:

15_18: Закон распределения

Элементами множеств А, P, Q являются натуральные числа, причём P = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}, Q = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}. Известно, что выражение

( (x ∈ A) → (x ∈ P) ) ∧ ( (x ∈ Q) → ¬(x ∈ A) )

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наибольшее возможное количество элементов в множестве A.

Типовые задания для тренировки

✍ Решение:

Введем обозначения:

P ≡ (x ∈ P); 
Q ≡ (x ∈ Q); 
A ≡ (x ∈ A).

Выполним преобразования:

Избавимся от импликации:
(¬A ∨ P) ∧ (¬Q ∨ ¬A) = 1
Применим распределительный закон (но можно вывести самостоятельно):
¬A ∨ (P ∧ ¬Q) = 1

Разделим выражение на две части — известную часть и неизвестную. Чтобы неизвестная часть (А) была непременно истинной, необходимо, чтобы известная часть была ложна:

¬A ∨ (P ∧ ¬Q) = 1
 ⁰      ¹

То есть получаем:

P ∧ ¬Q = 1,
или 
P = 1  и
¬Q = 1 отсюда Q = 0

Таким образом имеем разность двух множеств Q и P. То есть это новое множество, элементы которого принадлежат P, но не принадлежат Q:

A = {2, 4, 8, 10, 14, 16, 20}

Количество элементов = 7

Ответ: 7

Множества:

15_20:

Элементами множества А являются натуральные числа. Известно, что выражение

¬(x ∈ A) →¬(x ∈ {1, 3, 7}) ∨ (¬(x  ∈ {1, 2, 4, 5, 6}) ∧ (x ∈ {1, 3, 7}))

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное количество элементов множества A.

✍ Решение:

Введем обозначения:

P ≡ (x ∈ {1, 3, 7}); 
Q ≡ (x  ∈ {1, 2, 4, 5, 6}); 
A ≡ (x ∈ A).

Выполним преобразования:

Избавимся от импликации:
A ∨ ¬P ∨ (¬Q ∧ P) = 1
Применим закон поглощения (но можно вывести самостоятельно):
A ∨ ¬P ∨ ¬Q = 1

Разделим выражение на две части — известную часть и неизвестную. Чтобы неизвестная часть (А) была непременно истинной, необходимо, чтобы известная часть была ложна:

A ∨ ¬P ∨ ¬Q = 1
 ¹      ⁰

То есть получаем:

¬P ∨ ¬Q = 0,
или 
P = 1 и Q = 1

Таким образом имеем пересечение двух множеств Q и P:

A = {1}

Количество элементов = 1

Ответ: 1

Задания с отрезками на числовой прямой

Отрезки на числовой прямой:

15_3:

На числовой прямой даны два отрезка: P=[44,48] и Q=[23,35].

Укажите наибольшую возможную длину отрезка А, для которого формула

((x ϵ P) → (x ϵ Q)) ∧ (x ϵ A)

тождественно ложна, то есть принимает значение 0 при любом значении переменной x.

✍ Решение:

Упростим формулу, избавившись от ‘x ϵ‘:

(P → Q) ∧ A

Теперь преобразуем импликацию в скобках:

правило импликации: a → b = ¬a ∨ b

(¬P ∨ Q) ∧ A

Указанные в задании отрезки отобразим на числовой прямой. Разделим отрезки на части по точкам, соответствующим их границам.

Вернемся к преобразованному выражению. В нем есть известная часть (выделим ее) и неизвестная. По условию выражение должно быть ложно:

(¬P ∨ Q) ∧ A = 0

Внешняя операция выражения — конъюнкция — ложна в трех случаях и только в одном — истинна:

(¬P ∨ Q) ∧ A
    ⁰     ^∧ ⁰ ⁼ ⁰
    ⁰     ^∧ ¹ ⁼ ⁰
    ¹     ^∧ ⁰ ⁼ ⁰
    ¹     ^∧ ¹ ⁼ ¹

Теперь рассмотрим это выражение относительно наших отрезков на числовой прямой: если известная часть выражения (¬P ∨ Q) на каком-либо отрезке прямой дает истину, то неизвестная часть (A) должна возвращать ложь (по условию формула должна быть тождественно ложна).
Рассмотрим все отрезки числовой прямой для известной части выражения:

1. (¬P ∨ Q) = 1 ∨ 0 = 1  - на данном отрезке А должно равняться 0
2. (¬P ∨ Q) = 1 ∨ 1 = 1  - на данном отрезке А должно равняться 0
3. (¬P ∨ Q) = 1 ∨ 0 = 1  - на данном отрезке А должно равняться 0
4. (¬P ∨ Q) = 0 ∨ 0 = 0  - на данном отрезке А может! равняться 1
5. (¬P ∨ Q) = 1 ∨ 0 = 1  - на данном отрезке А должно равняться 0

Получаем, что на всех отрезках кроме 4-го выражение ¬P ∨ Q истинно, т.е. на отрезках 1, 2, 3 и 5 неизвестная часть A должна быть ложной (чтобы формула вернула ложь). Отсюда следует, что А может быть истинно только на отрезке 4.
Длина отрезка 4 составляет:

48 - 44 = 4

Результат: 4
✎ Решение 2 (программирование):
Внимание! этот способ подходит НЕ для всех заданий с отрезками!
Python:

def f(a1,a2,x):
    return((44<=x<=48)<=(23<=x<=35))and(a1<=x<=a2)
maxim = 0
for a1 in range (1,200):
    for a2 in range (a1+1,200):
        if all(f(a1,a2,x)==0 for x in range (1,200)):# если все ложны
            if a2-a1>maxim:
                maxim=a2-a1
                print(a1,a2, a2-a1) # сами точки отрезка и длина

Вывод:

PascalABC.net:

Вывод:

С подробным аналитическим решением задания 15 ЕГЭ по информатике можно ознакомиться по видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Отрезки на числовой прямой:

15_9:

На числовой прямой даны два отрезка: P = [10,20] и Q = [30,40].

Укажите наибольшую возможную длину отрезка A, для которого формула

((x ∈ P) → (x ∈ Q))  → ¬(x ∈ A)

тождественно истинна, то есть принимает значение 1 при любом значении переменной x.

Типовые задания для тренировки

✍ Решение:

Упростим выражение, введя обозначения:

A: x ∈ A
P: x ∈ P
Q: x ∈ Q

Запишем формулу с новыми обозначениями, учитывая, что по условию она должна быть тождественно истинной:

(P → Q) → ¬A = 1

Избавимся от импликации:

(P → Q) → ¬A = 1        =>
¬(P → Q) ∨ ¬A = 1       =>
¬(¬P ∨ Q) ∨ ¬A = 1

Используем закон Де Моргана для последующего преобразования:

¬(¬P ∨ Q) ∨ ¬A = 1    =>
P ∧ ¬Q ∨ ¬A = 1

А — наше неизвестное, а выделенную часть формулы можно найти. Необходимо, чтобы А = 1. Значит, предположим, что ¬А = 0, тогда P ∧ ¬Q = 1 (если P ∧ ¬Q = 0, то ¬А может равняться и 0 и 1, так как имеет место операция логического сложения ∨)
Значит, имеем P ∧ ¬Q = 1. Кроме того, в данном случае имеет место операция конъюнкция, которую проще вычислить, если выражение равно 1 (так как для конъюнкции существует один единственный случай истинности: 1 & 1 = 1). Таким образом имеем утверждения:

А = 1
P = 1
¬Q = 1 или Q = 0

Т.е. A истинно (=1) на промежутке пересечения отрезков P и ¬Q.
Отобразим отрезки на числовой прямой, чтобы найти искомое значение:

Очевидно, что А будет истинно, только в части 2 (на рис. желтым цветом), то есть соответствовать отрезку [10,20], имеющему длину 10.

Результат: 10

Отрезки на числовой прямой:

15_10:

На числовой прямой даны два отрезка: P = [3, 20] и Q = [6, 12].

Укажите наибольшую возможную длину отрезка A, для которого формула

((x ∈ P) ~ (x ∈ Q))  → ¬(x ∈ A)

тождественно истинна, то есть принимает значение 1 при любом значении переменной x.

✍ Решение:

Упростим выражение, введя обозначения:

A: x ∈ A
P: x ∈ P
Q: x ∈ Q

Запишем формулу с новыми обозначениями, учитывая, что по условию она должна быть тождественно истинной:

(P ~ Q) → ¬A = 1

Избавимся от импликации:

(P ~ Q) → ¬A = 1      =>
¬(P ~ Q) ∨ ¬A = 1

Далее возможно 2 способа решения.

✎ 1 способ:

Избавимся от эквивалентности по правилу преобразования эквивалентности:

(a ~ b) = a * b + ¬a * ¬b

¬(P ~ Q) = ¬((P ∧ Q) ∨ (¬P ∧ ¬Q)) =
= ¬(P ∧ Q) ∧ ¬(¬P ∧ ¬Q)

Преобразуем часть данного выражения по закону Де Моргана:

¬(P ∧ Q) ∧ ¬(¬P ∧ ¬Q) =
= ¬(P ∧ Q) ∧ (P ∨ Q)

В итоге получим:

¬(P ∧ Q) ∧ (P ∨ Q) ∨ ¬A = 1

А — наше неизвестное, а выделенную часть выражения можно найти. Необходимо, чтобы А = 1. Значит, предположим, что ¬А = 0, тогда, чтобы общее выражение было истинным (по условию), нужно чтобы ¬(P ∧ Q) ∧ (P ∨ Q) = 1.
Имеем:

¬(P ∧ Q) ∧ (P ∨ Q) = 1
А = 1

Отобразим отрезки на числовой прямой, чтобы найти искомое значение:

Очевидно, что А будет истинно в двух отмеченных на рисунке частях: 2 и 4 (на рис. желтым цветом). Но по условию нам необходимо найти А наибольшей длины, соответственно, выбираем отрезок [12,20], имеющий длину 8.

✎ 2 способ:
После того, как мы избавились от импликации, имеем:

¬(P ~ Q) ∨ ¬A = 1

А — наше неизвестное, а выделенную часть выражения можно найти. Необходимо, чтобы А = 1. Значит, предположим, что ¬А = 0, тогда ¬(P ~ Q) = 1 (чтобы общее выражение было истинным, как указанно в условии).
Иными словами ¬(P ~ Q) истинно для всех значений x, при которых P не равно Q (т.е. либо P = 1 и Q = 0, либо P = 0 и Q = 1).
Это соответствует двум отрезкам (см. рисунок выше, желтым цветом): [3,6] и [12,20]. Но по условию нам необходимо найти А наибольшей длины, соответственно выбираем отрезок [12,20], имеющий длину 8.

Результат: 8

С решением задания 15 вы также можете ознакомиться, посмотрев видео (аналитическое решение):

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Отрезки на числовой прямой:

15_11:

На числовой прямой даны два отрезка: P = [11, 21] и Q = [15, 40].

Укажите наибольшую возможную длину отрезка A, для которого формула

(x ∈ A) → ¬((x ∈ P)  ~ (x ∈ Q))

тождественно истинна, то есть принимает значение 1 при любом значении переменной x.

Типовые задания для тренировки

✍ Решение:

Упростим выражение, введя обозначения:

A: x ∈ A
P: x ∈ P
Q: x ∈ Q

Запишем формулу с новыми обозначениями, учитывая, что по условию она должна быть тождественно истинной:

A → ¬(P ~ Q) = 1

Избавимся от импликации:

A → ¬(P ~ Q) = 1    =>
¬A ∨ ¬(P ~ Q) = 1

А — наше неизвестное, тогда как выделенную часть формулы можно найти. Введем предположение, что А = 1. Значит, ¬А = 0 (т.е. А = 1), тогда ¬(P ~ Q) = 1 (так как общая формула должна быть истинной по условию).
Иными словами ¬(P ~ Q) истинно для всех значений x, при которых P не равно Q (т.е. либо P = 1 и Q = 0, либо P = 0 и Q = 1).
Отобразим отрезки на числовой прямой, чтобы найти искомое значение:

Получаем, что А соответствует двум отрезкам (см. рисунок, желтым цветом): [11,15] и [21,40]. Но по условию нам необходимо найти А наибольшей длины, соответственно выбираем отрезок [21,40], имеющий длину 19.

Результат: 19

Задания с ДЕЛ

Поиск наибольшего А, известная часть Дел ∨ Дел = 1

15_7:

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».

Для какого наибольшего натурального числа А формула

  (ДЕЛ(x, 40) ∨ ДЕЛ(x, 64))  → ДЕЛ(x, A)

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

Типовые задания для тренировки

✍ Решение:

✎ Решение 1 (теоретическое):

Введем обозначения:

A = ДЕЛ(x,A); 
D40 = ДЕЛ(x, 40); 
D64 = ДЕЛ(x, 64)

Перепишем исходную формулу, согласно введенным обозначениям. Укажем, что формула должна быть тождественно истинна (по условию):

(D40 ∨ D64)  → A = 1

Избавимся от импликации:

¬(D40 ∨ D64) ∨ A = 1
или
(¬D40 ∧ ¬D64) ∨ A = 1

Разделим данную формулу на две части: в одной из них — искомое A, а в другой — часть формулы с x, которую можно найти:

(¬D40 ∧ ¬D64) ∨ A = 1
      ¹          ²

В полученной формуле необходимо, чтобы искомая часть с A в конечном счете было истинно.
Т.е. (¬D40 ∧ ¬D64) должно быть = 0. Это нам ничего не дает, т.к. конъюнкция ложна в трех случаях (1*0, 0*1 и 0*0), т.е. D40 и D64 могут быть равны как 0, так и 1 (исключение составляет лишь вариант, когда оба D истинны, тогда логическое умножение 1 * 1 ≠ 0).
Преобразуем выражение первой части формулы по закону Де Моргана (чтобы оно равнялось 1):

¬D40 ∧ ¬D64 = 0
или
¬(¬D40 ∧ ¬D64) = 1

Преобразуем по закону Де Моргана и получим:
D40 ∨ D64 = 1

Далее можно решать задание либо с помощью кругов Эйлера, либо с помощью логических рассуждений.

Решение с помощью логических рассуждений:

Найдем все такие x, которые делятся на А и при этом делятся на 40 ИЛИ делятся на 64:

x/A : x/40 ∨ x/64

x = 40, 64, 80, 120, 128, 160, 192, 200, ...

Теперь найдем такие A, начиная с самого наименьшего (единицы), на которые делятся все x без исключения:

А = 1, 2, 4, 8

Наибольшее А равно 8.
Или то же самое можно найти поиском наибольшего общего делителя чисел 40 и 64 (используем формулу Евклида):

НОД (40,64) = 8 
40,64  (64 - 40 = 24)
40,24  (40 - 24 = 16)
24,16  (24 - 16 = 8)
16,8   (16 - 8 = 8)
8,8

Решение с помощью кругов Эйлера:

В этом случае логическое сложение тоже дает истину в трех случаях (1+1, 1+0, 0+1). Т.е. мы не сможем найти А с помощью функции ДЕЛ. Необходимо прибегнуть к решению с помощью кругов Эйлера.
В множество A должны входить все числа, которые попадают в объединение D40 + D64. Таким образом, нужно найти множество, в которое входят оба этих множества.
Найдем наибольший общий делитель чисел 40 и 64; это число 8:

64 / 40 = 1 (24 остаток)
40 / 24 = 1 (16 остаток)
24 / 16 = 1 (8 остаток)
16 / 8 = 2 (0 остаток) - НОД = 8
+++
40 / 8 = 5
64 / 8 = 8

Т.е. можно сказать, что A = D40 + D64 = D8*D5 + D8*D8 = D8*(D5 + D8). D8 входит в каждое из множеств D40 и D64. Объединение D40 + D64 тоже входит в D8:

8 — наибольший общий делитель числе 40 и 64, значит, оно соответствует максимальному значению A.

Результат: 8

✎ Решение 2 (программирование):
Python:

for A in range(1,500):
    OK = 1
    for x in range(1,1000):
        OK *= ((x % 40 == 0) or (x % 64 == 0))<=(x % A== 0)
    if OK:
        print( A )

Вывод:

PascalABC.net:

begin
  for var A := 1 to 500 do
  begin
    var ok := 1;
    for var x := 1 to 1000 do
    begin
      if (((x mod 40 = 0) or (x mod 64 = 0)) <= (x mod A = 0)) = false then
      begin
        ok := 0; 
        break;
      end;
    end;
    if (ok = 1) then print(A)
  end;
end.

Вывод:

Результат: 8

Поиск наименьшего А, известная часть Дел ∧ ¬Дел = 1

15_5:

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».

Для какого наименьшего натурального числа А формула

ДЕЛ(x, A) → (¬ДЕЛ(x, 28) ∨ ДЕЛ(x, 42))

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

Типовые задания для тренировки

✍ Решение:

✎ Решение 1 (теоретическое):

Имеем:

ДЕЛ(x, A) → (¬ДЕЛ(x, 28) ∨ ДЕЛ(x, 42)) = 1

Введем обозначения:

A = ДЕЛ(x,A); 
D28 = ДЕЛ(x, 28); 
D42 = ДЕЛ(x, 42)

Перепишем исходную формулу, согласно введенным обозначениям. Укажем, что формула должна быть тождественно истинна (по условию):

A → (¬D28 ∨ D42) = 1

Избавимся от импликации:

¬A ∨ (¬D28 ∨ D42) = 1

Разделим данную формулу на две части: в одной из них — искомое A, а в другой — часть формулы с x, которую можно найти:

¬A ∨ (¬D28 ∨ D42) = 1
 ¹        ²

В части 2 полученной формулы находится операция дизъюнкция, которую проще найти, когда логическое выражение равно 0 (только один случай: 0 ∨ 0 = 0):

(¬D28 ∨ D42) = 0   один случай: когда ¬D28 = 0 и D42 = 0

Т.е. имеем:

x/¬A : x/28 ∧ x/¬42

Иными словами найдем все такие x, которые НЕ делятся на А и при этом делятся на 28 И НЕ делятся на 42:

x = 28, 56, 84, 112, 140, 168, 196, 224, ...

Теперь найдем такие A, начиная с самого наименьшего (единицы), на которые НЕ делятся все x без исключения:

А = 1, 2, 3

Наименьшее А равно 3.

✎ Решение 2 (программирование). Язык Python, Pascal:

ДЕЛ(x, A) → (¬ДЕЛ(x, 28) ∨ ДЕЛ(x, 42)) = 1

Можно сделать вывод, что для некоторого диапазона натуральных значений А, необходимо рассмотреть диапазон натуральных значений x. Если выражение будет истинным для диапазона всех рассматриваемых х, то такое А необходимо вывести на экран.
То есть следует рассмотреть вложенный цикл: для внешнего цикла, перебирающего значения А (ограничим их числом 50, т.к. необходимо найти наименьшее А), будем запускать внутренний цикл, перебирающий значения х (х ограничим числом 1000, будем рассматривать данный диапазон, как «любое натуральное значение переменной х»).
Во внутреннем цикле расположим формулу:

Python:

for A in range(1,50):
    OK = 1
    for x in range(1,1000):
        OK *= (x % A == 0) <= ((x % 28 != 0) or (x % 42== 0))
    if OK:
        print( A )
        break

PascalABC.net:

begin
  for var A := 1 to 50 do
  begin
    var ok := 1;
    for var x := 1 to 1000 do
    begin
      if (x mod A = 0) <= ((x mod 28 <> 0)or (x mod 42 = 0)) = false then
      begin
        ok := 0; 
        break;
      end;
    end;
    if (ok = 1) then begin
      print(A);
      break;
      end
  end;
end.

OK — переменная-индикатор: если находится такое А при котором, диапазон всех значений x, подставленных в выражение, возвращает истинное значение выражения, то ОК остается равным 1, т.к. используется операция умножения (до цикла ОК необходимо присвоить единице).
Следует иметь в виду, что в программировании вместо операции импликация (->) можно использовать нестрогое неравенство: <=. Т.к. таблица истинности для операции импликация соответствует операции <=:

a b   F(a<=b)
0 0      1
0 1      1
1 0      0
1 1      1

После запуска программы выдается наименьшее значение А, т.к. используется оператор break для выхода из цикла после первого найденного значения:

Результат: 3

15_6:

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».

Для какого наименьшего натурального числа А формула

 (¬ДЕЛ(x, 19) ∨ ¬ДЕЛ(x, 15)) → ¬ДЕЛ(x, A)

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

✍ Решение:

✎ Решение 1 (Путём рассуждений):

Введем обозначения:

A = ДЕЛ(x,A); 
D19 = ДЕЛ(x, 19); 
D15 = ДЕЛ(x, 15)

Перепишем исходную формулу, согласно введенным обозначениям. Укажем, что формула должна быть тождественно истинна (по условию):

(¬D19 ∨ ¬D15) → ¬A = 1

Избавимся от импликации:

D19 ∧ D15 ∨ ¬A = 1

Разделим данную формулу на две части: в одной из них — искомое A, а в другой — часть формулы с x, которую можно найти:

¬A ∨ D19 ∧ D15 = 1
 ¹       ²

Начнем с известной части — части 2 формулы. В ней находится операция конъюнкция, которую проще найти, когда все ее операнды равны 1 (единственный случай для конъюнкции: 1 ∧ 1 = 1).
Вторая часть общей формулы может равняться только 1, когда ¬A = 0 (если ¬A = 1, то вторая часть может равнять 0, а нам нужно 1) :

¬A ∨ D19 ∧ D15 = 1
 ⁰  ^∨     ¹^{= 1}

Т.е. получаем:

¬A = 0 при D19 ∧ D15 = 1
или
A = 1 при D19 = 1 и D15 = 1

Таким образом, имеем:

A = 1
D19 = 1
D15 = 1

Очевидно, что наименьшим x можем взять число 285 (15 * 19 = 285): ДЕЛ(285, 19) и ДЕЛ(285, 15)
Поскольку мы ищем наименьшее A, такое что: ДЕЛ(x, A) и при этом ДЕЛ(x, 19) и ДЕЛ(x, 15), то нам необходимо найти наименьшее делимое чисел 19 и 15:

19 * 2 = 38 (38 не делится на 15)
19 * 3 = 57 (57 не делится на 15)
19 * 4 = 76 (76 не делится на 15)
19 * 5 = 95 (95 не делится на 15)
...
19 * 10 = 190 (190 не делится на 15)
19 * 15 = 285 (285 делится на 15)

A должно быть таким числом, при котором x принимает единственно возможное (наименьшее) значение 285.
Таким наименьшим A является само число 285.

✎ Решение 2 (программирование). Язык Python:

 (¬ДЕЛ(x, 19) ∨ ¬ДЕЛ(x, 15)) → ¬ДЕЛ(x, A)  = 1

Можно сделать вывод, что для некоторого диапазона натуральных значений А, необходимо рассмотреть диапазон натуральных значений x. Если выражение будет истинным для диапазона всех рассматриваемых х, то такое А необходимо вывести на экран.
То есть следует рассмотреть вложенный цикл: для внешнего цикла, перебирающего значения А (ограничим их числом 500, т.к. необходимо найти наименьшее А), будем запускать внутренний цикл, перебирающий значения х (х ограничим числом 1000, будем рассматривать данный диапазон, как «любое натуральное значение переменной х»).
Во внутреннем цикле расположим формулу:

for A in range(1,500):
    OK = 1
    for x in range(1,1000):
        OK *= ((x % 19 != 0) or (x % 15 != 0))<= (x % A!= 0)
    if OK:
            print( A )

a b   F(a<=b)
0 0      1
0 1      1
1 0      0
1 1      1

После запуска программы выдается одно значение А:

Результат: 285

Задания с поразрядной конъюнкцией

Поразрядная конъюнкция:

15_1:

Обозначим через m & n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 12&6 = 1100₂&0110₂ = 0100₂ = 4

Для какого наименьшего неотрицательного целого числа A формула

(X & A = 0) ∧ ¬(X & 35 ≠ 0 → X & 52 ≠ 0)

тождественно ложна (то есть принимает значение 0 при любом неотрицательном значении переменной X)?

✍ Решение:

Стоит заметить, что для такого типа задач, нет универсального единственного решения. Поэтому на видео, расположенном ниже, представлено два варианта решения.
✎ Способ 1:

Рассмотрим один из вариантов решения:

Удалим из формулы X&, чтобы сократить ее запись:

(A = 0) ∧ ¬(35 ≠ 0 → 52 ≠ 0)

Обратим внимание, что внешней операцией является конъюнкция — логическое умножение:

(A = 0) ∧ ¬(35 ≠ 0 → 52 ≠ 0)

Разделим общее выражение на две части относительно внешней операции. Первая часть — неизвестная, искомая, а вторая — известная, ее можно вычислить:

(A = 0) ∧ ¬(35 ≠ 0 → 52 ≠ 0)
   ¹               ²

Выполним некоторые преобразования во второй части формулы:
Зная свойство импликации, преобразуем формулу (избавимся от импликации в скобках):

правило импликации: a → b = ¬a ∨ b

(A = 0) ∧ ¬(35 = 0 ∨ 52 ≠ 0)
т.к. в результате получается отрицание того, что 35 ≠ 0, 
то убираем знак "не равно": было 35 ≠ 0, стало 35 = 0

Избавимся от отрицания перед скобками по закону Де Моргана:

закон де Моргана: ¬ (A ∨ B) = ¬ A ∧ ¬ B

A = 0 ∧ 35 ≠ 0 ∧ 52 = 0 = 0

По условию формула должна быть ложной. Вспомним таблицу истинности для конъюнкции (внешняя операция в нашей общей формуле):

0 ∧ 0 = 0
0 ∧ 1 = 0
1 ∧ 0 = 0
1 ∧ 1 = 1

Вторая часть формулы — вычислима, поэтому начнем с нее. В ней находится операция конъюнкция, которая имеет один единственный вариант решения, когда ¬ A ∧ ¬ B = 1. То есть примем вторую часть за истину (=1). В таком случае, для того чтобы общее выражение стало ложным (так требуется по заданию), необходимо, чтобы утверждение, что A = 0 было ложным (т.к. в обратном случае получим: 1 ∧ 1 = 1):

(A = 0) ∧ 35 ≠ 0 ∧ 52 = 0 = 0
   ⁰    ^∧        ¹    ^{= 0}

Вторая часть будет истинной только в том случае, если оба утверждения будут истинными:

35 ≠ 0 ∧ 52 = 0 = истинно (=1)  если:
35 ≠ 0 = истинно (=1)
и
52 = 0 = истинно (=1)

так как стоит логическое умножение ∧ - 
смотрим выше таблицу истинности для конъюнкции

Из двух последних пунктов получаем три утверждения:

35 ≠ 0  = 1  (истина)
и
52 = 0  = 1  (истина)
и
A = 0   = 0  (ложь)

Переведем числа в двоичную систему счисления:

35: 100011  (≠ 0)
52: 110100 (= 0)

Найдем такой X, который при поразрядной конъюнкции даст истинное значение для обеих частей.
Для начала рассмотрим ситуацию с числом 52 — это проще, т.к. для получения в результате нуля (52 = 0 => истина), достаточно во всех разрядах «перекрыть» единицы нулями:

52	1	1	0	1	0	0
X	0	0	?	0	?	?

Мы «перекрыли» все единицы нулями, чтобы в результате получить 0.
Теперь рассмотрим 35 ≠ 0 = истина (1):

35	1	0	0	0	1	1
X	1	?	?	?	1	1

Объединим обе маски в одну:

0 0 ? 0 ? ?  _&
1 ? ? ? 1 1
0 0 ? 0 1 1

Так как выражение X & A = 0 должно быть ложным, то найдем такое наименьшее А, при котором X & A ≠ 0. Для этого в тех разрядах Х, в которых находится единица, необходимо сохранить эту единицу и в соответствующих разрядах А:

X	0	0	?	0	1	1
A	0	0	0	0	1	1

Переведем результат в десятичную систему счисления:

000011₂ = 3₁₀

Ответ: 3

✎ Способ 2*:

Выполним последовательно следующие пункты:

Произвести замену (x & K = 0) на Zk
Выполнить преобразования по свойству импликации и закону Де Моргана.
Стремиться прийти к выражению с конъюнкциями без отрицаний типа: Zk * Zm.
Все выражения типа Zk * Zm преобразовать по свойству
Zk * Zm = Z_{k or m}.
Путем преобразований прийти к импликации: Zk → Zm.

Согласно первому пункту производим замену:

A ∧ ¬(¬Z35 → ¬Z52) = 0

Введем отрицание в выражение, чтобы оно было истинным:

¬(A ∧ ¬(¬Z35 → ¬Z52)) = 1

По закону де Моргана:

¬A ∨ (¬Z35 → ¬Z52) = 1

По свойству импликации:

¬A ∨ (Z35 ∨ ¬Z52) = 1

Объединим слагаемые с отрицанием:

¬A ∨ ¬Z52 ∨ Z35 = 1

Чтобы прийти к конъюнкции (пункт 3), используем закон де Моргана:

¬(A ∧ Z52) ∨ Z35 = 1

Чтобы прийти к импликации (пункт 5), используем свойство импликации:

(A ∧ Z52) → Z35 = 1

Получаем:

Z_{A ∨ 52} → Z35 = 1

Вспомним свойство:

Условие Zk → Zm истинно для любых натуральных значений x тогда и только тогда, когда все единичные биты двоичной записи числа M входят во множество единичных битов двоичной записи числа K.

В нашем случае это говорит о том, что все единичные биты двоичной записи числа 35 должны входить в результат Z_{A or 52}.
Рассмотрим подробно:

A       = ??0?11
52      = 110100
A or 52 = 110111
35      = 100011

поскольку мы ищем наименьшее А, то:

Аmin = 11₂ = 3₁₀

Результат: 3

Детальный разбор данного задания 15 ЕГЭ по информатике предлагаем посмотреть на видео:

Вариант решения №1 (универсальный, теоретический):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Вариант решения №2 (не универсальный, но простой):
📹 YouTube здесь

Поразрядная конъюнкция:

15_2:

Обозначим через m & n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 12&6 = 1100₂&0110₂ = 0100₂ = 4

Для какого наибольшего неотрицательного целого числа A формула

X & A ≠ 0 → (X & 36 = 0 → X & 6 ≠ 0)

тождественно истинна (то есть принимает значение 1 при любом неотрицательном значении переменной X)?

✍ Решение:

✎ Способ 1:

Произведем замену:

z36 = (x&36 = 0), z6 = (x&6 = 0), A = (x&A = 0)

Перепишем выражение:

¬A → (z36 → ¬ z6)

Избавимся от импликации (A → B = ¬ A ∨ B):
Сначала по правилу преобразования импликации:

¬A → (z36 → ¬ z6) = A + ¬z36 + ¬z6

По Закону де Моргана вынесем отрицание за скобки (¬ (A ∧ B) = ¬ A ∨ ¬ B):

A + ¬z36 + ¬z6 = A + ¬(z36 * z6)

Вернемся опять к импликации:

A + ¬(z36 * z6) = ¬(z36 * z6) + A = (z36 * z6) → A

Суть предыдущих действий в том, что нам необходимо прийти к импликации, но, избавившись от отрицания.
По следующему правилу Z_K * Z_M = Z_{K or M} (К. Поляков) заменим конъюнкцию:

z36 * z6 = z_{36 or 6}

Выполним поразрядную дизъюнкцию двоичных чисел 36 и 6:

100100₂ -> 36
110₂ -> 6

100100
   110
100110₂ -> 36 or 6 = 38₁₀

Получаем:

z38 → A

Необходимо обеспечить истинность данного выражения при всех x. Это возможно, когда единичные биты A входят в единичные биты числа 38. То есть:

A = 100110₂ = 38₁₀

✎ Способ 2:

Так как по заданию формула должна быть тождественно истинна, то перепишем ее так:

x&A ≠ 0 → (x&36 = 0 → x&6 ≠ 0) = 1

Введем обозначения:

A = (x&A = 0);
P = (x&36 = 0);
Q = (x&6 = 0);

Перепишем выражение согласно введенным обозначениям:

¬A → (P → ¬Q) = 1

Избавимся от импликации:

A ∨ (¬P ∨ ¬Q) = 1

A — наше неизвестное; для части выражения ¬P ∨ ¬Q нам необходимо подобрать такой вариант (равный 0 или 1), при котором единственно возможным значением A была бы единица (1).
Возьмем (¬P ∨ ¬Q) = 0, тогда А должно быть только единицей (чтобы общее выражение было = 1):

A ∨ (¬P ∨ ¬Q) = 1; 
или 
1 ∨ (0) = 1

Иными словами, выражение истинно, если при ¬P ∨ ¬Q = 0, A равно единице (1).
Получаем:

¬P ∨ ¬Q = 0
Отсюда имеем: 
¬P = 0 и ¬Q = 0 

(дизъюнкция равна 0 в единственном случае, когда все операнды равны 0)

Или запишем другим образом:

Q = 1 и P = 1

Построим побитовые маски:

100100  : 36
000110  : 6
0**0**  : маска P (x&36 = 0)
***00*  : маска Q (x&6 = 0)

Сопоставим обе маски и маску x&A = 0:

0**0**  : маска P (x&36 = 0)
***00*  : маска Q (x&6 = 0)
0**00*  : общая маска x
*00**0  : маска для A (x&A = 0)
т.е. в тех битах А, где может получиться единица (звездочки в обеих масках),
 мы поставили нули.

Так как нам необходимо получить наибольшее A (по заданию), то вместо всех «звездочек» ставим единицы:

100110 = 38₁₀

Результат: 38

Подробное решение данного задания 15 ЕГЭ по информатике предлагаем посмотреть в видео уроке:
Способ 1:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Способ 2:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Поразрядная конъюнкция:

15_8:

Определите наименьшее натуральное число А из интервала [43, 55], такое, что выражение

((x & 17 ≠ 0) → ((x & A ≠ 0) → (x & 58 ≠ 0))) →
→ ((x & 8 = 0) ∧ (x & A ≠ 0) ∧ (x & 58 = 0))

тождественно ложно (то есть принимает значение 0 при любом натуральном значении переменной х)?

Типовые задания для тренировки

✍ Решение:

Введем обозначения:

(¬Z17 → (¬A → ¬Z58)) → (z8 ∧ ¬A ∧ Z58) = 0

Для того, чтобы выражение было истинным, поставим его с отрицанием:

¬(((¬Z17 → (¬A → ¬Z58)) → (z8 ∧ ¬A ∧ Z58)) = 1

Упростим выделенную часть выражения (свойство 1, теория):

Z8 ∧ Z58 = Z_{8 or 58}  :

8  =   1000  _or
58 = 111010
     111010 = 58

Получили:

Z8 ∧ Z58 = Z58

Перепишем все выражение снова, избавившись от импликации:

¬(¬(Z17 ∨ A ∨ ¬Z58) ∨ (¬A ∧ Z58)) = 1

По закону Де Моргана получим:

(Z17 ∨ A ∨ ¬Z58) ∧ ¬(¬A ∧ Z58)) = 1

Еще раз применим закон теперь ко второй скобке:

(Z17 ∨ A ∨ ¬Z58) ∧  (A ∨ ¬Z58) = 1

Используем закон поглощения:

A ∨ ¬Z58 = 1

Приведем к импликации, чтобы избавиться от отрицания:

¬Z58 ∨ A => 
 Z58 → A = 1

Поскольку по заданию нас интересует диапазон [43;55], то проверять будет с числа 43.
По свойству 3 (теория), необходимо, чтобы единичные биты А входили в единичные биты двоичного представления числа 58:

43 = 101011 - не подходит!
58 = 111010

44 = 101100 - не подходит!
58 = 111010

45 = 101101 - не подходит!
58 = 111010

46 = 101110 - не подходит!
58 = 111010

47 = 101111 - не подходит!
58 = 111010

48 = 110000 - подходит!
58 = 111010

Результат: 48

Поразрядная конъюнкция:

15_15:

Определите набольшее натуральное число A, такое что выражение

((x & 26 = 0) ∨  (x & 13 = 0)) → ((x & 78 ≠ 0) → (x & A = 0))

тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной х)?

Типовые задания для тренировки:

✍ Решение:

Для упрощения восприятия введем обозначения:

z26 = (x & 26 = 0)
z13 = (x & 13 = 0)
z78 = (x & 78 = 0)
A = (x & A = 0)

Таким образом, получим следующее выражение:

(z26 ∨ z13) → (¬z78 → A) = 1

Упростим выражение по свойству импликации для второй скобки:

(z26 ∨ z13) → (z78 ∨ A) = 1

Упростим левую часть, используя свойство 2 (Z_k + Z_m = Z_{k and m}):

26 : 11010   единичные биты: 4, 3, 1
13 :  1101   единичные биты: 3, 2, 0
∧ =------------------------
     01000 = 8₁₀

То есть получили z26 ∨ z13 = z8
По правилу импликации: все единичные биты двоичной записи результата (z78 ∨ A) должны входить во множество единичных битов двоичной записи z8.
Рассмотрим:

z8 → (z78 ∨ A)
z78: не влияет на решение, так как операция дизъюнкция истинна тогда, 
когда хотя бы один операнд истинен
z8 → A     : ????

Для А единичными битами должны быть общие единичные биты для z8 (1000₂). Т.е. в нашим случае — это один бит — 3-й:

Наибольшее А = 1000 = 8₁₀

Результат: 8

Задания на поиск наибольшего или наименьшего числа А

Поиск наибольшего или наименьшего числа А:

15_4: 15 задание. Демоверсия ЕГЭ 2018 информатика:

Для какого наибольшего целого числа А формула

тождественно истинна, то есть принимает значение 1 при любых целых неотрицательных x и y?

✍ Решение:

✎ Способ 1 (программный):

Важно: Поскольку используется метод полного перебора, то возможна ситуация, когда транслятор будет работать слишком медленно. Но работоспособность представленного алгоритма проверена на онлайн компиляторах.

Pascalabc.net:

begin
  for var A := 200 downto -100 do
  begin
    var OK := 1;
    for var x := 0 to 100 do
      for var y := 0 to 100 do
        if ((x <= 9) <= (x * x <= A)) and ((y * y <= A) <= (y <= 9)) = false then 
        begin
          OK := 0;
          break;
        end;
    if OK = 1 then 
    begin
      print(A);
      break
    end;
  end;
end.

Бейсик:	Python: for A in range(200,-100,-1): OK = 1 for x in range(0,100): for y in range(0,100): OK = ((x<=9) <= (xx<=A)) and((y*y<=A) <= (y<=9)) if OK: print(A) break
С++:

✎ Способ 2 (теоретическое решение):

Условно разделим исходное выражение на части:

Главное действие (внешняя операция) в исходном выражении — это конъюнкция. Конъюнкция истинна, когда все операнды истинны. Т.е. в задаче обе части 1 и 2 должны быть истинными (т.к. по условию общая формула должна быть истинной).

Рассмотрим часть 1:

если в 1.1 имеем x > 9, то часть 1 будет истинна независимо от А. Значит, значение числа А влияет на решение только при выполнении условия:

x<=9

(импликация 0 → 0 = 1, 0 → 1 = 1)

теперь, для того чтобы в части 1, выражение было истинным, надо чтобы часть 1.2 была истинной:

x*x <= A

(импликация 1 → 1 = 1)

таким образом, получаем:

x <= 9
x² <= A

при любых x

так как нам необходимо найти наибольшее возможное А, то, значит, надо ограничить его значения сверху, а данная часть выражения ограничивает только снизу:

возьмем максимальное натуральное: x=9, тогда A>=81

Рассмотрим часть 2:

если 2.2 истинно (т.е. y <= 9), то часть 2 будет истинна независимо от А. Значит, значение числа А влияет на решение только при выполнении условия:

y > 9

теперь, для того чтобы в части 2 выражение было истинным, надо чтобы часть 2.1 была ложной:

y * y > A

(импликация 0 → 0 = 1)

таким образом, получаем:

y > 9
y² > A

при любых y

данная часть выражения ограничивает значения А сверху:

возьмем наименьшее возможное по условию натуральное: y = 10, тогда A < 100

Получаем, что наибольшее А меньшее 100: А = 99

Результат: 99

Подробное решение 15 задания демоверсии ЕГЭ 2018 года смотрите на видео (аналитическое решение):

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Поиск наибольшего или наименьшего числа А:

✍ Решение:

✎ Способ 1 (программный):

Pascalabc.net:

begin
  for var A := -100 to 200 do
  begin
    var OK := 1;
    for var x := 1 to 100 do
      for var y := 1 to 100 do
        if ((y+3*x<A) or (x >20)or(y>40)) = false then 
        begin
          OK := 0;
          break;
        end;
    if OK = 1 then 
    begin
      print(A);
      break
    end;
  end;
end.

Бейсик:	Python: for A in range(-100,200): OK = 1 for x in range(1,100): for y in range(1,100): OK = (y+3x<A) or (x > 20) or (y > 40) if OK: print(A) break
С++:

✎ Способ 2 (теоретическое решение):

Определим основные части выражения, выделив отдельно неизвестную часть — с А, и, так сказать, известную часть, то есть остальную.

    1                 2
(y+3x < A) ∨ (x > 20) ∨ (y > 40)

Поскольку основными операциями являются операции дизъюнкции (логического сложения) и порядок их выполнения не важен, то последней, внешней, операцией будем выполнять дизъюнкцию слева, т.к. она объединяет неизвестную и известную часть.
Сначала важно рассмотреть вторую часть выражения, известную, так как от нее будет зависеть значение A. Если вторая часть истинна, то А может быть как = 1, так и = 0. Такой вариант нам не подходит:

(y+3x < A) ∨ (x > 20) ∨ (y > 40)
  ^{1 или 0?                   1               = 1}
Не подходит!

Соответственно, рассмотрим вариант, когда вторая часть ложна, тогда часть выражения с неизвестным А будет обязательно истинной, т.е.:

1. (y+3x < A) = 1
2. (x > 20) ∨ (y > 40) = 0

Дизъюнкция ложна, когда оба операнда ложны, т.е. из второго пункта имеем:

x <= 20
y <= 40

Для того, чтобы перекрыть все x и все y, возьмем наибольшие из возможных значений: x = 20, y = 40.
Выразим А:

А > 3x + y
A > 3*20 + 40
A > 100

Поскольку требуется найти наименьшее значение А, то имеем А = 101.

Результат: 101

Подробное решение досрочного ЕГЭ 2018 года смотрите на видео (аналитическое решение):

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Поиск наибольшего или наименьшего числа А:

15_0:Разбор 15 задания. Демоверсия егэ по информатике 2019:

Для какого наибольшего целого неотрицательного числа А выражение

(48 ≠ y + 2x) ∨ (A < x) ∨ (A < y)

тождественно истинно, т.е. принимает значение 1 при любых целых неотрицательных x и y?

✍ Решение:
✎ Решение 1 (теоретическое):

Разделим общее выражение на две части. Выделим неизвестную часть красным:

(48 ≠ y + 2x) ∨ (A < x) ∨ (A < y)

Неизвестная часть должна быть истинной, она обязательно будет истинна, если известная часть — ложь:

(48 ≠ y + 2x) ∨ (A < x) ∨ (A < y) = 1
      ⁰                  ¹

Т.е. 48 ≠ y + 2x = 0 или y + 2x = 48. На графике это уравнение представляет линию. Из условия имеем два ограничения:(x > 0) and (y > 0). Отобразим линию для 1-й четверти, соответствующей положительным x и y:

y + 2x = 48  :
при x = 0, y = 48
при y = 0, 2x = 48 => x = 24

Возьмем некоторое значение A, например, A = 25, отметим его на графике белой областью так, чтобы выполнялось (A < x) ∨ (A < y). По условию имеем, что все точки данной части отрезка прямой y + 2x = 48 должны принадлежать отмеченной белой области. Заштрихуем область для всех точек прямой (голубым цветом):

То есть все точки голубого квадрата должны находиться под отрезком линии (включая вершину (A, A)), и данный квадрат, соответствует максимальному значению A.
Наибольшее значение голубая область приобретает в точке пересечения прямой y + 2x = 48 с прямой y = x:

Далее решаем полученное линейное уравнение (для x = y):

x + 2x = 48 =>
3x = 48
x = 16

Так как значение A должно быть меньше x, то наибольшее А = 15.

✎ Решение 2 (программное):
Python:

for A in range(200,0,-1):
    OK = 1
    for x in range(0,100):
        for y in range(0,100):
            OK *= (48!=y+2*x) or(A<x)or (A<y) 
    if OK:
        print(A)
        break

Результат: 15

Видео решения 15 задания демоверсии ЕГЭ 2019 (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Поиск наибольшего или наименьшего числа А:

15_19:

Для какого наименьшего целого числа А формула

(y + 5x <= 34) → ((y — x > 4) ∨ (y <= A))

тождественно истинна, т.е. принимает значение 1 при любых целых неотрицательных x и y?

✍ Решение:

Общая идея такова:
необходимо упростить формулу так, чтобы последняя операция (внешняя) выполнялась со скобкой, в которой находится искомое A. После чего разделить формулу на две части, в одной из которых находится искомое.
Избавимся от импликации, это даст нам возможность опустить общие скобки во второй части формулы:

¬(y + 5x <= 34) ∨ (y - x > 4) ∨ (y <= A)

Разделим формулу на две части таким образом, чтобы внешняя операции отделяла часть, в которой находится искомое A:

¬(y + 5x <= 34) ∨ (y - x > 4) ∨ (y <= A) = 1
        1 часть                  2 часть

Формула по условию должна быть истинной (=1). Внешняя операция — дизъюнкция — истинна аж в трех случаях: a=1 b=0, a=0 b=1, a=1 b=1.
Если мы допустим, что первая часть истинна, то вторая, искомая часть, может быть как истинной, так и ложной. Поэтому такой вариант не подходит.
Допустим, что первая часть ложна, тогда вторая, искомая часть, должна быть только истинной:

¬(y + 5x <= 34) ∨ (y - x > 4) ∨ (y <= A) = 1
        1 часть = 0               2 часть = 1

С учетом, что в первой части формулу находится операция дизъюнкция, которая ложна только в одном случае (a=0 b=0), то выпишем утверждения, получившиеся из первой части:

y + 5x > 34 = 0, значит:
1. y + 5x <= 34
y - x > 4 = 0, значит:
2. y - x <= 4

Кроме того, имеем еще одно утверждение второй части:

y <= A
или
A >= y

Отобразим получившиеся уравнения прямых на плоскости:

Раз A >= y, значит, искомая область лежит выше обеих прямых. Наименьшее значение А будет достигнуто в указанной точке пересечения двух прямых.
В точке пересечения прямых уравнения равны, т.е. имеем:

34 - 5x = 4 + x
30 = 6x
x = 5
Найдем y: 
y = 4 + 5 = 9

Поскольку имеем утверждение, что A >= y и в задании требуется найти наименьшее A, то получаем:

y = 9:
A >= 9 => наименьшее A = 9

✎ Решение 2 (программное):
Python:

for A in range(-100,100):
    OK = 1
    for x in range(0,100):
        for y in range(0,100):
            OK *= (y+5*x<=34)<=((y-x >4)or(y<=A)) 
    if OK:
        print( A )
        break

PascalABC.NET:

 
begin
  for var A := -100 to 100 do
  begin
    var OK := true;
    for var x := 0 to 100 do
    begin
      for var y := 0 to 100 do
      begin
        OK := (y + 5 * x <= 34) <= ((y - x > 4) or (y <= A));
        if OK = false then break;
      end;
      if OK = false then break;
    end;
    if OK then 
    begin
      print(A);
      break;
    end;
  end;
end.

Результат: 9

Поиск наибольшего или наименьшего числа А:

15_13:

Укажите наименьшее целое значение А при котором выражение

(2y + 5x < A) ∨ (2x + 4y > 100) ∨ (3x – 2y > 70)

истинно для любых целых положительных значений x и y.

Типовые задания для тренировки

✍ Решение:

Python:

for A in range(-200,200):
    OK = 1
    for x in range(1,100):
        for y in range(1,100):
            OK *= (2*y + 5*x < A) or (2*x + 4*y > 100) or (3*x - 2*y > 70) 
    if OK:
        print( A )
        break

PascalABC.NET:

begin
  for var A := -200 to 200 do
  begin
    var OK := true;
    for var x := 1 to 100 do
    begin
      for var y := 1 to 100 do
      begin
        OK := (2*y + 5*x < A) or (2*x + 4*y > 100) or (3*x - 2*y > 70);
        if OK = false then break;
      end;
      if OK = false then break;
    end;
    if OK then 
    begin
      print(A);
      break;
    end;
  end;
end.

Результат: 171

Видео разбора задания смотрите на видео (аналитическое решение):

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Поиск наибольшего или наименьшего числа А:

15_14:

Укажите наибольшее целое значение А при котором выражение

(3y – x > A) ∨ (2x + 3y < 30) ∨ (2y – x < –31)

истинно для любых целых положительных значений x и y.

Типовые задания для тренировки

✍ Решение:

✎ Решение 1 (теоретическое):

Разделим выражение на две части: часть с неизвестным = 1, часть известная = 0:

(3y – x > A) ∨ (2x + 3y < 30) ∨ (2y – x < –31) = 1

Выпишем отдельно обе скобки известной части:

(1) 
(2x + 3y) >= 30,
y >= (30 - 2x) / 3
x = (30 - 3y) /2

(2) 
(2y – x >=–31)
y >= (x - 31) / 2
x = 2y + 31

Подберем значения координат для x и y обеих частей, и отобразим линии на графике функций:

(1)
x | y
0 | 10
15| 0

(2)
x | y
0 | -15 ( целые)
30|0

Для первого уравнения:

Для второго уравнения:

Сопоставим обе области:

Добавим на график прямую A<3y-x:

Раз A < 3y – x, то будем перемещать А снизу вверх. Наибольшее значение А будет достигнуто в указанной точке пересечения с прямой (2).
Т.е. для уравнения (2) имеем:

если y = 1, то x = 2*1 + 31 = 33

Подставим в выражение для поиска А:

А < 3y - x
A < 3-33, A < -30, A=-31

✎ Решение (программное):
Python:

for A in range(200,-200,-1):
    OK = 1
    for x in range(1,100):
        for y in range(1,100):
            OK *= (3*y-x>A) or (2*x+3*y<30) or (2*y-x<-31) 
    if OK:
        print(A)
        break

Результат: -31

* В некоторых задачах использован метод, предложенный А.В. Здвижковой

Источник

11.05.2013

В файле содержится вся необходимая теория для подготовки к ЕГЭ по информатике для задания A1.

Изучив предложенный материал, вы обретёте знания и навык для решения этого типа заданий A1.

СКАЧАТЬ A1 в формате DOC

Сохранить ссылку:

Комментарии (0)
Добавить комментарий

Добавить комментарий

Комментарии без регистрации. Несодержательные сообщения удаляются.

Имя (обязательное)

E-Mail

Подписаться на уведомления о новых комментариях

Отправить

Источник

ЕГЭ информатика 15 задание разбор, теория, как решать.

Преобразование логических выражений, (П) — 1 балл

Е15.43 формула (x&35 ≠ 0 ∨ x&22 ≠ 0) → (x&15 = 0 → x&А ≠ 0) тождественно истинна

Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Например, 14&5 = 11102&01012 = 01002 = 4. Для какого наименьшего неотрицательного целого числа А формула (x&35 ≠ 0 ∨ x&22 ≠ 0) → (x&15 = 0 → x&А ≠ 0) тождественно истинна (т. е. принимает значение 1 при любом неотрицательном целом значении переменной …

Е15.42 Для какого наименьшего натурального числа А формула (ДЕЛ(x, 2) → ¬ДЕЛ(x, 3)) / (x + A ≥ 100)

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула (ДЕЛ(x, 2) → ¬ДЕЛ(x, 3)) / (x + A ≥ 100) тождественно истинна (т.е. принимает значение 1) при любом натуральном значении переменной х? Ответ: Демонстрационный вариант ЕГЭ 2023 г. – задание №15

Е15.41 для которого формула ((x ∈ Q) ≡ (x ∈ P)) ∨ (¬(x ∈ A) → ((x ∈ P) ∧ ¬(x ∈ Q))) тождественно истинна

На числовой прямой даны два отрезка: P = [ 6; 4 5] и Q = [18; 52]. Укажите наименьшую возможную длину такого отрезка A, для которого формула ((x ∈ Q) ≡ (x ∈ P)) ∨ (¬(x ∈ A) → ((x ∈ P) ∧ ¬(x ∈ Q))) тождественно истинна (т. е. принимает значение 1 при любом …

Е15.40 выражение (2у + 3х ≠ 135) ∨ (у > А) ∨ (x > A) истинно

Определите наибольшее целое значение A, при котором выражение (2у + 3х ≠ 135) ∨ (у > А) ∨ (x > A) истинно для любых целых положительных значений х и у. Ответ: Апробация ЕГЭ по информатике 19 февраля 2022 – задание №15 Тренировочный экзамен по информатике и ИКТ (КЕГЭ) в компьютерной форме

Е15.39 формула (x ∈ Q) → (((x ∈ P) ≡ (x ∈ Q)) ∨ (¬(x ∈ P) → (x ∈ A))) тождественно истинна

На числовой прямой даны два отрезка: P = [69; 91] и Q = [77; 114]. Укажите наименьшую возможную длину такого отрезка A, для которого формула (x ∈ Q) → (((x ∈ P) ≡ (x ∈ Q)) ∨ (¬(x ∈ P) → (x ∈ A))) тождественно истинна (т. е. принимает значение 1 при любом значении переменной …

Е15.38 выражение ((x & 26 ≠ 0) ∨ (x & 13 ≠ 0)) → ((x & 29 = 0) → (x & A ≠ 0)) тождественно истинно

Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14&5 = 11102&01012 = 01002 = 4 . Определите наименьшее натуральное число A, такое что выражение ( (x & 26 ≠ 0) ∨ (x & 13 ≠ 0)) → ((x & 29 = 0) → (x & A ≠ 0)) тождественно истинно …

Е15.37 формула (x ∈ Q) → (¬(x ∈ P) → ¬((x ∈ Q) ∧ ¬(x ∈ A))) тождественно истинна

На числовой прямой даны два отрезка: P = [19; 94] и Q = [4; 61]. Укажите наименьшую возможную длину такого отрезка A, для которого формула (x ∈ Q) → (¬(x ∈ P) → ¬((x ∈ Q) ∧ ¬(x ∈ A))) тождественно истинна (т. е. принимает значение 1 при любом значении переменной х). Ответ: источник: …

Е15.36 формула ( (x ∈ А) → (x ∈ P) ) / (x ∈ Q) тождественно истинна

На числовой прямой даны два отрезка: P = [5, 17] и Q = [13, 23]. Найдите наибольшую возможную длину отрезка A, при котором формула ( (x ∈ А) → (x ∈ P) ) / (x ∈ Q) тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Ответ: источник: informatikaexpert.ru

Е15.35 ДЕЛ(A, 40) / (ДЕЛ(780, x) → (¬ДЕЛ(A, x) → ¬ДЕЛ(180, x)))

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа A формула ДЕЛ(A, 40) / (ДЕЛ(780, x) → (¬ДЕЛ(A, x) → ¬ДЕЛ(180, x))) тождественно истинна, то есть принимает значение 1 при любом натуральном x? Ответ: СтатГрад Вариант ИН2010401 17.03.2021– задание №15

Е15.34 формула x & 85 = 0 → (x & 54 ≠ 0 → x & А ≠ 0) тождественно истинна

Обозначим через m & n поразрядную конъюнкцию неотрицательных целых чисел m и n. Например, 14 & 5 = 11102 & 01012 = 01002 = 4. Для какого наименьшего неотрицательного целого числа А формула x & 85 = 0 → (x & 54 ≠ 0 → x & А ≠ 0) тождественно истинна (т. е. принимает …

Источник

Сегодня посмотрим одно из самых интересных заданий из ЕГЭ по информатике 2023. Будем решать 24 задание. В этом задании нужно работать с файлами.

Все решения задач из задания 24 ЕГЭ по информатике 2023 будут приведены на языке программирования Python (Питон).

Поехали!

Задача (Самая простая)

Текстовый файл состоит не более чем из 10⁶ символов A, B и C. Определите максимальное количество идущих подряд символов B. Для выполнения этого задания следует написать программу. Ниже приведён файл, который необходимо обработать с помощью данного алгоритма.

Решение:

Решим данную задачу на языке Python.

f=open('24_1.txt')
s=f.read()
k=0
kmax=0

for i in range(0, len(s)):
    if s[i]=='B':
        k=k+1
        kmax=max(k, kmax)
    else:
        k=0

print(kmax)

С помощью команды open() подвязываемся к файлу. Чтобы не прописывать полный путь, файл должен лежать в той же папке, что и программа.

С помощью команды .read() зачитываем в переменную s всё содержимое файла.

Переменная k — это текущий счётчик символов «B». Задача переменной kmax сохранить максимальное значение k.

С помощью цикла for перебираем все символы из строки s. Переменная i пробегается по номерам всех симолов. Счёт символов начинается в строке с нуля. В начале берём нулевой символ, потом первый и т.д. Конструкция for i in range(0, len(s)) позволяет пройтись по всем символам строки до конца.

Если нам встретился нужный символ «B», то мы счётчик прибавляем на 1. Это значит, что мы подсчитываем текущую цепочку. Если будет стоять 3 символа «B» подряд, значит, счёт k покажет значение 3. Как только встретится дургой символ, то это означает, что цепочка прервалась и счётчик переводится в первоначальное положение 0.

При любом увеличении счётчика происходит анализ этого счётчика на максимальность. Функция max выбирает максимальное значение из старого значения kmax и нового показания счётчика k. Если счётчику k удалось победить kmax, то его значение будет считаться максимальным на данный момент времени.

В ответ идёт значение kmax. Это и есть длина максимальной цепочки. В этой задачке ответ получается 11.

Ответ: 11

Закрепим это простое задание из ЕГЭ по информатике 2023.

Задача (Простая, закрепление)

Текстовый файл состоит не более чем из 10⁶ символов X, Y и Z. Определите максимальное количество идущих подряд символов, среди которых нет символа Z. Для выполнения этого задания следует написать программу.

Решение:

Решение похоже на предыдущее.

f=open('24_2.txt')
s=f.read()
k=0
kmax=0

for i in range(0, len(s)):
    if s[i]!='Z':
        k=k+1
        kmax=max(k, kmax)
    else:
        k=0

print(kmax)

Если нет символов «Z», то подсчитываем, иначе сбрасываем.

Задача (Обращаемся к соседу)

Текстовый файл состоит не более чем из 10⁶ символов X, Y и Z. Определите максимальное количество идущих подряд символов, расположенных в алфавитном порядке (возможно с повторением симолов). Для выполнения этого задания следует написать программу.

Решение:

f=open('24_2.txt')
s=f.read()
k=1
kmax=0

for i in range(0, len(s)-1):
    if s[i]<=s[i+1]:
        k=k+1
        kmax=max(k, kmax)
    else:
        k=1

print(kmax)

В ответе получается 15. Символы можно сравнивать между собой с помощью знаков «>» или меньше «<» ( а так же «>=» или «<=»), причём это сравнение происходит в алфавитном порядке. Например, символ «B» будет больше, чем «A» и т.п. Теперь нам нужно уже обратится к соседу, уже важна связь между соседними символами. Раз мы обращаемся к следующему символу, то должны пробегать до len(s)-1, иначе куда мы будем обращаться, когда дойдём до последнего символа?

В самом начале цепочки мы анализируем два символа, а к счётчику прибавляем всего лишь 1. Чтобы это учесть, в начале счётчику (переменной k) присваиваем 1. Затем, по мере продвижения по цепочке, мы добавляем в наш анализ 1 новый символ, и к счётчику добавляется одна 1. Дальше уже таких проблем нет.

Раз мы присвоили в переменную k единицу, то и сбрасывать в ветке else мы тоже должны на 1. Эти значения обычно взаимосвязаны.

Если мы обращаемся к соседнему символу, как правило, счётчик и сброс устанавливаются в 1. Это не стопроцентная истина, но иметь ввиду это нужно.

Ответ: 15

Задача (Обращаемся к соседу, закрепление)

Текстовый файл состоит не более чем из 10⁶ символов арабских цифр (0, 1, …,9). Определите максимальное количество идущих подряд цифр, среди которых каждые две соседние различны. Для выполнения этого задания следует написать программу.

Решение:

f=open('24_3.txt')
s=f.read()
k=1
kmax=0

for i in range(0, len(s)-1):
    if s[i]!=s[i+1]:
        k=k+1
        kmax=max(k, kmax)
    else:
        k=1

print(kmax)

Если соседи различны, мы подсчитываем, иначе сбрасываем.

Ответ: 120

Задача (Обращаемся к соседу, ещё сложнее)

Текстовый файл состоит не более чем из 10⁶ символов арабских цифр (0, 1, …,9). Определите максимальное количество идущих подряд нечётных цифр, расположенных в неубывающем порядке. Для выполнения этого задания следует написать программу.

Решение:

f=open('24_3.txt')
s=f.read()
k=1
kmax=0

for i in range(0, len(s)-1):
    if s[i]<=s[i+1] and s[i] in '13579' and s[i+1] in '13579' :
        k=k+1
        kmax=max(k, kmax)
    else:
        k=1

print(kmax)

Здесь опять можно применить знаки сравнения прям к символам. Удобно проверить принадлежность к нечётным цифрам конструкцией s[i] in ‘13579’. Нечётной цифрой должна быть как текущая, так и следующая.

Ответ: 8

Решим ещё одну тренировочную задачу из ЕГЭ по информатике 2023.

Задача (Обращаемся к соседу, ещё сложнее, закрепление)

Текстовый файл состоит не более чем из 10⁶ символов 1, 2, 3, A, B, С. Определите максимальное количество идущих подряд символов, среди которых никакие две буквы и никакие две цифры не стоят рядом. Для выполнения этого задания следует написать программу.

Решение:

f=open('24_4.txt')
s=f.read()
k=1
kmax=0

for i in range(0, len(s)-1):
    if (s[i] in '123' and s[i+1] in 'ABC') or (s[i] in 'ABC' and s[i+1] in '123') :
        k=k+1
        kmax=max(k, kmax)
    else:
        k=1

print(kmax)

В этой задаче цифры и буквы должны чередоваться. Если у нас цифра, то следующая должны быть буква, или наоборот, если у нас буква, то следующая должна быть цифра. В этих двух случаях прибавляем к счётчику 1.

Ответ: 20

Задача (Исключаем строку из 2-х символов, демо 2022)

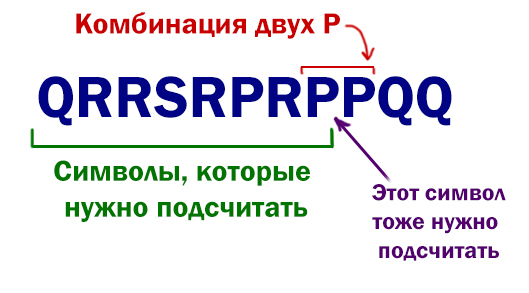
Текстовый файл состоит из символов P, Q, R и S.

Определите максимальное количество идущих подряд символов
в прилагаемом файле, среди которых нет идущих подряд символов P.
Для выполнения этого задания следует написать программу.

Решение:

Напишем решение на языке Python.

f=open('24_5.txt')
s=f.read()
k=1
kmax=0

for i in range(0, len(s)-1):
    if s[i]=='P' and s[i+1]=='P':
        k=1
    else:
        k=k+1
        kmax = max(k, kmax)

print(kmax)

Подсчитываем символы, пока не встретилась комбинация двух P подряд. Как только встретилась данная комбинация, сбрасываем счётчик на 1. Здесь мы сбрасываем счётчик на значение 1, чтобы учесть один символ, которые находится в самой комбинации PP. И в начале мы тоже устанавливаем счётчик в значение 1 по этой же причине.

Мы проходим в цикле for до длины строки минус один. Значение 1 в счётчике при сбросе и в начале программы так же компенсирует и тот момент, что мы не подсчитываем последний символ!

При изменении счётчика, сохраняем максимальное значение в переменной mx

Если бы у нас была вместо PP другая комбинация, состоящая к примеру из 5 символов, то мы бы тогда в начале и при сбросе писали в счётчик значение 5-1=4.

Здесь тоже работает негласное правило, обращаемся к соседу, значит, счётчик устанавливаем в 1.

В этой задаче получается ответ 188.

Ответ: 188

Задача (Исключаем подстроку из 3-х символов)

Текстовый файл состоит из символов арабских цифр(0, 1, …,9).

Определите максимальное количество идущих подряд символов
в прилагаемом файле, среди которых нет трёх символов 0, стоящих рядом.
Для выполнения этого задания следует написать программу.

Решение:

Напишем решение на языке Python.

f=open('24_6.txt')
s=f.read()
k=2
kmax=0

for i in range(0, len(s)-2):
    if s[i]=='0' and s[i+1]=='0' and s[i+2]=='0':
        k=2
    else:
        k=k+1
        kmax = max(k, kmax)

print(kmax)

Чтобы понять это решение, нужно посмотреть предыдущую задачу. Мы здесь обращаемся к двум соседям, значит, счётчик устанавливаем в 2. Так же проходим в цикле до len(s)-2. Нежелательная строка может состоять не только из одинаковых символов. Может быть строка «XYYZ», к примеру.

Ответ: 7684

Задача (Не более одного символа Z)

Текстовый файл состоит не более чем из 10⁶ символов X, Y и Z. Определите максимальное количество идущих подряд символов, среди которых символ Z встречается не более одного раза.

Решение:

В нашей цепочке один раз можно встретиь символ Z, а два раза уже нельзя. Здесь мы применим функцию .split(). Как работает эта фнкция? Напишем тестовую программу.

s='sadqttqtreq'
a=s.split('q')
print(a)

Результат данной программы будет следующим:

[‘sad’, ‘tt’, ‘tre’, »]

Команда split «разрезает» строку по символу «q». В результате мы получаем массив с кусочками этой строки.

Решение нашей задачи.

f=open('24_7.txt')
s=f.read()
a=s.split('Z')
k=0
kmax=0

for i in range(0, len(a)-1):
  k = len(a[i]) + 1 + len(a[i+1])
  kmax = max(k, kmax)

print(kmax)

Разрезаем нашу строку по символу «Z». Пробегаемся уже по массиву a. Цепочка-кандидат это текущий кусочек (a[i]), символ Z (1) и следующий кусочек (a[i+1]).

Каждого кандитата проверяем сразу на максимальность.

Ответ: 43

Задача (Не более двух символов Z)

Текстовый файл состоит не более чем из 10⁶ символов X, Y и Z. Определите максимальное количество идущих подряд символов, среди которых символ Z встречается не более двух раз.

Решение:

Решение аналогично предыдущему.

f=open('24_7.txt')
s=f.read()
a=s.split('Z')
k=0
kmax=0

for i in range(0, len(a)-2):
  k = len(a[i]) + 1 + len(a[i+1]) + 1 + len(a[i+2])
  kmax = max(k, kmax)

print(kmax)

Ответ: 50

Задача (Звенья)

Текстовый файл состоит не более чем из 10⁶ символов X, Y и Z. Определите максимальную длину цепочки символов, состоящей из повторяющихся фрагментов XYZ. Цепочка должна начинаться с символа X и заканчиваться символом Z. Например, для строки ZZZXYZXYZXZZZ длина цепочки равна 6: XYZ+XYZ

Решение:

Если мы подсчитаем количество идущих подряд звеньев XYZ, то, можно сказать, дело сделано.

f=open('24_8.txt')
s=f.read()
s=s.replace('XYZ', '1')
k=0
kmax=0

for i in range(0, len(s)):
    if s[i]=='1':
        k=k+1
        kmax=max(k, kmax)
    else:
        k=0

print(kmax*3)

Мы с помощью команды replace заменили звенья на «1» (на символ, которого точно нет в файле). Теперь задача свелась к самой простой, которую мы рассматривали в начале статьи. Нужно просто подсчитать количество идущих поряд единиц.

В ответе нас просили указать количество символов, а не звеньев, поэтому переменную kmax умножаем на 3.

Ответ: 66

Задача (Звенья, закрепление)

Текстовый файл состоит не более, чем из 10⁶ символов из набора A, B, С. Найдите максимальное количество идущих пар символов AC или AB. Искомая подстрока может включать только пары AB, только пары AC или содержать одновременно как пары AC, так и пары AB.

Решение:

f=open('24_9.txt')
s=f.read()
s=s.replace('AB', '1')
s=s.replace('AC', '1')
k=0
kmax=0

for i in range(0, len(s)):
    if s[i]=='1':
        k=k+1
        kmax=max(k, kmax)
    else:
        k=0

print(kmax)

Здесь нам подходит звено, как и AB, так и AC. В ответе нужно указать количество пар, поэтому не на что умножать переменную kmax не нужно.

Ответ: 19

Задача (Звенья, основная волна 20.06.22)

Текстовый файл состоит из символов A, B, C, D и O. Определите максимальное количество идущих подряд пар символов вида согласная + гласная в прилагаемом файле. Для выполенения этого задания следует написать программу.

Решение:

f=open('24_10.txt')
s=f.read()
s=s.replace('BA', '1')
s=s.replace('CA', '1')
s=s.replace('DA', '1')
s=s.replace('BO', '1')
s=s.replace('CO', '1')
s=s.replace('DO', '1')
k=0
kmax=0

for i in range(0, len(s)):
    if s[i]=='1':
        k=k+1
        kmax=max(k, kmax)
    else:
        k=0

print(kmax)

Ответ: 174

Задача (Звенья, последнее звено неполное)

Текстовый файл состоит не более чем из 10⁶ символов X, Y и Z. Определите максимальную длину цепочки вида XYZXYZXYZ… (составленной из фрагментов XYZ, последний фрагмент может быть неполным). Для выполнения этого задания следует написать программу. Ниже приведён файл, который необходимо обработать с помощью данного алгоритма.

Решение:

Т.к. последнее звено может быть неполным, здесь удобно применить другой алгоритм.

Пусть в начале показания счётчика равно нулю. Если мы находим нужный нам символ в нужной последовательности, то прибавляем к счётчику 1. Если последовательность сбивается, то ставим счётчик в ноль.

На рисунке представлен данный алгоритм. В нижней строке указано показание счётчика в момент анализа символа.

На данном рисунке максимальная длина цепочки нужных символов равна 9.

Видим, что для символа X, когда он находится на своём месте, остаток от деления значения счётчика на 3 равен 0.

Для символа Y, когда данный символ находится на своём месте, остаток от деления значения счётчика на 3 равен 1.

Для символа Z, когда данный символ находится на своём месте, остаток от деления значения счётчика на 3 равен 2.

Мы смотрим остаток от деления на 3, потому что у нас длина звена равна трём (XYZ).

Таким образом, мы и наш анализ очередного символа привяжем к показанию счётчика:

f=open('24_11.txt')
s=f.read()
k=0
kmax=0

for i in range(0, len(s)):
    if (s[i]=='X' and k%3==0) or  (s[i]=='Y' and k%3==1) or (s[i]=='Z' and k%3==2):
        k=k+1
        kmax = max(k, kmax)
    else:
        if s[i]=='X': k=1
        else: k=0


print(kmax)

Важный момент: Если нужную цепочку прервал символ X, то нужно счётчик сразу выставить в 1, иначе может произойти такая ошибка:

Т.е. первые три нужных символа в цепочке алгоритм не засчитал.

Поэтому мы не просто сбрасываем счётчик в ноль, а прописываем условие:

if s[i]=='X': k=1
else: k=0

Ответ: 13

Задача (Полезный приём)

Текстовый файл 24-157.txt состоит не более чем из 10⁶ символов и содержит только заглавные буквы латинского алфавита (ABC…Z). Определите символ, который чаще всего встречается в файле между двумя одинаковыми символами. Например, в тексте CCBAABABCBC есть комбинации ABA, BAB, BCB и CBC. Чаще всего – 2 раза – между двумя одинаковыми символами стоит B, в ответе для этого случая надо написать B2 (без пробелов и других разделителей). Если таких символов несколько, выведите тот, который стоит раньше в алфавите.

Решение:

f=open('24-157.txt')
s=f.read()
a=[0]*150

for i in range(0, len(s)-2):
    if s[i]==s[i+2]:
        a[ord(s[i+1])] = a[ord(s[i+1])] + 1

ch=''
mx=0
for i in range(0, 150):
    if a[i]>mx:
        mx=a[i]
        ch=chr(i)


print(ch, mx)

Здесь мы заводим массив a. Индексы этого массива — это коды ANSI всех букв латинского алфавита (ABC…Z). Ведь, как мы знаем, каждая буква кодируется определённым числом (кодом ANSI). Вот часть этой таблицы.

Например, буква A кодируется кодом 65. Коды увеличиваются в алфавитном порядке на 1. Буква Z кодируется числом 90. Таким образом, 150 ячеек точно хватит для нашего алфавита. Здесь берём с запасом, потому что на экзамене можно точно не вспомнить коды, но достаточно запомнить, что 150 ячеек вполне хватит для заглавных и строчных букв латинского алфавита.

Значит, ячейка 65 отвечает за букву A, ячейка 66 отвечает за букву B и т.д. Если мы встретили букву между двумя одинаковыми буквами, то её ячейка увеличивается на 1.

Функция ord() превращает символ в код ANSI.

После того, как мы прошли всю строку и собрали информацию о наших буквах, нужно пройти массив a и найти наибольшее число в нём.

Здесь мы уже не пользуемся функцией max, а используем условие, потому что нужно кроме максимального числа тянуть ещё один параметр — сам код (переменную i). Функция chr() превращает код ANSI обратно в символ.

Ответ: W1608

Задача (Строки различной длины)

Текстовый файл 24-164.txt состоит не более чем из 10⁶ символов и содержит только заглавные буквы латинского алфавита (ABC…Z). Текст разбит на строки различной длины. Необходимо найти строку, содержащую самую длинную цепочку стоящих подряд одинаковых букв. Если таких строк несколько, надо взять ту, которая в файле встретилась раньше. Определите, какая буква встречается в этой строке чаще всего. Если таких букв несколько, надо взять ту, которая стоит раньше в алфавите. Запишите в ответе эту букву, а затем – сколько раз она встречается во всем файле.

Пример. Исходный файл:

ZZQABA
ZALAAC
QRAQUT

В этом примере в первой и второй строках наибольшая длина цепочек одинаковых буквы равна 2 (ZZ в первой строке, AA во второй), в третьей – 1. Берём первую строку, т.к. она находится в файле раньше. В этой строке чаще других встречаются буквы Z и A (по 2 раза), выбираем букву A, т. к. она стоит раньше в алфавите. В ответе для этого примера надо записать A6, так как во всех строках файла буква A встречается 6 раз.

Решение:

Для считывания построчно файла, будем использовать конструкцию, как в задании 17. В начале найдём строчку, содержащую самую длинную цепочку стоящих подряд одинаковых букв.

f=open('24-164.txt')
kmax=0
count=0
n=-1
for s in f.readlines():
    count=count+1
    k=1
    for i in range(0, len(s)-1):
       if s[i]==s[i+1]:
           k=k+1
           if k>kmax:
               kmax=k
               n=count
       else:
           k=1

print(n)

Получается строка под номером 162. Переменная count считает строки по порядку. В переменную n сохраняем номер нужной строки. Опять пользуемся условием, а не функцией max, т.к. здесь нужно и обновлять kmax, и сохранять значение n. У нас условие строгое k>kmax, значит, сохранится первая строка с наибольшей искомой цепочкой.

f=open('24-164.txt')

count=0
a=[0]*150

for s in f.readlines():
    count=count+1
    k=1
    if count==162:
        for i in range(0, len(s)):
            a[ord(s[i])] = a[ord(s[i])] + 1
       
ch=''
mx=0
for i in range(0, 150):
    if a[i] > mx:
        mx=a[i]
        ch=chr(i)

print(ch)

Теперь нас интересует только строка под номером 162. Далее используем приём из прошлой задачи. Заводим массив a из 150 ячеек и используем таблицу кодов ANSI. Так определяем какая буква встретилась чаще всего в строке под номером 162. Получается буква K.

f=open('24-164.txt')
s=f.read()
print(s.count('K'))

Осталось найти количестов букв K во всём файле. Для этого используем функцию .count()

Ответ: K36582

В задаче 15 «Задача (Полезный приём)», созданы переменные k и kmax — напрасно, они не используются.

Убрал, по привычке написал.

Источник

Материалы для подготовки к ЕГЭ по информатике К. Ю. Полякова

Лицензионное соглашение

Все опубликованные ниже материалы для подготовки к ЕГЭ по информатике могут быть свободно использованы
в некоммерческих целях при условии сохранения авторства. Без письменного согласия автора
ЗАПРЕЩАЕТСЯ:

публикация материалов в любой форме, в том числе размещение материалов на других Web-сайтах;
распространение неполных или измененных материалов;
включение материалов в сборники на любых носителях информации;
получение коммерческой выгоды от продажи или другого использования материалов.

Скачивание материалов означает, что вы приняли условия этого лицензионного соглашения.

Информация (задания 4, 7, 8, 11)

Системы счисления (задание 14)

Логика (задания 2, 15)

Пользовательский курс (задания 1, 3, 9, 10, 13)

Алгоритмизация и основы программирования (задания 5, 6, 12, 16−27)

Ответы и решения

———-
Оригинал страницы: http://kpolyakov.spb.ru/school/ege.htm.

Источник

Автор материалов — Лада Борисовна Есакова.

Системы счисления и их разновидности.

Система счисления – это способ представления, записи чисел с помощью письменных знаков. Количество этих самых знаков (цифр), используемых для записи чисел, называется основанием системы счисления.

Различных систем счисления у разных народов существовало великое множество. Но все их можно поделить на непозиционные и позиционные. Позиционные системы в свою очередь подразделяются на однородные и смешанные.

1. Непозиционные системы счисления.

В непозиционных системах счисления число, обозначаемое цифрой, не зависит от положения цифры в записи числа.

Самым простым примером непозиционной системы счисления является единичная (унарная) система счисления. Это запись числа с помощью повторения зарубок на дощечке или узелков на веревке. Все зарубки, узелки или другие «цифры» абсолютно одинаковы, а потому их порядок не имеет значения, число получается простым суммированием количества символов.

Унарной системой счисления до сих пор пользуются маленькие дети, показывая количество на пальцах.

Еще одной используемой до сих пор почти непозиционной системой счисления является Римская:

Она названа почти непозиционной, потому что в Римской системе, кроме обычного сложения цифр в числе, действует правило: если младшая цифра стоит слева от старшей, она вычитается из суммы.
Т.е. число , а число

Непозиционных систем счисления известно очень много, но мы завершим на этом их рассмотрение. Использование непозиционных систем неудобно, а для очень больших чисел практически невозможно, и к тому же нет возможности записать дроби.

2. Позиционные системы счисления.

В позиционных системах счисления число, обозначаемое цифрой, зависит от положения цифры в записи числа.
Самой популярной позиционной системой является, конечно же, десятичная.

Мы видим, что числа 15 и 51 имеют совсем разные значения, хотя состоят из одних и тех же цифр. Разница обусловлена положением цифры в числе.

Но десятичная система ничем не лучше и не хуже другой позиционной системы, она просто привычная. Число 10 выбрано основанием по количеству пальцев на двух руках (для удобства счета). Однако, в Китае популярной была пятиречная система счисления (по количеству пальцев на одной руке), а двадцатиричная система использовалась у Ацтеков, Майя и некоторых народов Африки (по количеству пальцев на ногах и руках).

Еще одной известной позиционной системой счисления является двенадцатиричная (считали фаланги пальцев (кроме большого) на руке. Элементы двенадцатиричной системы сохранились в Англии: 1 фут = 12 дюймов, 1 шиллинг = 12 пенсов.

Ну и, наконец, незаменимая в наш компьютерный век двоичная система. Почему именно двоичная? Да потому что у компьютера только 2 «пальца», точнее два состояния: «есть ток», «нет тока».

2.1. Однородные системы счисления.

В однородной системе в каждой позиции числа может находиться любая цифра. Примером может быть запись числа в любой позиционной системе счисления (десятичной, двоичной и пр.). Т.е. когда мы пишем число в десятичной системе, в любой позиции мы можем написать цифру от 0 до 9.

2.2. Смешанные системы счисления.

В смешанной системе счисления набор используемых цифр может отличаться в зависимости от позиции. В качестве примера удобно рассмотреть запись времени в формате ЧЧ.ММ.СС (часы.минуты.секунды). В качестве часов может быть использовано число от 00 до 23, в качестве минут и секунд – число от 00 до 59.

Системы счисления. Перевод из одной системы в другую.

1. Порядковый счет в различных системах счисления.

В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».

Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.

Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.

Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение rm X_2 для 2-ной системы, rm X_3 для 3-ной и т.д.):

$rm X_{10}$
0	0	0	0
1	1	1	1
2	10	2	2
3	11	10	3
4	100	11	4
5	101	12	10
6	110	20	11
7	111	21	12
8	1000	22	13
9	1001	100	14
10	1010	101	20
11	1011	102	21
12	1100	110	22
13	1101	111	23
14	1110	112	24
15	1111	120	30

Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( rm A и rm B ):

$rm X_{10}$	$rm X_{12}$
0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
10
11
12	10
13	11
14	12
15	13

2.Перевод из десятичной системы счисления в любую другую.

Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.

Пример 1. Переведем десятичное число 46 в двоичную систему счисления.

Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.

Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.

$rm 934=3A6_{16}$

3. Перевод из любой системы счисления в десятичную.

Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.

$325_{10}=5+2 cdot 10 + 3 cdot 100.$

Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:

3;2;1;0

Это и есть десятичная запись нашего числа, т.е. $1201_3 = 46_{10}.$

Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.

$511_8=329_{10}.$

Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.

$1151_{16}=4433_{10}.$

4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).

Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.

Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. 8=2^3 ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:

Таблицу соответствия мы научились строить в п.1.

$rm X_{2}$
0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7

Т.е.

Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.

$rm X_{2}$	$rm X_{16}$
0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

$rm 1100001111010110_2 = 1100;0011;1101;0110_2 = C3D6_{16}.$

5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.

Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.

Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.

Для этого каждую цифру числа заменим группой из 4 цифр (т.к. 16=2^4 ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:
$rm C_{16}=1100_2$
$rm 3_{16}=0011_2$
$rm A_{16}=1010_2$
$rm 6_{16}=0110_2$

$rm C3A6_{16}=1100;0011;1010;0110_2.$

Десятичные дроби и смешанные числа в разных системах счисления.

Автор — Лада Борисовна Есакова.

Перевод целых чисел из одной системы счисления в другую обычно не вызывает проблем. А вот необходимость перевести десятичную дробь или смешанное число (число с целой и дробной частью) из системы в систему часто ставит в тупик даже сильных учеников.

1. Перевод смешанного числа в десятичную систему счисления из любой другой.

Для перевода смешанного числа в десятичную систему из любой другой следует пронумеровать разряды числа, начиная с нуля, справа налево от младшего целого разряда. Разряды дробной части нумеруются слева направо от -1 в убывающем порядке. Теперь представим число в виде суммы произведений его цифр на основание системы в степени разряда числа и ответ готов.

Пример 1.

Переведите число 105,4 из восьмеричной системы в десятичную.

Решение:

Пронумеруем целые разряды числа справа налево от 0, дробные – слева направо от -1 :

Посчитаем сумму произведений цифр числа на 8 (основание системы) в степени разряда числа: $4*8^{-1} + 5*8^{0} + 0*8^{1} + 1*8^{2} = 0,5 + 5 + 0 + 64 = 69,5_{10}$

Ответ: $69,5_{10}$

2. Перевод десятичных дробей из десятичной системы счисления в любую другую.

Для перевода десятичной дроби из десятичной системы в любую другую следует умножать дробь, а затем дробные части произведений, на основание новой системы пока дробная часть не станет равной 0 или до достижения указанной точности. Затем целые части выписать, начиная с первой.

Пример 2

Переведите десятичное число 0,816 в двоичную систему с точностью до сотых.

Решение:

Умножаем дробь 0,816, а затем дробную часть произведения (0,632) на 2 и выписываем целые части, начиная с первой:

$0,816_{10} = 0,11_{2}$

Ответ: $0,11_{2}$

Пример 3.

Переведите десятичное число 0,8125 в восьмеричную систему.

Решение:

Умножаем дробь 0,8125, а затем дробную часть произведения (0,5) на 8 и выписываем целые части, начиная с первой:

$0,8125_{10}=0,64_{8}$

Ответ: $0,64_{8}$

3. Перевод смешанных чисел из десятичной системы счисления в любую другую

Если необходимо перевести смешанное число из десятичной системы в любую другую, следует перевести целую и дробную части, а затем записать, разделив десятичной запятой.

Пример 4.

Сколько единиц в двоичной записи десятичного числа 14,125?

Решение:

Переведем целую часть числа в двоичную систему:

Переведем дробную часть числа в двоичную систему:

Соединим целую и дробную части:

$14,125_{10}=1110,001_{2}$
14,12510 = 1110,0012

Количество единиц равно 4.

Ответ: 4

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задача №1. Перевод из одной системы в другую, сравнение чисел в различных системах.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.03.2023

Источник