Теория для 1 задания егэ математика профиль 2023

7 сентября 2017

В закладки

Обсудить

Жалоба

Теория к заданиям первой части ЕГЭ по математике

Задачи 1-12 профильного уровня.

→ Решение задач на проценты: 1.pdf
→ Чтение графиков: 2.pdf
→ «Теория вероятностей»: 4.pdf
→ «Уравнения»: 5.pdf
→ Планиметрия: 6.pdf
→ «Производная»: 7.pdf
→ «Стереометрия»: 8.pdf
→ «Преобразование выражений»: 9.pdf
→ Задачи с физическим содержанием: 10.pdf
→ Движение. Работа. Смеси. Прогрессия: 11.pdf
→ Максимум (минимум) функции. Наибольшее (наименьшее): 12.pdf

Авторы: Александр и Наталья Крутицких | matematikalegko.ru

Источник

За это задание ты можешь получить 1 балл. На решение дается около 3 минут. Уровень сложности: базовый.
Средний процент выполнения: 80.6%
Ответом к заданию 1 по математике (профильной) может быть целое число или конечная десятичная дробь.

Разбор сложных заданий в тг-канале

Задачи для практики

Задача 1

В треугольнике $ABC$ угол $C$ равен $90^°$, $BC=7$, $cos A={3} / {5}$
(см. рис.). Найдите $AB$.

Решение

$sin A = {BC}/{AB}$.

$sin^2A + cos^2A = 1$, то есть $sin A = √{1 — {9}/{25}} = {4}/{5}$.

${4}/{5} = {7}/{AB}, AB = {35}/{4}=8.75$.

Ответ: 8.75

Задача 2

Угол $ACO$ равен $32^°$. Его сторона $CA$ касается окружности с центром в точке $O$. Сторона $CO$ пересекает окружность в точках $B$ и $D$ (см. рис.). Найдите градусную меру дуги $AD$ окружности, заключённой внутри этого угла. Ответ дайте в градусах.

Решение

$∠ AOC=90°-∠ ACO$, так как $∠ OAC=90°$ (радиус, проведённый в точку касания, перпендикулярен касательной). $∠ AOC=90°-32°=58°$. $∠ AOC$ — центральный и измеряется дугой $AB$, то есть $⌣ AB=58°$. Отсюда: дуга $AD$ равна $180°-58°=122°$, так как дуга $DB=180°$.

Ответ: 122

Задача 3

Через концы $A$ и $B$ дуги окружности с центром $O$ проведены касательные $AC$ и $BC$ (см. рис.). Меньшая дуга $AB$ равна $48^°$. Найдите угол $ACB$. Ответ дайте в градусах.

Решение

$∠C AB = ∠C BA$, как углы между хордой и касательной, они измеряются половиной дуги $AB$, то есть $∠C AB = {1}/{2} ︶ AB$ и $∠C BA = {1}/{2} ︶ AB$.

Отсюда, $∠AC B = 180°- ︶AB = 180° — 48° = 132°$.

Ответ: 132

Задача 4

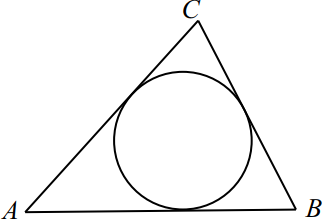
Периметр треугольника равен $73$, а радиус вписанной окружности равен $4$. Найдите площадь этого треугольника.

Решение

$S_{ABC} = p · r$, где $p$ — полупериметр треугольника, а $r$ — радиус вписанной окружности, тогда $S_{ABC} = {73}/{2} · 4 = 146$.

Ответ: 146

Задача 5

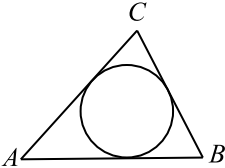
Периметр треугольника равен $40$, а радиус вписанной окружности равен $3$. Найдите площадь этого треугольника.

Решение

$S_{ABC} = p · r$, где $p$ — полупериметр треугольника, а $r$ — радиус вписанной окружности, тогда $S_{ABC} = {40}/{2} · 3 = 60$.

Ответ: 60

Задача 6

Отрезки $MN$ и $AB$ — диаметры окружности с центром $O$ (см. рис.). Угол $AOM$ равен $28^°$. Найдите вписанный угол $MNB$. Ответ дайте в градусах.

Решение

$∠AOM$ — центральный, он измеряется дугой $AM$, то есть $︶AM = 28°$. $AB$ — диаметр, значит $︶AB = 180°$, а $︶MB = 180° — 28° = 152°$. $∠MNB$ — вписанный и он измеряется половиной дуги $MB$, то есть $∠MNB = 76°$.

Ответ: 76

Задача 7

Отрезки $MN$ и $AB$ — диаметры окружности с центром $O$ (см. рис.). Угол $MOB$ равен $116^°$. Найдите вписанный угол $MAB$. Ответ дайте в градусах.

Решение

$∠ MOB$ — центральный, он измеряется дугой $MB$. $∠ MAB$ — вписанный и он измеряется половиной дуги $MB$, то есть $∠ MAB={116°} / {2}=58°$.

Ответ: 58

Задача 8

В треугольнике $ABC$ равны боковые стороны $AC=BC$, $AH$ — высота, $AB=15$,
$sin ∠ BAC=0{,}6$ (см. рис.). Найдите $BH$.

Решение

В равнобедренном треугольнике углы при основании равны.

$∠BAC = ∠ABC, sin ∠ABC = {AH}/{AB}, AH = AB sin ∠ABC. AH = 15 · 0.6 = 9$.

Из $△AHB: HB = √{AB^2 — AH^2} = √{225 — 81} = √{144} = 12$.

Ответ: 12

Задача 9

В треугольнике $ABC$ $AC=BC$, $AH$ — высота, $AB=15$, $sin ∠ BAC={√ {5}} / {3}$ (см. рис.). Найдите $BH$.

Решение

В треугольнике напротив равных сторон лежат равные углы. $∠ BAC=∠ ABC$, $sin ∠ ABC={AH} / {AB}$, $AH=AB sin ∠ ABC$. $AH=15⋅ {√ {5}} / {3}=5√ {5}$. Из $▵ AHB:$ $HB=√ {AB^2-AH^2}=√ {225-125}=√ {100}=10$.

Ответ: 10

Задача 10

В треугольнике $ABC$ угол $C$ равен $90^°$, $BC=9$, $sin A={4} / {11}$ (см. рис.). Найдите $AB$.

Решение

$sin A = {BC}/{AB}, AB = {BC}/{sin A} = {9}/{{4}/{11}} = {99}/{4} = 24.75$.

Ответ: 24.75

Задача 11

Найдите периметр прямоугольника, если его площадь равна $224$, а отношение соседних сторон равно ${2} / {7}$.

Решение

Рассмотрим прямоугольник $ABCD$

$AD : AB = 2 : 7, S_{ABCD} = AD · AB$

$S_{ABCD} = 224$, тогда $224 = AD · AB$

Пусть $x$ — некоторое положительное действительное число, тогда $AD = 2x, AB = 7x$

Отсюда, $224 = 2x · 7x$

$224 = 14x^2$

$x^2 = {224}/{14}$

$x^2 = 16$

$x = 4$

Следовательно, $P = 2(AD+AB) = 2(2·4+7·4) = 2·4(2+7) = 8·9 = 72$.

Ответ: 72

Задача 12

Найдите периметр прямоугольника, если его площадь равна $48$, а отношение соседних сторон равно $3:4$.

Решение

Рассмотрим прямоугольник $ABCD$ (см. рис.). $AD:AB=3:4$, $S_{ABCD}=AD⋅ AB$; $S_{ABCD}=48$, тогда
$48=AD⋅ AB$. Пусть $k$ — некоторое положительное действительное число и
$AD=3k$, $AB=4k$. Отсюда $48=3k⋅ 4k$; $48=12k^2$; $k^2=4$, $k=2$. Следовательно, $P=2(AD+AB)=2(3⋅ 2+4⋅ 2)=28$.

Ответ: 28

Задача 13

Площадь прямоугольника равна $22$. Найдите его большую сторону, если она на $9$ длиннее меньшей стороны.

Решение

$S_{ABCD} = AB·CB$.

Обозначим большую сторону через $x$, тогда меньшая сторона $x — 9$. Итак, $22 = x(x — 9)$

$ x^2 — 9x — 22 = 0$

$D = 81 + 88 = 169 = 13^2$

$ x = {9±13}/{2}$

$ x_1 = 11$

$ x_2 = -2$ (не подходит).

Ответ: 11

Задача 14

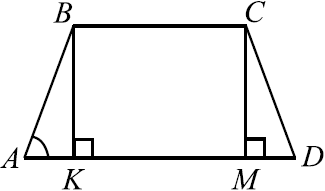
Основания равнобедренной трапеции равны $15$ и $9$. Высота трапеции равна $6$. Найдите тангенс острого угла.

Решение

Рассмотрим трапецию $ABCD$. Пусть $AB = CD, BK$ и $CM$ — высоты. Тогда $AK = MD$ и $AD = BC + 2AK$.

$tg ∠BAD = {BK}/{AK}, AK = {AD — BC}/{2} = {15 — 9}/{2} = 3, BK = 6$ (по условию). $tg ∠BAD = {6}/{3} = 2$.

Ответ: 2

Задача 15

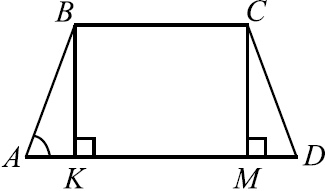
Основания равнобедренной трапеции равны $14$ и $6$. Высота трапеции равна $7$. Найдите тангенс острого угла.

Решение

Рассмотрим трапецию $ABCD$. Пусть $AB = CD, BK$ и $CM$ высоты. Тогда $AK = MD$ и $AD = BC + 2AK$.

$tg ∠BAD = {BK}/{AK}, AK = {AD — BC}/{2} = {14 — 6}/{2} = 4, BK = 7$ (по условию). $tg ∠BAD = {7}/{4} = 1.75$.

Ответ: 1.75

Задача 16

В треугольнике $ABC$ угол $C$ равен $90^°$, $AC=6√ {3}$, $tg A={√ {3}} / {3}$ (см. рис.). Найдите $AB$.

Решение

$tgA = {BC}/{AC}, {√3}/{3} = {BC}/{6√3}, BC = {6√3·√3}/{3} = 6$.

Из $△ABC: AB^2 = AC^2 + BC^2$;

$AB^2 = (6√3)^2 + 6^2 = 36·3 + 36 = 36·4 = 144, AB = 12$.

Ответ: 12

Задача 17

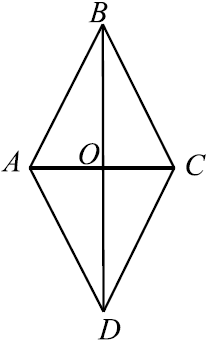
Найдите площадь ромба, если его диагонали равны $5$ и $16$.

Решение

Рассмотрим ромб $ABCD$.

$S_{ABCD} = {1}/{2}d_1d_2$, где $d_1$ и $d_2$ — диагонали ромба.

$S_{ABCD} = {1}/{2}·5·16 = 40$.

Ответ: 40

Задача 18

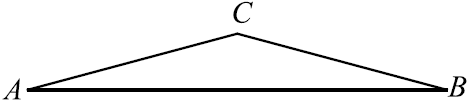
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен $150^°$. Боковая сторона треугольника равна $12$. Найдите площадь этого треугольника.

Решение

Пусть в $△ABC ∠C = 150°, AC = CB$.

$S_{ACB} = {1}/{2}AC·CB·sin∠ACB = {1}/{2}·12·12·sin150° = 72·sin 30° =72·{1}/{2} = 36$.

Ответ: 36

Задача 19

Угол при вершине, противолежащей основанию равнобедренного треугольника, равен $30^°$. Боковая сторона треугольника равна $7$. Найдите площадь этого треугольника.

Решение

Пусть в $▵ ABC$ $∠ C=30°$, $AC=BC=7$ (см. рис.). $S_{ACB}={1} / {2} AC⋅ CB⋅ sin ∠ ACB={1} / {2}⋅ 7⋅ 7⋅ sin 30°={1} / {2}⋅ 49⋅ {1} / {2}={49} / {4}=12{,}25$.

Ответ: 12.25

Задача 20

Периметр прямоугольника равен $28$, а площадь $48$. Найдите меньшую сторону прямоугольника.

Решение

Пусть $x$ и $y$ — две стороны прямоугольника. Из условия следует система уравнений:
${{table {2(x+y)=28{,}}; {xy=48{.}};}$

Из первого уравнения системы: $x+y=14$

$y=14-x$.

Подставляя выражение для переменной $y$ во второе уравнение системы, получим:

$x(14-x)=48$

$x^2-14x+48=0$

$x_1=8$

$x_2=6$

Тогда $y_1=14-8=6$

$y_2=14-6=8$

Следовательно, меньшая сторона прямоугольника равна $6$.

Ответ: 6

Рекомендуемые курсы подготовки

Источник

Профильный ЕГЭ по математике сдают не все. Это вариант для тех, кто намерен поступить в технический Вуз или освоить профессию, связанную с экономикой или математикой. Чтобы сдать данный экзамен, вам нужно будет показать глубокие знания предмета.

Основные требования

Во время сдачи базового госэкзамена вам понадобятся познания, которые были получены из школьного курса алгебры и геометрии. Вы должны уметь решать разнообразные неравенства и уравнения, а также знать терминологию и алгоритмы решения разных задач. А вот чтобы выполнить тесты высокой сложности, вы должны знать:

  • планиметрию;
  • стереометрию;
  • прогрессию.

Помимо этого от учащегося потребуется знание финансовой математики и умение работать с параметрическими системами, уравнениями, неравенствами, процентами.

Во время подготовки вам придется повторить теорию. При этом вы должны совмещать ее с практикой, чтобы уметь применять все выученные правила, теоремы, аксиомы.

Принципы подготовительного процесса

С самого начала года необходимо готовиться к ЕГЭ. Благодаря этому можно качественно усвоить весь необходимый материал.

Желательно повторять вслух все прочитанное, чтобы запомнить правила.

Некоторые аксиомы и теоремы нужно будет просто выучить. А после этого применять их при работе с тренировочными упражнениями.

Если вы готовитесь вместе с одноклассниками, контролируйте друг друга. Так материал быстрее усвоится.

Анализируйте ошибки во время решения задач. Благодаря этому вы значительно продвинетесь в подготовке.

Не забывайте про решение практических заданий. Во время сдачи тестирования этот навык вам очень пригодится.

Источник

Профильный уровень ЕГЭ по математике, в отличие от базового, более сложный и его должны сдавать выпускники, планирующие поступать в вузы на технические, инженерные, экономические специальности.

Задания в экзаменационной работе обычно выстроены от простого к сложному и первое задание это, как правило, самое легкое, как бы разминочное. Так и Задание 1 ЕГЭ по профильной математике – это задание базового уровня на знания элементарной математики, представляющее собой простейшую задачу на несложные арифметические действия.

• Вид задания — текстовая задача.

• Тип — с кратким ответом.

• Сложность — базовая.

• Максимальное количество получаемых баллов — 1.

• Период выполнения — 120 секунд.

Необходимые знания

1 задание егэ по математике

1-е Задание по профильной математике — это текстовая задача базового уровня сложности. Ответ должен быть дан в краткой форме в виде целого числа или конечной десятичной дроби, оценивается в 1 балл.

 Для выполнения задания необходимо знать:

  • арифметические действия;
  • простые и десятичные дроби и действия с ними;
  • проценты;
  • пропорции;
  • перевод одних единиц измерения в другие;
  • построение математической модели задачи;
  • интерпретация результата решения задачи;
  • учет реальных ограничений в интерпретации результата.

5 типов заданий

Наиболее часто встречаются задания пяти типов:

  • задачи, связанные с жизненными ситуациями (определение времени, веса, стоимости и т.д.);
  • на вычисление процентов;
  • на округление результата в большую или меньшую сторону;
  • на пропорции;
  • различные комбинации четырех предыдущих вариантов. 

Опыт подготовки к ЕГЭ прошлых лет показал, что у учащихся часто возникают трудности с решением задач на перевод из одних единиц измерения в другие (часы в сек., км в см, кг в гр. и т. п.). Следует обратить внимание на то, что часы и минуты считаются не в десятичной системе, ведь в часе – 60 минут, а в минуте – 60 секунд. Наиболее эффективным способом подготовки к профильной математике являются курсы «Уникум» РУДН по математике. Здесь вы получите разбор всех типов заданий, теорию и практику, пробные варианты ЕГЭ на протяжении всей подготовки. Преподаватель курсов, в том числе, сделает разбор 1-го задания ЕГЭ по математике профильного уровня.

Примеры

6 примеров по математике 1 заданиеПример 1

Автомобиль проехал 80 миль, в 1 миле 1609,34 метров. Сколько километров проехал автомобиль? Ответ округлить до целого значения.

Решение:

Определяем сколько км в 1 миле: 1 миля=1609,34 м:1000 м=1,60934 км

Сколько км проехал автомобиль: 80 миль*1,60934 км=128,7472 км

Округляем до целого значения по правилам математического округления: 128,7472  км

Ответ: 129

Пример 2

В магазине по акции продаются шоколадки. Обычная цена 1 шоколадки 35 рублей. По акции 3 шоколадки продаются по цене 2-х. Какое максимальное количество шоколадок может по акции приобрести покупатель, если он готов потратить на них не более 300 рублей?

Решение:

Определяем стоимость 3 шоколадок по акции: 2 шок.*35 руб.+1 шок.*0 руб.=70 руб. 

При продаже по акции 3 шоколадки являются одной товарной позицией. Определим, сколько таких товарных позиций можно купить на 300 руб.: 300 руб.:70 руб.=4,29

Округляем до целого, т.к. шоколадки продаются только по 3 шт.: 4*3 шок.= 12 шок.

Ответ: 12

Пример 3

Площадь стен в ванной составляет 23,8 м2. Сколько понадобится пластиковых панелей для отделки стен, если панель имеет размер 40 Х 120 см.

Решение:

Переведем размеры 1 панели из см в м: 40 см:100=0,4 м и 120 см:100=1,2 м

Площадь 1 панели в м2: 0,4м*1,2м=0,48 м2

В 23,8 м2 уложится: 23,8 м2:0,48 м2=49,58 шт.

Поскольку панели продаются целиком, для покрытия всей площади понадобится 50 панелей.

Ответ: 50

Пример 4

Средняя скорость полета самолета составляет 360 км/час. Определить его среднюю скорость в м/сек.

Решение:

Переводим км в метры: 360*1000 м=360 000 м

Часы в минуты: 1 час=60 мин, минуты в секунды: 60 мин=60*60сек= 3600 сек

Определяем скорость: 360 000 м:3600 сек=100 м/сек

Ответ: 100

Пример 5

Поезд отправился из Самары в Москву в 22 часа 10 минут (время московское) и прибыл в Москву в 10 часов 10 минут на следующие сутки. Сколько часов поезд находился в пути?

Решение:

В день отбытия из Самары поезд был в пути: 24 ч-22 ч 10 мин=23 ч 60 мин–22 ч 10 мин=1 ч 50 мин

В день прибытия поезд был в пути: 10 ч 10 мин

Общее время в пути: 1 ч 50 мин+10 ч 10 мин=11 ч 60 мин=12 ч

Ответ: 12

Пример 6

Олег живет в 9-этажном многоподъездном доме. На каждом этаже находится по 4 квартиры. Олег живёт в квартире №81. Укажите номер подъезда, в котором живёт Олег?

Решение:

Количество квартир в одном подъезде: 9 * 4=32

Значит квартиры распределяются по подъездам так:

1-й подъезд – с 1-й по 32-ю

2-й – с 33-й по 64-ю

3-й – с 65-й по 96-ю

Квартира №81 находится в 3-м подъезде

Ответ: 3

В Задании 1 профильной математики как правило встречаются задачи на действия с дробями в том или ином виде.

Действия с дробями

действие с дробями математика 1 заданиеДля того, чтобы получить правильный ответ на 1 задание ЕГЭ по математике, теорию нужно знать в первую очередь. Сложности у сдающих ЕГЭ возникают с дробями и задачами, где представлены дроби. Дробью называется форма представления числа. Сама дробная черта означает деление. Делимое — это числитель дроби, знаменатель — делитель. С дробями можно делать все то, что и с обычными числами: делить, умножать, складывать, вычитать.

Сложение дробей

Сложение дробей с одинаковыми знаменателями.

Пример: сложить дроби 

Числители 1-й и 2-й дроби складываются, знаменатель остается неизменным

Сложение дробей с различающимися знаменателями:

Пример: сложить дроби 

Сначала дроби нужно привести к общему знаменателю, таким знаменателем является произведение знаменателей 1-й и 2-й дроби, а числитель 1-й дроби умножается на знаменатель 2-й, числитель 2-й дроби на знаменатель 1-й. Затем числители складываются: 

Вычитание дробей проводится аналогично сложению. Просто числители не складываются, а вычитаются.

Умножение дробей

Пример: перемножить дроби: 

Просто перемножаются числители и знаменатели 

Деление дробей

Пример:  разделить 

Деление заменяем на умножение на дробь обратную дроби, на которую делим 

Как видите, задачи из Задания 1 по профильной математике легкие, на знания математики из курса младших и средних классов, что, однако не отменяет необходимость освежить в памяти эти знания и еще раз порешать эти несложные задачи. Особенно полезно решать реальные варианты заданий прошлых лет под контролем опытных преподавателей. А такую возможность и дают подготовительные курсы «Уникум» РУДН по математике.

Источник
  • Взрослым: Skillbox, Geekbrains, Хекслет, Eduson, XYZ, Яндекс.
  • 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
  • До 7 класса: Алгоритмика, Кодланд, Реботика.
  • Английский: Инглекс, Puzzle, Novakid.

ЕГЭ по профильной математике по заданиям 2022-2023

  • Задание 1
  • Задание 2
  • Задание 3
  • Задание 4
  • Задание 5
  • Задание 6
  • Задание 7
  • Задание 8
  • Задание 9
  • Задание 10
  • Задание 11
  • Задание 12
  • Задание 13
  • Задание 14
  • Задание 15
  • Задание 16
  • Задание 17
  • Задание 18
  • Взрослым: Skillbox, Geekbrains, Хекслет, Eduson, XYZ, Яндекс.
  • 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
  • До 7 класса: Алгоритмика, Кодланд, Реботика.
  • Английский: Инглекс, Puzzle, Novakid.
Источник

ЕГЭ – 2023
Алгоритм выполнения заданий 1-3.
Теория к заданиям
Подготовила
Халяпина Лариса Николаевна,
учитель русского языка и литературы
МБОУ «Гимназия №9 имени дважды
Героя Советского Союза С.Г.Горшкова»
г.о.Коломна Московской области

Задания 1 – 3
ЕГЭ – 23
Задание 1

  • 1. Внимательно прочитайте задание и необходимый отрезок текста/весь текст.
    2. Установите связь между предложением, в котором пропущено слово, и предыдущим предложением/ между предложением, в котором пропущено слово, и частью текста до этого предложения.
    3. Обратите внимание на искомую часть речи: важно подобрать слово, которое будет соответствовать заявленной характеристике. Например, в задании может быть предложено найти частицу или ограничительно-выделительную частицу. Для успешного выполнения задания важно знать не только различия между словами различных частей речи, но и разряды слов.

Задание 1
В тексте соединяются между собой не только соседние предложения, но и предложения, отделенные другими предложениями.
Между предложениями в тексте существуют различные смысловые отношения: предложения могут быть сопоставлены, противопоставлены, содержание второго предложения может раскрывать смысл первого, пояснять его и т.д.
В качестве средств связи предложений в тексте могут выступать лексические, синтаксические и морфологическиесредства, например, порядок слов, синонимы, антонимы, местоимения, союзы, синтаксический параллелизм и др.
Союз

  • Сочинительные союзы – союзы, связывающие однородные члены предложения и равноправные по смыслу простые предложения в составе сложного (сложносочиненного предложения).

Разряды сочинительных союзов

  • Соединительные: и, да (= и), не только, … но и, также, тоже, и…и, ни…ни, как,…так и; сколько…, столько и
  • Разделительные: или, или…или, либо, либо…либо, то…то, то ли…то ли, не то…не то
  • Противительные: а, но, да (= но), зато, же, однако, однако же, все же
  • Градационные: не только…, но и; не то чтобы…а; не столько…сколько
  • Присоединительные: тоже, также, да и, притом, причем
  • Пояснительные: а именно, то есть, или (= то есть)

Подчинительные союзы

  • Подчинительные союзы – союзы, которые связывают простые предложения в сложном предложении (СПП). 
  • Подчинительные союзы могут выступать в качестве средств связи между предложениями только в случае парцелляции (авторского членения текста)

Разделение подчинительных союзов на группы условно
Одни и те же союзы могут относиться к различным группам в зависимости от вопроса, который мы задаем от главного предложения к придаточному.

  • изъяснительные (что, чтобы, как, …)

    • обстоятельственные

  • времени (когда, лишь, едва, …)
  • места (где, куда, откуда, …)
  • образа действия, меры, степени (столько, настолько, так, до такой степени, до того, такой, … )
  • сравнения (как, как будто, словно, будто, точно, как бы)
  • причины (так как, потому что, …)
  • условия (если, если бы, коли, ежели, если … то,…)
  • уступки (несмотря на то, что, хотя, хоть, пускай, …)
  • цели (чтобы, дабы, с тем чтобы, …)
  • следствия (так что)

 Частицы

  • Частица – служебная часть речи, выражает различные добавочные смысловые оттенки слов и предложений, а также употребляется для образования новых слов или аналитических форм самостоятельных слов. 
  • Частицы бывают формообразующие

    •  (повелительное наклонение: пусть, пускай, давай, бы (б), да, бывало;
    условное наклонение: более, менее, самый) и смыслоразличительные (смысловые).

Разряды частиц

Отрицательные:

не, ни, вовсе не, далеко не, отнюдь не, нет

вопросительные

: неужели, разве, ли (ль), что, что ли, как

указательные

: вот, вон, это

уточняющие

: именно, как раз, прямо, точно, точь-в-точь

ограничительно-выделительные

: только, лишь, исключительно, почти, единственно, -то (я-то), всего, всего-навсего

восклицательные

: что за, ну и, как, куда как

усилительные

: даже, же, ни, ведь, уж, все-таки, ну, всё
со значением сомнения: едва ли; вряд ли
Среди частиц есть омонимичные: 
Например, ЭТО может быть как частицей, так и местоимением. 
ЧТО может быть частицей, а может быть местоимением. 
Местоимения

  • Разряды местоимений
  • Личные: я, ты, он, она, оно, мы, вы, они — во всех падежах (тебя, к нему, ее, с нами и т.д.)
  • Притяжательные: мой, твой, наш, ваш, его, ее, их — во всех падежах (моего, твоей и т.д.). Притяжательные местоимения указывают на принадлежность предмета лицу или другому предмету. 
  • Указательные: это, те, этот, таков, тот, столько, сей, оный и т.д.
  • Возвратное: себя
  • Вопросительные: кто, что, какой, каков, сколько, чей, чем, кому, кого и т.д.
  • Относительные: (те же, что и вопросительные, используются в качестве средств связи в сложноподчиненных предложениях)
  • Определительные: сам, самый, весь, всякий, каждый, иной, любой, другой, всяк, всяческий и т.д.
  • Неопределенные: некто, нечто, некоторый, некий, а также все местоимения, образованные от вопросительных местоимений приставкой кое- и частицей не, которая превращается в приставку или суффиксами -то, -либо, -нибудь.
  • Отрицательные: никто, ничто, никакой, ничей, ничего и т.д.

Числительные как средства связи

  • В качестве средств связи 

    • собирательные числительные используются без существительного, которое они определяют в количественном значении.
    Из собирательных числительных в качестве средств связи чаще других используются числительные 
    оба и двое

Наречия

  • Наречие — неизменяемая самостоятельная часть речи, которая обозначает признак действия, признака и предмета, отвечает на вопросы где, как, куда, откуда, зачем, почему и т.д. 
  • В качестве средств связи обычно выступают наречия времени, места, а также местоименные наречия в личных значениях. 

Разряды наречий
По функции:

  • Знаменательные: называют признаки действий или других признаков (громко, далеко, по-летнему)
  • Местоименные: там, так, тогда

    • По значению:
    образа действия: (как, каким образом?) так, по-летнему, по-товарищески, весело, громко, вдвое
    меры и степени: (сколько, в какой степени?) очень, чересчур, втрое, вдоволь, чуть-чуть, немного места: (где, куда, откуда?) вперед, издали, справа, вдалеке, здесь, куда-то
    времени: (когда, как долго, с каких пор, до каких пор)сегодня, ночью, давно, сейчас, послезавтра, всегда, тогда
    причины: (почему?)потому, сгоряча, поневоле
    цели: (зачем, с какой целью?)назло, нарочно, затем, назло, наперекор, специально

Вводные слова и словосочетания

  • обособляются запятыми  не являются членами предложения  к ним нельзя задать вопрос

    • Группы вводных слов 

  • Чувства говорящего (радость, злость, сожаление и т.д). К счастью, к несчастью, к ужасу, к стыду, на беду, на радость и т.д.
  •  Степень уверенности (предположение, возможность, неуверенность и т.д.). Может, может быть, по-видимому, по сути, кажется, казалось бы, бесспорно, правда, надо полагать, по сути, безусловно и т.д.
  • Связь мыслей, последовательность изложения . Итак, следовательно, к слову сказать, во-первых, во-вторых, с другой стороны, к примеру, главное, таким образом, кстати, значит, наоборот и т.д.
  • Источник сообщения. По слухам, говорят, по мнению кого-либо, на мой взгляд, по-моему, по преданию, помнится, сообщают, передают и т.д.
  • Приемы и способы оформления мыслей. Другими словами, иными словами, попросту сказать, мягко выражаясь, одним словом и т.д.
  • Призыв к собеседнику или читателю с целью привлечь внимание. Знаешь (ли), знаете (ли), пойми, извините, простите, послушайте, поверьте, согласитесь, вообразите , пожалуйста и т.д. 7
  • Оценка меры того, о чем говорится. По крайней мере, самое большее, самое меньшее и т.д.
  • Степень обычности сообщаемого. По обыкновению, бывает, бывало, случается и т.д. 
  • Выражение экспрессивности высказывания. Сказать по чести, честно говоря, по правде, по совести, смешно сказать и т.д.

 Средства связи, часто встречающиеся в 1 задании ЕГЭ 

  • Союзы.

    • То есть – пояснительный союз, который автор использует для уточнения сказанной ранее информации. 
    Но, зато, однако – противительные союзы, которые используются для противопоставления. 
    Потому что, так как, поскольку – используются, чтобы указать на причину того, о чем говорится в предыдущих предложениях. 
    Так что – используются перед выводом рассуждений. 

  • Частицы.

    • Даже – частица вносит значение уточнения и подчеркивает важность мысли. 
    Ведь, именно – эти частицы вносят значение усиления. 

Средства связи, часто встречающиеся в 1 задании ЕГЭ 

Вводные слова и конструкции:

  • Кроме того – конструкция используется, когда автор хочет дополнить ранее высказанную мысль. 
    Другими словами, иными словами – конструкция используется, если автор хочет сказать уже высказанную мысль иначе (более понятно). 
    Итак, таким образом, следовательно – автор использует данные вводные слова для подведения итога рассуждениям. 
    Конечно, разумеется, безусловно – указывают на степень уверенности в сказанных словах. 
    Например, так – вводные слова, которые используются для пояснения мысли. 
    Наоборот – вводное слово, употребляющееся для противопоставления одного предложения другому. 
    Во-первых, во-вторых, с одной стороны – автор указывает порядок следования мыслей.  

Задание 2

  • 1. В задании 2 предлагается определить, в каком значении употреблено в микротексте одно из слов. В словарной статье, данной в задании, приводится значение
  • 2. Вы уже прочитали микротекст, выполняя предыдущее задание. А теперь прочитайте его ещё раз и найдите в указанном предложении необходимое слово.
  • 3. Изучите значение сло́ва, данного в словарной статье. Не игнорируйте примеры, которые даны курсивом после каждого значения: именно они чаще всего и помогают выбрать правильный ответ.
  • 6. Лексическое значение толкуется (объясняется) в словарях часто путём подбора синонимичного слова, поэтому, чтобы проверить правильность своего выбора, подставьте в текст вместо анализируемого первое слово или словосочетание из словарной статьи. Если смысл предложения не нарушился, ваш ответ верен.

Задание 3
Задание №3 посвящено стилистическому анализу текста. Необходимо ориентироваться в такой науке, как стилистика.
Что это значит? Главным образом, то, что необходимо знать стили речи, а также уметь грамотно анализировать текст.
Задание 3

  • 1. ВНИМАТЕЛЬНО читаем предложенный текст. Читать нужно не механически, а вдумчиво. Желательно останавливаться на каждом абзаце и анализировать то, о чём говорит автор.
  • 2. ДО чтения вариантов ответов отвечаем на вопросы: какова тема текста и что хотел донести до нас автор, то есть какова проблема? Вопросы по содержанию обязательно встречаются в задании. Кроме того, это отличная тренировка для работы над №27, то есть над сочинением ЕГЭ.
  • 3. ДО чтения вариантов ответов определяем, какой стиль речи перед нами. В книжные стили входят научный, официально-деловой, публицистический и литературно-художественный стили. Разговорный стиль стоит особняком и в тренировочных КИМах не встречается.
  • 4. В соответствии с тем, каков стиль текста, разбираемся, могут ли в нём употребляться те или иные тропы и приёмы, есть ли в тексте термины, канцеляризмы, специальная лексика, определённые синтаксические конструкции, на какую аудиторию текст рассчитан. Утверждения, данные в ответах, и содержат информацию об этом.

Задание 3
Научный стиль

Это стиль, характерный для научной и учебной сфер деятельности. Используется в учебниках, справочниках, словарях и энциклопедиях. Его цель – передача объективной информации о природе, человеке и обществе, формирование научного мировоззрения.
Основные черты:
1) ясность и точность изложения;
2) подчёркнутая логичность, доказательность, обоснованность;
3) бесстрастность, объективность;
4) отсутствие эмоциональных оценок;
5) использование терминов, абстрактной лексики, а также сложных синтаксических конструкций;
6) насыщенность содержания и включение в текст цифровой и графической информации, знаков, схем.

Публицистический стиль
Это стиль, характерный для многих текстов, предлагаемых в КИМах ЕГЭ по русскому языку. Это стиль газет, журналов, выступлений перед общественностью, очерков. Его цели – воздействие на общественное мнение и информирование.
Основные черты:
1) логичность;
2) образность и эмоциональность;
3) оценочность (автор может прямо выразить своё мнение, дать оценку);
4) общедоступность и призывность (часто можно увидеть фигуры речи: риторические вопросы, восклицания, обращения);
5) точность, обоснованность;
6) общественная важность тематики;
7) заимствование средств и черт других стилей.
Литературно-художественный стиль

  • Это стиль художественной литературы. Его цель – передача информации о мире через художественные образы, эстетическое воздействие на читателя.
  • Основные черты:
  • образность, выразительность (достигается благодаря использованию средств художественной выразительности);
  • часто наличие вымысла;
  • субъективность оценок;
  • использование внелитературных элементов: просторечий, диалектизмов, жаргонных слов – в соответствии с задачей автора;
  • использование слов в переносных значениях;
  • использование средств всех других стилей в соответствии с эстетическим и идейным замыслом автора.

Официально-деловой стиль

  • Это стиль, использующийся в сфере деловых отношений, а также в сфере правовых отношений и управления, которая охватывает международные отношения, юриспруденцию, экономику, правительственную деятельность и т.д. Это юридические документы, в том числе тексты законов, нормативно-правовых актов, деловые бумаги: уставы, справки, инструкции, коммерческая корреспонденция, заявления, протоколы. Цель – передача информации (предписание, извещение, констатация) и формирование правового сознания. Основные черты:
  • 1) стереотипность, стандартизированность изложения, в том числе наличие определённой формы;
  • 2) точность изложения и использование канцелярских штампов;
  • 3) неэмоциональность;
  • 4) выражение долженствования;
  • 5) частое употребление отглагольных существительных и производных предлогов.

Разговорный стиль

  • Стиль повседневного неофициального общения. Цель – обмен мнениями, впечатлениями, новой информацией. Основные черты:

    • 1) непринуждённость и эмоциональность;
    2) использование разговорной лексики и фразеологии, сленга, жаргонизмов;
    3) оценочность;
    4) использование неполных предложений, междометий, вводных слов, обращений;
    5) диалогическая устная форма.

Информационные источники

  • https://dzen.ru/a/Ybd4aFBsDWS0mbyx
  • https://rustutors.ru/egeteoriya/1134-zadanie-1.html
  • https://rustutors.ru/egeteoriya/egepraktika/2637-zadanie-1-3-praktika-egje-po-russkomu-jazyku-2022.html
Источник
ЕГЭ по математике профиль

Материал для отработки заданий №1 в ЕГЭ по профильной математике — теория и практика.

Задание №1 в варианте ЕГЭ по математике профильного уровня  – одно из самых легких. И тем не менее ученики часто ошибаются, решая такие задачи. Почему?

Потому что не прочитали условие или допустили арифметическую ошибку.

Внимательно читайте условие и проверяйте решение.

Задачи в разъяснениях специально подобраны так, чтобы представить все возможные типы заданий.

Автор: Алькаева Лариса Рахимовна

→ скачать конспект

→ скачать практические задания

Виды задач в задании №1:

— вычисления, простейшие уравнения и пропорции;

— задачи на округление (с недостатком, с избытком);

— задачи на проценты

Источник информации: vk.com/club169850563

Связанные страницы:

Источник

Понравилась статья? Поделить с друзьями:
  • Теория егэ математика профиль пифагор
  • Теория егэ литература фипи
  • Теория егэ история сдать егэ
  • Теория егэ история раздробленность
  • Теория егэ информатика скачать