Планиметрия
Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.
Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)
- Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
- Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Признаки подобия треугольников:
- Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Площади фигур
Площадь треугольника
- $S={a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне $а$
- $S={a·b·sinα}/{2}$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
- Формула Герона $S=√{p(p-a)(p-b)(p-c)}$, где $р$ — это полупериметр $p={a+b+c}/{2}$
- $S=p·r$, где $r$ — радиус вписанной окружности
- $S={a·b·c}/{4R}$, где $R$ — радиус описанной окружности
- Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ — катеты прямоугольного треугольника.
- Для равностороннего треугольника $S={a^2 √3}/{4}$, где $а$ — длина стороны.
Площади четырехугольников
Прямоугольник
$S=a·b$, где $а$ и $b$ — смежные стороны.
Ромб
$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ — диагонали ромба
$S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
Трапеция
$S={(a+b)·h}/{2}$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
Квадрат
$S=a^2$, где $а$ — сторона квадрата.
Параллелограмм
$S=a·b·sinα$, где $а$ и $b$ — длины сторон параллелограмма, а $α$ — угол между этими сторонами.
Пропорциональные отрезки в прямоугольном треугольнике
В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
$CD^2=DB·AD$
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
$CB^2=AB·DB$
$AC^2=AB·AD$
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.
$AC·CB=AB·CD$
Метрические соотношения в окружности
1. Две касательные, проведенные к окружности из одной точки, равны, и центр окружности лежит на биссектрисе угла между ними.
2. Если хорды $АС$ и $BD$ пересекаются в некоторой точке $N$, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
$AN·NC=BN·ND$
Пример:
Хорды $АВ$ и $CD$ пересекаются в точке $Е$. Найдите $ЕD$, если $АЕ=16, ВЕ=9, СЕ=ED$.
Решение:
Если хорды $АВ$ и $СD$ пересекаются в некоторой точке $Е$, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
$AЕ·ЕВ=СЕ·ЕD$
Так как $СЕ=ED$, данное выражение можно записать в виде:
$ЕD^2=AЕ·ЕВ$
Подставим числовые значения
$ЕD^2=16·9$
$ЕD=√{16·9}=4·3=12$
Ответ: $12$
3. Если из одной точки к одной окружности проведены две секущие, то произведение первой секущей на ее внешнюю часть равно произведению второй секущей на свою внешнюю часть.
$АС·ВС=EC·DC$
4. Если из одной точки к окружности проведены секущая и касательная, то произведение секущей на ее внешнюю часть равно квадрату длины касательной.
$BD·СB=AB^2$
Вписанные и описанные окружности для четырехугольников.
1. Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
$АВ+CD=BC+AD$
2. Если сумма противоположных углов четырехугольника равна $180°$, то только тогда около него можно описать окружность.
$∠В+∠D=180°$
$∠A+∠C=180°$
Вневписанные окружности
Вневписанной окружностью треугольника называется окружность, касающаяся одной из его сторон и продолжений двух других.
Для каждого треугольника существует три вневписанных окружности, которые расположены вне треугольника, центрами вневписанных окружностей являются точки пересечения биссектрис внешних углов треугольника.
Точки $О_1, О_2$ и $О_3$ – центры вневписанных окружностей.
Связь площади треугольника с радиусами вневписанных окружностей.
Введем обозначения:
$S$ — площадь треугольника;
$p$ — полупериметр треугольника;
$a, b, c$ — стороны треугольника;
$r_a, r_b, r_c$ — радиусы вневписанных окружностей касающиеся соответственно сторон $a, b$ и $c$;
Для данных обозначений справедливы равенства:
$r_a={S}/{p-a};$
$r_b={S}/{p-b};$
$r_c={S}/{p-c}.$
Пример:
В прямоугольном треугольнике $АВС$ угол $С=90°, АС=6, ВС=8$. Найдите радиус вневписанной окружности, касающейся гипотенузы.
Решение:
Радиус вневписанной окружности, касающейся стороны $АВ$ равен:
$r_{АВ}={S}/{p-АВ}$, где $S$ — площадь треугольника, $р$ — полупериметр треугольника.
Чтобы подставить в формулу данные, найдем сначала площадь треугольника и его полупериметр.
Площадь прямоугольного треугольника равна половине произведения катетов:
$S={АС·АВ}/{2}={6·8}/{2}=24$
Нам неизвестна гипотенуза, найдем ее по теореме Пифагора:
$АВ=√{АС^2+СВ^2}=√{6^2+8^2}=√{100}=10$
Зная все стороны, вычислим полупериметр:
$р={6+8+10}/{2}=12$
Теперь можем все данные подставить в формулу нахождения радиуса вневписанной окружности:
$r_{АВ}={S}/{p-АВ}={24}/{12-10}={24}/{2}=12$
Ответ: $12$
Биссектриса
Биссектриса – это линия, которая делит угол пополам.
Свойства биссектрисы:
1. В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.
2. Если точка лежит на биссектрисе, то расстояния от неё до сторон угла равны.
$AD=DC$
3. Три биссектрисы в треугольнике пересекаются в одной точке, эта точка является центром вписанной в треугольник окружности.
4. Биссектриса угла в параллелограмме отсекает равнобедренный треугольник.
5. Биссектрисы смежных углов перпендикулярны.
6. В треугольнике биссектриса угла делит противоположную сторону на отрезки, отношение которых такое же, как отношение сторон треугольника, между которыми эта биссектриса прошла.
${AB}/{AC}={BA_1}/{A_1C}$
7. Для нахождения длины биссектрисы справедлива формула:
$АА_1=√{АВ·АС-ВА_1·А_1 С}$
Медиана
Медиана — это линия, проведенная из вершины треугольника к середине противоположной стороны.
Свойства медиан:
1. Медиана делит треугольник на два равновеликих треугольника, т.е. на два треугольника, у которых площади равны.
$S_1=S_2$
2. Медианы пересекаются в одной точке и этой точкой делятся в отношении два к одному, считая от вершины.
3. В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы и радиусу описанной около этого треугольника окружности.
4. Для нахождения длины медианы, проведенной к стороне «с», справедлива формула:
$М_с={√{2(а^2+b^2)-c^2}}/{2}$
Высота
Высота в треугольнике — это линия, проведенная из вершины треугольника к противоположной стороне под углом в 90 градусов.
$BB_1$ — высота
Свойства высот:
1. Три высоты (или их продолжения) пересекаются в одной точке.
2. При пересечении двух высот получаются подобные треугольники:
$∆АА_1 В~∆СС_1В;$
$∆АС_1 М~∆СМА1$
3. Угол между высотами в остроугольном треугольнике равен углу между сторонами, к которым эти высоты проведены.
4. Высоты треугольника обратно пропорциональны его сторонам:
$h_a:h_b:h_c={1}/{a}:{1}/{b}:{1}/{c}$
Теорема синусов
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
${a}/{sinα}={b}/{sinβ} ={c}/{sinγ} =2R$, где $R$ — радиус описанной около треугольника окружности.
Пример:
В треугольнике $АВС ВС=16, sin∠A={4}/{5}$. Найдите радиус окружности, описанной вокруг треугольника $АВС$.
Решение:
Воспользуемся теоремой синусов:
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности
${ВС}/{sinA} =2R$
Далее подставим числовые данные и найдем $R$
${16·5}/{4}=2R$
$R={16·5}/{4·2}=10$
Ответ: $10$
Теорема косинусов
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
$a^2=b^2+c^2-2·b·c·cosα.$
Геометрия на ЕГЭ по математике
Геометрия на профильном ЕГЭ по математике — одна из сложных тем для абитуриентов. Дело в том, что когда-то экзамен по геометрии в школе был обязательным, а сейчас — нет. В результате у большинства абитуриентов знания по геометрии близки к нулю.
Геометрия на профильном ЕГЭ — это три задачи в части 1 (сюда входит и планиметрия, и стереометрия), а также задача 14 (стереометрия) и для многих недосягаемая задача 16 (геометрия) из второй части. Как же научиться их решать?
Начнем с планиметрии. Прежде всего, выучите основные формулы геометрии.
На нашем сайте вы найдете курс геометрии с нуля — основные определения, формулы и теоремы, а также разбор множества экзаменационных задач по геометрии из части 1.
Для решения задач по геометрии из части 2 нужна более серьезная подготовка.
Первый этап — теория. Необходимый материал есть в учебнике по геометрии за 7-9 класс (автор — А. В. Погорелов или Л. С. Атанасян). Выпишите в тетрадь определения и формулировки теорем. Сделайте чертежи. Доказывать теоремы старайтесь самостоятельно.
Программа по геометрии.
1. Треугольники. Элементы треугольника. Вершины и стороны. Высоты, медианы, биссектрисы (определения).
2. Построение треугольника: практические задания.
а) Три стороны треугольника равны
и
сантиметров соответственно. Постройте треугольник
с помощью циркуля и линейки.
б) В треугольнике угол
равен
градусов, сторона
равна
,
равна
. Постройте треугольник
.
в) В треугольнике сторона
равна
, угол
равен
, угол
равен
. Постройте треугольник
.
3. Три признака равенства треугольников. Неравенство треугольника.
4. Постройте с помощью циркуля и линейки:
а) серединный перпендикуляр к отрезку;
б) биссектрису угла.
5. Углы при параллельных прямых и секущей. Вертикальные, смежные, соответственные, односторонние и накрест лежащие углы. Их определение и свойства.
6. Теорема о сумме углов треугольника.
7. Внешний угол треугольника.
8. Постройте в одном и том же треугольнике
а) Три высоты. Рассмотрите также случаи тупоугольного и прямоугольного треугольника.
б) Три биссектрисы.
в) Три медианы.
9. Равнобедренный треугольник. Определение и свойства. Высота в равнобедренном треугольнике.
10. Средняя линия треугольника и ее свойства.
11. Прямоугольный треугольник. Теорема Пифагора.
12. Определения синуса, косинуса и тангенса:
— для острого угла прямоугольного треугольника;
— для произвольного угла.
13. Четырехугольники. Сумма углов четырехугольника.
14. Параллелограмм. Определение и свойства. Площадь параллелограмма.
15. Виды параллелограммов и их свойства (ромб, прямоугольник, квадрат).
16. Трапеция. Средняя линия трапеции. Площадь трапеции.
17. Подобные треугольники. Три признака подобия треугольников.
18. Площадь треугольника. Формулы и
.
19. Теоремы синусов и косинусов.
20. Чему равно отношение площадей подобных фигур.
21. Свойство медианы (в каком отношении делятся медианы в точке пересечения?)
22. Свойство биссектрисы (в каком отношении биссектриса делит противоположную сторону?)
23. Окружность и круг. Длина окружности. Площадь круга. Длина дуги и площадь сектора.
24. Теорема о радиусе, проведенном в точку касания.
25. Центральный и вписанный углы. Связь между ними.
26. Теоремы о вписанных углах.
27. Теорема о пересекающихся хордах.
28. Теорема об отрезках длин касательных, проведенных из одной точки.
29. Теорема о секущей и касательной.
30. Дан треугольник . Постройте:
а) окружность, вписанную в данный треугольник;
б) окружность, описанную вокруг данного треугольника.
Где находятся центры этих окружностей?
31. Еще три формулы площади треугольника (через радиус вписанной окружности, через радиус описанной окружности и формула Герона).
32. Когда можно вписать окружность в четырехугольник? Когда — описать вокруг четырехугольника?
Программа по стереометрии
Разбирая и решая задания ЕГЭ по геометрии, вы заметите очень интересную вещь. Простые задачи из части 1, разобранные на нашем сайте, часто оказываются базовыми схемами, на которых строятся сложные задачи из части 2 профильного ЕГЭ.
Решая на ЕГЭ задачи по геометрии, обращайте особое внимание на оформление. Помните совет, который дал абитуриентам автор бестселлера «Математика — абитуриенту» В. В. Ткачук. Вот он, этот ценнейший совет:
«Подробность решения должна быть такова, чтобы его мог понять человек в 10 (десять) раз глупее вас».
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Геометрия на ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
09.03.2023
15 января 2013
В закладки
Обсудить
Жалоба
Теория по геометрии для сдачи ЕГЭ по математике
Немного теории, которая непременно пригодится на ЕГЭ.
Другие материалы смотрите в разделе ЕГЭ по математике.
Формулы для профильного ЕГЭ-2022 по математике
Формулы сокращённого умножения
Арифметическая и геометрическая прогрессии
Вероятность
Свойства степеней
Свойства логарифмов
Тригонометрия
Производные
Первообразные
Геометрия
Формулы сокращённого умножения
| `(a + b)^2=a^2 + 2ab + b^2` | |
| `(a − b)^2=a^2 − 2ab + b^2` | |
| `a^2 − b^2=(a + b)(a − b)` | |
| `a^3 + b^3=(a + b)(a^2 − ab + b^2)` | |
| `a^3 − b^3=(a − b)(a^2 + ab + b^2)` | |
| `(a + b)^3=a^3 + 3a^2b + 3ab^2 + b^3` | |
| `(a − b)^3=a^3 − 3a^2b + 3ab^2 − b^3` |
Прогрессии
Арифметическая прогрессия:
| `a_n=a_(n-1)+d` |
| `a_n=a_1+(n-1)*d` |
| `S_n=((a_1+a_n)*n)/2` |
Геометрическая прогрессия:
| `b_n=b_(n-1)*q` |
| `b_n=b_1*q^(n-1)` |
| `S_n=((q^n-1)*b_1)/(q-1)` |
| Бесконечно убывающая: `S=b_1/(1-q)` |
Вероятность
| Вероятность события A: | `P(A)=m/n` | |
| События происходят A и B происходят одновременно | `A*B` | |
| Независимые события: | `P(A*B)=P(A)*P(B)` | |
| Зависимые события: | `P(A*B)=P(A)*P(B|A)` | |
| Происходит или событие A, или B | `A+B` | |
| Несовместные события: | `P(A+B)=P(A)+P(B)` | |
| Совместные события: | `P(A+B)=P(A)+P(B)-P(A*B)` |
Свойства степеней
| `a^0=1` | `a^1=a` |
| `a^(-1)=1/a` | `a^(-n)=1/a^n` |
| `a^(1/2)=sqrt(a)` | `a^(1/n)=root(n)(a)` |
| `a^m*a^n=a^(m+n)` | `a^m/a^n=a^(m-n)` |
| `(a*b)^n=a^n*b^n` | `(a/b)^n=a^n/b^n` |
| `(a^m)^n=a^(m*n)` | `a^(m/n)=root(n)(a^m)` |
Свойства логарифмов
| `log_ab=c``a^c=b` | |
| `log_a1=0` | |
| `log_aa=1` | |
| `log_a(b*c)=log_ab+log_ac` | |
| `log_a(b/c)=log_ab-log_ac` | |
| `log_ab^n=n*log_ab` | |
| `log_(a^m)b=1/m*log_ab` | |
| `log_ab=1/(log_ba)` | |
| `log_ab=(log_cb)/(log_ca)` | |
| `a^(log_cb)=b^(log_ca)` | |
| `a^(log_ab)=b` |
Тригонометрия
| `alpha` | `0` | `pi/6` | `pi/4` | `pi/3` | `pi/2` | `pi` | `(3pi)/2` | `2pi` |
|---|---|---|---|---|---|---|---|---|
| `0^circ` | `30^circ` | `45^circ` | `60^circ` | `90^circ` | `180^circ` | `270^circ` | `360^circ` | |
| `sinalpha` | `0` | `1/2` | `sqrt(2)/2` | `sqrt(3)/2` | `1` | `0` | `-1` | `0` |
| `cosalpha` | `1` | `sqrt(3)/2` | `sqrt(2)/2` | `1/2` | `0` | `-1` | `0` | `1` |
| `text(tg)alpha` | `0` | `sqrt(3)/3` | `1` | `sqrt(3)` | `infty` | `0` | `infty` | `0` |
| `text(ctg)alpha` | `infty` | `sqrt(3)` | `1` | `sqrt(3)/3` | `0` | `infty` | `0` | `infty` |
Основные соотношения
| `sin^2alpha+cos^2alpha=1` | |
| `text(tg)alpha=sinalpha/cosalpha=1/(text(ctg)alpha)` |
Формулы двойного угла
| `cos2alpha={(cos^2alpha-sin^2alpha),(1-2sin^2alpha),(2cos^2alpha-1):}` | |
| `sin2alpha=2sinalphacosalpha` | |
| `text(tg)2alpha=(2text(tg)alpha)/(1-text(tg)^2alpha)` |
Формулы суммы и разности аргументов
| `sin(alpha+-beta)=sinalphacosbeta+-cosalphasinbeta` |
| `cos(alpha+-beta)=cosalphacosbeta∓sinalphasinbeta` |
| `text(tg)(alpha+-beta)=(text(tg)alpha+-text(tg)beta)/(1∓text(tg)alpha*text(tg)beta)` |
Преобразование суммы и разности в произведение
| `sinalpha+-sinbeta=2sin((alpha+-beta)/2)cos((alpha∓beta)/2)` |
| `cosalpha+cosbeta=2cos((alpha+beta)/2)cos((alpha-beta)/2)` |
| `cosalpha-cosbeta=-2sin((alpha+beta)/2)sin((alpha-beta)/2)` |
Формулы половинного аргумента
| `sin(alpha/2)=+-sqrt((1-cosalpha)/2)` | |
| `cos(alpha/2)=+-sqrt((1+cosalpha)/2)` | |
| `text(tg)(alpha/2)=+-sqrt((1-cosalpha)/(1+cosalpha))=(1-cosalpha)/sinalpha=sinalpha/(1+cosalpha)` |
Обратные тригонометрические функции
| `sinx=A` | `x=(-1)^k*arcsinA + pik` или `{(x=arcsinA + 2pik),(x=pi-arcsinA+2pik):}` |
`kinZZ` |
| `cosx=A` | `x=±arccosA + 2pik` | `kinZZ` |
| `tg x=A` | `x=text(arctg) A + pik` | `kinZZ` |
| `ctg x=A` | `x=text(arcctg) A + pik` | `kinZZ` |
Также некоторые тригонометрические соотношения смотрите в разделе Геометрия.
Производные
Основные правила дифференцирования
| `(u+-v)’=u’+-v’` | |
| `(u*v)’=u’*v+u*v’` | |
| `(u/v)^’=(u’*v-u*v’)/v^2` | |
| `[f(g(x))]’=f'(g(x))*g'(x)` |
Уравнение касательной
| `y=f(x_0)+f'(x_0)*(x-x_0)` |
Производные элементарных функций
| `C’=0` | `(C*x)’=C` | |
| `(x^m)’=mx^(m-1)` | `(sqrtx)’=1/(2sqrtx)` | |
| `(1/x)^’=-1/x^2` | ||
| `(e^x)’=e^x` | `(lnx)’=1/x` | |
| `(a^x)’=a^x*lna` | `(log_ax)’=1/(xlna)` | |
| `(sinx)’=cosx` | `(cosx)’=-sinx` | |
| `(text(tg)x)’=1/cos^2x` | `(text(ctg)x)’=-1/sin^2x` | |
| `(arcsinx)’=1/sqrt(1-x^2)` | `(arccosx)’=-1/sqrt(1-x^2)` | |
| `(text(arctg))=1/(1+x^2)’` | `(text(arcctg))’=-1/(1+x^2)` |
Также некоторые сведения про производные смотрите в описании задач
№14 (база), №7 (профиль), №12 (профиль).
Первообразные
| Первообразная: | `F'(x)=f(x)` | |||
| Неопределённый интеграл: | `intf(x)dx=F(x)+C` | |||
| Определённый интеграл (формула Ньютона-Лейбница): | `int_a^bf(x)dx=F(b)-F(a)` |
Таблица первообразных
| `f(x)` | `F(x)` | `f(x)` | `F(x)` | |
|---|---|---|---|---|
| `a` | `ax` | |||
| `x^n` | `x^(n+1)/(n+1)` | `1/x` | `lnx` | |
| `e^x` | `e^x` | `a^x` | `a^x/lna` | |
| `sinx` | `-cosx` | `cosx` | `sinx` | |
| `1/cos^2x` | `text(tg)x` | `1/sin^2x` | `-text(ctg)x` | |
| `1/(x^2+a^2)` | `1/atext(arctg)x/a` | `1/(x^2-a^2)` | `1/(2a)ln|(x-a)/(x+a)|` | |
| `1/sqrt(a^2-x^2)` | `text(arcsin)x/a` | `1/sqrt(x^2+a)` | `ln|x+sqrt(x^2+a)|` |
Геометрия
Планиметрия (2D)
Площади фигур:
| Окружность: | `S=pir^2` | |
| Треугольник: | `S=1/2ah` | |
| Параллелограмм: | `S=ah` | |
| Четырёхугольник: | `S=1/2d_1d_2sinvarphi` | |
| Трапеция: | `S=(a+b)/2*h` |
Стереометрия (3D)
| Призма: | `V=S_(осн)h` | |
| Пирамида: | `V=1/3S_(осн)h` | |
| Конус: | `V=1/3S_(осн)h` | |
| `S_(бок)=pirl` | ||
| Цилиндр: | `V=pir^2h` | |
| `S_(бок)=2pirh` | ||
| Шар: | `V=4/3pir^3` | |
| `S=4pir^2` |
Этапы закрепощения крестьян в России
Крепостное право на Руси появилось позже, чем во многих средневековых европейских королевствах. Это было связано с объективными причинами – низкая плотность населения, зависимость от ордынского ига.
Задания 12-18 досрочного ЕГЭ по математике
3 примера по каждому заданию. Досрочный ЕГЭ по математике прошёл 28 марта.
ОГЭ по математике. Тренировочный вариант СтатГрад
Видеоуроки ОГЭ | Вчера, 21:46
Решение тестовой части (№1-19) тренировочной работы по математике от 18 апреля 2022 года.
Факт 1.
(bullet) Множество натуральных чисел (mathbb{N}) – это числа (1,
2, 3, 4 ) и т.д.
(bullet) Множество целых чисел (mathbb{Z}) состоит из натуральных чисел, противоположных им ((-1, -2, -3 ) и т.д.) и нуля (0).
(bullet) Рациональные числа (mathbb{Q}) – числа вида (dfrac ab), где (ain mathbb{Z}), (bin mathbb{N}).
Таким образом, существует включение: (mathbb{N}) содержится в (mathbb{Z}), а (mathbb{Z}) содержится в (mathbb{Q}).
Факт 2.
(bullet) Правила сложения дробей: [begin{aligned} &dfrac ab+dfrac cb=dfrac{a+c}b[2ex]
&dfrac ab+dfrac cd=dfrac{ad+bc}{bd}end{aligned}] Пример: (dfrac {31}6+dfrac {67}6=dfrac{31+67}6=dfrac{98}6)
(bullet) Правила умножения дробей: [dfrac abcdot dfrac cd=dfrac{ac}{bd}] Пример: (dfrac 47cdot dfrac{14}5=dfrac{4cdot 14}{7cdot 5})
(bullet) Правила деления дробей: [dfrac ab: dfrac cd=dfrac abcdot dfrac dc] Пример: (dfrac 45 :dfrac 67=dfrac 45cdot dfrac 76)
Факт 2.
(bullet) Сокращение дробей – деление числителя и знаменателя на одно и то же число, отличное от нуля.
Пример:
(begin{aligned} &dfrac{98}6=dfrac{49cdot
2llap{/}}{3cdot
2llap{/}}=dfrac{49}3[2ex]
&dfrac{4cdot 14}{7cdot 5}=dfrac{4cdot 2cdot
7llap{/}}{7llap{/}cdot
5}=dfrac 85[2ex]
&dfrac{4cdot 7}{5cdot 6}=dfrac {2llap{/}cdot 2cdot 7}{5cdot
3cdot
2llap{/}}=dfrac{14}{15}end{aligned})
(bullet) Если (dfrac ab) – несократимая дробь, то ее можно представить в виде конечной десятичной дроби тогда и только тогда, когда знаменатель (b) делится только на числа (2) и (5).
Пример: дробь (dfrac2{65}) нельзя представить в виде конечной десятичной дроби, так как (65=5cdot 13), то есть (dfrac2{65}=0,0307…)
дробь (dfrac3{160}) можно представить в виде конечной десятичной дроби, так как (160=2^5cdot 5), то есть (dfrac3{160}=0,01875).
Факт 3.
(bullet) Формулы сокращенного умножения:
(blacktriangleright) Квадрат суммы и квадрат разности: [(a+b)^2=a^2+2ab+b^2] [(a-b)^2=a^2-2ab+b^2]
(blacktriangleright) Куб суммы и куб разности: [(a+b)^3=a^3+3a^2b+3ab^2+b^3quad {small{text{или}}}quad
(a+b)^3=a^3+b^3+3ab(a+b)] [(a-b)^3=a^3-3a^2b+3ab^2-b^3quad {small{text{или}}}quad
(a-b)^3=a^3-b^3-3ab(a-b)]
Заметим, что применение данных формул справа налево часто помогает упростить вычисления:
(13^3+3cdot 13^2cdot 7+3cdot 13cdot 49+7^3=(13+7)^3=20^3=8000)
(blacktriangleright) Разность квадратов: [a^2-b^2=(a-b)(a+b)]
(blacktriangleright) Сумма кубов и разность кубов: [a^3+b^3=(a+b)(a^2-ab+b^2)] [a^3-b^3=(a-b)(a^2+ab+b^2)]
Заметим, что не существует формулы суммы квадратов (a^2+b^2).
Заметим, что применение данных формул слева направо часто помогает упростить вычисления:
(dfrac{7^6-2^6}{7^4+14^2+16}=
dfrac{(7^2-2^2)(7^4+7^2cdot2^2+2^4)}
{7^4+(7cdot2)^2+2^4}=7^2-2^2=45)
Факт 4.
(bullet) Квадрат суммы нескольких слагаемых равен сумме квадратов этих слагаемых и удвоенных попарных произведений: [begin{aligned}
&(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc[2ex]
&(a+b+c+d)^2=a^2+b^2+c^2+d^2+2ab+2ac+2ad+2bc+2bd+2cd[2ex]
&{small{text{и т.д.}}}end{aligned}]
Геометрия на профильном ЕГЭ по математике — одна из сложных тем для абитуриентов. Дело в том, что когда-то экзамен по геометрии в школе был обязательным, а сейчас — нет. В результате у большинства абитуриентов знания по геометрии близки к нулю.
Геометрия на профильном ЕГЭ — это три в части 1 (сюда входит и планиметрия, и стереометрия), а также задача 14 (стереометрия) и для многих недосягаемая 16 (геометрия) из второй части. Как же научиться их решать?
Начнем с планиметрии. Прежде всего, выучите основные формулы геометрии.
На нашем сайте вы найдете курс геометрии с нуля — основные определения, формулы и теоремы, а также разбор множества экзаменационных задач по геометрии из части 1.
Для решения задач по геометрии из части 2 нужна более серьезная подготовка.
Первый этап — теория. Необходимый материал есть в учебнике по геометрии за 7-9 класс (автор — А. В. Погорелов или Л. С. Атанасян). Выпишите в тетрадь определения и формулировки теорем. Сделайте чертежи. Доказывать теоремы старайтесь самостоятельно.
Программа по геометрии.
1. Треугольники. Элементы треугольника. Вершины и стороны. Высоты, медианы, биссектрисы (определения).
2. Построение треугольника: практические задания.
а) Три стороны треугольника равны
и
сантиметров соответственно. Постройте треугольник
с помощью циркуля и линейки.
б) В треугольнике угол
равен
градусов, сторона
равна двум,
равна
. Постройте треугольник
.
в) В треугольнике сторона
равна
, угол
равен
, угол
равен
. Постройте треугольник
.
3. Три признака равенства треугольников. Неравенство треугольника.
4. Постройте с помощью циркуля и линейки:
а) серединный перпендикуляр к отрезку;
б) биссектрису угла.
5. Углы при параллельных прямых и секущей. Вертикальные, смежные, соответственные, односторонние и накрест лежащие углы. Их определение и свойства.
6. Теорема о сумме углов треугольника.
7. Внешний угол треугольника.
8. Постройте в одном и том же треугольнике
а) три высоты. Рассмотрите также случаи тупоугольного и прямоугольного треугольника.
б) три биссектрисы.
в) три медианы.
9. Равнобедренный треугольник. Определение и свойства. Высота в равнобедренном треугольнике.
10. Средняя линия треугольника и ее свойства.
11. Прямоугольный треугольник. Теорема Пифагора.
12. Определения синуса, косинуса и тангенса
— для острого угла прямоугольного треугольника
— для произвольного угла.
13. Четырехугольники. Сумма углов четырехугольника.
14. Параллелограмм. Определение и свойства. Площадь параллелограмма.
15. Виды параллелограммов и их свойства. (ромб, прямоугольник, квадрат).
16. Трапеция. Средняя линия трапеции. Площадь трапеции.
17. Подобные треугольники. Три признака подобия треугольников.
18. Площадь треугольника. Формулы и
.
19. Теоремы синусов и косинусов.
20. Чему равно отношение площадей подобных фигур.
21. Свойство медианы (в каком отношении делятся медианы в точке пересечения?)
22. Свойство биссектрисы (в каком отношении биссектриса делит противоположную сторону?)
23. Окружность и круг. Длина окружности. Площадь круга. Длина дуги и площадь сектора.
24. Теорема о радиусе, проведенном в точку касания.
25. Центральный и вписанный углы. Связь между ними.
26. Теоремы о вписанных углах.
27. Теорема о пересекающихся хордах.
28. Теорема об отрезках длин касательных, проведенных из одной точки.
29. Теорема о секущей и касательной.
30. Дан треугольник . Постройте
а) окружность, вписанную в данный треугольник
б) окружность, описанную вокруг данного треугольника.
Где находятся центры этих окружностей?
31. Еще три формулы площади треугольника (через радиус вписанной окружности, через радиус описанной окружности и формула Герона).
32. Когда можно вписать окружность в четырехугольник? Когда — описать вокруг четырехугольника?
Программа по стереометрии
Разбирая и решая задания ЕГЭ по геометрии, вы заметите очень интересную вещь. Простые задачи из части 1, разобранные на нашем сайте, часто оказываются базовыми схемами, на которых строятся сложные задачи из части 2 профильного ЕГЭ.
Решая на ЕГЭ задачи по геометрии, обращайте особое внимание на оформление. Помните совет, который дал абитуриентам автор бестселлера «Математика — абитуриенту» В. В. Ткачук. Вот он, этот ценнейший совет:
«Подробность решения должна быть такова, чтобы его мог понять человек в 10 (десять) раз глупее вас».
Русский, Математика, Обществознание, Физика, История, Биология, Химия, Английский, Информатика, Литература, География
О правах / ctege.info@gmail.com / Архив: 2020; 2021; 2022;
2005-2023 © ctege.info При использовании материалов указывайте гиперссылку.
- Поиск
- Доска
- О проекте
- Контакты
X
Код для вставки банера 220×110
- Главная
- Новости
- ОГЭ
- ЕГЭ
- 4 класс
- Учебник
- Задачники
- Тесты
- 5 класс
- Учебник
- Задачники
- Тесты
- 6 класс
- Учебник
- Задачники
- Тесты
- 7 класс
- Учебник
- Задачники
- Тесты
- 8 класс
- Учебник
- Задачники
- Тесты
- 9 класс
- Учебник
- Задачники
- Тесты
- ОГЭ
- Дидактические задачи
- Тематические задачи
- Экзамена- ционные тематические задачи
- Экзамена- ционные тесты
- 10 класс
- Учебник
- Задачники
- Тесты
- 11 класс
- Учебник
- Задачники
- Тесты
- ЕГЭ
Базовый уровень- Дидактические задачи
- Тематические задачи
- Экзамена- ционные тематические задачи
- Экзамена- ционные тесты
- ЕГЭ
Профильный уровень- Дидактические задачи
- Тематические задачи
- Экзамена- ционные тематические задачи
- Экзамена- ционные тесты
- Информатика
- Внеклассное чтение
- Учись учиться
- Видео
- Малый мехмат МГУ
Задание 16. ГЕОМЕТРИЯ. ПЛАНИМЕТНИЯ
Теоретический материал
1. Медиана прямоугольного треугольника |
 |
 |
 |
2. Удвоение медианы |
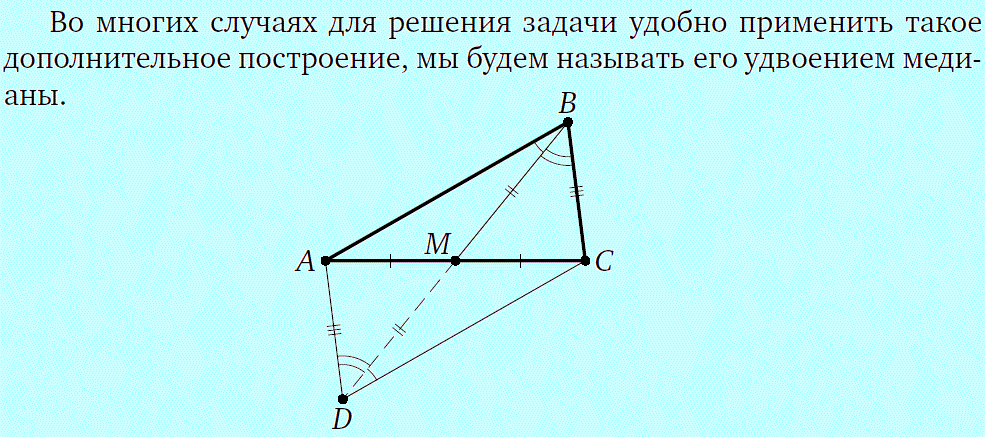 |
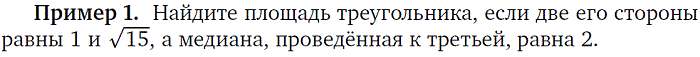 |
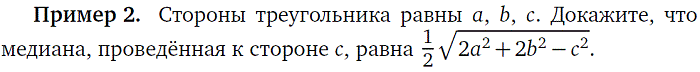 |
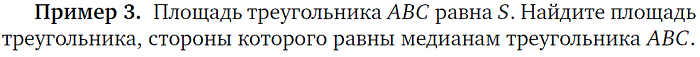 |
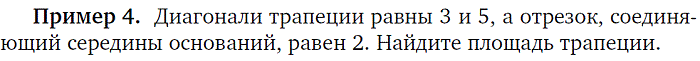 |
3. Параллелограмм
|
 |
 |
 |
 |
 |
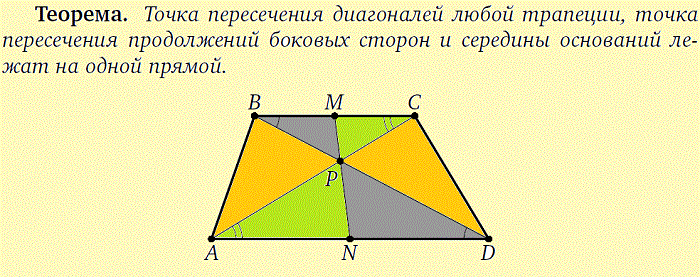
4. Трапеция |
 |
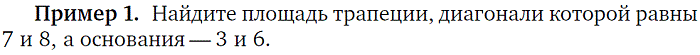 |
 |
 |
 |
5. Нахождение высоты и биссектриссы треугольника |
 |
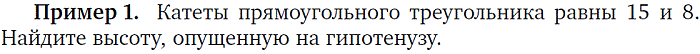 |
 |
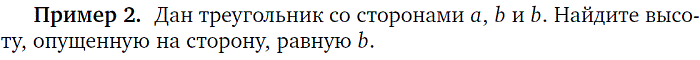 |
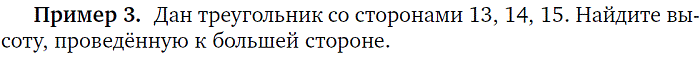 |
 |
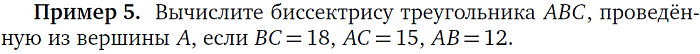 |
 |
6. Отношение отрезков |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Паровая турбина |
 |
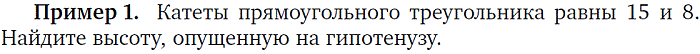 |
 |
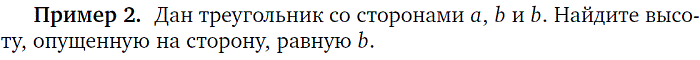 |
 |
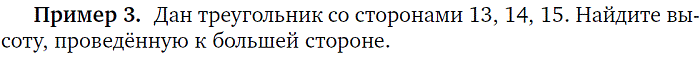 |
Демографическая пирамида |
 |
 |
 |
 |
 |
 |
 |
 |
Геометрия на плоскости (планиметрия)
Задание
1
#199
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle B = 81^{circ}), (angle C = 25^{circ}). Найдите внешний угол при вершине (A). Ответ дайте в градусах.
Согласно теореме о внешнем угле треугольника, (angle B + angle C =) внешнему углу при вершине (A), следовательно (A_{text{внеш}}) ( = 81^{circ} + 25^{circ} = 106^{circ}).
Ответ: 106
Задание
2
#200
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle A = 22^{circ}), внешний угол при вершине (C) равен (130^{circ}). Найдите (angle B). Ответ дайте в градусах.
Согласно теореме о внешнем угле треугольника, (angle A + angle B = C_{text{внеш}}), тогда (22^{circ} + angle B = 130^{circ}), откуда находим (angle B = 130^{circ} — 22^{circ} = 108^{circ}).
Ответ: 108
Задание
3
#201
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle C = 35^{circ}), внешний угол при вершине (B) равен (91^{circ}). Найдите (angle A). Ответ дайте в градусах.
Согласно теореме о внешнем угле треугольника, (angle C + angle A = B_{text{внеш}}), тогда (35^{circ} + angle A = 91^{circ}), откуда находим (angle A = 91^{circ} — 35^{circ} = 56^{circ}).
Ответ: 56
Задание
4
#202
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle C = 70^{circ}), (AB = BC). Найдите (angle B). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle A = angle C = 70^{circ}). Так как у любого треугольника сумма углов равна (180^{circ}), то (angle B = 180^{circ} — 70^{circ} — 70^{circ} = 40^{circ}).
Ответ: 40
Задание
5
#203
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle A = 47^{circ}), (AB = BC). Найдите (angle B). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle C = angle A = 47^{circ}). Так как у любого треугольника сумма углов равна (180^{circ}), то (angle B = 180^{circ} — 47^{circ} — 47^{circ} = 86^{circ}).
Ответ: 86
Задание
6
#204
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle C = 36^{circ}), (AB = BC). Найдите (angle B). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle A = angle C = 36^{circ}). Так как у любого треугольника сумма углов равна (180^{circ}), то (angle B = 180^{circ} — 36^{circ} — 36^{circ} = 108^{circ}).
Ответ: 108
Задание
7
#205
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle B = 38^{circ}), (AB = BC). Найдите (angle C). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle A = angle C). Так как у любого треугольника сумма углов равна (180^{circ}), то (180^{circ} = 38^{circ} + angle A + angle C = 38^{circ} + 2cdot angle A), откуда (2cdot angle A = 142^{circ}), тогда (angle A = 71^{circ}).
Ответ: 71