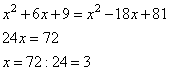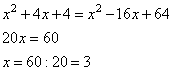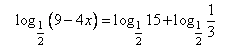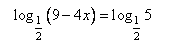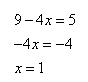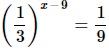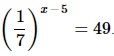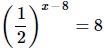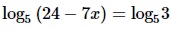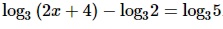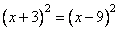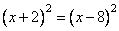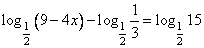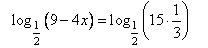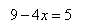Теория к 7 заданию егэ по математике базовый уровень

---

Простейшие уравнения

---

В задании №7 базового уровня ЕГЭ по математике необходимо решить простейшие уравнения. Для этого нам понадобятся знания логарифмов, степеней и методы решения квадратных уравнений. Перейдем к рассмотрению и разбору подобных примеров.

---

Разбор типовых вариантов заданий №7 ЕГЭ по математике базового уровня

---

Вариант 7МБ1

[su_note note_color=”#defae6″]

Найдите корень уравнения 

[/su_note]

Алгоритм выполнения

1. Раскрыть скобки с левой и с правой стороны равенства, применив формулы приведения.
2. Все, выражения, содержащие переменную перенести в левую часть, а не содержащие в правую.
3. Преобразовать левую часть.
4. Преобразовать правую часть.
5. Решить уравнение относительно x, то есть найти неизвестный множитель.

Решение:

Раскроем скобки с левой и с правой стороны равенства, применив формулы приведения.

Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.

(x + 3)² = x² + 2 · x · 3 + 3² = x² + 6x + 9

Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.

(x – 9)² = x² – 2 · x · 9 + 9² = x² – 18x + 81

После преобразования выражение примет вид:

x² + 6x + 9 = x² – 18x + 81

Все выражения, содержащие переменную перенесем в левую часть, а не содержащие – в правую.

При переносе из одной части равенства в другую знак меняется на противоположный.

x² + 6x – x² + 18x = 81 – 9

Преобразуем левую часть. Приведем подобные слагаемые. Объединим в скобки, сохранив знаки, те выражения, где содержится x² и x.

x² + 6x – x² + 18x = (x² – x²) + (6x +18x) = 0 + 24x = 24x

Выражение примет вид:

24x = 81 – 9

Преобразуем правую часть. 81 – 9 = 72

Выражение примет вид:

24x = 72

Решим уравнение относительно x, то есть найдем неизвестный множитель. Для того чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.

x = 72 : 24

x = 3

Решение в общем виде:

Раскроем скобки в уравнении, получим:

 

 

 

Ответ: 3.

---

Вариант 7МБ2

[su_note note_color=”#defae6″]

Найдите корень уравнения 

[/su_note]

Алгоритм выполнения

1. Раскрыть скобки с левой и с правой стороны равенства, применив формулы приведения.
2. Все, выражения, содержащие переменную перенести в левую часть, а не содержащие в правую.
3. Преобразовать левую часть.
4. Преобразовать правую часть.
5. Решить уравнение относительно x, то есть найти неизвестный множитель.

Решение:

Раскроем скобки с левой и с правой стороны равенства, применив формулы приведения.

Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.

(x + 2)² = x² + 2 · x · 2 + 2² = x² + 4x + 4

Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.

(x – ² = x² – 2 · x · 8 + 8² = x² – 16x + 64

После преобразования выражение примет вид:

x² + 4x + 4 = x² – 16x + 64

Все выражения, содержащие переменную перенесем в левую часть, а не содержащие – в правую.

При переносе из одной части равенства в другую знак меняется на противоположный.

x² + 4x – x² + 16x = 64 – 4

Преобразуем левую часть. Приведем подобные слагаемые. Объединим в скобки, сохранив знаки, те выражения, где содержится x² и x.

x² + 4x – x² + 16x = (x² – x²) + (4x +16x) = 0 + 20x = 20x

Выражение примет вид:

20x = 64 – 4

Преобразуем правую часть. 64 – 4 = 60

Выражение примет вид:

20x = 60

Решим уравнение относительно x, то есть найдем неизвестный множитель. Для того чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.

x = 60 : 20

x = 3

Решение в общем виде:

Раскроем скобки, получим:

Ответ: 3.

---

Вариант 7МБ3

[su_note note_color=”#defae6″]

Найдите корень уравнения 

[/su_note]

Алгоритм выполнения

1. Перенести вычитаемое в правую сторону равенства с противоположным знаком.
2. Преобразовать правую часть с учетом свойства: log_a x + log_a y = log_a (x · y).
3. Приравнять логарифмические выражения. Можно так поступить, так как основания логарифмов в левой и правой части одинаковы.
4. Решить уравнение относительно x.

Решение:

Перенесем вычитаемое в правую сторону равенства с противоположным знаком.

Преобразуем правую часть с учетом свойства: log_a x + log_a y = log_a (x · y).

Выполним преобразование:

Приравняем логарифмические выражения. Можно так поступить, так как основания логарифмов в левой и правой части одинаковы.

Решим уравнение относительно x.

Ответ: 1.

---

Вариант 7МБ4

[su_note note_color=”#defae6″]

Найдите корень уравнения 3^{x− 3} = 81.

[/su_note]

Алгоритм выполнения

1. Привести выражения в степенях к одинаковому основанию. В данном случае – это 3. Теперь необходимо вспомнить, какой степенью тройки является 81.
2. Когда основания равны, можно приравнять значения степеней

Если вы забыли, то для этого необходимо делить 81 на 3 до тех пор, пока не получим 3. Чтобы получить три из 81, нам нужно поделить 81 на 3 три раза: при первом делении мы получим 27, при втором – 9, при третьем – три.

Значит, 81 это три в четвертой степени. Запишем это:

Решение:

3^{x− 3} = 3⁴

х – 3 = 4

Откуда:

х = 7

Ответ: 7

---

Вариант 7МБ5

[su_note note_color=”#defae6″]

Найдите корень уравнения log₂( x − 3) = 6 .

[/su_note]

Алгоритм выполнения

1. Логарифм по основанию два показывает нам число, в степень которого нам необходимо возвести основание, то есть двойку, чтобы получить число под логарифмом.

Решение:

x − 3 = 2⁶

x − 3 = 64

x = 67

Ответ: 67

---

Вариант 7МБ6

[su_note note_color=”#defae6″]

Найдите отрицательный корень уравнения x² − x − 6 = 0.

[/su_note]

Алгоритм выполнения

1. Вычислить дискриминант
2. Найти корни
3. Выбрать необходимый корень

D = b² − 4ac

Решение:

D = -(1)² − 4 • 1 • (-6) = 25

x = (- b ±√D) : 2a

x = (1 + 5) : 2 = 3

x = (1 – 5) : 2 = -2

Так как нам необходим отрицательный корень – ответ -2

Ответ: -2.

---

Вариант 7МБ7

[su_note note_color=”#defae6″]

Решите уравнение х² = –2х + 24.

Если уравнение имеет больше одного корня, в ответе укажите больший из них.

[/su_note]

Алгоритм выполнения

1. Переносим влево часть ур-ния, стоящую справа от знака «=». Получаем кв.уравнение стандартного вида.
2. Поскольку уравнение является приведенным, используем для нахождения корней т.Виета.
3. Записываем в качестве ответа большее из полученных 2 чисел.

Решение:

х² = –2х +24

х² +2х – 24 = 0

По т.Виета х₁+х₂=–b, x₁·x₂=c. В нашем ур-нии b=2, c=24. Подбираем подходящую пару чисел, получаем: х₁=–6, х₂=4.

Поскольку требуется указать больший из корней, то ответом будет 4.

Ответ: 4

---

Вариант 7МБ8

[su_note note_color=”#defae6″]

Найдите корни уравнения 4^х–6 = 64.

[/su_note]

Алгоритм выполнения

1. Представляем 64 как степень с основанием 4, т.е. приводим выражения справа и слева к степеням с одинаковым основанием.
2. Опускаем одинаковые основания и переходим к равенству показателей. Ур-ние стало простейшим линейным.
3. Находим корень ур-ния.

Решение:

4^х–6 = 64

4^х–6 = 4³

х – 6 = 3

х = 9

Ответ: 9

---

Вариант 7МБ9

[su_note note_color=”#defae6″]

Найдите корень уравнения log₃ (2x – 5) = 2.

[/su_note]

Алгоритм выполнения

1. Преобразуем часть уравнения справа от знака «=», используя св-ва логарифмов log_xx=1 и log_xyⁿ=nlog_xy.
2. Переходим от равенства логарифмов к равенству выражений, стоящих под их знаками.
3. Решаем полученное линейное ур-ние.

Решение:

log₃ (2x – 5) = 2

log₃ (2x – 5) = 2 · log₃3

log₃ (2x – 5) = log₃3²

2x – 5 = 3²

2x – 5 = 9

2x = 14

x=7

Ответ: 7

---

Вариант 7МБ10

[su_note note_color=”#defae6″]

Найдите корень уравнения

[/su_note]

Алгоритм выполнения

1. Преобразовываем обе части ур-ния: приводим их к степеням с основанием 3. Для этого используем св-во степеней (1/а)^х=а^–х.
2. Поскольку основания степеней слева и справа в ур-нии теперь одинаковы, то можем их опустить и приравнять показатели.
3. Решаем полученное линейное ур-ние.

Решение:

–x + 9 = –2

–x = –2–9

x = 11

Ответ: 11

---

Вариант 7МБ11

[su_note note_color=”#defae6″]

Найдите корень уравнения (х – ² = (х – 2)².

[/su_note]

Алгоритм выполнения

1. Раскрываем скобки слева и справа, используя ф-лу сокращенного умножения (х–у)²=х²–2ху–у².
2. Переносим влево часть уравнения справа от знака «=». Справа получаем 0.
3. Приводим подобные слагаемые. В результате уравнение стало линейным.
4. Решаем полученное уравнение.

Решение:

(х – ² = (х – 2)²

х² – 2 · х ·8 + 8² = х² – 2 · х · 2 + 2²

х² – 16х + 64 = х² – 4х + 4

х² – 16х +64 – х² + 4х – 4 = 0

–12х + 60 = 0

–12х = –60

х = 5

Ответ: 5

---

Вариант 7МБ12

[su_note note_color=”#defae6″]

Найдите корень уравнения

[/su_note]

Алгоритм выполнения

1. Преобразовываем обе части ур-ния так, чтобы привести их к степеням с одинаковым основанием 7. Для выражения слева применяем св-во степеней (1/а)^х=а^–х.
2. Применяем св-во показат.уравнений: если степени с одинаковыми основаниями равны, то равны и их показатели. Отсюда переходим к линейному ур-нию.
3. Решаем его.

Решение:

–(x–5) = 2

5 – x = 2

–x = 2 – 5

x = 5 – 2

x = 3

Ответ: 3

---

Вариант 7МБ13

[su_note note_color=”#defae6″]

Решите уравнение х² – 25 = 0

[/su_note]

Алгоритм выполнения

1. Переносим 25 в правую часть ур-ния.
2. Выражаем из ур-ния х путем извлечения корня из 25.
3. Определяем корни, сравниваем их, определяем больший.

Решение:

х² – 25 = 0

х² = 25

х = ±√25

х₁ = –5, х₂ = 5

Для ответа берем 5.

Ответ: 5

---

Вариант 7МБ14

[su_note note_color=”#defae6″]

Найдите корень уравнения

[/su_note]

Алгоритм выполнения

1. Применим св-во логарифмических равенств: если логарифмы с одинаковыми основания равны, то равны и их подлогарифменные выражения. В результате получаем равенство из выражений, стоящих под знаком логарифма.
2. Решаем полученное линейное ур-ние.

Решение:

log₅ (24 – 7x) = log₅ 3

24 – 7x = 3

–7x = 3 – 24

7x = 21

x = 3

Ответ: 3

---

Вариант 7МБ15

[su_note note_color=”#defae6″]

Найдите корень уравнения

[/su_note]

Алгоритм выполнения

1. Приводим обе части ур-ния к степеням с основанием 2. При этом для преобразования выражения слева используем св-во степеней (1/а)^х=а^–х.
2. Получив слева и справа степени с одинаковым основанием, опускаем это основание и приравниваем показатели этих степеней. Получаем линейное ур-ние.
3. Решаем его.

Решение:

2^–(x–8) = 2³

–x+8 = 3

–x = 3–8

x = 5

Ответ: 5

---

Вариант 7МБ16

[su_note note_color=”#defae6″]

Найдите корень уравнения

[/su_note]

Алгоритм выполнения

1. К левой части уравнения применяем св-во логарифмов log_a(x/y)=log_ax–log_ay.
2. Поскольку в обеих частях ур-ния имеем логарифмы по одинаковым основаниям, то можем их знаки, оставив только подлогарифменные выражения. Получаем линейное ур-ние.
3. Решаем его.

Решение:

log₃ (2x + 4) – log₃ 2 = log₃ 5

log₃ (2x + 4)/2 = log₃ 5

log₃ (x + 2) = log₃ 5

x + 2 = 5

x = 3

Ответ: 3

Даниил Романович | Просмотров: 11.2k

Практика по заданию №7 ЕГЭ по математике базового уровня — вычисления и преобразования.

Для выполнения задания №7 необходимо уметь выполнять вычисления и преобразования.

Практика

Источник	Задания
time4math.ru	Скачать задания
math100.ru	Вычисления и преобразования

Коды проверяемых элементов содержания (по кодификатору) — 1.1–1.4

Уровень сложности задания — базовый

Максимальный балл за выполнение задания — 1

Примерное время выполнения задания выпускником, изучавшим математику на базовом уровне (в мин.) — 7

Связанные страницы:

• Взрослым: Skillbox, Хекслет, Eduson, XYZ, GB, Яндекс, Otus, SkillFactory.
• 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
• До 7 класса: Алгоритмика, Кодланд, Реботика.
• Английский: Инглекс, Puzzle, Novakid.

• Оценивание (первичные баллы) — 1
• Время на выполнение (мин) — 7
• Сложность — базовая

Теория по заданию 7

3.1.1. Функция, область определения функции

3.1.2. Множество значений функции

3.1.3. График функции. Примеры функциональных зависимостей в реальных процессах и явлениях

3.2.1. Монотонность функции. Промежутки возрастания и убывания

3.2.5. Точки экстремума (локального максимума и минимума) функции

3.2.6. Наибольшее и наименьшее значения функции

4.1.1. Понятие о производной функции, геометрический смысл производной

4.1.2. Физический смысл производной, нахождение скорости для процесса, заданного формулой или графиком

6.2.1. Табличное и графическое представление данных

Решите уравнения

1	2+9x=4x+3	Смотреть видеоразбор >>
2	2(3-2x)-7=-3x+8	Смотреть видеоразбор >>
3	x^2+11x=-28. Если уравнение имеет более одного корня, в ответе укажите меньший из них.	Смотреть видеоразбор >>
4	x^2=3x. Если уравнение имеет более одного корня, в ответе укажите больший из них.	Смотреть видеоразбор >>
5	4^{x-11}=frac{1}{16}	Смотреть видеоразбор >>
6	log_3(x-3)+log_32=log_310	Смотреть видеоразбор >>
7	5x-2=10x+4	Смотреть видеоразбор >>
8	(x-8)^2=(x-2)^2	Смотреть видеоразбор >>
9	x^2+8=6x. Если уравнение имеет более одного корня, в ответе укажите больший из них.	Смотреть видеоразбор >>
10	sqrt{3x-8}=5	Смотреть видеоразбор >>
11	(frac{1}{7})^{x-5}=49	Смотреть видеоразбор >>
12	log_3(2x+4)-log_32=log_35	Смотреть видеоразбор >>
13	1+8(3x+7)=9	Смотреть видеоразбор >>
14	x^2-7x-18=0. Если уравнение имеет более одного корня, в ответе укажите больший из них.	Смотреть видеоразбор >>
15	x^2=9. Если уравнение имеет более одного корня, в ответе укажите меньший из них.	Смотреть видеоразбор >>
16	sqrt{13-x}=3	Смотреть видеоразбор >>
17	log_3(2x-5)=2	Смотреть видеоразбор >>
18	1+8(-x+10)=9	Смотреть видеоразбор >>
19	x^2+10x+21=0. Если уравнение имеет более одного корня, в ответе укажите меньший из них.	Смотреть видеоразбор >>
20	x^2-4=0. Если уравнение имеет более одного корня, в ответе укажите больший из них.	Смотреть видеоразбор >>
21	8^{5+x}=64	Смотреть видеоразбор >>
22	log_5(-2x+9)=2	Смотреть видеоразбор >>
23	5-6(-2x+5)=-1	Смотреть видеоразбор >>
24	x^2=-2x+24. Если уравнение имеет более одного корня, в ответе укажите больший из них.	Смотреть видеоразбор >>
25	x^2+3x=0. Если уравнение имеет более одного корня, в ответе укажите меньший из них.	Смотреть видеоразбор >>
26	(frac{1}{3})^{x-9}=frac{1}{9}	Смотреть видеоразбор >>
27	log_2(-5x+3)=-1	Смотреть видеоразбор >>

Задание №7 ЕГЭ по математике базового уровня

Простейшие уравнения

В задании №7 базового уровня ЕГЭ по математике необходимо решить

Простейшие (Protozoa) — тип одноклеточных животных.

Разбор типовых вариантов заданий №7 ЕГЭ по математике базового уровня

Вариант 7МБ1

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Алгоритм выполнения

1. Раскрыть скобки с левой и с правой стороны равенства, применив формулы приведения.
2. Все, выражения, содержащие переменную перенести в левую часть, а не содержащие в правую.
3. Преобразовать левую часть.
4. Преобразовать правую часть.
5. Решить уравнение относительно x, то есть найти неизвестный множитель.

Решение:

Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.

(x + 3) 2 = x 2 + 2 · x · 3 + 3 2 = x 2 + 6x + 9

Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.

(x – 9) 2 = x 2 – 2 · x · 9 + 9 2 = x 2 – 18x + 81

После преобразования выражение примет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

x 2 + 6x + 9 = x 2 – 18x + 81

Все выражения, содержащие переменную перенесем в левую часть, а не содержащие – в правую. При переносе из одной части равенства в другую знак меняется на противоположный.

x 2 + 6x – x 2 + 18x = 81 – 9

Преобразуем левую часть. Приведем подобные слагаемые. Объединим в скобки, сохранив знаки, те выражения, где содержится x 2 и x.

x 2 + 6x – x 2 + 18x = (x 2 – x 2 ) + (6x +18x) = 0 + 24x = 24x

Выражение примет вид:

Преобразуем правую часть. 81 – 9 = 72

Выражение примет вид:

Решим уравнение относительно x, то есть найдем неизвестный множитель. Для того чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.

Решение в общем виде:

Вариант 7МБ2

Алгоритм выполнения

1. Раскрыть скобки с левой и с правой стороны равенства, применив формулы приведения.
2. Все, выражения, содержащие переменную перенести в левую часть, а не содержащие в правую.
3. Преобразовать левую часть.
4. Преобразовать правую часть.
5. Решить уравнение относительно x, то есть найти неизвестный множитель.

Решение:

Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.

(x + 2) 2 = x 2 + 2 · x · 2 + 2 2 = x 2 + 4x + 4

Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.

(x – 2 = x 2 – 2 · x · 8 + 8 2 = x 2 – 16x + 64

После преобразования выражение примет вид:

x 2 + 4x + 4 = x 2 – 16x + 64

Все выражения, содержащие переменную перенесем в левую часть, а не содержащие – в правую. При переносе из одной части равенства в другую знак меняется на противоположный.

x 2 + 4x – x 2 + 16x = 64 – 4

Преобразуем левую часть. Приведем подобные слагаемые. Объединим в скобки, сохранив знаки, те выражения, где содержится x 2 и x.

x 2 + 4x – x 2 + 16x = (x 2 – x 2 ) + (4x +16x) = 0 + 20x = 20x

Выражение примет вид:

Преобразуем правую часть. 64 – 4 = 60

Выражение примет вид:

Решим уравнение относительно x, то есть найдем неизвестный множитель. Для того чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.

Решение в общем виде:

Вариант 7МБ3

Алгоритм выполнения

1. Перенести вычитаемое в правую сторону равенства с противоположным знаком.
2. Преобразовать правую часть с учетом свойства: log_ax + log_ay = log_a (x · y).
3. Приравнять логарифмические выражения. Можно так поступить, так как основания логарифмов в левой и правой части одинаковы.
4. Решить уравнение относительно x.

Решение:

Вариант 7МБ4

Найдите корень уравнения 3 x− 3 = 81.

Алгоритм выполнения

1. Привести выражения в степенях к одинаковому основанию. В данном случае – это 3. Теперь необходимо вспомнить, какой степенью тройки является 81.
2. Когда основания равны, можно приравнять значения степеней

Если вы забыли, то для этого необходимо делить 81 на 3 до тех пор, пока не получим 3. Чтобы получить три из 81, нам нужно поделить 81 на 3 три раза: при первом делении мы получим 27, при втором – 9, при третьем – три.

Значит, 81 это три в четвертой степени. Запишем это:

Решение:

Ответ: 7

Вариант 7МБ5

Найдите корень уравнения log₂( x − 3) = 6 .

Алгоритм выполнения

1. Логарифм по основанию два показывает нам число, в степень которого нам необходимо возвести основание, то есть двойку, чтобы получить число под логарифмом.

Решение:

Вариант 7МБ6

Найдите отрицательный корень уравнения x 2 − x − 6 = 0.

Алгоритм выполнения

1. Вычислить дискриминант
2. Найти корни
3. Выбрать необходимый корень

Решение:

D = -(1) 2 − 4 • 1 • (-6) = 25

Так как нам необходим отрицательный корень – ответ -2

Вариант 7МБ7

Решите уравнение х 2 = –2х + 24.

Если уравнение имеет больше одного

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Алгоритм выполнения

1. Переносим влево часть ур-ния, стоящую справа от знака «=». Получаем кв.уравнение стандартного вида.
2. Поскольку уравнение является приведенным, используем для нахождения корней т.Виета.
3. Записываем в качестве ответа большее из полученных 2 чисел.

Решение:

Поскольку требуется указать больший из корней, то ответом будет 4.

Вариант 7МБ8

Найдите корни уравнения 4 х–6 = 64.

Алгоритм выполнения

1. Представляем 64 как степень с основанием 4, т.е. приводим выражения справа и слева к степеням с одинаковым основанием.
2. Опускаем одинаковые основания и переходим к равенству показателей. Ур-ние стало простейшим линейным.
3. Находим корень ур-ния.

Решение:

Вариант 7МБ9

Найдите корень уравнения log₃ (2x – 5) = 2.

Алгоритм выполнения

1. Преобразуем часть уравнения справа от знака «=», используя св-ва логарифмов log_xx=1 и log_xy n =nlog_xy.
2. Переходим от равенства логарифмов к равенству выражений, стоящих под их знаками.
3. Решаем полученное линейное ур-ние.

Решение:

Вариант 7МБ10

Найдите корень уравнения

Алгоритм выполнения

1. Преобразовываем обе части ур-ния: приводим их к степеням с основанием 3. Для этого используем св-во степеней (1/а) х =а –х .
2. Поскольку основания степеней слева и справа в ур-нии теперь одинаковы, то можем их опустить и приравнять показатели.
3. Решаем полученное линейное ур-ние.

Решение:

Вариант 7МБ11

Найдите корень уравнения (х – 2 = (х – 2) 2 .

Алгоритм выполнения

1. Раскрываем скобки слева и справа, используя ф-

Луб — это сложная проводящая ткань, по которой продукты фотосинтеза (органические вещества) транспортируются из листьев ко всем органам растения (к корневищам, плодам, семенам и т. д.).

Решение:

х 2 – 2 · х ·8 + 8 2 = х 2 – 2 · х · 2 + 2 2

Вариант 7МБ12

Найдите корень уравнения

Алгоритм выполнения

1. Преобразовываем обе части ур-ния так, чтобы привести их к степеням с одинаковым основанием 7. Для выражения слева применяем св-во степеней (1/а) х =а –х .
2. Применяем св-во показат.уравнений: если степени с одинаковыми основаниями равны, то равны и их показатели. Отсюда переходим к линейному ур-нию.
3. Решаем его.

Решение:

Вариант 7МБ13

Решите уравнение х 2 – 25 = 0

Алгоритм выполнения

1. Переносим 25 в правую часть ур-ния.
2. Выражаем из ур-ния х путем извлечения корня из 25.
3. Определяем корни, сравниваем их, определяем больший.

Решение:

Для ответа берем 5.

Вариант 7МБ14

Найдите корень уравнения

Алгоритм выполнения

1. Применим св-во логарифмических равенств: если логарифмы с одинаковыми основания равны, то равны и их подлогарифменные выражения. В результате получаем равенство из выражений, стоящих под знаком логарифма.
2. Решаем полученное линейное ур-ние.

Решение:

Вариант 7МБ15

Найдите корень уравнения

Алгоритм выполнения

1. Приводим обе части ур-ния к степеням с основанием 2. При этом для преобразования выражения слева используем св-во степеней (1/а) х =а –х .
2. Получив слева и справа степени с одинаковым основанием, опускаем это основание и приравниваем показатели этих степеней. Получаем линейное ур-ние.
3. Решаем его.

Решение:

Вариант 7МБ16

Найдите корень уравнения

Репетитор по математике

Меня зовут Виктор Андреевич, — я репетитор по математике . Последние десять лет я занимаюсь только преподаванием. Я не «натаскиваю» своих учеников. Моя цель — помочь ребенку понять предмет, научить его мыслить, а не применять шаблоны, передать свои знания, а не просто «добиться результата».

Предусмотрен дистанционный формат занятий (через Skype или Zoom). На первом же уроке оцениваем уровень подготовки ребенка. Если ребенка устраивает моя подача материала, то принимаем решение о дальнейшем сотрудничестве — составляем расписание и индивидуальный план работы. После каждого занятия дается домашнее задание — оно всегда обязательно для выполнения. [в личном кабинете родители могут контролировать успеваемость ребенка]

Стоимость занятий

Набор на 2020/2021 учебный год открыт. Предусмотрен дистанционный формат.

Видеокурсы подготовки к ЕГЭ-2021

Решения авторские, то есть мои (автор ютуб-канала mrMathlesson — Виктор Осипов). На видео подробно разобраны все задания.

Теория представлена в виде лекционного курса, для понимания методик, которые используются при решении заданий.

Группа Вконтакте

В группу выкладываются самые свежие решения и разборы задач. Подпишитесь, чтобы быть в курсе и получать помощь от других участников.

Преимущества

Педагогический стаж

Сейчас существует много сайтов, где вам подберут репетитора по цене/опыту/возрасту, в зависимости от желаний. Но большинство анкет там принадлежат либо студентам, либо школьным учителям. Для них репетиторство — дополнительный временный заработок, из этого формируется отношение к деятельности. У студентов нет опыта и желания совершенствоваться, у школьных учителей — нет времени и сил после основной деятельности. Я занимаюсь только репетиторством с 2010 года. Все свои силы и знания трачу на совершенствование только в этой области.

Собственная методика

За время работы я накопил огромное количество материала для подготовки к итоговым экзаменам. Ребенку не будет даваться неадаптированная школьная программа. С каждым я разберу поэтапно специфичные примеры, темы, способы решений, необходимые для успешной сдачи ЕГЭ и ОГЭ. При этом это не будет «натаскиванием» на решение конкретных задач, но полноценная структурированная подготовка. Естественно, если таковые найдутся, устраню «пробелы» и в школьной программе.

Гарантированный результат

За время моей работы не было ни одного случая, где не прослеживалась бы четкая тенденция к улучшению знаний у ученика. Ни один откровенно не «завалил» экзамен. Каждый вырос в «понимании» математики в сравнении со своим первоначальным уровнем. Естественно, я не могу гарантировать, что двоечник за полгода подготовится на твердую «пять». Но могу с уверенностью сказать, что я подготовлю ребенка на его максимально возможный уровень за то время, что осталось до экзамена.

Индивидуальная работа

Все дети разные, поэтому способ и форма объяснения корректируются в зависимости от уровня понимания ребенком предмета. Индивидуальная работа с каждым учеником — каждому даются отдельные задания, теоретический материал.

Уравнения. Базовый уровень

Автор: Толмачева Надежда Алексеевна.

Шкала перевода баллов ОГЭ 2022

Рекомендации по переводу суммы первичных баллов за экзаменационные работы основного государственного экзамена (ОГЭ) в пятибалльную систему оценивания в 2022 году.

Итоги собеседования по русскому языку

98,7% девятиклассников, сдававших итоговое собеседование по русскому языку в основной срок 9 февраля, успешно справились с заданиями и получили «зачёт». Участие в итоговом собеседовании приняли 1 млн. 373 тыс. учащихся 9 классов из 1 млн. 462 тыс. зарегистрированных.

Единый государственный экзамен по математике базового уровня состоит из 20 заданий. В задании 7 проверяются навыки решения простейших уравнений. Школьник должен уметь решать квадратные, показательные, логарифмические, тригонометрические и другие уравнения. Здесь вы можете узнать, как решать задание 7 ЕГЭ по математике базового уровня, а также изучить примеры и способы решения на основе подробно разобранных заданий.

Простейшие уравнения

---

В задании №7 базового уровня ЕГЭ по математике необходимо решить простейшие уравнения. Для этого нам понадобятся знания логарифмов, степеней и методы решения квадратных уравнений. Перейдем к рассмотрению и разбору подобных примеров.

---

Разбор типовых вариантов заданий №7 ЕГЭ по математике базового уровня

---

Вариант 7МБ1

Найдите корень уравнения  

Алгоритм выполнения

1. Раскрыть скобки с левой и с правой стороны равенства, применив формулы приведения.
2. Все, выражения, содержащие переменную перенести в левую часть, а не содержащие в правую.
3. Преобразовать левую часть.
4. Преобразовать правую часть.
5. Решить уравнение относительно x, то есть найти неизвестный множитель.

Решение:

Раскроем скобки с левой и с правой стороны равенства, применив формулы приведения.

Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.

(x + 3)² = x² + 2 · x · 3 + 3² = x² + 6x + 9

Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.

(x — 9)² = x² — 2 · x · 9 + 9² = x² — 18x + 81

После преобразования выражение примет вид:

x² + 6x + 9 = x² — 18x + 81

Все выражения, содержащие переменную перенесем в левую часть, а не содержащие – в правую.

При переносе из одной части равенства в другую знак меняется на противоположный.

x² + 6x — x² + 18x = 81 — 9

Преобразуем левую часть. Приведем подобные слагаемые. Объединим в скобки, сохранив знаки, те выражения, где содержится x² и x.

x² + 6x — x² + 18x = (x² — x²) + (6x +18x) = 0 + 24x = 24x

Выражение примет вид:

24x = 81 — 9

Преобразуем правую часть. 81 – 9 = 72

Выражение примет вид:

24x = 72

Решим уравнение относительно x, то есть найдем неизвестный множитель. Для того чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.

x = 72 : 24

x = 3

Решение в общем виде:

Раскроем скобки в уравнении, получим:

Ответ: 3.

---

Вариант 7МБ2

Найдите корень уравнения  

Алгоритм выполнения

1. Раскрыть скобки с левой и с правой стороны равенства, применив формулы приведения.
2. Все, выражения, содержащие переменную перенести в левую часть, а не содержащие в правую.
3. Преобразовать левую часть.
4. Преобразовать правую часть.
5. Решить уравнение относительно x, то есть найти неизвестный множитель.

Решение:

Раскроем скобки с левой и с правой стороны равенства, применив формулы приведения.

Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.

(x + 2)² = x² + 2 · x · 2 + 2² = x² + 4x + 4

Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.

(x — ² = x² — 2 · x · 8 + 8² = x² — 16x + 64

После преобразования выражение примет вид:

x² + 4x + 4 = x² — 16x + 64

Все выражения, содержащие переменную перенесем в левую часть, а не содержащие – в правую.

При переносе из одной части равенства в другую знак меняется на противоположный.

x² + 4x — x² + 16x = 64 — 4

Преобразуем левую часть. Приведем подобные слагаемые. Объединим в скобки, сохранив знаки, те выражения, где содержится x² и x.

x² + 4x — x² + 16x = (x² — x²) + (4x +16x) = 0 + 20x = 20x

Выражение примет вид:

20x = 64 — 4

Преобразуем правую часть. 64 — 4 = 60

Выражение примет вид:

20x = 60

Решим уравнение относительно x, то есть найдем неизвестный множитель. Для того чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.

x = 60 : 20

x = 3

Решение в общем виде:

Раскроем скобки, получим:

Ответ: 3.

---

Вариант 7МБ3

Найдите корень уравнения  

Алгоритм выполнения

1. Перенести вычитаемое в правую сторону равенства с противоположным знаком.
2. Преобразовать правую часть с учетом свойства: log_a x + log_a y = log_a (x · y).
3. Приравнять логарифмические выражения. Можно так поступить, так как основания логарифмов в левой и правой части одинаковы.
4. Решить уравнение относительно x.

Решение:

Перенесем вычитаемое в правую сторону равенства с противоположным знаком.

Преобразуем правую часть с учетом свойства: log_a x + log_a y = log_a (x · y).

Выполним преобразование:

Приравняем логарифмические выражения. Можно так поступить, так как основания логарифмов в левой и правой части одинаковы.

Решим уравнение относительно x.

Ответ: 1.

---

Вариант 7МБ4

Найдите корень уравнения 3^{x− 3} = 81.

Алгоритм выполнения

1. Привести выражения в степенях к одинаковому основанию. В данном случае — это 3. Теперь необходимо вспомнить, какой степенью тройки является 81.
2. Когда основания равны, можно приравнять значения степеней

Если вы забыли, то для этого необходимо делить 81 на 3 до тех пор, пока не получим 3. Чтобы получить три из 81, нам нужно поделить 81 на 3 три раза: при первом делении мы получим 27, при втором — 9, при третьем — три.

Значит, 81 это три в четвертой степени. Запишем это:

Решение:

3^{x− 3} = 3⁴

х — 3 = 4

Откуда:

х = 7

Ответ: 7

---

Вариант 7МБ5

Найдите корень уравнения log₂( x − 3) = 6 .

Алгоритм выполнения

1. Логарифм по основанию два показывает нам число, в степень которого нам необходимо возвести основание, то есть двойку, чтобы получить число под логарифмом.

Решение:

x − 3 = 2⁶

x − 3 = 64

x = 67

Ответ: 67

---

Вариант 7МБ6

Найдите отрицательный корень уравнения x² − x − 6 = 0.

Алгоритм выполнения

1. Вычислить дискриминант
2. Найти корни
3. Выбрать необходимый корень

D = b² − 4ac

Решение:

D = -(1)² − 4 • 1 • (-6) = 25

x = (- b ±√D) : 2a

x = (1 + 5) : 2 = 3

x = (1 — 5) : 2 = -2

Так как нам необходим отрицательный корень — ответ -2

Ответ: -2.

---

Вариант 7МБ7

Решите уравнение х² = –2х + 24.

Если уравнение имеет больше одного корня, в ответе укажите больший из них.

Алгоритм выполнения

1. Переносим влево часть ур-ния, стоящую справа от знака «=». Получаем кв.уравнение стандартного вида.
2. Поскольку уравнение является приведенным, используем для нахождения корней т.Виета.
3. Записываем в качестве ответа большее из полученных 2 чисел.

Решение:

х² = –2х +24

х² +2х – 24 = 0

По т.Виета х₁+х₂=–b, x₁·x₂=c. В нашем ур-нии b=2, c=24. Подбираем подходящую пару чисел, получаем: х₁=–6, х₂=4.

Поскольку требуется указать больший из корней, то ответом будет 4.

Ответ: 4

---

Вариант 7МБ8

Найдите корни уравнения 4^х–6 = 64.

Алгоритм выполнения

1. Представляем 64 как степень с основанием 4, т.е. приводим выражения справа и слева к степеням с одинаковым основанием.
2. Опускаем одинаковые основания и переходим к равенству показателей. Ур-ние стало простейшим линейным.
3. Находим корень ур-ния.

Решение:

4^х–6 = 64

4^х–6 = 4³

х – 6 = 3

х = 9

Ответ: 9

---

Вариант 7МБ9

Найдите корень уравнения log₃ (2x – 5) = 2.

Алгоритм выполнения

1. Преобразуем часть уравнения справа от знака «=», используя св-ва логарифмов log_xx=1 и log_xyⁿ=nlog_xy.
2. Переходим от равенства логарифмов к равенству выражений, стоящих под их знаками.
3. Решаем полученное линейное ур-ние.

Решение:

log₃ (2x – 5) = 2

log₃ (2x – 5) = 2 · log₃3

log₃ (2x – 5) = log₃3²

2x – 5 = 3²

2x – 5 = 9

2x = 14

x=7

Ответ: 7

---

Вариант 7МБ10

Найдите корень уравнения

Алгоритм выполнения

1. Преобразовываем обе части ур-ния: приводим их к степеням с основанием 3. Для этого используем св-во степеней (1/а)^х=а^–х.
2. Поскольку основания степеней слева и справа в ур-нии теперь одинаковы, то можем их опустить и приравнять показатели.
3. Решаем полученное линейное ур-ние.

Решение:

–x + 9 = –2

–x = –2–9

x = 11

Ответ: 11

---

Вариант 7МБ11

Найдите корень уравнения (х – ² = (х – 2)².

Алгоритм выполнения

1. Раскрываем скобки слева и справа, используя ф-лу сокращенного умножения (х–у)²=х²–2ху–у².
2. Переносим влево часть уравнения справа от знака «=». Справа получаем 0.
3. Приводим подобные слагаемые. В результате уравнение стало линейным.
4. Решаем полученное уравнение.

Решение:

(х – ² = (х – 2)²

х² – 2 · х ·8 + 8² = х² – 2 · х · 2 + 2²

х² – 16х + 64 = х² – 4х + 4

х² – 16х +64 – х² + 4х – 4 = 0

–12х + 60 = 0

–12х = –60

х = 5

Ответ: 5

---

Вариант 7МБ12

Найдите корень уравнения

Алгоритм выполнения

1. Преобразовываем обе части ур-ния так, чтобы привести их к степеням с одинаковым основанием 7. Для выражения слева применяем св-во степеней (1/а)^х=а^–х.
2. Применяем св-во показат.уравнений: если степени с одинаковыми основаниями равны, то равны и их показатели. Отсюда переходим к линейному ур-нию.
3. Решаем его.

Решение:

–(x–5) = 2

5 – x = 2

–x = 2 – 5

x = 5 – 2

x = 3

Ответ: 3

---

Вариант 7МБ13

Решите уравнение х² – 25 = 0

Алгоритм выполнения

1. Переносим 25 в правую часть ур-ния.
2. Выражаем из ур-ния х путем извлечения корня из 25.
3. Определяем корни, сравниваем их, определяем больший.

Решение:

х² – 25 = 0

х² = 25

х = ±√25

х₁ = –5, х₂ = 5

Для ответа берем 5.

Ответ: 5

---

Вариант 7МБ14

Найдите корень уравнения

Алгоритм выполнения

1. Применим св-во логарифмических равенств: если логарифмы с одинаковыми основания равны, то равны и их подлогарифменные выражения. В результате получаем равенство из выражений, стоящих под знаком логарифма.
2. Решаем полученное линейное ур-ние.

Решение:

log₅ (24 – 7x) = log₅ 3

24 – 7x = 3

–7x = 3 – 24

7x = 21

x = 3

Ответ: 3

---

Вариант 7МБ15

Найдите корень уравнения

Алгоритм выполнения

1. Приводим обе части ур-ния к степеням с основанием 2. При этом для преобразования выражения слева используем св-во степеней (1/а)^х=а^–х.
2. Получив слева и справа степени с одинаковым основанием, опускаем это основание и приравниваем показатели этих степеней. Получаем линейное ур-ние.
3. Решаем его.

Решение:

2^–(x–8) = 2³

–x+8 = 3

–x = 3–8

x = 5

Ответ: 5

---

Вариант 7МБ16

Найдите корень уравнения 

Алгоритм выполнения

1. К левой части уравнения применяем св-во логарифмов log_a(x/y)=log_ax–log_ay.
2. Поскольку в обеих частях ур-ния имеем логарифмы по одинаковым основаниям, то можем их знаки, оставив только подлогарифменные выражения. Получаем линейное ур-ние.
3. Решаем его.

Решение:

log₃ (2x + 4) – log₃ 2 = log₃ 5

log₃ (2x + 4)/2 = log₃ 5

log₃ (x + 2) = log₃ 5

x + 2 = 5

x = 3

Ответ: 3