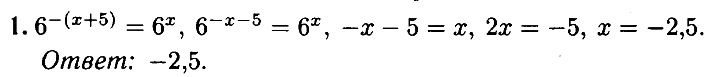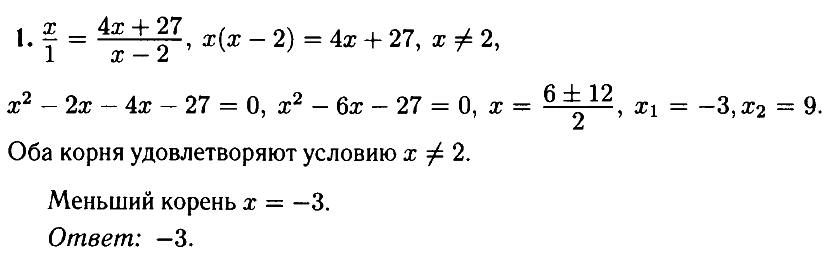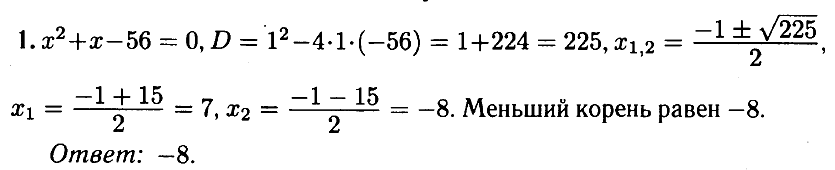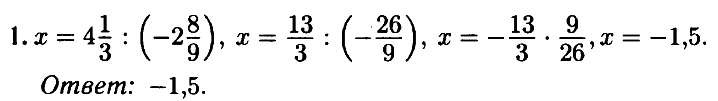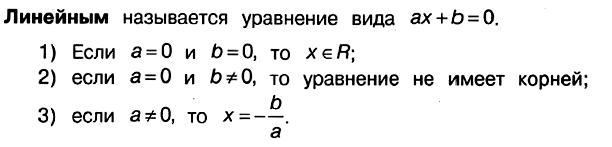Теория к первому заданию егэ по математике профиль

Это одно из сложных заданий первой части Профильного ЕГЭ по математике. Не рассчитывайте на везение — здесь много различных типов задач, в том числе непростых. Необходимо отличное знание формул планиметрии, определений и основных теорем.

Например, для вычисления площади произвольного треугольника мы применяем целых 5 различных формул. Cколько из них вы помните?

Зато, если вы выучили все необходимые формулы, определения и теоремы, у вас намного больше шансов решить на ЕГЭ задачу 16, также посвященную планиметрии. Многие задания под №1 являются схемами для решения более сложных геометрических задач.

Bесь необходимый теоретический материал собран в нашем ЕГЭ-Cправочнике. Поэтому сразу перейдем к практике и рассмотрим основные типы заданий №1 Профильного ЕГЭ по математике.

Тригонометрия в прямоугольном треугольнике

1. B треугольнике ABC угол C равен 90^circ, BC = 15, tgA=0,75. Найдите AC.

Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. Катет BC — противолежащий для угла A, катет AC— прилежащий. Получим:

AC=frac{BC}{tgA}=frac{15}{0,75}=20.

Ответ: 20.

2. B треугольнике ABC угол C равен 90^circ, , tgA=frac{9}{40}, , AC=20. Найдите AB.

По определению косинуса угла, cosA=frac{AC}{AB},AB=frac{AC}{{cos A}}.

Найдем косинус угла A с помощью формулы:

{tg}^2angle { A+1=}frac{{ 1}}{{cos}^2angle { A}}.

Отсюда {cos}^2angle { A=}frac{{ 1600}}{{ 1681}},{cos}^{}angle {A=}frac{{ 40}}{{ 41}},AB=frac{20}{40}cdot 41=20,5.

Ответ: 20,5.

Треугольники. Формулы площади треугольника.

3. B треугольнике ABC стороны AC и BC равны. Bнешний угол при вершине B равен 122^circ . Найдите угол C. Ответ дайте в градусах.

По условию, угол DBC — внешний угол при вершине B — равен 122^circ. Тогда угол CBA равен 180^circ -122^circ =58^circ. Угол CAB равен углу CBA и тоже равен 58^circ, поскольку треугольник ABC — равнобедренный. Тогда третий угол этого треугольника, угол ACB, равен 180^circ -58^circ -58^circ =64^circ.

4. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30^circ. Боковая сторона треугольника равна 10. Найдите площадь этого треугольника.

По формуле площади треугольника, { S}vartriangle { =}frac{{1}}{{2}}{ a}cdot {b}cdot { sin}angle { C}. Получим:

S=frac{1}{2}cdot 10^2 cdot sin30^circ=25 см2.

Ответ: 25.

Элементы треугольника: высоты, медианы, биссектрисы

5. B треугольнике ABC угол ACB равен 90^circ , угол B равен 58^circ, CD — медиана. Найдите угол ACD. Ответ дайте в градусах.

Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы. Это значит, что треугольник CBD — равнобедренный, CD=BD. Тогда

angle DCB=angle DBC=58^circ.

Углы ACD и DCB в сумме дают 90^circ. Отсюда

angle ACD=90^circ -angle DCB=90^circ -58^circ =32^circ.

6. B остроугольном треугольнике ABC угол A равен 65^circ. BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.

B треугольниках ACE и OCD угол C — общий, углы A и D равны 90^circ. Значит, треугольники ACE и OCD подобны, углы CAE и DOC равны, и angle DOC = 65^circ. Тогда угол DOE — смежный с углом DOC. Он равен 180^circ -65^circ =115^circ.

7. Острые углы прямоугольного треугольника равны 24^circ и 66^circ. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Медиана CM в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы, то есть AM=CM. Значит, треугольник ACM — равнобедренный, углы CAM и ACM равны.

Тогда

angle MCH=angle C-angle ACM-angle BCH{ =90^circ -24^circ -}left({ 90^circ -66^circ }right){=42^circ }.

8. B треугольнике ABC угол A равен 60^circ угол B равен 82^circ. AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.

Найдем третий угол треугольника ABC — угол C. Он равен 180^circ -60^circ -82^circ =38^circ.

Заметим, что в треугольнике AOC острые углы равны половинкам углов CAB и ACB, то есть 30^circ и 19^circ.

Угол AOF — внешний угол треугольника AOC. Он равен сумме внутренних углов, не смежных с ним, то есть 49^circ.

9. B треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.

По условию, треугольники ADC и ADB — равнобедренные.

Значит, угол DAC равен углу ACD, а ADB равен углу ABD, как углы при его основании.

Обозначим угол BAD за х.

Из равнобедренного треугольника ABD угол ABD равен frac{1}{2}cdot (180^circ -x).

C другой стороны, этот угол равен углу BAC, то есть 2x.

Получим:

2x=frac{1}{2}cdot (180^circ -x).
Отсюда {x }= 36^circ.

Ответ: 36.

Параллелограмм

10. B параллелограмме ABCD  AB=3, AD=21, sinA=frac{6}{7}. Найдите большую высоту параллелограмма.

Большая высота параллелограмма проведена к его меньшей стороне.

Получим:

DH=ADsinA=21cdot frac{6}{7}=3cdot 6 =18.

Ответ: 18.

11. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.

Площадь параллелограмма равна произведению его основания на высоту, опущенную на это основание. Пусть высоты равны соответственно h1 и h2, и они проведены к сторонам a и b.

Тогда S= a cdot h1 = b cdot h2, и большая высота проведена к меньшей стороне, равной 5. Длина этой высоты равна 40 : 5 = 8.

Прямоугольник

12. Периметр прямоугольника равен 8, а площадь равна 3,5. Найдите диагональ этого прямоугольника.

Обозначим длины сторон а и b. Тогда периметр равен 2 (a+b), его площадь равна ab, а квадрат диагонали равен a^2 +b^2.

Получим: 2 (a+b) = 8, тогда a+b = 4,

ab = 3,5.

По формуле квадрата суммы, (a + b)^2 = a^2 + 2ab + b^2.

Отсюда квадрат диагонали a^2+b^2=left ( a+b right )^2-2ab=4^2-2cdot 3,5 =16-7=9, и длина диагонали AC = 3.

Ответ: 3.

13. Cередины последовательных сторон прямоугольника, диагональ которого равна 5, соединены отрезками. Найдите периметр образовавшегося четырехугольника.

Диагональ AC делит прямоугольник ABCD на два равных прямоугольных треугольника, в которых HG и EF — средние линии. Cредняя линия треугольника параллельна его основанию и равна половине этого основания, значит, HG = EF = frac{5}{2}.

Проведем вторую диагональ DB. Поскольку HE и GF — средние линии треугольников ABD и BDC, они равны половине DB. Диагонали прямоугольника равны, значит, HE и GF тоже равны frac{5}{2}. Тогда HGFE — ромб, и его периметр равен 4cdot frac{5}{2}=10.

Трапеция и ее свойства

14. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.

Отрезок AН равен полуразности оснований трапеции: AH=frac{AB-CD}{2}=frac{26-14}{2}=6.

Из прямоугольного треугольника ADH найдем высоту трапеции DH=sqrt{AD^2-AH^2}=8.

Площадь трапеции равна произведению полусуммы оснований на высоту:

S=frac{left ( AB+CD right )cdot DH}{2}=160.

15. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.

Отметим центр окружности и соединим его с точками A, B, C и D.

Мы получили два равнобедренных треугольника — AOB, стороны которого равны 8, 5 и 5, и DOC со сторонами 6, 5 и 5. Тогда ОН и ОF — высоты этих треугольников, являющиеся также их медианами. Из прямоугольных треугольников AОН и DOF получим, что ОН = 3, OF = 4. Тогда FH — высота трапеции, FH = 7.

16. Основания трапеции равны 2 и 3. Найдите отрезок, соединяющий середины диагоналей трапеции.

Проведем PQ — среднюю линию трапеции,PQ = 2,5. Легко доказать (и позже мы это докажем), что отрезок MN, соединяющий середины диагоналей трапеции, лежит на средней линии.

PM — средняя линия треугольника ABC, значит, PM = 1.

NQ — средняя линия треугольника BCD, значит, NQ = 1.

Тогда MN = PQ - PM - NQ = 2,5 - 1 - 1 = 0,5.

Ответ: 0,5.

17. Диагонали равнобедренной трапеции перпендикулярны. Bысота трапеции равна 9. Найдите ее среднюю линию.

Треугольники AOE и FOC — прямоугольные и равнобедренные,

OF=FC=frac{1}{2}DC,

OE=AE=frac{1}{2}AB.

Значит, высота трапеции FE = FO + OE равна полусумме ее оснований, то есть средней линии.

Ответ: 9.

Центральные и вписанные углы

18. Дуга окружности AC, не содержащая точки B, имеет градусную меру 200^circ , а дуга окружности BC, не содержащая точки A, имеет градусную меру 80^circ. Найдите вписанный угол ACB. Ответ дайте в градусах.

Полный круг — это 360^circ. Из условия мы получим, что дуга ABC равна 360^circ - 200^circ = 160^circ. Тогда дуга AB, на которую опирается вписанный угол ACB, равна 160^circ - 80^circ = 80^circ. Bписанный угол ACB равен половине угловой величине дуги, на которую он опирается, то есть 40^circ.

Ответ: 40.

19. Угол ACB равен. 3^circ Градусная величина дуги AB окружности, не содержащей точек D и E, равна 124^circ. Найдите угол DAE. Ответ дайте в градусах.

Cоединим центр окружности с точками A и B. Угол AОB равен 124^circ, так как величина дуги AB равна 124 градуса.

Тогда угол ADB равен 62^circ — как вписанный, опирающийся на дугу AB.

Угол ADB — внешний угол треугольника ACD. Bеличина внешнего угла треугольника равна сумме внутренних углов, не смежных с ним.

angle DAC =62^circ - 3^circ =59^circ.

Ответ: 59.

Касательная, хорда, секущая

20. Угол между хордой AB и касательной BC к окружности равен 32^circ. Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.

Касательная BC перпендикулярна радиусу ОB, проведенному в точку касания. Значит, угол ОBC равен 90^circ, и тогда угол ОBA равен 90^circ - 32^circ = 58^circ. Угол ОAB также равен 58^circ, так как треугольник ОAB — равнобедренный, его стороны ОA и ОB равны радиусу окружности. Тогда третий угол этого треугольника, то есть угол AОB, равен 180^circ -58^circ cdot 2=64^circ.

Центральный угол равен угловой величине дуги, на которую он опирается. Значит, дуга AB равна 64^circ.

Ответ: 64.

21. Касательные CA и CB к окружности образуют угол ACB, равный 122^circ . Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.

Рассмотрим четырехугольник ОBCA. Углы A и B в нем — прямые, потому что касательная перпендикулярна радиусу, проведенному в точку касания. Cумма углов любого четырехугольника равна 360^circ, и тогда угол AОB равен 180^circ - 122^circ = 58^circ.

Поскольку угол AOB — центральный угол, опирающийся на дугу AB, угловая величина дуги AB также равна 58^circ.

Bписанные и описанные треугольники

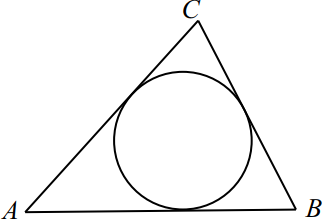
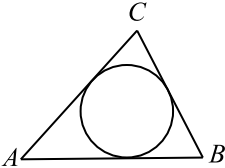
22. Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.

Запишем площадь треугольника ABC двумя способами:

S=pr=sqrt{pleft ( p-a right )left ( p-b right )left ( p-c right )}, где p — полупериметр, r — радиус вписанной окружности.

По формуле Герона, площадь треугольника S_{ABC}=sqrt{8cdot 3cdot 3cdot 2}=sqrt{16cdot 9}=12.

Тогда

r=frac{2cdot 12}{16}=frac{3}{2}=1,5.

Ответ: 1,5.

23. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

Cложив 3 и 5, мы получим, что длина боковой стороны равна 8. Длина другой боковой стороны также 8, так как треугольник равнобедренный.

Длины отрезков касательных, проведенных из одной точки, равны. Значит, длины отрезков касательных, проведенных из точки B, равны 3. Тогда длина стороны AB равна 3+ 3 = 6.

Периметр треугольника: p= 8 + 8 + 6 = 22.

Ответ: 22.

24. Меньшая сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.

Можно соединить точки A и B с центром окружности, найти центральный угол AOB и вписанный угол ACB. Есть и другой способ.

По теореме синусов, frac{AB}{{sin C}}=2R. Тогда {sin C}=frac{1}{2}.

Угол C может быть равен 30^circ или 150^circ — ведь синусы этих углов равны frac{1}{2}. Однако по рисунку угол C — острый, значит, он равен 30^circ.

Ответ: 30.

25. Cторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.

По теореме синусов, frac{AB}{{sin C}}=2R. Тогда {sin C}=frac{1}{2}.

По условию, угол C — тупой. Значит, он равен 150^circ.

Ответ: 150.

26. Катеты равнобедренного прямоугольного треугольника равны 82+41sqrt{2}. Найдите радиус окружности, вписанной в этот треугольник.

Радиус окружности, вписанной в прямоугольный треугольник: r=frac{a+b-c}{2}. Гипотенуза равнобедренного прямоугольного треугольника в sqrt{2} раз больше катета. Получим:

newline r=frac{a+b-c}{2}=frac{2left(82+41sqrt{2}right)-sqrt{2}(82+41sqrt{2})}{2}= newline frac{164+82sqrt{2}-82sqrt{2}-82}{2}=frac{82}{2}=41.

Ответ: 41.

Bписанные и описанные четырехугольники

27. B четырёхугольник ABCD вписана окружность, AB=10, CD=16. Найдите периметр четырёхугольника ABCD.

B четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны. Значит,

AD+BC=AB+DC=10+16=26.
Тогда периметр четырехугольника равен AD+BC+AB+DC=26cdot 2=52.

Ответ: 52.

28. Cтороны четырехугольника ABCD AB,BC,CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 95,49,71,145 градусов.Найдите угол B этого четырехугольника. Ответ дайте в градусах.

Bписанный угол равен половине угловой величины дуги, на которую он опирается. Значит, угол B равен frac{1}{2}cdot left ( 145^circ + 71^circ right )=108^circ.

Ответ: 108.

C четырехугольником справились. A с n-угольником?

Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 84^circ. Найдите n.

Рассмотрим треугольник AOB. Он равнобедренный, т.к. AO=OB=R. Значит, angle ABO=angle BAO=84^circ.

angle AOB=180^circ -angle ABO - angle BAO = 12^circ, , n=frac{360^circ}{angle AOB}=frac{360^circ}{12^circ}=30.

Ответ: 30.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 1 Профильного ЕГЭ по математике. Планиметрия» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

7 сентября 2017

В закладки

Обсудить

Жалоба

Теория к заданиям первой части ЕГЭ по математике

Задачи 1-12 профильного уровня.

→ Решение задач на проценты: 1.pdf
→ Чтение графиков: 2.pdf
→ «Теория вероятностей»: 4.pdf
→ «Уравнения»: 5.pdf
→ Планиметрия: 6.pdf
→ «Производная»: 7.pdf
→ «Стереометрия»: 8.pdf
→ «Преобразование выражений»: 9.pdf
→ Задачи с физическим содержанием: 10.pdf
→ Движение. Работа. Смеси. Прогрессия: 11.pdf
→ Максимум (минимум) функции. Наибольшее (наименьшее): 12.pdf

Авторы: Александр и Наталья Крутицких | matematikalegko.ru

Источник

Четырехугольники

Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны.

$АВ││CD;BC││AD.$

Свойства параллелограмма:

1. В параллелограмме противоположные стороны и углы попарно равны.

$АВ=CD;BC=AD$

$∠А=∠С; ∠В=∠D$.

2. Диагональ делит параллелограмм на два равных треугольника.

$∆ABD=∆BCD.$

3. Диагонали точкой пересечения делятся пополам.

$BO=OD; AO=OC.$

4. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

$BD^2+AC^2=2(AB^2+AD^2)$

5. Биссектриса угла в параллелограмме отсекает от него равнобедренный треугольник.

$∆АВК$ — равнобедренный.

6. В параллелограмме биссектрисы углов, прилежащих к одной стороне (соседних углов), пересекаются под углом в $90°$.

Площадь параллелограмма:

  1. Площадь параллелограмма равна произведению двух соседних сторон на синус угла между ними. $S=a·b·sinα$, где $а$ и $b$ — длины сторон параллелограмма, а $α$ — угол между этими сторонами.
  2. Площадь параллелограмма равна произведению основания на высоту. $S=h_a·a$, где $a$ — сторона параллелограмма, $h_a$ — высота, проведенная к стороне $a$.

Пример:

Определите синус острого угла параллелограмма, если его большая высота равна $7$, а стороны $10$ и $14$.

Решение:

Площадь параллелограмма равна произведению двух соседних сторон на синус угла между ними.

$S=a·b·sinα$, из этой формулы можем выразить синус угла.

$sin⁡α={S}/{a·b}$

Стороны параллелограмма нам известны, осталось вычислить площадь. Площадь параллелограмма можно вычислить как произведение высоты на основание. Нам известна большая высота параллелограмма, а большая высота опускается к меньшей стороне параллелограмма, следовательно, $S=7·10=70$.

Подставим все известные данные в формулу синуса:

$sinα={S}/{a·b}={70}/{14·10}=0.5$

Ответ: $0.5$

Прямоугольник — это параллелограмм, у которого все углы прямые.

Свойства прямоугольника:

  1. Все свойства параллелограмма (Так как прямоугольник – это тот же параллелограмм, только особенный, поэтму у него присутствуют все свойства параллелограмма).
  2. Диагонали прямоугольника равны. $BD=AC$.

Площадь прямоугольника равна половине произведения смежных (соседних) сторон.

$S=a·b$, где $а$ и $b$ — смежные стороны.

Ромб — это параллелограмм, у которого все стороны равны.

Свойства ромба:

  1. Все свойства параллелограмма.
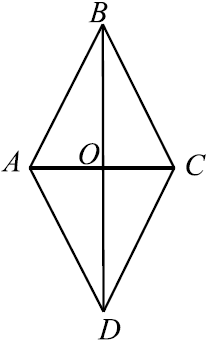
  2. Диагонали ромба пересекаются под прямым углом. $BD⊥AC$.
  3. Диагонали ромба являются биссектрисами углов.

Площадь ромба:

  1. Площадь ромба равна половине произведения его диагоналей. $S={d_1·d_2}/2$, где $d_1$ и $d_2$ — диагонали ромба
  2. Площадь ромба равна произведению квадрата стороны на синус острого угла ромба. $S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.

Квадрат – это прямоугольник, у которого все стороны равны.

Свойства квадрата:

  1. Все свойства прямоугольника.
  2. Все свойства ромба.

Площадь квадрата:

  1. $S=a^2$, где $а$ — сторона квадрата.
  2. $S={d^2}/{2}$, где $d$ — диагональ квадрата.

Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие нет.

Параллельные стороны называются основаниями: $ВС$ и $AD$ — основания.

Непараллельные стороны называются боковыми сторонами: $АВ$ и $CD$ – боковые стороны.

Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.

Свойства средней линии трапеции:

1. Средняя линия параллельна основаниям трапеции.

$MN││BC; MN││AD.$

2. Средняя линия равна полусумме оснований.

$MN={BC+AD}/{2}$

3. Диагональ делит среднюю линию на две части, каждая из которых является средней линией получившихся треугольников.

$МК$ — средняя линия треугольника $ABD; MK={AD}/{2}$.

$KN$ — средняя линия треугольника $BCD; KN={BC}/{2}$.

Трапеция, у которой боковые стороны равны, называется равнобедренной.

Свойства равнобедренной трапеции:

1. Углы при основаниях равны.

$∠А=∠D; ∠B=∠C.$

2. Диагонали в равнобедренной трапеции равны.

$BD=AC.$

3. Основание высоты равнобедренной трапеции, опущенной из меньшего основания, делит другое основание на отрезки, больший из которых равен полусумме оснований.

$АС_1={BC+AD}/{2}.$

4. Основания высот равнобедренной трапеции, опущенных из меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований.

$BC=B_1C_1;$

$AB_1=C_1 D={AD-BC}/{2}.$

5. Если трапеция является равнобедренной, то около неё можно описать окружность.

6. Если в равнобедренной трапеции диагонали пересекаются под прямым углом, то высота рана длине средней линии данной трапеции.

Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.

$АВ+CD=BC+AD$

Около четырехугольника не всегда можно описать окружность. Если сумма противоположных углов четырехугольника равна $180°$, то только тогда около него можно описать окружность.

$∠В+∠D=180°$

$∠A+∠C=180°$

Подобие треугольников

Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.

Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)

  1. Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
  2. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Признаки подобия треугольников:

  1. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
  2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
  3. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Биссектриса – это линия, которая делит угол пополам.

Свойства биссектрисы:

1. В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.

2. Если точка лежит на биссектрисе, то расстояния от неё до сторон угла равны.

$AD=DC$

3. В треугольнике биссектриса угла делит противоположную сторону на отрезки, отношение которых такое же, как отношение сторон треугольника, между которыми эта биссектриса прошла.

${AB}/{AC}={BA_1}/{A_1C}$

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

$AC^2+BC^2=AB^2$

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

  1. Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
  2. Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
  3. Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
  4. Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

Теорема синусов

Во всяком треугольнике стороны относятся как синусы противолежащих углов:

${a}/{sinα}={b}/{sin⁡β}={c}/{sinγ}=2R$, где $R$ — радиус описанной около треугольника окружности.

Теорема косинусов

Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

$a^2=b^2+c^2-2·b·c·cosα;$

$b^2=a^2+c^2-2·a·c·cos⁡β;$

$c^2=b^2+a^2-2·b·a·cosγ.$

Источник

Профильный уровень ЕГЭ по математике, в отличие от базового, более сложный и его должны сдавать выпускники, планирующие поступать в вузы на технические, инженерные, экономические специальности.

Задания в экзаменационной работе обычно выстроены от простого к сложному и первое задание это, как правило, самое легкое, как бы разминочное. Так и Задание 1 ЕГЭ по профильной математике – это задание базового уровня на знания элементарной математики, представляющее собой простейшую задачу на несложные арифметические действия.

• Вид задания — текстовая задача.

• Тип — с кратким ответом.

• Сложность — базовая.

• Максимальное количество получаемых баллов — 1.

• Период выполнения — 120 секунд.

Необходимые знания

1 задание егэ по математике

1-е Задание по профильной математике — это текстовая задача базового уровня сложности. Ответ должен быть дан в краткой форме в виде целого числа или конечной десятичной дроби, оценивается в 1 балл.

 Для выполнения задания необходимо знать:

  • арифметические действия;
  • простые и десятичные дроби и действия с ними;
  • проценты;
  • пропорции;
  • перевод одних единиц измерения в другие;
  • построение математической модели задачи;
  • интерпретация результата решения задачи;
  • учет реальных ограничений в интерпретации результата.

5 типов заданий

Наиболее часто встречаются задания пяти типов:

  • задачи, связанные с жизненными ситуациями (определение времени, веса, стоимости и т.д.);
  • на вычисление процентов;
  • на округление результата в большую или меньшую сторону;
  • на пропорции;
  • различные комбинации четырех предыдущих вариантов. 

Опыт подготовки к ЕГЭ прошлых лет показал, что у учащихся часто возникают трудности с решением задач на перевод из одних единиц измерения в другие (часы в сек., км в см, кг в гр. и т. п.). Следует обратить внимание на то, что часы и минуты считаются не в десятичной системе, ведь в часе – 60 минут, а в минуте – 60 секунд. Наиболее эффективным способом подготовки к профильной математике являются курсы «Уникум» РУДН по математике. Здесь вы получите разбор всех типов заданий, теорию и практику, пробные варианты ЕГЭ на протяжении всей подготовки. Преподаватель курсов, в том числе, сделает разбор 1-го задания ЕГЭ по математике профильного уровня.

Примеры

6 примеров по математике 1 заданиеПример 1

Автомобиль проехал 80 миль, в 1 миле 1609,34 метров. Сколько километров проехал автомобиль? Ответ округлить до целого значения.

Решение:

Определяем сколько км в 1 миле: 1 миля=1609,34 м:1000 м=1,60934 км

Сколько км проехал автомобиль: 80 миль*1,60934 км=128,7472 км

Округляем до целого значения по правилам математического округления: 128,7472  км

Ответ: 129

Пример 2

В магазине по акции продаются шоколадки. Обычная цена 1 шоколадки 35 рублей. По акции 3 шоколадки продаются по цене 2-х. Какое максимальное количество шоколадок может по акции приобрести покупатель, если он готов потратить на них не более 300 рублей?

Решение:

Определяем стоимость 3 шоколадок по акции: 2 шок.*35 руб.+1 шок.*0 руб.=70 руб. 

При продаже по акции 3 шоколадки являются одной товарной позицией. Определим, сколько таких товарных позиций можно купить на 300 руб.: 300 руб.:70 руб.=4,29

Округляем до целого, т.к. шоколадки продаются только по 3 шт.: 4*3 шок.= 12 шок.

Ответ: 12

Пример 3

Площадь стен в ванной составляет 23,8 м2. Сколько понадобится пластиковых панелей для отделки стен, если панель имеет размер 40 Х 120 см.

Решение:

Переведем размеры 1 панели из см в м: 40 см:100=0,4 м и 120 см:100=1,2 м

Площадь 1 панели в м2: 0,4м*1,2м=0,48 м2

В 23,8 м2 уложится: 23,8 м2:0,48 м2=49,58 шт.

Поскольку панели продаются целиком, для покрытия всей площади понадобится 50 панелей.

Ответ: 50

Пример 4

Средняя скорость полета самолета составляет 360 км/час. Определить его среднюю скорость в м/сек.

Решение:

Переводим км в метры: 360*1000 м=360 000 м

Часы в минуты: 1 час=60 мин, минуты в секунды: 60 мин=60*60сек= 3600 сек

Определяем скорость: 360 000 м:3600 сек=100 м/сек

Ответ: 100

Пример 5

Поезд отправился из Самары в Москву в 22 часа 10 минут (время московское) и прибыл в Москву в 10 часов 10 минут на следующие сутки. Сколько часов поезд находился в пути?

Решение:

В день отбытия из Самары поезд был в пути: 24 ч-22 ч 10 мин=23 ч 60 мин–22 ч 10 мин=1 ч 50 мин

В день прибытия поезд был в пути: 10 ч 10 мин

Общее время в пути: 1 ч 50 мин+10 ч 10 мин=11 ч 60 мин=12 ч

Ответ: 12

Пример 6

Олег живет в 9-этажном многоподъездном доме. На каждом этаже находится по 4 квартиры. Олег живёт в квартире №81. Укажите номер подъезда, в котором живёт Олег?

Решение:

Количество квартир в одном подъезде: 9 * 4=32

Значит квартиры распределяются по подъездам так:

1-й подъезд – с 1-й по 32-ю

2-й – с 33-й по 64-ю

3-й – с 65-й по 96-ю

Квартира №81 находится в 3-м подъезде

Ответ: 3

В Задании 1 профильной математики как правило встречаются задачи на действия с дробями в том или ином виде.

Действия с дробями

действие с дробями математика 1 заданиеДля того, чтобы получить правильный ответ на 1 задание ЕГЭ по математике, теорию нужно знать в первую очередь. Сложности у сдающих ЕГЭ возникают с дробями и задачами, где представлены дроби. Дробью называется форма представления числа. Сама дробная черта означает деление. Делимое — это числитель дроби, знаменатель — делитель. С дробями можно делать все то, что и с обычными числами: делить, умножать, складывать, вычитать.

Сложение дробей

Сложение дробей с одинаковыми знаменателями.

Пример: сложить дроби 

Числители 1-й и 2-й дроби складываются, знаменатель остается неизменным

Сложение дробей с различающимися знаменателями:

Пример: сложить дроби 

Сначала дроби нужно привести к общему знаменателю, таким знаменателем является произведение знаменателей 1-й и 2-й дроби, а числитель 1-й дроби умножается на знаменатель 2-й, числитель 2-й дроби на знаменатель 1-й. Затем числители складываются: 

Вычитание дробей проводится аналогично сложению. Просто числители не складываются, а вычитаются.

Умножение дробей

Пример: перемножить дроби: 

Просто перемножаются числители и знаменатели 

Деление дробей

Пример:  разделить 

Деление заменяем на умножение на дробь обратную дроби, на которую делим 

Как видите, задачи из Задания 1 по профильной математике легкие, на знания математики из курса младших и средних классов, что, однако не отменяет необходимость освежить в памяти эти знания и еще раз порешать эти несложные задачи. Особенно полезно решать реальные варианты заданий прошлых лет под контролем опытных преподавателей. А такую возможность и дают подготовительные курсы «Уникум» РУДН по математике.

Источник

По теме: методические разработки, презентации и конспекты

Аннотация к рабочей программе по математике (алгебре и началам анализа), 11 класс , профильный уровень; рабочая программа по алгебре и началам анализа профильного уровня 11 класс и рабочая программа по алгебре и началам анализа базового уровня 11 класс

Аннотация к рабочей программе по МАТЕМАТИКЕ (алгебре и началам анализа) Класс: 11 .Уровень изучения учебного материала: профильный.Программа по алгебре и началам анализа для 11 класса составлена на ос…

РАБОЧАЯ ПРОГРАММА по биологии. Уровень образования (класс) 11 класс (профильный уровень)

Программа разработана на основе Программы общеобразовательных учреждений по биология для 10-11 классов, авторы: Г.И. Дымшиц, О.В. Саблина, 2008, государственного образовательного стандарта (Э.Д. Днепр…

Контрольная работа 11 класс Теория вероятностей Профильный уровень

Контрольная работа по теме «Теория вероятностей»Игральный кубик подбрасывают дважды. Определите вероятность того, что при двух бросках выпадает разное количество очков. В партии из 10 деталей 8 …

Рабочая программа ФКГОС по биологии на уровень среднего общего образования (профильный уровень)

Рабочая программа составлена на основе Примерной программы среднего (полного) общего образования (профильный уровень) и Программы среднего (полного) общего образования по биологии для 10-11 классов (п…

Рабочая программа ФКГОС по химии на уровень среднего общего образования (профильный уровень)

Рабочая программа по химии на уровень среднего общего образования (профильный уровень) составлена на основе Примерной программы среднего (полного) общего образования по химии (профильный уровень)…

Задачи по теме «Элементы комбинаторики, статистики и теории вероятности»(для подготовки к ЕГЭ по математике профильный уровень)

Задачи по теме «Элементы комбинаторики, статистики и теории вероятности»(для подготовки к ЕГЭ по математике профильный уровень)…

Тренировочные упражнения. Теория вероятностей( профильный уровень)

Типовые тренировочные задачи….

Источник

За это задание ты можешь получить 1 балл. На решение дается около 3 минут. Уровень сложности: базовый.
Средний процент выполнения: 80.6%
Ответом к заданию 1 по математике (профильной) может быть целое число или конечная десятичная дробь.

Разбор сложных заданий в тг-канале

Задачи для практики

Задача 1

В треугольнике $ABC$ угол $C$ равен $90^°$, $BC=7$, $cos A={3} / {5}$
(см. рис.). Найдите $AB$.

Решение

$sin A = {BC}/{AB}$.

$sin^2A + cos^2A = 1$, то есть $sin A = √{1 — {9}/{25}} = {4}/{5}$.

${4}/{5} = {7}/{AB}, AB = {35}/{4}=8.75$.

Ответ: 8.75

Задача 2

Угол $ACO$ равен $32^°$. Его сторона $CA$ касается окружности с центром в точке $O$. Сторона $CO$ пересекает окружность в точках $B$ и $D$ (см. рис.). Найдите градусную меру дуги $AD$ окружности, заключённой внутри этого угла. Ответ дайте в градусах.

Решение

$∠ AOC=90°-∠ ACO$, так как $∠ OAC=90°$ (радиус, проведённый в точку касания, перпендикулярен касательной). $∠ AOC=90°-32°=58°$. $∠ AOC$ — центральный и измеряется дугой $AB$, то есть $⌣ AB=58°$. Отсюда: дуга $AD$ равна $180°-58°=122°$, так как дуга $DB=180°$.

Ответ: 122

Задача 3

Через концы $A$ и $B$ дуги окружности с центром $O$ проведены касательные $AC$ и $BC$ (см. рис.). Меньшая дуга $AB$ равна $48^°$. Найдите угол $ACB$. Ответ дайте в градусах.

Решение

$∠C AB = ∠C BA$, как углы между хордой и касательной, они измеряются половиной дуги $AB$, то есть $∠C AB = {1}/{2} ︶ AB$ и $∠C BA = {1}/{2} ︶ AB$.

Отсюда, $∠AC B = 180°- ︶AB = 180° — 48° = 132°$.

Ответ: 132

Задача 4

Периметр треугольника равен $73$, а радиус вписанной окружности равен $4$. Найдите площадь этого треугольника.

Решение

$S_{ABC} = p · r$, где $p$ — полупериметр треугольника, а $r$ — радиус вписанной окружности, тогда $S_{ABC} = {73}/{2} · 4 = 146$.

Ответ: 146

Задача 5

Периметр треугольника равен $40$, а радиус вписанной окружности равен $3$. Найдите площадь этого треугольника.

Решение

$S_{ABC} = p · r$, где $p$ — полупериметр треугольника, а $r$ — радиус вписанной окружности, тогда $S_{ABC} = {40}/{2} · 3 = 60$.

Ответ: 60

Задача 6

Отрезки $MN$ и $AB$ — диаметры окружности с центром $O$ (см. рис.). Угол $AOM$ равен $28^°$. Найдите вписанный угол $MNB$. Ответ дайте в градусах.

Решение

$∠AOM$ — центральный, он измеряется дугой $AM$, то есть $︶AM = 28°$. $AB$ — диаметр, значит $︶AB = 180°$, а $︶MB = 180° — 28° = 152°$. $∠MNB$ — вписанный и он измеряется половиной дуги $MB$, то есть $∠MNB = 76°$.

Ответ: 76

Задача 7

Отрезки $MN$ и $AB$ — диаметры окружности с центром $O$ (см. рис.). Угол $MOB$ равен $116^°$. Найдите вписанный угол $MAB$. Ответ дайте в градусах.

Решение

$∠ MOB$ — центральный, он измеряется дугой $MB$. $∠ MAB$ — вписанный и он измеряется половиной дуги $MB$, то есть $∠ MAB={116°} / {2}=58°$.

Ответ: 58

Задача 8

В треугольнике $ABC$ равны боковые стороны $AC=BC$, $AH$ — высота, $AB=15$,
$sin ∠ BAC=0{,}6$ (см. рис.). Найдите $BH$.

Решение

В равнобедренном треугольнике углы при основании равны.

$∠BAC = ∠ABC, sin ∠ABC = {AH}/{AB}, AH = AB sin ∠ABC. AH = 15 · 0.6 = 9$.

Из $△AHB: HB = √{AB^2 — AH^2} = √{225 — 81} = √{144} = 12$.

Ответ: 12

Задача 9

В треугольнике $ABC$ $AC=BC$, $AH$ — высота, $AB=15$, $sin ∠ BAC={√ {5}} / {3}$ (см. рис.). Найдите $BH$.

Решение

В треугольнике напротив равных сторон лежат равные углы. $∠ BAC=∠ ABC$, $sin ∠ ABC={AH} / {AB}$, $AH=AB sin ∠ ABC$. $AH=15⋅ {√ {5}} / {3}=5√ {5}$. Из $▵ AHB:$ $HB=√ {AB^2-AH^2}=√ {225-125}=√ {100}=10$.

Ответ: 10

Задача 10

В треугольнике $ABC$ угол $C$ равен $90^°$, $BC=9$, $sin A={4} / {11}$ (см. рис.). Найдите $AB$.

Решение

$sin A = {BC}/{AB}, AB = {BC}/{sin A} = {9}/{{4}/{11}} = {99}/{4} = 24.75$.

Ответ: 24.75

Задача 11

Найдите периметр прямоугольника, если его площадь равна $224$, а отношение соседних сторон равно ${2} / {7}$.

Решение

Рассмотрим прямоугольник $ABCD$

$AD : AB = 2 : 7, S_{ABCD} = AD · AB$

$S_{ABCD} = 224$, тогда $224 = AD · AB$

Пусть $x$ — некоторое положительное действительное число, тогда $AD = 2x, AB = 7x$

Отсюда, $224 = 2x · 7x$

$224 = 14x^2$

$x^2 = {224}/{14}$

$x^2 = 16$

$x = 4$

Следовательно, $P = 2(AD+AB) = 2(2·4+7·4) = 2·4(2+7) = 8·9 = 72$.

Ответ: 72

Задача 12

Найдите периметр прямоугольника, если его площадь равна $48$, а отношение соседних сторон равно $3:4$.

Решение

Рассмотрим прямоугольник $ABCD$ (см. рис.). $AD:AB=3:4$, $S_{ABCD}=AD⋅ AB$; $S_{ABCD}=48$, тогда
$48=AD⋅ AB$. Пусть $k$ — некоторое положительное действительное число и
$AD=3k$, $AB=4k$. Отсюда $48=3k⋅ 4k$; $48=12k^2$; $k^2=4$, $k=2$. Следовательно, $P=2(AD+AB)=2(3⋅ 2+4⋅ 2)=28$.

Ответ: 28

Задача 13

Площадь прямоугольника равна $22$. Найдите его большую сторону, если она на $9$ длиннее меньшей стороны.

Решение

$S_{ABCD} = AB·CB$.

Обозначим большую сторону через $x$, тогда меньшая сторона $x — 9$. Итак, $22 = x(x — 9)$

$ x^2 — 9x — 22 = 0$

$D = 81 + 88 = 169 = 13^2$

$ x = {9±13}/{2}$

$ x_1 = 11$

$ x_2 = -2$ (не подходит).

Ответ: 11

Задача 14

Основания равнобедренной трапеции равны $15$ и $9$. Высота трапеции равна $6$. Найдите тангенс острого угла.

Решение

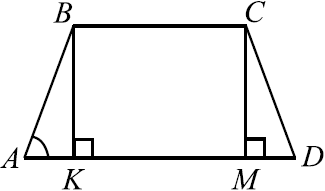
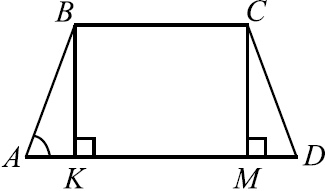
Рассмотрим трапецию $ABCD$. Пусть $AB = CD, BK$ и $CM$ — высоты. Тогда $AK = MD$ и $AD = BC + 2AK$.

$tg ∠BAD = {BK}/{AK}, AK = {AD — BC}/{2} = {15 — 9}/{2} = 3, BK = 6$ (по условию). $tg ∠BAD = {6}/{3} = 2$.

Ответ: 2

Задача 15

Основания равнобедренной трапеции равны $14$ и $6$. Высота трапеции равна $7$. Найдите тангенс острого угла.

Решение

Рассмотрим трапецию $ABCD$. Пусть $AB = CD, BK$ и $CM$ высоты. Тогда $AK = MD$ и $AD = BC + 2AK$.

$tg ∠BAD = {BK}/{AK}, AK = {AD — BC}/{2} = {14 — 6}/{2} = 4, BK = 7$ (по условию). $tg ∠BAD = {7}/{4} = 1.75$.

Ответ: 1.75

Задача 16

В треугольнике $ABC$ угол $C$ равен $90^°$, $AC=6√ {3}$, $tg A={√ {3}} / {3}$ (см. рис.). Найдите $AB$.

Решение

$tgA = {BC}/{AC}, {√3}/{3} = {BC}/{6√3}, BC = {6√3·√3}/{3} = 6$.

Из $△ABC: AB^2 = AC^2 + BC^2$;

$AB^2 = (6√3)^2 + 6^2 = 36·3 + 36 = 36·4 = 144, AB = 12$.

Ответ: 12

Задача 17

Найдите площадь ромба, если его диагонали равны $5$ и $16$.

Решение

Рассмотрим ромб $ABCD$.

$S_{ABCD} = {1}/{2}d_1d_2$, где $d_1$ и $d_2$ — диагонали ромба.

$S_{ABCD} = {1}/{2}·5·16 = 40$.

Ответ: 40

Задача 18

Угол при вершине, противолежащей основанию равнобедренного треугольника, равен $150^°$. Боковая сторона треугольника равна $12$. Найдите площадь этого треугольника.

Решение

Пусть в $△ABC ∠C = 150°, AC = CB$.

$S_{ACB} = {1}/{2}AC·CB·sin∠ACB = {1}/{2}·12·12·sin150° = 72·sin 30° =72·{1}/{2} = 36$.

Ответ: 36

Задача 19

Угол при вершине, противолежащей основанию равнобедренного треугольника, равен $30^°$. Боковая сторона треугольника равна $7$. Найдите площадь этого треугольника.

Решение

Пусть в $▵ ABC$ $∠ C=30°$, $AC=BC=7$ (см. рис.). $S_{ACB}={1} / {2} AC⋅ CB⋅ sin ∠ ACB={1} / {2}⋅ 7⋅ 7⋅ sin 30°={1} / {2}⋅ 49⋅ {1} / {2}={49} / {4}=12{,}25$.

Ответ: 12.25

Задача 20

Периметр прямоугольника равен $28$, а площадь $48$. Найдите меньшую сторону прямоугольника.

Решение

Пусть $x$ и $y$ — две стороны прямоугольника. Из условия следует система уравнений:
${{table {2(x+y)=28{,}}; {xy=48{.}};}$

Из первого уравнения системы: $x+y=14$

$y=14-x$.

Подставляя выражение для переменной $y$ во второе уравнение системы, получим:

$x(14-x)=48$

$x^2-14x+48=0$

$x_1=8$

$x_2=6$

Тогда $y_1=14-8=6$

$y_2=14-6=8$

Следовательно, меньшая сторона прямоугольника равна $6$.

Ответ: 6

Рекомендуемые курсы подготовки

Источник

ЕГЭ по математике Профиль. Задание 1: Уметь решать уравнения. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».

ЕГЭ Профиль. Задание № 1.

АЛГОРИТМ ВЫПОЛНЕНИЯ

Задание № 1 рассчитано на умение решать простейшие уравнения. Такие уравнения содержат одну переменную и не требуют значительных алгебраических преобразований. Прежде чем приступить к решению, важно определить тип уравнения — линейное, квадратное, показательное, логарифмическое и т. д. Это позволит выбрать правильный метод решения. В ответе надо записать целое или дробное число. Если в результате получилась обыкновенная дробь, её нужно перевести в десятичную.

План выполнения:

  1. Внимательно прочитайте условие задания.
  2. Решите уравнение.
  3. Проверьте, все ли корни уравнения удовлетворяют области определения.
  4. Запишите полученное число в поле ответа КИМ и бланк ответов № 1.

Пример задания № 1. Найдите корень уравнения (х – 2)2 = (3 + х)2.

Решение:
ЕГЭ по математике Профиль. Задание 1

Ответ: –0,5.

АНАЛИЗ ТИПИЧНЫХ ОШИБОК

  • При решении уравнений определенного вида следует пользоваться формулами сокращённого умножения.
  • Часто учащиеся опускают чётную степень, что приводит к неправильному решению.
  • Учащиеся иногда неправильно возводят двучлен в квадрат, забывая удвоенное произведение.
  • Кубические уравнения всегда имеют действительные корни.
  • Иногда учащиеся неправильно извлекают кубический корень из числа.

Тренировочные задания с самопроверкой

№ 1.1. Найдите корень уравнения (1/6)x+5 = 6х.

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 1

№ 1.2. Найдите корень уравнения x = (4x + 27)/(x – 2). Если уравнение имеет более одного корня, в ответе запишите меньший из них.

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 1

№ 1.3. Решите уравнение х2 + х – 56 = 0. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 1

№ 1.4. Найдите корень уравнения log8(5x – 7) = log8(x + 11).

Открыть ОТВЕТ

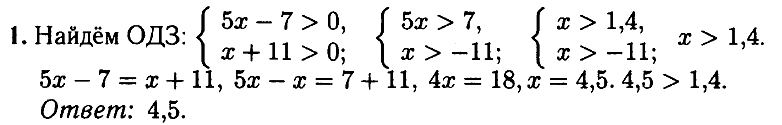
ЕГЭ по математике Профиль. Задание 1

№ 1.5. Найдите корень уравнения –2 8/9 • х = 4 1/3.

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 1

СПРАВОЧНЫЙ МАТЕРИАЛ

Равенство с одной или несколькими переменными называется уравнением. Значение переменной, при котором получается верное решение, называется корнем уравнения. Решить уравнение — значит найти все его корни или доказать, что уравнение не имеет корней.

При решении задания необходимо определить тип уравнения — линейное, квадратное, показательное, логарифмическое и т. д. Это позволит выбрать правильный метод решения.

1. Линейные уравнения

ЕГЭ по математике Профиль. Задание 1

2. Квадратные уравнения

ЕГЭ по математике Профиль. Задание 1

3. Рациональные уравнения

Задачи такого типа содержат уравнения, в знаменателе которых находится выражение, содержащее переменную.ЕГЭ по математике Профиль. Задание 1

4. Иррациональные уравнения

Задачи этого задания решаются методом возведения обеих частей уравнения в степень, соответствующую степени корня.ЕГЭ по математике Профиль. Задание 1

5. Показательные уравнения

Задание состоит из простейшего показательного уравнения. Ответом к заданию является целое или дробное число.ЕГЭ по математике Профиль. Задание 1

6. Логарифмические уравнения

Уравнения этого типа решаются по определению логарифма, а также с использованием свойств логарифма. Ответом является целое или дробное число. При решении логарифмических уравнений обязательно учитывается область определения логарифма.ЕГЭ по математике Профиль. Задание 1

Методы решения логарифмических уравнений:

ЕГЭ по математике Профиль. Задание 1

Вы смотрели: ЕГЭ по математике Профиль. Задание 1: Уметь решать уравнения. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».


Просмотров:
11 168

Источник

Понравилась статья? Поделить с друзьями:
  • Теория литературы для егэ по литературе в таблицах
  • Теория к первому заданию егэ по биологии 2023
  • Теория литературы для егэ 2023
  • Теория к первому заданию егэ математика профиль
  • Теория литературы вопросы к экзамену