Теория множеств информатика егэ - Помощь в подготовке к экзаменам и поступлению

На уроке рассматривается разбор 15 задания ЕГЭ по информатике, дается подробное объяснение того, как решать подобные задачи

Содержание:

Объяснение задания 15 ЕГЭ по информатике
- Элементы математической логики
- Математическая логика и теория множеств
- Задания с отрезками и ДЕЛ
- Задания с поразрядной конъюнкцией
Решение заданий 15 ЕГЭ по информатике
- Задания с множествами
- Задания с отрезками на числовой прямой
- Задания с ДЕЛ
- Задания с поразрядной конъюнкцией
- Задания на поиск наибольшего или наименьшего числа А

15-е задание: «Основные законы алгебры логики»

Уровень сложности

— повышенный,

Требуется использование специализированного программного обеспечения

— нет,

Максимальный балл

— 1,

Примерное время выполнения

— 5 минут.

Проверяемые элементы содержания: Знание основных понятий и законов математической логики

До ЕГЭ 2021 года — это было задание № 18 ЕГЭ

Типичные ошибки и рекомендации по их предотвращению:

«Важно понимать, что выражение должно быть тождественно истинно, т.е. истинно при любых допустимых значениях переменных x и у, а не только при некоторых наборах значений»

ФГБНУ «Федеральный институт педагогических измерений»

Элементы математической логики

Для выполнения задания рекомендуется повторить следующие темы:

Преобразование логических операций:

операцию импликация можно преобразовать в операции ИЛИ и НЕ:

A → B = ¬ A ∨ B
или
A → B = A + B

операцию эквивалентность можно преобразовать:

A ↔ B = A ⊕ B = A ∧ B ∨ A ∧ B
или
A ↔ B = A ⊕ B = A · B + A · B

операцию XOR (сложение по модулю 2) можно преобразовать так:

A ⊕ B = (¬A ∧ B) ∨ (A ∧ ¬B)
или
A ⊕ B = (A · B) + (A · B)

Законы алгебры логики:

кроме того, могут пригодиться базовые аксиомы и формулы:

Закон двойного отрицания:	¬¬ A = A
Закон исключения третьего:	A ∧ ¬ A = 0 или A · A = 0 A ∨ ¬ A = 1 или A + A = 1
Закон повторения (идемпотентности):	A ∧ A = A или A · A = A A ∨ A = A или A + A = A
Законы исключения логических констант:	A ∧ 0 = 0 A ∧ 1 = A A ∨ 0 = A A ∨ 1 = 1
Переместительный (коммутативный) закон:	A ∧ B = B ∧ A A ∨ B = B ∨ A
Сочетательный (ассоциативный) закон:	(A ∧ B) ∧ C = A ∧ (B ∧ C) (A ∨ B) ∨ С = A ∨ (B ∨ С)
Распределительный (дистрибутивный) закон:	(A ∧ B) ∨ C = (A ∨ C) ∧ (B ∨ C) (A ∨ B) ∧ С = (A ∧ С) ∨ (B ∧ С) и наоборот: (A ∨ B) ∧ (A ∨ C) = A ∨ (B ∧ C) (A ∧ B) ∨ (A ∧ C) = A ∧ (B ∨ C)
Закон общей инверсии (Законы де Моргана):	¬ (A ∧ B) = ¬ A ∨ ¬ B ¬ (A ∨ B) = ¬ A ∧ ¬ B
Закон исключения (склеивания):	(A ∧ B) ∨(¬A ∧ B) = B (A ∨ B) ∧(¬A ∨ B) = B
Упрощать выражения можно с помощью формул:
Закон поглощения:	A ∨ A ∧ B = A A ∧ (A ∨ B) = A A ∨ ¬A ∧ B = A ∨ B ¬A ∨ A ∧ B = ¬A ∨ B A ∧ (¬A ∨ B) = A ∧ B ¬A ∧ (A ∨ B) = ¬A ∧ B

Порядок выполнения логических операций:

выражения в скобках,
операции «НЕ»,
операции «И»,
операции «ИЛИ»,
операции «импликация»
операции «эквиваленция»

последовательность из операций импликации выполняется слева направо (при этом соблюдается принцип «операции с одинаковым приоритетом выполняются слева направо»):

A → B → C → D = ((A → B) → C) → D

Математическая логика и теория множеств

пересечение множеств соответствует логическому умножению, а объединение – логическому сложению;
пересечением двух множеств называется новое множество, состоящее из элементов, принадлежащих одновременно обеим множествам:

Пример:

объединением двух множеств называется новое множество, состоящее из элементов, принадлежащих отдельно каждому из множеств (без повторений);

Пример:

пустое множество ∅ – это множество, в котором не содержится ни одного элемента; пустому множеству в теории множеств соответствует 0;
универсальное множество U (на кругах Эйлера обозначается в виде прямоугольника) – это множество, содержащее все возможные элементы определенного типа (например, все вещественные числа):

универсальное множество соответствует логической единице: для любого множества целых чисел X справедливы равенства:

X ∨ U = U и X ∧ U = X

разностью двух множеств A и B называется новое множество, элементы которого принадлежат A, но не принадлежат B:

Пример разности множеств:

дополнение множества X – это разность между универсальным множеством U и множеством X (например, для целых чисел ¬ X – все целые числа, не входящие в X)

пусть требуется выбрать множество A так, чтобы выполнялось равенство A ∨ X = I; в этом случае множество A должно включать дополнение ¬ X, то есть A ≥¬ X (или A ⊇¬ X), то есть A_min = ¬ X
пусть требуется выбрать множество A так, чтобы выполнялось равенство ¬ A ∨ X = I, в этом случае множество ¬ A должно включать дополнение ¬ X, то есть ¬ A ⊇ ¬ X; отсюда A ⊆ X, то есть A_max = X

Для большей определенности стоит рассмотреть тему круги Эйлера

Задания с отрезками и ДЕЛ

Для решения заданий необходимо знать рассмотренную тему о множествах.

Для упрощения решений можно пользоваться следующими законами.

1. Если в задании формула тождественно истинна (равна 1), и
2. после упрощения A без отрицания
то используется закон:

A_min = ¬B

где B — известная часть выражения.

1. Если в задании формула тождественно истинна (равна 1), и
2. после упрощения A с отрицанием
то используется закон:

A_max = B

где B — известная часть выражения.

1. Если в задании формула тождественно ложна (равна 0), и
2. после упрощения A без отрицания
то используется закон:

A_max = ¬B

где B — известная часть выражения.

1. Если в задании формула тождественно ложна (равна 0), и
2. после упрощения A с отрицанием
то используется закон:

A_min = B

где B — известная часть выражения.

Задания с поразрядной конъюнкцией

В задании 15 ЕГЭ встречаются задачи, связанные с поразрядной конъюнкцией.
Например:

5 & 26

означает поразрядную конъюнкцию (логическое «И») между двоичными значениями двух чисел — 5 и 26. Выполняется так:

5  =   101₂ 
26 = 11010₂
0  = 00000₂

Задания, связанные с поразрядной конъюнкцией, решаются несколькими способами. Рассмотрим один из них.

Обозначим:

(x & K = 0) как Z_k

Для решения методом, предложенным А.В. Здвижковой, пригодится использование следующих свойств:

Z_k * Z_m = Z_{k or m}

Так, например, если в задании имеем:

(X & 5 = 0) ∧ (X & 26 = 0)

то сначала введем замену:

Z₅ ∧ Z₂₆

а затем, используя свойство 1, вычислим поразрядную дизъюнкцию двоичного значения чисел 26 и 5:

Z₅ ∧ Z₂₆ = Z_{26 or 5}
помним, что дизъюнкция - это операция логическое "ИЛИ" (сложение)
5  =   101₂ 
26 = 11010₂
31 = 11111₂

таким образом, получили:

Z₅ ∧ Z₂₆ = Z₃₁

Z_k + Z_m = Z_{k and m}

Так, например, если в задании имеем:

(X & 28 = 0) ∨ (X & 22 = 0)

то сначала введем замену:

Z₂₈ ∨ Z₂₂

а затем, используя свойство 2, вычислим поразрядную конъюнкцию двоичного значения чисел 28 и 22:

Z₂₈ ∨ Z₂₂ = Z_{28 and 22}
помним, что конъюнкция - это операция логическое "И" (умножение)
28 = 11100₂ 
22 = 10110₂
     10100₂ = 20₁₀

таким образом, получили:

Z₂₈ ∨ Z₂₂ = Z₂₀

Условие Z_k → Z_m истинно для любых натуральных значений x тогда и только тогда, когда все единичные биты двоичной записи числа M входят во множество единичных битов двоичной записи числа K.

На деле, это означает, что если имеем:

X & 29 = 0 → X & 5 = 0  Истинно или Ложно?

то сначала введем замену:

Z₂₉ → Z₅

а затем, используя свойство 3, определим истинность высказывания Z₂₉ → Z₅:

Z₂₉ → Z₅ = 1 (истине), тогда, когда:
29 = 11101₂
5  =   101₂  
единичные биты двоичного числа 5 входят в единичные биты двоичного числа 29 
(совпадают с ними)

таким образом, получили:

Z₂₉ → Z₅ = 1 (истинно)

(x & 125 = 5) то же самое, что и
Z₁₂₀ * ¬Z₄ * ¬Z₁ = 1 (истине)

Так, например, если в задании имеем:

X & 130 = 3

то сначала введем замену и, используя свойство 4, получим:

X & 130 = 3 то же самое, что и
Z₁₂₇ * ¬Z₂ * ¬Z₁

т.е. 3 = 2 + 1 :	

2 = 10
1 = 01
3 = 11

Решение заданий 15 ЕГЭ по информатике

Плейлист видеоразборов задания на YouTube:

Задание демонстрационного варианта 2022 года ФИПИ

Задания с множествами

Множества:

15_16:

Элементами множества А являются натуральные числа. Известно, что выражение

((x ∈ {1, 3, 5, 7, 9, 11}) → ¬(x ∈ {3, 6, 9, 12})) ∨ (x ∈ A)

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное значение суммы элементов множества A.

✍ Решение:

Введем обозначения:

P ≡ (x ∈ {1, 3, 5, 7, 9, 11}) ; 
Q ≡ (x ∈ {3, 6, 9, 12}) ; 
A ≡ (x ∈ A).

Выполним преобразования:

(P → ¬Q) ∨ A = 1
Избавимся от импликации:
¬P ∨ ¬Q ∨ A = 1

Разделим выражение на две части — известную часть и неизвестную. Чтобы неизвестная часть (А) была непременно истинной, необходимо, чтобы известная часть была ложна:

¬P ∨ ¬Q ∨ А = 1
    ⁰      ¹

То есть получаем:

¬P ∨ ¬Q = 0,
или 
¬P = 0  отсюда P = 1
¬Q = 0 отсюда Q = 1

Таким образом имеем пересечение (умножение) двух множеств Q и P. То есть необходимо выбрать элементы, которые встречаются в обоих множествах одновременно:

A = {3,9}

Сумма элементов:

3 + 9 = 12

Ответ: 12

Аналитическое решение:
📹 YouTube здесь

📹 Видеорешение на RuTube здесь

Множества:

15_17:

Элементами множества А являются натуральные числа. Известно, что выражение

(x ∈ {2, 4, 6, 8, 10, 12}) → (((x ∈ {3, 6, 9, 12, 15}) ∧ ¬(x ∈ A)) → 
→ ¬(x ∈ {2, 4, 6, 8, 10, 12}))

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное значение суммы элементов множества A.

Типовые задания для тренировки

✍ Решение:

Введем обозначения:

P≡(x ∈ {2, 4, 6, 8, 10, 12}) ; 
Q ≡ (x ∈ {3, 6, 9, 12, 15}) ; 
A ≡ (x ∈ A).

Выполним преобразования:

P → ((Q ∧ ¬A) → ¬P) = 
P → (¬(Q ∧ ¬А) ∨ ¬P) = 
¬P ∨ (¬(Q ∧ ¬А) ∨ ¬P) = 
¬P ∨ ¬Q ∨ А.

Разделим выражение на две части — известную часть и неизвестную. Чтобы неизвестная часть (А) была непременно истинной, необходимо, чтобы известная часть была ложна:

¬P ∨ ¬Q ∨ А = 1
    ⁰      ¹

То есть получаем:

¬P ∨ ¬Q = 0,
или 
¬P = 0  отсюда P = 1
¬Q = 0 отсюда Q = 1

Таким образом имеем пересечение (умножение) двух множеств Q и P. То есть необходимо выбрать элементы, которые встречаются в обоих множествах одновременно:

A = {6,12}

Сумма элементов:

6 + 12 = 18

Ответ: 18

Множества:

15_18: Закон распределения

Элементами множеств А, P, Q являются натуральные числа, причём P = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}, Q = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}. Известно, что выражение

( (x ∈ A) → (x ∈ P) ) ∧ ( (x ∈ Q) → ¬(x ∈ A) )

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наибольшее возможное количество элементов в множестве A.

Типовые задания для тренировки

✍ Решение:

Введем обозначения:

P ≡ (x ∈ P); 
Q ≡ (x ∈ Q); 
A ≡ (x ∈ A).

Выполним преобразования:

Избавимся от импликации:
(¬A ∨ P) ∧ (¬Q ∨ ¬A) = 1
Применим распределительный закон (но можно вывести самостоятельно):
¬A ∨ (P ∧ ¬Q) = 1

Разделим выражение на две части — известную часть и неизвестную. Чтобы неизвестная часть (А) была непременно истинной, необходимо, чтобы известная часть была ложна:

¬A ∨ (P ∧ ¬Q) = 1
 ⁰      ¹

То есть получаем:

P ∧ ¬Q = 1,
или 
P = 1  и
¬Q = 1 отсюда Q = 0

Таким образом имеем разность двух множеств Q и P. То есть это новое множество, элементы которого принадлежат P, но не принадлежат Q:

A = {2, 4, 8, 10, 14, 16, 20}

Количество элементов = 7

Ответ: 7

Множества:

15_20:

Элементами множества А являются натуральные числа. Известно, что выражение

¬(x ∈ A) →¬(x ∈ {1, 3, 7}) ∨ (¬(x  ∈ {1, 2, 4, 5, 6}) ∧ (x ∈ {1, 3, 7}))

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное количество элементов множества A.

✍ Решение:

Введем обозначения:

P ≡ (x ∈ {1, 3, 7}); 
Q ≡ (x  ∈ {1, 2, 4, 5, 6}); 
A ≡ (x ∈ A).

Выполним преобразования:

Избавимся от импликации:
A ∨ ¬P ∨ (¬Q ∧ P) = 1
Применим закон поглощения (но можно вывести самостоятельно):
A ∨ ¬P ∨ ¬Q = 1

Разделим выражение на две части — известную часть и неизвестную. Чтобы неизвестная часть (А) была непременно истинной, необходимо, чтобы известная часть была ложна:

A ∨ ¬P ∨ ¬Q = 1
 ¹      ⁰

То есть получаем:

¬P ∨ ¬Q = 0,
или 
P = 1 и Q = 1

Таким образом имеем пересечение двух множеств Q и P:

A = {1}

Количество элементов = 1

Ответ: 1

Задания с отрезками на числовой прямой

Отрезки на числовой прямой:

15_3:

На числовой прямой даны два отрезка: P=[44,48] и Q=[23,35].

Укажите наибольшую возможную длину отрезка А, для которого формула

((x ϵ P) → (x ϵ Q)) ∧ (x ϵ A)

тождественно ложна, то есть принимает значение 0 при любом значении переменной x.

✍ Решение:

Упростим формулу, избавившись от ‘x ϵ‘:

(P → Q) ∧ A

Теперь преобразуем импликацию в скобках:

правило импликации: a → b = ¬a ∨ b

(¬P ∨ Q) ∧ A

Указанные в задании отрезки отобразим на числовой прямой. Разделим отрезки на части по точкам, соответствующим их границам.

Вернемся к преобразованному выражению. В нем есть известная часть (выделим ее) и неизвестная. По условию выражение должно быть ложно:

(¬P ∨ Q) ∧ A = 0

Внешняя операция выражения — конъюнкция — ложна в трех случаях и только в одном — истинна:

(¬P ∨ Q) ∧ A
    ⁰     ^∧ ⁰ ⁼ ⁰
    ⁰     ^∧ ¹ ⁼ ⁰
    ¹     ^∧ ⁰ ⁼ ⁰
    ¹     ^∧ ¹ ⁼ ¹

Теперь рассмотрим это выражение относительно наших отрезков на числовой прямой: если известная часть выражения (¬P ∨ Q) на каком-либо отрезке прямой дает истину, то неизвестная часть (A) должна возвращать ложь (по условию формула должна быть тождественно ложна).
Рассмотрим все отрезки числовой прямой для известной части выражения:

1. (¬P ∨ Q) = 1 ∨ 0 = 1  - на данном отрезке А должно равняться 0
2. (¬P ∨ Q) = 1 ∨ 1 = 1  - на данном отрезке А должно равняться 0
3. (¬P ∨ Q) = 1 ∨ 0 = 1  - на данном отрезке А должно равняться 0
4. (¬P ∨ Q) = 0 ∨ 0 = 0  - на данном отрезке А может! равняться 1
5. (¬P ∨ Q) = 1 ∨ 0 = 1  - на данном отрезке А должно равняться 0

Получаем, что на всех отрезках кроме 4-го выражение ¬P ∨ Q истинно, т.е. на отрезках 1, 2, 3 и 5 неизвестная часть A должна быть ложной (чтобы формула вернула ложь). Отсюда следует, что А может быть истинно только на отрезке 4.
Длина отрезка 4 составляет:

48 - 44 = 4

Результат: 4
✎ Решение 2 (программирование):
Внимание! этот способ подходит НЕ для всех заданий с отрезками!
Python:

def f(a1,a2,x):
    return((44<=x<=48)<=(23<=x<=35))and(a1<=x<=a2)
maxim = 0
for a1 in range (1,200):
    for a2 in range (a1+1,200):
        if all(f(a1,a2,x)==0 for x in range (1,200)):# если все ложны
            if a2-a1>maxim:
                maxim=a2-a1
                print(a1,a2, a2-a1) # сами точки отрезка и длина

Вывод:

PascalABC.net:

Вывод:

С подробным аналитическим решением задания 15 ЕГЭ по информатике можно ознакомиться по видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Отрезки на числовой прямой:

15_9:

На числовой прямой даны два отрезка: P = [10,20] и Q = [30,40].

Укажите наибольшую возможную длину отрезка A, для которого формула

((x ∈ P) → (x ∈ Q))  → ¬(x ∈ A)

тождественно истинна, то есть принимает значение 1 при любом значении переменной x.

Типовые задания для тренировки

✍ Решение:

Упростим выражение, введя обозначения:

A: x ∈ A
P: x ∈ P
Q: x ∈ Q

Запишем формулу с новыми обозначениями, учитывая, что по условию она должна быть тождественно истинной:

(P → Q) → ¬A = 1

Избавимся от импликации:

(P → Q) → ¬A = 1        =>
¬(P → Q) ∨ ¬A = 1       =>
¬(¬P ∨ Q) ∨ ¬A = 1

Используем закон Де Моргана для последующего преобразования:

¬(¬P ∨ Q) ∨ ¬A = 1    =>
P ∧ ¬Q ∨ ¬A = 1

А — наше неизвестное, а выделенную часть формулы можно найти. Необходимо, чтобы А = 1. Значит, предположим, что ¬А = 0, тогда P ∧ ¬Q = 1 (если P ∧ ¬Q = 0, то ¬А может равняться и 0 и 1, так как имеет место операция логического сложения ∨)
Значит, имеем P ∧ ¬Q = 1. Кроме того, в данном случае имеет место операция конъюнкция, которую проще вычислить, если выражение равно 1 (так как для конъюнкции существует один единственный случай истинности: 1 & 1 = 1). Таким образом имеем утверждения:

А = 1
P = 1
¬Q = 1 или Q = 0

Т.е. A истинно (=1) на промежутке пересечения отрезков P и ¬Q.
Отобразим отрезки на числовой прямой, чтобы найти искомое значение:

Очевидно, что А будет истинно, только в части 2 (на рис. желтым цветом), то есть соответствовать отрезку [10,20], имеющему длину 10.

Результат: 10

Отрезки на числовой прямой:

15_10:

На числовой прямой даны два отрезка: P = [3, 20] и Q = [6, 12].

Укажите наибольшую возможную длину отрезка A, для которого формула

((x ∈ P) ~ (x ∈ Q))  → ¬(x ∈ A)

тождественно истинна, то есть принимает значение 1 при любом значении переменной x.

✍ Решение:

Упростим выражение, введя обозначения:

A: x ∈ A
P: x ∈ P
Q: x ∈ Q

Запишем формулу с новыми обозначениями, учитывая, что по условию она должна быть тождественно истинной:

(P ~ Q) → ¬A = 1

Избавимся от импликации:

(P ~ Q) → ¬A = 1      =>
¬(P ~ Q) ∨ ¬A = 1

Далее возможно 2 способа решения.

✎ 1 способ:

Избавимся от эквивалентности по правилу преобразования эквивалентности:

(a ~ b) = a * b + ¬a * ¬b

¬(P ~ Q) = ¬((P ∧ Q) ∨ (¬P ∧ ¬Q)) =
= ¬(P ∧ Q) ∧ ¬(¬P ∧ ¬Q)

Преобразуем часть данного выражения по закону Де Моргана:

¬(P ∧ Q) ∧ ¬(¬P ∧ ¬Q) =
= ¬(P ∧ Q) ∧ (P ∨ Q)

В итоге получим:

¬(P ∧ Q) ∧ (P ∨ Q) ∨ ¬A = 1

А — наше неизвестное, а выделенную часть выражения можно найти. Необходимо, чтобы А = 1. Значит, предположим, что ¬А = 0, тогда, чтобы общее выражение было истинным (по условию), нужно чтобы ¬(P ∧ Q) ∧ (P ∨ Q) = 1.
Имеем:

¬(P ∧ Q) ∧ (P ∨ Q) = 1
А = 1

Отобразим отрезки на числовой прямой, чтобы найти искомое значение:

Очевидно, что А будет истинно в двух отмеченных на рисунке частях: 2 и 4 (на рис. желтым цветом). Но по условию нам необходимо найти А наибольшей длины, соответственно, выбираем отрезок [12,20], имеющий длину 8.

✎ 2 способ:
После того, как мы избавились от импликации, имеем:

¬(P ~ Q) ∨ ¬A = 1

А — наше неизвестное, а выделенную часть выражения можно найти. Необходимо, чтобы А = 1. Значит, предположим, что ¬А = 0, тогда ¬(P ~ Q) = 1 (чтобы общее выражение было истинным, как указанно в условии).
Иными словами ¬(P ~ Q) истинно для всех значений x, при которых P не равно Q (т.е. либо P = 1 и Q = 0, либо P = 0 и Q = 1).
Это соответствует двум отрезкам (см. рисунок выше, желтым цветом): [3,6] и [12,20]. Но по условию нам необходимо найти А наибольшей длины, соответственно выбираем отрезок [12,20], имеющий длину 8.

Результат: 8

С решением задания 15 вы также можете ознакомиться, посмотрев видео (аналитическое решение):

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Отрезки на числовой прямой:

15_11:

На числовой прямой даны два отрезка: P = [11, 21] и Q = [15, 40].

Укажите наибольшую возможную длину отрезка A, для которого формула

(x ∈ A) → ¬((x ∈ P)  ~ (x ∈ Q))

тождественно истинна, то есть принимает значение 1 при любом значении переменной x.

Типовые задания для тренировки

✍ Решение:

Упростим выражение, введя обозначения:

A: x ∈ A
P: x ∈ P
Q: x ∈ Q

Запишем формулу с новыми обозначениями, учитывая, что по условию она должна быть тождественно истинной:

A → ¬(P ~ Q) = 1

Избавимся от импликации:

A → ¬(P ~ Q) = 1    =>
¬A ∨ ¬(P ~ Q) = 1

А — наше неизвестное, тогда как выделенную часть формулы можно найти. Введем предположение, что А = 1. Значит, ¬А = 0 (т.е. А = 1), тогда ¬(P ~ Q) = 1 (так как общая формула должна быть истинной по условию).
Иными словами ¬(P ~ Q) истинно для всех значений x, при которых P не равно Q (т.е. либо P = 1 и Q = 0, либо P = 0 и Q = 1).
Отобразим отрезки на числовой прямой, чтобы найти искомое значение:

Получаем, что А соответствует двум отрезкам (см. рисунок, желтым цветом): [11,15] и [21,40]. Но по условию нам необходимо найти А наибольшей длины, соответственно выбираем отрезок [21,40], имеющий длину 19.

Результат: 19

Задания с ДЕЛ

Поиск наибольшего А, известная часть Дел ∨ Дел = 1

15_7:

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».

Для какого наибольшего натурального числа А формула

  (ДЕЛ(x, 40) ∨ ДЕЛ(x, 64))  → ДЕЛ(x, A)

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

Типовые задания для тренировки

✍ Решение:

✎ Решение 1 (теоретическое):

Введем обозначения:

A = ДЕЛ(x,A); 
D40 = ДЕЛ(x, 40); 
D64 = ДЕЛ(x, 64)

Перепишем исходную формулу, согласно введенным обозначениям. Укажем, что формула должна быть тождественно истинна (по условию):

(D40 ∨ D64)  → A = 1

Избавимся от импликации:

¬(D40 ∨ D64) ∨ A = 1
или
(¬D40 ∧ ¬D64) ∨ A = 1

Разделим данную формулу на две части: в одной из них — искомое A, а в другой — часть формулы с x, которую можно найти:

(¬D40 ∧ ¬D64) ∨ A = 1
      ¹          ²

В полученной формуле необходимо, чтобы искомая часть с A в конечном счете было истинно.
Т.е. (¬D40 ∧ ¬D64) должно быть = 0. Это нам ничего не дает, т.к. конъюнкция ложна в трех случаях (1*0, 0*1 и 0*0), т.е. D40 и D64 могут быть равны как 0, так и 1 (исключение составляет лишь вариант, когда оба D истинны, тогда логическое умножение 1 * 1 ≠ 0).
Преобразуем выражение первой части формулы по закону Де Моргана (чтобы оно равнялось 1):

¬D40 ∧ ¬D64 = 0
или
¬(¬D40 ∧ ¬D64) = 1

Преобразуем по закону Де Моргана и получим:
D40 ∨ D64 = 1

Далее можно решать задание либо с помощью кругов Эйлера, либо с помощью логических рассуждений.

Решение с помощью логических рассуждений:

Найдем все такие x, которые делятся на А и при этом делятся на 40 ИЛИ делятся на 64:

x/A : x/40 ∨ x/64

x = 40, 64, 80, 120, 128, 160, 192, 200, ...

Теперь найдем такие A, начиная с самого наименьшего (единицы), на которые делятся все x без исключения:

А = 1, 2, 4, 8

Наибольшее А равно 8.
Или то же самое можно найти поиском наибольшего общего делителя чисел 40 и 64 (используем формулу Евклида):

НОД (40,64) = 8 
40,64  (64 - 40 = 24)
40,24  (40 - 24 = 16)
24,16  (24 - 16 = 8)
16,8   (16 - 8 = 8)
8,8

Решение с помощью кругов Эйлера:

В этом случае логическое сложение тоже дает истину в трех случаях (1+1, 1+0, 0+1). Т.е. мы не сможем найти А с помощью функции ДЕЛ. Необходимо прибегнуть к решению с помощью кругов Эйлера.
В множество A должны входить все числа, которые попадают в объединение D40 + D64. Таким образом, нужно найти множество, в которое входят оба этих множества.
Найдем наибольший общий делитель чисел 40 и 64; это число 8:

64 / 40 = 1 (24 остаток)
40 / 24 = 1 (16 остаток)
24 / 16 = 1 (8 остаток)
16 / 8 = 2 (0 остаток) - НОД = 8
+++
40 / 8 = 5
64 / 8 = 8

Т.е. можно сказать, что A = D40 + D64 = D8*D5 + D8*D8 = D8*(D5 + D8). D8 входит в каждое из множеств D40 и D64. Объединение D40 + D64 тоже входит в D8:

8 — наибольший общий делитель числе 40 и 64, значит, оно соответствует максимальному значению A.

Результат: 8

✎ Решение 2 (программирование):
Python:

for A in range(1,500):
    OK = 1
    for x in range(1,1000):
        OK *= ((x % 40 == 0) or (x % 64 == 0))<=(x % A== 0)
    if OK:
        print( A )

Вывод:

PascalABC.net:

begin
  for var A := 1 to 500 do
  begin
    var ok := 1;
    for var x := 1 to 1000 do
    begin
      if (((x mod 40 = 0) or (x mod 64 = 0)) <= (x mod A = 0)) = false then
      begin
        ok := 0; 
        break;
      end;
    end;
    if (ok = 1) then print(A)
  end;
end.

Вывод:

Результат: 8

Поиск наименьшего А, известная часть Дел ∧ ¬Дел = 1

15_5:

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».

Для какого наименьшего натурального числа А формула

ДЕЛ(x, A) → (¬ДЕЛ(x, 28) ∨ ДЕЛ(x, 42))

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

Типовые задания для тренировки

✍ Решение:

✎ Решение 1 (теоретическое):

Имеем:

ДЕЛ(x, A) → (¬ДЕЛ(x, 28) ∨ ДЕЛ(x, 42)) = 1

Введем обозначения:

A = ДЕЛ(x,A); 
D28 = ДЕЛ(x, 28); 
D42 = ДЕЛ(x, 42)

Перепишем исходную формулу, согласно введенным обозначениям. Укажем, что формула должна быть тождественно истинна (по условию):

A → (¬D28 ∨ D42) = 1

Избавимся от импликации:

¬A ∨ (¬D28 ∨ D42) = 1

Разделим данную формулу на две части: в одной из них — искомое A, а в другой — часть формулы с x, которую можно найти:

¬A ∨ (¬D28 ∨ D42) = 1
 ¹        ²

В части 2 полученной формулы находится операция дизъюнкция, которую проще найти, когда логическое выражение равно 0 (только один случай: 0 ∨ 0 = 0):

(¬D28 ∨ D42) = 0   один случай: когда ¬D28 = 0 и D42 = 0

Т.е. имеем:

x/¬A : x/28 ∧ x/¬42

Иными словами найдем все такие x, которые НЕ делятся на А и при этом делятся на 28 И НЕ делятся на 42:

x = 28, 56, 84, 112, 140, 168, 196, 224, ...

Теперь найдем такие A, начиная с самого наименьшего (единицы), на которые НЕ делятся все x без исключения:

А = 1, 2, 3

Наименьшее А равно 3.

✎ Решение 2 (программирование). Язык Python, Pascal:

ДЕЛ(x, A) → (¬ДЕЛ(x, 28) ∨ ДЕЛ(x, 42)) = 1

Можно сделать вывод, что для некоторого диапазона натуральных значений А, необходимо рассмотреть диапазон натуральных значений x. Если выражение будет истинным для диапазона всех рассматриваемых х, то такое А необходимо вывести на экран.
То есть следует рассмотреть вложенный цикл: для внешнего цикла, перебирающего значения А (ограничим их числом 50, т.к. необходимо найти наименьшее А), будем запускать внутренний цикл, перебирающий значения х (х ограничим числом 1000, будем рассматривать данный диапазон, как «любое натуральное значение переменной х»).
Во внутреннем цикле расположим формулу:

Python:

for A in range(1,50):
    OK = 1
    for x in range(1,1000):
        OK *= (x % A == 0) <= ((x % 28 != 0) or (x % 42== 0))
    if OK:
        print( A )
        break

PascalABC.net:

begin
  for var A := 1 to 50 do
  begin
    var ok := 1;
    for var x := 1 to 1000 do
    begin
      if (x mod A = 0) <= ((x mod 28 <> 0)or (x mod 42 = 0)) = false then
      begin
        ok := 0; 
        break;
      end;
    end;
    if (ok = 1) then begin
      print(A);
      break;
      end
  end;
end.

OK — переменная-индикатор: если находится такое А при котором, диапазон всех значений x, подставленных в выражение, возвращает истинное значение выражения, то ОК остается равным 1, т.к. используется операция умножения (до цикла ОК необходимо присвоить единице).
Следует иметь в виду, что в программировании вместо операции импликация (->) можно использовать нестрогое неравенство: <=. Т.к. таблица истинности для операции импликация соответствует операции <=:

a b   F(a<=b)
0 0      1
0 1      1
1 0      0
1 1      1

После запуска программы выдается наименьшее значение А, т.к. используется оператор break для выхода из цикла после первого найденного значения:

Результат: 3

15_6:

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».

Для какого наименьшего натурального числа А формула

 (¬ДЕЛ(x, 19) ∨ ¬ДЕЛ(x, 15)) → ¬ДЕЛ(x, A)

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

✍ Решение:

✎ Решение 1 (Путём рассуждений):

Введем обозначения:

A = ДЕЛ(x,A); 
D19 = ДЕЛ(x, 19); 
D15 = ДЕЛ(x, 15)

Перепишем исходную формулу, согласно введенным обозначениям. Укажем, что формула должна быть тождественно истинна (по условию):

(¬D19 ∨ ¬D15) → ¬A = 1

Избавимся от импликации:

D19 ∧ D15 ∨ ¬A = 1

Разделим данную формулу на две части: в одной из них — искомое A, а в другой — часть формулы с x, которую можно найти:

¬A ∨ D19 ∧ D15 = 1
 ¹       ²

Начнем с известной части — части 2 формулы. В ней находится операция конъюнкция, которую проще найти, когда все ее операнды равны 1 (единственный случай для конъюнкции: 1 ∧ 1 = 1).
Вторая часть общей формулы может равняться только 1, когда ¬A = 0 (если ¬A = 1, то вторая часть может равнять 0, а нам нужно 1) :

¬A ∨ D19 ∧ D15 = 1
 ⁰  ^∨     ¹^{= 1}

Т.е. получаем:

¬A = 0 при D19 ∧ D15 = 1
или
A = 1 при D19 = 1 и D15 = 1

Таким образом, имеем:

A = 1
D19 = 1
D15 = 1

Очевидно, что наименьшим x можем взять число 285 (15 * 19 = 285): ДЕЛ(285, 19) и ДЕЛ(285, 15)
Поскольку мы ищем наименьшее A, такое что: ДЕЛ(x, A) и при этом ДЕЛ(x, 19) и ДЕЛ(x, 15), то нам необходимо найти наименьшее делимое чисел 19 и 15:

19 * 2 = 38 (38 не делится на 15)
19 * 3 = 57 (57 не делится на 15)
19 * 4 = 76 (76 не делится на 15)
19 * 5 = 95 (95 не делится на 15)
...
19 * 10 = 190 (190 не делится на 15)
19 * 15 = 285 (285 делится на 15)

A должно быть таким числом, при котором x принимает единственно возможное (наименьшее) значение 285.
Таким наименьшим A является само число 285.

✎ Решение 2 (программирование). Язык Python:

 (¬ДЕЛ(x, 19) ∨ ¬ДЕЛ(x, 15)) → ¬ДЕЛ(x, A)  = 1

Можно сделать вывод, что для некоторого диапазона натуральных значений А, необходимо рассмотреть диапазон натуральных значений x. Если выражение будет истинным для диапазона всех рассматриваемых х, то такое А необходимо вывести на экран.
То есть следует рассмотреть вложенный цикл: для внешнего цикла, перебирающего значения А (ограничим их числом 500, т.к. необходимо найти наименьшее А), будем запускать внутренний цикл, перебирающий значения х (х ограничим числом 1000, будем рассматривать данный диапазон, как «любое натуральное значение переменной х»).
Во внутреннем цикле расположим формулу:

for A in range(1,500):
    OK = 1
    for x in range(1,1000):
        OK *= ((x % 19 != 0) or (x % 15 != 0))<= (x % A!= 0)
    if OK:
            print( A )

a b   F(a<=b)
0 0      1
0 1      1
1 0      0
1 1      1

После запуска программы выдается одно значение А:

Результат: 285

Задания с поразрядной конъюнкцией

Поразрядная конъюнкция:

15_1:

Обозначим через m & n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 12&6 = 1100₂&0110₂ = 0100₂ = 4

Для какого наименьшего неотрицательного целого числа A формула

(X & A = 0) ∧ ¬(X & 35 ≠ 0 → X & 52 ≠ 0)

тождественно ложна (то есть принимает значение 0 при любом неотрицательном значении переменной X)?

✍ Решение:

Стоит заметить, что для такого типа задач, нет универсального единственного решения. Поэтому на видео, расположенном ниже, представлено два варианта решения.
✎ Способ 1:

Рассмотрим один из вариантов решения:

Удалим из формулы X&, чтобы сократить ее запись:

(A = 0) ∧ ¬(35 ≠ 0 → 52 ≠ 0)

Обратим внимание, что внешней операцией является конъюнкция — логическое умножение:

(A = 0) ∧ ¬(35 ≠ 0 → 52 ≠ 0)

Разделим общее выражение на две части относительно внешней операции. Первая часть — неизвестная, искомая, а вторая — известная, ее можно вычислить:

(A = 0) ∧ ¬(35 ≠ 0 → 52 ≠ 0)
   ¹               ²

Выполним некоторые преобразования во второй части формулы:
Зная свойство импликации, преобразуем формулу (избавимся от импликации в скобках):

правило импликации: a → b = ¬a ∨ b

(A = 0) ∧ ¬(35 = 0 ∨ 52 ≠ 0)
т.к. в результате получается отрицание того, что 35 ≠ 0, 
то убираем знак "не равно": было 35 ≠ 0, стало 35 = 0

Избавимся от отрицания перед скобками по закону Де Моргана:

закон де Моргана: ¬ (A ∨ B) = ¬ A ∧ ¬ B

A = 0 ∧ 35 ≠ 0 ∧ 52 = 0 = 0

По условию формула должна быть ложной. Вспомним таблицу истинности для конъюнкции (внешняя операция в нашей общей формуле):

0 ∧ 0 = 0
0 ∧ 1 = 0
1 ∧ 0 = 0
1 ∧ 1 = 1

Вторая часть формулы — вычислима, поэтому начнем с нее. В ней находится операция конъюнкция, которая имеет один единственный вариант решения, когда ¬ A ∧ ¬ B = 1. То есть примем вторую часть за истину (=1). В таком случае, для того чтобы общее выражение стало ложным (так требуется по заданию), необходимо, чтобы утверждение, что A = 0 было ложным (т.к. в обратном случае получим: 1 ∧ 1 = 1):

(A = 0) ∧ 35 ≠ 0 ∧ 52 = 0 = 0
   ⁰    ^∧        ¹    ^{= 0}

Вторая часть будет истинной только в том случае, если оба утверждения будут истинными:

35 ≠ 0 ∧ 52 = 0 = истинно (=1)  если:
35 ≠ 0 = истинно (=1)
и
52 = 0 = истинно (=1)

так как стоит логическое умножение ∧ - 
смотрим выше таблицу истинности для конъюнкции

Из двух последних пунктов получаем три утверждения:

35 ≠ 0  = 1  (истина)
и
52 = 0  = 1  (истина)
и
A = 0   = 0  (ложь)

Переведем числа в двоичную систему счисления:

35: 100011  (≠ 0)
52: 110100 (= 0)

Найдем такой X, который при поразрядной конъюнкции даст истинное значение для обеих частей.
Для начала рассмотрим ситуацию с числом 52 — это проще, т.к. для получения в результате нуля (52 = 0 => истина), достаточно во всех разрядах «перекрыть» единицы нулями:

52	1	1	0	1	0	0
X	0	0	?	0	?	?

Мы «перекрыли» все единицы нулями, чтобы в результате получить 0.
Теперь рассмотрим 35 ≠ 0 = истина (1):

35	1	0	0	0	1	1
X	1	?	?	?	1	1

Объединим обе маски в одну:

0 0 ? 0 ? ?  _&
1 ? ? ? 1 1
0 0 ? 0 1 1

Так как выражение X & A = 0 должно быть ложным, то найдем такое наименьшее А, при котором X & A ≠ 0. Для этого в тех разрядах Х, в которых находится единица, необходимо сохранить эту единицу и в соответствующих разрядах А:

X	0	0	?	0	1	1
A	0	0	0	0	1	1

Переведем результат в десятичную систему счисления:

000011₂ = 3₁₀

Ответ: 3

✎ Способ 2*:

Выполним последовательно следующие пункты:

Произвести замену (x & K = 0) на Zk
Выполнить преобразования по свойству импликации и закону Де Моргана.
Стремиться прийти к выражению с конъюнкциями без отрицаний типа: Zk * Zm.
Все выражения типа Zk * Zm преобразовать по свойству
Zk * Zm = Z_{k or m}.
Путем преобразований прийти к импликации: Zk → Zm.

Согласно первому пункту производим замену:

A ∧ ¬(¬Z35 → ¬Z52) = 0

Введем отрицание в выражение, чтобы оно было истинным:

¬(A ∧ ¬(¬Z35 → ¬Z52)) = 1

По закону де Моргана:

¬A ∨ (¬Z35 → ¬Z52) = 1

По свойству импликации:

¬A ∨ (Z35 ∨ ¬Z52) = 1

Объединим слагаемые с отрицанием:

¬A ∨ ¬Z52 ∨ Z35 = 1

Чтобы прийти к конъюнкции (пункт 3), используем закон де Моргана:

¬(A ∧ Z52) ∨ Z35 = 1

Чтобы прийти к импликации (пункт 5), используем свойство импликации:

(A ∧ Z52) → Z35 = 1

Получаем:

Z_{A ∨ 52} → Z35 = 1

Вспомним свойство:

Условие Zk → Zm истинно для любых натуральных значений x тогда и только тогда, когда все единичные биты двоичной записи числа M входят во множество единичных битов двоичной записи числа K.

В нашем случае это говорит о том, что все единичные биты двоичной записи числа 35 должны входить в результат Z_{A or 52}.
Рассмотрим подробно:

A       = ??0?11
52      = 110100
A or 52 = 110111
35      = 100011

поскольку мы ищем наименьшее А, то:

Аmin = 11₂ = 3₁₀

Результат: 3

Детальный разбор данного задания 15 ЕГЭ по информатике предлагаем посмотреть на видео:

Вариант решения №1 (универсальный, теоретический):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Вариант решения №2 (не универсальный, но простой):
📹 YouTube здесь

Поразрядная конъюнкция:

15_2:

Обозначим через m & n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 12&6 = 1100₂&0110₂ = 0100₂ = 4

Для какого наибольшего неотрицательного целого числа A формула

X & A ≠ 0 → (X & 36 = 0 → X & 6 ≠ 0)

тождественно истинна (то есть принимает значение 1 при любом неотрицательном значении переменной X)?

✍ Решение:

✎ Способ 1:

Произведем замену:

z36 = (x&36 = 0), z6 = (x&6 = 0), A = (x&A = 0)

Перепишем выражение:

¬A → (z36 → ¬ z6)

Избавимся от импликации (A → B = ¬ A ∨ B):
Сначала по правилу преобразования импликации:

¬A → (z36 → ¬ z6) = A + ¬z36 + ¬z6

По Закону де Моргана вынесем отрицание за скобки (¬ (A ∧ B) = ¬ A ∨ ¬ B):

A + ¬z36 + ¬z6 = A + ¬(z36 * z6)

Вернемся опять к импликации:

A + ¬(z36 * z6) = ¬(z36 * z6) + A = (z36 * z6) → A

Суть предыдущих действий в том, что нам необходимо прийти к импликации, но, избавившись от отрицания.
По следующему правилу Z_K * Z_M = Z_{K or M} (К. Поляков) заменим конъюнкцию:

z36 * z6 = z_{36 or 6}

Выполним поразрядную дизъюнкцию двоичных чисел 36 и 6:

100100₂ -> 36
110₂ -> 6

100100
   110
100110₂ -> 36 or 6 = 38₁₀

Получаем:

z38 → A

Необходимо обеспечить истинность данного выражения при всех x. Это возможно, когда единичные биты A входят в единичные биты числа 38. То есть:

A = 100110₂ = 38₁₀

✎ Способ 2:

Так как по заданию формула должна быть тождественно истинна, то перепишем ее так:

x&A ≠ 0 → (x&36 = 0 → x&6 ≠ 0) = 1

Введем обозначения:

A = (x&A = 0);
P = (x&36 = 0);
Q = (x&6 = 0);

Перепишем выражение согласно введенным обозначениям:

¬A → (P → ¬Q) = 1

Избавимся от импликации:

A ∨ (¬P ∨ ¬Q) = 1

A — наше неизвестное; для части выражения ¬P ∨ ¬Q нам необходимо подобрать такой вариант (равный 0 или 1), при котором единственно возможным значением A была бы единица (1).
Возьмем (¬P ∨ ¬Q) = 0, тогда А должно быть только единицей (чтобы общее выражение было = 1):

A ∨ (¬P ∨ ¬Q) = 1; 
или 
1 ∨ (0) = 1

Иными словами, выражение истинно, если при ¬P ∨ ¬Q = 0, A равно единице (1).
Получаем:

¬P ∨ ¬Q = 0
Отсюда имеем: 
¬P = 0 и ¬Q = 0 

(дизъюнкция равна 0 в единственном случае, когда все операнды равны 0)

Или запишем другим образом:

Q = 1 и P = 1

Построим побитовые маски:

100100  : 36
000110  : 6
0**0**  : маска P (x&36 = 0)
***00*  : маска Q (x&6 = 0)

Сопоставим обе маски и маску x&A = 0:

0**0**  : маска P (x&36 = 0)
***00*  : маска Q (x&6 = 0)
0**00*  : общая маска x
*00**0  : маска для A (x&A = 0)
т.е. в тех битах А, где может получиться единица (звездочки в обеих масках),
 мы поставили нули.

Так как нам необходимо получить наибольшее A (по заданию), то вместо всех «звездочек» ставим единицы:

100110 = 38₁₀

Результат: 38

Подробное решение данного задания 15 ЕГЭ по информатике предлагаем посмотреть в видео уроке:
Способ 1:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Способ 2:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Поразрядная конъюнкция:

15_8:

Определите наименьшее натуральное число А из интервала [43, 55], такое, что выражение

((x & 17 ≠ 0) → ((x & A ≠ 0) → (x & 58 ≠ 0))) →
→ ((x & 8 = 0) ∧ (x & A ≠ 0) ∧ (x & 58 = 0))

тождественно ложно (то есть принимает значение 0 при любом натуральном значении переменной х)?

Типовые задания для тренировки

✍ Решение:

Введем обозначения:

(¬Z17 → (¬A → ¬Z58)) → (z8 ∧ ¬A ∧ Z58) = 0

Для того, чтобы выражение было истинным, поставим его с отрицанием:

¬(((¬Z17 → (¬A → ¬Z58)) → (z8 ∧ ¬A ∧ Z58)) = 1

Упростим выделенную часть выражения (свойство 1, теория):

Z8 ∧ Z58 = Z_{8 or 58}  :

8  =   1000  _or
58 = 111010
     111010 = 58

Получили:

Z8 ∧ Z58 = Z58

Перепишем все выражение снова, избавившись от импликации:

¬(¬(Z17 ∨ A ∨ ¬Z58) ∨ (¬A ∧ Z58)) = 1

По закону Де Моргана получим:

(Z17 ∨ A ∨ ¬Z58) ∧ ¬(¬A ∧ Z58)) = 1

Еще раз применим закон теперь ко второй скобке:

(Z17 ∨ A ∨ ¬Z58) ∧  (A ∨ ¬Z58) = 1

Используем закон поглощения:

A ∨ ¬Z58 = 1

Приведем к импликации, чтобы избавиться от отрицания:

¬Z58 ∨ A => 
 Z58 → A = 1

Поскольку по заданию нас интересует диапазон [43;55], то проверять будет с числа 43.
По свойству 3 (теория), необходимо, чтобы единичные биты А входили в единичные биты двоичного представления числа 58:

43 = 101011 - не подходит!
58 = 111010

44 = 101100 - не подходит!
58 = 111010

45 = 101101 - не подходит!
58 = 111010

46 = 101110 - не подходит!
58 = 111010

47 = 101111 - не подходит!
58 = 111010

48 = 110000 - подходит!
58 = 111010

Результат: 48

Поразрядная конъюнкция:

15_15:

Определите набольшее натуральное число A, такое что выражение

((x & 26 = 0) ∨  (x & 13 = 0)) → ((x & 78 ≠ 0) → (x & A = 0))

тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной х)?

Типовые задания для тренировки:

✍ Решение:

Для упрощения восприятия введем обозначения:

z26 = (x & 26 = 0)
z13 = (x & 13 = 0)
z78 = (x & 78 = 0)
A = (x & A = 0)

Таким образом, получим следующее выражение:

(z26 ∨ z13) → (¬z78 → A) = 1

Упростим выражение по свойству импликации для второй скобки:

(z26 ∨ z13) → (z78 ∨ A) = 1

Упростим левую часть, используя свойство 2 (Z_k + Z_m = Z_{k and m}):

26 : 11010   единичные биты: 4, 3, 1
13 :  1101   единичные биты: 3, 2, 0
∧ =------------------------
     01000 = 8₁₀

То есть получили z26 ∨ z13 = z8
По правилу импликации: все единичные биты двоичной записи результата (z78 ∨ A) должны входить во множество единичных битов двоичной записи z8.
Рассмотрим:

z8 → (z78 ∨ A)
z78: не влияет на решение, так как операция дизъюнкция истинна тогда, 
когда хотя бы один операнд истинен
z8 → A     : ????

Для А единичными битами должны быть общие единичные биты для z8 (1000₂). Т.е. в нашим случае — это один бит — 3-й:

Наибольшее А = 1000 = 8₁₀

Результат: 8

Задания на поиск наибольшего или наименьшего числа А

Поиск наибольшего или наименьшего числа А:

15_4: 15 задание. Демоверсия ЕГЭ 2018 информатика:

Для какого наибольшего целого числа А формула

тождественно истинна, то есть принимает значение 1 при любых целых неотрицательных x и y?

✍ Решение:

✎ Способ 1 (программный):

Важно: Поскольку используется метод полного перебора, то возможна ситуация, когда транслятор будет работать слишком медленно. Но работоспособность представленного алгоритма проверена на онлайн компиляторах.

Pascalabc.net:

begin
  for var A := 200 downto -100 do
  begin
    var OK := 1;
    for var x := 0 to 100 do
      for var y := 0 to 100 do
        if ((x <= 9) <= (x * x <= A)) and ((y * y <= A) <= (y <= 9)) = false then 
        begin
          OK := 0;
          break;
        end;
    if OK = 1 then 
    begin
      print(A);
      break
    end;
  end;
end.

Бейсик:	Python: for A in range(200,-100,-1): OK = 1 for x in range(0,100): for y in range(0,100): OK = ((x<=9) <= (xx<=A)) and((y*y<=A) <= (y<=9)) if OK: print(A) break
С++:

✎ Способ 2 (теоретическое решение):

Условно разделим исходное выражение на части:

Главное действие (внешняя операция) в исходном выражении — это конъюнкция. Конъюнкция истинна, когда все операнды истинны. Т.е. в задаче обе части 1 и 2 должны быть истинными (т.к. по условию общая формула должна быть истинной).

Рассмотрим часть 1:

если в 1.1 имеем x > 9, то часть 1 будет истинна независимо от А. Значит, значение числа А влияет на решение только при выполнении условия:

x<=9

(импликация 0 → 0 = 1, 0 → 1 = 1)

теперь, для того чтобы в части 1, выражение было истинным, надо чтобы часть 1.2 была истинной:

x*x <= A

(импликация 1 → 1 = 1)

таким образом, получаем:

x <= 9
x² <= A

при любых x

так как нам необходимо найти наибольшее возможное А, то, значит, надо ограничить его значения сверху, а данная часть выражения ограничивает только снизу:

возьмем максимальное натуральное: x=9, тогда A>=81

Рассмотрим часть 2:

если 2.2 истинно (т.е. y <= 9), то часть 2 будет истинна независимо от А. Значит, значение числа А влияет на решение только при выполнении условия:

y > 9

теперь, для того чтобы в части 2 выражение было истинным, надо чтобы часть 2.1 была ложной:

y * y > A

(импликация 0 → 0 = 1)

таким образом, получаем:

y > 9
y² > A

при любых y

данная часть выражения ограничивает значения А сверху:

возьмем наименьшее возможное по условию натуральное: y = 10, тогда A < 100

Получаем, что наибольшее А меньшее 100: А = 99

Результат: 99

Подробное решение 15 задания демоверсии ЕГЭ 2018 года смотрите на видео (аналитическое решение):

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Поиск наибольшего или наименьшего числа А:

✍ Решение:

✎ Способ 1 (программный):

Pascalabc.net:

begin
  for var A := -100 to 200 do
  begin
    var OK := 1;
    for var x := 1 to 100 do
      for var y := 1 to 100 do
        if ((y+3*x<A) or (x >20)or(y>40)) = false then 
        begin
          OK := 0;
          break;
        end;
    if OK = 1 then 
    begin
      print(A);
      break
    end;
  end;
end.

Бейсик:	Python: for A in range(-100,200): OK = 1 for x in range(1,100): for y in range(1,100): OK = (y+3x<A) or (x > 20) or (y > 40) if OK: print(A) break
С++:

✎ Способ 2 (теоретическое решение):

Определим основные части выражения, выделив отдельно неизвестную часть — с А, и, так сказать, известную часть, то есть остальную.

    1                 2
(y+3x < A) ∨ (x > 20) ∨ (y > 40)

Поскольку основными операциями являются операции дизъюнкции (логического сложения) и порядок их выполнения не важен, то последней, внешней, операцией будем выполнять дизъюнкцию слева, т.к. она объединяет неизвестную и известную часть.
Сначала важно рассмотреть вторую часть выражения, известную, так как от нее будет зависеть значение A. Если вторая часть истинна, то А может быть как = 1, так и = 0. Такой вариант нам не подходит:

(y+3x < A) ∨ (x > 20) ∨ (y > 40)
  ^{1 или 0?                   1               = 1}
Не подходит!

Соответственно, рассмотрим вариант, когда вторая часть ложна, тогда часть выражения с неизвестным А будет обязательно истинной, т.е.:

1. (y+3x < A) = 1
2. (x > 20) ∨ (y > 40) = 0

Дизъюнкция ложна, когда оба операнда ложны, т.е. из второго пункта имеем:

x <= 20
y <= 40

Для того, чтобы перекрыть все x и все y, возьмем наибольшие из возможных значений: x = 20, y = 40.
Выразим А:

А > 3x + y
A > 3*20 + 40
A > 100

Поскольку требуется найти наименьшее значение А, то имеем А = 101.

Результат: 101

Подробное решение досрочного ЕГЭ 2018 года смотрите на видео (аналитическое решение):

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Поиск наибольшего или наименьшего числа А:

15_0:Разбор 15 задания. Демоверсия егэ по информатике 2019:

Для какого наибольшего целого неотрицательного числа А выражение

(48 ≠ y + 2x) ∨ (A < x) ∨ (A < y)

тождественно истинно, т.е. принимает значение 1 при любых целых неотрицательных x и y?

✍ Решение:
✎ Решение 1 (теоретическое):

Разделим общее выражение на две части. Выделим неизвестную часть красным:

(48 ≠ y + 2x) ∨ (A < x) ∨ (A < y)

Неизвестная часть должна быть истинной, она обязательно будет истинна, если известная часть — ложь:

(48 ≠ y + 2x) ∨ (A < x) ∨ (A < y) = 1
      ⁰                  ¹

Т.е. 48 ≠ y + 2x = 0 или y + 2x = 48. На графике это уравнение представляет линию. Из условия имеем два ограничения:(x > 0) and (y > 0). Отобразим линию для 1-й четверти, соответствующей положительным x и y:

y + 2x = 48  :
при x = 0, y = 48
при y = 0, 2x = 48 => x = 24

Возьмем некоторое значение A, например, A = 25, отметим его на графике белой областью так, чтобы выполнялось (A < x) ∨ (A < y). По условию имеем, что все точки данной части отрезка прямой y + 2x = 48 должны принадлежать отмеченной белой области. Заштрихуем область для всех точек прямой (голубым цветом):

То есть все точки голубого квадрата должны находиться под отрезком линии (включая вершину (A, A)), и данный квадрат, соответствует максимальному значению A.
Наибольшее значение голубая область приобретает в точке пересечения прямой y + 2x = 48 с прямой y = x:

Далее решаем полученное линейное уравнение (для x = y):

x + 2x = 48 =>
3x = 48
x = 16

Так как значение A должно быть меньше x, то наибольшее А = 15.

✎ Решение 2 (программное):
Python:

for A in range(200,0,-1):
    OK = 1
    for x in range(0,100):
        for y in range(0,100):
            OK *= (48!=y+2*x) or(A<x)or (A<y) 
    if OK:
        print(A)
        break

Результат: 15

Видео решения 15 задания демоверсии ЕГЭ 2019 (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Поиск наибольшего или наименьшего числа А:

15_19:

Для какого наименьшего целого числа А формула

(y + 5x <= 34) → ((y — x > 4) ∨ (y <= A))

тождественно истинна, т.е. принимает значение 1 при любых целых неотрицательных x и y?

✍ Решение:

Общая идея такова:
необходимо упростить формулу так, чтобы последняя операция (внешняя) выполнялась со скобкой, в которой находится искомое A. После чего разделить формулу на две части, в одной из которых находится искомое.
Избавимся от импликации, это даст нам возможность опустить общие скобки во второй части формулы:

¬(y + 5x <= 34) ∨ (y - x > 4) ∨ (y <= A)

Разделим формулу на две части таким образом, чтобы внешняя операции отделяла часть, в которой находится искомое A:

¬(y + 5x <= 34) ∨ (y - x > 4) ∨ (y <= A) = 1
        1 часть                  2 часть

Формула по условию должна быть истинной (=1). Внешняя операция — дизъюнкция — истинна аж в трех случаях: a=1 b=0, a=0 b=1, a=1 b=1.
Если мы допустим, что первая часть истинна, то вторая, искомая часть, может быть как истинной, так и ложной. Поэтому такой вариант не подходит.
Допустим, что первая часть ложна, тогда вторая, искомая часть, должна быть только истинной:

¬(y + 5x <= 34) ∨ (y - x > 4) ∨ (y <= A) = 1
        1 часть = 0               2 часть = 1

С учетом, что в первой части формулу находится операция дизъюнкция, которая ложна только в одном случае (a=0 b=0), то выпишем утверждения, получившиеся из первой части:

y + 5x > 34 = 0, значит:
1. y + 5x <= 34
y - x > 4 = 0, значит:
2. y - x <= 4

Кроме того, имеем еще одно утверждение второй части:

y <= A
или
A >= y

Отобразим получившиеся уравнения прямых на плоскости:

Раз A >= y, значит, искомая область лежит выше обеих прямых. Наименьшее значение А будет достигнуто в указанной точке пересечения двух прямых.
В точке пересечения прямых уравнения равны, т.е. имеем:

34 - 5x = 4 + x
30 = 6x
x = 5
Найдем y: 
y = 4 + 5 = 9

Поскольку имеем утверждение, что A >= y и в задании требуется найти наименьшее A, то получаем:

y = 9:
A >= 9 => наименьшее A = 9

✎ Решение 2 (программное):
Python:

for A in range(-100,100):
    OK = 1
    for x in range(0,100):
        for y in range(0,100):
            OK *= (y+5*x<=34)<=((y-x >4)or(y<=A)) 
    if OK:
        print( A )
        break

PascalABC.NET:

 
begin
  for var A := -100 to 100 do
  begin
    var OK := true;
    for var x := 0 to 100 do
    begin
      for var y := 0 to 100 do
      begin
        OK := (y + 5 * x <= 34) <= ((y - x > 4) or (y <= A));
        if OK = false then break;
      end;
      if OK = false then break;
    end;
    if OK then 
    begin
      print(A);
      break;
    end;
  end;
end.

Результат: 9

Поиск наибольшего или наименьшего числа А:

15_13:

Укажите наименьшее целое значение А при котором выражение

(2y + 5x < A) ∨ (2x + 4y > 100) ∨ (3x – 2y > 70)

истинно для любых целых положительных значений x и y.

Типовые задания для тренировки

✍ Решение:

Python:

for A in range(-200,200):
    OK = 1
    for x in range(1,100):
        for y in range(1,100):
            OK *= (2*y + 5*x < A) or (2*x + 4*y > 100) or (3*x - 2*y > 70) 
    if OK:
        print( A )
        break

PascalABC.NET:

begin
  for var A := -200 to 200 do
  begin
    var OK := true;
    for var x := 1 to 100 do
    begin
      for var y := 1 to 100 do
      begin
        OK := (2*y + 5*x < A) or (2*x + 4*y > 100) or (3*x - 2*y > 70);
        if OK = false then break;
      end;
      if OK = false then break;
    end;
    if OK then 
    begin
      print(A);
      break;
    end;
  end;
end.

Результат: 171

Видео разбора задания смотрите на видео (аналитическое решение):

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Поиск наибольшего или наименьшего числа А:

15_14:

Укажите наибольшее целое значение А при котором выражение

(3y – x > A) ∨ (2x + 3y < 30) ∨ (2y – x < –31)

истинно для любых целых положительных значений x и y.

Типовые задания для тренировки

✍ Решение:

✎ Решение 1 (теоретическое):

Разделим выражение на две части: часть с неизвестным = 1, часть известная = 0:

(3y – x > A) ∨ (2x + 3y < 30) ∨ (2y – x < –31) = 1

Выпишем отдельно обе скобки известной части:

(1) 
(2x + 3y) >= 30,
y >= (30 - 2x) / 3
x = (30 - 3y) /2

(2) 
(2y – x >=–31)
y >= (x - 31) / 2
x = 2y + 31

Подберем значения координат для x и y обеих частей, и отобразим линии на графике функций:

(1)
x | y
0 | 10
15| 0

(2)
x | y
0 | -15 ( целые)
30|0

Для первого уравнения:

Для второго уравнения:

Сопоставим обе области:

Добавим на график прямую A<3y-x:

Раз A < 3y – x, то будем перемещать А снизу вверх. Наибольшее значение А будет достигнуто в указанной точке пересечения с прямой (2).
Т.е. для уравнения (2) имеем:

если y = 1, то x = 2*1 + 31 = 33

Подставим в выражение для поиска А:

А < 3y - x
A < 3-33, A < -30, A=-31

✎ Решение (программное):
Python:

for A in range(200,-200,-1):
    OK = 1
    for x in range(1,100):
        for y in range(1,100):
            OK *= (3*y-x>A) or (2*x+3*y<30) or (2*y-x<-31) 
    if OK:
        print(A)
        break

Результат: -31

* В некоторых задачах использован метод, предложенный А.В. Здвижковой

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Элементами множеств А, P, Q являются натуральные числа, причём P = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}, Q = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}. Известно, что выражение

( (x ∈ A) → (x ∈ P) ) ∧ ( (x ∈ Q) → ¬(x ∈ A) )

истинно (то есть принимает значение 1) при любом значении переменной х. Определите наибольшее возможное количество элементов в множестве A.

Элементами множества А являются натуральные числа. Известно, что выражение

(x ∈ {2, 4, 6, 8, 10, 12}) → (((x ∈ {3, 6, 9, 12, 15}) ∧ ¬(x ∈ A)) → ¬(x ∈ {2, 4, 6, 8, 10, 12}))

истинно (т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A.

Элементами множеств А, P, Q являются натуральные числа, причём P = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}, Q  =  {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}.

Известно, что выражение

((x ∈ P) → (x ∈ A)) ∨ (¬(x ∈ A) → ¬(x ∈ Q))

Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 18 января 2017 года Вариант ИН10304

Элементами множеств А, P, Q являются натуральные числа, причём P = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}, Q = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}.

Известно, что выражение

((x A) → (x P)) ∨ (¬(x Q) → ¬(x A))

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наибольшее возможное количество элементов в множестве A.

Элементами множеств А, P, Q являются натуральные числа, причём P = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21}, Q  =  {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}. Известно, что выражение

((x ∈ P) → (x ∈ A)) ∨ (¬(x ∈ A) → ¬(x ∈ Q))

истинно ( т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A.

Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 18 января 2017 года Вариант ИН10303

Пройти тестирование по этим заданиям

Источник

Теория и практика решения задания 15 ЕГЭ по информатике

Мнемоническое правило

Соционика – это информационная психология

Один из ее главных принципов – дополнение до целого ( дополнение противоположностью )

Решающая формула

В алгебре логики есть формула дополнения до целого:

А  ¬А = 1

В некоторых задачах мы будем использовать вместо этой формулы умножение противоположностей:

А  ¬А = 0

Типы задания 15

Задания на отрезки
Задания на множества
Задания на поразрядную конъюнкцию
Задания на условие делимости
Задания на функции

Задания на отрезки

( № 376 ) На числовой прямой даны два отрезка: P=[4,15] и Q=[12,20]. Укажите наименьшую возможную длину такого отрезка A, что формула ((x ∈ P) ∧ (x ∈ Q)) → (x ∈ A)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

Источник — сайт Полякова К.Ю.

Решающая формула

Для выбора решающей формулы важно внимательно прочитать требование задачи.

В нашей задаче в требовании сказано:

принимает значение 1 при любом значении переменной х.

Выбор решающей формулы очевиден:

А  ¬А = 1

Решение задачи на отрезки

Разделим решение задачи на этапы:

Легенда
Формализация условия
Решение логического уравнения
Интерпретация полученного результата

Решение задачи на отрезки

Легенда – это удобные нам условные обозначения, которые мы будем использовать при решении.

Введем следующие обозначения:

P = x  P

Q = x  Q

A = x  A

Решение задачи на отрезки

2) Формализация условия – перепишем формулу из условия задачи в соответствие с легендой.

Было:

((x ∈ P) ∧ (x ∈ Q)) → (x ∈ A) = 1

Стало:

(P ∧ Q) → A = 1

Решение задачи на отрезки

3) Решение логического уравнения – вначале это, возможно, самый сложный этап в решении задачи. Но позже, при накоплении опыта, он уже не будет казаться таким уж сложным 

Рассмотрим решение логического уравнения по шагам.

Решение задачи на отрезки

3.1. Представим логическое следование в базовых логических операциях по формуле: А → В = ¬А  В :

(P ∧ Q) → A = 1

¬ (P ∧ Q)  A = 1

Решение задачи на отрезки

3.2. Сведем получившееся выражение к решающей формуле: А  ¬А = 1 (в алгебре логики справедлив закон коммутативности, т.е. А  ¬А = ¬А  А) :

¬(P ∧ Q)  A = 1, отсюда

¬А = ¬(P ∧ Q)

Ответом в логическом уравнении будет:

А = P ∧ Q.

Решение задачи на отрезки

4) Интерпретация полученного результата .

Наш ответ: А = P ∧ Q .

В алгебре логики это выражение означает пересечение объемов двух логических объектов. По условию нашей задачи – это пересечение отрезков P и Q .

Решение задачи на отрезки

Пересечение отрезков P и Q можно визуализировать: P=[4,15] и Q=[12,20].

По условию нашей задачи, нам нужна минимальная длина отрезка А . Находим ее: 15 – 12 = 3 .

Ответ: 3 .

Ответ на сайте Полякова К.Ю.: 3

Задания на отрезки

(№ 360) На числовой прямой даны три отрезка: P=[10,25], Q=[15,30] и R=[25,40]. Какова максимальная длина отрезка A, при котором формула ((x ∈ Q) → (x ∉ R) ) ∧ (x ∈ A) ∧ (x ∉ P)

тождественно ложна, то есть принимает значение 0 при любом значении переменной х?

Источник — сайт Полякова К.Ю.

Решающая формула

Для выбора решающей формулы важно внимательно прочитать требование задачи.

В нашей задаче в требовании сказано:

принимает значение 0 при любом значении переменной х.

Выбор решающей формулы очевиден:

А  ¬А = 0

Решение задачи на отрезки

Легенда
Формализация условия
Решение логического уравнения
Интерпретация полученного результата

Решение задачи на отрезки

Легенда

R = x  R

Q = x  Q

A = x  A

P = x  P

Решение задачи на отрезки

2) Формализация условия

Было:

((x ∈ Q) → (x ∉ R) ) ∧ (x ∈ A) ∧ (x ∉ P) = 0

Стало:

( Q → ¬R ) ∧ A ∧ ¬ P = 0

Решение задачи на отрезки

3) Решение логического уравнения

( Q → ¬R ) ∧ A ∧ ¬ P = 0

3.1. Представим логическое следование в базовых логических операциях по формуле: А → В = ¬А  В , и переставим множители согласно закону коммутативности умножения:

A ∧ (¬ Q  ¬R ) ∧ ¬ P = 0

Решение задачи на отрезки

3) Решение логического уравнения

A ∧ ( ¬ Q  ¬R ) ∧ ¬ P = 0

3.2. Сведем получившееся выражение к решающей формуле: А  ¬А = 0 и найдем, чему равно ¬А :

¬А = (¬ Q  ¬R ) ∧ ¬ P

Решение задачи на отрезки

3) Решение логического уравнения

¬А = (¬ Q  ¬R ) ∧ ¬ P

3.3. Упростим выражение для ¬А по закону де Моргана ¬А  ¬В=¬(А  В) :

¬А = ¬ (Q  R ) ∧ ¬ P,

и по другому закону де Моргана ¬А  ¬В =¬(А  В ) :

¬А = ¬ (Q  R  P)

Решение задачи на отрезки

3) Решение логического уравнения

¬А = ¬ (Q  R  P)

3.4. Очевидно, что

А = Q  R  P

Решение задачи на отрезки

4) Интерпретация полученного результата

А = Q  R  P

Отрезок А – это пересечение отрезков Q и R и его объединение с отрезком Р .

Решение задачи на отрезки

Пересечение отрезков R и Q можно визуализировать: Q=[15,30] и R=[25,40].

Отрезок P=[10,25] нанесем на наш чертеж и объединим с пересечением:

Решение задачи на отрезки

А = Q  R  P

По условию нашей задачи, нам нужна максимальная длина отрезка А . Находим ее: 30 – 10 = 20 .

Ответ: 20 .

Ответ на сайте Полякова К.Ю.: 20

2. Задания на множества

(№ 386) Элементами множеств А, P, Q являются натуральные числа, причём P={1,2,3,4,5,6}, Q={3,5,15}. Известно, что выражение (x ∉ A) → ((x ∉ P) ∧ (x ∈ Q)) ∨ (x ∉ Q)

истинно (т.е. принимает значение 1 при любом значении переменной х. Определите наименьшее возможное количество элементов в множестве A.

Источник — сайт Полякова К.Ю.

Решение задачи на множества

Легенда
Формализация условия
Решение логического уравнения
Интерпретация полученного результата

Решение задачи на множества

Легенда

A = x ∈ A

P = x ∈ P

Q = x ∈ Q

Решение задачи на множества

2) Формализация условия

Было:

(x ∉ A) → ((x ∉ P) ∧ (x ∈ Q)) ∨ (x ∉ Q) = 1

Стало:

¬ A → (¬P ∧ Q)  ¬ Q = 1

Решение задачи на множества

3) Решение логического уравнения

¬ A → (¬P ∧ Q)  ¬ Q = 1

3.1. Представим логическое следование в базовых логических операциях и сгруппируем:

A  ((¬P ∧ Q)  ¬ Q) = 1

Решение задачи на множества

A  (( ¬P ∧ Q)  ¬Q) = 1

3.2. Сведем получившееся выражение к решающей формуле:

А  ¬А = 1

и найдем, чему равно ¬А :

¬А = (¬P ∧ Q)  ¬Q

Решение задачи на множества

¬А = (¬P ∧ Q)  ¬Q

3.3. Упростим выражение для ¬А, раскрыв скобки по закону дистрибутивности сложения:

¬А = ( ¬P  ¬Q)  (Q  ¬Q)

Q  ¬Q = 1

¬А = ( ¬P  ¬Q)

Решение задачи на множества

¬А = ( ¬P  ¬Q)

По закону де Моргана:

¬А = ¬(P  Q)

3.4. Очевидно, что

А = P  Q

Решение задачи на множества

А = P  Q

4) Интерпретация полученного результата

Искомое множество А представляет собой пересечение множеств P и Q.

Решение задачи на множества

Искомое множество А есть пересечение множеств

P =  1, 2, 3 , 4, 5 , 6  и Q = { 3 , 5 ,15}, таким образом A = { 3 , 5 }

и содержит только 2 элемента.

Ответ: 2

Ответ на сайте Полякова: 2

2. Задания на множества

(№ 368) Элементами множеств А, P, Q являются натуральные числа, причём P={2,4,6,8,10,12} и Q={4,8,12,116}. Известно, что выражение (x ∈ P) → (((x ∈ Q) ∧ (x ∉ A)) → (x ∉ P))

истинно (т. е. принимает значение 1 ) при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A.

Источник — сайт Полякова К.Ю.

Решение задачи на множества

Легенда
Формализация условия
Решение логического уравнения
Интерпретация полученного результата

Решение задачи на множества

Легенда

A = x ∈ A

P = x ∈ P

Q = x ∈ Q

Решение задачи на множества

2) Формализация условия

Было:

(x ∈ P)→(((x ∈ Q) ∧ (x ∉ A))→(x ∉ P)) = 1

Стало:

P → ((Q ∧ ¬ A) → ¬ P) = 1

Решение задачи на множества

3) Решение логического уравнения

P → ((Q ∧ ¬ A) → ¬ P) = 1

3.1. Представим первое логическое следование (в скобках) в базовых логических операциях :

P → ( ¬ (Q ∧ ¬ A)  ¬ P) = 1

Решение задачи на множества

P → ( ¬ (Q ∧ ¬ A)  ¬ P) = 1

Представим второе логическое следование в базовых логических операциях, применим закон де Моргана и перегруппируем:

¬ P  ( ¬ (Q ∧ ¬ A)  ¬ P) = 1

¬ P  ¬ Q  A  ¬ P = 1

Решение задачи на множества

A  ( ¬ P  ¬ Q  ¬ P) = 1

3.2. Сведем получившееся выражение к решающей формуле:

А  ¬А = 1

и найдем, чему равно ¬А :

¬А = ( ¬ P  ¬ Q  ¬ P)

Решение задачи на множества

¬А = ¬ P  ¬ Q  ¬ P

3.3. Упростим выражение для ¬А по формуле А  А = А :

¬А = ¬ P  ¬ Q

Далее, по закону де Моргана получаем:

¬А = ¬( P  Q)

Решение задачи на множества

¬А = ¬(P  Q)

3.4. Очевидно, что

А = P  Q

4) Интерпретация полученного результата

Искомое множество А представляет собой пересечение множеств P и Q.

Решение задачи на множества

Искомое множество А есть пересечение множеств

P =  2, 4 , 6, 8 , 10, 12  и

Q = { 4 , 8 , 12 , 16}, таким образом

A = { 4 , 8 , 12 }

и содержит только 3 элемента, сумма которых 4+8+12=24 .

Ответ: 24

Ответ на сайте Полякова: 24

3. Задания на поразрядную конъюнкцию

(№ 379) Обозначим через m & n пораз-рядную конъюнкцию неотрицательных целых чисел m и n . Так, например, 14 & 5 = 1110 2 & 0101 2 = 0100 2 = 4. Для какого наименьшего неотрицательного целого числа А формула (x & 29 ≠ 0) → ((x & 12 = 0) → (x & А ≠ 0))

тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной х)?

Решение задачи на поразрядную конъюнкцию

Легенда
Формализация условия
Решение логического уравнения
Интерпретация полученного результата

Решение задачи на поразрядную конъюнкцию

Легенда

Легенда для задач на поразрядную конъюнкцию отличается от всех остальных случаев:

B = (x & 29 ≠ 0)

C = (x & 12 ≠ 0)

A = (x & А ≠ 0)

Решение задачи на поразрядную конъюнкцию

Мы принимаем за истинное высказывание поразрядную конъюнкцию, отличную от нуля, иначе поразрядная конъюнкция теряет свой логический смысл, т.к. всегда можно представить Х всеми нулями.

Решение задачи на поразрядную конъюнкцию

2) Формализация условия

Было:

(x & 29 ≠ 0)→((x & 12 = 0)→(x & А ≠ 0))=1

Стало:

В → ( ¬С → А) = 1

Решение задачи на поразрядную конъюнкцию

3) Решение логического уравнения

В → ( ¬С → А) = 1

В → (С  А) = 1

(¬В  С)  А = 1

¬А = ¬В  С

¬А = ¬(В  ¬ С)

Очевидно, что

А = В  ¬ С

Решение задачи на поразрядную конъюнкцию

4) Интерпретация полученного результата

Искомое двоичное значение поразрядной конъюнкции А – это двоичное значение поразрядной конъюнкции значения В и инверсии двоичного значения С .

Решение задачи на поразрядную конъюнкцию

B = (x & 29 ≠ 0)

В или 29 = 11101 2

C = (x & 12 ≠ 0)

12 = 1100 2

¬С или инверсия 12 = 0011 2

Решение задачи на поразрядную конъюнкцию

В или 29 = 11101 2

¬С или инверсия 12 = 0011 2

А = В  ¬ С

х 11101 2

0011 2

10001 2

А = 1 0001 2 = 17

Ответ на сайте Полякова: 17

3. Задания на поразрядную конъюнкцию

(№ 375) Введём выражение M & K, обозначающее поразрядную конъюнкцию M и K (логическое «И» между соответ-ствующими битами двоичной записи). Определите наименьшее натуральное число A, такое что выражение (X & 49 ≠ 0) → ((X & 33 = 0) → (X & A ≠ 0))

тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной X)?

Решение задачи на поразрядную конъюнкцию

Легенда
Формализация условия
Решение логического уравнения
Интерпретация полученного результата

Решение задачи на поразрядную конъюнкцию

Легенда

Легенда для задач на поразрядную конъюнкцию отличается от всех остальных случаев:

B = (x & 49 ≠ 0)

C = (x & 33 ≠ 0)

A = (x & А ≠ 0)

Решение задачи на поразрядную конъюнкцию

2) Формализация условия

Было:

(X & 49 ≠ 0) → ((X & 33 = 0) → (X & A ≠ 0))=1

Стало:

В → ( ¬С → А) = 1

Решение задачи на поразрядную конъюнкцию

3) Решение логического уравнения

В → ( ¬С → А) = 1

В → (С  А) = 1

(¬В  С)  А = 1

¬А = (¬В  С)

Очевидно:

А = В  ¬С

Решение задачи на поразрядную конъюнкцию

4) Интерпретация полученного результата

Решение задачи на поразрядную конъюнкцию

B = (x & 49 ≠ 0)

В или 49 = 110001 2

C = (x & 33 ≠ 0)

33 = 100001 2

¬С или инверсия 33 = 011110 2

Решение задачи на поразрядную конъюнкцию

В или 49 = 110001 2

¬С или инверсия 33 = 011110 2

А = В  ¬ С

х 110001 2

011110 2

010000 2

А = 1 0000 2 = 16

Ответ на сайте Полякова: 16

4. Задания на условие делимости

(№ 372) Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула ¬ДЕЛ(x,А) → (¬ДЕЛ(x,21) ∧ ¬ДЕЛ(x,35))

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

Источник — сайт Полякова К.Ю.

Решение задачи

на условие делимости

Легенда
Формализация условия
Решение логического уравнения
Интерпретация полученного результата

Решение задачи

на условие делимости

Легенда

Легенда простая: А = ДЕЛ(x,А)

21 = ДЕЛ(х,21)

35 = ДЕЛ(x,35)

Решение задачи

на условие делимости

2) Формализация условия

Было:

¬ДЕЛ(x,А) → (¬ДЕЛ(x,21) ∧ ¬ДЕЛ(x,35))

тождественно истинна (то есть принимает значение 1)

Стало:

¬А → (¬21 ∧ ¬35) = 1

Решение задачи

на условие делимости

3) Решение логического уравнения

¬А → (¬21 ∧ ¬35) = 1

А  (¬21 ∧ ¬35) = 1

¬А = ¬21 ∧ ¬35

Очевидно, что

А = 21  35

Решение задачи

на условие делимости

4) Интерпретация полученного результата

А = 21  35

В данной задаче это самый сложный этап решения. Нужно понять, что же представляет из себя число А – НОК или НОД или …

Решение задачи

на условие делимости

4) Интерпретация полученного результата

А = 21  35

Итак, наше число А таково, что Х делится на него без остатка, тогда и только тогда, когда Х делится без остатка на 21 или на 35. В этом случае ищем

А = НОД (21, 35) = 7

Ответ на сайте Полякова: 7

4. Задания на условие делимости

(№ 370) Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула ¬ДЕЛ(x,А) → ((ДЕЛ(x,6) → ¬ДЕЛ(x,4))

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

Источник — сайт Полякова К.Ю.

Решение задачи

на условие делимости

Легенда
Формализация условия
Решение логического уравнения
Интерпретация полученного результата

Решение задачи

на условие делимости

Легенда

А = ДЕЛ(x,А)

6 = ДЕЛ(x,6)

4 = ДЕЛ(x,4)

Решение задачи

на условие делимости

2) Формализация условия

Было:

¬ДЕЛ(x,А) → ((ДЕЛ(x,6) → ¬ДЕЛ(x,4))

тождественно истинна (то есть принимает значение 1

Стало:

¬А → (6 → ¬4) = 1

Решение задачи

на условие делимости

3) Решение логического уравнения

¬А → (6 → ¬4) = 1

¬А → (¬ 6  ¬4) = 1

А  (¬ 6  ¬4) = 1

¬А = ¬ 6  ¬4

Очевидно:

А = 6  4

Решение задачи

на условие делимости

4) Интерпретация полученного результата

А = 6  4

Итак, А таково, что Х делится на него без остатка тогда и только тогда, когда Х делится без остатка и на 6, и на 4. Т.е. А = НОК(6, 4) = 12

Ответ на сайте Полякова: 12

A ) ∨ ( x A ) истинно для любых целых положительных значений x и y . » width=»640″

5. Задания на функции

Укажите наибольшее целое значение А, при котором выражение

( y + 2 x  99) ∨ ( y A ) ∨ ( x A )

истинно для любых целых положительных значений x и y .

A ) or ( x A ) выполнялось при всех x и y , для которых ложно ( y + 2 x  99) , то есть истинно ( y + 2 x = 99) или y = –2 x + 99 » width=»640″

Решение задачи

на функции

1) первое выражение не зависит от выбора A :

( y + 2 x  99)

2) таким образом, нам нужно выбрать значение A так, чтобы условие ( y A ) or ( x A ) выполнялось при всех x и y , для которых ложно ( y + 2 x  99) , то есть истинно ( y + 2 x = 99) или y = –2 x + 99

A ) or ( x A ) для некоторого значения A , например, для A = 50 (конечно, нужно учесть, что x и y положительны и добавить ещё два ограничения: ( x 0) and ( y 0) ): » width=»640″

Решение задачи

на функции

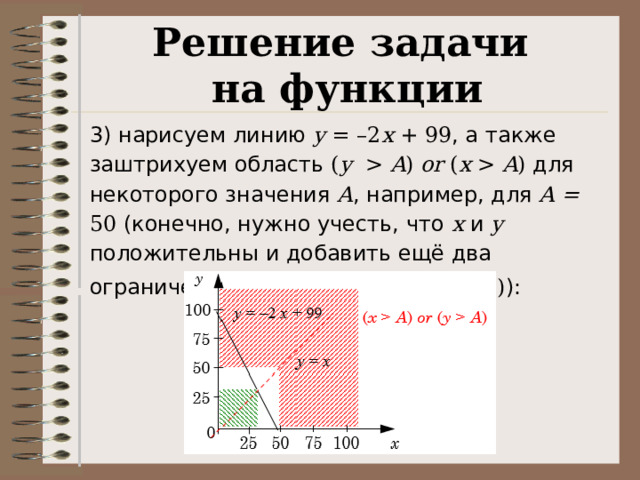
3) нарисуем линию y = –2 x + 99 , а также заштрихуем область ( y A ) or ( x A ) для некоторого значения A , например, для A = 50 (конечно, нужно учесть, что x и y положительны и добавить ещё два ограничения: ( x 0) and ( y 0) ):

Решение задачи

на функции

4) по условию задачи нужно, чтобы все точки отрезка прямой y = –2 x + 99 в первой четверти плоскости оказались в заштрихованной зоне

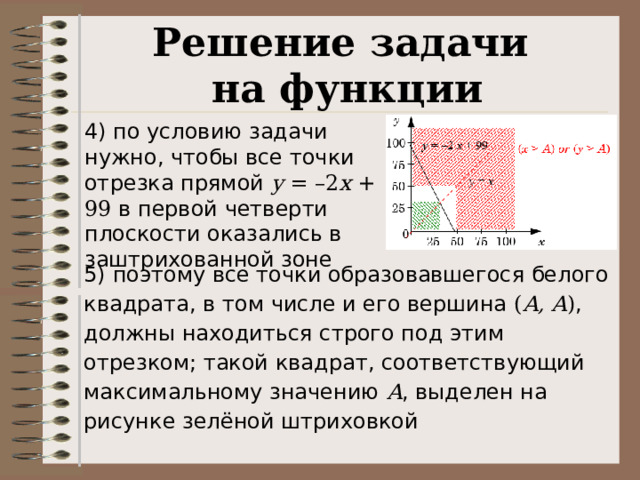
5) поэтому все точки образовавшегося белого квадрата, в том числе и его вершина ( A, A ) , должны находиться строго под этим отрезком; такой квадрат, соответствующий максимальному значению A , выделен на рисунке зелёной штриховкой

Решение задачи

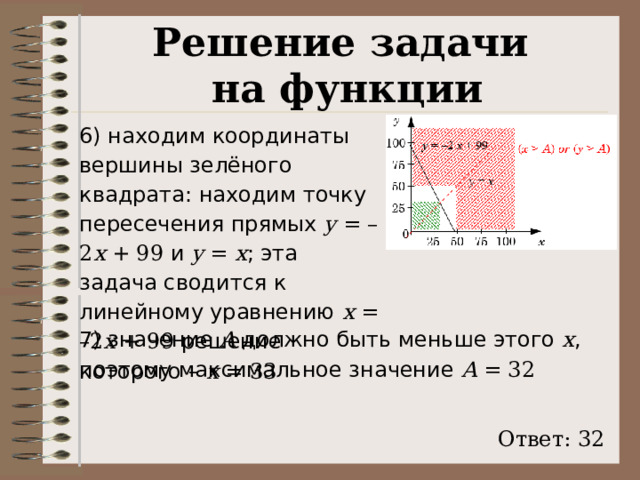
на функции

6) находим координаты вершины зелёного квадрата: находим точку пересечения прямых y = –2 x + 99 и y = x ; эта задача сводится к линейному уравнению x = –2 x + 99 решение которого – x = 33

7) значение A должно быть меньше этого x , поэтому максимальное значение A = 32

Ответ: 32

50) ∨ (4 y – x истинно для любых целых положительных значений x и y . » width=»640″

5. Задания на функции

Укажите наименьшее целое значение А, при котором выражение

( y + 3 x A ) ∨ (2 y +x 50) ∨ (4 y – x

истинно для любых целых положительных значений x и y .

50) or (4 y – x 2) таким образом, нам нужно выбрать значение A так, чтобы условие ( y + 3 x A ) выполнялось при всех x и y , для которых ложно (2 y +x 50) or (4 y – x y +x  50) and (4 y – x  40) 3) последние два условия можно переписать в виде ( y  – x /2 + 25) and ( y  x /4 + 10) » width=»640″

Решение задачи

на функции

1) второе и третье выражения не зависят от выбора A : (2 y +x 50) or (4 y – x

2) таким образом, нам нужно выбрать значение A так, чтобы условие ( y + 3 x A ) выполнялось при всех x и y , для которых ложно (2 y +x 50) or (4 y – x y +x  50) and (4 y – x  40)

3) последние два условия можно переписать в виде

( y  – x /2 + 25) and ( y  x /4 + 10)

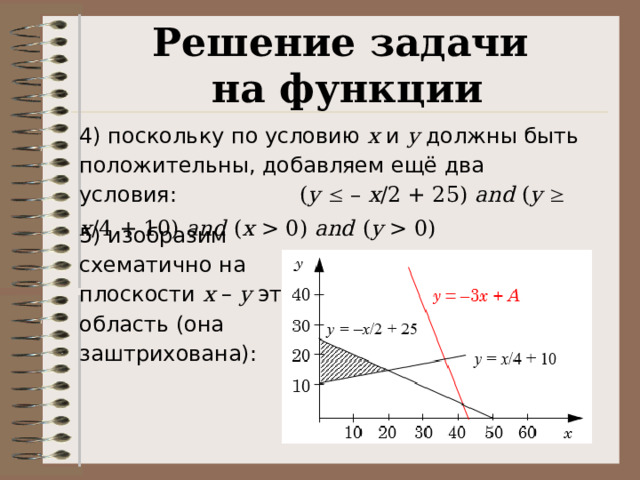
0) and ( y 0) 5) изобразим схематично на плоскости x – y эту область (она заштрихована): » width=»640″

Решение задачи

на функции

4) поскольку по условию x и y должны быть положительны, добавляем ещё два условия: ( y  – x /2 + 25) and ( y  x /4 + 10) and ( x 0) and ( y 0)

5) изобразим схематично на плоскости x – y эту область (она заштрихована):

Решение задачи

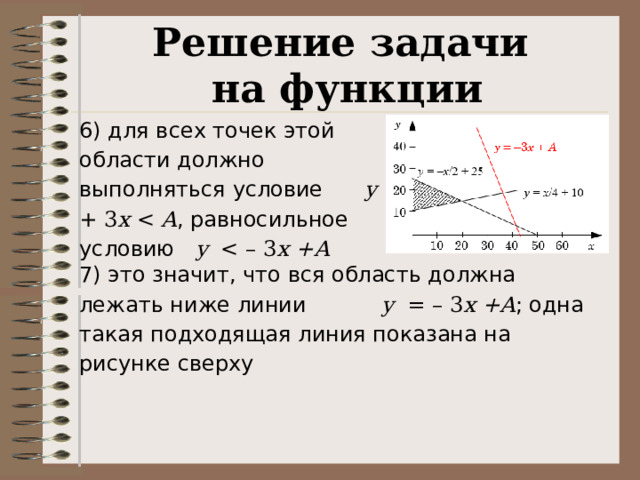
на функции

6) для всех точек этой области должно выполняться условие y + 3 x A , равносильное условию y x +A

7) это значит, что вся область должна лежать ниже линии y = – 3 x +A ; одна такая подходящая линия показана на рисунке сверху

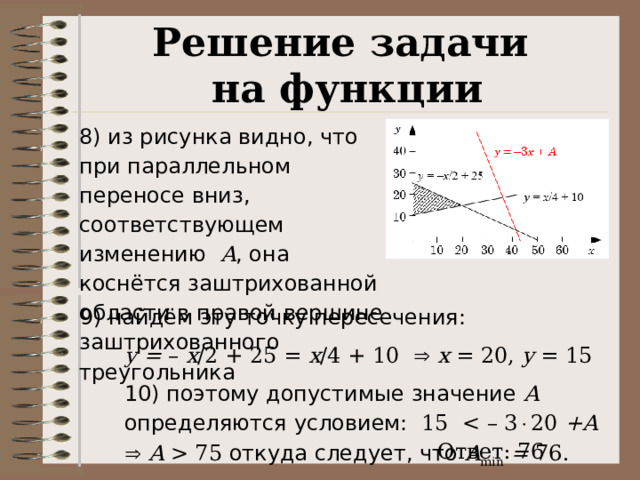
75 откуда следует, что A min = 76. Ответ: 76 » width=»640″

Решение задачи

на функции

из рисунка видно, что при параллельном переносе вниз, соответствующем изменению A , она коснётся заштрихованной области в правой вершине заштрихованного треугольника

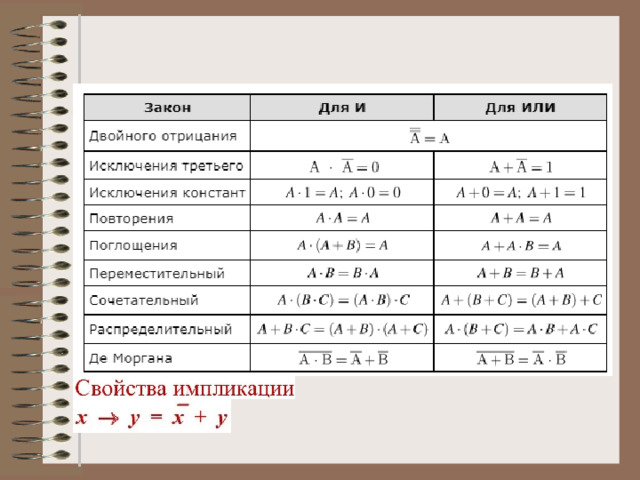
9) найдём эту точку пересечения:

y = – x /2 + 25 = x /4 + 10  x = 20, y = 15

10) поэтому допустимые значение A определяются условием: 15 +A  A 75 откуда следует, что A min = 76.

Ответ: 76

Источник