Теория на экзамене по математике огэ

Подписаться

В данном разделе представлены все необходимые материалы для подготовки к ОГЭ по математике 2022. Мы предоставляем как разобранные варианты с теорией по заданиям, так и тестовые варианты для самоподготовки. Пройдя курс подготовки к ОГЭ на нашем сайте, вы уверенно напишете экзамен в 9 классе в 2022 году!

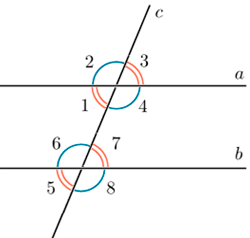
1. Углы

Вертикальные углы равны (на рис. 1 и 3; 6 и 8 и др.).

Внутренние накрест лежащие углы при параллельных прямых и секущей равны. (на рис. 4 и 6; 1 и 7).

Сумма внутренних односторонних углов при параллельных прямых и секущей равна 180˚ (на рис. 4 и 7; 1 и 6).

Соответственные углы при параллельных прямых и секущей равны. (на рис. 3 и 7; 1 и 5 и др.).

Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая перпендикулярна третьей прямой.

2. Медиана, биссектриса, высота

Биссектриса треугольника — отрезок, соединяющий вершину треугольника с точкой на противоположной стороне и делящий угол треугольника пополам.

Высота треугольника – перпендикуляр опущенный из вершины угла на противоположную сторону.

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

В любом треугольники все биссектрисы пересекаются в одной точке, все медианы пересекаются в одной точке, все медианы пересекаются в одной точке.

3. Треугольник

Сумма углов в любом треугольнике 180˚.

Средняя линия треугольника – прямая проходящая через середины двух сторон. Средняя линия параллельна одной из сторон и равна половине этой стороны.

Виды треугольников: тупоугольный (один угол тупой), прямоугольный (один угол прямой 90˚), остроугольный (все углы острые, меньше 90˚).

Равнобедренный треугольник — треугольник, у которого равны две стороны.

Свойства равнобедренного треугольника:

• в равнобедренном треугольнике углы при основании равны;
• в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой;

Равносторонний треугольник — треугольник,
у которого все стороны равны. (все углы по 60 градусов)

Всякий равносторонний треугольник является равнобедренным,
но не всякий равнобедренный — равносторонним.

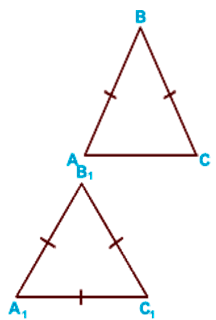
Три признака равенства треугольников

I признак по двум сторонам и углу между ними

II признак (по стороне и прилежащим углам)

III признак (по трем сторонам)

Признаки подобия треугольников

I признак по двум равным углам

II признак по двум пропорциональным сторонам и углу между ними

III признак по трем пропорциональным сторонам

Площади подобных фигур относятся как коэффициент подобия в квадрате.

Объемы подобных фигур относятся как коэффициент подобия в кубе.

Треугольник называется прямоугольным, если один из его углов прямой.

Стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла, – гипотенузой. (самая большая сторона это гипотенуза, две др катеты).

Свойства прямоугольного треугольника

Сумма острых углов прямоугольного треугольника равна 90 градусов.

Катет, лежащий против угла в 30˚, равен половине гипотенузы.

Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы.

Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности.

Теорема Пифагора:

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: a² + b² = c².

Пифагоровы тройки:

• 3, 4, 5
• 6, 8, 10
• 5, 12, 13
• 9, 12, 15

Признаки равенства прямоугольных треугольников

• По двум катетам.
• По гипотенузе и катету.
• По катету и прилежащему острому углу.
• По катету и противолежащему острому углу.
• По гипотенузе и острому углу.

Признаки подобия прямоугольных треугольников:

• По острому углу.
• По пропорциональности двух катетов.
• По пропорциональности катета и гипотенузы.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

Высота, проведенная из вершины прямого угла, разбивает прямоугольный треугольник на два подобных треугольника. Каждый из этих треугольников подобен исходному.

Высота прямоугольного треугольника: h=ab/c или h = (где АВ гипотенуза, СЕ высота опущенная на гипотенузу).

В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равна половине гипотенузы: m=c/2 (R=​с/2=m​c).

3. Четырехугольники

Сумма углов в любом четырехугольнике 360˚.

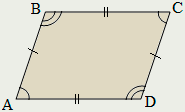
Параллелограмм

Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны.

У параллелограмма противолежащие стороны равны и противолежащие углы равны.

Сумма любых двух соседних углов параллелограмма равна 180°.

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

Каждая диагональ делит параллелограмм на два равных треугольника.

Две диагонали параллелограмма делят его на четыре равновеликих треугольника.

Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

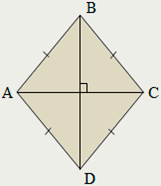
Ромб

Ромбом называется параллелограмм, у которого все стороны равны.

Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.

Прямоугольник

Прямоугольником называется параллелограмм, у которого все углы прямые.

Диагонали прямоугольника равны и точкой пересечения делятся на четыре равных отрезка.

Квадрат.

Квадрат – это прямоугольник, у которого все стороны равны.

Диагонали квадрата равны и перпендикулярны.

Сторона и диагональ квадрата связаны соотношениями: .

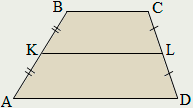
Трапеция

Трапецией называется четырёхугольник у которого только две противолежащие стороны параллельны.

Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.

Средняя линия трапеции параллельна её основаниям и равна их полусумме.

Равнобокой называется трапеция, у которой боковые стороны равны.

У равнобокой трапеции: диагонали равны; углы при основании равны; сумма противолежащих углов равна 180.

Стороны и диагональ равнобокой трапеции связаны соотношением: d² = ab+c².

Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям.

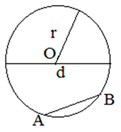
4. Окружность

Отрезок, соединяющий центр окружности с любой точкой окружности называется радиусом (r) окружности.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром окружности.

Прямая, имеющая с окружностью одну общую точку, называется касательной. Касательная и радиус проведенный в точку касания пересекаются под прямым углом.

Прямая, имеющая с окружностью две общие точки, называется секущей.

Центральный угол окружности – это угол, вершина которого лежит в центре окружности. Центральный угол равен дуге на которую он опирается.

Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают ее. Вписанный угол равен половине дуги на которую опирается.

Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.

Вписанный угол, опирающийся на диаметр равен 90˚.

Все вписанные углы, опирающиеся на одну и туже дугу равны.

Теорема косинусов:

a² = b² + c² – 2bccosa

Теорема синусов:

5. Формулы площадей

См. продолжение статьи

Конспекты для подготовки к ОГЭ по Математике

Автор Г.Д. Соловьева

Для быстрого и эффективного повторения материала при подготовке к ОГЭ по математике вам помогут опорные конспекты. Например, по таким темам:

Уравнения с одной переменной

Уравнение – это равенство с переменной.

Например:

Корень уравнения – это значение переменной, при котором уравнение обращается в верное равенство.
Например, уравнение

Если , тогда . Число 2 – корень данного уравнения.

Решить уравнение – значит найти все его корни или доказать, что их нет.

Равносильные уравнения – это уравнения, имеющие одни и те же корни или не имеющие корней.

Примеры:

Уравнения и равносильны. Их корни 7 и -7.
Уравнения и равносильны. Они оба не имеют корней

к оглавлению ▴

Правила решения уравнений:

1) Можем переносить слагаемое из одной части уравнения в другую, изменяя его знак на противоположный.

2) Можем умножать (делить) левую и правую части уравнения на одно и то же число, отличное от нуля.

Линейное уравнение с одной переменной

Это уравнение вида , где – переменная, и — некоторые числа.

Виды линейных уравнений:

1) ax = b, где a ≠ 0, b ≠ 0. Например, 2х = 4.

Такое уравнение имеет единственный корень:

Например,

.

Корень уравнения:

.

Решаем уравнение:

,

2) Уравнение

В этом уравнении , .

Такое уравнение не имеет корней.

Например:

2x + 9 = 2(x+6)

2x + 9 = 2x + 12

0 = 3.

3) Уравнение

Здесь a = 0, b= 0. Уравнение имеет бесконечно много корней. Любое число х является его корнем.

Например:

к оглавлению ▴

Линейная функция

Прямая пропорциональность – это функция вида , где — переменная, .

График прямой пропорциональности – прямая, проходящая через начало координат

Случай k > 0. Пример:

Строим график.

Случай k < 0. Пример:

Линейная функция – это функция вида , где – переменная, k и b числа.

График линейной функции – прямая

Пример для k > 0 – функция

ГРАФИК

Пример для k < 0 – функция

График функции , где , — прямая, параллельная прямой .

– частный случай линейной функции при

Если k = 0, то y = b – прямая, параллельная оси x

Если k = 0, b = 0, то y = 0 – ось x

к оглавлению ▴

Взаимное расположение графиков линейных функций

Угловой коэффициент прямой – это число k в формуле функции y = kx + b

Если k > 0, то угол наклона к оси х – острый.

Если k<0, то угол наклона к оси х – тупой.

Если для двух прямых угловые коэффициенты различны, прямые пересекаются

РИСУНОК

Если для двух прямых угловые коэффициенты равны, прямые параллельны.

Например, ,

РИСУНОК

к оглавлению ▴

Степень с натуральными показателями

Определение: Степенью числа а с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен а.

— возведение в степень

Выражение — степень числа а,

а — основание степени (показывает, какой множитель умножается),

n — показатель степени (показывает, сколько множителей умножается).

Запомним: для любого числа а.

для любого а, не равного нулю.

Выражение «ноль в нулевой степени» не имеет смысла.

Примеры:

1)

2)

3)

4)

5)

6)

к оглавлению ▴

Свойства степени с натуральным показателем

Умножение степеней.

При умножении степеней с одинаковым основанием показатели складывают. Основание остается прежним.

Примеры:

1) 

2)

3)

Деление степеней

При делении степеней с одинаковым основанием из показателя делимого вычитают показатель делителя. Основание остается прежним.

Примеры:

1)

2)

3)

Возведение степени в степень

При возведении степени в степень основание оставляют прежним, а показатели умножают.

Примеры:

1)

2)

Возведение произведения в степень

При возведении произведения в степень в эту степень возводят каждый множитель и результаты перемножают.

Примеры:

1)

2)

Формулы сокращенного умножения

Примеры:
1)

2)

4)

5)

Квадратное уравнение и разложение квадратного трехчлена на множители.

, где , — корни квадратного трехчлена

Квадратное уравнение – уравнение вида .

Дискриминант квадратного уравнения: .

Если > 0, уравнение имеет два корня

Если , уравнение имеет один корень

Если < 0, уравнение не имеет корней

Такие конспекты для подготовки к ОГЭ по математике легко сделать самим. Сделай конспекты по темам:

— Неравенство с одной переменной

— Квадратное неравенство

— Вероятность

— Квадратичная функция, обратная пропорциональность

— Арифметическая прогрессия

— Геометрическая прогрессия