Теория по электричеству физика егэ - Помощь в подготовке к экзаменам и поступлению

Главная
Теория ЕГЭ
Физика — теория ЕГЭ
Полная теория Электростатики, ЕГЭ по физике

Полная теория Электростатики, ЕГЭ по физике

29.09.2013

Полный материал по физике на тему: Электростатика.

Материал содержит в себе необходимую теорию по теме, а также множество различных практических заданий и тестов, ориентированных на ЕГЭ.

Вместе с этим материалом вы сможете максимально качественно изучить раздел физики «Электростатика» для ЕГЭ.

Смотреть в PDF:

Или прямо сейчас: Скачайте в pdf файле.

Сохранить ссылку:

Комментарии (0)
Добавить комментарий

Добавить комментарий

Комментарии без регистрации. Несодержательные сообщения удаляются.

Имя (обязательное)

E-Mail

Подписаться на уведомления о новых комментариях

Отправить

Источник

Основные теоретические сведения
- Электрический ток. Сила тока. Сопротивление
- Закон Ома. Последовательное и параллельное соединение проводников
- ЭДС. Закон Ома для полной цепи
- Работа и мощность тока. Закон Джоуля-Ленца
- Энергобаланс замкнутой цепи
- Электролиз
- Электрический ток в газах и в вакууме

Основные теоретические сведения

Электрический ток. Сила тока. Сопротивление

К оглавлению…

В проводниках при определенных условиях может возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда. Такое движение называется электрическим током. За направление электрического тока принято направление движения положительных свободных зарядов, хотя в большинстве случае движутся электроны – отрицательно заряженные частицы.

Количественной мерой электрического тока служит сила тока I – скалярная физическая величина, равная отношению заряда q, переносимого через поперечное сечение проводника за интервал времени t, к этому интервалу времени:

Если ток не постоянный, то для нахождения количества прошедшего через проводник заряда рассчитывают площадь фигуры под графиком зависимости силы тока от времени.

Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным. Сила тока измеряется амперметром, который включается в цепь последовательно. В Международной системе единиц СИ сила тока измеряется в амперах [А]. 1 А = 1 Кл/с.

Средняя сила тока находится как отношение всего заряда ко всему времени (т.е. по тому же принципу, что и средняя скорость или любая другая средняя величина в физике):

Если же ток равномерно меняется с течением времени от значения I₁ до значения I₂, то можно значение среднего тока можно найти как среднеарифметическое крайних значений:

Плотность тока – сила тока, приходящаяся на единицу поперечного сечения проводника, рассчитывается по формуле:

При прохождении тока по проводнику ток испытывает сопротивление со стороны проводника. Причина сопротивления – взаимодействие зарядов с атомами вещества проводника и между собой. Единица измерения сопротивления 1 Ом. Сопротивление проводника R определяется по формуле:

где: l – длина проводника, S – площадь его поперечного сечения, ρ – удельное сопротивление материала проводника (будьте внимательны и не перепутайте последнюю величину с плотностью вещества), которое характеризует способность материала проводника противодействовать прохождению тока. То есть это такая же характеристика вещества, как и многие другие: удельная теплоемкость, плотность, температура плавления и т.д. Единица измерения удельного сопротивления 1 Ом·м. Удельное сопротивление вещества – табличная величина.

Сопротивление проводника зависит и от его температуры:

где: R₀ – сопротивление проводника при 0°С, t – температура, выраженная в градусах Цельсия, α – температурный коэффициент сопротивления. Он равен относительному изменению сопротивления, при увеличении температуры на 1°С. Для металлов он всегда больше нуля, для электролитов наоборот, всегда меньше нуля.

Диод в цепи постоянного тока

Диод – это нелинейный элемент цепи, сопротивление которого зависит от направления протекания тока. Обозначается диод следующим образом:

Стрелка в схематическом обозначении диода показывает, в каком направлении он пропускает ток. В этом случае его сопротивление равно нулю, и диод можно заменить просто на проводник с нулевым сопротивлением. Если ток течет через диод в противоположном направлении, то диод обладает бесконечно большим сопротивлением, то есть не пропускает ток совсем, и является разрывом в цепи. Тогда участок цепи с диодом можно просто вычеркнуть, так как ток по нему не идет.

Закон Ома. Последовательное и параллельное соединение проводников

К оглавлению…

Немецкий физик Г.Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (то есть проводнику, в котором не действуют сторонние силы) сопротивлением R, пропорциональна напряжению U на концах проводника:

Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Это соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.

Проводники, подчиняющиеся закону Ома, называются линейными. Графическая зависимость силы тока I от напряжения U (такие графики называются вольт-амперными характеристиками, сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при достаточно больших токах наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.

Проводники в электрических цепях можно соединять двумя способами: последовательно и параллельно. У каждого способа есть свои закономерности.

1. Закономерности последовательного соединения:

Формула для общего сопротивления последовательно соединенных резисторов справедлива для любого числа проводников. Если же в цепь последовательно включено n одинаковых сопротивлений R, то общее сопротивление R₀ находится по формуле:

2. Закономерности параллельного соединения:

Формула для общего сопротивления параллельно соединенных резисторов справедлива для любого числа проводников. Если же в цепь параллельно включено n одинаковых сопротивлений R, то общее сопротивление R₀ находится по формуле:

Электроизмерительные приборы

Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы – вольтметры и амперметры.

Вольтметр предназначен для измерения разности потенциалов, приложенной к его клеммам. Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением R_B. Для того чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен.

Амперметр предназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением R_A. В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи.

ЭДС. Закон Ома для полной цепи

К оглавлению…

Для существования постоянного тока необходимо наличие в электрической замкнутой цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками постоянного тока. Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами.

Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.

При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу. Физическая величина, равная отношению работы A_ст сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):

Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).

Закон Ома для полной (замкнутой) цепи: сила тока в замкнутой цепи равна электродвижущей силе источника, деленной на общее (внутреннее + внешнее) сопротивление цепи:

Сопротивление r – внутреннее (собственное) сопротивление источника тока (зависит от внутреннего строения источника). Сопротивление R – сопротивление нагрузки (внешнее сопротивление цепи).

Падение напряжения во внешней цепи при этом равно (его еще называют напряжением на клеммах источника):

Важно понять и запомнить: ЭДС и внутреннее сопротивление источника тока не меняются, при подключении разных нагрузок.

Если сопротивление нагрузки равно нулю (источник замыкается сам на себя) или много меньше сопротивления источника, то тогда в цепи потечет ток короткого замыкания:

Сила тока короткого замыкания – максимальная сила тока, которую можно получить от данного источника с электродвижущей силой ε и внутренним сопротивлением r. У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик, и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.

Несколько источников ЭДС в цепи

Если в цепи присутствует несколько ЭДС подключенных последовательно, то:

1. При правильном (положительный полюс одного источника присоединяется к отрицательному другого) подключении источников общее ЭДС всех источников и их внутреннее сопротивление может быть найдено по формулам:

Например, такое подключение источников осуществляется в пультах дистанционного управления, фотоаппаратах и других бытовых приборах, работающих от нескольких батареек.

2. При неправильном (источники соединяются одинаковыми полюсами) подключении источников их общее ЭДС и сопротивление рассчитывается по формулам:

В обоих случаях общее сопротивление источников увеличивается.

При параллельном подключении имеет смысл соединять источники только c одинаковой ЭДС, иначе источники будут разряжаться друг на друга. Таким образом суммарное ЭДС будет таким же, как и ЭДС каждого источника, то есть при параллельном соединении мы не получим батарею с большим ЭДС. При этом уменьшается внутреннее сопротивление батареи источников, что позволяет получать большую силу тока и мощность в цепи:

В этом и состоит смысл параллельного соединения источников. В любом случае при решении задач сначала надо найти суммарную ЭДС и полное внутреннее сопротивление получившегося источника, а затем записать закон Ома для полной цепи.

Работа и мощность тока. Закон Джоуля-Ленца

К оглавлению…

Работа A электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в теплоту Q, выделяющееся на проводнике. Эту работу можно рассчитать по одной из формул (с учетом закона Ома все они следуют друг из друга):

Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж.Джоулем и Э.Ленцем и носит название закона Джоуля–Ленца. Мощность электрического тока равна отношению работы тока A к интервалу времени Δt, за которое эта работа была совершена, поэтому она может быть рассчитана по следующим формулам:

Работа электрического тока в СИ, как обычно, выражается в джоулях (Дж), мощность – в ваттах (Вт).

Энергобаланс замкнутой цепи

К оглавлению…

Рассмотрим теперь полную цепь постоянного тока, состоящую из источника с электродвижущей силой ε и внутренним сопротивлением r и внешнего однородного участка с сопротивлением R. В этом случае полезная мощность или мощность, выделяемая во внешней цепи:

Максимально возможная полезная мощность источника достигается, если R = r и равна:

Если при подключении к одному и тому же источнику тока разных сопротивлений R₁ и R₂ на них выделяются равные мощности то внутреннее сопротивление этого источника тока может быть найдено по формуле:

Мощность потерь или мощность внутри источника тока:

Полная мощность, развиваемая источником тока:

КПД источника тока:

Электролиз

К оглавлению…

Электролитами принято называть проводящие среды, в которых протекание электрического тока сопровождается переносом вещества. Носителями свободных зарядов в электролитах являются положительно и отрицательно заряженные ионы. К электролитам относятся многие соединения металлов с металлоидами в расплавленном состоянии, а также некоторые твердые вещества. Однако основными представителями электролитов, широко используемыми в технике, являются водные растворы неорганических кислот, солей и оснований.

Прохождение электрического тока через электролит сопровождается выделением вещества на электродах. Это явление получило название электролиза.

Электрический ток в электролитах представляет собой перемещение ионов обоих знаков в противоположных направлениях. Положительные ионы движутся к отрицательному электроду (катоду), отрицательные ионы – к положительному электроду (аноду). Ионы обоих знаков появляются в водных растворах солей, кислот и щелочей в результате расщепления части нейтральных молекул. Это явление называется электролитической диссоциацией.

Закон электролиза был экспериментально установлен английским физиком М.Фарадеем в 1833 году. Закон Фарадея определяет количества первичных продуктов, выделяющихся на электродах при электролизе. Итак, масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит:

Величину k называют электрохимическим эквивалентом. Он может быть рассчитан по формуле:

где: n – валентность вещества, N_A – постоянная Авогадро, M – молярная масса вещества, е – элементарный заряд. Иногда также вводят следующее обозначение для постоянной Фарадея:

Электрический ток в газах и в вакууме

К оглавлению…

Электрический ток в газах

В обычных условиях газы не проводят электрический ток. Это объясняется электрической нейтральностью молекул газов и, следовательно, отсутствием носителей электрических зарядов. Для того чтобы газ стал проводником, от молекул необходимо оторвать один или несколько электронов. Тогда появятся свободные носителя зарядов — электроны и положительные ионы. Этот процесс называется ионизацией газов.

Ионизировать молекулы газа можно внешним воздействием — ионизатором. Ионизаторами может быть: поток света, рентгеновские лучи, поток электронов или α-частиц. Молекулы газа также ионизируются при высокой температуре. Ионизация приводит к возникновению в газах свободных носителей зарядов — электронов, положительных ионов, отрицательных ионов (электрон, объединившийся с нейтральной молекулой).

Если создать в пространстве, занятом ионизированным газом, электрическое поле, то носители электрических зарядов придут в упорядоченное движение – так возникает электрический ток в газах. Если ионизатор перестает действовать, то газ снова становится нейтральным, так как в нем происходит рекомбинация – образование нейтральных атомов ионами и электронами.

Электрический ток в вакууме

Вакуумом называется такая степень разрежения газа, при котором можно пренебречь соударением между его молекулами и считать, что средняя длина свободного пробега превышает линейные размеры сосуда, в котором газ находится.

Электрическим током в вакууме называют проводимость межэлектродного промежутка в состоянии вакуума. Молекул газа при этом столь мало, что процессы их ионизации не могут обеспечить такого числа электронов и ионов, которые необходимы для ионизации. Проводимость межэлектродного промежутка в вакууме может быть обеспечена лишь с помощью заряженных частиц, возникших за счет эмиссионных явлений на электродах.

Источник

Электроэнергия

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: производство, передача и потребление электрической энергии.

Электрическая энергия играет в нашей жизни исключительную роль. Если в доме нет света, мы оказываемся практически беспомощны. Функционирование предприятий, средств транспорта, коммуникаций и прочих достижений цивилизации основано на использовании электроэнергии.

Электроэнергия обладает замечательными свойствами, которые и обеспечивают возможность её повсеместного применения.

• Простота производства. В мире функционирует огромное множество разнообразных генераторов электроэнергии.
• Передача на большие расстояния. Электроэнергия транспортируется по высоковольтным линиям электропередачи без существенных потерь.
• Преобразование в другие виды энергии. Электроэнергия легко преобразуется в механическую энергию (электродвигатели), внутреннюю энергию (нагревательные приборы), энергию света (осветительные приборы) и т. д.
• Распределение между потребителями. Специальные устройства позволяют распределять электроэнергию между потребителями с самыми разными «запросами» — промышленными предприятиями, городскими электросетями, жилыми домами и т. д.

Рассмотрим подробнее вопросы производства, передачи и потребления электрической энергии.

Производство электроэнергии

Среди генераторов электроэнергии наиболее распространены электромеханические генераторы переменного тока. Они преобразуют механическую энергию вращения ротора в энергию индукционного переменного тока, возникающего благодаря явлению электромагнитной индукции.

На рис. 1 проиллюстрирована основная идея генератора переменного тока: проводящая рамка (называемая якорем) вращается в магнитном поле.

Рис.1. Схема генератора переменного тока

Магнитный поток сквозь рамку меняется со временем и порождает ЭДС индукции, которая приводит к возникновению индукционного тока в рамке. С помощью специальных приспособлений (колец и щёток) переменный ток передаётся из рамки во внешнюю цепь.

Если рамка вращается в однородном магнитном поле с постоянной угловой скоростью omega , то возникающий переменный ток будет синусоидальным. Покажем это.

Выберем направление вектора нормали vec{n} к плоскости рамки. Вектор vec{n} , таким образом, вращается вместе с рамкой. Направление обхода рамки считается положительным, если с конца вектора vec{n} этот обход видится против часовой стрелки.

Напомним, что ток считается положительным, если он течёт в положительном направлении (и отрицательным в противном случае). ЭДС индукции считается положительной, если она создаёт ток в положительном направлении (и отрицательной в противном случае).

Предположим, что в начальный момент времени векторы vec{n} и vec{B} сонаправлены. За время рамка повернётся на угол . Магнитный поток через рамку в момент времени равен:

(1)

где — площадь рамки. Дифференцируя по времени, находим ЭДС индукции:

(2)

Если сопротивление рамки равно , то в ней возникает ток:

$i = frac{displaystyle e}{displaystyle R vphantom{1^a}}=frac{displaystyle BS omega}{displaystyle R vphantom{1^a}} sin omega t.$ (3)

Как видим, ток действительно меняется по гармоническому закону, то есть является синусоидальным.

В реальных генераторах переменного тока рамка содержит не один виток, как в нашей схеме, а большое число витков. Это позволяет увеличить в раз ЭДС индукции в рамке. Почему?

Объяснить это несложно. В самом деле, магнитный поток через каждый виток площади по-прежнему определяется выражением (1), так что ЭДС индукции в одном витке согласно формуле (2) равна: . Все эти ЭДС индукции, возникающие в каждом витке, складываются друг с другом, и суммарная ЭДС в рамке окажется равной:

Сила тока в рамке:

$i = frac{displaystyle NBS omega}{displaystyle R vphantom{1^a}} sin omega t,$

где есть по-прежнему сопротивление рамки.

Кроме того, рамку снабжают железным (или стальным) сердечником. Железо многократно усиливает магнитное поле внутри себя, и поэтому наличие сердечника позволяет увеличить магнитный поток сквозь рамку в сотни и даже тысячи раз. Как следует из формул (2) и (3), ЭДС индукции и ток в рамке увеличатся во столько же раз.

Передача электроэнергии

Электроэнергия производится в основном на тепловых электростанциях (ТЭС), гидроэлектростанциях (ГЭС) и атомных электростанциях (АЭС).

Роторы генераторов ТЭС вращаются за счёт энергии сгорающего топлива (чаще всего этим топливом является уголь). Экономически целесообразным является строительство ТЭС вблизи крупных угольных месторождений.

Роторы генераторов ГЭС приводятся во вращение энергией падающей воды. Поэтому ГЭС строятся на реках.

В любом случае возникает проблема передачи выработанной электроэнергии потребителям, находящимся за много километров от электростанций.

Электроэнергия транспортируется по проводам. Потери энергии на нагревание проводов должны быть сведены к минимуму. Оказывается, для этого нужно высокое напряжение в линии электропередачи. Покажем это.

Рассмотрим двухпроводную линию электропередачи, связывающую источник переменного напряжения u с потребителем П (рис. 2).

Рис.2. Передача электроэнергии по двухпроводной линии

Длина линии равна , так что общая длина проводов составит . Если rho — удельное сопротивление материала провода, — площадь поперечного сечения провода, то сопротивление линии будет равно:

$R = frac{displaystyle 2 rho l}{displaystyle S vphantom{1^a}}.$ (4)

Потребителю должна быть передана мощность с заданным действующим значением . Обозначим через и действующие значения напряжения в линии и силы тока. Если alpha — сдвиг фаз между током и напряжением, то, как мы знаем из предыдущего листка, .

Отсюда

$I = frac{displaystyle P}{displaystyle U cos alpha vphantom{1^a}}.$ (5)

Часть мощности Delta P теряется на нагревание проводов:

Подставляя сюда выражения (4) и (5), получим:

$Delta P = frac{displaystyle 2 rho l P^2}{displaystyle SU^2 cos^2 alpha vphantom{1^a}}.$ (6)

Мы видим из формулы (6), что потеря мощности обратно пропорциональна квадрату напряжения в линии. Следовательно, для уменьшения потерь надо повышать напряжение при передаче. Вот почему линии электропередач являются высоковольтными. Например, Волжская ГЭС передаёт в Москву электроэнергию при напряжении 500 киловольт.

Трансформатор

Генераторы электростанций имеют ЭДС порядка 10-20 кВ. Как мы только что видели, для передачи электроэнергии на большие расстояния нужно повышать напряжение до нескольких сотен киловольт.

С другой стороны, напряжение бытовой электросети составляет 220 В. Поэтому при доставке энергии обычному потребителю требуется понижение напряжения до сотен вольт.

Замечательно, что повышение и понижение напряжения в случае синусоидального переменного тока не представляет никаких сложностей. Для этого используются специальные устройства — трансформаторы.

Простейшая схема трансформатора приведена на рис. 3. На замкнутом стальном сердечнике расположены две обмотки.

Рис.3. Трансформатор

Первичная обмотка содержит N_1 витков; на неё подаётся входное напряжение u_1 . Это напряжение как раз и требуется преобразовать — повысить или понизить.

Вторичная обмотка содержит N_2 витков. К ней подсоединяется нагрузка, условно обозначенная резистором . Это — потребитель, для работы которого нужно преобразованное напряжение u_2 .

Режим холостого хода

Наиболее прост для рассмотрения холостой ход трансформатора, когда нагрузка отключена (ключ разомкнут).

Пусть напряжение на первичной обмотке меняется по закону косинуса с амплитудой $U_{01}$ :

$u_1 = U_{01} cos omega t.$

Активное сопротивление R_1 первичной обмотки считаем очень малым по сравнению с её индуктивным сопротивлением. В таком случае, как мы знаем, сила тока i_1 в первичной обмотке отстаёт по фазе от напряжения на pi/2 :

$i_1 = I_{01} cos left ( omega t - frac{displaystyle pi}{displaystyle 2 vphantom{1^a}} right ) = I_{01} sin omega t.$

При этом трансформатор не потребляет энергию из сети, к которой он подключён.

Магнитный поток Phi , пронизывающий витки первичной обмотки, пропорционален току i_1 и поэтому также меняется по закону синуса:

В каждом витке первичной обмотки возникает ЭДС индукции:

$e = -dot{Phi}= - omega Phi_0 cos omega t.$ (7)

Следовательно, полная ЭДС индукции в первичной обмотке равна:

(8)

Стальной сердечник практически не выпускает магнитное поле наружу — линии магнитного поля почти целиком идут внутри сердечника. Магнитный поток в любом сечении сердечника одинаков; в частности, каждый виток вторичной обмотки пронизывает тот же самый магнитный поток Phi . Поэтому в одном витке вторичной обмотки возникает та же ЭДС индукции , даваемая выражением (7), а полная ЭДС индукции во вторичной обмотке равна:

(9)

Как видим, обе ЭДС индукции в первичной и вторичной обмотках меняются синфазно. Мгновенные значения ЭДС индукции относятся друг к другу как числа витков в обмотках:

$frac{displaystyle e_1}{displaystyle e_2 vphantom{1^a}}= frac{displaystyle N_1}{displaystyle N_2 vphantom{1^a}}.$ (10)

Ввиду малости активного сопротивления первичной обмотки мы можем считать, что выполнено приближённое равенство:

(11)

(вспомните рассуждение из листка «Переменный ток. 1», раздел «Катушка в цепи переменного тока»). Так как цепь вторичной обмотки разомкнута и ток в ней отсутствует, имеем точное равенство:

Итак, . Следовательно, мгновенные значения напряжений в первичной и вторичной обмотках также меняются почти синфазно. С учётом равенства (10) получаем:

$frac{displaystyle u_1}{displaystyle u_2 vphantom{1^a}}= frac{displaystyle N_1}{displaystyle N_2 vphantom{1^a}}.$ (12)

Величина называется коэффициентом трансформации. Отношение мгновенных значений напряжений в (12) можно заменить отношением действующих значений U_1 и U_2 :

$frac{displaystyle U_1}{displaystyle U_2 vphantom{1^a}}= frac{displaystyle N_1}{displaystyle N_2 vphantom{1^a}}=k.$

Если k > 1 , то трансформатор является понижающим. В этом случае вторичная обмотка содержит меньше витков, чем первичная; потребитель получает меньшее напряжение, чем то, что поступает на вход трансформатора. На рис. 3 изображён как раз понижающий трансформатор.

Если же k < 1 , то трансформатор будет повышающим. Вторичная обмотка содержит больше витков, чем первичная, и потребитель получает напряжение более высокое, чем на входе трансформатора.

Режим нагрузки

Теперь рассмотрим вкратце работу нагруженного трансформатора, когда ключ на рис. 3 замкнут. В этом случае трансформатор выполняет свою прямую задачу — передаёт энергию потребителю, подключённому ко вторичной обмотке.

Согласно закону сохранения энергии, передача энергии потребителю возможна только за счёт увеличения потребления энергии из внешней сети. Так оно в действительности и происходит. Давайте попробуем понять, какие физические процессы приводят к этому.

Главное заключается в том, что ввиду малого омического сопротивления первичной обмотки сохраняется приближённое равенство (11), т. е.

Напряжение u_1 задаётся внешней сетью, поэтому амплитуда ЭДС индукции e_1 остаётся прежней — равной амплитуде внешнего напряжения.

Но, с другой стороны, из выражения (8) мы знаем, что амплитуда величины e_1 равна .

Стало быть, при подключении нагрузки остаётся неизменной амплитуда Phi_0 магнитного потока Phi , пронизывающего витки первичной и вторичной обмоток.

При холостом ходе магнитный поток Phi порождался магнитным полем тока i_1 первичной обмотки (во вторичной обмотке тока не было). Теперь в создании магнитного потока участвуют два магнитных поля: поле B_1 тока i_1 первичной обмотки (оно создаёт поток Phi_1 ) и поле B_2 тока i_2 вторичной обмотки (оно создаёт поток Phi_2 ). Таким образом,

В отличие от тока i_1 , который «навязывается» первичной обмотке внешней сетью, ток i_2 — индукционный, и его направление определяется правилом Ленца: магнитное поле B_2 стремится уменьшить изменение суммарного магнитного потока Phi . Но амплитуда Phi_0 этого потока, как мы уже говорили, остаётся той же, что и при холостом ходе. Как же так?

Очень просто — чтобы обеспечить неизменность величины Phi_0 , приходится увеличиваться магнитному потоку Phi_1 . Возрастает амплитуда тока i_1 первичной обмотки! Вот почему увеличивается потребление энергии из сети по сравнению с режимом холостого хода.

Первичная обмотка потребляет из сети мощность

(как и выше, в данной формуле фигурируют действующие значения мощности, напряжения и силы тока).

Нагрузка получает от вторичной обмотки мощность

Эта мощность является полезной с точки зрения потребителя. Отношение полезной мощности, получаемой нагрузкой, к мощности, потребляемой из сети — это КПД трансформатора:

$eta = frac{displaystyle P_2}{displaystyle P_1 vphantom{1^a}} = frac{displaystyle U_2 I_2 cos alpha_2}{displaystyle U_1 I_1 cos alpha_1 vphantom{1^a}}$

Разумеется, — часть мощности теряется в трансформаторе. Потери мощности состоят из двух частей.

1. Так называемые «потери в меди», обозначаемые $Delta P_{MED}$ . Это мощность, расходуемая на нагревание первичной и вторичной обмоток:

$Delta P_{MED} = I_1^2R_1 + I_2^2R_2$

Сколь бы малыми не были активные сопротивления R_1 и R_2 этих обмоток, они не равны нулю, и при больших токах с ними приходится считаться.

2. Так называемые «потери в стали», обозначаемые $Delta P_{CT}$ . Сюда относятся:

• Мощность, расходуемая на перемагничивание сердечника, т. е. на изменение ориентации элементарных токов под действием внешнего магнитного поля.

• Мощность, расходуемая на нагревание сердечника индукционными вихревыми токами (которые называются ещё токами Фуко). Эти токи возникают в сердечнике под действием вихревого электрического поля, порождаемого переменным магнитным полем. Для уменьшения токов Фуко сердечники собираются из листов специальной трансформаторной стали, но полностью ликвидировать эти токи, конечно же, не удаётся.

Оказывается, потери в стали не зависят от нагрузки — они определяются только амплитудой магнитного потока, которая, как мы знаем, при любой нагрузке остаётся неизменной.

Таким образом, имеем:

$P_1 = P_2 + Delta P_{MED} + Delta P_{CT},$

и для КПД трансформатора получаем следующее выражение:

$eta = frac{displaystyle P_2}{displaystyle P_2 + Delta P_{MED} + Delta P_{CT} vphantom{1^a}}.$ (13)

Если полезная мощность P_2 мала (недогрузка трансформатора), то и КПД мал. Действительно, числитель в (13) маленький, а знаменатель — не меньше постоянной величины потерь в стали $Delta P_{CT}$ .

Если полезная мощность P_2 чрезмерно велика(перегрузка трансформатора), то КПД опятьтаки мал. Дело в том, что в этом случае велики токи I_1 и I_2 в обмотках трансформатора, и, следовательно, большой величины достигают потери в меди $Delta P_{MED}$ .

Для трансформатора существует оптимальная (так называемая номинальная) нагрузка, на которую он рассчитан. При номинальной нагрузке оказывается, что КПД трансформатора близок к единице, т. е. , или, с учётом выражений для мощностей:

Кроме того, сдвиги фаз приближённо равны нулю, так что

Следовательно, при нагрузках, близких к номинальной, имеем:

$frac{displaystyle I_2}{displaystyle I_1 vphantom{1^a}} approx frac{displaystyle U_1}{displaystyle U_2 vphantom{1^a}} approx k,$

где — введённый выше коэффициент трансформации. Например, у понижающего трансформатора k > 1 , и при номинальной нагрузке ток в его вторичной обмотке в раз больше тока первичной обмотки.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Электроэнергия» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

ЭЛЕКТРОСТАТИКА
Теория и формулы (кратко и сжато)

Электростатика – раздел электродинамики, изучающий покоящиеся электрически заряженные тела. Существует два вида электрических зарядов: положительные (стекло о шелк) и отрицательные (эбонит о шерсть).

Элементарный заряд – минимальный заряд (е = 1,6∙10^-19Кл)

Заряд любого тела кратен целому числу элементарных зарядов: q = N∙е

Электризация тел – перераспределение заряда между телами. Способы электризации: трение, касание, влияние.

Закон сохранения электрического заряда – в замкнутой системе алгебраическая сумма зарядов всех частиц остается неизменной. q_{1 +} q ₂+ q ₃+ …..+ q_n = const

Пробный заряд – точечный положительный заряд.

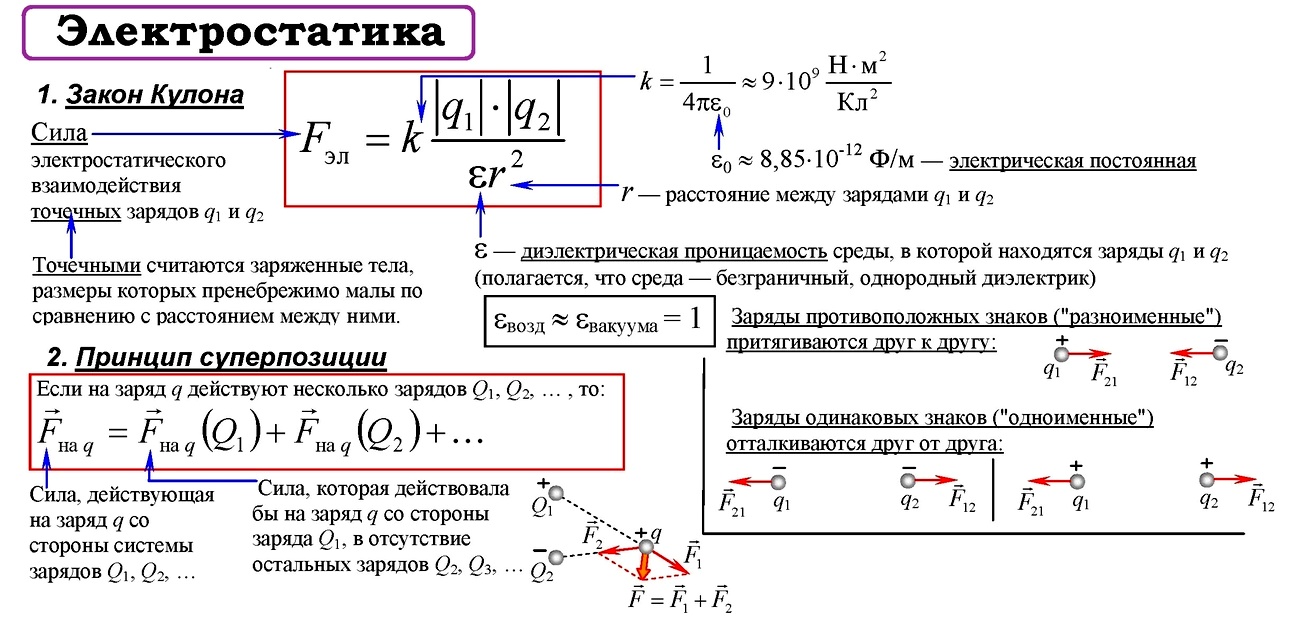
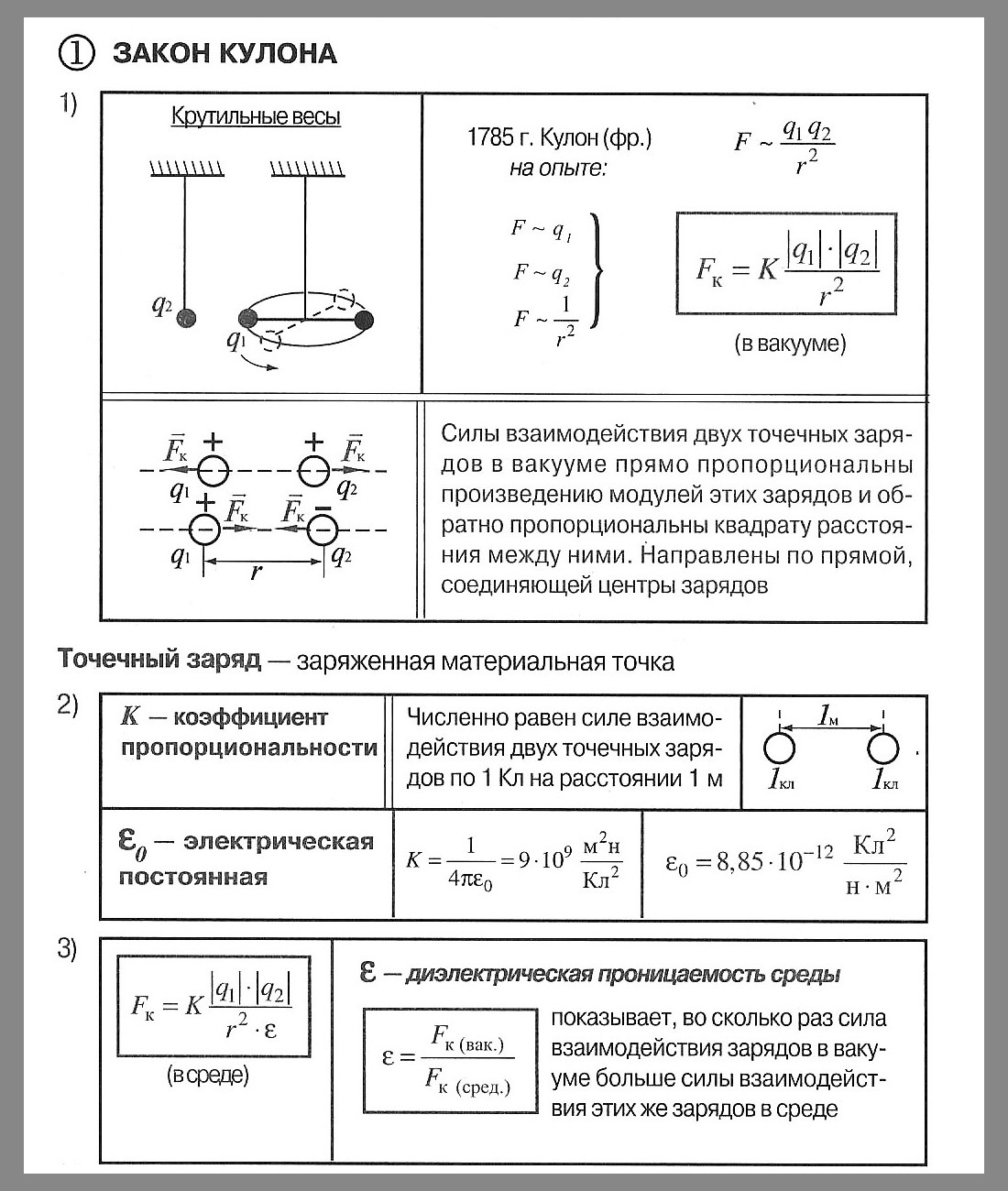
Закон Кулона

Закон Кулона (установлен опытным путем в 1785 году) Сила взаимодействия двух неподвижных точечных зарядов в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорционально квадрату расстояния между ними.

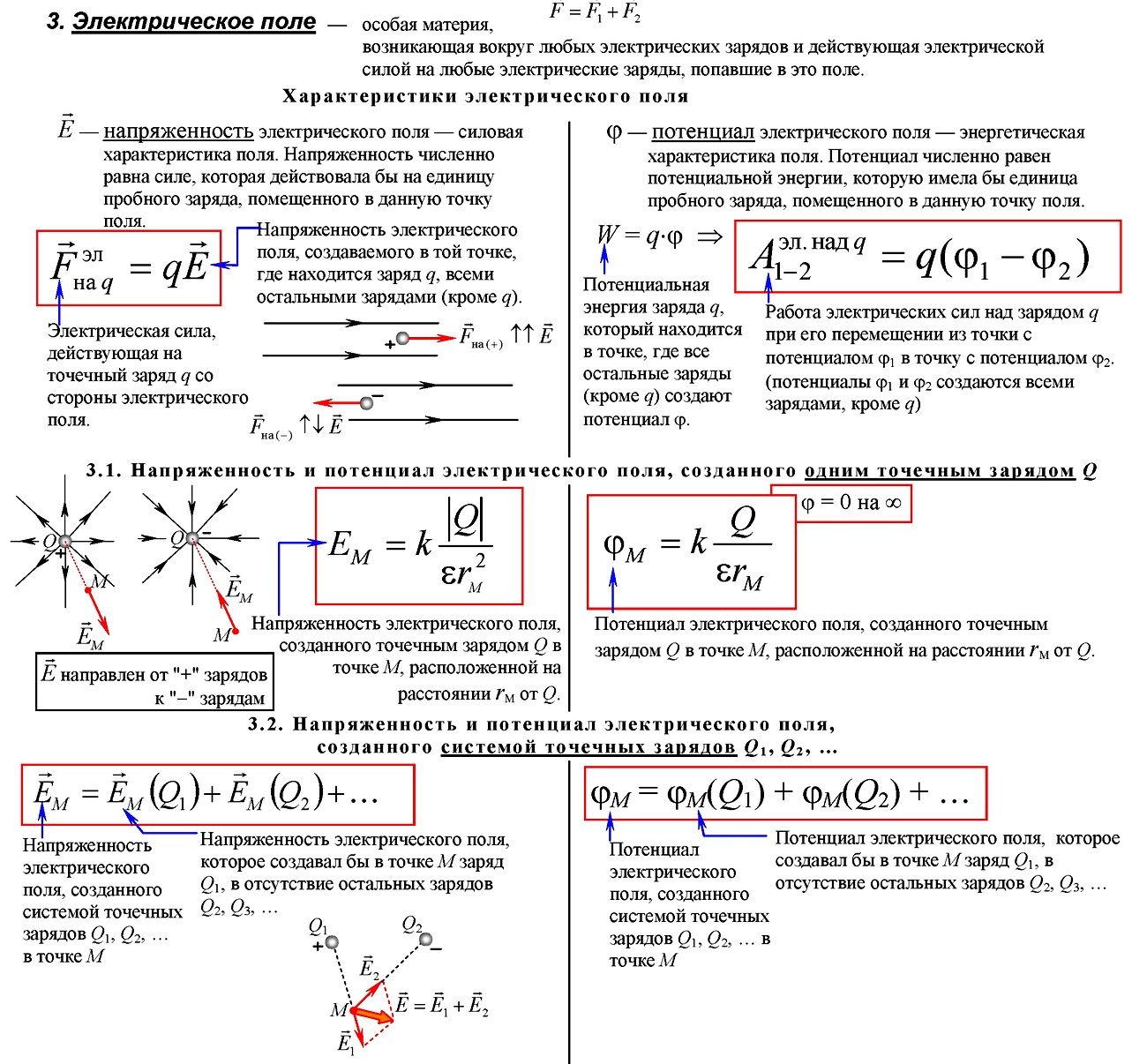
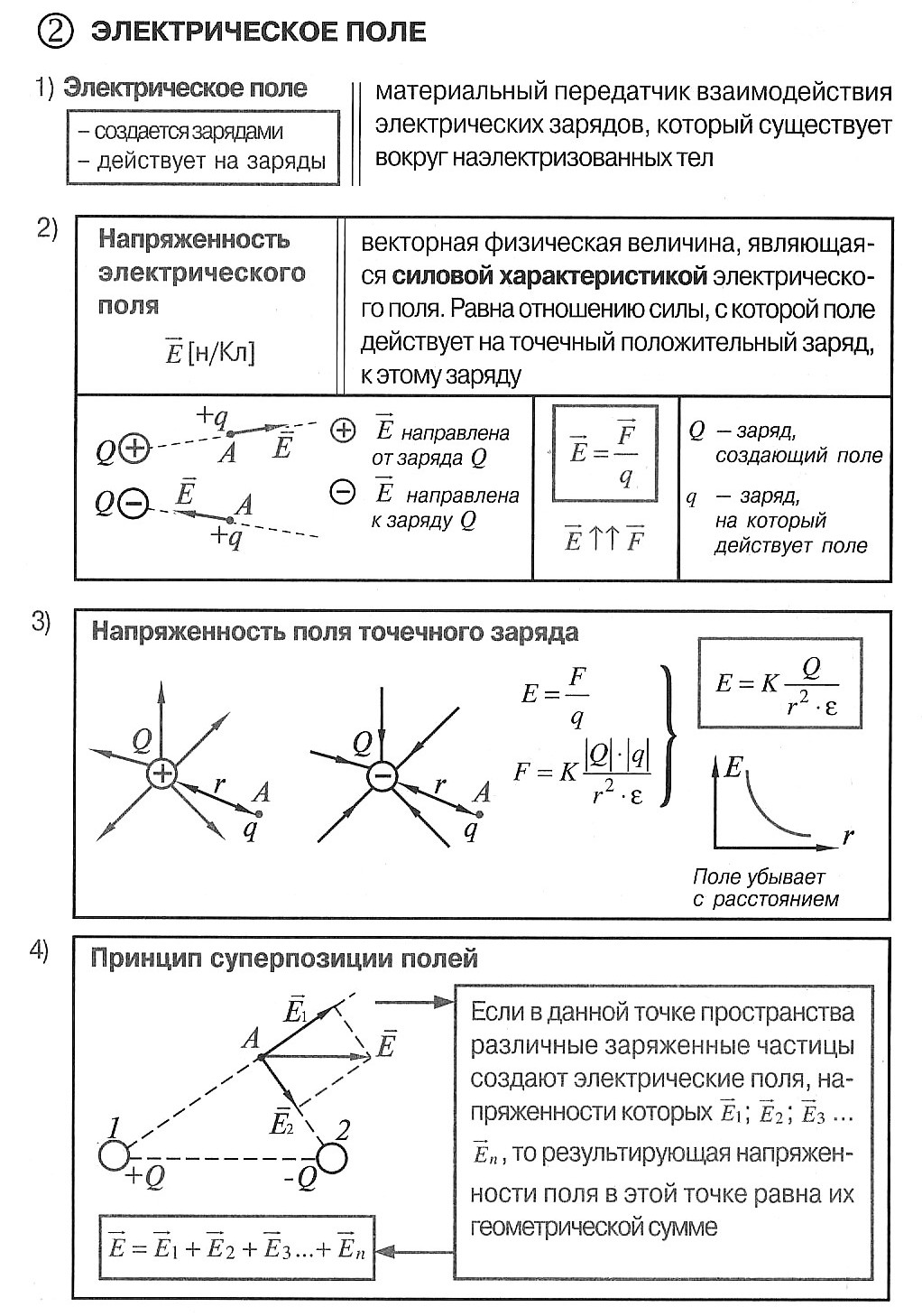
Электрическое поле

Электрическое поле – вид материи, осуществляющий взаимодействие между электрическими зарядами, возникает вокруг зарядов, действует только на заряды

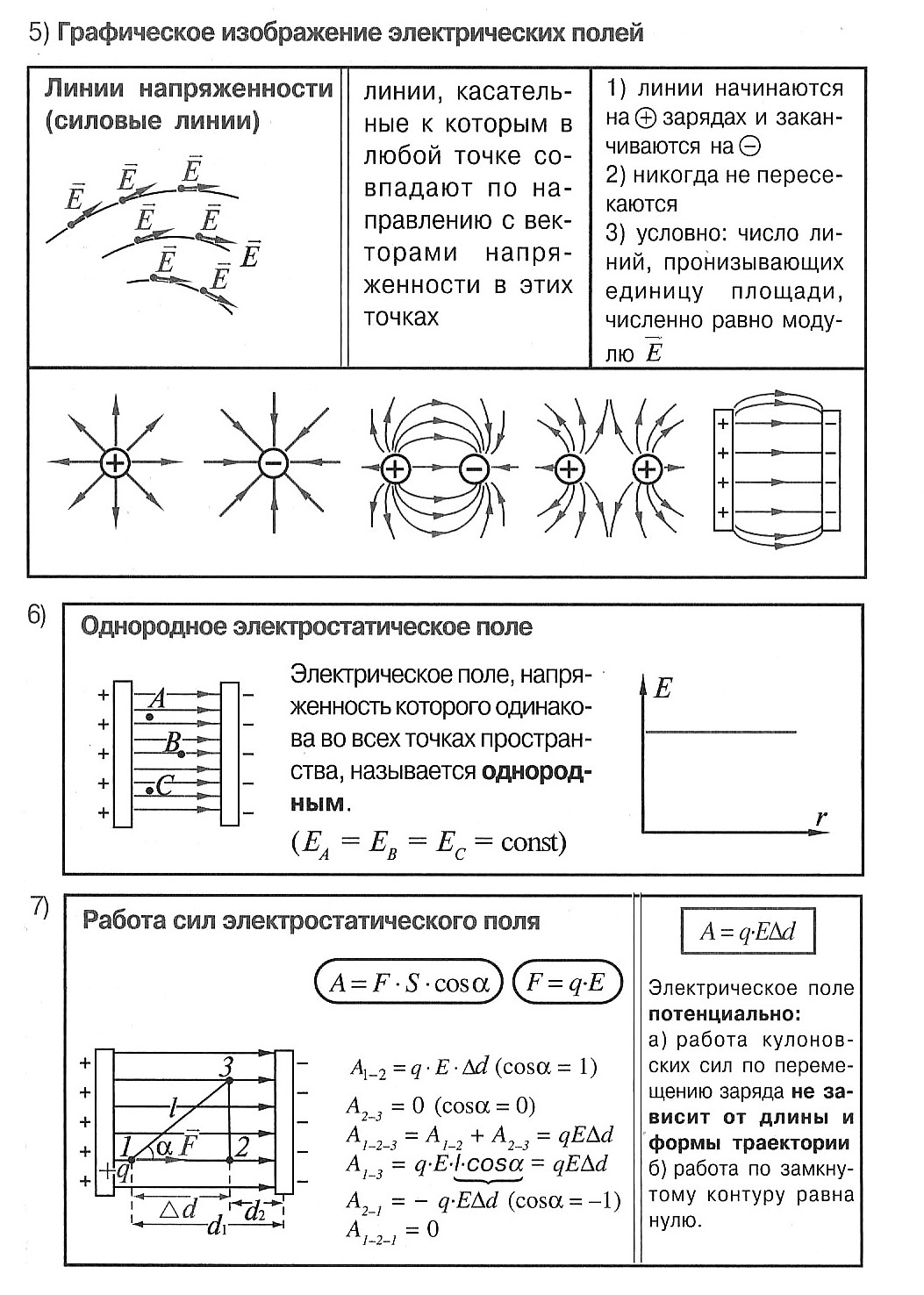
Силовые линии напряженности электрического поля – непрерывные линии, касательные к которым в каждой точке, через которые они проходят, совпадают с вектором напряженности.

Свойства силовых линий:

не замкнуты;
не пересекаются;
непрерывны;
направление совпадает с направлением вектора напряжённости;
начало на + q или в бесконечности, конец на – q или в бесконечности;
гуще вблизи зарядов (где больше напряжённость).
перпендикулярны поверхности проводника

Разность потенциалов или напряжение (Δφ или U) — это разность потенциалов в начальной и конечной точках траектории заряда Δφ = φ₁ – φ₂

Чем меньше меняется потенциал на отрезке пути, тем меньше напряженность поля.
Напряженность электрического поля направлена в сторону уменьшения потенциала.

Электроемкость

Электроемкость С — характеризует способность проводника накапливать электрический заряд на своей поверхности.

— не зависит от электрического заряда и напряжения.
— зависит от геометрических размеров проводников, их формы, взаимного расположения, электрических свойств среды между проводниками.

Проводники и диэлектрики

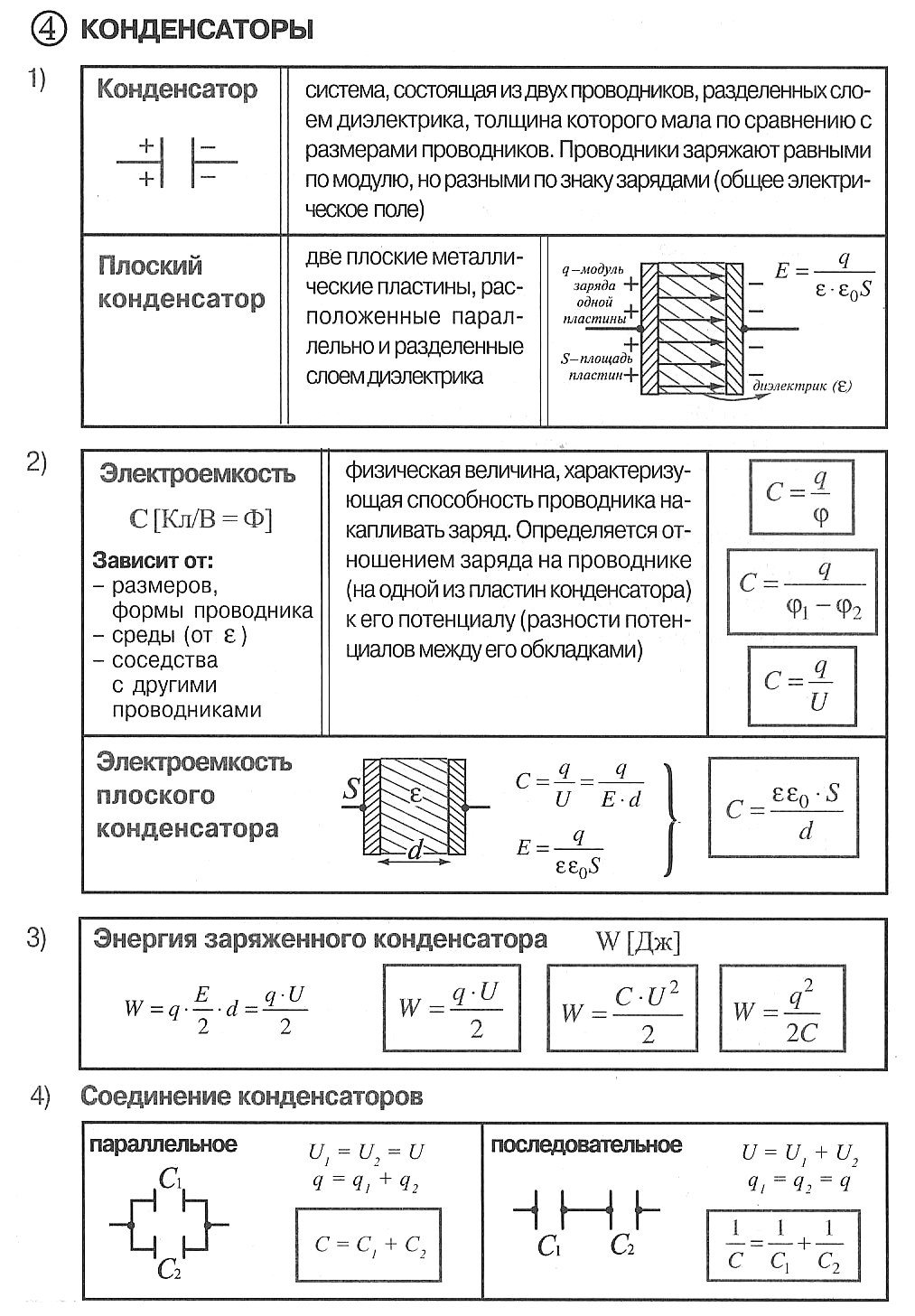
Конденсаторы

Конденсатор — электротехническое устройство, служащее для быстрого накопления электрического заряда и быстрой отдачи его в цепь (два проводника, разделенных слоем диэлектрика ).

Скачать таблицы по теме «Электростатика»

Конспект уроков по теме «Электростатика. Теория и формулы» + шпаргалка.

Еще конспекты для 10-11 классов:

Источник

Проводники и диэлектрики в электростатическом поле. Диэлектрическая проницаемость вещества. Электроемкость. Конденсаторы. Поле плоского конденсатора. Электроемкость плоского конденсатора. Последовательное и параллельное соединение конденсаторов. Энергия заряженного конденсатора.

Проводники и диэлектрики в электростатическом поле

Вещества в природе можно разделить на проводники и диэлектрики.

Основная особенность — наличие свободных зарядов (электронов), которые участвуют в тепловом движении и могут перемещаться по всему объему проводника.

Типичные проводники — металлы.

Диэлектрическая проницаемость вещества

В отсутствие внешнего поля в любом элементе объема проводника отрицательный свободный заряд компенсируется положительным зарядом ионной решетки. В проводнике, внесенном в электрическое поле, происходит перераспределение свободных зарядов, в результате чего на поверхности проводника возникают нескомпенсированные положительные и отрицательные заряды. Этот процесс называют электростатической индукцией, а появившиеся на поверхности проводника заряды — индукционными зарядами.

В отличие от проводников, в диэлектриках (изоляторах) нет свободных электрических зарядов. Они состоят из нейтральных атомов или молекул. Заряженные частицы в нейтральном атоме связаны друг с другом и не могут перемещаться под действием электрического поля по всему объему диэлектрика.

Физическая величина, равная отношению модуля напряженности (vec{E}_0) внешнего электрического поля в вакууме к модулю напряженности (vec{E}) полного поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества (varepsilon).

[varepsilon=dfrac{vec{E}_0}{vec{E}}]

Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда (q) одного из проводников к разности потенциалов (Delta varphi) между ними:

[fbox{$C=dfrac{q}{Delta varphi}$}]

Единицы измерения: (displaystyle [text{Ф}]) (фарад).

Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники.

Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, — обкладками.

Плоский конденсатор — система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика.

Электроемкость плоского конденсатора

Разность потенциалов (Delta varphi) между пластинами в однородном электрическом поле равна (Ed), где (d) — расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:

[C=dfrac{q}{Delta varphi}=dfrac{sigma S}{Ed}=dfrac{varepsilon_0S}{d}]

Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в (varepsilon) раз:

[fbox{$C=dfrac{varepsilon_0varepsilon S}{d}$}]

Электрическое поле плоского конденсатора в основном локализовано между пластинами; однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния. В целом ряде задач приближенно можно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками.

Последовательное и параллельное соединение конденсаторов

Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.

Последовательное соединение конденсаторов

При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику тока одной из своих пластин. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.

Напряжение на данном участке цепи соотносятся следующим образом:

[fbox{$U=U_1+U_2$}]

Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:

[dfrac{q}{C}=dfrac{q}{C_1}+dfrac{q}{C_2}]

Сократив выражение на (Q), получим формулу:

[fbox{$dfrac{1}{C}=dfrac{1}{C_1}+dfrac{1}{C_2}$}]

Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:

[fbox{$C=dfrac{C_1C_2}{C_1+C_2}$}]
Параллельное соединение конденсаторов

При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.

Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:

[fbox{$q=q_1+q_2$}]

Так как заряд конденсатора

[q=CU]

А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов

[CU=C_1U+C_2U]

[fbox{$C=C_1+C_2$}]
По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.

Энергия заряженного конденсатора

Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии того, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится. Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке.

Вычислим эту энергию: начнём с плоского воздушного конденсатора.

Ответим на такой вопрос: какова силу притяжения его обкладок друг к другу. Величины используем следующие: заряд конденсатора (q), площадь обкладок (S). Возьмём на второй обкладке настолько маленькую площадку, что заряд (q_0) этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой

[F_0 = q_0E_1,]

где (E_1) — напряжённость поля первой обкладки:

[E_1=dfrac{sigma}{2varepsilon_0}=dfrac{q}{2varepsilon_0S}]

Значит

[F_0=dfrac{qq_0}{2varepsilon_0S}]

Направлена эта сила параллельно линиям поля (т.е. перпендикулярно пластинам). Результирующая сила (F) притяжения второй обкладки к первой складывается из всех этих сил (F_0), с которыми притягиваются к первой обкладке всевозможные маленькие заряды (q_0) второй обкладки. При этом суммировании постоянный множитель (displaystyledfrac{q}{2varepsilon_0S}) вынесется за скобку, а в скобке просуммируются все (q_0) и дадут (q). В результате получим

[F=dfrac{q^2}{2varepsilon_0S}]

Предположим теперь, что расстояние между обкладками изменилось от начальной величины (d_1) до конечной величины (d_2). Сила притяжения пластин совершает при этом работу [A = F(d_1 -d_2)]

Знак правильный: если пластины сближаются ((d_2 < d_1)), то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины ((d_2 > d_1)), то работа силы притяжения получается отрицательной, как и должно быть.

Получаем

[A=dfrac{q^2}{2varepsilon_0S}(d_1-d_2)=dfrac{q^2d_1}{2varepsilon_0S}-dfrac{q^2d_2}{2varepsilon_0S}=dfrac{q^2}{2C_1}-dfrac{q^2}{2C_2}=W_1-W_2]

Это можно переписать следующим образом: [A =-(W_2-W_1) =-Delta W,]

где [fbox{$W=dfrac{q^2}{2C}$}, (1)]

Работа потенциальной силы (F) притяжения обкладок оказалась равна изменению со знаком минус величины (W). Это как раз и означает, что (W) — потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора. Используя соотношение (q = CU), можно получить ещё две формулы для энергии конденсатора (проделать это самостоятельно).

[fbox{$W=dfrac{qU}{2}$}, (2)]

[fbox{$W=dfrac{CU^2}{2}$}, (3)]

Формулы (1)—(3) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.

Источник

Пришла пора начать разбирать новую тему: Электростатика на ЕГЭ по физике. Как видите, даже само название говорит о том, что речь пойдет об электричестве и магнетизме.

Конечно же, проще всего осваивать электромагнетизм с опытным педагогом, который подробно и понятно разберет основные вопросы. Наше обучающее видео посвящено введению в электричество и электромагнетизм. А вся теория электростатики для ЕГЭ с задачами – на нашем канале.

Магнитное поле и его основные свойства

Итак, что нужно знать о магнитном поле. В первую очередь то, что источниками магнитного поля являются электрические движущиеся заряды. В отличие от электрического магнитное не воздействует на сам заряд, сила возникает только при движении.

Основные свойства магнитного поля, о которых стоит помнить для решения задач на ЕГЭ:

магнитное поле материально;
магнитное поле порождается только движущимся электрическим зарядом;
там, где двигается электрический заряд с определенной силой, всегда есть магнитное поле;
скорость магнитного поля конечна и равна скорости света в вакууме.

Электричество

Как проще освоить тему? Конечно, разбить ее на подтемы. Именно это и делает преподаватель учебного центра Годограф, чтобы облегчить понимание для каждого ученика.

Итак, электричество делим на 2 подтемы:

Электростатика. В этом случае заряды никуда не двигаются.
Электродинамика. Здесь заряды уже можно двигать, появляются различные схемы и т.д.

Электродинамика и электростатика в ЕГЭ – важный раздел, на который отводится немало задач. Внимательно изучив теорию по электростатике для ЕГЭ, вы сможете легче справиться с практическими заданиями и испытывать меньшую нагрузку на экзамене.

Электростатика на ЕГЭ: способы упрощение подготовки

Если вы только начинаете готовиться к экзамену, вооружите себя всеми доступными методическими материалами. Учебники, специальная литература, старые тесты, методички – все это станет вашим путеводителем в мир знаний. Кроме того, задачи на электростатику ЕГЭ прошлых годов помогут оценить сложность заданий.

Однако чтобы освоить нелегкую тему электромагнетизма самому, бывает недостаточно усидчивости и самоконтроля. В этом случае обратите внимание на курсы, которые предлагают учебные центры. С опытными педагогами, имеющими под рукой готовую программу и многолетний опыт, значительно проще получить желаемый результат на экзамене по физике.

О том, как выбрать репетитора для подготовки к ЕГЭ, вы можете почитать в нашей статье.

Опытные преподаватели физики учебного центра Годограф помогут восстановить пробелы в знаниях и подготовиться к ЕГЭ на 80+ баллов. Наш рейтинг на Яндекс.Картах – 5.0! Записывайтесь на пробный урок и продолжайте знакомиться с нашими видеообзорами по физике.