15 января 2013
В закладки
Обсудить
Жалоба
Теория по геометрии для сдачи ЕГЭ по математике
Немного теории, которая непременно пригодится на ЕГЭ.
Другие материалы смотрите в разделе ЕГЭ по математике.
Геометрия на ЕГЭ по математике
Геометрия на профильном ЕГЭ по математике — одна из сложных тем для абитуриентов. Дело в том, что когда-то экзамен по геометрии в школе был обязательным, а сейчас — нет. В результате у большинства абитуриентов знания по геометрии близки к нулю.
Геометрия на профильном ЕГЭ — это три задачи в части 1 (сюда входит и планиметрия, и стереометрия), а также задача 14 (стереометрия) и для многих недосягаемая задача 16 (геометрия) из второй части. Как же научиться их решать?
Начнем с планиметрии. Прежде всего, выучите основные формулы геометрии.
На нашем сайте вы найдете курс геометрии с нуля — основные определения, формулы и теоремы, а также разбор множества экзаменационных задач по геометрии из части 1.
Для решения задач по геометрии из части 2 нужна более серьезная подготовка.
Первый этап — теория. Необходимый материал есть в учебнике по геометрии за 7-9 класс (автор — А. В. Погорелов или Л. С. Атанасян). Выпишите в тетрадь определения и формулировки теорем. Сделайте чертежи. Доказывать теоремы старайтесь самостоятельно.
Программа по геометрии.
1. Треугольники. Элементы треугольника. Вершины и стороны. Высоты, медианы, биссектрисы (определения).
2. Построение треугольника: практические задания.
а) Три стороны треугольника равны
и
сантиметров соответственно. Постройте треугольник
с помощью циркуля и линейки.
б) В треугольнике угол
равен
градусов, сторона
равна
,
равна
. Постройте треугольник
.
в) В треугольнике сторона
равна
, угол
равен
, угол
равен
. Постройте треугольник
.
3. Три признака равенства треугольников. Неравенство треугольника.
4. Постройте с помощью циркуля и линейки:
а) серединный перпендикуляр к отрезку;
б) биссектрису угла.
5. Углы при параллельных прямых и секущей. Вертикальные, смежные, соответственные, односторонние и накрест лежащие углы. Их определение и свойства.
6. Теорема о сумме углов треугольника.
7. Внешний угол треугольника.
8. Постройте в одном и том же треугольнике
а) Три высоты. Рассмотрите также случаи тупоугольного и прямоугольного треугольника.
б) Три биссектрисы.
в) Три медианы.
9. Равнобедренный треугольник. Определение и свойства. Высота в равнобедренном треугольнике.
10. Средняя линия треугольника и ее свойства.
11. Прямоугольный треугольник. Теорема Пифагора.
12. Определения синуса, косинуса и тангенса:
— для острого угла прямоугольного треугольника;
— для произвольного угла.
13. Четырехугольники. Сумма углов четырехугольника.
14. Параллелограмм. Определение и свойства. Площадь параллелограмма.
15. Виды параллелограммов и их свойства (ромб, прямоугольник, квадрат).
16. Трапеция. Средняя линия трапеции. Площадь трапеции.
17. Подобные треугольники. Три признака подобия треугольников.
18. Площадь треугольника. Формулы и
.
19. Теоремы синусов и косинусов.
20. Чему равно отношение площадей подобных фигур.
21. Свойство медианы (в каком отношении делятся медианы в точке пересечения?)
22. Свойство биссектрисы (в каком отношении биссектриса делит противоположную сторону?)
23. Окружность и круг. Длина окружности. Площадь круга. Длина дуги и площадь сектора.
24. Теорема о радиусе, проведенном в точку касания.
25. Центральный и вписанный углы. Связь между ними.
26. Теоремы о вписанных углах.
27. Теорема о пересекающихся хордах.
28. Теорема об отрезках длин касательных, проведенных из одной точки.
29. Теорема о секущей и касательной.
30. Дан треугольник . Постройте:
а) окружность, вписанную в данный треугольник;
б) окружность, описанную вокруг данного треугольника.
Где находятся центры этих окружностей?
31. Еще три формулы площади треугольника (через радиус вписанной окружности, через радиус описанной окружности и формула Герона).
32. Когда можно вписать окружность в четырехугольник? Когда — описать вокруг четырехугольника?
Программа по стереометрии
Разбирая и решая задания ЕГЭ по геометрии, вы заметите очень интересную вещь. Простые задачи из части 1, разобранные на нашем сайте, часто оказываются базовыми схемами, на которых строятся сложные задачи из части 2 профильного ЕГЭ.
Решая на ЕГЭ задачи по геометрии, обращайте особое внимание на оформление. Помните совет, который дал абитуриентам автор бестселлера «Математика — абитуриенту» В. В. Ткачук. Вот он, этот ценнейший совет:
«Подробность решения должна быть такова, чтобы его мог понять человек в 10 (десять) раз глупее вас».
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Геометрия на ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами с границами $М$ и $М_1$. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.
Образующие цилиндрической поверхности называются образующими цилиндра, на рисунке образующая $L$.
Цилиндр называется прямым, если его образующие перпендикулярны основаниям.
Осевое сечение цилиндра — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра.
Основные понятия и свойства цилиндра:
- Основания цилиндра равны и лежат в параллельных плоскостях.
- Все образующие цилиндра параллельны и равны.
- Радиусом цилиндра называется радиус его основания ($R$).
- Высотой цилиндра называется расстояние между плоскостями оснований (в прямом цилиндре высота равна образующей).
- Осью цилиндра называется отрезок, соединяющий центры оснований ($ОО_1$).
- Если радиус или диаметр цилиндра увеличить в n раз, то объем цилиндра увеличится в $n^2$ раз.
- Если высоту цилиндра увеличить в m раз, то объем цилиндра увеличится в то же количество раз.
- Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра — образующими цилиндра.
- Если цилиндр вписан в призму, то ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра.
- Если в цилиндр вписана сфера, то радиус сферы равен радиусу цилиндра и равен половине высоты цилиндра.
$R_{сферы}=R_{цилиндра}={h_{цилиндра}}/{2}$
Площадь поверхности и объем цилиндра.
Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.
$S_{бок.пов.}=2πR·h$
Площадь поверхности цилиндра равна сумме двух площадей оснований и площади боковой поверхности.
$S_{полной.пов.}=2πR^2+2πR·h=2πR(R+h)$
Объем цилиндра равен произведению площади основания на высоту.
$V=πR^2·h$
Объем части цилиндра, в основании которого лежит сектор: $V={πR^2·n°·h}/{360}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.
Пример:
Цилиндр описан около шара. Объём цилиндра равен $30$. Найдите объём шара.
Решение:
Если в цилиндр вписан шар, то радиус цилиндра равен радиусу шара, а высота цилиндра в два раза больше радиуса шара.
$R_{цилиндр}=R_{шар}; h_{цилиндр}=2R_{шар}$
Распишем формулы объема цилиндра и шара.
$V_{цилиндра}=πR_{цилиндр}^2·h_{цилиндр}=πR_{шар}^2·2R_{шар}=2πR_{шар}^3$
$V_{шара}={4π·R_{шар}^3}/{3}$
Далее надо сравнить во сколько раз объем цилиндра больше объема шара, для этого разделим объемы друг на друга.
${V_{цилиндра}}/{V_{шара}}={2πR_{шар}^3·3}/{4π·R_{шар}^3}={3}/{2}=1.5$
Объем цилиндра больше объема шара в $1.5$ раза, следовательно, чтобы найти объем шара, надо объем цилиндра разделить на $1.5$.
$V_{шара}=30:1.5=20$
Ответ: $20$
Конусом (круговым конусом) называется тело, которое состоит из круга, точки, не лежащей в плоскости этого круга, и всех отрезков, соединяющих заданную точку с точками круга.
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими и обозначаются (l).
$l=SA$
Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Ось прямого конуса и его высота равны.
$SО$ — высота и ось конуса.
Свойства конуса:
- Все образующие конуса равны.
- Осевым сечением конуса является равнобедренный треугольник, основание которого равно двум радиусам, а боковые стороны равны образующим конуса.
- Если боковая поверхность конуса – полукруг, то осевым сечением является равносторонний треугольник, угол при вершине равен $60°$.
- Если радиус или диаметр конуса увеличить в n раз, то его объем увеличится в $n^2$ раз.
- Если высоту конуса увеличить в m раз, то объем конуса увеличится в то же количество раз.
Площадь поверхности и объем конуса.
Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.
$S_{бок.пов.}=πR·l$
Площадь поверхности конуса равна сумме площади основания и площади боковой поверхности.
$S_{полной.пов.}=πR^2+πR·l=πR(R+l)$
Объем конуса равен трети произведения площади основания на высоту.
$V={πR^2·h}/{3}$
Объем части конуса, в основании которого лежит сектор: $V={πR^2·n°·h}/{360·3}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии ($R$) от данной точки (центра сферы $О$).
Тело, ограниченное сферой, называется шаром.
Осевое сечение шара это круг, радиус которого равен радиусу шара. Осевым сечением является самый большой круг шара.
Площадь поверхности сферы: $S_{п.п}=4π·R^2=π·d^2$, где $R$ — радиус сферы, $d$ — диаметр сферы
Объем шара: $V={4π·R^3}/{3}={π·d^3}/{6}$, где $R$ — радиус шара, $d$ — диаметр шара.
Если радиус или диаметр шара увеличить в n раз, то площадь поверхности увеличится в $n^2$ раз, а объем в $n^3$ раз.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$:
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Признаки подобия треугольников:
- Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Русский, Математика, Обществознание, Физика, История, Биология, Химия, Английский, Информатика, Литература, География
О правах / ctege.info@gmail.com / Архив: 2020; 2021; 2022;
2005-2023 © ctege.info При использовании материалов указывайте гиперссылку.
- Поиск
- Доска
- О проекте
- Контакты
X
Код для вставки банера 220×110
- Главная
- Новости
- ОГЭ
- ЕГЭ
- 4 класс
- Учебник
- Задачники
- Тесты
- 5 класс
- Учебник
- Задачники
- Тесты
- 6 класс
- Учебник
- Задачники
- Тесты
- 7 класс
- Учебник
- Задачники
- Тесты
- 8 класс
- Учебник
- Задачники
- Тесты
- 9 класс
- Учебник
- Задачники
- Тесты
- ОГЭ
- Дидактические задачи
- Тематические задачи
- Экзамена- ционные тематические задачи
- Экзамена- ционные тесты
- 10 класс
- Учебник
- Задачники
- Тесты
- 11 класс
- Учебник
- Задачники
- Тесты
- ЕГЭ
Базовый уровень- Дидактические задачи
- Тематические задачи
- Экзамена- ционные тематические задачи
- Экзамена- ционные тесты
- ЕГЭ
Профильный уровень- Дидактические задачи
- Тематические задачи
- Экзамена- ционные тематические задачи
- Экзамена- ционные тесты
- Информатика
- Внеклассное чтение
- Учись учиться
- Видео
- Малый мехмат МГУ
Задание 16. ГЕОМЕТРИЯ. ПЛАНИМЕТНИЯ
Теоретический материал
1. Медиана прямоугольного треугольника |
 |
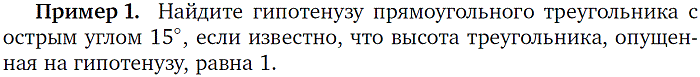 |
 |
2. Удвоение медианы |
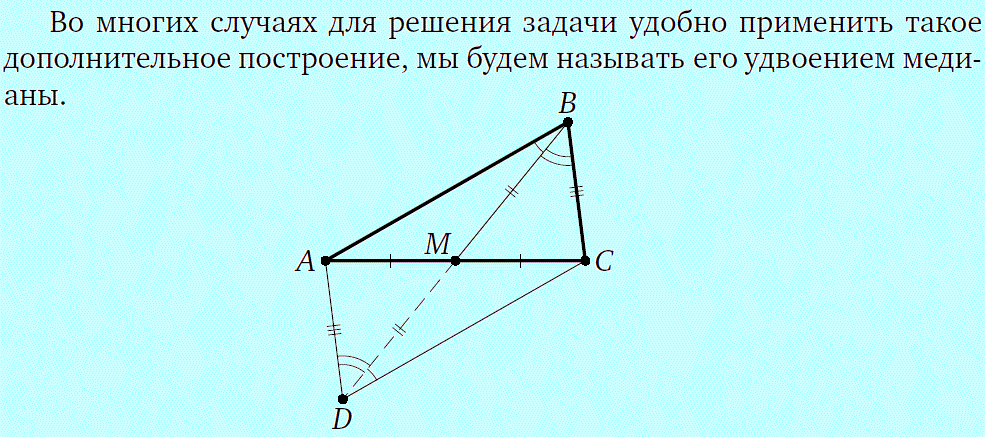 |
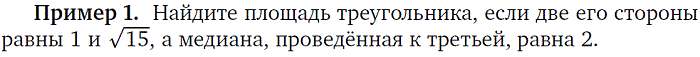 |
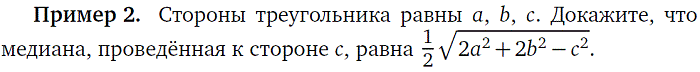 |
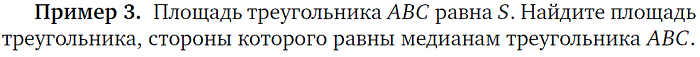 |
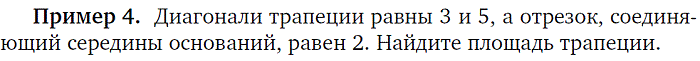 |
3. Параллелограмм
|
 |
 |
 |
 |
 |
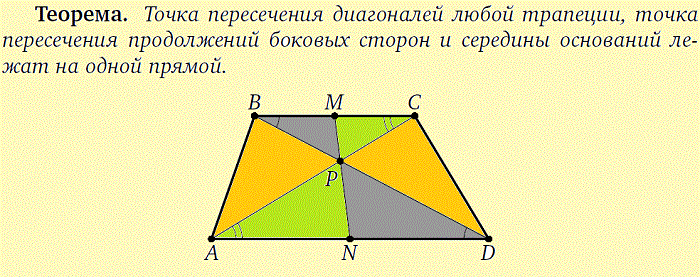
4. Трапеция |
 |
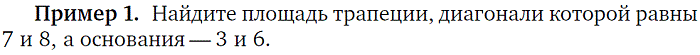 |
 |
 |
 |
5. Нахождение высоты и биссектриссы треугольника |
 |
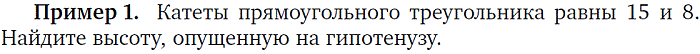 |
 |
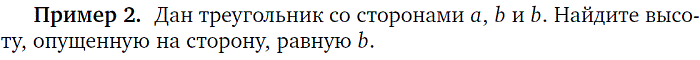 |
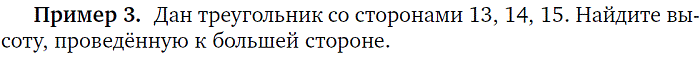 |
 |
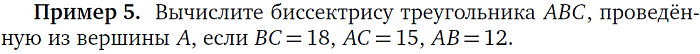 |
 |
6. Отношение отрезков |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Паровая турбина |
 |
 |
 |
 |
 |
 |
Демографическая пирамида |
 |
 |
 |
 |
 |
 |
 |
 |







