15 января 2013
В закладки
Обсудить
Жалоба
Теория по геометрии для сдачи ЕГЭ по математике
Немного теории, которая непременно пригодится на ЕГЭ.
Другие материалы смотрите в разделе ЕГЭ по математике.
Справочник
«ОСНОВНЫЕ ТЕОРЕМЫ
ГЕОМЕТРИИ»
Содержание:
1.
Теоремы базового уровня……………………………………….3 – 11 стр.
1.1.
Теорема Фалеса Милетского……………………………..……3 стр. 1.2. Теорема
Пифагора………………………………………………3 стр. 1.3.
Теорема синусов………………………………………………..4 стр. 1.4. Теорема косинусов……………………………………………..4 стр.
1.5.
Теорема биссектрис…………………………………………….5 стр.
1.6.
Теорема о пересечении медиан треугольника……………..…5 стр. 1.7. Теорема о высотах
треугольника………………………………5 стр. 1.8.
Площади треугольников……………………………….………6 стр.
1.9.
Вписанный и центральный углы……………………………….7 стр.
1.10.
Вписанная окружность треугольника………………………..8 стр.
1.11.
Описанная окружность треугольника……………………..…8 стр.
1.12.
Вневписанная окружность треугольника……………………..8 стр. 1.13. Площади
четырехугольников……….……………………..….9 стр.
1.14.
Вписанный четырехугольник………………..………………10 стр.
1.15.
Описанный четырехугольник…………..……………………10 стр.
1.16.
Теорема о двух секущих……..………………………………11 стр. 1.17. Теорема о касательной и
секущей……………………………11 стр.
1.18. Теорема
о двух хордах………………………………………..11 стр.
2.
Теоремы профильного уровня…………………………………12 – 13 стр.
2.1.
Теорема Менелая………………………………………………12 стр. 2.2. Теорема
Чевы…………………………………………………..12 стр.
2.3.
Теорема Ван – Обеля………………………………………….12 стр.
2.4.
Теорема Стюарта………………………………………………13 стр.
2.5.
Теорема Птолемея…………………………………………….13 стр.
2.6.
Теорема Аполлония……………………………………………13 стр.
Теорема Фалеса
Милетского «Несколько параллельных прямых a║b║c║d и т.д., отсекающие на
одной из сторон угла равные отрезки, и на другой стороне угла также отсекающие
на одной из сторон угла равные отрезки, и на другой стороне угла также отсекают
равные отрезки»

Теорема Пифагора
1. Квадрат
гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
2. Если
квадрат стороны треугольника равен сумме квадратов двух других его сторон, то
треугольник – прямоугольный.

Теорема синусов
Пусть a, b, c – стороны треугольника; α, β, γ –
противолежащие им углы; R – радиус описанной окружности. Тогда:
Теорема косинусов
Пусть a, b, c – стороны треугольника; α – угол,
противолежащий стороне a. Тогда:
α
Теорема биссектрис
Биссектриса треугольника делит противоположную сторону на два
отрезка, длины которых относятся так же, как длины соответствующих сторон.
Теорема о пересечении медиан треугольника
В треугольнике три медианы пересекаются в одной точке. Точка
пересечения делит каждую медиану в отношении 2:1, если считать от вершины, из
которой проведена медиана.

Теорема о высотах треугольника
В треугольнике высоты пересекаются в одной точке.
Площади треугольников
;
;
;
(формула
Герона)
где:
•
a,b,c – стороны треугольника
•
ha – высота треугольника
•
p – полупериметр треугольника
•
r – радиус вписанной окружности
•
R – радиус описанной окружности
•
β – угол между сторонами
Вписанный и центральный углы
Угол называется вписанным в окружность, если его вершина
лежит на окружности, а стороны пересекают эту окружность.
На рисунке вписанным углом является ABC.
Центральным называется угол вершиной в центре окружности. На
рисунке центральным углом является угол AOC.
Вписанная окружность треугольника

вписать единственную окружность. Центр окружности, вписанной в треугольник, совпадает
с точной пересечения его биссектрис.
Описанная окружность треугольника
Около любого треугольника можно описать
единственную окружность. Центр окружности, описанной около треугольника,
совпадает с точкой пресечения серединных перпендикуляров к его сторонам

Вневписанная окружность треугольника
В любом треугольнике биссектрисы двух
внешних углов и биссектриса внутреннего угла, не смежного с ними, пересекаются
в одной точке.
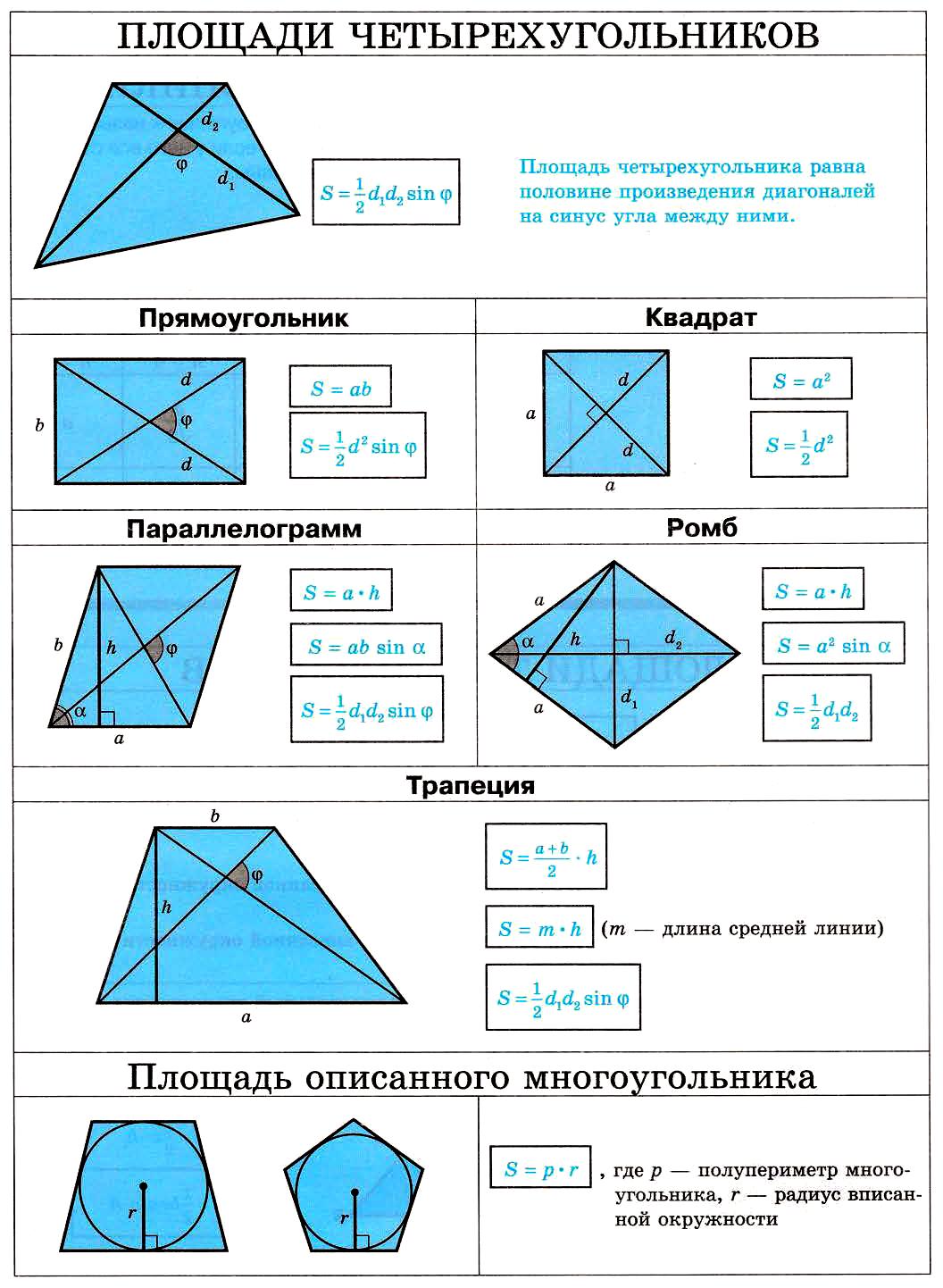
Площади четырехуголников
— площадь любого четырехугольника, где
•
d1 – первая диагональ
•
d2 – вторая диагональ
•
α – угол между диагоналями
— площадь четырехугольника,
вписанного в окружность (формула Герона), где
•
p – полупериметр четырехугольника
•
a, b, c и d – стороны четырехугольника
S = aha – площадь паралелограмма, где
•
a – основание паралелограмма
•
ha – высота, проведенная к основанию
S = ab sinβ – площадь параллелограмма, где
•
a и b – стороны паралелограмма
•
β – угол между смежными сторонами
S = ab – площадь прямоугольника, где
a и b – стороны квадрата
S = – площадь квадрата, где
a – сторона квадрата
S = aha – площадь ромба, где
•
a – сторона ромба
•
ha – высота, проведенная к стороне
S = – площадь ромба, где
•
a – сторона ромба
•
β – угол между сторонами ромба
Вписанный четырехугольник
Четырехугольник можно вписать в окружность тогда и только
тогда, когда суммы его противоположных углов равны 180.

Описанный четырехугольник
Четырехугольник можно описать вокруг окружности тогда и
только тогда, когда суммы длин его противоположных сторон равны.

DC
+ AB = DA + BC
Теорема о двух секущих
Если из точки, лежащей вне окружности, проведены две секущие,
то произведение одной секущей на ее внешнюю часть равно произведению другой
секущей на ее внешнюю часть:

MAMB = MC
MD
Теорема о касательной и секущей
Если из точки, лежащей вне окружности
проведены касательная и секущая, то квадрат длины касательной равен
произведению секущей на ее внешнюю часть

= MA MB
M
B
Теорема о двух
хордах Если две хорды окружности AB и CD пересекаются в точке S, то
произведение отрезков одной хорды равно произведению отрезков другой хорды. AS SD = CS
SB
D

SD = CS
SB
A
Теорема Менелая

Теорема Чевы
Отрезок, соединяющий вершину треугольника с точкой на
противоположной стороне или ее продолжении, называется чевианой.

Теорема Ван-Обеля

Теорема Стюарта

py
a
Теорема
Птолемея
Если
четырехугольник вписан в окружность, то
 AB
AB + AD
+ AD = AC
= AC
Теорема Аполлония
A
Если AD – медиана треугольника ABC, то
Желаем вам успехов!
Слайд 1
Разбор типовых заданий ЕГЭ по математике базового уровня Геометрия
Слайд 2
Прикладная геометрия 1. Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота h1 перил равна 1,25 м, а наибольшая высота h2 равна 2,25 м. Ответ дайте в метрах. ! Алгоритм выполнения Определить, что за фигура на рисунке. Вспомнить определение средней линии трапеции. Записать формулу для нахождения средней линии трапеции. Подставить данные. Вычислить среднюю линию трапеции.
Слайд 3
2. План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м х 1 м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах. ! Алгоритм выполнения Определить что за фигура на рисунке. Записать формулу нахождения площади данной фигуры. Определить по чертежу все необходимые данные. Вычислить площадь участка.
Слайд 4
3. План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м х 1 м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах. ! Алгоритм выполнения Определить что за фигура на рисунке. Записать формулу нахождения площади данной фигуры. Определить по чертежу все необходимые данные. Вычислить площадь участка.
Слайд 5
4. Дачный участок имеет форму прямоугольника со сторонами 25 метров и 30 метров. Хозяин планирует обнести его забором и разделить таким же забором на две части, одна из которых имеет форму квадрата. Найдите суммарную длину забора в метрах . ! Алгоритм выполнения Вычислить периметр прямоугольника. Прибавить длину разделяющей части. P = 30 м + 30 м + 25 м + 25 м = 110 м. 110 м – длина забора без перегородки. Прибавим длину разделяющей части. По рисунку видно, что длина разделяющей части 25 м. 110 м + 25 м = 135 м.
Слайд 6
5. Какой угол (в градусах) образуют минутная и часовая стрелки в 16:00? ! Алгоритм выполнения Сначала мы найдем, сколько в градусах занимает один час. Затем найдем угол, который образуют стрелки в 16:00 Так как вся окружность — 360°, а часов 12, то один час: 360° : 12 = 30° Значит, в четыре часа угол будет равен: 30° • 4 = 120°
Слайд 7
6. Пожарную лестницу длиной 10 м приставили к окну дома. Нижний конец лестницы отстоит от стены на 6 м. На какой высоте находится верхний конец лестницы? Ответ дайте в метрах. ! Алгоритм выполнения Приставленная к стене лестница образует с этой стеной и горизонтальной площадкой возле дома прямоугольный треугольник. Высота, на которой находится верхний конец лестницы, является одним из катетов этого треугольника. Следовательно, для нахождения ее величины нужно использовать теореме Пифагора.
Слайд 8
7. Дачный участок имеет форму прямоугольника, стороны которого равны 35 и 45 м. Дом, расположенный на участке, имеет на плане форму квадрата со стороной 7 м. Найдите площадь оставшейся части участка, не занятой домом. Ответ дайте в квадратных метрах. ! Алгоритм выполнения Находим площадь прямоугольного участка. Находим площадь квадратного дома. Находим разность этих площадей, отняв от большего числа меньшее. 35 · 45 = 1575 ( кв.м ) – площадь всего участка 7 · 7 = 49 ( кв.м ) – площадь дома 1575 – 49 = 1526 ( кв.м ) – площадь оставшейся части участка
Слайд 9
8. На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 5 м? ! Алгоритм выполнения Рассматриваем 2 подобных треугольника. В первом стороны образуют линия фонаря и расстояние от его основания до верхней точки тени от человека. Во втором – линия роста человека и линия его тени. Поскольку треугольники подобны, то можем соотнести соответствующие стороны и оставить из этих отношений пропорцию. Из полученной пропорции выражаем искомую величину. Вычисляем ее. Обозначим искомое расстояние через х . Из рисунка имеем 2 треугольника. Один (больший) построен на сторонах 5 м и ( х +9) м. Другой (меньший) – 1,8 м и 9 м. Составим пропорцию из отношений соответствующих сторон этих треугольников: 5 : 1,8 = ( х + 9) : 9. Из пропорции получим: 5 · 9 = 1,8 · ( х + 9) 1,8 х + 16,2 = 45 1,8 х = 28,8 х = 16 (м)
Слайд 10
Наглядная стереометрия 9. Вода в сосуде цилиндрической формы находится на уровне h = 80 см. На каком уровне окажется вода, если ее перелить в другой цилиндрический сосуд, у которого радиус основания в 4 раза больше, чем у данного? Ответ дайте в сантиметрах. ! Алгоритм выполнения: Записать формулу объема цилиндра. Подставить значения для цилиндра с жидкостью в первом и во втором случае. Объем жидкости не изменялся, следовательно, можно приравнять объемы. Полученное уравнение решить относительно второй высоты h 2 . Подставить данные и вычислить искомую величину. V 1 = π r 1 2 h 1 V 2 = π r 2 2 h 2 Объем жидкости не изменялся, следовательно, можно приравнять объемы. V 1 = V 2 π r 1 2 h 1 = π r 2 2 h 2 h 2 =( π r 1 2 h 1 )/ π r 2 2 По условию площадь основания стала в 4 раза больше, то есть r 2 = 4 r 1 . Подставим r 2 = 4 r 1 в выражение для h 1. Получим: h 2 =( π r 1 2 h 1 )/ π (4 r 1 ) 2 Полученную дробь сократим на π, получим h 2 =( r 1 2 h 1 )/ 16 r 1 2 Полученную дробь сократим на r 1 , получим h 2 = h 1 / 16. Подставим известные данные: h 2 = 80/ 16 = 5 см. Ответ: 5.
Слайд 11
10. Даны две коробки, имеющие форму правильной четырёхугольной призмы. Первая коробка в четыре с половиной раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой коробки меньше объёма второй? ! Алгоритм выполнения: Записать формулу, для вычисления объема правильной четырехугольной призмы. Записать в общем виде формулу для нахождения объема в первом и втором случае. Найти отношение объемов. Преобразовать полученное выражение с учетом соотношения измерений первой и второй призмы. Сократить получившуюся дробь. V 1 = a 1 · b 1 · c 1 V 2 = a 2 · b 2 · c 2 Найдем отношение объемов. V 1 / V 2 = (a 1 · b 1 · c 1 )/ ( a 2 · b 2 · c 2 ) По условию c 1 = 4,5 c 2 (первая коробка в четыре с половиной раза выше второй), b 2 = 3 b 1 (вторая коробка втрое шире первой). Так как это правильные четырехугольные призмы, то в основании лежит квадрат, а значит глубина второй коробки тоже втрое больше глубины первой, то есть a 2 = 3 a 1 Подставим эти выражения в формулу отношения объемов: V 1 / V 2 = (a 1 · b 1 · c 1 )/ ( a 2 · b 2 · c 2 ) = (a 1 · b 1 · 4,5c 2 )/ ( 3a 1 · 3b 1 · c 2 ) = (a 1 · b 1 · 4,5c 2 )/ ( 9a 1 · b 1 · c 2 ) Сократим получившуюся дробь на a 1 · b 1 · c 2 . Получим: V 1 / V 2 = (a 1 · b 1 · 4,5c 2 )/ ( 9a 1 · b 1 · c 2 ) = 4,5/9 = ½. Объем первой коробочки в 2 раза меньше объема второй. Ответ: 2.
Слайд 12
11. От деревянного кубика отпилили все его вершины (см. рис.). Сколько граней у получившегося многогранника (невидимые ребра на рисунке не изображены)? ! Сначала вспомним сколько всего граней и вершин у куба: шесть граней и восемь вершин. Теперь на месте каждой вершины образуется новая грань после отпила, значит у модифицированного в задании куба шесть родных граней и восемь новых (после отпила). Итого получаем: 6 + 8 = 14 граней. Ответ: 14. Если бы нас спросили, а сколько вершин у нового «куба». Очевидно, если вместо одной становится три, а их всего восемь, то получаем: 8 • 3 = 24
Слайд 13
12. Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6, а второго – 6 и 4. Во сколько раз объем второго цилиндра больше объема первого? ! Алгоритм выполнения Записываем ф- лу для вычисления объема цилиндра. Вводим обозначения для радиуса основания и высоты 1-го цилиндра. Выражаем подобным образом аналогичные параметры 2-го цилиндра. Формируем формулы для объема 1-го и 2-го цилиндров. Вычисляем отношение объемов. V 1 =πR 1 2 H 1 , V 2 =πR 2 2 H 2 .
Слайд 14
13. В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке поднялся в 1,4 раза. Найдите объем детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров. ! Алгоритм выполнения Вводим обозначения для объема до погружения детали и после. Пусть это будет соответственно V 1 и V 2 . Фиксируем значение для V 1 . Выражаем V 2 через V 1 . Находим значение V 2 . Переводим результат, полученный в литрах, в куб.см . Объем бака до погружения V 1 =5 (л). Т.к. после погружения детали объем стал равным V 2 . Согласно условию, увеличение составило 1,4 раза, поэтому V 2 =1,4 V 1 . Отсюда получаем: V 2 =1,4·5=7 (л). Т.о ., разница объемов, которая и составляет объем детали, равна: V 2 –V 1 =7–5=2 (л). 2 л=2·1000=2000 ( куб.см ).
Слайд 15
14. В сосуде, имеющем форму конуса, уровень жидкости достигает ½ высоты. Объем сосуда 1600 мл. Чему равен объем налитой жидкости? Ответ дайте в миллилитрах. ! Алгоритм выполнения Доказываем, что данные в условии конусы подобны. Определяем коэффициент подобия. Используя свойство для объемов подобных тел, находим объем жидкости. Если рассматривать сечение конуса по двум его противоположно расположенным образующим (осевое сечение), то видим, что полученные таким способом треугольники большого конуса и малого (образованного жидкостью) подобны. Это следует из равенства их углов. Т.е. имеем: у конусов подобны высоты и радиусы основания. Отсюда делаем вывод: т.к. линейные параметры конусов подобны, то и конусы подобны. По условию высота малого конуса (жидкости) составляет ½ высоты конуса. Значит, коэффициент подобия малого и большого конусов равен ½. Применяем св -во подобия тел, которое заключается в том, их объемы относятся как коэффициет подобия в кубе. Обозначим объем большого конуса V 1 , малого – V 2 . Получим: Поскольку по условию V 1 =1600 мл, то V 2 =1600/8=200 мл.
Слайд 16
15. Даны два шара с радиусами 4 и 1. Во сколько раз объем большего шара больше объема меньшего? ! Алгоритм выполнения Записываем формулу для вычисления объема шара. Адаптируем формулу для каждого из шаров. Для этого используем индексы 1 и 2. Записываем отношение объемов, вычисляем его, подставив числовые данные из условия. Вывод: объем большего шара в 64 раза больше.
Слайд 17
16. Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 4 и 18, а второго – 2 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго? ! Алгоритм выполнения Записываем формулу для определения площади бок.поверхности цилиндра. Переписываем ее дважды с использованием соответствующих индексов – для 1-го (большего) и 2-го (меньшего) цилиндров. Находим отношение площадей. Вычисляем отношения, используя числовые данные из условия. Вывод: площадь боковой поверхности 1-го цилиндра больше в 12 раз.
Слайд 18
17. Однородный шар диаметром 3 см весит 162 грамма. Сколько граммов весит шар диаметром 2 см, изготовленный из того же материала? ! Алгоритм выполнения Записываем формулу для определения массы большего шаров через плотность и объем. Объем в этой формуле расписываем через ф- лу объема шара (через его радиус). Записываем ф- лу для массы меньшего шара, расписываем объем через радиус (по аналогии с пп.1 и 2). Поскольку оба шара изготовлены из одного и того же материала, то найденное значение для плотности можем использовать в ф- ле для массы меньшего шара. Вычисляем искомую массу. m 1 = ρ V 1 . V 1 = (4/3)π R 1 3 . Отсюда получаем: m 1 =(4/3)πρ R 1 3 . m 2 =ρ V 2 V 2 =(4/3)π R 2 3
Слайд 19
Планиметрия. №15 18 . В треугольнике ABC угол ACB равен 90°, cos A = 0,8, AC = 4. Отрезок CH – высота треугольника ABC(см. рисунок). Найдите длину отрезка AH . ! Алгоритм выполнения: Вспомнить определение косинуса угла. Записать выражение для нахождения косинуса угла. Выразить неизвестную величину. Вычислить. cos A = АН/АС. АН = АС · cos A АН = АС · cos A = 4 · 0,8 = 3,2 Ответ: 3,2.
Слайд 20
19. Найдите вписанный угол, опирающийся на дугу, длина которой равна 5/18 длины окружности. Ответ дайте в градусах. ! Алгоритм выполнения: Вспомнить соотношение величины вписанного угла и градусной меры угла, на который он опирается. Вычислить градусную меру угла, на который опирается дуга. Вычислить вписанный угол. Весь круг составляет 360°, а 5/18 от его длины это Так как вписанный угол равен половине градусной меры дуги, на которую он опирается, вписанный угол равен 100°:2 = 50°. Ответ: 50.
Слайд 21
20.В треугольнике АВС известно, что АВ=ВС=15, АС=24. Найдите длину медианы ВМ ! Алгоритм выполнения Определяем вид треугольника. Доказываем, что медиана ВМ является и высотой. Из прямоугольного треугольника АМВ по т. Пифагора находим медиану ВМ. Если АВ=ВС, то ∆АВС – равнобедренный. Т.к. АМ медиана, то AM=АС:2=24:2=12.
Слайд 22
21. На стороне ВС прямоугольника АВСD, у которого АВ=12 и АD=17, отмечена точка Е так, что треугольник АВЕ равнобедренный. Найдите ЕD. ! Алгоритм выполнения Находим ЕС. Определяем значение СD. Из прямоугольного треугольника АСD по т.Пифагора находим ЕD. Т.к. по условию ∆АВЕ равнобедренный, то ВЕ=АВ=12. Т.к. АВСD прямоугольник, то ВС=АD=17, СD=АВ=12. ЕС=ВС–ВЕ=17–12=5. ∆ЕСD прямоугольный. Тогда по т.Пифагора ЕD 2 =ЕC 2 +СD 2 .
Слайд 23
22. В треугольнике АВС угол С равен 90 0 , АВ=25, АС=24. Найдите cos B. ! Алгоритм выполнения По т.Пифагора находим величину катета ВС. По формуле-определению для косинуса находим cos B как отношение прилежащего катета к гипотенузе. Из прямоугольного ∆АВС по теореме Пифагора имеем: АВ 2 =АС 2 +ВС 2 .
Слайд 24
23. В равнобедренном треугольнике АВС боковая сторона АВ=25, sin A=3/5. Найдите площадь треугольника АВС. ! Алгоритм выполнения Из вершины В проводим высоту BD к основанию ∆АВС. Получаем прямоугольного ∆ADB. Из ∆ADB находим катет ВD, используя sin A. Находим АD из ∆ADB по т.Пифагора . Далее определяем АС как 2AD. Находим площадь ∆АВС по формуле S= ah /2 . В ∆ ADB sin A=BD/AB → BD = AB · sin A = 25 · 3 / 5 = 15. Из ∆ ADB по т.Пифагора имеем: AB 2 =AD 2 +BD 2 АС=2АD=2·20=40.
Слайд 25
24. В треугольнике АВС угол В равен 120 0 . Медиана ВМ делит угол В пополам и равна 27. Найдите длину стороны АВ. ! Алгоритм выполнения Определяем величину угла АВМ. Доказываем, что ∆АМВ прямоугольный. Находим АВ, используя формулу-определение для косинуса. По условию угол АВМ равен половине угла В. Значит, угол АВМ составляет 120 0 :2=60 0 . Т.к. ВМ – медиана, опущенная на основание равнобедренного ∆АВС, то ВМ является и высотой. Поэтому ∆АМВ прямоугольный с прямым углом АМВ.
Слайд 26
25. В равнобедренном треугольнике АВС медиана ВК=10, боковая сторона ВС=26. Найдите длину отрезка МN, если известно, что он соединяет середины боковых сторон. ! Алгоритм выполнения Доказываем, что ∆АКВ прямоугольный. Из ∆АКВ по т.Пифагора находим АК. Находим АС как 2АК. Находим МN как среднюю линию. Из прямоугольного ∆АКВ по т.Пифагора АВ 2 =АК 2 +ВК 2 . Поскольку ВК медиана, то АС=2АК=2·24=48. Значит, MN=AC:2=48:2=24.
Слайд 27
26. В треугольнике АВС высота АС=56, ВМ – медиана, ВН – высота, ВС=ВМ. Найдите длину отрезка АН. ! Алгоритм выполнения Находим длину отрезков АМ и МС как половину от АС. Доказываем, что ВН является медианой в ∆МВС. Отсюда определяем, что МН – половина от МС. 3. Находим АН как сумму АМ и МН. Рассмотрим ∆АВС. Т.к. ВМ медиана, то АМ=МС=АС/2=56/2=28. МН=НС=МС/2=28/2=14. АН=АМ+МН=28+14=42.
Слайд 28
Стереометрия (№16) 27. Радиус основания цилиндра равен 13, а его образующая 18. Сечение, параллельное оси цилиндра, удалено от нее на расстояние, равное 12. Найдите площадь этого сечения. ! Алгоритм выполнения: Определить тип фигуры, образующей сечение. Записать формулу для нахождения площади фигуры, образующей сечение. Вычислить недостающие данные. Вычислить искомую площадь сечения. Сечение является прямоугольником, одна из сторон которого образующая цилиндра. Длина прямоугольника – 18, из условия. Осталось вычислить ширину. Сделаем дополнительный чертеж цилиндра сверху :
Слайд 29
Ширина прямоугольника – CD. По условию «Сечение, параллельное оси цилиндра, удалено от нее на расстояние, равное 12». Расстояние от точки до прямой – это длина перпендикуляра, проведенного из этой точки на прямую. То есть на чертеже АВ = 12. СD = СВ + ВD. СВ = ВD Рассмотрим треугольник ВСА. Треугольник ВСА – прямоугольный. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. В данном случае СА 2 = СВ 2 + АВ 2 СВ 2 — неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое. СВ 2 = СА 2 — АВ 2 СВ = √(СА 2 — АВ 2 ) СВ = √(13 2 — 12 2 ) = √(169 — 144) = √25 = 5 Для решения задачи необходимо знать СD = СВ + ВD = 5 + 5 = 10 Вычислим искомую площадь сечения. 10 · 18 = 180 Ответ: 180.
Слайд 30
29. Стороны основания правильной треугольной пирамиды равны 24, а боковые рёбра равны 37. Найдите площадь боковой поверхности этой пирамиды. ! Алгоритм выполнения: Проанализировать какие данные необходимо вычислить для ответа на вопрос задачи. Найти площади треугольников. Найти площадь боковой поверхности пирамиды. В основании правильной треугольной пирамиды лежит равносторонний треугольник. Боковые ребра пирамиды, равные 37, образуют три равнобедренных треугольника, которые составляют ее боковую поверхность. Найдем площади треугольников. Так как треугольник равнобедренный, AH=AC:2=24:2=12. Р/м треугольник АВН. АВ 2 = ВН 2 + АН 2 . ВН 2 = АВ 2 — АН 2 Боковая поверхность пирамиды состоит из трех треугольников
Слайд 31
30. Найдите объем правильной четырехугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно √17. Вспомним формулу площади правильной пирамиды — одна треть от произведения площади основания и высоты . После этого перейдем к нахождению высоты. Для этого нам необходимо рассмотреть прямоугольный (так как основание перпендикулярно высоте) треугольник AMH. AH — половина диагонали квадрата, которая равна √2 его стороны, то есть в нашем случае диагональ равна 4√2, ну а половина — AH = 2√2. Зная гипотенузу и один из катетов, найдем высоту: V = 1/3 • 16 •3 = 16
Слайд 32
31. Сторона основания правильной треугольной призмы АВСА 1 В 1 С 1 равна 2, а высота этой призмы равна 4√3. Найдите объем призмы АВСА 1 В 1 С 1 . ! Алгоритм выполнения Находим площадь основы призмы через формулу для площади правильного треугольника. Записываем формулу для объема призмы. Подставляем в нее числовые данные, вычисляем искомую величину. Объем призмы: V= Sh
Слайд 33
32. Объем конуса равен 25π, а его высота равна 3. Найдите радиус основания конуса. ! Алгоритм выполнения Записываем формулу для объема конуса. Из нее выражаем площадь основания. Площадь основания расписываем по формуле площади круга, поскольку именно круг лежит в основании конуса. Из этих двух формул выражаем искомую величину. Вычисляем ее. S осн =3 V / h . S = π R 2 Поскольку в данном случае S осн = S , то π R 2 =3 V / h
Слайд 34
33. Два ребра прямоугольного параллелепипеда равны 8 и 5, а объем параллелепипеда равен 280. Найдите площадь поверхности этого параллелепипеда. ! Алгоритм выполнения Записываем формулу для объема прямоугольного параллелепипеда. Из нее выражаем 3-е (неизвестное) ребро. Вычисляем величину этого ребра. Записываем формулу для площади поверхности. Подставляем в него числовые данные, находим искомое значение. Объем прямоугольного параллелепипеда равен: V= abc , где a, b, c – ребра. Будем считать, что a и b нам известны, а с – неизвестно. Тогда: с=V / ( ab ). с=280 /(8·5)=7. Площадь поверхности прямоугольного параллелепипеда вычисляется так: S =2( ab+bc+ac ). Отсюда имеем: S=2(8·5+5·7+8·7)=2(40+35+56)=2·131=262.
Слайд 35
34. Объем конуса равен 24π, а радиус его основания равен 2. Найдите высоту конуса. ! Алгоритм выполнения Записываем формулу для объема конуса. Из нее выражаем высоту. Записываем формулу для площади круга, лежащего в основе конуса. Вычисляем эту площадь. Подставляем числовые данные в формулу для объема, вычисляем искомую величину. Площадь основания (как площадь круга) равна: S осн =π R 2 . Вычисляем площадь: Sосн =π·2 2 =4π.
-
ЕГЭ по математике (база) 2023
- /
- Теория по математике (база)
- /
Теоремы и определения по Планиметрии
Теоремы и определения по Планиметрии. Справочник по геометрии для 7-11 классов, для подготовки к ОГЭ и ЕГЭ. Часть 1 «Планиметрия». Автор: Нелин Е.П. Использованы цитаты из пособия «Геометрия. 7-11 классы. Определения, свойства, методы решения задач в таблицах / М.: Илекса, 2018» из серии «Комплексная подготовка к ЕГЭ и ГИА (ОГЭ). Цитаты использованы в учебных целях.
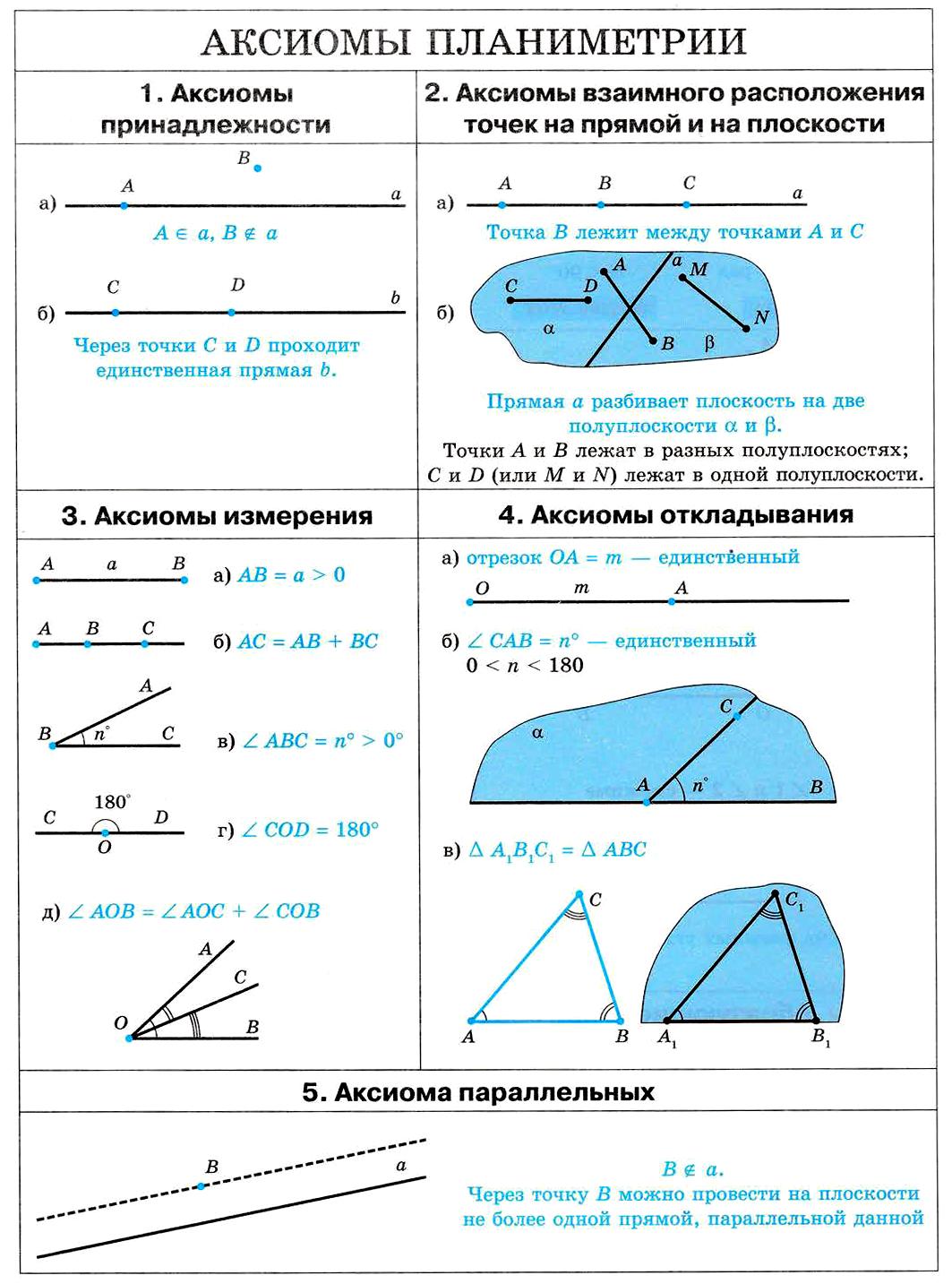
01. Аксиомы планиметрии.
Аксиомы принадлежности. Аксиомы взаимного расположения точек на прямой и плоскости. Аксиомы измерения. Аксиомы откладывания. Аксиома параллельных
02. Углы
Смежные углы. Вертикальные углы. Углы при пересечении
03. Параллельные прямые. Перпендикулярные прямые. Перпендикуляр к прямой
03. Параллельные прямые. Перпендикулярные прямые. Перпендикуляр к прямой
04. Свойства сторон и углов треугольника
Свойства сторон и углов треугольника. Внешний угол. Свойства. Неравенство треугольника. Равнобедренный треугольник
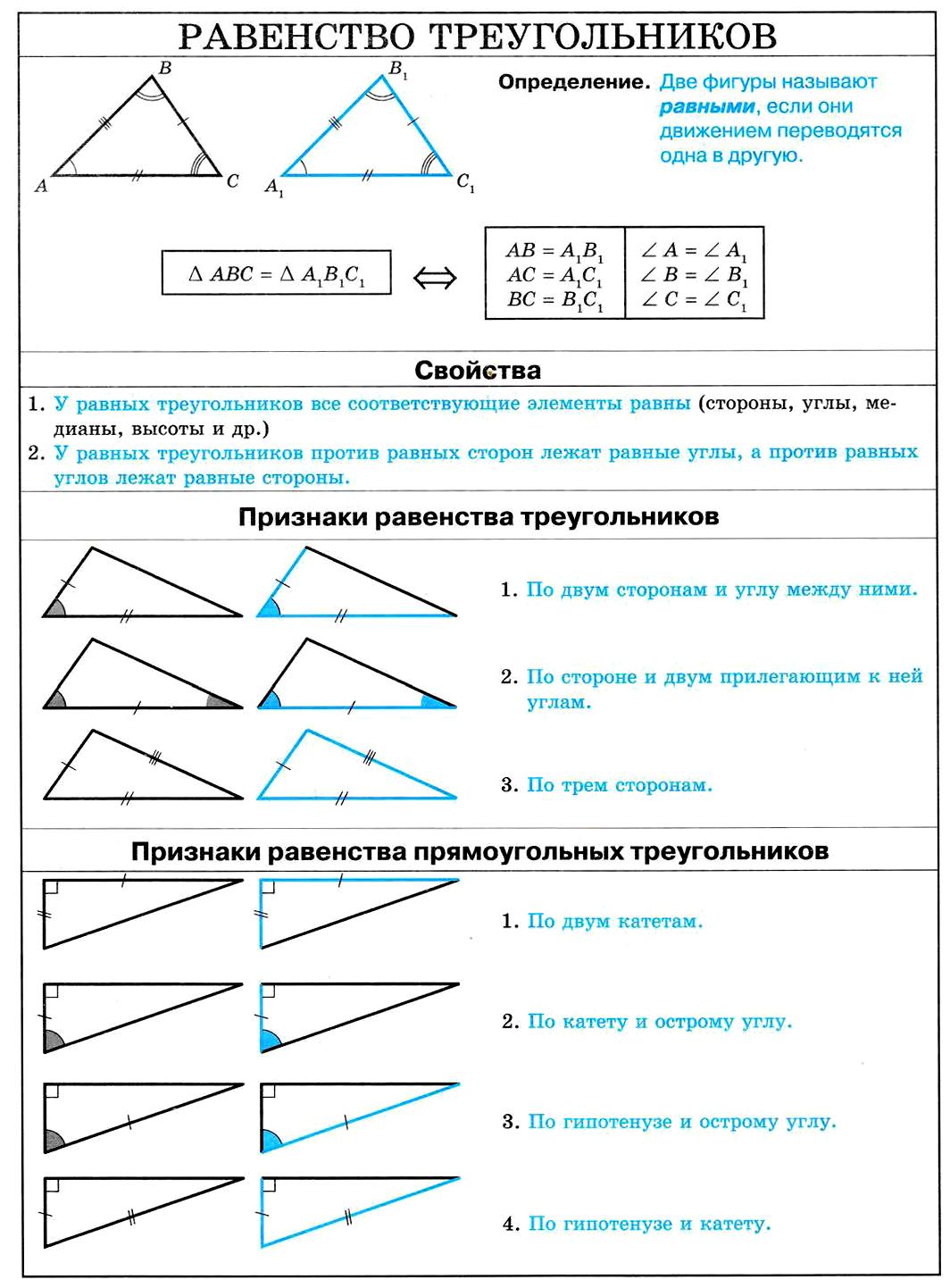
05. Равенство треугольников.
Равенство треугольников. Свойства. Признаки равенства треугольников. Признаки равенства прямоугольных треугольников
06. Медиана треугольника.
Медиана треугольника. Свойства.
07. Биссектриса треугольника.
Биссектриса треугольника. Свойства
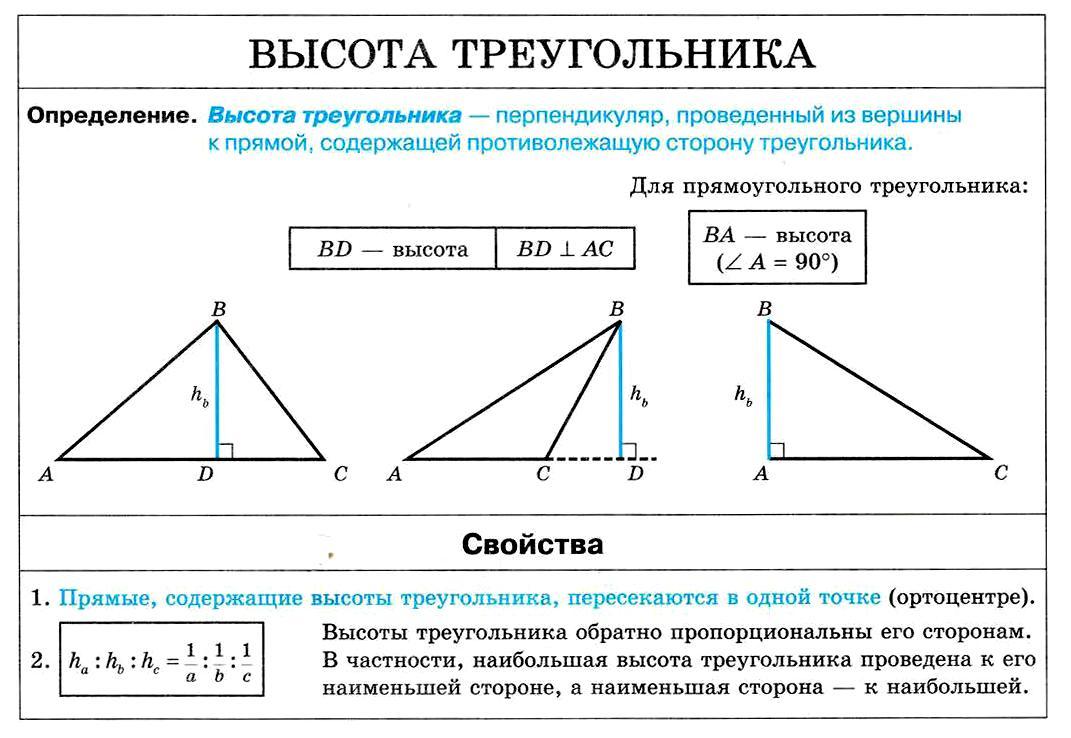
08. Высота треугольника
Высота треугольника. Свойства
09. Средняя линия треугольника
Средняя линия треугольника. Свойства
10. Соотношение между элементами прямоугольного треугольника
Соотношение между элементами прямоугольного треугольника
11. Соотношение между сторонами и углами в произвольном треугольнике
Соотношение между сторонами и углами в произвольном треугольнике
12. Преобразование фигур. Движение
Преобразование фигур. Движение. Симметрия относительно точки. Поворот. Симметрия относительно прямой. Параллельный перенос
13. Преобразование подобия
Преобразование подобия. Свойства. Гомотетия.
14. Подобие треугольников.
Подобие треугольников. Свойства. Признаки подобия треугольников
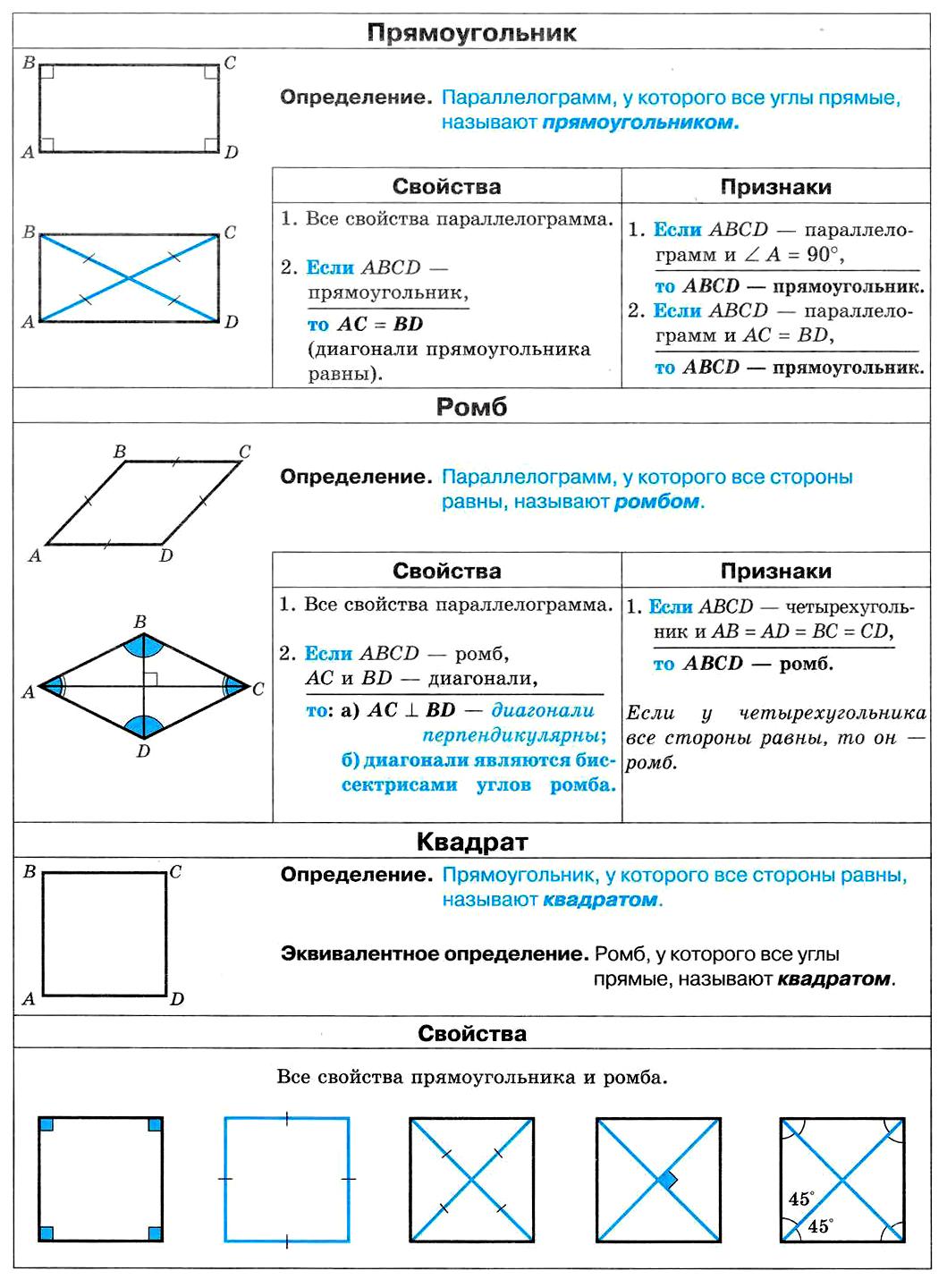
15. Параллелограмм и его виды.
Параллелограмм и его виды. Свойства. Признаки
Прямоугольник. Ромб. Квадрат.
16. Трапеция
Трапеция. Частные случаи трапеции. Средняя линия трапеции. Дополнительные построения для трапеции
17. Окружность, хорды и дуги
Окружность, хорды и дуги. Свойства
18. Окружность. Касательные и секущие.
Окружность. Касательные и секущие.
19. Взаимное расположение прямой и окружности. Взаимное расположение двух окружностей.
Взаимное расположение прямой и окружности. Взаимное расположение двух окружностей.
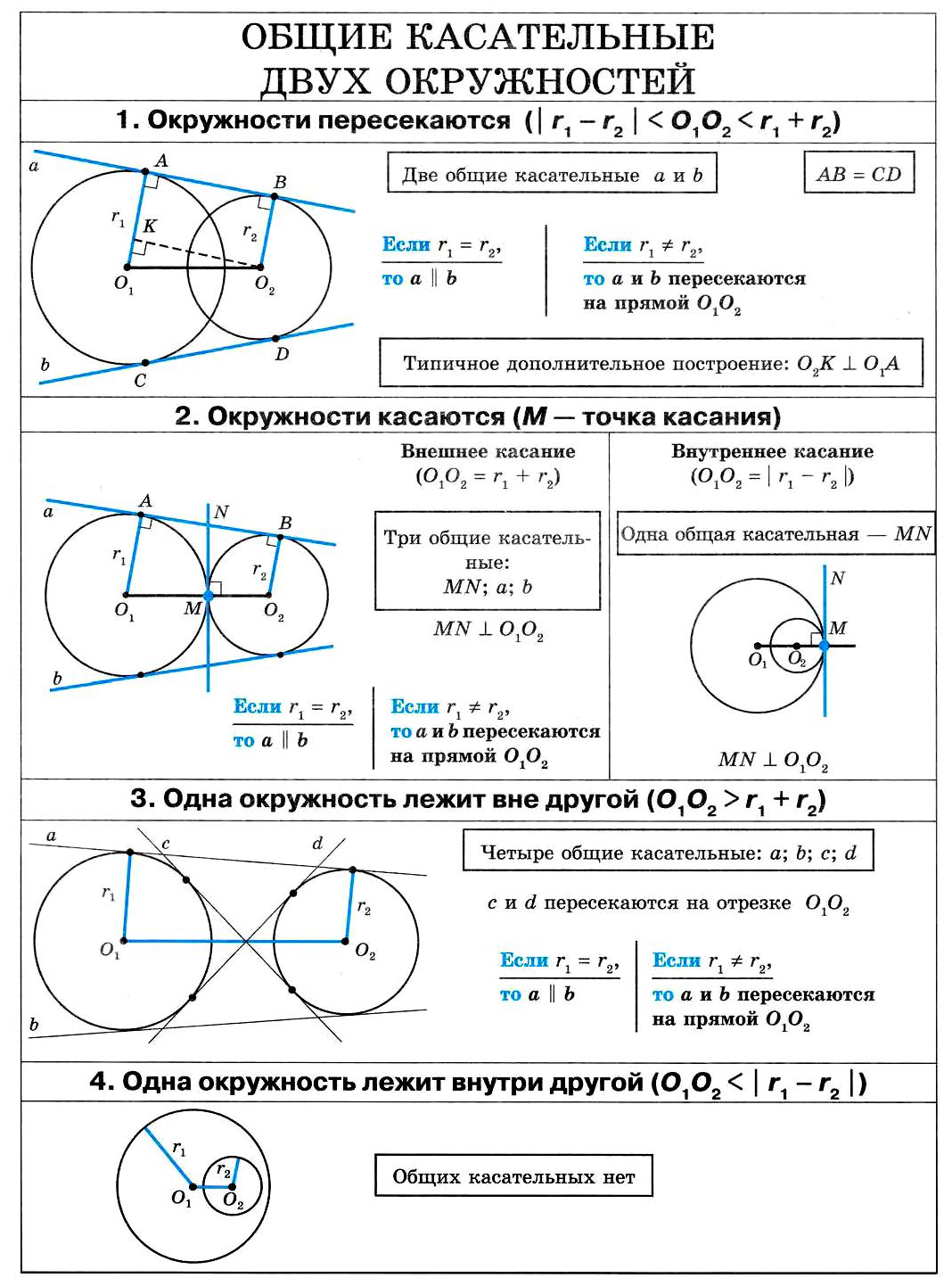
20. Общие касательные двух окружностей.
Общие касательные двух окружностей.
21. Углы в окружности.
Углы в окружности.
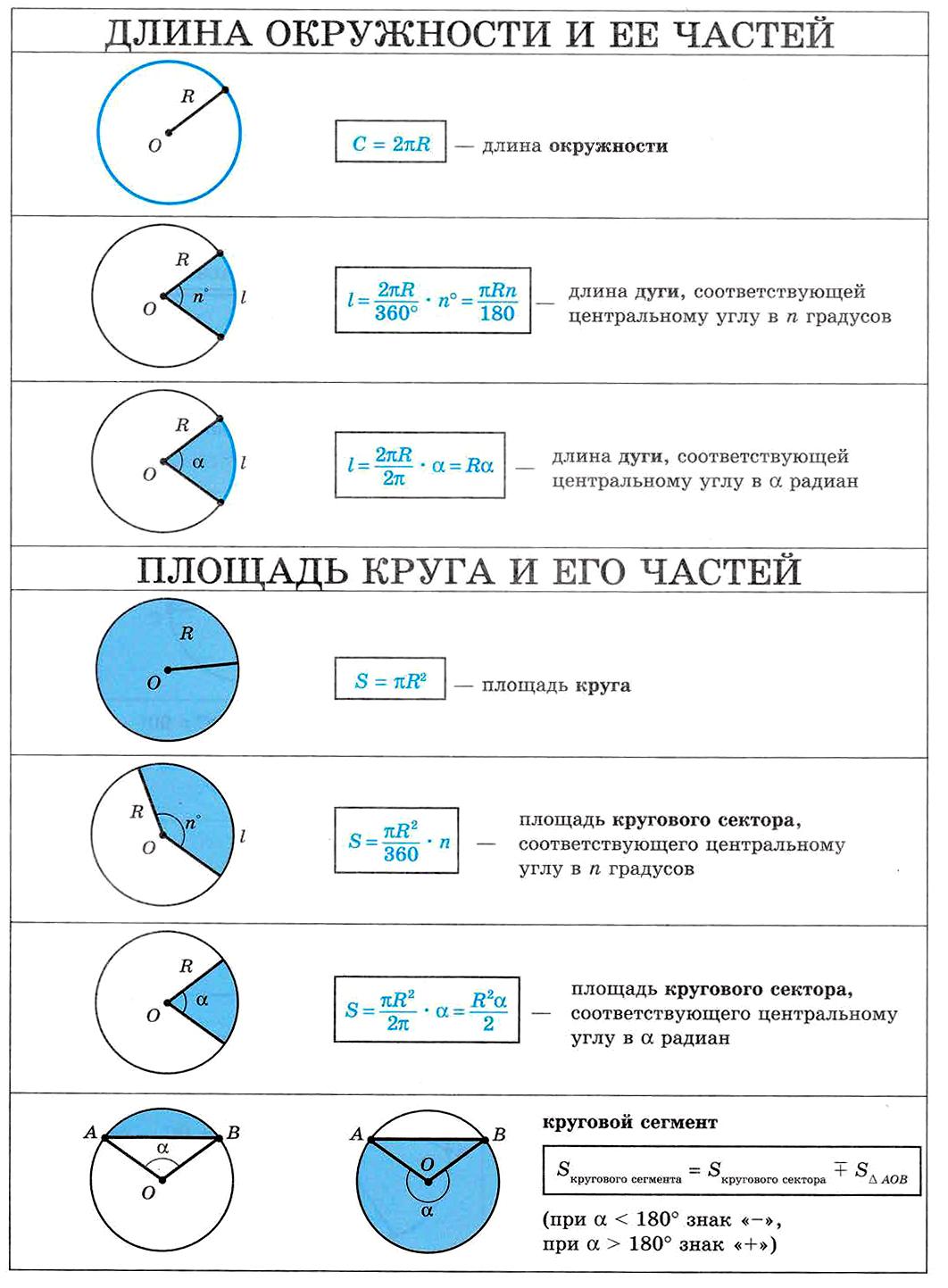
22. Длина окружности и её частей. Площадь круга и его частей
Длина окружности и её частей. Площадь круга и его частей
23. Вписанный и описанный многоугольники. Вписанный и описанный четырехугольники. Прямоугольник. Трапеция и ромб. Квадрат.
Вписанный и описанный многоугольники. Вписанный и описанный четырехугольники. Прямоугольник. Трапеция и ромб. Квадрат.
24. Окружность, описанная около треугольника, и окружность, вписанная в треугольник.
25. Окружности, описанные и вписанные в правильные многоугольники
Окружности, описанные и вписанные в правильные многоугольники
26. Площади треугольников.
Площади треугольников.
27. Площади четырехугольников.
Площади четырехугольников. Площадь описанного многоугольника
Вы смотрели справочник по геометрии для 7-11 классов «Теоремы и определения по Планиметрии».