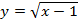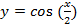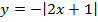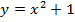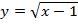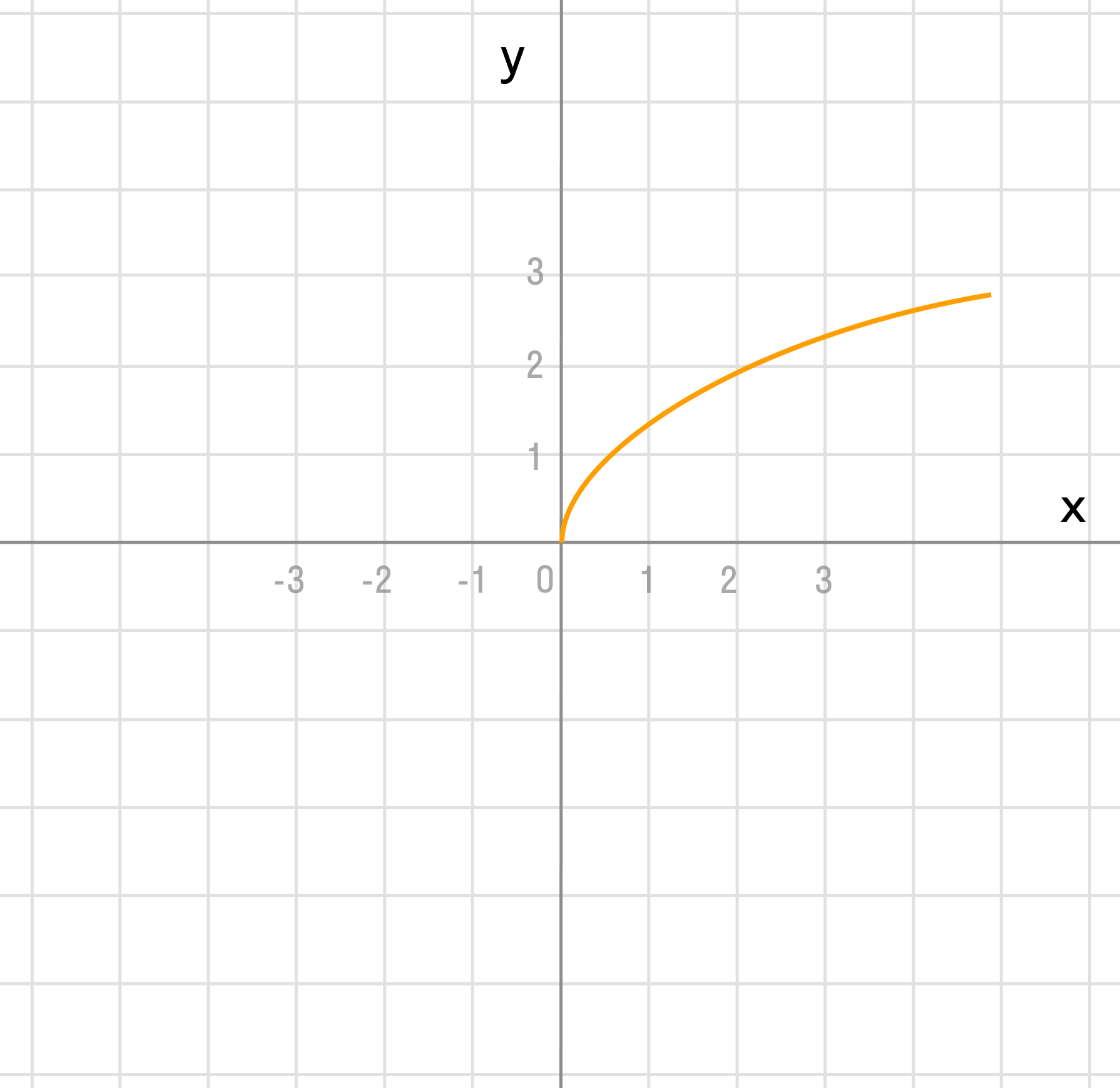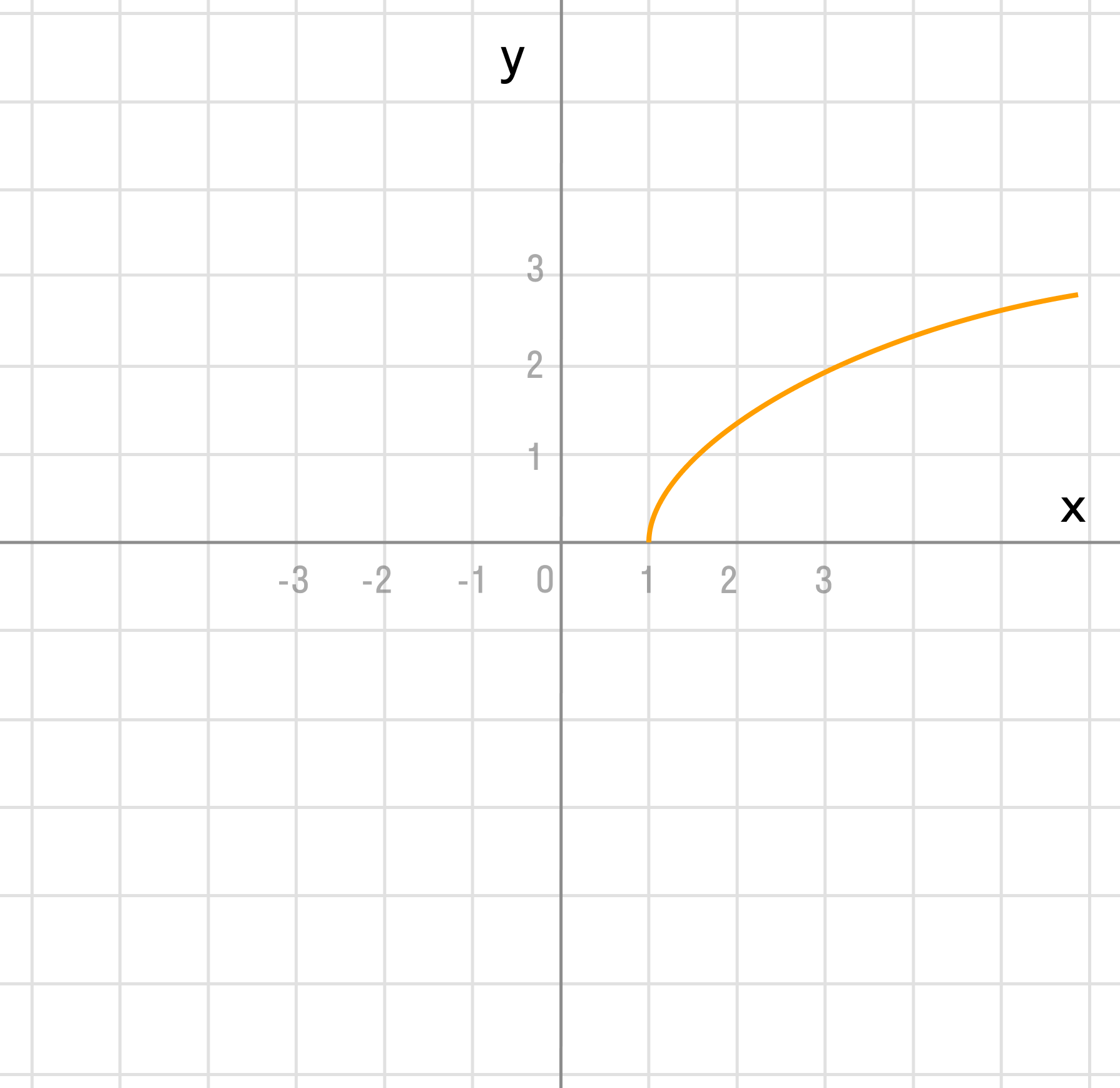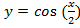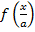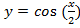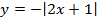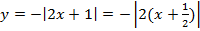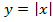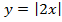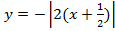Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания,
берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта
готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием
сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом
администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта
и представлены на сайте исключительно для ознакомления. Авторские права на материалы
принадлежат их законным авторам. Частичное или полное копирование материалов сайта без
письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой
зрения авторов.
Понятие функции
Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие значения функции. Вот, какими способами ее можно задать:
-
Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
-
Графический способ — наглядно.
-
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
-
Словесный способ.
Область определения функции — это множество всех допустимых значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.
Например, для функции вида
область определения выглядит так
-
х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): (-∞; 0) ⋃ (0; +∞).
Область значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.
Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): [0; +∞).
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
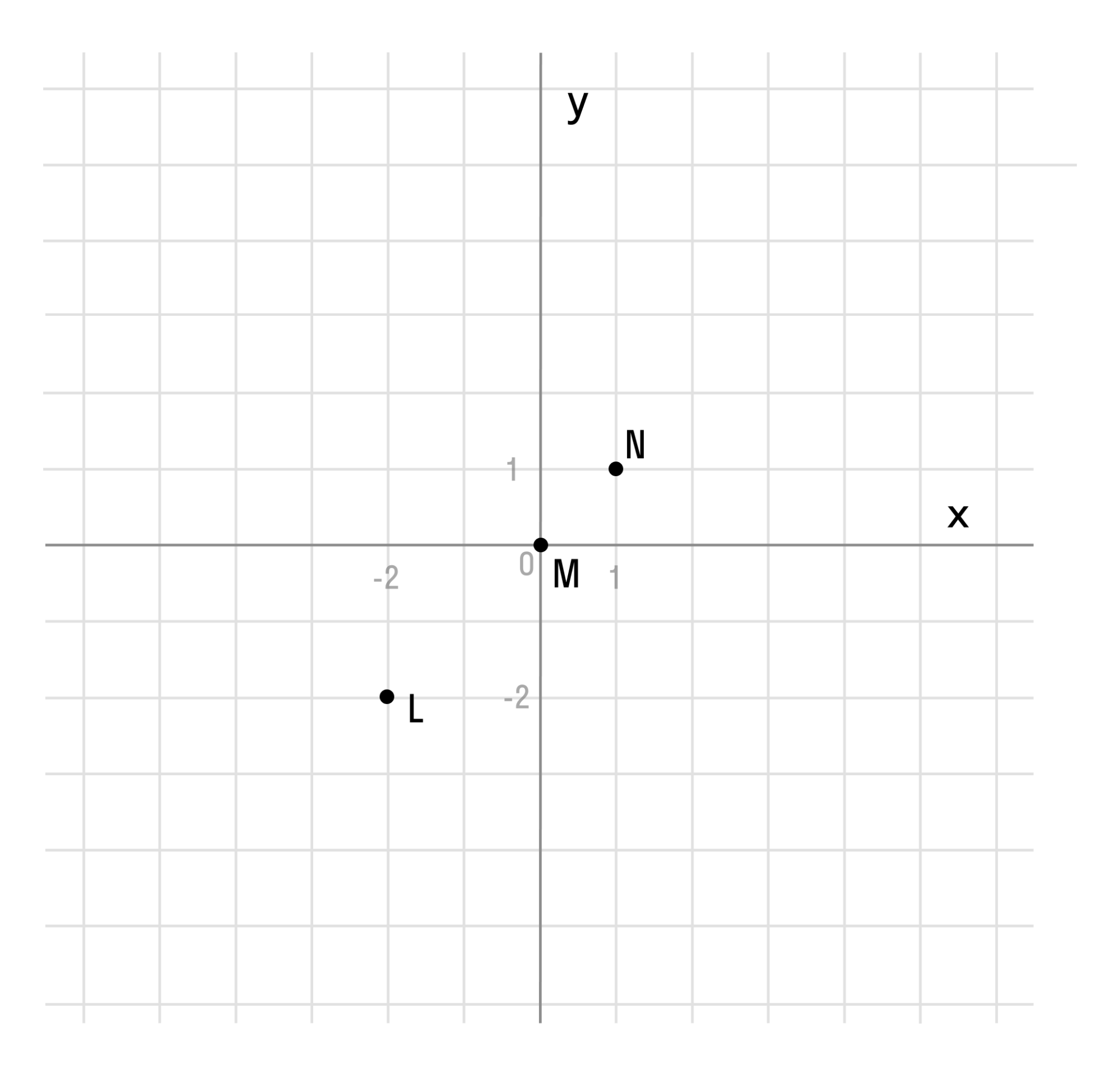
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться при решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Запоминаем!
Не обязательно делать чертеж на целый тетрадный лист, можно выбрать удобный для вас масштаб, который отразит суть задания.
Исследование функции
Важные точки графика функции y = f(x):
-
стационарные и критические точки;
-
точки экстремума;
-
нули функции;
-
точки разрыва функции.
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых значение функции равно нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
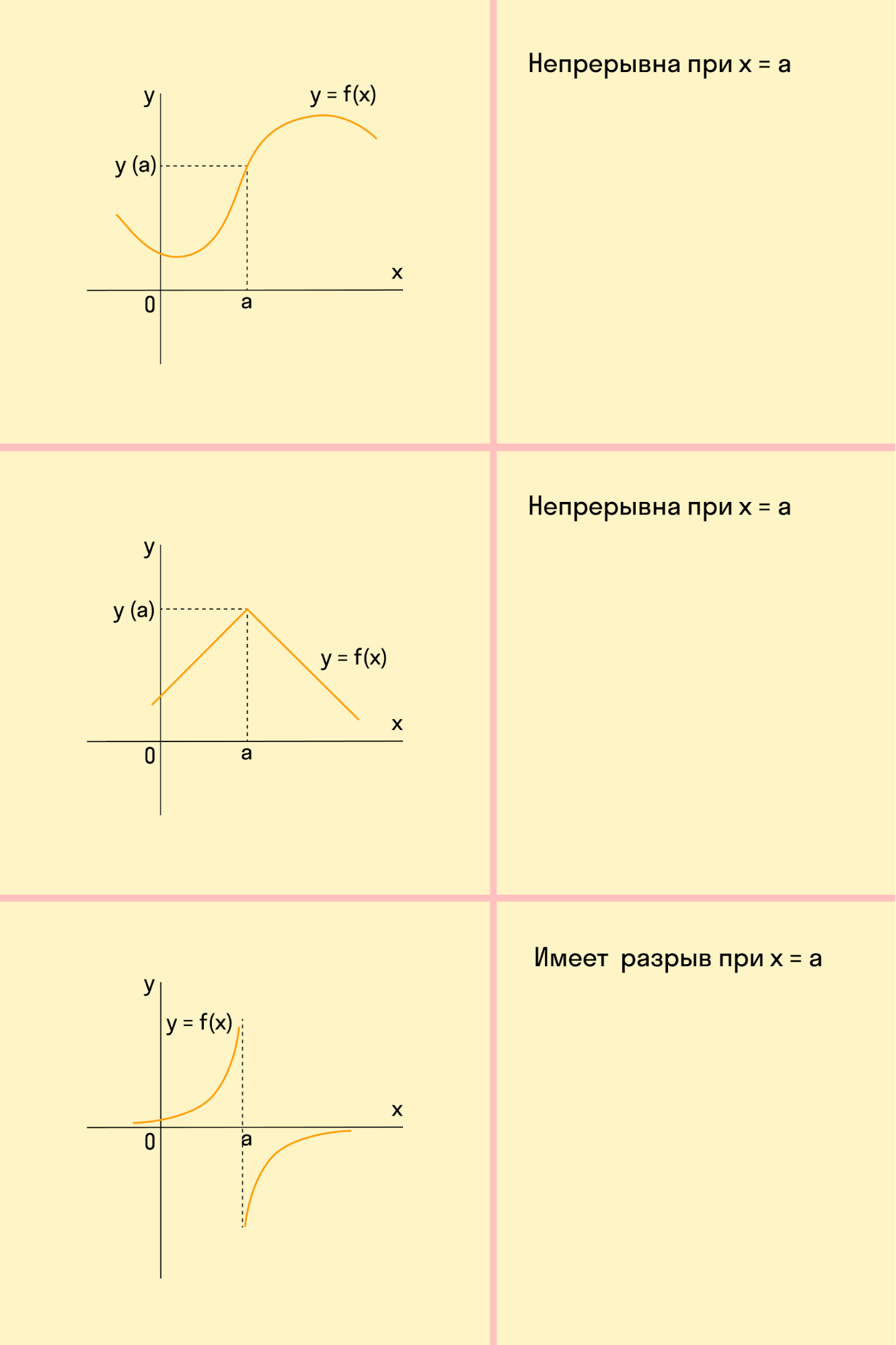
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
-
Найти область определения функции.
-
Найти область допустимых значений функции.
-
Проверить не является ли функция четной или нечетной.
-
Проверить не является ли функция периодической.
-
Найти точку пересечения с осью OY (если она есть).
-
Вычислить производную и найти критические точки, определить промежутки возрастания и убывания.
-
Промежутки знакопостоянства.
-
Асимптоты.
-
На основании проведенного исследования построить график функции.
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах или воспользуйтесь онлайн тренажером.
Задача 1. Построим график функции
Как решаем:
Упростим формулу функции:
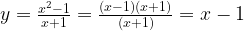
График функции — прямая y = x — 1 с выколотой точкой M (-1; -2).
Задача 2. Построим график функции
Как решаем:
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Задача 3. Построить графики функций:
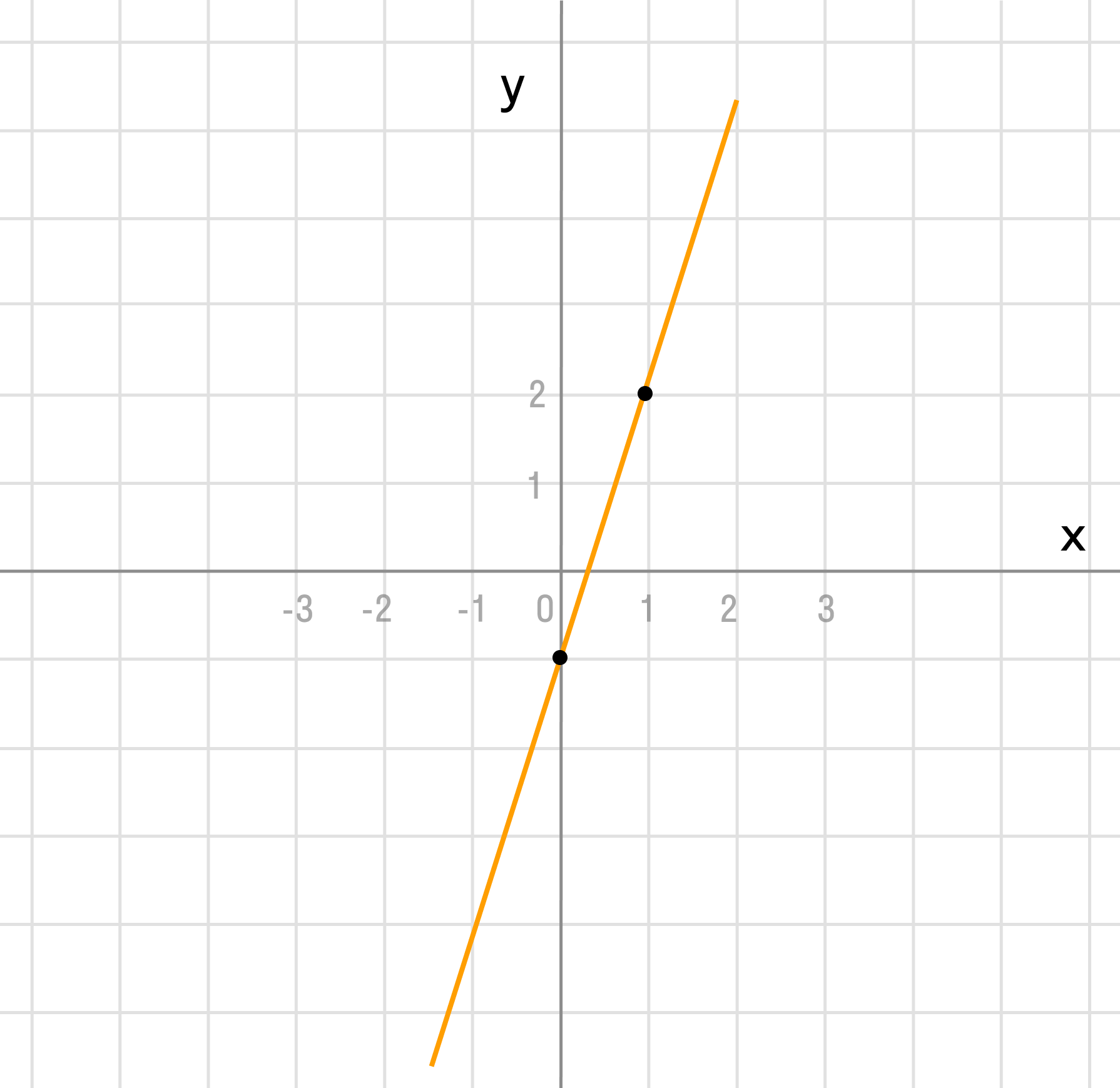
а) y = 3x — 1
б) y = -x + 2
в) y = 2x
г) y = -1
Как решаем:
Воспользуемся методом построения линейных функций «по точкам».
а) y = 3x — 1
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
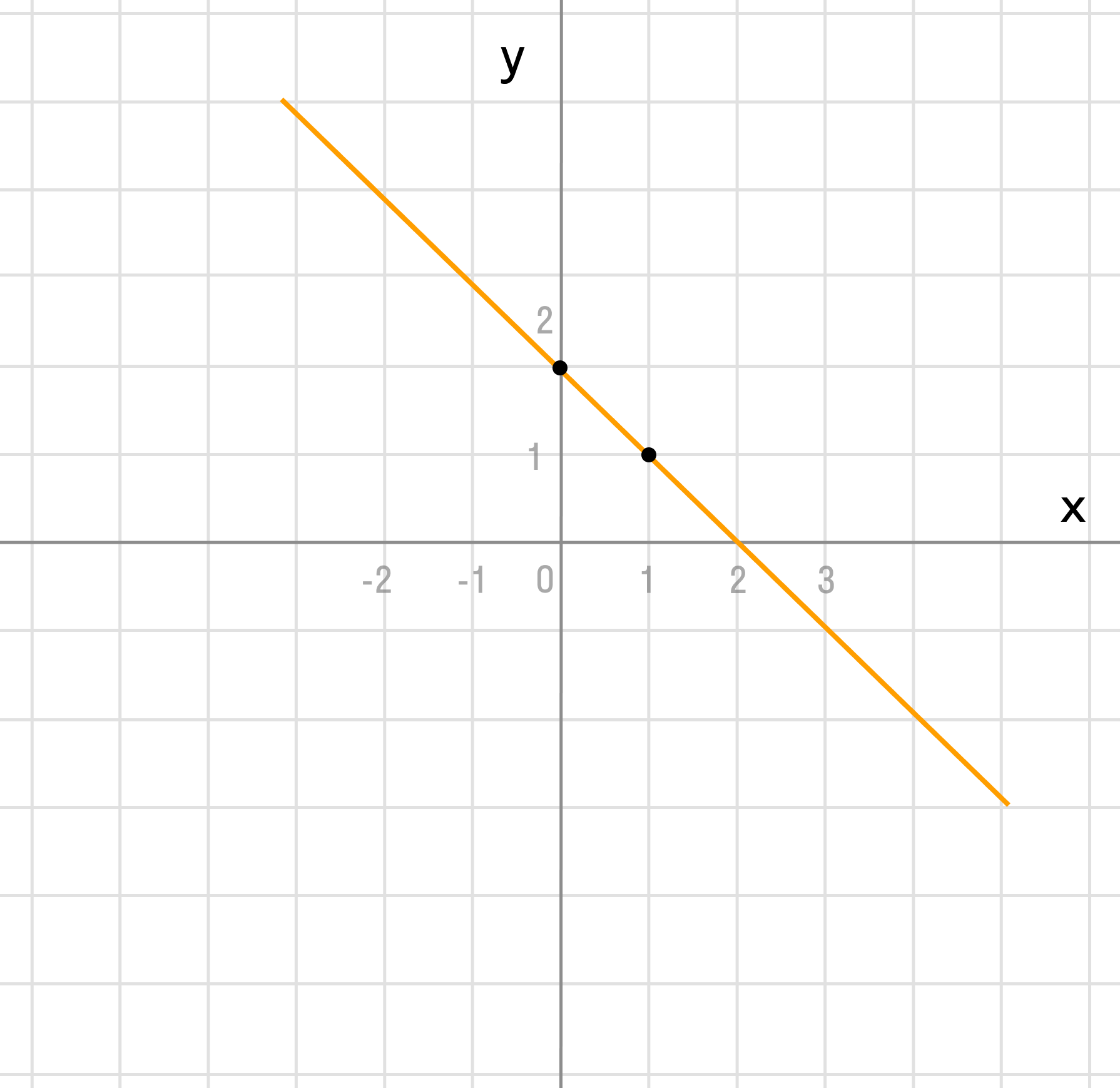
б) y = -x + 2
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
в) y = 2x
k = 2 > 0 — угол наклона к оси Ox острый, b = 0 — график проходит через начало координат.
г) y = -1
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
Задача 4. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Как решаем:
Вспомним, как параметры a, b и c определяют положение параболы.
-
Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины
-
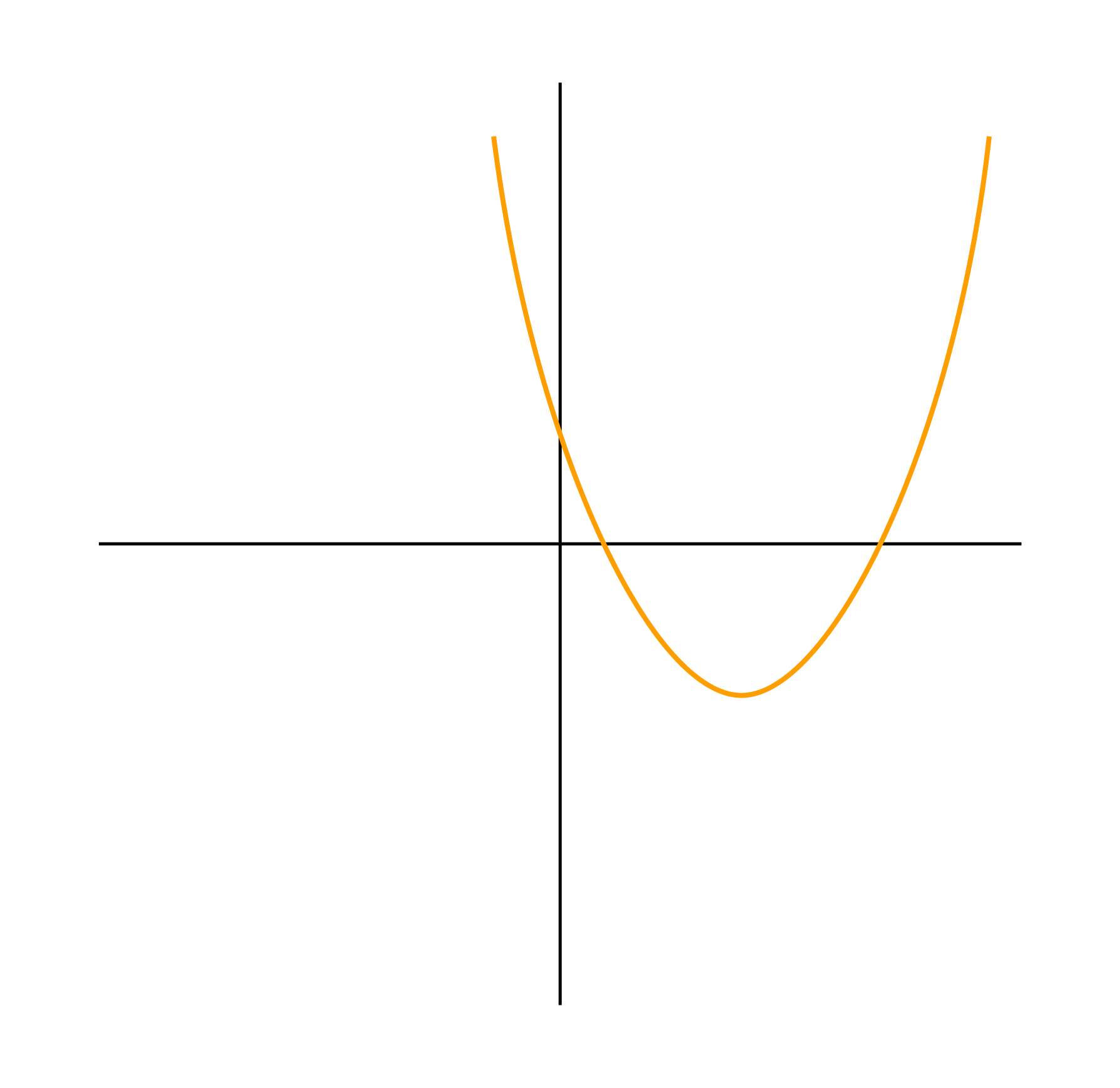
Ветви вверх, следовательно, a > 0.
Точка пересечения с осью Oy — c > 0.
Координата вершины
, т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
-
Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c > 0.
Координата вершины
, т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.
Задача 5. Построить графики функций:
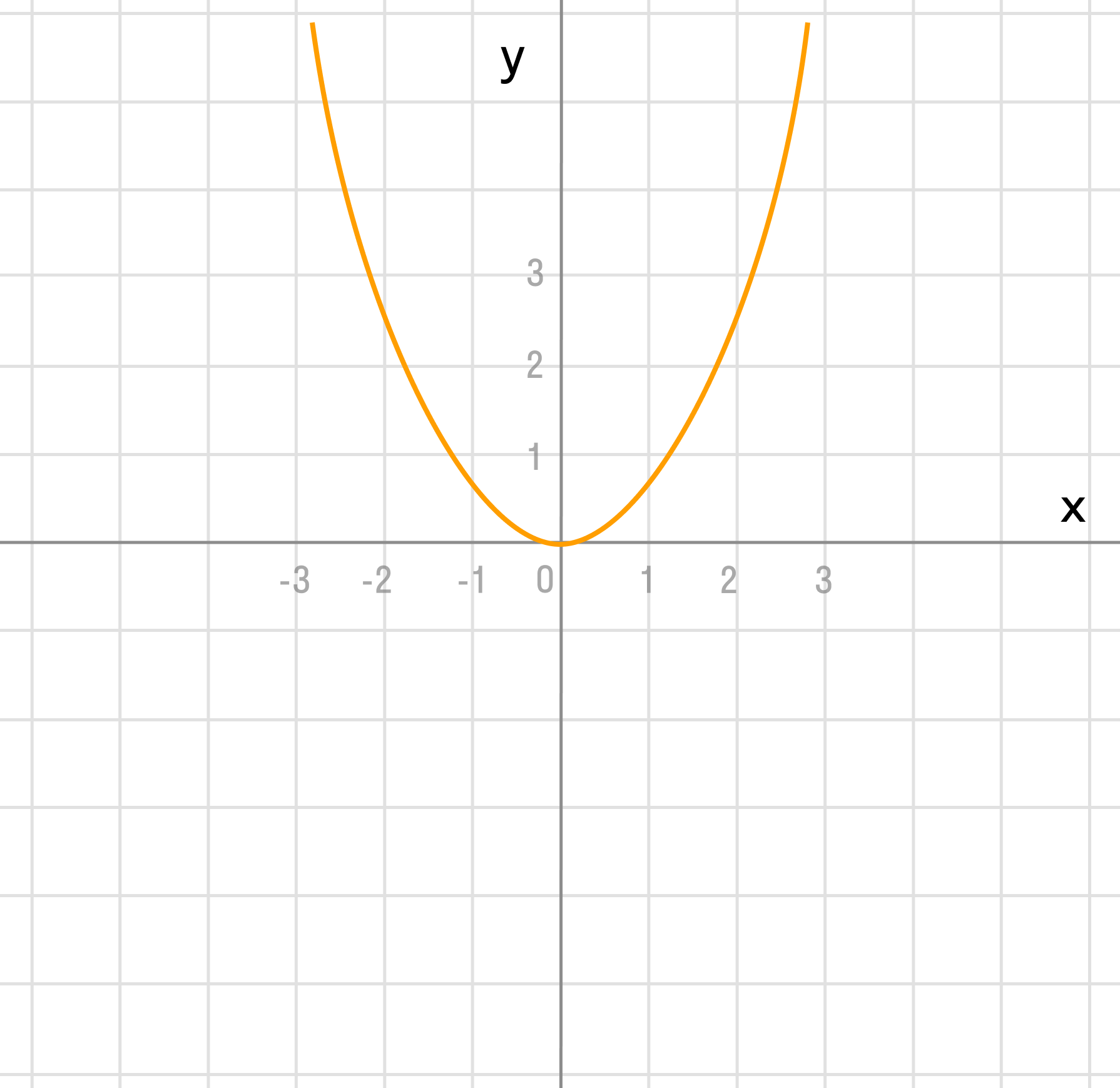
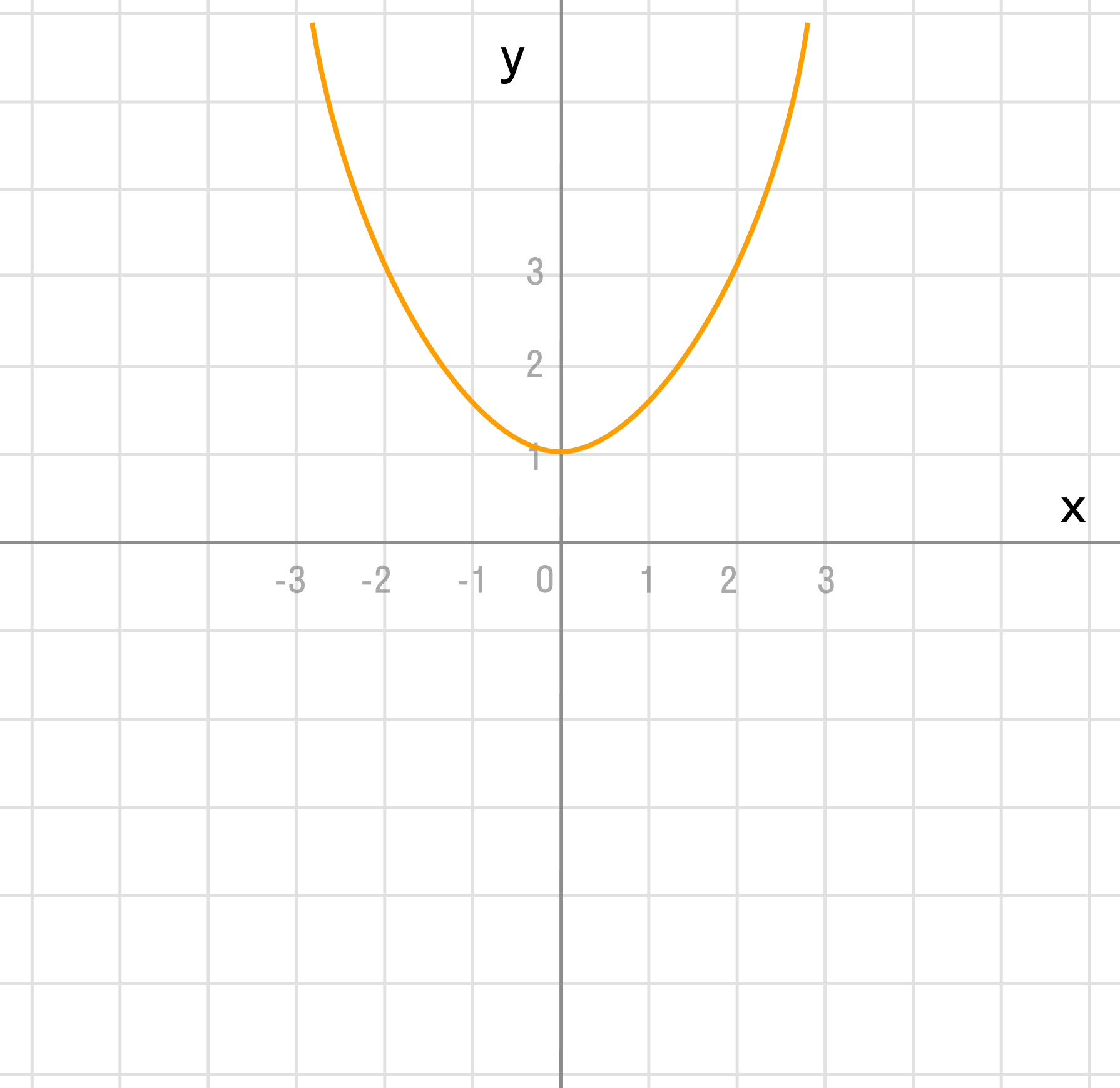
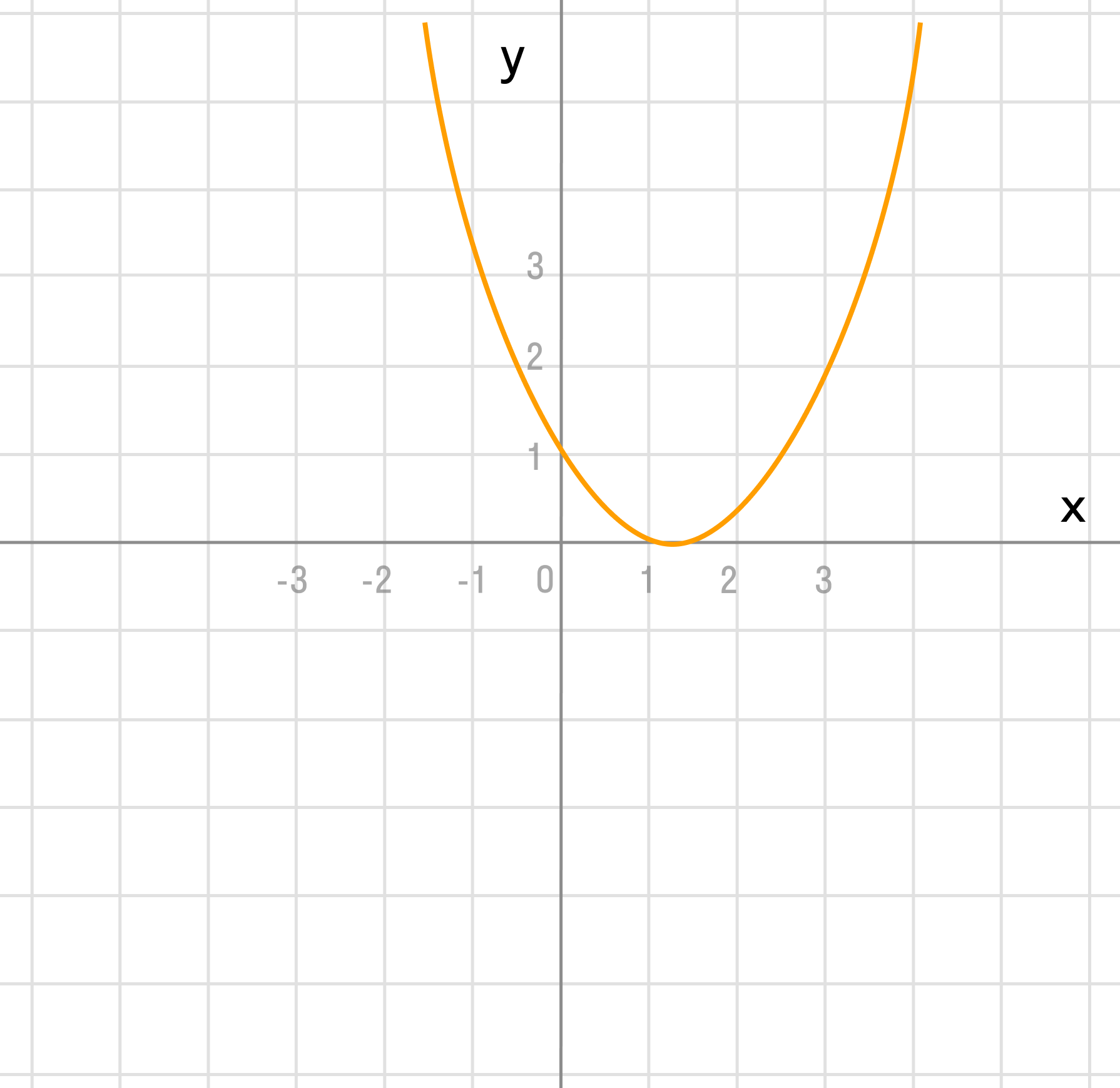
а) y = x² + 1
б)
в) y = (x — 1)² + 2
г)
д)
Как решаем:
Построить графики можно при помощи элементарных преобразований.
Если построен график функции y = f(x), то при a > 0 следующие графики получаются с помощью сдвига графика f(x).
-
y = f(x) + a — график функции y = f(x) сдвигается на a единиц вверх;
-
y = f(x) − a — график функции y = f(x) сдвигается на a единиц вниз;
-
y = f(x + a) — график функции y = f(x) сдвигается на a единиц влево;
-
y = f(x − a) — график функции у = f(x) сдвигается на a единиц вправо.
Преобразование график по типу y = mf(x): y = f(x) → y = mf(x), где m — положительное число.
-
Если m > 1, то такое преобразование графика называют растяжением вдоль оси y с коэффициентом m.
-
Если m < 1, то такое преобразование графика называют сжатием к оси x с коэффициентом 1/m.
а)
Преобразование в одно действие типа f(x) + a.
y = x²
Сдвигаем график вверх на 1:
y = x² + 1
б)
Преобразование в одно действие типа f(x — a).
Сдвигаем график вправо на 1:
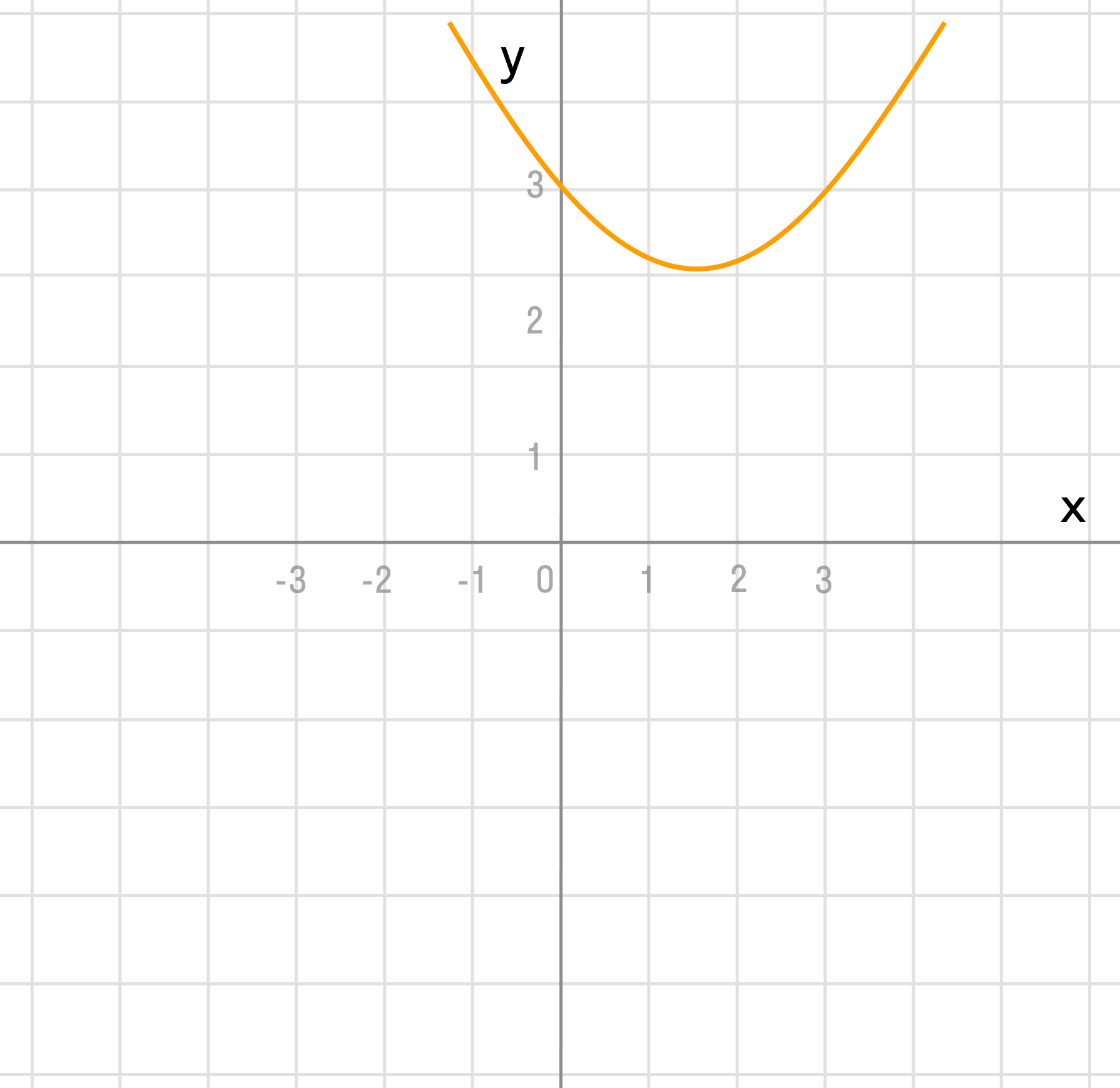
в) y = (x — 1)² + 2
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.
y = x²
Сдвигаем график вправо на 1:
y = (x — 1)²
Сдвигаем график вверх на 2:
y = (x — 1)² + 2
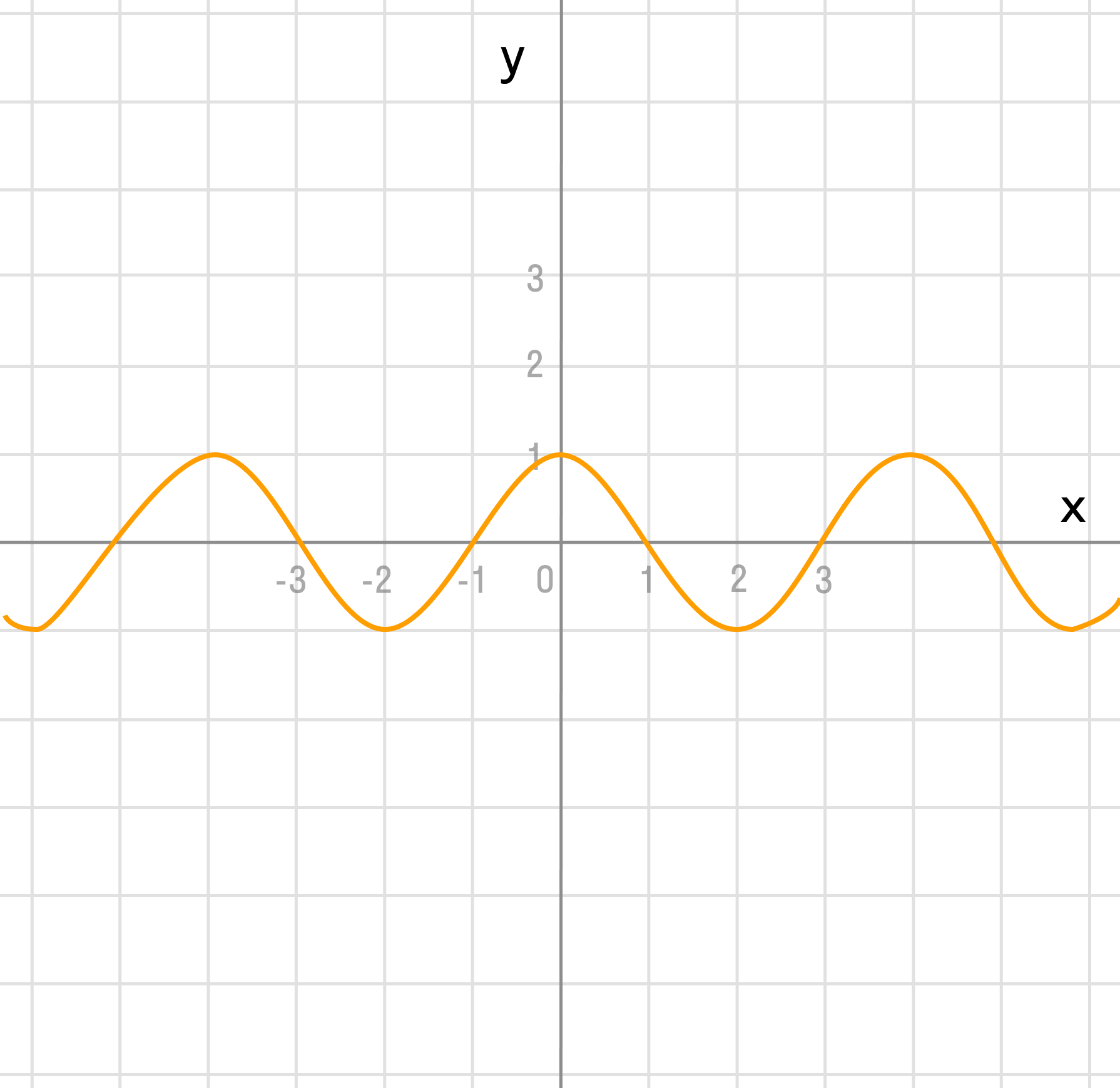
г)
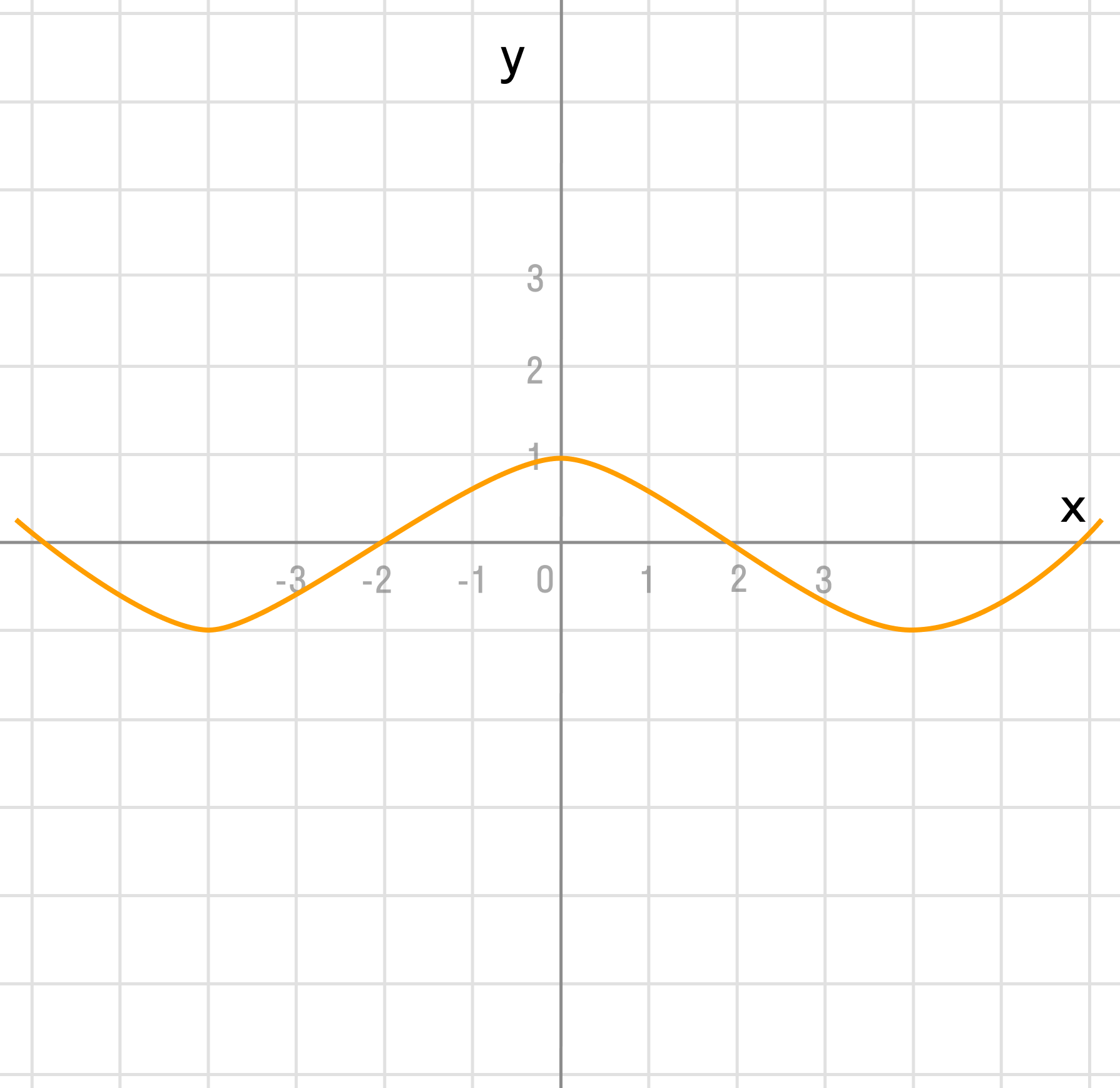
Преобразование в одно действие типа
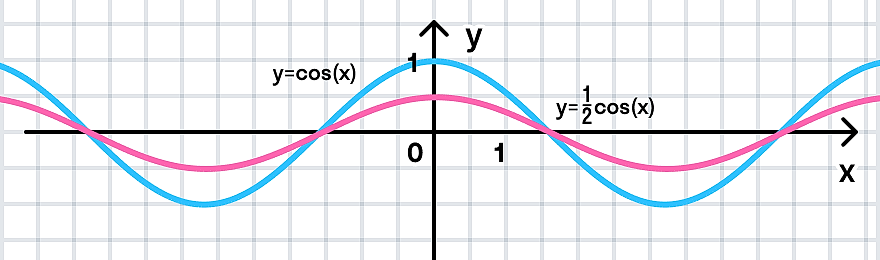
y = cos(x)
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
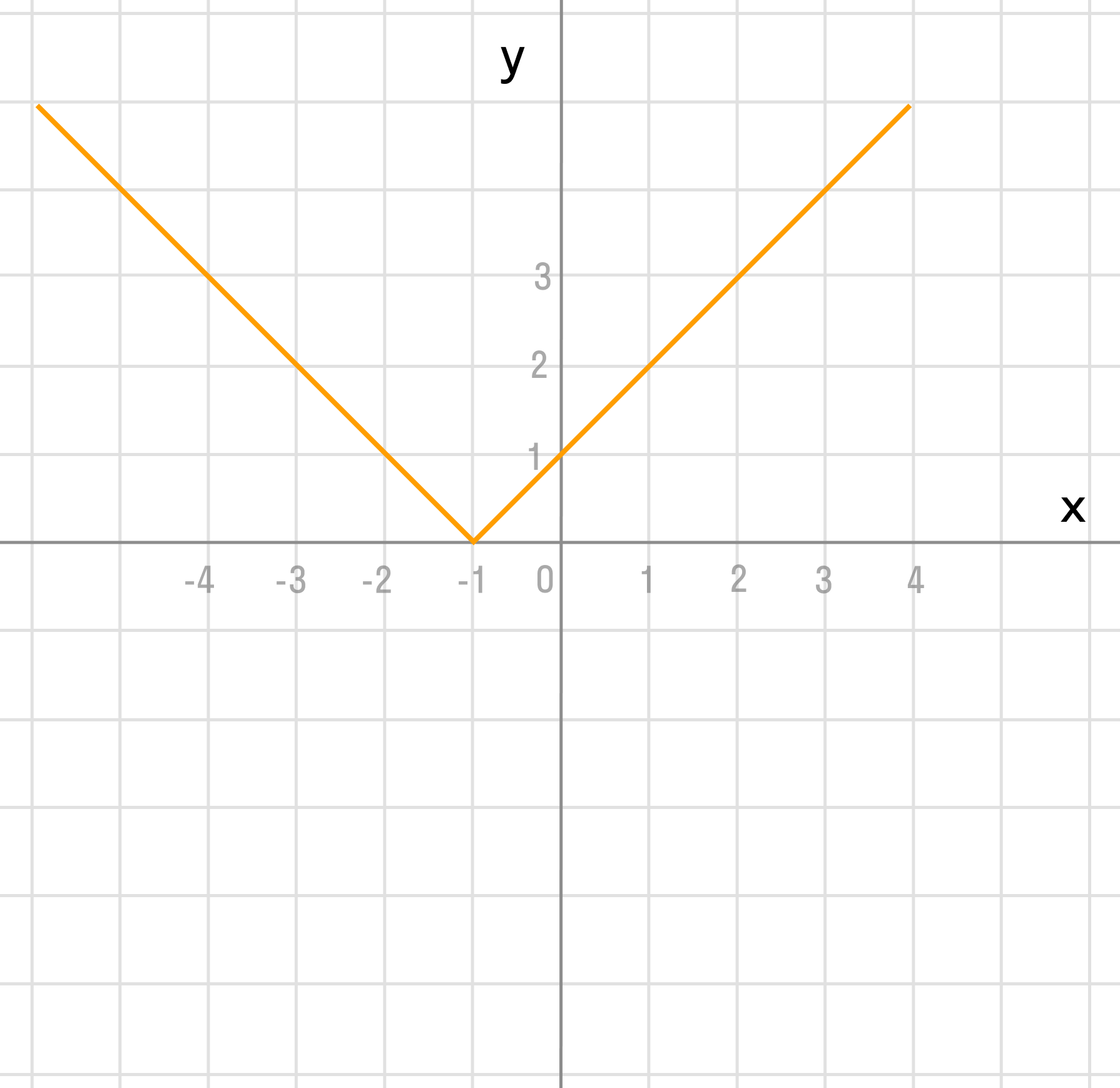
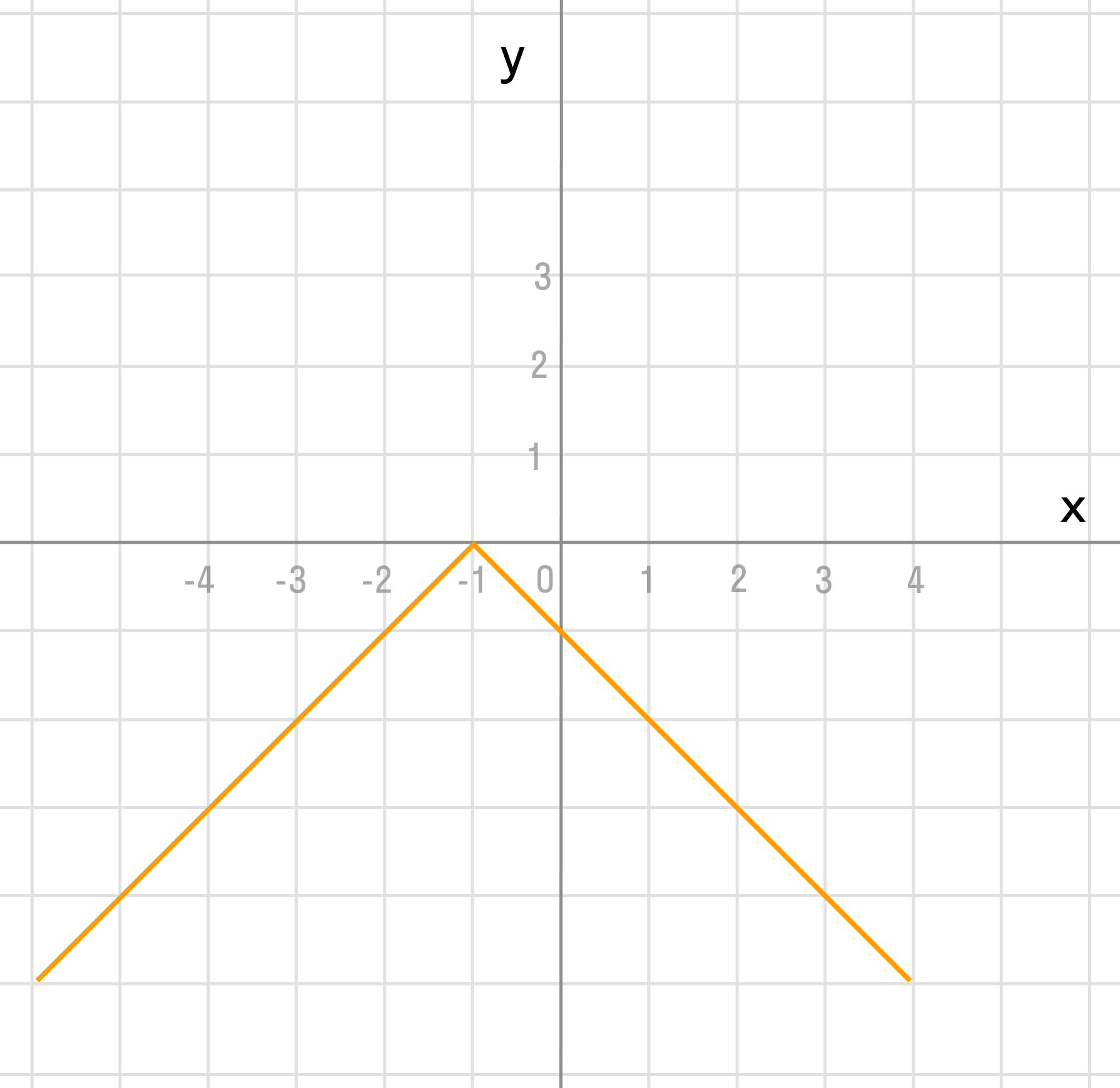
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.
Сжимаем график в два раза вдоль оси абсцисс:
Сдвигаем график влево на 1/2 вдоль оси абсцисс:
Отражаем график симметрично относительно оси абсцисс:
Оглавление:
- Основные теоретические сведения
- Координаты и базовые понятия о функциях
- График линейной функции
- График квадратичной функции (Парабола)
- Графики других функций
- Графики периодических (тригонометрических) функций
Основные теоретические сведения
Координаты и базовые понятия о функциях
К оглавлению…
Длина отрезка на координатной оси находится по формуле:
Длина отрезка на координатной плоскости ищется по формуле:
Для нахождения длины отрезка в трёхмерной системе координат используется следующая формула:
Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы) вычисляются по формулам:
Функция – это соответствие вида y = f(x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой переменной величины x (аргумента или независимой переменной) соответствует определенное значение другой переменной величины, y (зависимой переменной, иногда это значение просто называют значением функции). Обратите внимание, что функция подразумевает, что одному значению аргумента х может соответствовать только одно значение зависимой переменной у. При этом одно и то же значение у может быть получено при различных х.
Область определения функции – это все значения независимой переменной (аргумента функции, обычно это х), при которых функция определена, т.е. ее значение существует. Обозначается область определения D(y). По большому счету Вы уже знакомы с этим понятием. Область определения функции по другому называется областью допустимых значений, или ОДЗ, которую Вы давно умеете находить.
Область значений функции – это все возможные значения зависимой переменной данной функции. Обозначается Е(у).
Функция возрастает на промежутке, на котором большему значению аргумента соответствует большее значение функции. Функция убывает на промежутке, на котором большему значению аргумента соответствует меньшее значение функции.
Промежутки знакопостоянства функции – это промежутки независимой переменной, на которых зависимая переменная сохраняет свой положительный или отрицательный знак.
Нули функции – это такие значения аргумента, при которых величина функции равна нулю. В этих точках график функции пересекает ось абсцисс (ось ОХ). Очень часто необходимость найти нули функции означает необходимость просто решить уравнение. Также часто необходимость найти промежутки знакопостоянства означает необходимость просто решить неравенство.
Функцию y = f(x) называют четной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:
Это означает, что для любых противоположных значений аргумента, значения четной функции равны. График чётной функции всегда симметричен относительно оси ординат ОУ.
Функцию y = f(x) называют нечетной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:
Это означает, что для любых противоположных значений аргумента, значения нечетной функции также противоположны. График нечётной функции всегда симметричен относительно начала координат.
Сумма корней чётной и нечетной функций (точек пересечения оси абсцисс ОХ) всегда равна нулю, т.к. на каждый положительный корень х приходится отрицательный корень –х.
Важно отметить: некоторая функция не обязательно должна быть четной либо нечетной. Существует множество функций не являющихся ни четными ни нечетными. Такие функции называются функциями общего вида, и для них не выполняется ни одно из равенств или свойств приведенных выше.
График линейной функции
К оглавлению…
Линейной функцией называют функцию, которую можно задать формулой:
График линейной функции представляет из себя прямую и в общем случае выглядит следующим образом (приведен пример для случая когда k > 0, в этом случае функция возрастающая; для случая k < 0 функция будет убывающей, т.е. прямая будет наклонена в другую сторону — слева направо):
График квадратичной функции (Парабола)
К оглавлению…
График параболы задается квадратичной функцией:
Квадратичная функция, как и любая другая функция, пересекает ось ОХ в точках являющихся её корнями: (x1; 0) и (x2; 0). Если корней нет, значит квадратичная функция ось ОХ не пересекает, если корень один, значит в этой точке (x0; 0) квадратичная функция только касается оси ОХ, но не пересекает её. Квадратичная функция всегда пересекает ось OY в точке с координатами: (0; c). График квадратичной функции (парабола) может выглядеть следующим образом (на рисунке примеры, которые далеко не исчерпывают все возможные виды парабол):
При этом:
- если коэффициент a > 0, в функции y = ax2 + bx + c, то ветви параболы направлены вверх;
- если же a < 0, то ветви параболы направлены вниз.
Координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины (p — на рисунках выше) параболы (или точка в которой квадратный трехчлен достигает своего наибольшего или наименьшего значения):
Игрек вершины (q — на рисунках выше) параболы или максимальное, если ветви параболы направлены вниз (a < 0), либо минимальное, если ветви параболы направлены вверх (a > 0), значение квадратного трехчлена:
Графики других функций
К оглавлению…
Степенной функцией называют функцию, заданную формулой:
Приведем несколько примеров графиков степенных функций:
Обратно пропорциональной зависимостью называют функцию, заданную формулой:
В зависимости от знака числа k график обратно пропорциональной зависимости может иметь два принципиальных варианта:
Асимптота — это линия, к которой линия графика функции бесконечно близко приближается, но не пересекает. Асимптотами для графиков обратной пропорциональности приведенных на рисунке выше являются оси координат, к которым график функции бесконечно близко приближается, но не пересекает их.
Показательной функцией с основанием а называют функцию, заданную формулой:
В зависимости от того больше или меньше единицы число a график показательной функции может иметь два принципиальных варианта (приведем также примеры, см. ниже):
Логарифмической функцией называют функцию, заданную формулой:
В зависимости от того больше или меньше единицы число a график логарифмической функции может иметь два принципиальных варианта:
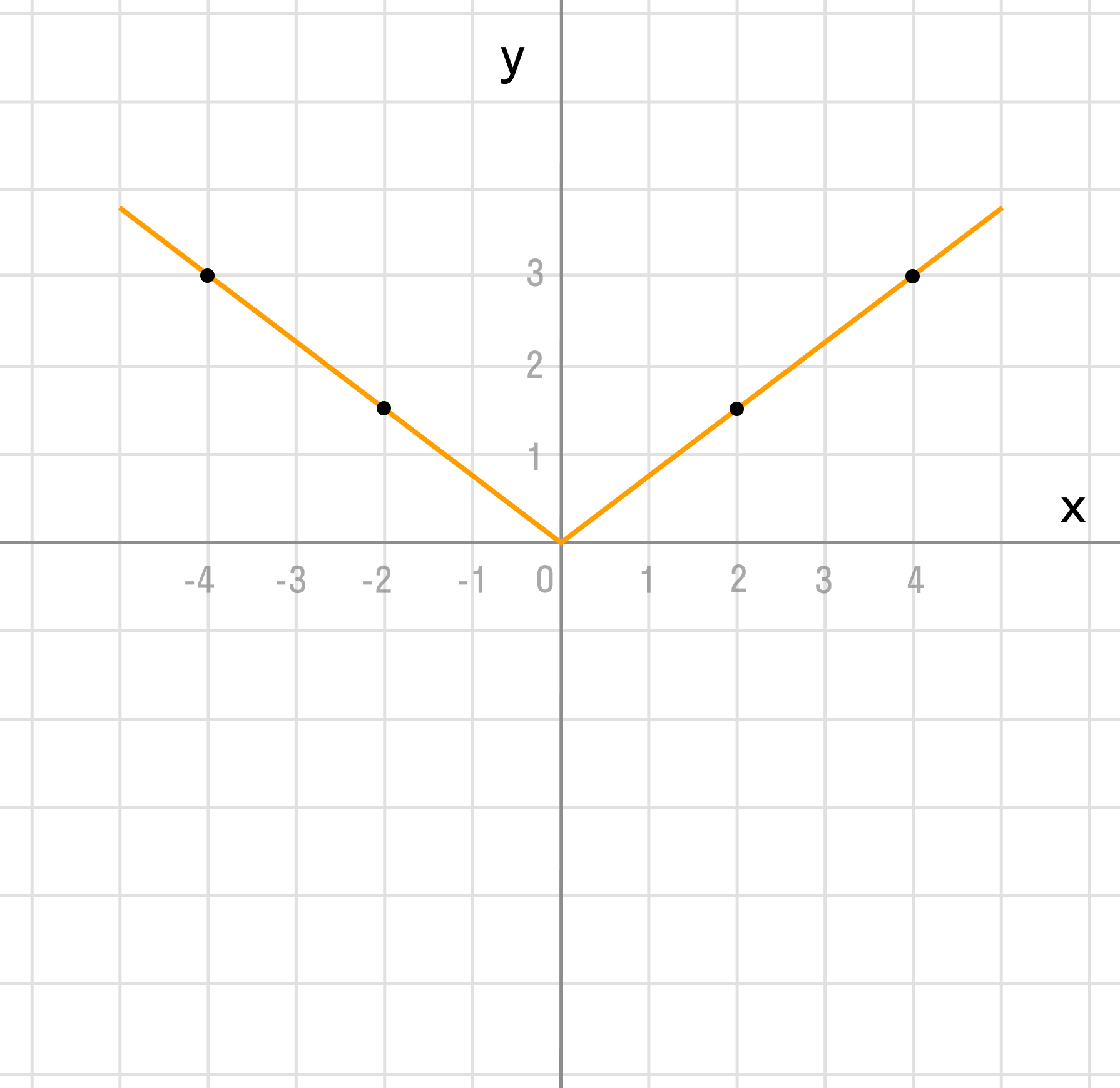
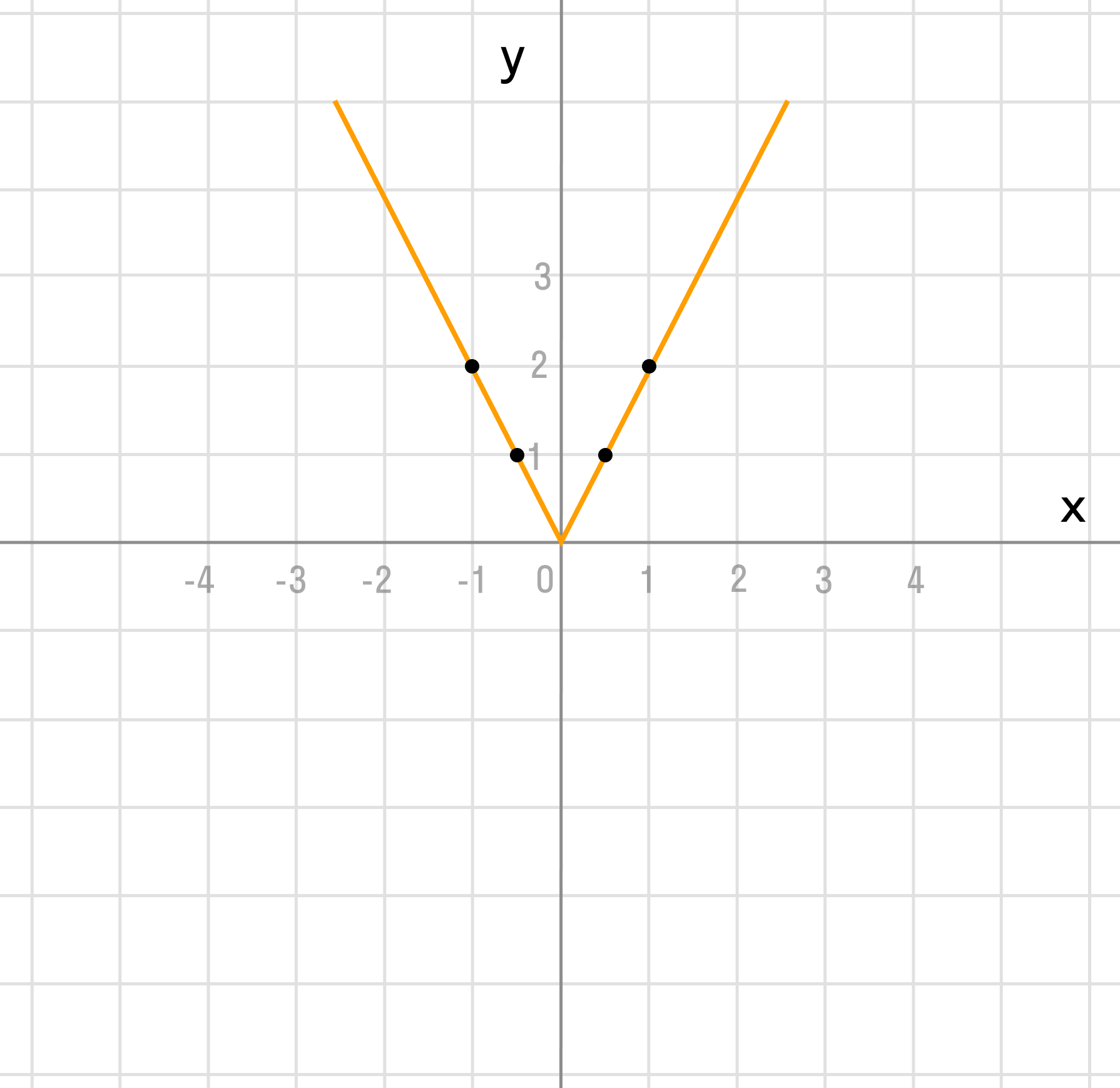
График функции y = |x| выглядит следующим образом:
Графики периодических (тригонометрических) функций
К оглавлению…
Функция у = f(x) называется периодической, если существует такое, неравное нулю, число Т, что f(x + Т) = f(x), для любого х из области определения функции f(x). Если функция f(x) является периодической с периодом T, то функция:
где: A, k, b – постоянные числа, причем k не равно нулю, также периодическая с периодом T1, который определяется формулой:
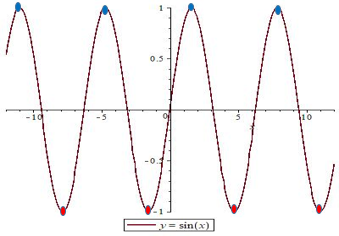
Большинство примеров периодических функций — это тригонометрические функции. Приведем графики основных тригонометрических функций. На следующем рисунке изображена часть графика функции y = sinx (весь график неограниченно продолжается влево и вправо), график функции y = sinx называют синусоидой:
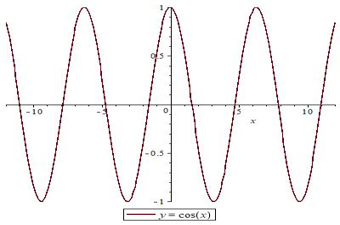
График функции y = cosx называется косинусоидой. Этот график изображен на следующем рисунке. Так как и график синуса он бесконечно продолжается вдоль оси ОХ влево и вправо:
График функции y = tgx называют тангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.
Ну и наконец, график функции y = ctgx называется котангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических и тригонометрических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.
В ЕГЭ 2022 года добавили новую задачу на графики функций. Для решения этой задачи нужно сначала определить формулу функции, а затем вычислить ответ на вопрос задачи. И если вычисление ответа по известной формуле обычно не составляет труда, то вот определение самой формулы часто ставит школьников в тупик. Поэтому мы разберем три разных подхода к этому вопросу.
Замечание. Про то как определяется формула у прямой и параболы я написала в этой и этой статьях. Поэтому здесь в примерах я буду использовать другие функции – дробные, иррациональные, показательные и логарифмические, но все три описанных здесь способа работают и для линейных, и для квадратичных функций в том числе.
1 способ – находим формулу по точкам
Этот способ подходит вообще для любой девятой задачи, но занимает достаточно много времени и требует хорошего навыка решения систем уравнений.
Давайте разберем алгоритм на примере конкретной 9-ой задачи ЕГЭ:

Алгоритм:
1. Находим 2 точки с целыми координатами. Обычно они выделены жирно, но если это не так, то не проблема найти их самому.
Пример:
2. Подставляем эти координаты в «полуфабрикат» функции. Вместо (f(x))– координату игрек, вместо (x) – икс. Получается система.

3. Решаем эту систему и получаем готовую формулу.

4. Готово, функция найдена, можно переходить ко второму этапу – вычислению (f(-8)). Если вы вдруг не знаете, что это значит – в конце статьи я рассматриваю этот момент более подробно.

Давайте посмотрим метод еще раз на примере с логарифмической функцией.
Пример:

2 способ – преобразование графиков функций
Этот способ сильно быстрее первого, но требует больше знаний. Для использования преобразований функций нужно знать, как выглядят функции без изменения и как преобразования их меняют. Наиболее удобно использовать этот способ для иррациональной функции ((y=sqrt{x}) ) и функции обратной пропорциональности ((y=frac{1}{x})).
Вот как выглядит применение этого способа:

Для использования этого способа надо знать, как выглядят изначальные функции:

И понимать, как меняются функции от преобразований:




Часто даже по «полуфабрикату» функции понятно, какие преобразования сделали с функцией:

Пример:

3 способ – гибридный
Идеально подходит для логарифмических и показательных функций, так как обычно у таких функций неизвестно основание и с помощью преобразований его не найти. С другой стороны, независимо от оснований любая показательная функция должна проходить через точку ((0;1)), а любая логарифмическая — через точку ((1;0)).

По смещению этих точек легко понять, как именно двигали функцию, но только если ее не растягивали, а лишь перемещали вверх-вниз, влево-вправо (как обычно и бывает в задачах на ЕГЭ).
Основание же лучше находить уже следующим действием, используя подстановку координат точки в «полуфабрикат» функции.


Как отвечать на вопросы в задаче, когда уже определили функцию
— Если просят найти (f)(любое число), то нужно это число подставить в готовую функцию вместо икса.
Пример:
— Если просят найти «при каком значении x значение функции равно *любому числу*», то надо решить уравнение, в одной части которого будет функция, а в другой — то самое число. Аналогично надо поступить, если просят «найти корень уравнения (f(x)=) *любое число*».
Пример:
— Если просят найти абсциссу точки пересечения – надо приравнять 2 функции и решить получившееся уравнение. Корень уравнения и будет искомой абсциссой. Аналогично надо делать в задачах, где даны две точки пересечения (A)(*любое число*;*другое число*) и (B(x_0;y_0)) и просят найти (x_0).
Пример:

— Если просят найти ординату точки пересечения – надо приравнять 2 функции, найти иксы и подставить подходящий икс в любую функцию. Точно также решаем если просят найти (y_0) точки пересечения двух функций.
Пример:

— Иногда просят найти просто какой-либо из коэффициентов функции. Тогда надо просто восстановить функцию и записать в ответ то, о чем спросили:
Пример:

Самый наглядный способ представления информации – графический. Этот тезис применим и в математике. А при правильном подходе график может дать гораздо больше информации о поведении функции, чем просто положении точек на координатной плоскости.
Что может рассказать график $ y=f(x) $?
1. Область определения функции – значения аргумента $ x $, которые можно «подать на вход». Аргумент откладывается на горизонтальной оси.
2. Область значения функции – значения функции $ y $, получаемые «на выходе». Значения отмечаются на вертикальной оси.
3. Непрерывность функции. Для всех ли аргументов существуют значения?
4. Промежутки монотонности функции (возрастания или убывания).
Функция называется возрастающей, если большему значению аргумента соответствует большее значение функции то есть $ x_{1} < x_{2}Rightarrow y_{1} < y_{2} $.
Если же большему значению аргумента соответствует меньшее значение функции (то есть $ x_{1} < x_{2}Rightarrow y_{1} > y_{2} $), то функция называется убывающей.
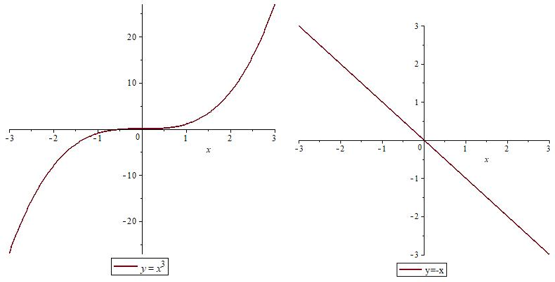
Существуют функции, которые всегда возрастают (например, $ y=x^{3} $) или всегда убывают (например, $ y=-x $).
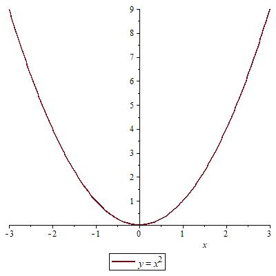
Но чаще функции имеют несколько промежутков возрастания и убывания. Например, функция $ y=x^{2} $ убывает при $ x in (0; +infty) $ и возрастает при $ x in (- infty; 0) $.
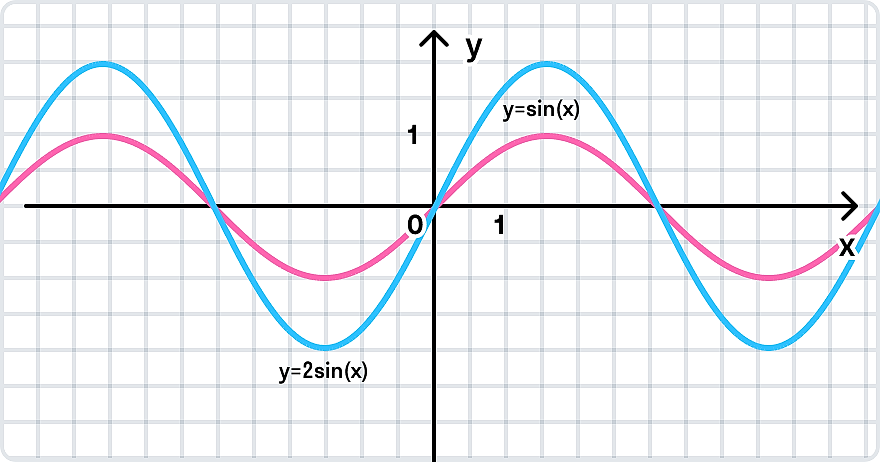
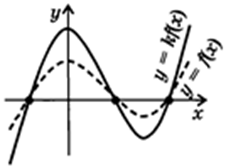
А график функции косинус имеет множество таких промежутков, сменяющих друг друга.
5. Точки минимума и максимума.
Значения аргумента, в которых функция перестает возрастать и начинает убывать, называются точками максимума. Если же в них, наоборот, функция перестает убывать и начинает возрастать – точками минимума. На графике $ y = sin(x) $ красным отмечены точки минимума, синим – максимума.
Всегда возрастающие и убывающие функции таких точек не имеют.
6. Ограниченность функции. Есть ли значения, за которые функция «не заходит»?
Функции могут быть неограниченными; ограниченными сверху, снизу, слева, справа, а также сразу с нескольких сторон.
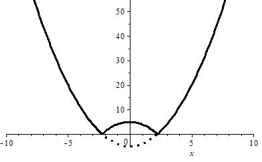
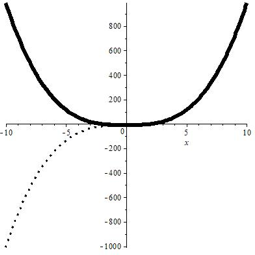
Уже знакомая нам функция косинуса, например, ограничена и сверху, и снизу. Парабола $ y=x^{2} $ ограничена снизу. А график функции $ y=x^{3} $неограничен нигде.
7. Четность функции.
Функция называется четной, если выполняется равенство $ f(-x)=f(x) $. Такой функцией является парабола $ y=x^{2} $ так как верно, что $ -x^{2} = x^{2} $. Наглядным признаком четности является симметрия графика относительно оси ОY.
Если выполняется равенство $ f(-x)=-f(x) $, то функция считается нечетной. Примером такого типа функций может служить кубическая парабола $ y=x^{3} $ для которой $ (-x)^{3} = -x^{3} $. График нечетной функции будет симметричен относительно начала координат.
Не всякую функцию можно отнести одной из этих групп. Если не выполняется ни одно из названных условий, говорят, что функция не обладает четностью.
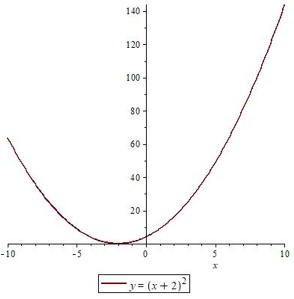
Рассмотрим функцию $ y = (x+2)^{2} $ и исследуем ее $ на четность.
$ y(-x) = (-x+2)^{2} = (-1(x-2))^{2} = (-1)^{2} cdot (x-2)^{2} = (x-2)^{2} $
Видно, что $ (x-2)^{2} neq (x+2)^{2} = y(x);$ и $ (x-2)^{2} neq -(x+2)^{2} = -y(x) $
То есть данная функция не является ни четной, ни нечетной.
8. Периодичность функции.
Если с какого-то момента график функции начинает повторяться, то такая функция называется периодичной. Таким свойством обладают все тригонометрические функции.
Помимо вышеназванных свойств у функций и их графиков есть особенные признаки, которые позволяют быстро и схематично их изобразить. Рассмотрим самые часто встречающиеся в математике зависимости.
Линейная функция
| Формула | $ y=kx+b, k neq 0 $ |
| График | 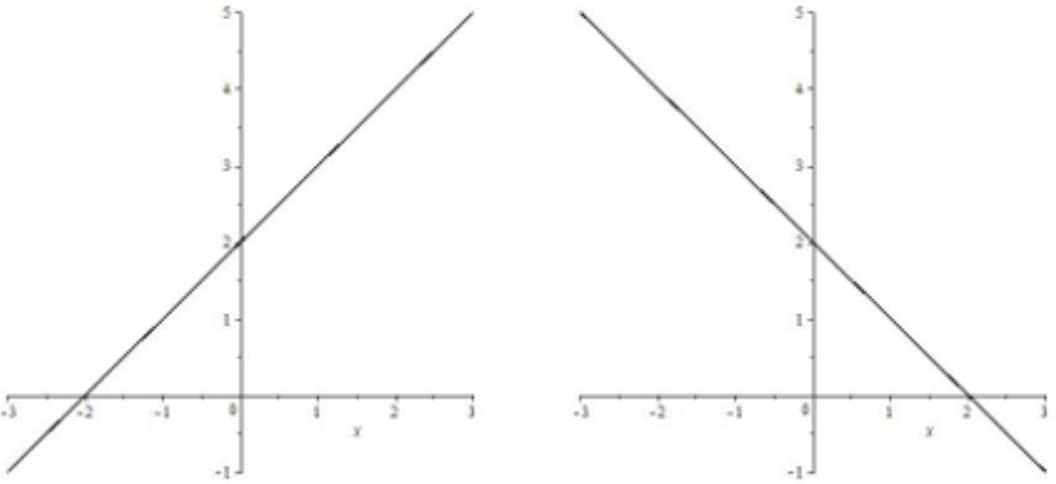 |
| Особые свойства | $ k=tga $ тангенс угла наклона, $ b $ точка пересечения с $ OY $ |
| Область определения | $ R $ |
| Область значения | $ R $ |
| Непрерывность | да |
| Монотонность | $ k > 0 $ — возростает, $ k < 0 $ — убывает |
| Точки минимума и максимума | нет |
| Ограниченность | неограничено |
| Четность | нечетная |
| Периодичность | нет |
Квадратичная функция (парабола)
| Формула | $ y=ax^{2}+bx+c, a neq 0 $ |
| График |  |
| Особые свойства | $ a > 0 $ ветви направлены вверх, $ a < 0 $ $ b $ — точка пересечения с $ OY $ $ x_{вершины}=frac{-b}{2a} $ |
| Область определения | $ R $ |
| Область значения | $ R $ |
| Непрерывность | да |
| Монотонность | При $ a > 0 (-infty;x_{вершины}) $ — убывает $ x_{вершины};+infty $ — возростает. При $ a < 0 $ — наоборот. |
| Точки минимума и максимума | $ a > 0 x_{вершины} $ — точка минимума, при $ a < 0 $ — максимума |
| Ограниченность | При $ a > 0 $ ограничена снизу, при $ a < 0 $ — сверху |
| Четность | $ b=0 $ — четная, $ b neq 0 $ — не обладает четностью |
| Периодичность | нет |
Кубическая парабола
| Формула | $ y=ax^{3}+b, a neq 0 $ |
| График | 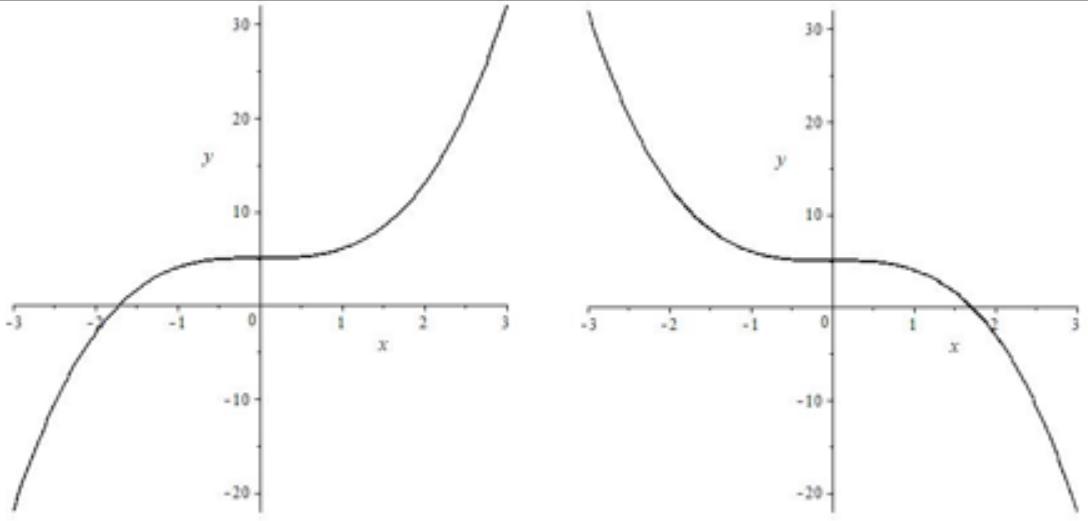 |
| Особые свойства | $ b $ — точка пересечения с $ OY $ |
| Область определения | $ R $ |
| Область значения | $ R $ |
| Непрерывность | да |
| Монотонность | При $ a > 0 $ — возростает, $ a < 0 $ — убывает. |
| Точки минимума и максимума | нет |
| Ограниченность | Неограничена |
| Четность | $ b=0 $ — нечетная, иначе — не обладает четностью |
| Периодичность | нет |
Квадратный корень
| Формула | $ y=a sqrt {x}, a neq 0 $ |
| График | 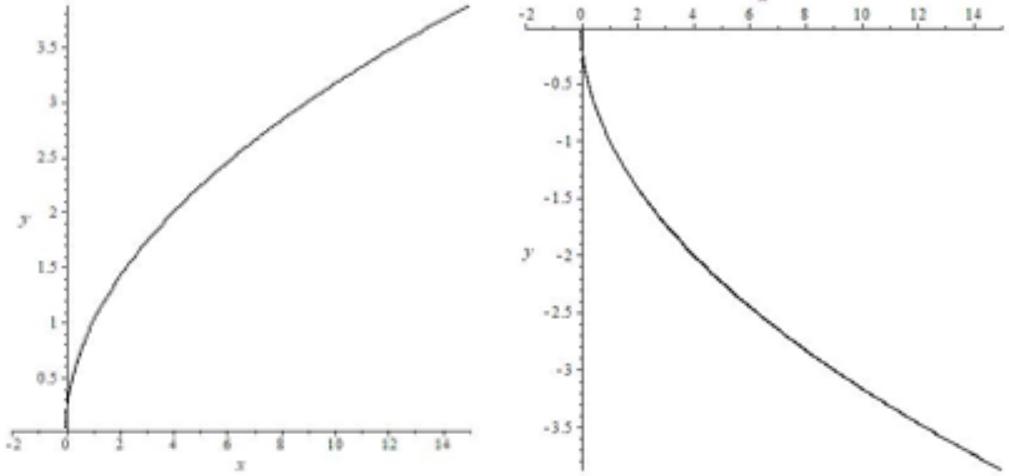 |
| Особые свойства | График располагается справа от нуля |
| Область определения | $ x geq 0 $ |
| Область значения | $ a geq 0 Rightarrow y geq 0 $ $ a leq 0 Rightarrow y leq 0 $ |
| Непрерывность | да |
| Монотонность | При $ a > 0 $ — возростает, $ a < 0 $ — убывает. |
| Точки минимума и максимума | $ a > 0 — x = 0 $ точка минимума, $ a < 0 — x = 0 $ точка максимума |
| Ограниченность | При $ a > 0 $ ограничена снизу и слева, при $ a < 0 $ — сверху и слева |
| Четность | Не обладает четностью |
| Периодичность | нет |
Гипербола
| Формула | $ y= frac{k}{x}, k neq 0 $ |
| График | 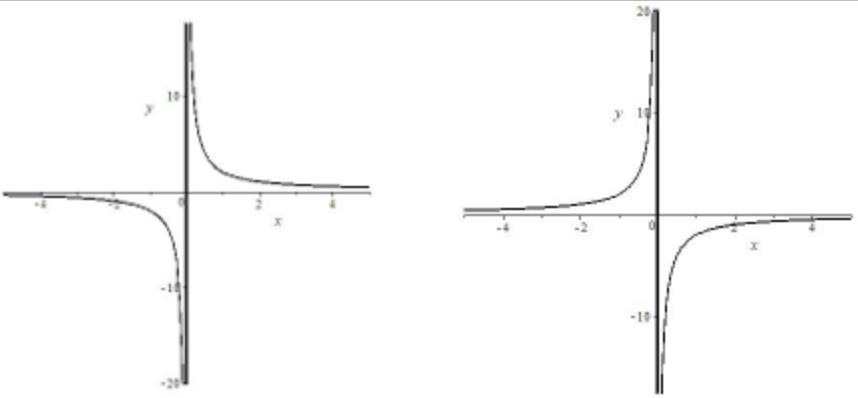 |
| Особые свойства | График имеет 2 асимптоты (прямые, к которым бесконечно приближается, но никогда не пересекает) $ x=0, y=0 $ |
| Область определения | $ x neq 0 $ |
| Область значения | $ y neq 0 $ |
| Непрерывность | Разрыв в точке $ x neq 0 $ |
| Монотонность | $ k > 0 $ убывает $ (-infty ; 0) $, возрастает $ (0;+infty) $ \ $ k < 0 $ возрастает $ (-infty ; 0) $, убывает $ (0;+infty) $ |
| Точки минимума и максимума | нет |
| Ограниченность | Неограничена |
| Четность | Нечетная |
| Периодичность | Нет |
Окружность
| Формула | $ (x-a)^{2} + (y-b)^{2}= R^{2} $ |
| График | 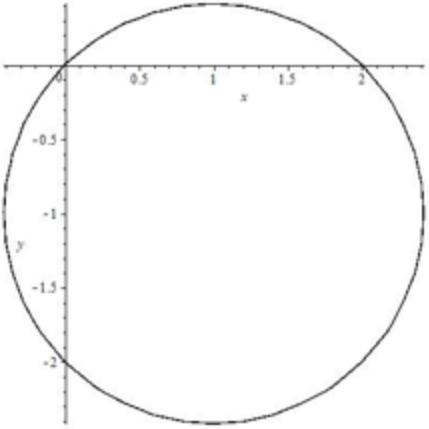 |
| Особые свойства | Центр окружности в точке $ a, b $, радиус $ R $ |
| Область определения | $ R $ |
| Область значения | $ R $ |
| Непрерывность | Да |
| Монотонность | |
| Точки минимума и максимума | нет |
| Ограниченность | С 4 сторон |
| Четность | При $ a=b=0 $ — четная, иначе не обладает четностью |
| Периодичность | Нет |
Показательная функция
| Формула | $ y=a^{x}, a > 0, a neq 1 $ |
| График | 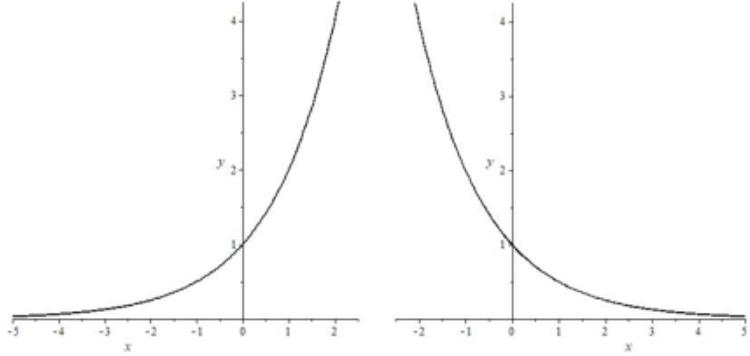 |
| Особые свойства | Все показательные функции проходят через точку (0,1) |
| Область определения | $ R $ |
| Область значения | $ (0;+infty) $ |
| Непрерывность | Да |
| Монотонность | $ a > 1 $ — возрастает, $ 0 < a < 1 $ — убывает |
| Точки минимума и максимума | нет |
| Ограниченность | Ограничена с низу |
| Четность | Не обладает четностью |
| Периодичность | Нет |
Логарифмическая функция
| Формула | $ y=log_{a}x, a > 0, a neq 1 $ |
| График | 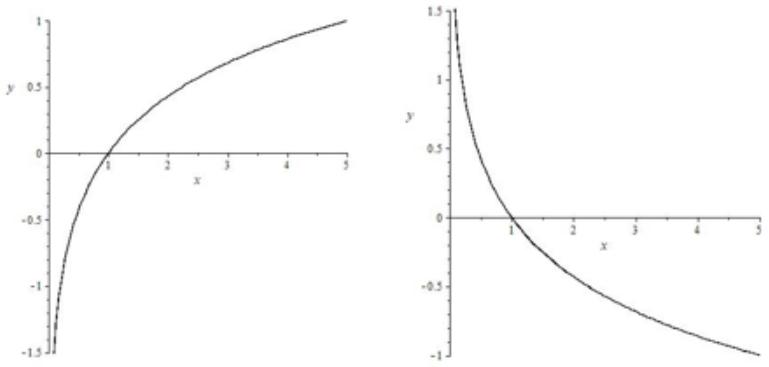 |
| Особые свойства | Все показательные функции проходят через точку (1,0) |
| Область определения | $ (0;+infty) $ |
| Область значения | $ R $ |
| Непрерывность | Да |
| Монотонность | $ a > 1 $ — возрастает, $ 0 < a < 1 $ — убывает |
| Точки минимума и максимума | нет |
| Ограниченность | Нет |
| Четность | Нет |
| Периодичность | Нет |
Синус
| Формула | $ y=sin(x) $ |
| График |  |
| Особые свойства | |
| Область определения | $ R $ |
| Область значения | [-1;1] |
| Непрерывность | Да |
| Монотонность | Да |
| Точки минимума и максимума | Точки минимума $ frac{pi}{2}+2pi k, kin Z $, точки минимума $ -frac{pi}{2}+2pi k, kin Z $ |
| Ограниченность | Сверху и снизу |
| Четность | Нечетная |
| Периодичность | Период $ 2pi $ |
Косинус
| Формула | $ y=cos(x) $ |
| График | 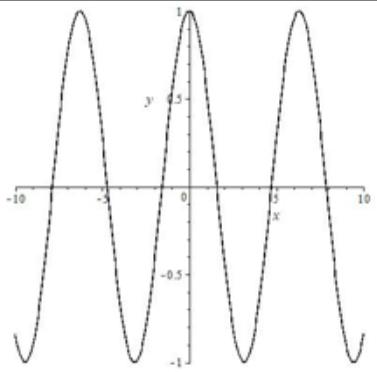 |
| Особые свойства | |
| Область определения | $ R $ |
| Область значения | [-1;1] |
| Непрерывность | Да |
| Монотонность | Да |
| Точки минимума и максимума | Точки минимума $ 2pi k, kin Z $, точки минимума $ pi+2pi k, kin Z $ |
| Ограниченность | Сверху и снизу |
| Четность | Четная |
| Периодичность | Период $ 2pi $ |
Тангенс
| Формула | $ y=tgx $ |
| График | 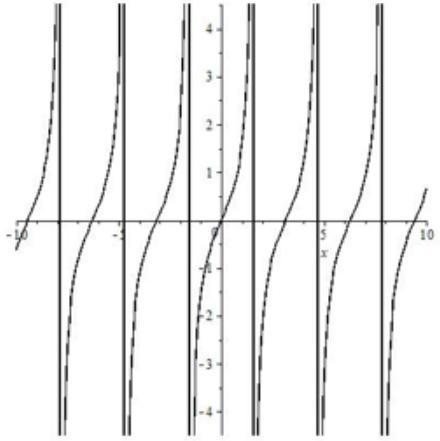 |
| Особые свойства | Имеет бесконечное число асимптот |
| Область определения | $ x neq frac{pi}{2}+pi k, kin Z $ |
| Область значения | $ R $ |
| Непрерывность | Разрыв в точках $ (-frac{pi}{2}+pi k; frac{pi}{2}+pi k), k in Z $ |
| Монотонность | Возрастает на каждом промежутке $ x neq frac{pi}{2}+pi k, kin Z $ |
| Точки минимума и максимума | Нет |
| Ограниченность | Нет |
| Четность | Четная |
| Периодичность | Период $ pi $ |
Котангенс
| Формула | $ y=ctgx $ |
| График | 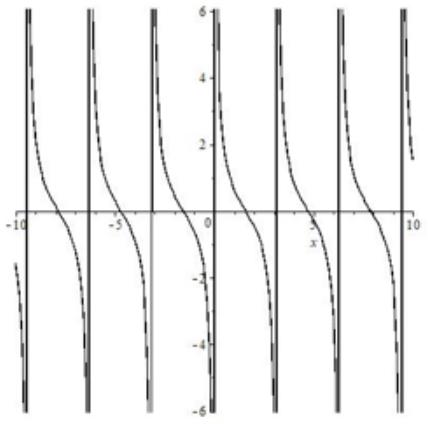 |
| Особые свойства | Имеет бесконечное число асимптот |
| Область определения | $ x neq pi k, kin Z $ |
| Область значения | $ R $ |
| Непрерывность | Разрыв в точках $ x = pi k, kin Z $ |
| Монотонность | Убывает на каждом промежутке $ (pi k, pi + pi k), k in Z $ |
| Точки минимума и максимума | Нет |
| Ограниченность | Нет |
| Четность | Нечетная |
| Периодичность | Период $ pi $ |
Преобразование графиков функции
График любой зависимости можно построить по точкам. Но в некоторых случаях гораздо проще преобразовать график какой-либо известной функции с помощью сдвигов, отражений и растяжений.
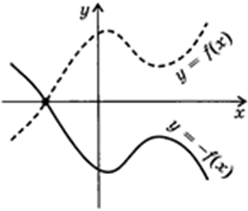
1. Симметрия относительно оси $ OX: f(x) rightarrow — f(x) $
Все абсциссы остаются неизменными, а все ординаты меняют знак на противоположный.
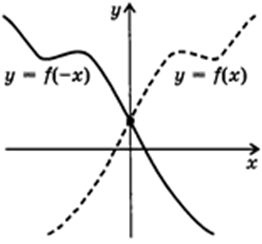
2. Симметрия относительно оси $ OY: f(x) rightarrow f(-x) $
Все ординаты графика остаются неизменными, а абсциссы меняют знак на противоположный.
При таком преобразовании четной функции, график остается неизменным.
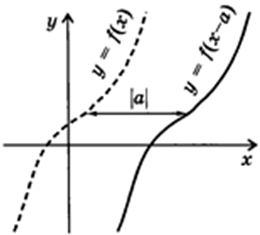
3. Сдвиг вдоль оси $ OX: f(x) rightarrow f(x-a) $
Ординаты остаются неизменными, а абсциссам прибавляется $ a $. Если $ a > 0 $, то график сдвигается вправо, иначе – влево.
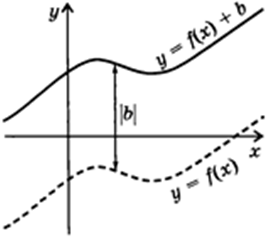
4. Сдвиг вдоль оси $ OY: f(x) rightarrow f(x)+b $
Абсциссы не меняются, а к ординатам прибавляется $ : b $. При $ b > 0 $ график сдвигается вверх, иначе – вниз.
Обратите внимание, что в пункте 3. перед $ a $ стоит знак «–», в то время как в 4. перед $ b $ стоит «+». При этом знаки параметров $ a,b $ могут быть любыми.
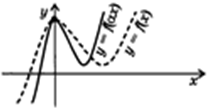
5. Сжатие и растяжение вдоль оси $ OX: f(x) rightarrow f(ax), a > 0 $
Ординаты остаются неизменными, а абсциссы делятся на $ a $. Точки пересечения графика функции с осью $ OY $ остаются на месте.
6. Сжатие и растяжение вдоль оси $ OY: f(x) rightarrow kf(x), k > 0 $
Абсциссы остаются неизменными, а ординаты умножаются на $ k $. Точки пересечения графика функции с осью $ OX $ остаются на месте.
7. Модуль функции: $ f(x) rightarrow|;f(x);| $
Точки с положительными ординатами остаются на месте, точки с отрицательными ординатами отбражаются симметрично относительно оси $ OX $.
8. Модуль аргумента: $ f(x) rightarrow f(|x|) $
Точки, соответствующие отрицательным абсциссами, стираются. Точки с положительными абсциссами остаются на месте, а так же отображаются симметрично относительно оси $ OY $. Функция становится четной.
Приведенные выше преобразования можно комбинировать и выполнять друг за другом.
Пример 1.
Построите график функции $ y=-2(x-3)^{2}+4 $.
Данный график можно получить из $ y=x^{2} $ последовательными сжатием вдоль оси $ OY $ в 2 раза, сдвигом вдоль оси $ OX $ на 3 вправо, сдвигом вдоль оси $ OY $ на 4 вверх и отражением относительно оси $ OX $.
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Декартова система координат
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.
Координатные оси – прямые, образующие систему координат.
Ось абсцисс (ось x ) – горизонтальная ось.
Ось ординат (ось y ) – вертикальная ось.
Функция
Функция – это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.
Прямая
Линейная функция – функция вида y = a x + b где a и b – любые числа.
Графиком линейной функции является прямая линия.
Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :
Если a > 0 , прямая будет проходить через I и III координатные четверти.
b – точка пересечения прямой с осью y .
Если a < 0 , прямая будет проходить через II и IV координатные четверти.
b – точка пересечения прямой с осью y .
Если a = 0 , функция принимает вид y = b .
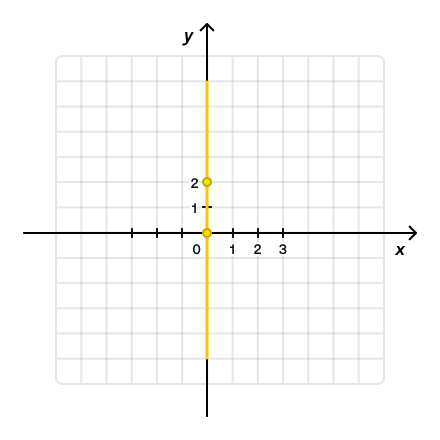
Отдельно выделим график уравнения x = a .
Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».
Парабола
Графиком функции y = a x 2 + b x + c является парабола.
Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a , b , c :
- Коэффициент a указывает на то, куда направлены ветки параболы.
- Если a > 0 , ветки параболы направлены вверх.
- Если a < 0 , ветки параболы направлены вниз.
- Коэффициент c указывает, в какой точке парабола пересекает ось y.
- Коэффициент b помогает найти x в – координату вершины параболы.
x в = − b 2 a
- Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .
- Если D > 0 – две точки пересечения.
- Если D = 0 – одна точка пересечения.
- Если D < 0 – нет точек пересечения.



Гипербола
Графиком функции y = k x является гипербола.
Характерная особенность гиперболы в том, что у неё есть асимптоты.
Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.
Ось x – горизонтальная асимптота гиперболы
Ось y – вертикальная асимптота гиперболы.
На графике асимптоты отмечены зелёной пунктирной линией.
Если коэффициент k > 0 , то ветви гиперолы проходят через I и III четверти.
Если k < 0, ветви гиперболы проходят через II и IV четверти.
Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y .
Квадратный корень
Функция y = x имеет следующий график:
Возрастающие/убывающие функции
Функция y = f ( x ) возрастает на интервале, если большему значению аргумента (большему значению x ) соответствует большее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)
Примеры возрастающих функций:
Функция y = f ( x ) убывает на интервале, если большему значению аргумента (большему значению x ) соответствует меньшее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).
Примеры убывающих функций:

Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наибольшим значением функции.
Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наименьшим значением функции.
Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.
Скачать домашнее задание к уроку 5.
Функции ЕГЭ по математике
- 08.11.2013
Материал для подготовки к ЕГЭ по математике на тему: «Функции».
Содержание темы:
3. ФУНКЦИИ
3.1. Основные понятия и определения
3.2. Графики элементарных функций
3.3. Преобразования графиков функций
3.4. Изображения некоторых множеств точек на плоскости
Тест для проверки теоретических знаний
Примеры
Задачи для самостоятельного решения
Контрольный тест
Рекомендуем использовать этот материал при тщательной подготовке к сдаче ЕГЭ на высокий балл.
В теме содержатся теория и практические задания различного уровня сложности.
Смотреть в PDF:
Или прямо сейчас: Скачайте в pdf файле.


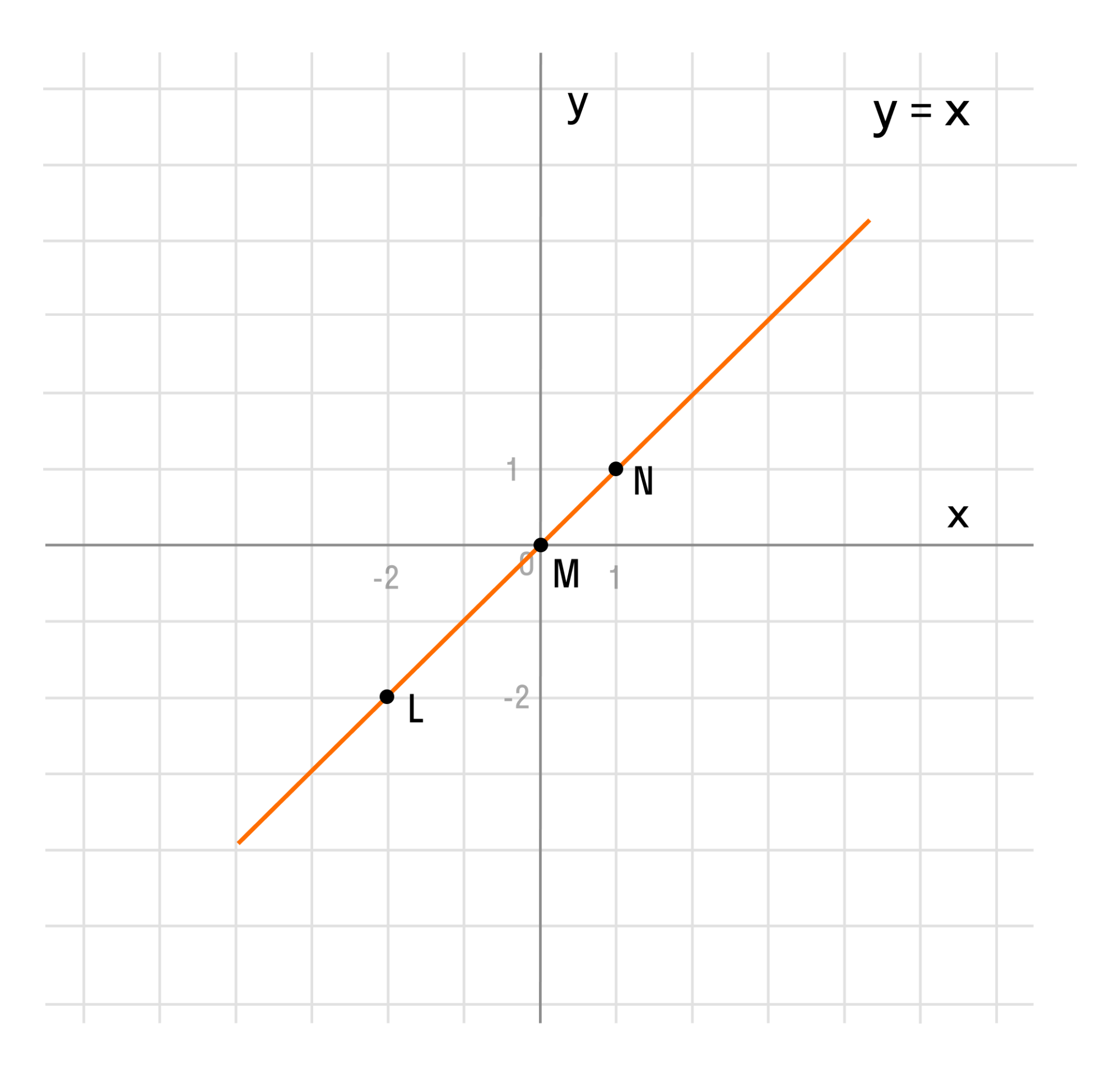
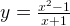
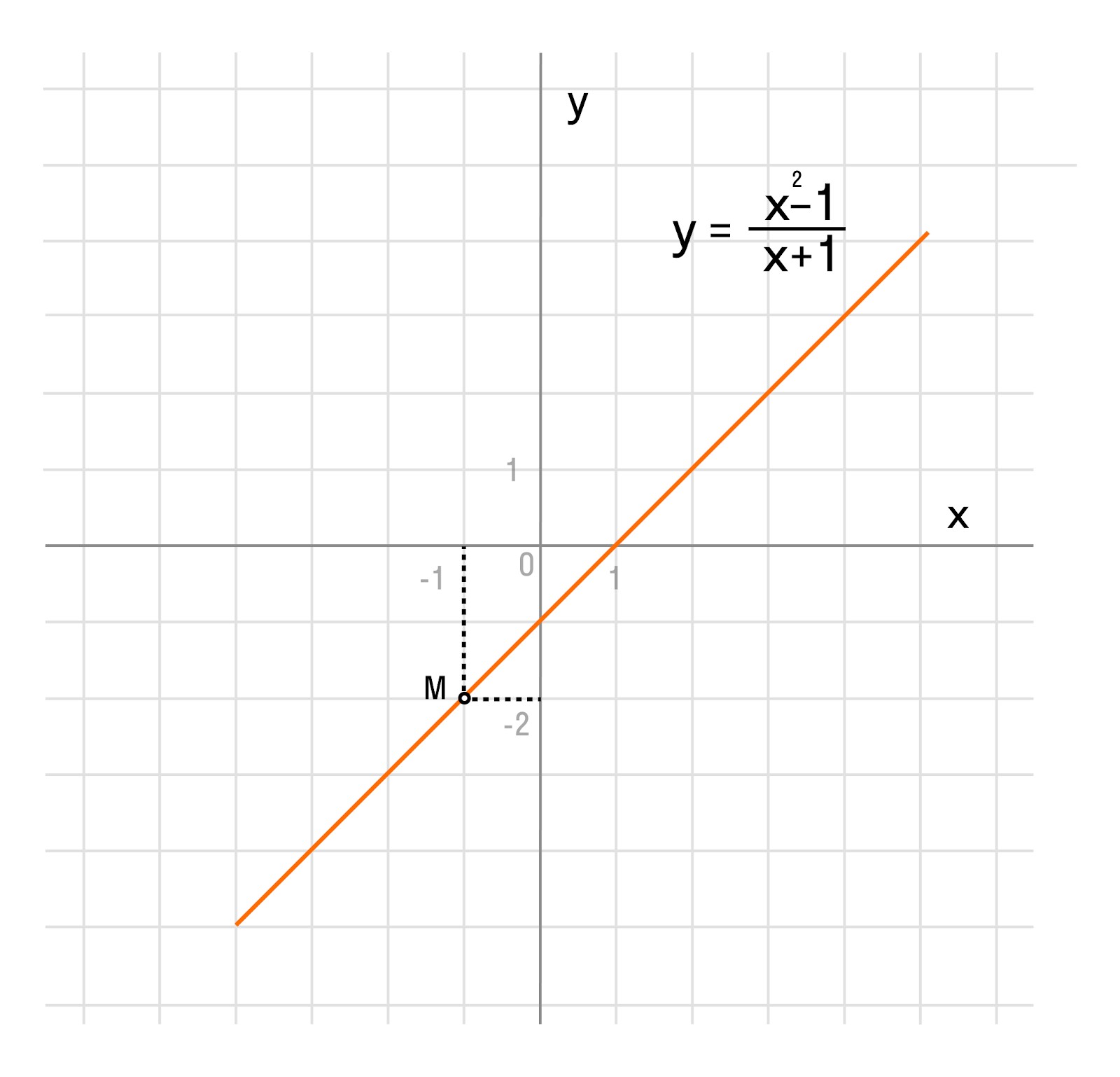
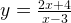
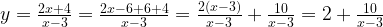
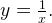
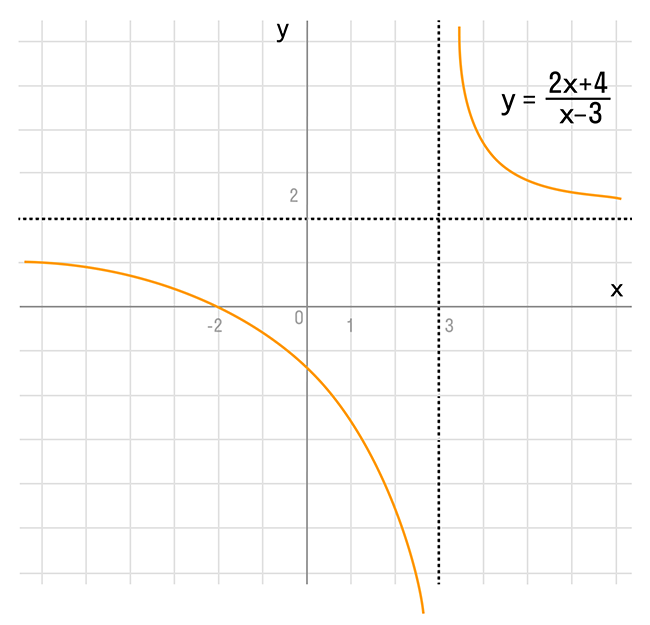
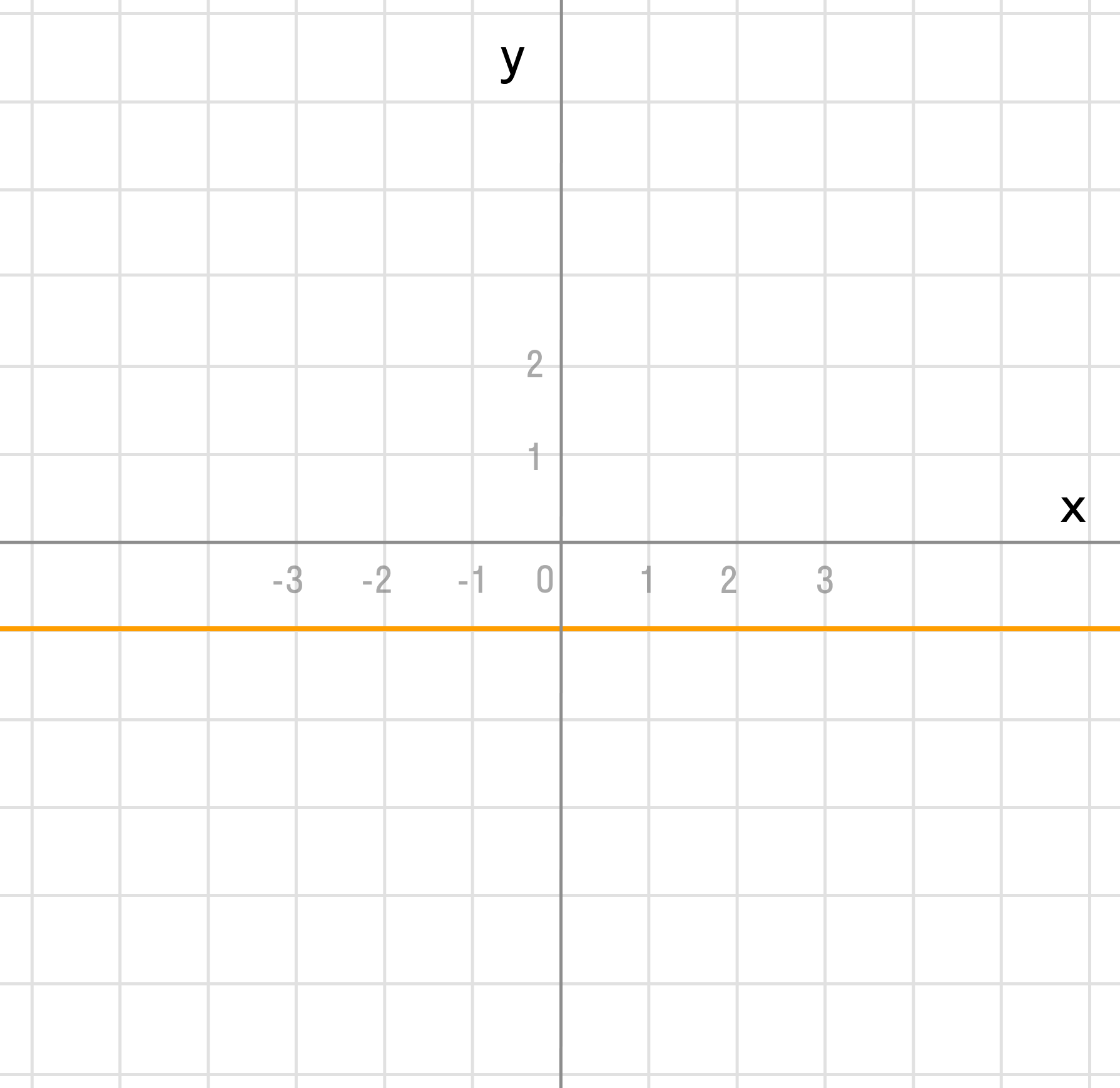
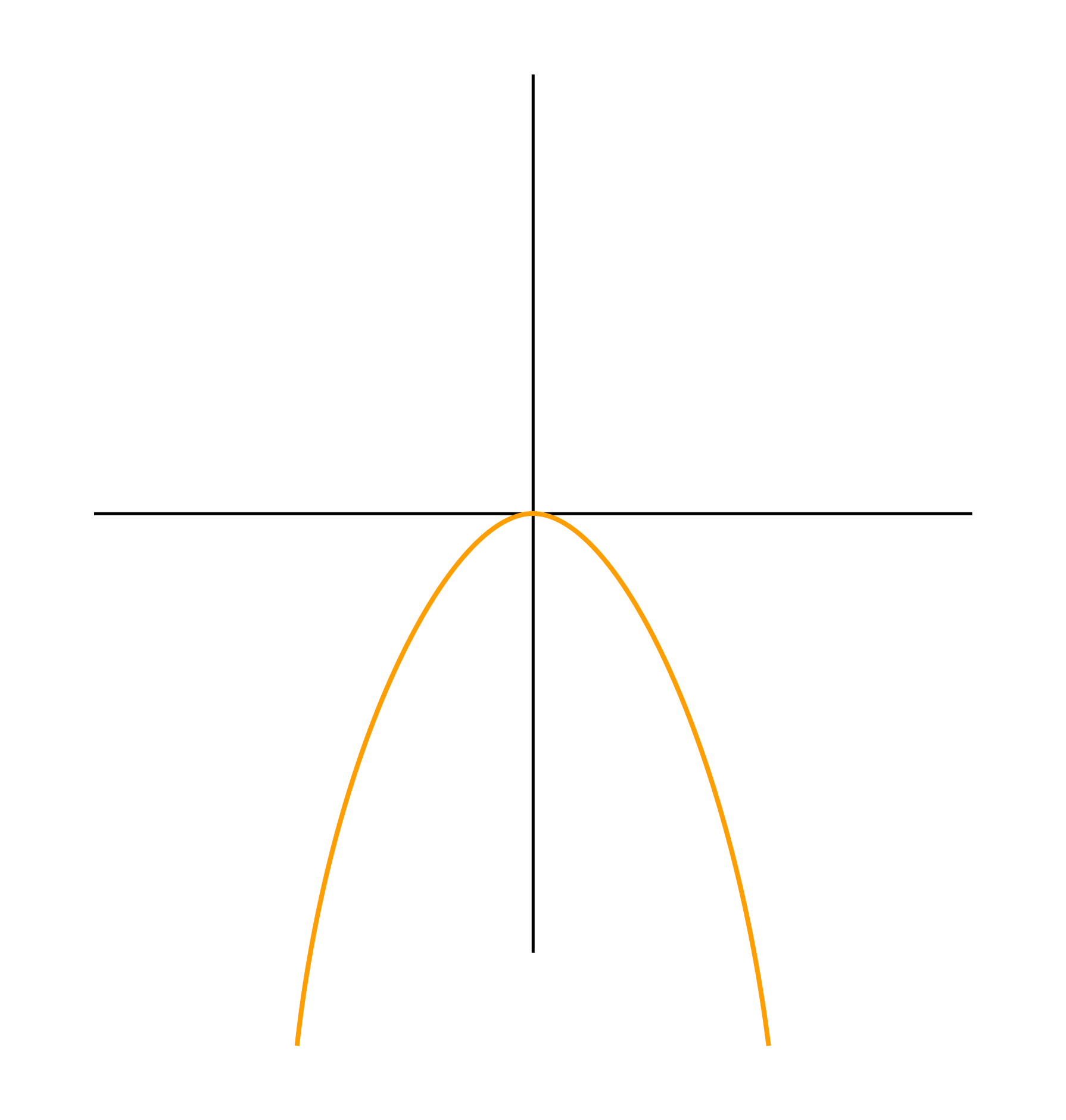
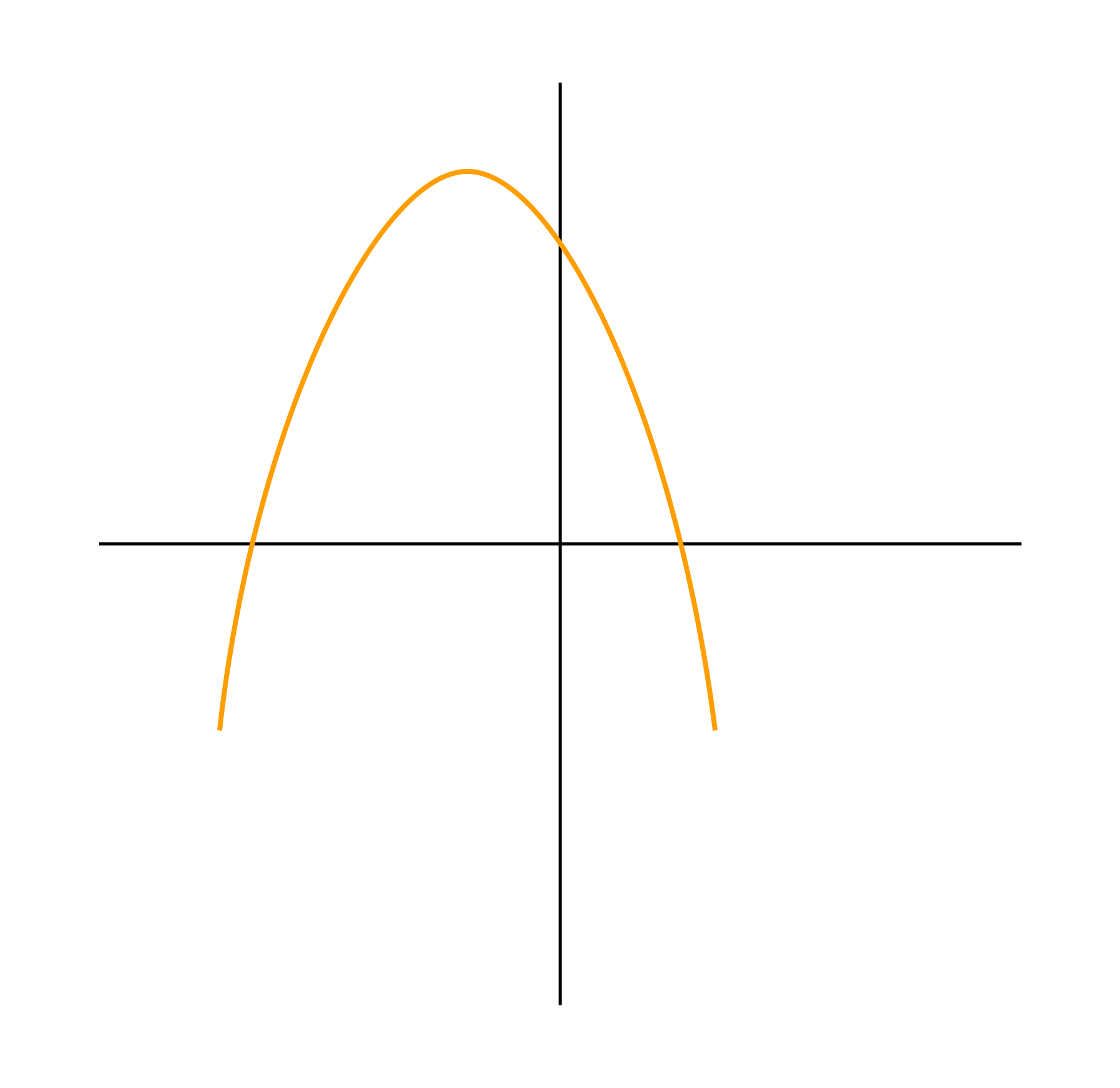
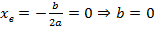
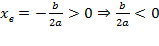 , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
, т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.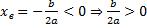 , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.
, т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.