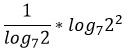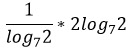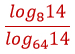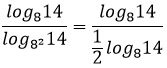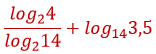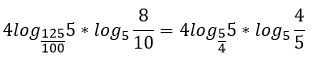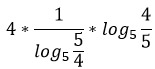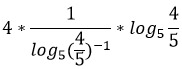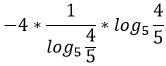Теория по логарифмам для егэ профиль

Логарифмом положительного числа $b$ по основанию а, где $a>0$, $a≠1$, называется показатель степени, в которую надо возвести число $а$, чтобы получить $b$.

Особенно можно выделить три формулы:

$log_{a}a=1;$

$log_{a}1=0;$

$log_{a}a^b=b.$

Десятичным логарифмом числа называют логарифм этого числа по основанию $10$ и пишут $lg⁡b$ вместо $log_{10}b$.

Натуральным логарифмом числа называют логарифм этого числа по основанию $е$, где $е$ – иррациональное число, приближенно равное $2.7$. При этом пишут $lnb$, вместо $log_{e}b$

Свойства логарифмов.

Все свойства логарифмов мы будем рассматривать для $a>0, a≠1, b>0, c>0, m$ – любое действительное число.

1. Для любых действительных чисел $m$ и $n$ справедливы равенства:

$log{_а}b^m=mlog_{a}b;$

$log_{a^m}b={1}/{m}log_{a}b.$

$log_{a^n}b^m={m}/{n}log_{a}b$

2. Логарифм произведения равен сумме логарифмов по тому же основанию от каждого множителя.

$log_{a}(bc)=log_{a}b+log_{a}c$

3. Логарифм частного равен разности логарифмов от числителя и знаменателя по тему же основанию

$log_{a}{b}/{c}=log_{a}b-log_{a}c$

4. При умножении двух логарифмов можно поменять местами их основания

$log_{a}b·log_{c}d=log_{c}b·log_{a}d$, если $a$, $b$, $c$, $d>0$, $a≠1$, $b≠1.$

5. $c^{log_{a}b}=b^{log_{a}c}$, где $а, b, c>0, a≠1$

6. Формула перехода к новому основанию

$log_{a}b={log_{c}b}/{log_{c}a}$

7. В частности, если необходимо поменять местами основание и подлогарифмическое выражение

$log_{a}b={1}/{log_{b}a}$

Логарифм и его свойства

Логарифм — это показатель степени, в которую надо возвести основание степени, чтобы получилось некоторое число.

Ничего не понятно! Будем разбираться на простых примерах.

Пусть дано уравнение: 2^х = 4 (2 — основание степени, х — неизвестный показатель степени, 4 — некоторое число).

Это показательное уравнение. Интуитивно понятно, что неизвестная переменная х равна 2, т.к. 2² = 4.

Модернизируем уравнение: 2^х = 5.

Хм… И как?

х = 2 — мало, а х = 3 много, т.е. х — это какое-то дробное число, скорее всего, даже иррациональное. В любом случае, точно подобрать не получится, разве что на калькуляторе и с округлением.

И поэтому для таких вот случаев ленивые математики придумали определение логарифма. В общем, корнем этого уравнения будет являться х = log₂5 (читается: логарифм числа 5 по основанию 2).

Естественно, что у логарифма есть ограничения, числа a и b должны быть положительными и а не должно быть равно 1 (Если пораскинуть мозгами, станет понятно почему).

Пришло время красиво записать полное определение логарифма на математическом языке, с помощью которого ты сможешь решать простейшие показательные уравнения (наподобие тех, что были выше).

Мы рассмотрели самый приятный вид логарифма. Есть еще два вида, десятичный и натуральный.

В десятичном логарифме основание равно 10, а в натуральном — е (е ≈ 2,718…).

Такие логарифмы пишутся немного по-другому:

log₁₀b = lgb;

log_eb = lnb.

Основные свойства логарифмов.

Свойства работают в обе стороны, при этом a, b, c — положительные и основания логарифмов не равны 1.

Прототипы заданий из ЕГЭ по математике (ФИПИ). Базовый и профильный уровни.

Задание 1.

Найдите корень уравнения 

___________

Для решения этого уравнения используем определение логарифма. Продублирую его еще раз:

Наша задача основание логарифма 3 возвести в третью степень и приравнять выражению в скобках. Уравнение примет вид:

2х — 7 = 3³.

При этом важно не забыть, что (2х — 7) должно быть больше нуля. Это важно.

Решаем обычное линейное уравнение:

2х — 7 = 27;

2х = 34;

х = 17.

Надо убедится, что корень подходит области определения логарифма: 2 · 17 — 7 > 0. Неравенство верно.

Ответ: 17.

Задание 2.

Найдите корень уравнения

___________

Основания у логарифмов одинаковые, значит можно приравнять (5х — 23) и 17.

Снова получаем обычное линейное уравнение:

5х — 23 = 17;

5х = 40;

х = 8.

Удовлетворяет ли корень области определения логарифма? Да (5 · 8 — 23 > 0).

Ответ: 8.

Задание 3.

Найдите значение выражения

___________

Воспользуемся 8-м свойством: изменим основание первого логарифма на удобное нам. А еще представим 4 как 2 в квадрате.

Теперь преобразуем второй логарифм, используя свойство 4.

Одинаковые логарифмы сокращаются…

Ответ: 2.

Задание 4.

Найдите значение выражения

___________

Представим основание нижнего логарифма как 8² и по свойству 5 вынесем показатель степени вперед.

Логарифмы сокращаются, остается разделить 1 на ½.

Ответ: 2.

Задание 5.

Найдите значение выражения

___________

У логарифмов одинаковые основания, значит сработает свойство 2.

В какую степени надо возвести число 7, чтобы получилось 49? Правильно, 2.

Ответ: 2.

Задание 6.

Найдите значение выражения

___________

Для дроби используем свойство 7, только наоборот, а затем — свойство 2.

Ответ: 1.

Задание 7.

Найдите значение выражения

___________

Представим десятичные дроби в виде обыкновенных и сократим их.

Поменяем основание у первого логарифма, используя свойство 8.

Представим дробь 5/4 как 4/5 в минус первой степени.

По свойству 4 выносим -1 вперед.

Логарифмы равны и сокращаются.

Ответ: -4.

Факт 1.
(bullet) Логарифм по основанию (a) от (b) – это число (t), которое показывает, в какую степень нужно возвести (a), чтобы получить (b).
Ограничения: числа (a) и (b) такие, что (a>0, ane 1, b>0).
[Large{{color{blue}{log_a{b}=tquadLeftrightarrowquad
a^t=b }}}]
Т.к. мы имеем право возводить в любую степень, то (tin
mathbb{R}).
Таким образом, верно основное логарифмическое тождество [{Large{a^{log_ab}=b}}]
(bullet) Справедливы следующие формулы: [{large{begin{array}{|ll|l|}
hline qquad qquad qquad qquad {small{text{Формулы}}}
&& qquad qquad{small{text{Ограничения}}}\
&&\
hline textbf{(1)} log_a1=0&&a>0, ane 1\
&&\
textbf{(2)} log_aa=1 &&a>0, ane 1\
&&\
textbf{(3)} log_{a}{b^m}=mlog_a|b|&(m —
{small{text{четн.}}})&a>0, ane 1, bne 0\
&&\
textbf{(4)}log_{a}{b^m}=mlog_ab& (m —
{small{text{нечетн.}}})&a>0, ane 1, b>0\
&&\
textbf{(5)} log_{a^n}{b}=frac 1nlog_{|a|}b&(n —
{small{text{четн.}}})&ane 0, ane 1, b>0\
&&\
textbf{(6)}log_{a^n}b=frac1nlog_ab&(n —
{small{text{нечетн.}}})&a>0, ane 1, b>0\
&&\
textbf{(7)} log_a{bc}=log_a|b|+log_a|c|&&a>0, ane 1, bcne 0\
&&\
textbf{(8)}
log_a{dfrac bc}=log_a|b|-log_a|c|&&a>0, ane 1,bcne 0 \
&&\
textbf{(9)}
a^{log_ab}=b &&a>0, ane 1, b>0\
&&\
textbf{(10)}c^{log_ab}=b^{log_ac}&&a>0, ane 1, b>0, c>0\
&&\
textbf{(11)} log_abcdot log_bc=log_ac && a>0, ane 1,b>0, bne 1, c>0\
&&\
textbf{(11′}) log_bc=dfrac{log_ac}{log_ab}&&a>0, ane 1,b>0, bne 1, c>0\
&&\
&&\
{small{text{ЧАСТНЫЕ СЛУЧАИ:}}}&& \
textbf{(12)} log_abcdot log_ba=1 && a>0, ane 1, b>0, bne 1\
&&\
textbf{(12′}) log_ab=dfrac1{log_ba}&&a>0, ane 1, b>0, bne 1\
&&\ hline
end{array}}}]

Заметим, что при выполнении ограничений данные формулы верны в обе стороны!

Свойства  и графики логарифмических функций

 

1.    
Область определения: D( y ): x ϵ (0; +∞).

2.    
Множество значений: E( y ): y ϵ (-∞;+∞).

3.    
Функция не является четной и не является нечетной.

4.    
Нули функции: при x = 1 логарифмическая функция y = log a x
приобретает значение, равное 0.

5.    
График пересекает ось O x в точке (1; 0).

6.    
Интервалы монотонности: При a > 1 функция возрастает на
интервале (0; +∞). При 0 < a < 1 функция убывает на интервале (0; +∞)

7.    
Интервалы выпуклости / вогнутости: При a > 1 график функции
выпуклый на интервале (0; +∞). При 0 < a < 1 график функции вогнутый на
интервале (0; +∞).

8.    
Из равенства логарифмов двух чисел по одному и тому же основанию
следует равенство самих чисел: log a x = log a y => x = y , a > 0, a ≠ 1.

Примеры решения логарифмических уравнений

Краткий алгоритм решения логарифмических
уравнений:

1. Привести логарифмы в разных частях уравнения к одному
основанию, исключая коэффициенты перед ними с помощью свойства логарифмов.

2. Исключить логарифмы, прибегая к правилу потенцирования.

3. Решить стандартное уравнение.

4. Проверить результат.

5.Записать ответ.

Несколько схем решений логарифмических
уравнений

Схема выполнения равносильных преобразований
логарифмических неравенств (потенцирование неравенств)

 

Обобщенный метод интервалов

Схема:

1. Привести неравенство к такому виду, где в
левой части находится функция f(x), а в правой 0.

2. Найти область определения функции f(x).

3. Найти нули функции f(x), то есть – решить
уравнение f(x) = 0 (а решать уравнение обычно проще, чем решать неравенство)

4. Изобразить на числовой прямой область
определения и нули функции.

5. Определить знаки функции f(x) на полученных
интервалах.

6. Выбрать интервалы, где функция принимает
необходимые значения и записать ответ.

Запомни:
знаки расставляются только на области определения функции!

Метод рационализации

(метод
декомпозиции, метод замены множителей, метод замены функции, правило знаков)

Метод рационализации заключается в замене сложного выражения F(x)ü0 на более простое выражение G(x)ü0 равносильно неравенству F(x)ü0 в области определения выражения F(x).

Выделим некоторые выражения F и
соответствующие им рационализирующие выражения G, где f, g, h, p, q – выражения с переменной x (h>0; h≠1; f>0, g>0), a –
фиксированное число (a>0; a≠1)

 

Схема

1. Найти ОДЗ неравенства

2. Подобрать нужное
рационализирующее выражение

3. Решить неравенство, полученное в
п.2

4. Найти пересечение множеств п 2 и
п. 3

5.
Записать ответ

Интернет-ресурсы для подготовки к профильному
ЕГЭ по математике

1.       alexlarin.net
— каждую неделю публикуются качественные пробники.

2.       ege.sdamgia.ru
— лучший онлайн-тренажёр с решениями заданий.

3.       yandex.ru/tutor/
— Яндекс.Репетитор — тренировочные варианты онлайн.

4.       alleng.org/edu/math3.htm
— книги в pdf формате.

5.       berdov.com/ege/
— хорошие пробники, много нестандартных и сложных заданий.

6.       4ege.ru/video-matematika/50912…
— видеокурс с теорией и практикой.

7.       https://math100.ru/ege/ege-profil/-
задание ЕГЭ в pdf формате, с ответами.

8.       https://www.mathm.ru- задания разделены
по темам и уровням сложности

Шпаргалка для подготовки к ЕГЭ по математике

(профильный уровень) по теме:

Логарифмы.

Уравнения. Неравенства

10 июня 2022

В закладки

Обсудить

Жалоба

Логарифмы для ЕГЭ с нуля

Решаем задачи на логарифмы от простых к сложным.

00:28 — Что такое логарифм
02:51 — Мини-практика
04:37 — Что такое lg
05:02 — Основное логарифмическое тождество
07:21 — Формула суммы логарифмов
08:43 — Формула разности логарифмов
09:30 — Еще одно свойство логарифмов
11:54 — Логарифмическое уравнение
13:21 — Опасный момент
14:46 — ОДЗ
16:51 — Реальные примеры из ЕГЭ

Автор: Марсель Нуртдинов.

Источник: vk.com/marsel_tutor

Логарифмические уравнения

Логарифмом положительного числа $b$ по основанию $а$, где $a>0, a ≠ 1$, называется показатель степени, в которую надо возвести число $а$, чтобы получить $b$.

$log_<2>8 = 3$, т.к. $2^3 = 8;$

Особенно можно выделить три формулы:

Основное логарифмическое тождество:

Это равенство справедливо при $b> 0, a> 0, a≠ 1$

Некоторые свойства логарифмов

Все свойства логарифмов мы будем рассматривать для $a> 0, a≠ 1, b> 0, c> 0, m$ – любое действительное число.

1. Для любого действительного числа $m$ справедливы равенства:

2. Для решения задач иногда полезно следующее свойство: Если числа $а$ и $b$ на числовой оси расположены по одну сторону от единицы, то $log_b>0$, а если по разные, то $log_b 0$

Представим обе части уравнения в виде логарифма по основанию 2

Если логарифмы по одинаковому основанию равны, то подлогарифмические выражения тоже равны.

Т.к. основания одинаковые, то приравниваем подлогарифмические выражения

Перенесем все слагаемые в левую часть уравнения и приводим подобные слагаемые

Проверим найденные корни по условиям: $<table x^2-3x-5>0; 7-2x>0;$

При подстановке во второе неравенство корень $х=4$ не удовлетворяет условию, следовательно, он посторонний корень

4. Уравнения вида $a^x=b$. Решаются логарифмированием обеих частей по основанию $а$.

Решить уравнение $log_5log_2(x+1)=1$

Сделаем в обеих частях уравнения логарифмы по основанию $5$

Т.к. основания одинаковые, то приравниваем подлогарифмические выражения

Далее представим обе части уравнения в виде логарифма по основанию $2$

ОДЗ данного уравнения $x+1>0$

Подставим вместо х в неравенство $31$ и проверим, получиться ли верное условие $32>0$, следовательно, $31$ корень уравнения.

Логарифмические уравнения

Прежде чем решать логарифмические уравнения, повторим еще раз определение логарифма и основные формулы.

Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести a, чтобы получить b.

При этом 0,;a> 0,;aneq 1′ alt=’b> 0,;a> 0,;aneq 1′ />.

Обратим внимание на область допустимых значений логарифма:

Основное логарифмическое тождество:

Основные формулы для логарифмов:

(Логарифм произведения равен сумме логарифмов)

(Логарифм частного равен разности логарифмов)
(Формула для логарифма степени)

Формула перехода к новому основанию:

Мы знаем, как выглядит график логарифмической функции. Эта функция монотонна. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает. Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. И в любом случае каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, то равны и сами числа.

Все это пригодится нам в решении логарифмических уравнений.

Простейшие логарифмические уравнения

Основания логарифмов равны, сами логарифмы тоже равны – значит, равны и числа, от которых они берутся.
Обычно ученики запоминают это правило в краткой жаргонной формулировке: «Отбросим логарифмы!» Конечно, мы «отбрасываем» их не просто так, а пользуясь свойством монотонности логарифмической функции.

Решая логарифмические уравнения, не забываем про область допустимых значений логарифма. Помним, что выражение определено при 0,;a> 0,;aneq 1′ alt=’b> 0,;a> 0,;aneq 1′ />.

Очень хорошо, если вы, найдя корень уравнения, просто подставите его в уравнение. Если после такой подстановки левая или правая часть уравнения не имеют смысла – значит, найденное число не является корнем уравнения и не может быть ответом задачи. Это хороший способ проверки на ЕГЭ.

2. Решите уравнение:

В левой части уравнения – логарифм, в правой – число 7. Применив основное логарифмическое тождество, представим число 7 в виде . Дальше все просто.

3. Решите уравнение:

Видите число 2 перед логарифмом в правой части уравнения? Сейчас оно мешает вам «отбросить логарифмы». Что с ним сделать, чтобы в левой и правой частях были просто логарифмы по основанию 5? Конечно же, поможет формула для логарифма степени.

4. Решите уравнение:

Область допустимых значений: 0.’ alt=’4+x> 0.’ /> Значит, -4.’ alt=’x> -4.’ />

Представим 2 в правой части уравнения как — чтобы слева и справа в уравнении были логарифмы по основанию 5.

Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом -4′ alt=’x> -4′ />.

5. Решите уравнение:

Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:

0\ x^<2>-4> 0\ x^<2>+x=x^<2>-4 endright.Leftrightarrow left <beginx^<2>+x> 0\ x^<2>-4> 0\ x=-4 endright.Leftrightarrow x=-4′ alt=’log _<8>left ( x^<2>+x right )=log _<8>left ( x^<2>-4 right )Leftrightarrow left <beginx^<2>+x> 0\ x^<2>-4> 0\ x^<2>+x=x^<2>-4 endright.Leftrightarrow left <beginx^<2>+x> 0\ x^<2>-4> 0\ x=-4 endright.Leftrightarrow x=-4′ />
Ответ: –4.

Заметим, что решения логарифмических уравнений лучше всего записывать в виде цепочки равносильных переходов. Это поможет нам не забыть про область допустимых значений.

Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:

Запишем решение как цепочку равносильных переходов.

0 endright.Leftrightarrow left <beginleft (2^<log _<2>left ( 4x+5 right )> right )^<frac<1><2>>=9\ x> -1frac<1> <4>endright.Leftrightarrow left <beginleft ( 4x+5 right )^<frac<1><2>>=9\ x> -1frac<1> <4>endright.Leftrightarrow left <beginsqrt<4x+5>=9\ x> -1frac<1> <4>endright.Leftrightarrow left <begin4x+5=81\ x> -1frac<1> <4>endright.Leftrightarrow left <beginx=19\ x> -1frac<1> <4>endright.’ alt=’2^<log _<4>left ( 4x+5 right )>=9Leftrightarrow left <begin2^frac<<log _<2>left ( 4x+5 right )>><2>=9\ 4x+5> 0 endright.Leftrightarrow left <beginleft (2^<log _<2>left ( 4x+5 right )> right )^<frac<1><2>>=9\ x> -1frac<1> <4>endright.Leftrightarrow left <beginleft ( 4x+5 right )^<frac<1><2>>=9\ x> -1frac<1> <4>endright.Leftrightarrow left <beginsqrt<4x+5>=9\ x> -1frac<1> <4>endright.Leftrightarrow left <begin4x+5=81\ x> -1frac<1> <4>endright.Leftrightarrow left <beginx=19\ x> -1frac<1> <4>endright.’ />

Обратите внимание: переменная х и под логарифмом, и в основании логарифма. Мы помним, что основание логарифма должно быть положительно и не равно 1.

ОДЗ:
0\ x> 0\ xneq 1 endright.’ alt=’left <begin12-x> 0\ x> 0\ xneq 1 endright.’ />

Теперь можно «убрать» логарифмы.

— посторонний корень, поскольку должно выполняться условие 0′ alt=’x> 0′ />.

8. Решите уравнение .

ОДЗ уравнения: 0′ alt=’x> 0′ />

Сделаем замену . Как и в алгебраических уравнениях, мы делаем замену переменной всегда, когда только возможно.

Вернемся к переменной х:

Выражение под логарифмом всегда положительно – поскольку к неотрицательной величине прибавляем 25. Выражение под корнем в правой части также положительно. Значит, х может быть любым действительным числом.

Представим сумму логарифмов в левой части как логарифм произведения. В правой части – перейдем к логарифму по основанию 3. И используем формулу логарифма степени.

Такое уравнение называется биквадратным. В него входят выражения и . Сделаем замену

Вернемся к переменной х. Получим:

. Мы нашли все корни исходного уравнения.

Логарифмические уравнения могут встретиться вам и в задании №1 Профильного ЕГЭ по математике, и в задании №12. И если в задании №1 нужно решить простейшее уравнение, то в задаче 12 решение состоит из двух пунктов. Второй пункт – отбор корней на заданном отрезке или интервале.

Поверните устройство

1. Классы
2. ЕГЭ (профиль)
3. 01. Простейшие уравнения
4. Теория: 07. Элементарные логарифмические уравнения

Найдите корень уравнения:

Решим уравнение (displaystyle log_7(13-3x)=2<small .>)

Если (displaystyle a>0,, b>0 ) и (displaystyle acancel<=>1), то по определению логарифма

(displaystyle log_a b=c) равносильно (displaystyle b=a^c <small .>)

(displaystyle log_7(13-3x)=2) равносильно (displaystyle 13-3x=7^2 <small .>)

Решим линейное уравнение (displaystyle 13-3x=7^2 <small :>)

Так как (displaystyle 13-3x=7^2 <small ,>) то ограничение (displaystyle 13-3x>0 ) будет верным для решения линейного уравнения.