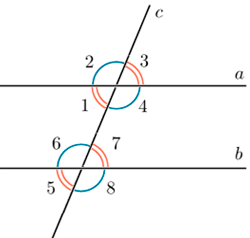
Теория по математике 9 класс к экзамену - Помощь в подготовке к экзаменам и поступлению

1. Углы

Вертикальные углы равны (на рис. 1 и 3; 6 и 8 и др.).

Внутренние накрест лежащие углы при параллельных прямых и секущей равны. (на рис. 4 и 6; 1 и 7).

Сумма внутренних односторонних углов при параллельных прямых и секущей равна 180˚ (на рис. 4 и 7; 1 и 6).

Соответственные углы при параллельных прямых и секущей равны. (на рис. 3 и 7; 1 и 5 и др.).

Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая перпендикулярна третьей прямой.

2. Медиана, биссектриса, высота

Биссектриса треугольника — отрезок, соединяющий вершину треугольника с точкой на противоположной стороне и делящий угол треугольника пополам.

Высота треугольника – перпендикуляр опущенный из вершины угла на противоположную сторону.

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

В любом треугольники все биссектрисы пересекаются в одной точке, все медианы пересекаются в одной точке, все медианы пересекаются в одной точке.

3. Треугольник

Сумма углов в любом треугольнике 180˚.

Средняя линия треугольника – прямая проходящая через середины двух сторон. Средняя линия параллельна одной из сторон и равна половине этой стороны.

Виды треугольников: тупоугольный (один угол тупой), прямоугольный (один угол прямой 90˚), остроугольный (все углы острые, меньше 90˚).

Равнобедренный треугольник — треугольник, у которого равны две стороны.

Свойства равнобедренного треугольника:

в равнобедренном треугольнике углы при основании равны;
в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой;

Равносторонний треугольник — треугольник,
у которого все стороны равны. (все углы по 60 градусов)

Всякий равносторонний треугольник является равнобедренным,
но не всякий равнобедренный — равносторонним.

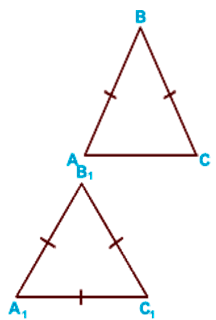
Три признака равенства треугольников

I признак по двум сторонам и углу между ними

II признак (по стороне и прилежащим углам)

III признак (по трем сторонам)

Признаки подобия треугольников

I признак по двум равным углам

II признак по двум пропорциональным сторонам и углу между ними

III признак по трем пропорциональным сторонам

Площади подобных фигур относятся как коэффициент подобия в квадрате.

Объемы подобных фигур относятся как коэффициент подобия в кубе.

Треугольник называется прямоугольным, если один из его углов прямой.

Стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла, – гипотенузой. (самая большая сторона это гипотенуза, две др катеты).

Свойства прямоугольного треугольника

Сумма острых углов прямоугольного треугольника равна 90 градусов.

Катет, лежащий против угла в 30˚, равен половине гипотенузы.

Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы.

Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности.

Теорема Пифагора:

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: a² + b² = c².

Пифагоровы тройки:

3, 4, 5
6, 8, 10
5, 12, 13
9, 12, 15

Признаки равенства прямоугольных треугольников

По двум катетам.
По гипотенузе и катету.
По катету и прилежащему острому углу.
По катету и противолежащему острому углу.
По гипотенузе и острому углу.

Признаки подобия прямоугольных треугольников:

По острому углу.
По пропорциональности двух катетов.
По пропорциональности катета и гипотенузы.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

Высота, проведенная из вершины прямого угла, разбивает прямоугольный треугольник на два подобных треугольника. Каждый из этих треугольников подобен исходному.

Высота прямоугольного треугольника: h=ab/c или h = (где АВ гипотенуза, СЕ высота опущенная на гипотенузу).

В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равна половине гипотенузы: m=c/2 (R=с/2=mc).

3. Четырехугольники

Сумма углов в любом четырехугольнике 360˚.

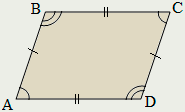
Параллелограмм

Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны.

У параллелограмма противолежащие стороны равны и противолежащие углы равны.

Сумма любых двух соседних углов параллелограмма равна 180°.

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

Каждая диагональ делит параллелограмм на два равных треугольника.

Две диагонали параллелограмма делят его на четыре равновеликих треугольника.

Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

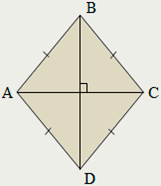
Ромб

Ромбом называется параллелограмм, у которого все стороны равны.

Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.

Прямоугольник

Прямоугольником называется параллелограмм, у которого все углы прямые.

Диагонали прямоугольника равны и точкой пересечения делятся на четыре равных отрезка.

Квадрат.

Квадрат – это прямоугольник, у которого все стороны равны.

Диагонали квадрата равны и перпендикулярны.

Сторона и диагональ квадрата связаны соотношениями: .

Трапеция

Трапецией называется четырёхугольник у которого только две противолежащие стороны параллельны.

Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.

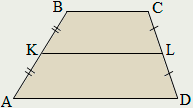
Средняя линия трапеции параллельна её основаниям и равна их полусумме.

Равнобокой называется трапеция, у которой боковые стороны равны.

У равнобокой трапеции: диагонали равны; углы при основании равны; сумма противолежащих углов равна 180.

Стороны и диагональ равнобокой трапеции связаны соотношением: d² = ab+c².

Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям.

4. Окружность

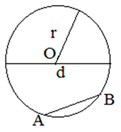
Отрезок, соединяющий центр окружности с любой точкой окружности называется радиусом (r) окружности.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром окружности.

Прямая, имеющая с окружностью одну общую точку, называется касательной. Касательная и радиус проведенный в точку касания пересекаются под прямым углом.

Прямая, имеющая с окружностью две общие точки, называется секущей.

Центральный угол окружности – это угол, вершина которого лежит в центре окружности. Центральный угол равен дуге на которую он опирается.

Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают ее. Вписанный угол равен половине дуги на которую опирается.

Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.

Вписанный угол, опирающийся на диаметр равен 90˚.

Все вписанные углы, опирающиеся на одну и туже дугу равны.

Теорема косинусов:

a² = b² + c² – 2bccosa

Теорема синусов:

5. Формулы площадей

См. продолжение статьи

Источник

Теория для успешной подготовки по математике для ОГЭ

Вся необходимая теория для успешной подготовки к Государственной итоговой аттестации в 9 классе по математике, которая с 2015 года называется ОГЭ — общий государственный экзамен.

Содержимое разработки

9 класс Алгебра №1

Чтобы перемножить десятичные дроби, надо умножать, не обращая внимания на запятую, а в полученном результате отсчитать справа налево столько знаков, сколько их после запятой во всех множителях.
Чтобы перемножить десятичную дробь и смешанное число, надо числа записать в каком-то одном виде.
Если смешанное число не переводится в десятичную дробь, то десятичную дробь переводят в обыкновенную следующим образом: дробную часть записывают в числитель, а в знаменатель надо записать единицу с таким количеством нулей, сколько знаков после запятой в дробной части десятичной дроби.
Чтобы записать смешанное число в виде неправильной дроби, надо целую часть умножить на знаменатель, прибавить числитель и результат записать в числитель, знаменатель оставить тот же.
Чтобы записать смешанное число в виде неправильной дроби, надо целую часть умножить на знаменатель, прибавить числитель и результат записать в числитель, знаменатель оставить тот же.
Чтобы сократить дробь, надо числитель и знаменатель разделить на одно и то же число, не равное нулю.
Если в знаменателе дроби стоит 10, 100, 1000 и т.д., то не следует на них сокращать, а лучше перевести обыкновенную дробь в десятичную.
Если числитель дроби меньше знаменателя, то дробь называется правильной, и ее целая часть равна нулю.
Если числитель дроби меньше знаменателя, то дробь называется правильной, и ее целая часть равна нулю.
Если числитель дроби больше знаменателя, то дробь называется неправильной, и из нее можно выделить целую часть.
При сравнении десятичных дробей сначала надо сравнить целые части. Та дробь больше, у которой целая часть больше.
Чтобы привести дроби к общему знаменателю (желательно к наименьшему), надо найти НОК знаменателей дробей, далее новый знаменатель разделить на старый знаменатель каждой дроби (получим дополнительный множитель для каждой дроби), далее свой дополнительный множитель умножить на числитель и знаменатель своей дроби.
Чтобы разделить смешанные числа, надо записать их в виде неправильных дробей и разделить по правилу обыкновенных дробей.
Чтобы разделить смешанные числа, надо записать их в виде неправильных дробей и разделить по правилу обыкновенных дробей.
Чтобы число умножить на сумму, надо это число умножить на каждое слагаемое.
Чтобы из меньшего числа вычесть большее, надо из большего модуля вычесть меньший и перед полученным результатом поставить знак «минус».
Квадрат числа можно вычислить следующим образом: а² = а ∙ а.
Произведение взаимно обратных чисел равно единице.
Чтобы умножить десятичную дробь на 100, надо запятую перенести на два знака вправо.
Чтобы умножить десятичную дробь на 0,1, надо запятую перенести влево на один знак.
Четная степень отрицательного числа дает «положительный» результат.
Нечетная степень отрицательного числа дает «отрицательный» результат.
Сумма противоположных чисел равна нулю.
Чтобы сложить отрицательные числа, надо сложить их модули, а перед полученным результатом поставить знак «минус».
Чтобы из одного числа вычесть другое, надо к первому числу прибавить число, противоположное другому.
Если в дробях одинаковые числители, то та дробь больше, у которой знаменатель меньше.
Если разделить два числа с разными знаками, то получится «отрицательный» результат.
Из двух отрицательных чисел больше то, модуль которого меньше.
Чем в большую степень возводить правильную десятичную дробь, тем больше знаков после запятой получится.

Содержимое разработки

9 класс Алгебра №2

Если из меньшего числа вычесть большее, то результат будет отрицательный.
Если из большего числа вычесть меньшее, то результат будет положительный.
Чтобы сложить числа с разными знаками, надо из большего модуля вычесть меньший, и поставить знак числа с большим модулем.
При решении неравенств можно переносить слагаемые из одной части в другую, меняя знак слагаемых на противоположный.
Чтобы вычесть из одного числа другое, надо к первому числу прибавить число противоположное второму.
Чтобы сложить два отрицательных числа, надо сложить их модули, а перед полученным ответом поставить знак «минус».
Если из нуля вычесть положительное число, то результат будет отрицательный.
Если 0
Если -1
На координатной (числовой) прямой числа, которые лежат левее нуля, называются отрицательными.
На координатной (числовой) прямой ценой деления называется длина каждого деления в единичных отрезках.
На координатной (числовой) прямой числа, которые лежат правее нуля, называются положительными.
На координатной (числовой) прямой число, которое находится правее, имеет большую координату.
По одному из свойств неравенств: если аb, то
По одному из свойств неравенств: если аb, то –а–b
Произведение двух отрицательных чисел дает положительный результат.
Чем число на координатной (числовой) прямой дальше от нуля, тем больше его модуль.
Сумма двух отрицательных чисел дает отрицательный результат.
Если из меньшего числа вычесть большее, то получится отрицательное число.
Если данное число положительное, то противоположное ему число — отрицательное.
Квадрат любого числа есть число неотрицательное.
Если число умножить на правильную дробь, то оно уменьшается.
Если к обеим частям неравенства прибавить одно и то же число, то получим равносильное неравенство.
Если обе части неравенства разделить на одно и то же положительное число, то получим равносильное неравенство, при этом знак неравенства не изменится.
Нечетная степень числа сохраняет его знак.
Если из меньшего числа вычесть большее, то получится отрицательное число.
Частное двух чисел с разными знаками дает отрицательный результат.
По свойству транзитивности, если ab, то ab.
Если обе части неравенства умножить или разделить на -1, то знак неравенства изменится на противоположный..
Если обе части неравенства разделить или умножить на положительное число, то получим равносильное неравенство, при этом знак неравенства не меняется.
Чтобы найти делимое при делении с остатком, надо умножить неполное частное на делитель и к полученному произведению прибавить остаток.
При решении неравенств можно прибавлять ко всем частям неравенства одно и то же число, знак неравенства при этом не меняется.
Если при решении неравенств разделить все части неравенства одно и то же положительное число, знак неравенства при этом не меняется.

Содержимое разработки

9 класс Алгебра №3

Чтобы сравнить выражения, содержащие радикал (в частности квадратные корни), надо внести множители под знак корня и сравнить подкоренные выражения.
Чтобы внести множитель под знак корня, надо этот множитель возвести в квадрат и записать его под знаком корня.
Чтобы перемножить квадратные корни из неотрицательных множителей, надо перемножить эти множители под общим знаком корня.
Чтобы сравнить квадратные корни, надо сравнить подкоренные выражения. Тот корень больше, у которого подкоренное выражение больше.
Чтобы возвести в степень произведение, надо каждый множитель возвести в данную степень.
Возведение числа в квадрат и извлечение квадратного корня из этого же числа – два взаимно обратные действия, поэтому эти действия друг друга взаимно уничтожают.
Чтобы сократить дробь, надо числитель и знаменатель дроби разделить на одно и то же число, не равное нулю.
Чтобы записать смешанное число в виде неправильной дроби, надо целую часть умножить на знаменатель, прибавить числитель и результат записать в числитель, знаменатель оставить тот же.
Если в дроби и числитель и знаменатель содержат квадратные корни, то можно записать дробь под общим знаком корня.
Если в ответе получили обыкновенную дробь, то по возможности надо ее перевести в десятичную. Для этого надо числитель разделить на знаменатель.
Чтобы сложить дроби с разными знаменателями, надо дроби привести к общему знаменателю и сложить числители.
Чтобы вынести множитель из-под знака корня, надо подкоренное число разложить на такие множители, чтобы из одного из них извлекался корень.
Подобными слагаемыми называются те, которые имеют одну и ту же буквенную часть (Общий множитель). Квадратный корень из одного и того же числа может играть роль такого же общего множителя
Чтобы сравнить данные числа с ближайшими с точкой А координатами, надо эти координаты записать с виде квадратных корней.
Чтобы сравнить данное число с координатами, надо эти координаты записать с виде квадратных корней.
Квадрат суммы двух выражений вычисляется по формуле .
Квадрат разности двух выражений вычисляется по формуле
Разность квадратов двух выражений вычисляется по формуле

Содержимое разработки

9 класс. Алгебра №4

В уравнении можно делить обе части уравнения на одно и то же число, не равное нулю.
Чтобы разделить число на обыкновенную дробь, надо первое число умножить на взаимно обратное дроби.
При умножении двух чисел в разными знаками результат будет отрицательным.
Чтобы умножить число на скобку, надо число умножить на каждое слагаемое скобки.
При решении уравнения можно переносить слагаемые из одной части уравнения в другую, меняя знак слагаемых на противоположный.
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить числители, а знаменателями оставить без изменения.
Сократить дробь, значит разделить и числитель, и знаменатель на одно и то же число.
Чтобы умножить одночлен на многочлен, надо одночлен умножить на каждый член многочлена.
Чтобы сложить (вычесть) дроби с разными знаменателями, надо привести дроби к общему знаменателю и сложить (вычесть) числители.
Чтобы умножить обыкновенные дроби, надо перемножить отдельно числители и знаменатели.
Чтобы выделить целую часть из неправильной дроби, надо числитель разделить на знаменатель, неполное частное – целая часть, остаток – числитель, знаменатель без изменения
Чтобы «избавиться» от дробей, надо уравнение почленно умножить на общий знаменатель дробей, входящих в уравнение.
Сумма противоположных чисел равна нулю.
Подобными слагаемыми называются те, которые имеют одинаковую буквенную часть или не имеют ее вовсе.
Дробно-рациональное уравнение имеет смысл тогда, когда знаменатель дробей, входящих в уравнение, не равен нулю.
Дробно-рациональное уравнение можно свести к целому, если обе его части умножить на общий знаменатель.
В верной пропорции произведение крайних членов равно произведению средних членов.
Собираем подобные слагаемые, т.е. переносим их из одной части уравнения в другую, меняя их знаки на противоположные.
Если сложить числа с противоположными знаками, то надо из большего модуля вычесть меньший, поставив в ответе знак числа с большим модулем.
Квадратным уравнением называется уравнение вида ax²+bx+c=0
Дискриминант – различитель можно найти по формуле
Так как D0, то уравнение имеет два корня.
Корни квадратного уравнения можно вычислить по формулам:
Если все числовые коэффициенты уравнения имеют общий делитель, то их можно сократить на этот делитель.
Приведенным называется квадратное уравнение, старший коэффициент которого равен единице.
Если числа х₁ и х₂ таковы, что х₁+х₂=-b, х₁∙х₂=с, то эти числа – корни уравнения (обратная теорема Виета).
Чтобы решить систему уравнений методом подстановки, надо вместо у во втором уравнении подставить 2х, и получим уравнение с одной переменной.
Чтобы найти значение второй переменной (у), надо в первое уравнение подставить вместо х значение равное 2 и решить получившееся уравнение.
Решение системы уравнений записывают парой чисел в виде координат точки.
Если пред скобкой стоит знак «минус», то при раскрытии скобок скобки и этот знак опускают, а знаки в скобках меняют на противоположные.
Умножить почленно каждое уравнение на такие множители, чтобы при одной из переменных получить противоположные коэффициенты.
Надо сложить почленно уравнения чтобы исключить одну из переменных (в данном случае х), и решить получившееся уравнение с одной переменной.
Если одно из уравнений не имеет решения, то и система не имеет решения.

Содержимое разработки

9 класс Алгебра №5

Функции и их свойства

Функция — одно из важнейших математических понятий. Функцией называют такую зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у.

Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Говорят также, что переменная у является функцией от переменной х. Значения зависимой переменной называют значениями функции.

Если зависимость переменной у от переменной х является функцией, то коротко это записывают так: y=f(x). (Читают: у равно f от х.) Символом f(x) обозначают значение функции, соответствующее значению аргумента, равному х.

Все значения независимой переменной образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.

Если функция задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений аргумента, при которых формула имеет смысл.

Способы задания функции:

1. аналитический способ (функция задается с помощью математической формулы;

2. табличный способ (функция задается с помощью таблицы)

3. описательный способ (функция задается словесным описанием)

4. графический способ (функция задается с помощью графика).

Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.

ОСНОВНЫЕ СВОЙСТВА ФУНКЦИЙ

1. Нули функции

Нуль функции – такое значение аргумента, при котором значение функции равно нулю .

2. Промежутки знакопостоянства функции

Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.

3. Возрастание (убывание) функции.

Возрастающая в некотором промежутке функция — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.

Функция у = f (x) называется возрастающей на интервале (а; b), если для любых x₁ и x₂ из этого интервала таких, что x₁x₂ , справедливо неравенство f(x₁)f(x₂).

Убывающая в некотором промежутке функция — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Функция у =f (x) называется убывающей на интервале (а; b), если для любых x₁ и x₂ из этого интервала таких, что x₁x₂, справедливо неравенство f(x₁)f(x₂).

4. Четность (нечетность) функции

Четная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.

Например, у = х² — четная функция.

Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = — f(x). График нечетной функции симметричен относительно начала координат.

Например: у = х³ — нечетная функция.

Функция общего вида не является четной или нечетной (у = х²+х).

Свойства некоторых функций и их графики

1.      Линейной функцией называется функция вида , где k и b – числа.

Область определения линейной функции – множество R действительных чисел.

Графиком линейной функции у = kx + b (k ≠ 0) является прямая проходящая через точку (0; b) и параллельная прямой у = kx.

Прямая, не параллельная оси Оу, является графиком линейной функции.

Свойства линейной функции.

1. При k 0 функция у = kx + b возрастающая в области определения.

2. При k 0 функция у = kx + b убывающая в области определения.

3. Множеством значений функции y = kx + b(k ≠ 0) является вся числовая прямая, т.е. множество R действительных чисел.

При k = 0 множество значений функции у = kx + b состоит из одного числа b.

3.      При b = 0 и k = 0 функция не является ни четной, ни нечетной.

При k = 0 линейная функция имеет вид у = b и при b ≠ 0 она является четной.

При k = 0 и b = 0 линейная функция имеет вид у = 0 и являете одновременно четной и нечетной.

Графиком линейной функции у = b является прямая, проходящая через точку (0; b) и параллельная оси Ох. Заметим, что при b = 0 график функции у = b совпадаете осью Ох.

5. При k 0 имеем, что у 0, если и у 0, если . При k 0 имеем, что у 0, если и у .

2. Функция y = x²

Область определения этой функции — множество R действительных чисел.

Придавая переменной х несколько значений из области определения функции и вычисляя соответствующие значения у по формуле y = x² , изображаем график функции.

График функции y = x²называется параболой.

Свойства функции у = х².

1. Если х = 0, то у = 0, т.е. парабола имеет с осями координат общую точку (0; 0) — начало координат.

2. Если х ≠ 0, то у 0, т.е. все точки параболы, кроме начала координат, лежат над осью абсцисс.

3.   Множеством значений функции у = х² является промежуток [0; + ∞).

4. Если значения аргумента отличаются только знаком, то значения функции равны, т.е. парабола симметрична относительно оси ординат (функция у = х² — четная).

5. На промежутке [0; + ∞) функция у = х² возрастает.

6. На промежутке (-∞; 0] функция у = х² убывает.

7. Наименьшее значение функция принимает в точке х = 0, оно равно 0. Наибольшего значения не существует.

3.Фунуция

Область определения этой функции — промежуток [0;+∞), т. е. все неотрицательные числа.

Придавая переменной х несколько значений из области определения функции и вычисляя соответствующие значения у по формуле , изображаем график функции.

Свойства функции.

1. Если х = 0, то у = 0, т.е. график функции имеет с осями координат общую точку (0; 0) — начало координат.

2. Если х 0, то у 0, т.е. все точки графика функции, кроме начала координат, лежат над осью абсцисс.

3. Множеством значений функции    является промежуток [0;+∞).

4. Функция не является ни четной, ни нечетной.

5. Функция возрастающая в области определения.

6. Наименьшее значение функция принимает в точке х = 0, оно равно 0. Наибольшего значения не существует.

4. Функция y = x³

Область определения этой функции — множество R действительных чисел,

Придавая переменной х несколько значений из области определения функции и вычисляя соответствующие значения у по формуле у = х³, изображаем график функции.

График функции у= х³ называется кубической параболой.

Свойства функции y = x³.

1. Если х = 0, то у = 0, т.е. кубическая парабола пересекает оси координат в точке (0; 0) — начале координат.

2. Если х 0, то у 0, а если х 0, то у

3. Множеством значений функции у = х³ является вся числовая прямая.

4.   Если значения аргумента отличаются только знаком, то и значения функции отличаются только знаком, т.е.   кубическая парабола симметрична относительно начала координат (функция у = х³ — нечетная).

4.      Функция у = х³ возрастающая в области определения.

5.      Функция y = |x|

Область определения этой функции — множество R действительных чисел.

Пользуясь определением модуля числа х при х О получим у = х, а при х у = — х. Таким образом, имеем:

График функции состоит из двух частей: части прямой у = х при х ≥ 0 и из части прямой у =- х при х

Свойства функции

1. Если х = 0, то у = 0, т.е. график пересекает оси координат в точке (0; 0) — начале координат.

2. Если х ≠ 0, то у 0, т.е. все точки графика   функции y = |x|,   кроме   начала координат, лежат над осью абсцисс.

3.   Множеством значений функции y = |x| является промежуток [0;+∞).

4. Если значения аргумента отличаются только знаком, то значения функции равны, т.е. график функции симметричен относительно ординат (функция y = |x| — четная).

5. На промежутке [0;+∞) функция y = |x| возрастает.

6. На промежутке (-∞;0] функция y = |x| убывает.

7. Наименьшее значение функция принимает в точке х, оно равно 0. Наибольшего значения не существует.

6.      Функция

Область определения функции: .

Область значений функции: .

График — гипербола.

1. Нули функции.

                             у ≠ 0, нулей нет.

2. Промежутки знакопостоянства,

Если k 0, то у 0 при х 0; у х

Если k у х 0; у 0 при х

3. Промежутки возрастания и убывания.

Если k 0, то функция убывает при .

Если k .

4. Четность (нечетность) функции.

Функция нечетная.

Квадратный трехчлен

Уравнение вида ax²+bx+c = 0, где a, b и с — некоторые числа, причем а≠0, называется квадратным.

В квадратном уравнении ax²+bx+c = 0 коэффициент а называется первым коэффициентом, b — вторым коэффициентам, с — свободным членом.

Формула корней квадратного уравнения имеет вид:

.

Выражение называется дискриминантом квадратного уравнения и обозначается через D.

Если D = 0, то существует только одно число, удовлетворяющее уравнению ax²+bx+c = 0. Однако условились говорить, что в этом случае квадратное уравнение имеет два равных действительных корня, а само число называют двукратным корнем.

Если D

Если D 0, то квадратное уравнение имеет два различных действительных корня.

Пусть дано квадратное уравнение ax²+bx+c = 0. Так как а≠0, то, разделив обе части данного уравнения на а, получим уравнение . Полагая и , приходим к уравнению , в котором первый коэффициент равен 1. Такое уравнение называется приведенным.

Формула корней приведенного квадратного уравнения имеет вид:

.

Уравнения вида

аx² +bx = 0,   ax² + с =0,   аx² = 0

называются неполными квадратными уравнениями. Неполные квадратные уравнения решаются разложением левой части уравнения на множители.

Теорема Виета.

Сумма корней квадратного уравнения равна взятому с противоположным знаком отношению второго коэффициента к первому, а произведение корней — отношению свободного члена к первому коэффициенту, т.е.

; .

Обратная теорема.

Если сумма каких-нибудь двух чисел х₁ и х₂ равна , а их произведение равно , то эти числа являются корнями квадратного уравнения ах²   + bх + с = 0.

Функция вида ах² +bх + с называется квадратным трехчленом.   Корни этой функции являются корнями соответствующего квадратного уравнения ах²   + bх + с = 0.

Если дискриминант квадратного трехчлена больше нуля, то этот трехчлен можно представить в виде:

ах² +bх + с =а(х-х₁)(х-х₂)

где х₁   и   х₂   —   корни   трехчлена

Если дискриминант квадратного трехчлена равен нулю, то этот трехчлен можно представить в виде:

ах² +bх + с =а(х-х₁)²

где х₁ — корень трехчлена.

Например, 3х² — 12х + 12 = 3(х — 2)².

Уравнение вида ах⁴   + bх²   + с = 0 называется биквадратным. С помощью замены переменной по формуле х² = y оно приводится к квадратному уравнению аy² + by + с = 0.

Квадратичная функция

Квадратичной функцией называется функция, которую можно записать формулой вида y = ax² + bx + c, где x – независимая переменная, a, b и c – некоторые числа, причем a≠0.

            Свойства функции и вид ее графика определяются, в основном, значениями коэффициента a и дискриминанта .

Свойства квадратичной функции

            — Область определения: R;

— Область значений:

при а 0          [-D/(4a); ∞)

при а D/(4a)];

— Четность, нечетность:

при b= 0     функция четная

при b≠0    функция не является ни четной, ни нечетной

— Нули:

при D 0      два нуля: ,

при D = 0      один нуль:

при D

— Промежутки знакопостоянства:

если, а 0, D 0, то

если, а 0, D = 0, то

eсли а 0, D

если а D 0, то

если а D = 0, то

если а D

—         Промежутки монотонности

при а 0

при а

            Графиком квадратичной функции является парабола – кривая, симметричная относительно прямой , проходящей через вершину параболы (вершиной параболы называется точка пересечения параболы с осью симметрии).

Чтобы построить график квадратичной функции, нужно:

1) найти координаты вершины параболы и отметить ее в координатной плоскости;

2) построить еще несколько точек, принадлежащих параболе;

3) соединить отмеченные точки плавной линией.

            Координаты вершины параболы определяются по формулам:

; .

Преобразование графиков функции

            1. Растяжение графика у = х² вдоль оси у в |а| раз (при |а| 1 — это сжатие в 1/|а| раз).

Если, а х (ветви параболы будут направлены вниз).

Результат: график функции у = ах².

2.      Параллельный перенос графика функции у = ах² вдоль оси х на |m| (вправо при

m 0 и влево при т 0).

Результат: график функции у = а(х — т)².

3. Параллельный перенос графика функции вдоль оси у на |n| (вверх при п 0 и вниз при п 0).

Результат: график функции у = а(х — т)² + п.

Квадратичные неравенства

Неравенства вида ах² + bх + с 0 и ах² + bх + с 0, где х — переменная, a, b и с — некоторые числа, причем, а≠0, называют неравенствами второй степени с одной переменной.

Решение неравенства второй степени с одной переменной можно рассматривать как нахождение промежутков, в которых соответствующая квадратичная функция принимает положительные или отрицательные значения.

Для решения неравенств вида ах² + bх + с 0 и ах² + bх + с 0 поступают следующим образом:

1) находят дискриминант квадратного трехчлена и выясняют, имеет ли трехчлен корни;

2) если трехчлен имеет корни, то отмечают их на оси х и через отмеченные точки проводят схематически параболу, ветви которой направлены вверх при а 0 или вниз при а 0; если трехчлен не имеет корней, то схематически изображают параболу, расположенную в верхней полуплоскости при а 0 или в нижней при а

3) находят на оси х промежутки, для которых точки параболы расположены выше оси х (если решают неравенство ах² + bх + с 0) или ниже оси х (если решают неравенство ах² + bх + с

Пример:

Решим неравенство .

Рассмотрим функцию

Ее графиком является парабола, ветви которой направлены вниз (т. к. ).

Выясним, как расположен график относительно оси х. Решим для этого уравнение . Получим, что х = 4. Уравнение имеет единственный корень. Значит, парабола касается оси х.

Изобразив схематически параболу, найдем, что функция принимает отрицательные значения при любом х, кроме 4.

Ответ можно записать так: х — любое число, не равное 4.

Решение неравенств методом интервалов

схема решения

1. Найти нули функции, стоящей в левой части неравенства.

2. Отметить положение нулей на числовой оси и определить их кратность (если k_i четное, то нуль четной кратности, если k_i нечетное — то нечетной).

3. Найти знаки функции в промежутках между ее нулями, начиная с крайнего правого промежутка: в этом промежутке функция в левой части неравенства всегда положительна для приведенного вида неравенств.   При переходе справа налево через нуль функции от одного промежутка к соседнему следует учитывать:

•    если нуль нечетной кратности, знак функции изменяется,

•    если нуль четной кратности, знак функции сохраняется.

4.      Записать ответ.

Пример:

(х + 6) (х + 1) (х — 4)

            Найден нули функции. Они равны: х₁ = -6; х₂ = -1; х₃ = 4.

Отметим на координатной прямой нули функции f(x) = (х + 6) (х + 1) (х — 4).

Найдем знаки этой функции в каждом из промежутков (-∞; -6), (-6; -1), (-1; 4) и

(4; +∞).

Из рисунка видно, что множеством решений неравенства является объединение промежутков (-∞; -6) и (-1; 4).

Ответ: (-∞_; -6) и (-1; 4).

Рассмотренный способ решения неравенств называют методом интервалов.

13

Содержимое разработки

9 класс. Алгебра№7

Арифметическая прогрессия

Определение: Последовательность, у которой задан первый член a₁, а каждый следующий равен предыдущему, сложенному с одним и тем же числом d, называется арифметической прогрессией:

a_n₊₁ = a_n + d, где d – разность прогрессии.

Геометрическая прогрессия

Определение: Последовательность, у которой задан первый член b₁ 0, а каждый следующий равен предыдущему, умноженному на одно и то же число q  0, называется геометрической прогрессией:

b_n₊₁ = b_n q, где q – знаменатель прогрессии.

Содержимое разработки

9 класс. Алгебра №7.

Квадрат суммы (разности) двух выражений равен квадрату первого выражения плюс (минус) удвоенное произведение первого и второго выражений и плюс квадрат второго выражения.
Если у слагаемых одинаковая буквенная часть, то они подобны. При сложении таких слагаемых складывают коэффициенты и умножают на общую буквенную часть.
Произведение разности двух выражений на их сумму равно разности квадратов этих выражений.
Если квадратный корень возвести в квадрат, то получим подкоренное выражение.
Чтобы сократить дробь, надо и числитель, и знаменатель разложить на множители.
Чтобы перевести обыкновенную дробь в десятичную, надо числитель разделить на знаменатель.
Разность квадратов равна произведению разности этих выражений на из сумму.
Квадратный трехчлен можно разложить на множители по формуле

Корни квадратного трехчлена можно найти по формулам:

Чтобы сократить дробь, надо и числитель и знаменатель разделить на одно и тоже выражение, не равное нулю.
Чтобы сократить дробь, надо и числитель и знаменатель разделить на одно и тоже выражение, не равное нулю.
Если у слагаемых есть общий множитель, то при разложении многочлена на множители этот множитель можно вынести за скобку.
Чтобы сложить дроби с разными знаменателями, надо привести дроби к общему знаменателю и сложить числители.
Чтобы умножить дроби, надо отдельно умножить числители и знаменатели.
В процессе умножения дробей можно сокращать. Для этого надо числители и знаменатели дробей разложить на множители
Сумма противоположных слагаемых равна нулю.
Чтобы разделить дробь на дробь, надо первую дробь умножить на обратную второй дроби.
Чтобы сложить с дробью натуральное число, надо это число представить в виде дроби со знаменателем 1 и сложить по правилу дробей.
Произведение двух одинаковых множителей можно записать в виде квадрата этого множителя.
Сумму кубов двух выражений можно разложить по формуле

Дробь, знаменатель которой равен единице, является целым выражением.
Чтобы сложить дробь с одночленом, надо одночлен заменить дробью со знаменателем 1 и выполнить сложение дробей.
Чтобы разложить многочлен на множители (в случае, если формулы сокращенного умножения на подходят), можно применить способ группировки.
Далее надо каждую скобку разложить на множители своим способом.
Далее общий множитель в виде многочлена вынести за скобку.
Чтобы упростить запись дроби, ее надо сократить, а для этого надо числитель и знаменатель разложить на множители.
Чтобы вынести общий множитель за скобки, надо разделить каждое слагаемое на этот множитель.
Чтобы записать натуральное число в виде квадрата, надо его заключить под знак квадратного корня.
Чтобы «избавиться» от иррациональности в знаменателе, надо числитель и знаменатель умножить на иррациональный множитель.
Если квадратный корень возвести в квадрат, то получится подкоренное число.
Произведение квадратных корней из неотрицательных множителей равно квадратному корню из произведения этих множителей.

Содержимое разработки

9 класс. Алгебра №8

При решении неравенства можно переносить слагаемые из одной части в другую, меняя знак слагаемых на противоположный.
Уравнение вида aх+b≥0 называется линейным.
Числа, которые больше данного числа, на числовой прямой лежат правее данного числа.
Если неравенство содержит нестрогий знак (≥), то соответствующая точка на числовой прямой будет темной, а скобка в ответе квадратной.
Если обе части неравенства разделить на одно и то же отрицательное число, то необходимо изменить знак неравенства на противоположный.
Если в промежуток входит светлая точка, то этот промежуток разбивается на две части, а в ответ записывается круглая скобка, соответствующая светлой точке.
Если числитель дроби меньше знаменателя, то дробь правильная, если же числитель больше знаменателя, то дробь неправильная.
Неправильная дробь больше правильной, и соответственно правее на числовой прямой.
Решением системы неравенств является тот промежуток, где штриховки совпадают.
Неравенство вида ах²+bx+с0 называется квадратным (неравенством второй степени с одной переменной)
Приведенным называется квадратное уравнение, старший коэффициент которого равен единице.
Если числа х₁ и х₂ таковы, что х₁+х₂=-b, х₁∙х₂=с, то эти числа – корни уравнения

(обратная теорема Виета).

Дискриминант – различитель можно найти по формуле
Так как D0, то уравнение имеет два корня.
Корни квадратного уравнения можно вычислить по формулам:
Неравенства вида (х-a)(x—b)(x—c)∙…0 решаются методом интервалов.
Произведение равно нулю тогда, когда один из множителей равен нулю (при условии, что другие множители не теряют смысла)
В данных неравенствах знаки на промежутке постоянен, и меняются при переходе через нуль функции.
Если в неравенстве вида (х-a)(x—b)(x—c)∙…0 во всех скобках коэффициенты при х равны +1 и a≠b≠c то можно расставить знаки на промежутках таким образом: на самом правом ставится знак «+», а далее знаки чередуются
Если обе части неравенства разделить на одно и тоже положительное число, то при этом знак неравенства не меняется.
Т.к. неравенство содержит знак «меньше 0», то на рисунке надо взять промежуток, где часть «кривой знаков» ниже оси Ох.
Квадрат любого числа есть число неотрицательное.
Чтобы сократить дробь, надо числитель и знаменатель разделить на одно и то же выражение, не равное нулю.

Содержимое разработки

9 класс Геометрия №10

Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему
В прямоугольном треугольнике сумма острых углов равна 90⁰
Если в треугольнике два угла равны, то такой треугольник равнобедренный
Высота в прямоугольном треугольнике, проведенная к основанию является биссектрисой и медианой
В прямоугольном треугольнике катет, лежащий против угла в 30⁰, равен половине гипотенузы
Биссектриса – это луч, который делит угол пополам
Периметр многоугольника – это сумма длин всех сторон многоугольника
При пересечении двух параллельных прямых накрест лежащие углы равны
Если два угла в треугольнике равны, то треугольник — равнобедренный
Прямоугольник – это параллелограмм с прямыми углами
Катет, лежащий против угла в 30⁰, равен половине гипотенузы
Если две параллельные прямые пересечены третьей, то накрест лежащие углы равны
Если отрезок точкой разделен на части, то его длина равна сумме его частей
Диагонали ромба пересекаются под прямым углом и делят углы ромба пополам
Диагонали параллелограмма (ромба) точкой пересечения делятся пополам
Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон трапеции
Средняя линия трапеции равна полусумме оснований трапеции
Параллельные прямые, проведенные через концы равных отрезков на одной из сторон угла, отсекают равные отрезки на другой стороне угла
Средняя линия треугольника равна половине третьей стороны треугольника
Если в четырехугольнике противоположные стороны параллельны, то такой четырехугольник — параллелограмм
В параллелограмме противоположные стороны равны
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого треугольника, то треугольники равны
Если в четырехугольник можно вписать окружность, то суммы противоположных сторон четырехугольника равны
Радиус окружности, проведенный в точку касания перпендикулярен касательной
Радиус окружности равен половине диаметра
Перпендикуляры между параллельными прямыми равны
Прямой угол, вписанный в окружность опирается на диаметр окружности

Содержимое разработки

9 класс Геометрия №11

Площадь треугольника равна половине произведения двух сторон на синус угла между ними
Площадь прямоугольного треугольника равна половине произведения катетов
Сумма квадратов синуса и косинуса одного и того же угла равна единице
Высота треугольника – это отрезок, проведенный из вершины к противоположной стороне под прямым углом
Площадь треугольника равна половине произведения основания на высоту
Вписанной в треугольник окружностью называется окружность, которая касается всех сторон треугольника
Если в треугольник вписана окружность, то площадь треугольника равна произведению полупериметра треугольника на радиус вписанной окружности
Площадь параллелограмма равна произведению двух сторон на синус угла между ними
Ромб – это параллелограмм с равными сторонами
Площадь ромба равна половине произведения его диагоналей
Трапеция – это четырехугольник, две стороны которого параллельны
Площадь трапеции равна произведению полусуммы оснований на высоту
Диагонали прямоугольника равны и делятся точкой пересечения пополам
В равнобедренном треугольнике углы при основании равны
Если угол разбит на части, то его градусная мера равна сумме его частей
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Площадь прямоугольника равна произведению соседних сторон
Средняя линия трапеции равна полусумме оснований
Если в прямоугольном треугольнике острый угол равен 45⁰, то и другой острый угол равен 45⁰
Периметр треугольника – это сумма длин сторон треугольника
Высота в равнобедренном треугольнике, проведенная к основанию является медианой
Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе
Высота прямоугольного треугольника, проведенная к основанию, является медианой
Если в четырехугольник можно вписать окружность, то суммы противоположных сторон четырехугольника равны
Если фигура разбита на части, то площадь фигуры равна сумме площадей ее частей
Радиус, проведенный в точку касания перпендикулярен касательной
Диагонали ромба перпендикулярны и делят углы ромба пополам
Площадь ромба равна половине произведения его диагоналей
Треугольник, в котором стороны равны 3,4,5 называется Пифагоровым (т.е. треугольник является прямоугольным)
Длина окружности равна удвоенному произведению числа π на радиус окружности
Площадь кругового сектора вычисляется по формуле
Площадь круга равна произведению числа π на квадрат радиуса круга
Сторона правильного треугольника, в который вписана окружность, равна
Радиусы вписанной и описанной окружности около правильного многоугольника связаны формулой
Сторона правильного четырехугольника, в который вписана окружность, равна

-80%

Скачать разработку

Сохранить у себя:

Теория для успешной подготовки по математике для ОГЭ (939.39 KB)

Вы смотрели

Источник

Начни онлайн-курс ОГЭ по математике прямо сейчас

Приложение Android

Начать подготовку

Приложение iOS

Начать подготовку

Источник

В данном разделе представлены все необходимые материалы для подготовки к ОГЭ по математике 2022. Мы предоставляем как разобранные варианты с теорией по заданиям, так и тестовые варианты для самоподготовки. Пройдя курс подготовки к ОГЭ на нашем сайте, вы уверенно напишете экзамен в 9 классе в 2022 году!

Источник

Русский, Математика, Обществознание, Физика, История, Биология, Химия, Английский, Информатика, Литература, География

О правах / ctege.info@gmail.com / Архив: 2020; 2021; 2022;

2005-2023 © ctege.info При использовании материалов указывайте гиперссылку.

Источник

Конспекты для подготовки к ОГЭ по Математике

Уравнения с одной переменной
Правила решения уравнений:
Линейное уравнение с одной переменной
Виды линейных уравнений:
Линейная функция
Взаимное расположение графиков линейных функций
Степень с натуральными показателями
Свойства степени с натуральным показателем

Автор Г.Д. Соловьева

Для быстрого и эффективного повторения материала при подготовке к ОГЭ по математике вам помогут опорные конспекты. Например, по таким темам:

Уравнения с одной переменной

Уравнение – это равенство с переменной.

Например:

$x^{2} = 9$

Корень уравнения – это значение переменной, при котором уравнение обращается в верное равенство.
Например, уравнение

Если x = 2 , тогда . Число 2 – корень данного уравнения.

Решить уравнение – значит найти все его корни или доказать, что их нет.

Равносильные уравнения – это уравнения, имеющие одни и те же корни или не имеющие корней.

Примеры:

Уравнения $x^{2} = 49$ и равносильны. Их корни 7 и -7.
Уравнения $x^{2} = -5$ и y-4 = y равносильны. Они оба не имеют корней

к оглавлению ▴

Правила решения уравнений:

1) Можем переносить слагаемое из одной части уравнения в другую, изменяя его знак на противоположный.

2) Можем умножать (делить) левую и правую части уравнения на одно и то же число, отличное от нуля.

Линейное уравнение с одной переменной

Это уравнение вида ax = b , где – переменная, и — некоторые числа.

Виды линейных уравнений:

1) ax = b, где a ≠ 0, b ≠ 0. Например, 2х = 4.

Такое уравнение имеет единственный корень: $x=frac{b}{a}$

Например,

$x=frac{b}{a}4x= 1$ .

Корень уравнения: $x=frac{1}{4}$

$frac{1}{3}x=12$ .

Решаем уравнение:

, x = 36

2) Уравнение

В этом уравнении a = 0 , b neq 0 .

Такое уравнение не имеет корней.

Например:

2x + 9 = 2(x+6)

2x + 9 = 2x + 12

0 = 3.

3) Уравнение

Здесь a = 0, b= 0. Уравнение имеет бесконечно много корней. Любое число х является его корнем.

Например:

0 = 0

к оглавлению ▴

Линейная функция

Прямая пропорциональность – это функция вида y=kx , где — переменная, kneq 0 .

График прямой пропорциональности – прямая, проходящая через начало координат

Случай k > 0. Пример: y = 3x

Строим график.

Случай k < 0. Пример: $y =-frac{1}{2}x$

Линейная функция – это функция вида , где – переменная, k и b числа.

График линейной функции – прямая

Пример для k > 0 – функция

ГРАФИК

Пример для k < 0 – функция $y =-frac{1}{2}x-2$

График функции , где kneq 0 , — прямая, параллельная прямой y = kx .

y = kx – частный случай линейной функции при b = 0

Если k = 0, то y = b – прямая, параллельная оси x

Если k = 0, b = 0, то y = 0 – ось x

к оглавлению ▴

Взаимное расположение графиков линейных функций

Угловой коэффициент прямой – это число k в формуле функции y = kx + b

Если k > 0, то угол наклона к оси х – острый.

Если k<0, то угол наклона к оси х – тупой.

Если для двух прямых угловые коэффициенты различны, прямые пересекаются

РИСУНОК

Если для двух прямых угловые коэффициенты равны, прямые параллельны.

Например, $y_{1}=frac{1}{2} x+1$ , $y_{2}=frac{1}{2} x-2$

РИСУНОК

к оглавлению ▴

Степень с натуральными показателями

Определение: Степенью числа а с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен а.

— возведение в степень

Выражение a^n — степень числа а,

а — основание степени (показывает, какой множитель умножается),

n — показатель степени (показывает, сколько множителей умножается).

Запомним: $a^{2} geq 0$ для любого числа а.

$a^{1} = a$

$a^{0} = 1$ для любого а, не равного нулю.

Выражение «ноль в нулевой степени» не имеет смысла.

Примеры:

1) $left ( 1frac{2}{5} right )^{2}=left ( frac{7}{5} right )^{2}=left ( frac{7}{5} right )cdot left ( frac{7}{5} right )=frac{49}{25} =1frac{24}{25}$

2) $0,3^{3}=0,3cdot 0,3cdot 0,3=0,027$

3) $-1^{4} + (-2)^{3} = -1 + (-8) = -9$

4) $-6^{2} - (-1)^{4} = -36 -1 = -37$

5) $8 cdot 0,5^{3} + 25 cdot 0,2^{2} = 8 cdot 0,125 + 25 cdot 0,04 = 1 + 1 = 2$

6) $8 cdot 0,11^{0} + 4 cdot 5^{2} = 8 cdot 1 + 4cdot 25 = 8 + 100 = 108$

к оглавлению ▴

Свойства степени с натуральным показателем

Умножение степеней.

При умножении степеней с одинаковым основанием показатели складывают. Основание остается прежним.

$boldsymbol{a^{n}cdot a^{m}=a^{n+m}}$

Примеры:

1) $a^{8} cdot a^{7} = a^{8+7} = a^{15}$

2) $a cdot a^{3} cdot a^{4} cdot a^{2} = a^{1+3+4+2} = a^{10}$

3) $5^{8}cdot 25=5^{8}cdot 5^{2}=5^{8+2}=5^{10}$

Деление степеней

При делении степеней с одинаковым основанием из показателя делимого вычитают показатель делителя. Основание остается прежним.

$boldsymbol{a^{m}:a^{n}=a^{m-n}}$

Примеры:

1) $a^{8} : a^{7} = a^{8-7} = a^{1} = a$

2) $a^{9} : a = a^{9-1} = a^{8}$

3) $2^{6} : 4 = 2^{6} : 2^{2} = 2^{6-2} = 2^{4} = 16$

Возведение степени в степень

При возведении степени в степень основание оставляют прежним, а показатели умножают.

$boldsymbol{(a^{n})^{m}=a^{n-m}}$

Примеры:

1) $(x^{3})^{2} = x^{3cdot 2} = x^{6}$

2) $25^{4} = (5^{2})^{4} = 5^{2cdot 4} = 5^{8}$

Возведение произведения в степень

При возведении произведения в степень в эту степень возводят каждый множитель и результаты перемножают.

$boldsymbol{(ab)^{n}=a^{n}cdot b^{n}}$

Примеры:

1) $(2x)^{3} = 2^{3}cdot x^{3} = 8x^{3}$

2) $2^{4} cdot 5^{4} = (2cdot 5)^{4} = 10^{4} = 10000$

Формулы сокращенного умножения

$boldsymbol{(a+b)^{2}=a^{2}+2ab+b^{2}=(-a-b)^{2}}$

$boldsymbol{(a-b)^{2}=a^{2}-2ab+b^{2}=(b-a)^{2}}$

$boldsymbol{a^{2}-b^{2}=(a-b)(a+b)}$

Примеры:
1) $(x+9)^{2} = x^{2} + 2cdot xcdot 9 + 9^{2} = x^{2}+18x+81$

2) $(2x-3y)^{2} = (2x)^{2} - 2cdot 2xcdot 3y +(3y)^{2} = 4x^{2}-12xy+9y^{2}$

4) $(-3a+b^{4})^{2} = (b^{4}-3a)^{2} = b^{8} - 6ab^{4} + 9a^{2}$

$boldsymbol{a^3 + b^3 = (a+b) (a^2 - ab + b^2 )}$

$boldsymbol{a^{3} - b^{3} = (a-b) (a^{2} + ab+b^{2})}$

Квадратное уравнение и разложение квадратного трехчлена на множители.

$ax^{2} +bx+c =a (x-x_{1})(x - x_{2})$ , где x_1 , x_2 — корни квадратного трехчлена

Квадратное уравнение – уравнение вида $ax^{2} + bx +c = 0$ .

Дискриминант квадратного уравнения: $boldsymbol{D = b^2 - 4ac}$ .

Если $D=b^{2} - 4ac$ > 0, уравнение имеет два корня $x = frac{-bpm sqrt{D}}{2a}$

Если , уравнение имеет один корень $x = frac{-b}{2a}$

Если $D=b^{2} - 4ac$ < 0, уравнение не имеет корней

Такие конспекты для подготовки к ОГЭ по математике легко сделать самим. Сделай конспекты по темам:

— Неравенство с одной переменной

— Квадратное неравенство

— Вероятность

— Квадратичная функция, обратная пропорциональность

— Арифметическая прогрессия

— Геометрическая прогрессия

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Конспекты для подготовки к ОГЭ по Математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник