Анна Малкова
На этой странице – всё, что необходимо для отличного освоения планиметрии и решения задачи 16 Профильного ЕГЭ по математике. В том числе – уникальные авторские материалы.
New: Теорема Менелая, теорема Чевы – нужны на ЕГЭ или нет?
Знаете ли вы, что задание 16 Профильного ЕГЭ по математике в 2018 и 2019 годах было значительно проще, чем «параметры» или «экономическая» задача? Получается, те, кто не брался за планиметрию на ЕГЭ, добровольно отказались от трех первичных баллов, и кому-то не хватило их для поступления.
Да, мы знаем, что в школе планиметрией занимаются мало.
У нас даже статья есть о том, как там всё печально: Геометрия в школе: засада для абитуриента
Однако выучить геометрию и сдать ЕГЭ все равно надо. Как же это сделать: Вам поможет наша Программа по геометрии. Список необходимых фактов и теорем.
Учим определения, формулы и теоремы. Вспоминаем, что такое синус и что такое косинус острого угла в прямоугольном треугольнике. Учим определения и свойства биссектрисы, медианы и высоты треугольника. И 5 (да, 5) формул площади треугольника.
В общем, всё, что необходимо для решения задания №1 первой части Профильного ЕГЭ по математике. До второй части и задачи 16 мы тоже дойдем!
Кратко – в нашем Справочнике.
Подробно – здесь:
Геометрия. Формулы площадей фигур
Синус, косинус и тангенс острого угла прямоугольного треугольника
Тригонометрический круг: вся тригонометрия на одном рисунке
Внешний угол треугольника. Синус и косинус внешнего угла
Высота в прямоугольном треугольнике
Сумма углов треугольника
Углы при параллельных прямых и секущей
Высоты, медианы, биссектрисы треугольника
Четырёхугольники
Параллелограмм
Прямоугольник
Ромб
Квадрат
Трапеция
Окружность. Центральный и вписанный угол
Касательная к окружности
Вписанные и описанные треугольники. Теорема синусов
Вписанные и описанные четырёхугольники
Правильный треугольник
Правильный шестиугольник
Обратите внимание на тему «Векторы»:
Векторы на ЕГЭ по математике
Задание 16 из второй части ЕГЭ состоит из пунктов (а) и (б). Пункт (а) — это доказательство. Как правило, доказать нужно не самый тривиальный факт, и нужно уметь это делать.
Вам помогут «домашние заготовки» — наши Полезные факты для решения задач по планиметрии (с доказательствами)
Докажите их все и проверьте, что у вас получилось. После этого вы сможете доказать любое утверждение, которое вам может встретиться на ЕГЭ в задаче 16.
Но это не всё. Знаете ли вы, что многие задачи 16 Профильного ЕГЭ строятся по одной из так называемых классических схем? И эти Классические схемы для решения задач по планиметрии (с доказательствами) надо знать.
А для тех, кому скучно на уроке, — два геометрических парадокса. Готовы ли вы поверить, что прямой угол равен тупому? И что катет равен гипотенузе? Попробуйте найти ошибку в этих «доказательствах».
Геометрический парадокс: Прямой угол равен тупому
Геометрический парадокс: Катет равен гипотенузе
Как оформить решение задачи №16 (планиметрия)? Смотри образец решения и оформления!
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 2, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 4, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 6, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 12, задача 16
Задача на доказательство. Планиметрия.
И несколько полезных советов:
1) Задачи ЕГЭ по планиметрии решаются без сложных формул. Все необходимые факты, определения и теоремы – на этой странице.
2) Часто пункт (а) задачи 16 Профильного ЕГЭ содержит подсказку для решения пункта (б).
3) Обратите внимание на теорему о секущей и касательной, а также на свойство биссектрисы. Их трудно найти в учебнике. А в задачах ЕГЭ они применяются постоянно.
4) Старшеклассники очень любят теорему Фалеса. Но на самом деле применяется она очень редко. Намного чаще применяются три признака подобия треугольников:
— по двум углам,
— по углу и двум прилежащим к нему сторонам,
— по трем пропорциональным сторонам.
5) Самое важное – правильная методика подготовки. Не нужно начинать с реальных задач ЕГЭ. Сначала – теория. Затем – доказательство полезных фактов и классических схем. И только после этого – задачи №16 Профильного ЕГЭ.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Планиметрия» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Планиметрия
Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.
Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)
- Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
- Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Признаки подобия треугольников:
- Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Площади фигур
Площадь треугольника
- $S={a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне $а$
- $S={a·b·sinα}/{2}$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
- Формула Герона $S=√{p(p-a)(p-b)(p-c)}$, где $р$ — это полупериметр $p={a+b+c}/{2}$
- $S=p·r$, где $r$ — радиус вписанной окружности
- $S={a·b·c}/{4R}$, где $R$ — радиус описанной окружности
- Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ — катеты прямоугольного треугольника.
- Для равностороннего треугольника $S={a^2 √3}/{4}$, где $а$ — длина стороны.
Площади четырехугольников
Прямоугольник
$S=a·b$, где $а$ и $b$ — смежные стороны.
Ромб
$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ — диагонали ромба
$S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
Трапеция
$S={(a+b)·h}/{2}$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
Квадрат
$S=a^2$, где $а$ — сторона квадрата.
Параллелограмм
$S=a·b·sinα$, где $а$ и $b$ — длины сторон параллелограмма, а $α$ — угол между этими сторонами.
Пропорциональные отрезки в прямоугольном треугольнике
В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
$CD^2=DB·AD$
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
$CB^2=AB·DB$
$AC^2=AB·AD$
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.
$AC·CB=AB·CD$
Метрические соотношения в окружности
1. Две касательные, проведенные к окружности из одной точки, равны, и центр окружности лежит на биссектрисе угла между ними.
2. Если хорды $АС$ и $BD$ пересекаются в некоторой точке $N$, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
$AN·NC=BN·ND$
Пример:
Хорды $АВ$ и $CD$ пересекаются в точке $Е$. Найдите $ЕD$, если $АЕ=16, ВЕ=9, СЕ=ED$.
Решение:
Если хорды $АВ$ и $СD$ пересекаются в некоторой точке $Е$, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
$AЕ·ЕВ=СЕ·ЕD$
Так как $СЕ=ED$, данное выражение можно записать в виде:
$ЕD^2=AЕ·ЕВ$
Подставим числовые значения
$ЕD^2=16·9$
$ЕD=√{16·9}=4·3=12$
Ответ: $12$
3. Если из одной точки к одной окружности проведены две секущие, то произведение первой секущей на ее внешнюю часть равно произведению второй секущей на свою внешнюю часть.
$АС·ВС=EC·DC$
4. Если из одной точки к окружности проведены секущая и касательная, то произведение секущей на ее внешнюю часть равно квадрату длины касательной.
$BD·СB=AB^2$
Вписанные и описанные окружности для четырехугольников.
1. Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
$АВ+CD=BC+AD$
2. Если сумма противоположных углов четырехугольника равна $180°$, то только тогда около него можно описать окружность.
$∠В+∠D=180°$
$∠A+∠C=180°$
Вневписанные окружности
Вневписанной окружностью треугольника называется окружность, касающаяся одной из его сторон и продолжений двух других.
Для каждого треугольника существует три вневписанных окружности, которые расположены вне треугольника, центрами вневписанных окружностей являются точки пересечения биссектрис внешних углов треугольника.
Точки $О_1, О_2$ и $О_3$ – центры вневписанных окружностей.
Связь площади треугольника с радиусами вневписанных окружностей.
Введем обозначения:
$S$ — площадь треугольника;
$p$ — полупериметр треугольника;
$a, b, c$ — стороны треугольника;
$r_a, r_b, r_c$ — радиусы вневписанных окружностей касающиеся соответственно сторон $a, b$ и $c$;
Для данных обозначений справедливы равенства:
$r_a={S}/{p-a};$
$r_b={S}/{p-b};$
$r_c={S}/{p-c}.$
Пример:
В прямоугольном треугольнике $АВС$ угол $С=90°, АС=6, ВС=8$. Найдите радиус вневписанной окружности, касающейся гипотенузы.
Решение:
Радиус вневписанной окружности, касающейся стороны $АВ$ равен:
$r_{АВ}={S}/{p-АВ}$, где $S$ — площадь треугольника, $р$ — полупериметр треугольника.
Чтобы подставить в формулу данные, найдем сначала площадь треугольника и его полупериметр.
Площадь прямоугольного треугольника равна половине произведения катетов:
$S={АС·АВ}/{2}={6·8}/{2}=24$
Нам неизвестна гипотенуза, найдем ее по теореме Пифагора:
$АВ=√{АС^2+СВ^2}=√{6^2+8^2}=√{100}=10$
Зная все стороны, вычислим полупериметр:
$р={6+8+10}/{2}=12$
Теперь можем все данные подставить в формулу нахождения радиуса вневписанной окружности:
$r_{АВ}={S}/{p-АВ}={24}/{12-10}={24}/{2}=12$
Ответ: $12$
Биссектриса
Биссектриса – это линия, которая делит угол пополам.
Свойства биссектрисы:
1. В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.
2. Если точка лежит на биссектрисе, то расстояния от неё до сторон угла равны.
$AD=DC$
3. Три биссектрисы в треугольнике пересекаются в одной точке, эта точка является центром вписанной в треугольник окружности.
4. Биссектриса угла в параллелограмме отсекает равнобедренный треугольник.
5. Биссектрисы смежных углов перпендикулярны.
6. В треугольнике биссектриса угла делит противоположную сторону на отрезки, отношение которых такое же, как отношение сторон треугольника, между которыми эта биссектриса прошла.
${AB}/{AC}={BA_1}/{A_1C}$
7. Для нахождения длины биссектрисы справедлива формула:
$АА_1=√{АВ·АС-ВА_1·А_1 С}$
Медиана
Медиана — это линия, проведенная из вершины треугольника к середине противоположной стороны.
Свойства медиан:
1. Медиана делит треугольник на два равновеликих треугольника, т.е. на два треугольника, у которых площади равны.
$S_1=S_2$
2. Медианы пересекаются в одной точке и этой точкой делятся в отношении два к одному, считая от вершины.
3. В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы и радиусу описанной около этого треугольника окружности.
4. Для нахождения длины медианы, проведенной к стороне «с», справедлива формула:
$М_с={√{2(а^2+b^2)-c^2}}/{2}$
Высота
Высота в треугольнике — это линия, проведенная из вершины треугольника к противоположной стороне под углом в 90 градусов.
$BB_1$ — высота
Свойства высот:
1. Три высоты (или их продолжения) пересекаются в одной точке.
2. При пересечении двух высот получаются подобные треугольники:
$∆АА_1 В~∆СС_1В;$
$∆АС_1 М~∆СМА1$
3. Угол между высотами в остроугольном треугольнике равен углу между сторонами, к которым эти высоты проведены.
4. Высоты треугольника обратно пропорциональны его сторонам:
$h_a:h_b:h_c={1}/{a}:{1}/{b}:{1}/{c}$
Теорема синусов
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
${a}/{sinα}={b}/{sinβ} ={c}/{sinγ} =2R$, где $R$ — радиус описанной около треугольника окружности.
Пример:
В треугольнике $АВС ВС=16, sin∠A={4}/{5}$. Найдите радиус окружности, описанной вокруг треугольника $АВС$.
Решение:
Воспользуемся теоремой синусов:
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности
${ВС}/{sinA} =2R$
Далее подставим числовые данные и найдем $R$
${16·5}/{4}=2R$
$R={16·5}/{4·2}=10$
Ответ: $10$
Теорема косинусов
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
$a^2=b^2+c^2-2·b·c·cosα.$
Планиметрия – профильный ЕГЭ по математике (оглавление)
Планиметрия плохо дается многим ученикам. На ЕГЭ эта задача №16 – одна из самых сложных задач и многие даже не пытаются за нее браться.
Весь секрет в том, что понимание планиметрии приходит не постепенно, а сразу. Вчера не получалось, а сегодня уже все понятно. Большинству просто не хватает терпения дойти до этого момента.
Надеемся, что ты не такой и не бросишь занятия на полпути. И вот тебе в помощь все, что нужно знать по планиметрии + несколько вебинаров для отработки навыков!
Планиметрия – часть 1. ЕГЭ №3 (бывшая №6)
Если вы плохо знаете планиметрию, начинайте с этой части и смотрите вебинар за вебинаром, ставьте на паузу и решайте задачи вместе с ведущим вебинаров Алексеем Шевчуком.
Помните, планиметрия требует нарешенности. Чтобы научиться решать любую задачу по планиметрии, нужно решать много задач.
Начните с самого начала.
Планиметрия – прямоугольный треугольник
Итак, прямоугольный треугольник, его свойства, площадь и углы прямоугольного треугольника, теорема Пифагора, тригонометрический функции острых углов, медиана и высота.
Планиметрия – равнобедренный треугольник и произвольный треугольник
В этом видео мы вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ.
Очень часто все “проблемы” с решением задач на равнобедренный треугольник решаются построением высоты. Также мы научимся решать и “обычные” треугольники.
Убедимся в достоверности утверждении из прошлого урока о прямоугольных треугольниках – очень часто решение задач сводится к нескольким прямоугольным треугольникам.
Вписанная окружность
В этом видео мы узнаем, что такое вписанная окружность, где находится её центр, и другие ее свойства. В какие фигуры можно, а в какие нельзя вписать окружность.
Научимся решать задачи на вписанную окружность – очень важный навык в понимании планиметрии.
Описанная окружность. Многоугольники
Вы этом видео вы узнаете, что такое описанная окружность, где находится её центр, и другие свойства. Около каких фигур можно, а вокруг каких нельзя описать окружность.
Также мы узнаем, что такое правильные многоугольники, и какие у них свойства; как они связаны с описанной окружностью.
Научимся решать задачи из ЕГЭ на описанную окружность и правильные многоугольники.
Что приблизит нас к умению решать любые задачи по планиметрии.
Теорема косинусов и синусов
Универсальный инструмент при решении треугольников – это теоремы косинусов и синусов.
Они подходят для любых треугольников, а не только для прямых (как теорема Пифагора).
А как мы уже знаем, почти любая задача в планиметрии сводится именно к треугольникам.
На этом уроке мы выучим сами теоремы и научимся применять их при решении задач первой части.
Планиметрия – часть 2. ЕГЭ №16
Эта часть планиметрии – для продвинутых, для тех, кто уже хорошо усвоил планиметрию из первой части.
Принцип тот же – смотрите вебинар за вебинаром и, самое главное, ставьте на паузу и решайте задачи.
Планиметрия. Подобие треугольников. Задачи на доказательство. ЕГЭ №16
Подобие треугольников. Это одна из самых сложных задачи планиметрии в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников!
Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства.
Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы.
В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение.
Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем.
Вы научитесь также применять подобие треугольников не только для доказательств, а и для расчётных задач.
Метод вспомогательной окружности. Из реального ЕГЭ 2016 года
Метод вспомогательной окружности – это очень классный метод, используемый в планиметрии но, к сожалению, он не всегда очевиден. Иногда в задаче нет даже намёка ни на какие окружности, но тем не менее, если догадаться её на рисунке достроить, решение становится в разы проще!
Как минимум, сразу же становятся равными друг другу очень неочевидные углы – те, которые опираются на одну дугу, но без окружности увидеть это было бы нереально сложно. Либо произведения отрезков хорд равны друг другу.
Это очень крутой и удобный метод – но нужно понимать, в каких ситуациях он применяется, ведь далеко не всегда нужно на и без того сложный рисунок лепить ещё и окружность.
Теорема Менелая и Чевы. “Секретный” метод решения самой сложной задачи ЕГЭ по математике
Задача №16. Планиметрия. Одна из самых сложных задач на ЕГЭ. Редко кто (менее 1% учеников!) набирает полные баллы по ней и поэтому грех не воспользоваться шорткатами и лайфхаками, если они есть.
Теорема Менелая и Чевы – один из таких шорткатов. Эти теоремы не входят в стандартную школьную программу, но они невероятно мощный инструмент! Они могут очень-очень упростить решение и сами по себе они красивые и легко запоминаются.
Итак, смотрите видео, учите теорему Менелая и Чевы, используйте ее на ЕГЭ.
Теорема Менелая и Чевы — её уже запретили, наконец, или нет?
Каждый год начинают ходить слухи, что теоремами Менелая и Чевы В ЭТОМ ГОДУ НЕЛЬЗЯ будет пользоваться на ЕГЭ. Правда ли это? Чтобы понять это, достаточно заглянуть в обычный…
Впрочем, смотрите это видео и узнаете, как понять, какими теоремами можно, а какими нельзя пользоваться. А также, на этом вебе мы разберём, что это за теоремы такие, и как ими пользоваться.
Вы узнаете, насколько они крутые и мощные, и насколько экономят нам время в некоторых задачах.
Планиметрия Статград март 2021
Задача №16 из мартовского статграда на планиметрию ничем не удивляет: снова окружность и пропорциональные отрезки в ней, прямоугольные треугольники, вот это всё.
Скучно… Раз-два, и ответ готов!
Но погодите-ка, а почему у нас с вами ответ получился разный? И вроде бы оба делаем всё правильно…
На уроках нашего курса я рассказывал о таких задачах, но их уже давненько не попадалось на ЕГЭ, и все уж думали, что ушла эпоха. Конечно, никакого парадокса в этой задаче нет, нужно всего лишь (ха-ха) быть очень внимательными:)
Смотрите видео, и узнаете, в чём же особенность этой задачи, как её правильно решать и оформлять, а также – как ничего не упустить на экзамене и не потерять баллы!
Планиметрия. Окружности. Задача из олимпиады Физтеха 2020
Планиметрия и окружности! Куда же деться от них в 16 задаче на ЕГЭ?
Те, кто ходил на наш курс подготовки, посвященный 16 задаче, знают, что окружности в задачах на планиметрию попадаются чаще всего.
Иногда вписанные. Иногда описанные. С разными вписанными или описанными фигурами. Иногда одна окружность . Иногда две. Они касаются друг друга или пересекаются друг с другом. Никуда не деться от окружностей – остается только научится их решать и получать удовольствие от красивых задач!
В этом видео мы разберём, что бы вы думали? Задачу 16 из ЕГЭ?
Нет! Пойдём дальше – разберём задачу из олимпиады Физтеха прошлого года.
Стойте, не разбегайтесь! Олимпиады далеко не всегда бывают сложными (особенно, если вы прошли наш курс по 16-й задаче). Эта задача вполне себе ЕГЭ-шного уровня. Про окружности и прямоугольные треугольники.
Готовьтесь и “разминайте” свои теоремы Пифагора, теорему синусов и прочих косинусов.
Разбор задачи №16 (б) из реального варианта ЕГЭ 2021 по профильной математике
Продолжение предыдущего видео. Разбор части (б):
Теперь слово вам…
Как вам наш гид по планиметрии? Что нового вы узнали? Что еще хотите узнать?
Как вам теорема Менелая и Чевы? Один из моих знакомых сказал: “В школе ее от нас утаивали!”. Шутка, в которой есть доля… шутки.
Готовьтесь к планиметрии и забирайте свои 3 балла на ЕГЭ.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук – ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 – WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org – email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж – c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов – как обычно дурацкая ошибка:);
- отзыв на Профи.ру: “Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами”.
Планиметрия на ЕГЭ
- 08.11.2013
Материал для подготовки к ЕГЭ по математике на тему: «Планиметрия».
Содержание темы:
21. ПЛАНИМЕТРИЯ
21.1. Углы и прямые
21.2. Многоугольник
21.3. Соотношения между сторонами и углами в треугольнике
21.4. Линии в треугольнике
21.5. Формулы для вычисления площади треугольника
21.6. Признаки равенства и подобия треугольников
21.7. Четырехугольники
21.8. Окружность и круг
22.9. Вписанные и центральные углы
11.2. Вписанная и описанная окружность
11.3. Формулы для вычисления радиусов вписанной и описанной окружностей
11.4. Шестиугольник
Тест для проверки теоретических знаний
Примеры
Задачи для самостоятельного решения
Контрольный тест
Рекомендуем использовать этот материал при тщательной подготовке к сдаче ЕГЭ на высокий балл.
В теме содержатся теория и практические задания различного уровня сложности.
Смотреть в PDF:
Или прямо сейчас: Скачайте в pdf файле.
Теоремы и определения по Планиметрии
Теоремы и определения по Планиметрии. Справочник по геометрии для 7-11 классов, для подготовки к ОГЭ и ЕГЭ. Часть 1 «Планиметрия». Автор: Нелин Е.П. Использованы цитаты из пособия «Геометрия. 7-11 классы. Определения, свойства, методы решения задач в таблицах / М.: Илекса, 2018» из серии «Комплексная подготовка к ЕГЭ и ГИА (ОГЭ). Цитаты использованы в учебных целях.
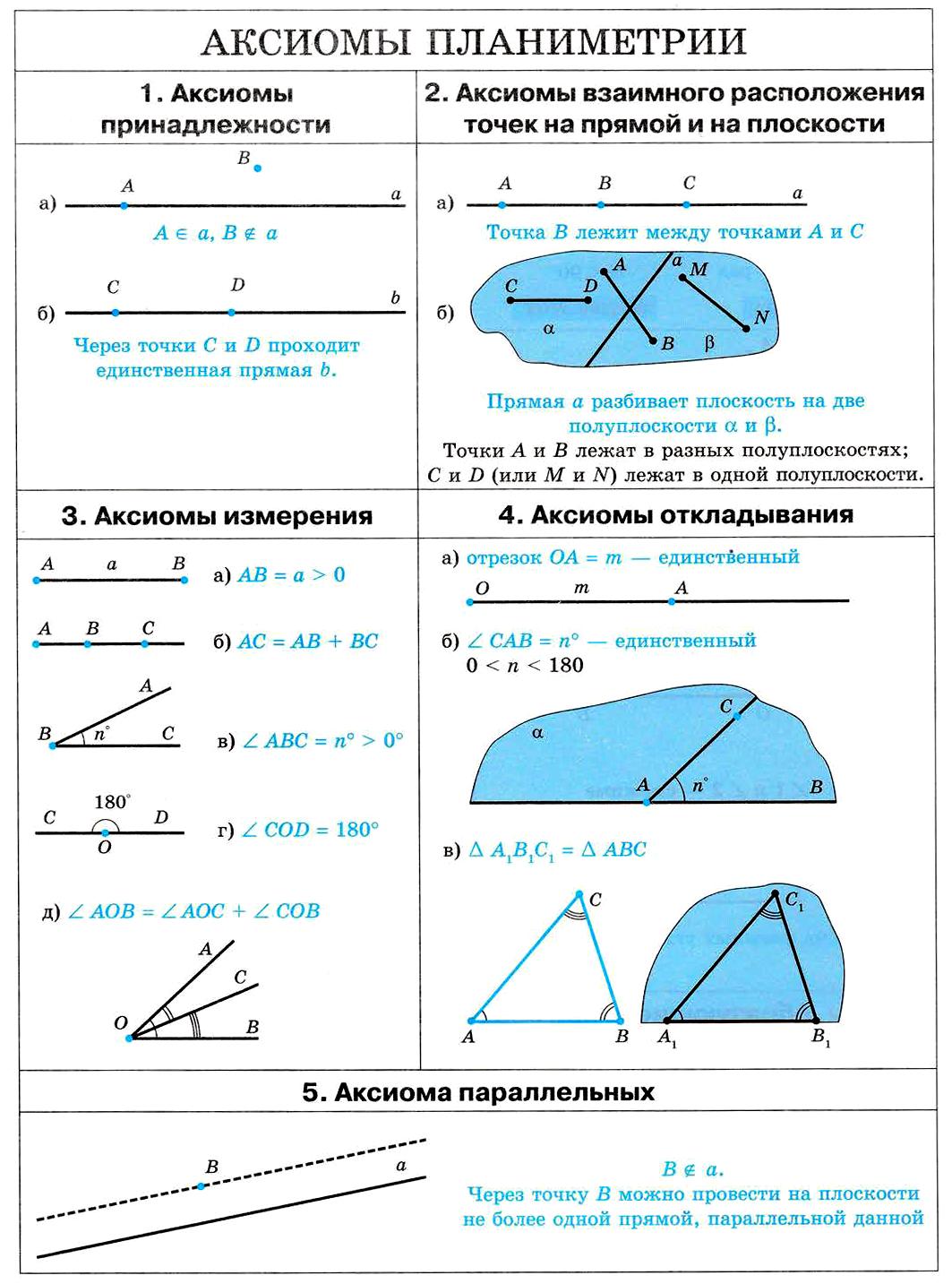
01. Аксиомы планиметрии.
Аксиомы принадлежности. Аксиомы взаимного расположения точек на прямой и плоскости. Аксиомы измерения. Аксиомы откладывания. Аксиома параллельных
02. Углы
Смежные углы. Вертикальные углы. Углы при пересечении
03. Параллельные прямые. Перпендикулярные прямые. Перпендикуляр к прямой
03. Параллельные прямые. Перпендикулярные прямые. Перпендикуляр к прямой
04. Свойства сторон и углов треугольника
Свойства сторон и углов треугольника. Внешний угол. Свойства. Неравенство треугольника. Равнобедренный треугольник
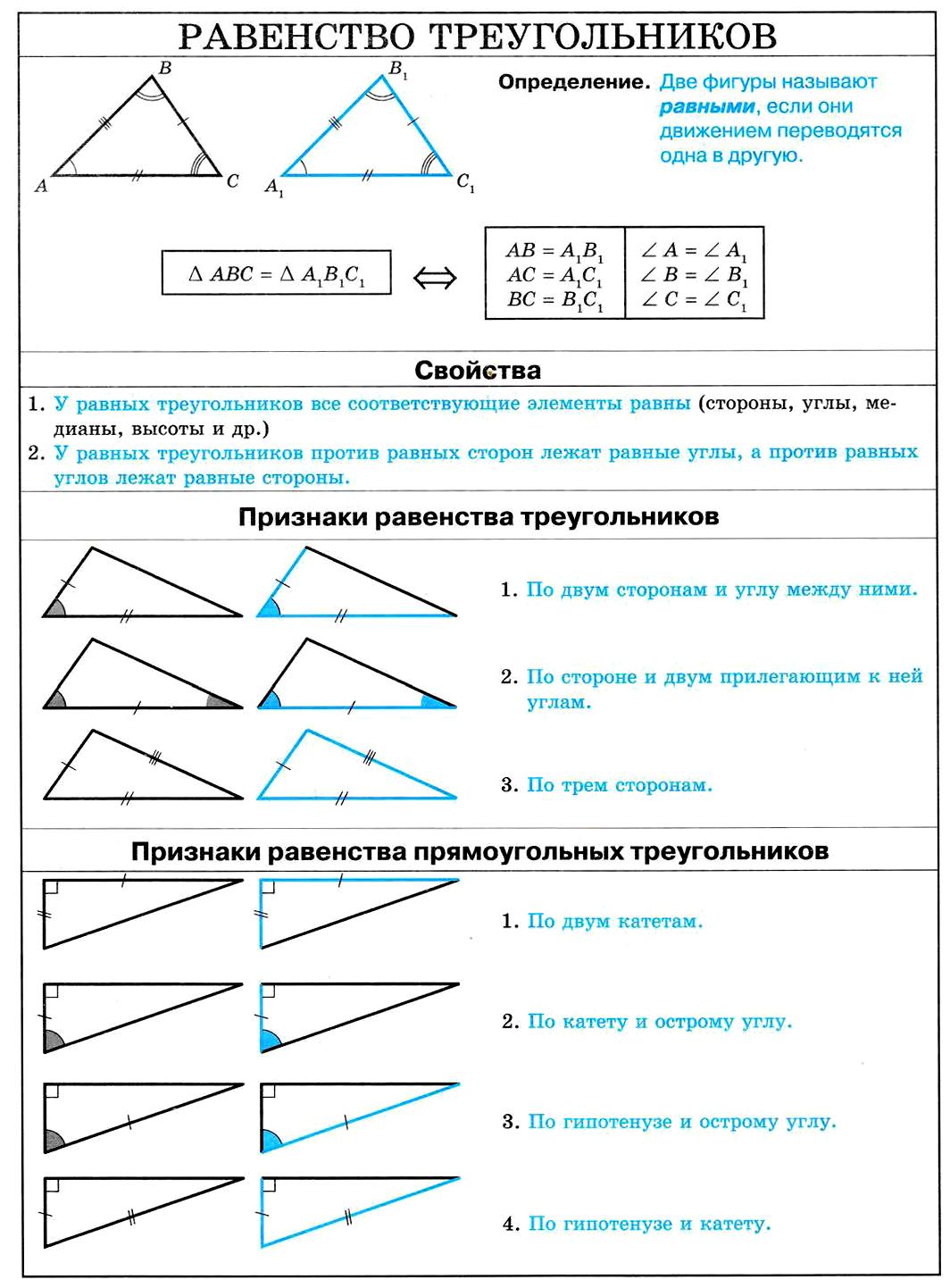
05. Равенство треугольников.
Равенство треугольников. Свойства. Признаки равенства треугольников. Признаки равенства прямоугольных треугольников
06. Медиана треугольника.
Медиана треугольника. Свойства.
07. Биссектриса треугольника.
Биссектриса треугольника. Свойства
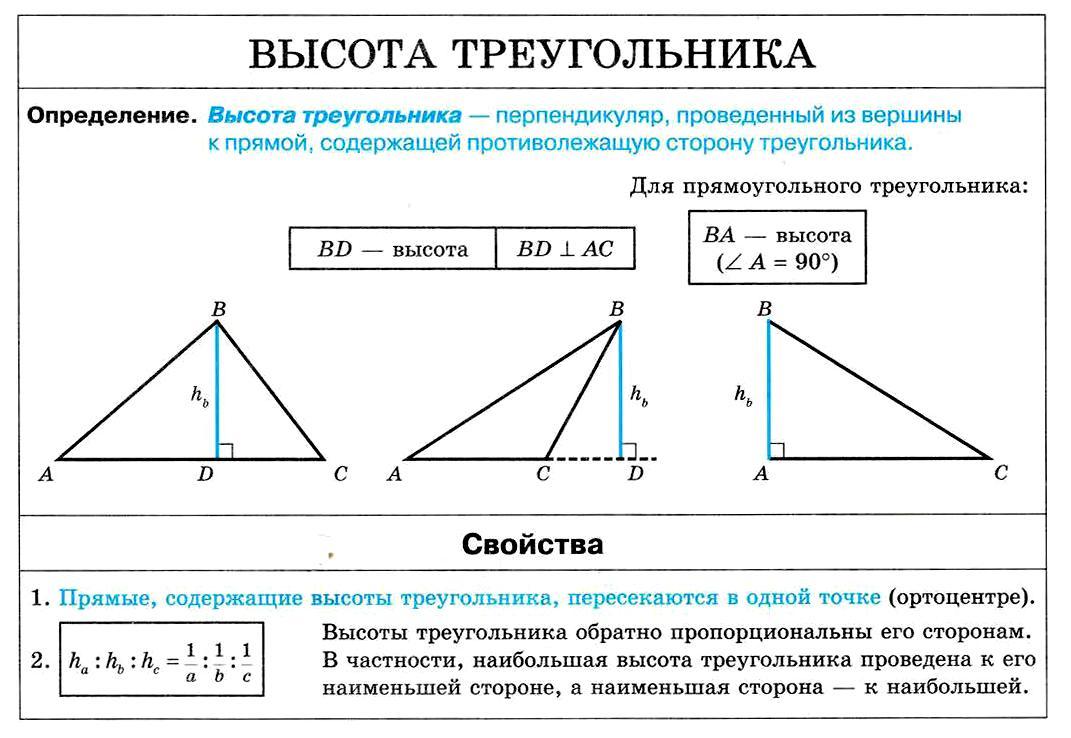
08. Высота треугольника
Высота треугольника. Свойства
09. Средняя линия треугольника
Средняя линия треугольника. Свойства
10. Соотношение между элементами прямоугольного треугольника
Соотношение между элементами прямоугольного треугольника
11. Соотношение между сторонами и углами в произвольном треугольнике
Соотношение между сторонами и углами в произвольном треугольнике
12. Преобразование фигур. Движение
Преобразование фигур. Движение. Симметрия относительно точки. Поворот. Симметрия относительно прямой. Параллельный перенос
13. Преобразование подобия
Преобразование подобия. Свойства. Гомотетия.
14. Подобие треугольников.
Подобие треугольников. Свойства. Признаки подобия треугольников
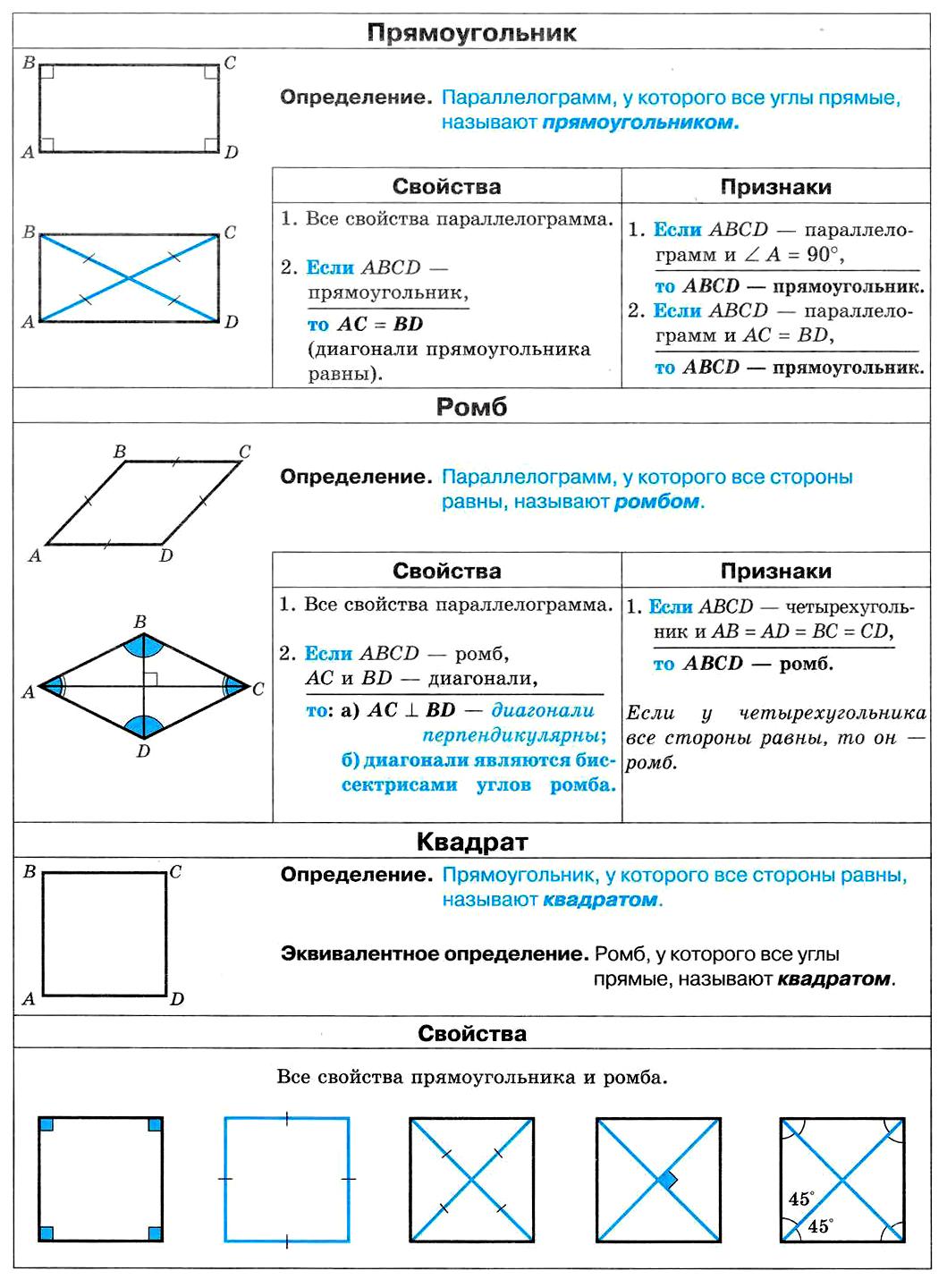
15. Параллелограмм и его виды.
Параллелограмм и его виды. Свойства. Признаки
Прямоугольник. Ромб. Квадрат.
16. Трапеция
Трапеция. Частные случаи трапеции. Средняя линия трапеции. Дополнительные построения для трапеции
17. Окружность, хорды и дуги
Окружность, хорды и дуги. Свойства
18. Окружность. Касательные и секущие.
Окружность. Касательные и секущие.
19. Взаимное расположение прямой и окружности. Взаимное расположение двух окружностей.
Взаимное расположение прямой и окружности. Взаимное расположение двух окружностей.
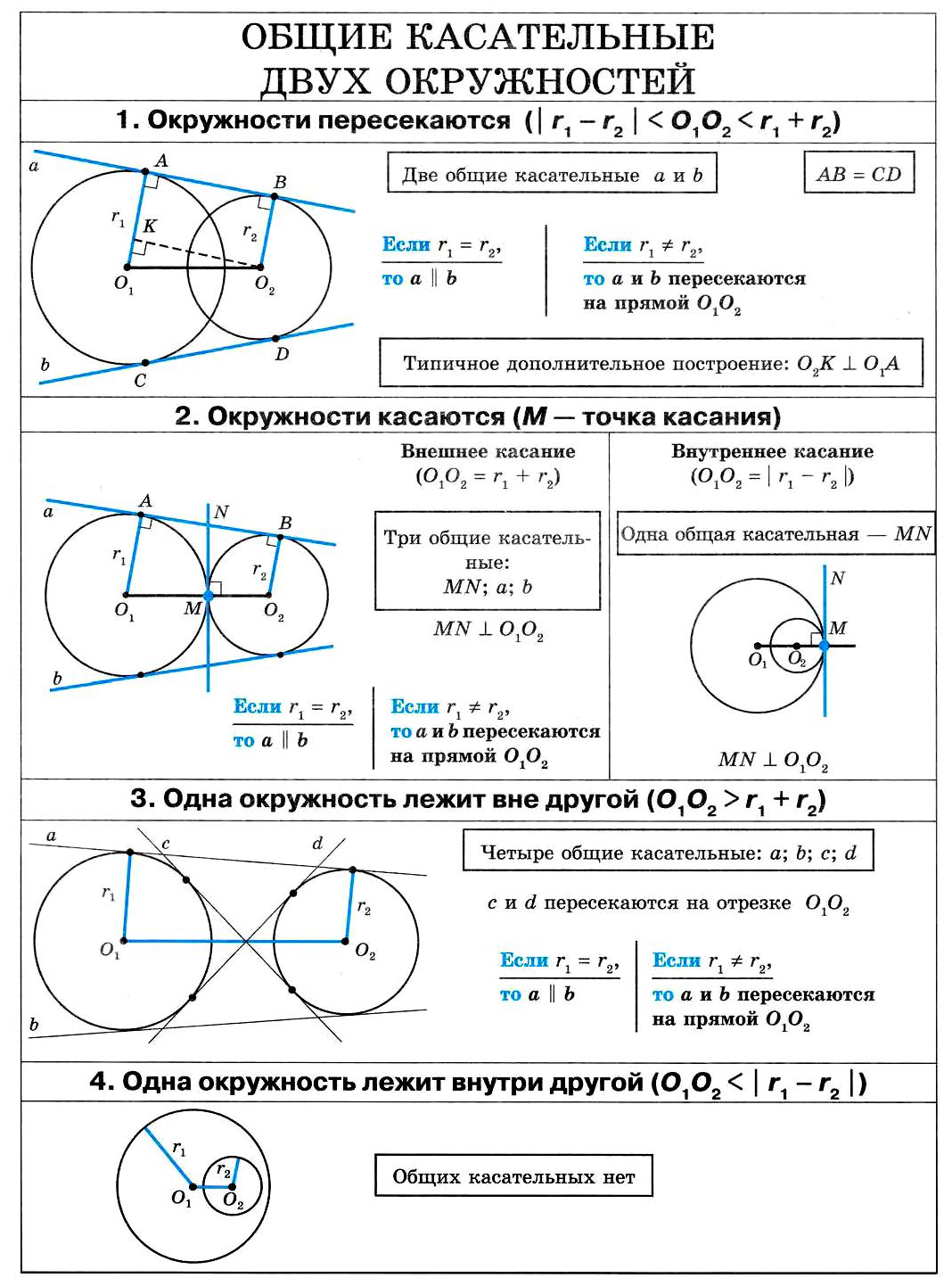
20. Общие касательные двух окружностей.
Общие касательные двух окружностей.
21. Углы в окружности.
Углы в окружности.
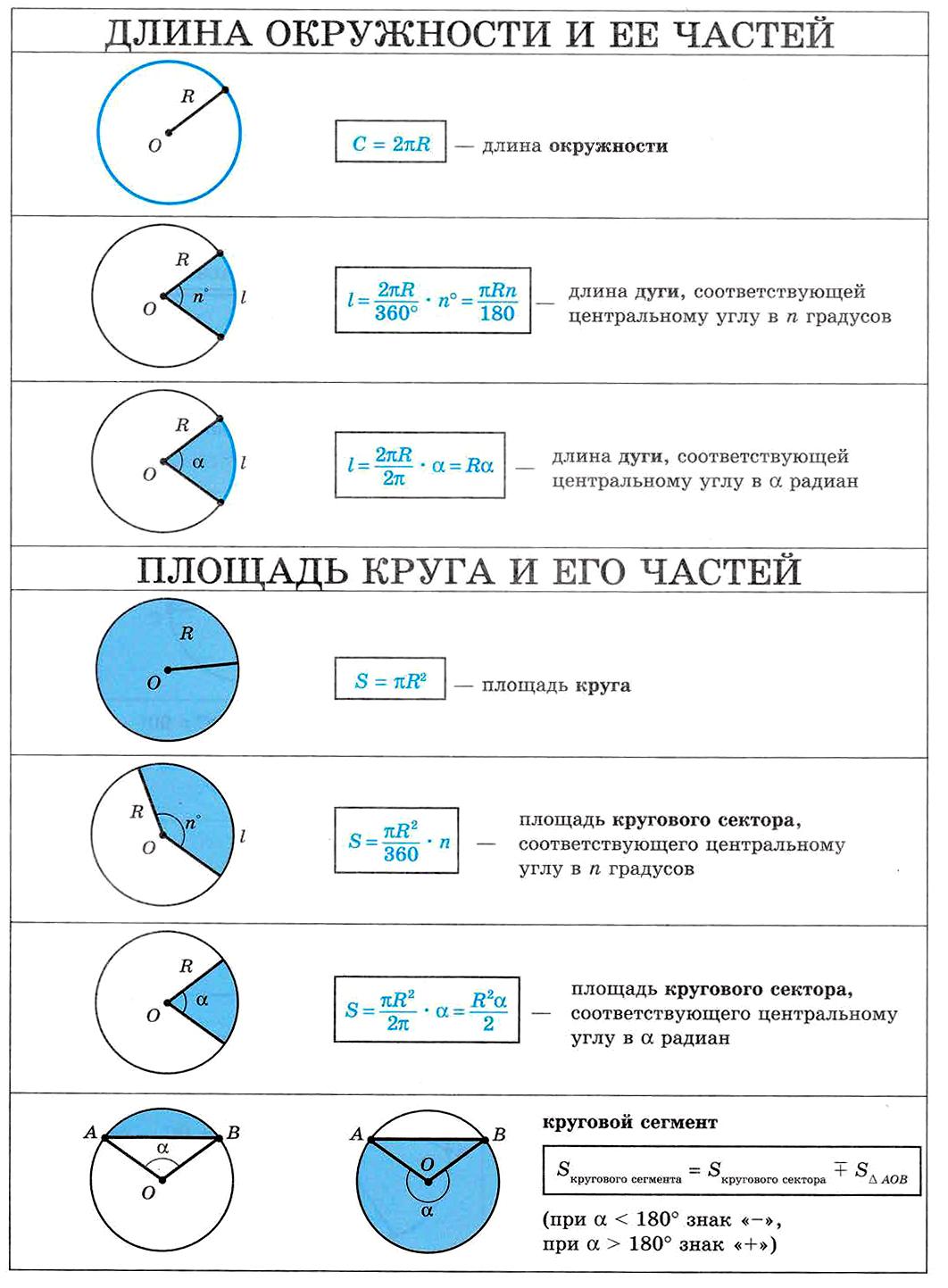
22. Длина окружности и её частей. Площадь круга и его частей
Длина окружности и её частей. Площадь круга и его частей
23. Вписанный и описанный многоугольники. Вписанный и описанный четырехугольники. Прямоугольник. Трапеция и ромб. Квадрат.
Вписанный и описанный многоугольники. Вписанный и описанный четырехугольники. Прямоугольник. Трапеция и ромб. Квадрат.
24. Окружность, описанная около треугольника, и окружность, вписанная в треугольник.
25. Окружности, описанные и вписанные в правильные многоугольники
Окружности, описанные и вписанные в правильные многоугольники
26. Площади треугольников.
Площади треугольников.
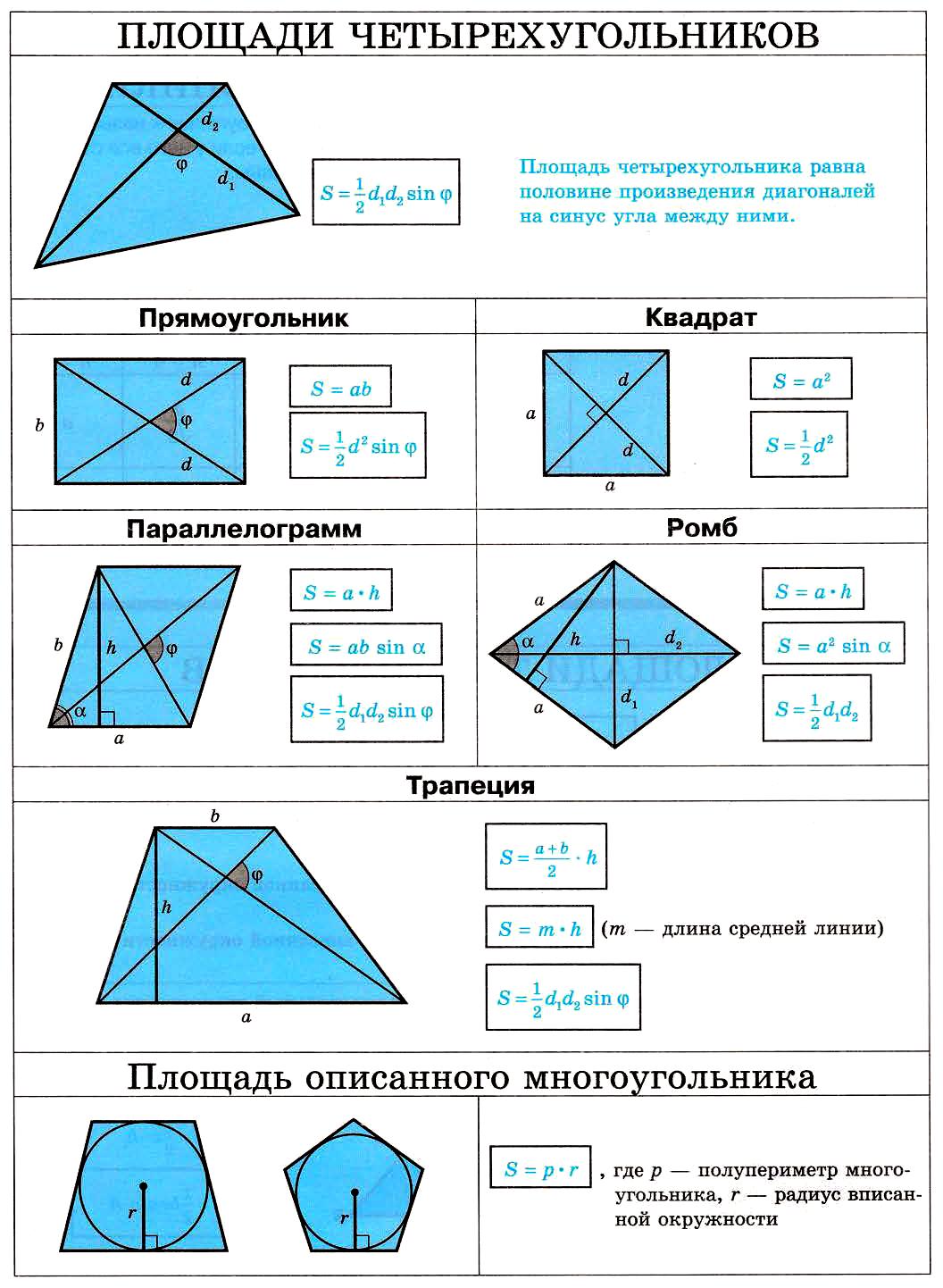
27. Площади четырехугольников.
Площади четырехугольников. Площадь описанного многоугольника
Вы смотрели справочник по геометрии для 7-11 классов «Теоремы и определения по Планиметрии».
Справочный материал по планиметрии
Геометрия на плоскости (планиметрия)
Задание
1
#199
Уровень задания: Легче ЕГЭ
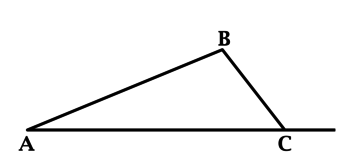
В треугольнике (ABC): (angle B = 81^{circ}), (angle C = 25^{circ}). Найдите внешний угол при вершине (A). Ответ дайте в градусах.
Согласно теореме о внешнем угле треугольника, (angle B + angle C =) внешнему углу при вершине (A), следовательно (A_{text{внеш}}) ( = 81^{circ} + 25^{circ} = 106^{circ}).
Ответ: 106
Задание
2
#200
Уровень задания: Легче ЕГЭ
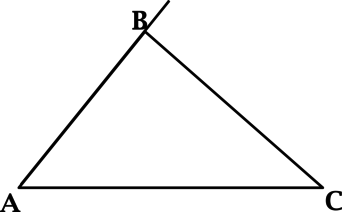
В треугольнике (ABC): (angle A = 22^{circ}), внешний угол при вершине (C) равен (130^{circ}). Найдите (angle B). Ответ дайте в градусах.
Согласно теореме о внешнем угле треугольника, (angle A + angle B = C_{text{внеш}}), тогда (22^{circ} + angle B = 130^{circ}), откуда находим (angle B = 130^{circ} — 22^{circ} = 108^{circ}).
Ответ: 108
Задание
3
#201
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle C = 35^{circ}), внешний угол при вершине (B) равен (91^{circ}). Найдите (angle A). Ответ дайте в градусах.
Согласно теореме о внешнем угле треугольника, (angle C + angle A = B_{text{внеш}}), тогда (35^{circ} + angle A = 91^{circ}), откуда находим (angle A = 91^{circ} — 35^{circ} = 56^{circ}).
Ответ: 56
Задание
4
#202
Уровень задания: Легче ЕГЭ
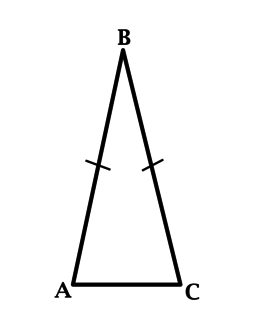
В треугольнике (ABC): (angle C = 70^{circ}), (AB = BC). Найдите (angle B). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle A = angle C = 70^{circ}). Так как у любого треугольника сумма углов равна (180^{circ}), то (angle B = 180^{circ} — 70^{circ} — 70^{circ} = 40^{circ}).
Ответ: 40
Задание
5
#203
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle A = 47^{circ}), (AB = BC). Найдите (angle B). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle C = angle A = 47^{circ}). Так как у любого треугольника сумма углов равна (180^{circ}), то (angle B = 180^{circ} — 47^{circ} — 47^{circ} = 86^{circ}).
Ответ: 86
Задание
6
#204
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle C = 36^{circ}), (AB = BC). Найдите (angle B). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle A = angle C = 36^{circ}). Так как у любого треугольника сумма углов равна (180^{circ}), то (angle B = 180^{circ} — 36^{circ} — 36^{circ} = 108^{circ}).
Ответ: 108
Задание
7
#205
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle B = 38^{circ}), (AB = BC). Найдите (angle C). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle A = angle C). Так как у любого треугольника сумма углов равна (180^{circ}), то (180^{circ} = 38^{circ} + angle A + angle C = 38^{circ} + 2cdot angle A), откуда (2cdot angle A = 142^{circ}), тогда (angle A = 71^{circ}).
Ответ: 71