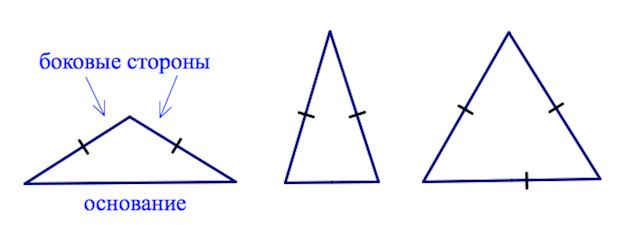
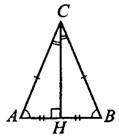
Равнобедренный треугольник — это такой треугольник, у которого две стороны равны. Равные стороны называются боковыми. Третья сторона называется основанием.
Свойства:
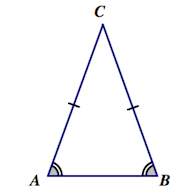
1. В равнобедренном треугольнике углы при основании равны.
2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
3. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
4. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
5. Углы, противолежащие равным сторонам равнобедренного треугольника, всегда острые.
6. В равнобедренном треугольнике:
— биссектрисы, проведенные из вершин при основании, равны;
— высоты, проведенные из вершин при основании, равны;
— медианы, проведенные из вершин при основании, равны.
7. Центры вписанной и описанной окружностей лежат на высоте, биссектрисе и медиане, проведенных к основанию.
8. Вписанная окружность точкой касания делит основание пополам.
Внешним углом треугольника называется угол, смежный с каким-либо углом этого треугольника.
Внешний угол треугольника равен сумме двух углов, не смежных с ним.
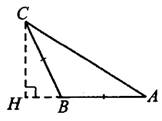
$∠BCD$ — внешний угол треугольника $АВС$.
$∠BCD=∠A+∠B$
Теорема Пифагора.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$.
Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом ($ctg$) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
Пример:
В прямоугольном треугольнике $АВС$ для острого угла $В$:
$sinB={AC}/{AB};$
$cosB={BC}/{AB};$
$tg B={AC}/{BC};$
$ctg B={BC}/{AC}$.
- В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
- Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
- Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
$sin BOA=sin BOC;$
$cos BOA= — cos BOC;$
$tg BOA= — tg BOC;$
$ctg BOA= — ctg BOC.$
Пример:
В треугольнике $ABC$ $AB=BC, AH$ — высота, $AC=34, cos ∠BAC=0.15$. Найдите $CH$.
Решение:
Так как треугольник $АВС$ равнобедренный, то $∠A=∠С$ (как углы при основании)
Косинусы равных углов равны, следовательно, $cos∠BAC=cos∠ВСА=0.15$
Рассмотрим прямоугольный треугольник $АНС$.
Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Распишем косинус $∠НСА$ (он же $∠ВСА$) по определению:
$cos∠НСА={НС}/{АС}={НС}/{34}=0.15$
Из последнего равенства найдем $НС$, для этого $0.15$ представим в виде обыкновенной дроби и воспользуемся свойством пропорции:
${НС}/{34}={15}/{100}$
$НС={34·15}/{100}=5.1$
Ответ: $5.1$
Теорема Менелая:
Если на сторонах $ВС, АВ$ и продолжении стороны $АС$ треугольника $АВС$ за точку $С$ отмечены соответственно $А_1,С_1,В_1$, лежащие на одной прямой, то
${АС_1}/{С_1 В}·{ВА_1}/{А_1 С}·{СВ_1}/{В_1 А}=1$
Теорема синусов.
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
${a}/{sinα}={b}/{sinβ}={c}/{sinγ}=2R$, где $R$ — радиус описанной около треугольника окружности.
Пример:
В треугольнике $АВС$ $ВС=16, sin∠A={4}/{5}$. Найдите радиус окружности, описанной вокруг треугольника $АВС$.
Решение:
Воспользуемся теоремой синусов:
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности
${ВС}/{sinA}=2R$
Далее подставим числовые данные и найдем $R$
${16·5}/{4}=2R$
$R={16·5}/{4·2}=10$
Ответ: $10$
Теорема косинусов.
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
$a^2=b^2+c^2-2·b·c·cosα.$
22
Июл 2013
Категория: Справочные материалы
Равнобедренный треугольник
2013-07-22
2021-08-08
Равнобедренный треугольник – треугольник, у которого две стороны равны между собой.
Равные стороны называются боковыми, третья сторона называется основанием.
Свойства равнобедренного треугольника
1. Углы при основании равны
2. Биссектриса, медиана и высота, проведенные к основанию совпадают между собой
3. Углы при основании равнобедренного треугольника вычисляются по следующей формуле:
,
где – угол напротив основания.
4. Биссектрисы, медианы и высоты, проведённые из углов при основании равны между собой
5. Центры вписанной и описанной окружностей лежат на медиане=высоте=биссектрисе, проведенной к основанию
Признаки равнобедренного треугольника
1. Если в треугольнике два угла равны, то он равнобедренный.
2. Если в треугольнике медиана является и высотой (биссектрисой), то такой треугольник равнобедренный.
Автор: egeMax |
Нет комментариев
Доказательство равенства треугольников
Посмотри внимательно, у нас есть:
- ( displaystyle underbrace{AB}_{гипотенуза в Delta ABH}=underbrace{BC}_{гипотенуза в Delta СBH})
- ( displaystyle BHtext{ }=text{ }BH) (ещё говорят, ( displaystyle BH)– общая)
И, значит, ( displaystyle AHtext{ }=text{ }CH)!
Почему?
Да мы просто найдём и ( displaystyle AH), и ( displaystyle CH) из теоремы Пифагора (помня ещё при этом, что ( displaystyle AB=BC))
( displaystyle AH=sqrt{A{{B}^{2}}-B{{H}^{2}}})
( displaystyle CH=sqrt{B{{C}^{2}}-B{{H}^{2}}})
Удостоверились? Ну вот, теперь у нас
( displaystyle begin{array}{l}AB=BC\BH=BH\AH=CHend{array})
А уж по трём сторонам – самый легкий (третий) признак равенства треугольников.
Ну вот, наш равнобедренный треугольник разделился на два одинаковых прямоугольных.
Отметим на картинке все одинаковые элементы (углы и стороны).
Видишь, как интересно? Получилось, что:
- В равнобедренном треугольнике углы при основании равны: ( displaystyle angle A=angle C);
- Высота, проведенная к основанию ( displaystyle (ВH)), совпадает с медианой и биссектрисой
- ( displaystyle AH=CH)
- ( displaystyle angle 1=angle 2).
Вспоминаем тут, что медиана – линия, проведённая из вершины, которая делит сторону пополам, а биссектриса – делит угол.)
Ну вот, здесь мы обсудили, что хорошего можно увидеть, если дан равнобедренный треугольник.
Мы вывели, что у равнобедренного треугольника углы при основании равны, а высота, биссектриса и медиана, проведенные к основанию, совпадают.
И теперь возникает другой вопрос: а как узнать, равнобедренный ли треугольник?
То есть, как говорят математики, каковы признаки равнобедренного треугольника?
Определение равнобедренного треугольника
Какой треугольник называется равнобедренным?
Равнобедренным называется треугольник, у которого две стороны равны.
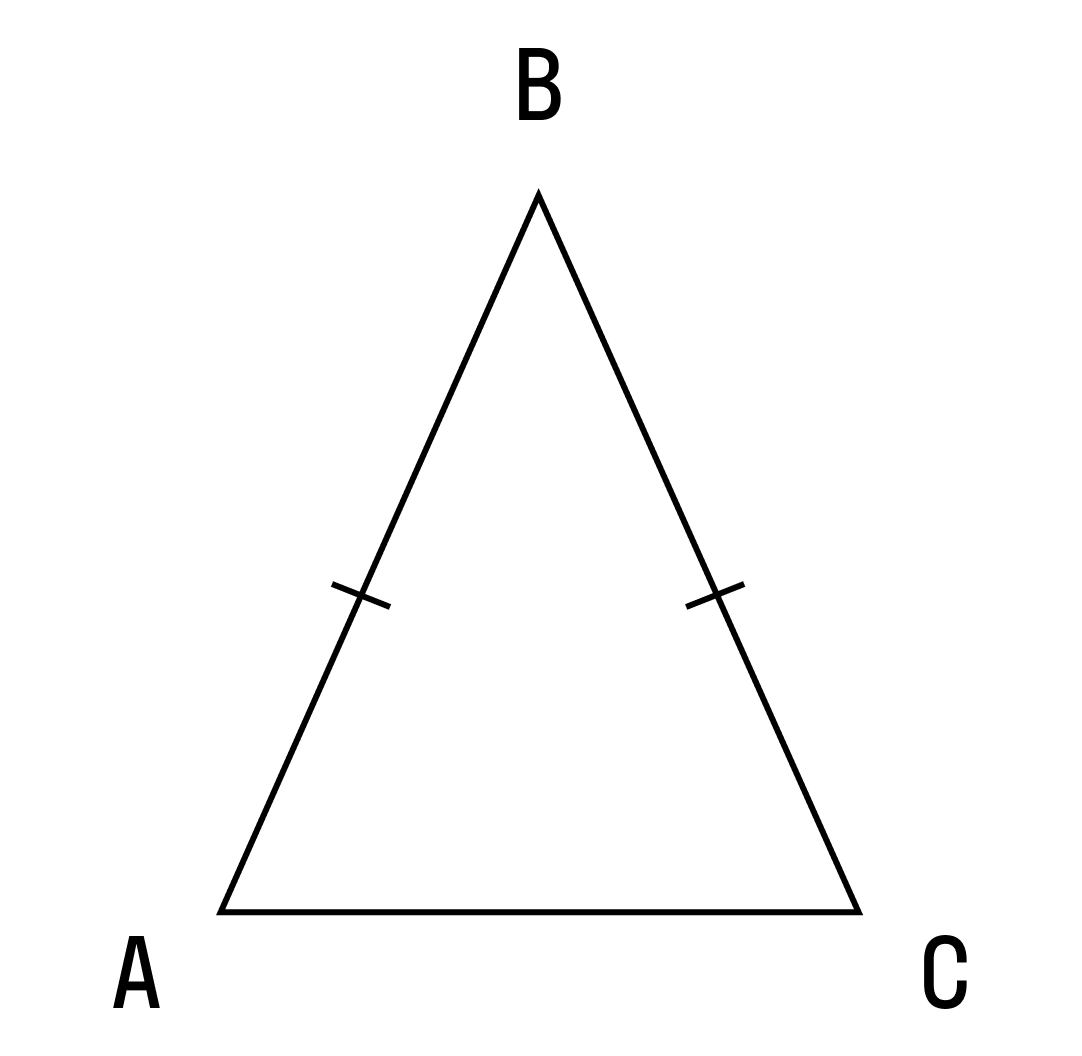
Давайте посмотрим на такой треугольник:
На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.
А вот как называются стороны равнобедренного треугольника:
AB и BC — боковые стороны,
AC — основание треугольника.
Для понимания материала нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.
Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.
Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.
Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.
Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».
В данном треугольнике медианой является отрезок BH.
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.
Высотой в представленном равнобедренном треугольнике является отрезок BH.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Признаки равнобедренного треугольника
Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.
- Если у треугольника два угла равны, то этот треугольник — равнобедренный.
- Если высота треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник — равнобедренный.
- Если высота треугольника совпадает с его биссектрисой, проведенной из того же угла, то такой треугольник — равнобедренный.
- Если биссектриса треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник снова равнобедренный!
Свойства равнобедренного треугольника
Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Доказательство теоремы:
Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!
Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
-
Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
-
Значит, во-первых, AH = HC и BH — медиана.
-
Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.
Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
-
Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
-
Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
-
Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.
Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
-
Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
-
Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
-
Во-вторых, AH = HC и BH — медиана.
Примеры решения задач
Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.
Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.
Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.
Значит, ∠A = ∠C = 80°.
Не должно вас удивить и то, что сумма углов треугольника равна 180°.
∠B = 180° − 80° − 80° = 20°.
Ответ: ∠B = 20°.
Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.
-
Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.
-
А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.
-
Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.
Ответ: 5 см.
Изучать свойства и признаки равнобедренного треугольника лучше всего
на курсах по математике с опытными преподавателями в Skysmart.
«Равнобедренный треугольник
+ ЗАДАЧИ по теме»
Равнобедренный треугольник — треугольнику которого две стороны равны.
Равные стороны называют боковыми сторонами, а третью сторону — основанием.
Свойства равнобедренного треугольника были известны с давних времен. Еще древние вавилоняне (II в. до н.э.) знали, что углы у основания равнобедренного треугольника равны. Любой треугольник можно разрезать на равнобедренные треугольники.
Свойства и признаки равнобедренного треугольника
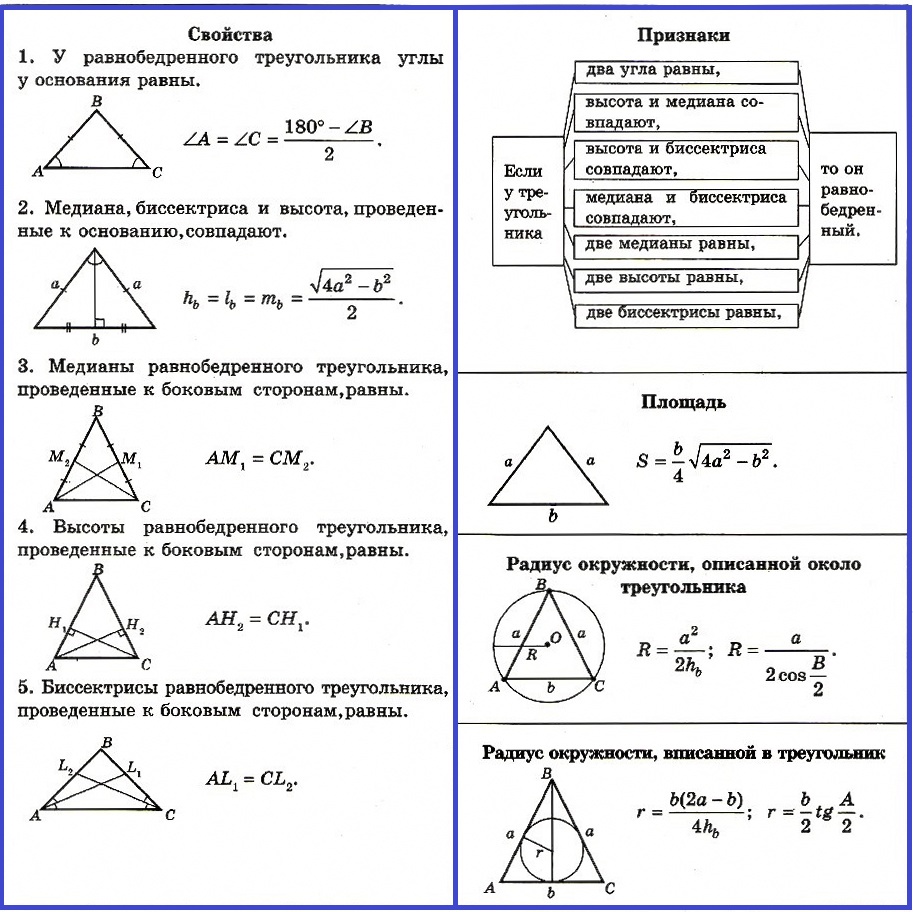
Свойства равнобедренного треугольника:
1. У равнобедренного треугольника углы у основания равны (теорема).
2. Медиана, биссектриса и высота, проведенные к основанию, совпадают (теорема).
3. Медианы равнобедренного треугольника, проведенные к боковым сторонам, равны.
4. Высоты равнобедренного треугольника, проведенные к боковым сторонам, равны.
5. Биссектрисы равнобедренного треугольника, проведенные к боковым сторонам, равны.
Признаки равнобедренного треугольника:
Если у треугольника есть один из нижеуказанных признаков, то он равнобедренный:
— два угла равны,
— высота и медиана совпадают,
— высота и биссектриса совпадают,
— медиана и биссектриса совпадают,
— две медианы равны,
— две высоты равны,
— две биссектрисы равны.
ПРИМЕРЫ РЕШЕНИЯ
КЛЮЧЕВЫХ ЗАДАЧ:
Уважаемые учителя!
Ранее размещенные здесь материалы удалены по требованию Издательства «Аверсэв» от 20 октября 2022 года. Кроме того, указанные материалы содержали ошибки, опечатки и не соответствовали ФГОС. В связи с этим не рекомендуем пользоваться учебными пособиями Издательства «Аверсэв» (Беларусь). Мы поддерживаем позицию этого издательства, что бесплатно рекламировать их учебные пособия нельзя, пусть рекламируют свои книги только за большие деньги, только через рекламу, только по предоплате!
В ближайшее время мы разместим здесь учебные материалы, которые полностью соответствуют ФГОС и рекомендованы УМК Атанасян и УМК Мерзляк.
С уважением, редакция сайта.
Теоретический тест
с последующей самопроверкой
- Медиана в равнобедренном треугольнике является его биссектрисой и высотой. Это утверждение:
а) всегда верно;
б) может быть верно;
в) всегда неверно. - Если треугольник равносторонний, то:
а) он равнобедренный;
б) все его углы равны;
в) любая его высота является биссектрисой и медианой. - В каком треугольнике только одна его высота делит треугольник на два равных треугольника?
а) в любом;
б) в равнобедренном;
в) в равностороннем. - Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение:
а) всегда верно;
б) может быть верно;
в) всегда неверно. - Если треугольник равнобедренный, то:
а) он равносторонний;
б) любая его медиана является биссектрисой и высотой;
в) два его угла равны. - В каком треугольнике любая его высота делит треугольник на два равных треугольника?
а) в любом;
б) в равнобедренном;
в) в равностороннем. - Если в треугольнике два угла равны, то этот треугольник является:
а) равносторонним;
б) равнобедренным;
в) прямоугольным. - Если в треугольнике две стороны равны, то:
а) у него равны два угла;
б) у него все углы равны;
в) этот треугольник равносторонний.
Нажмите на спойлер, чтобы увидеть ОТВЕТЫ
Вы смотрели конспект по теме «Равнобедренный треугольник + ЗАДАЧИ по теме». Выберите дальнейшие действия:
- Смотреть самостоятельную работу с ответами на тему «Равнобедренный треугольник»
- Перейти к следующему конспекту: Свойства сторон и углов треугольника + ЗАДАЧИ по теме
- Вернуться к Списку конспектов по геометрии
Равнобедренный треугольник
Равнобедренный треугольник – треугольник, у которого две стороны равны между собой.
Равные стороны называются боковыми , третья сторона называется основанием .
Свойства равнобедренного треугольника
1. Углы при основании равны
2. Биссектриса, медиана и высота, проведенные к основанию совпадают между собой
3. Углы при основании равнобедренного треугольника вычисляются по следующей формуле:
,
где – угол напротив основания.
4. Биссектрисы, медианы и высоты, проведённые из углов при основании равны между собой
5. Центры вписанной и описанной окружностей лежат на медиане=высоте=биссектрисе, проведенной к основанию
Признаки равнобедренного треугольника
1. Если в треугольнике два угла равны, то он равнобедренный.
2. Если в треугольнике медиана является и высотой (биссектрисой), то такой треугольник равнобедренный.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Равнобедренные треугольники
Равнобедренный треугольник — это такой треугольник, у которого две стороны равны. Равные стороны называются боковыми. Третья сторона называется основанием.
1. В равнобедренном треугольнике углы при основании равны.
2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
3. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
4. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
5. Углы, противолежащие равным сторонам равнобедренного треугольника, всегда острые.
6. В равнобедренном треугольнике:
— биссектрисы, проведенные из вершин при основании, равны;
— высоты, проведенные из вершин при основании, равны;
— медианы, проведенные из вершин при основании, равны.
7. Центры вписанной и описанной окружностей лежат на высоте, биссектрисе и медиане, проведенных к основанию.
8. Вписанная окружность точкой касания делит основание пополам.
Внешним углом треугольника называется угол, смежный с каким-либо углом этого треугольника.
Внешний угол треугольника равен сумме двух углов, не смежных с ним.
$∠BCD$ — внешний угол треугольника $АВС$.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$.
Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом ($ctg$) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
В прямоугольном треугольнике $АВС$ для острого угла $В$:
- В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
- Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
- Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
$cos BOA= — cos BOC;$
$ctg BOA= — ctg BOC.$
В треугольнике $ABC$ $AB=BC, AH$ — высота, $AC=34, cos ∠BAC=0.15$. Найдите $CH$.
Так как треугольник $АВС$ равнобедренный, то $∠A=∠С$ (как углы при основании)
Косинусы равных углов равны, следовательно, $cos∠BAC=cos∠ВСА=0.15$
Рассмотрим прямоугольный треугольник $АНС$.
Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Распишем косинус $∠НСА$ (он же $∠ВСА$) по определению:
Из последнего равенства найдем $НС$, для этого $0.15$ представим в виде обыкновенной дроби и воспользуемся свойством пропорции:
Если на сторонах $ВС, АВ$ и продолжении стороны $АС$ треугольника $АВС$ за точку $С$ отмечены соответственно $А_1,С_1,В_1$, лежащие на одной прямой, то
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
В треугольнике $АВС$ $ВС=16, sin∠A=<4>/<5>$. Найдите радиус окружности, описанной вокруг треугольника $АВС$.
Воспользуемся теоремой синусов:
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности
Далее подставим числовые данные и найдем $R$
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
Свойства и признаки равнобедренного треугольника
Равнобедренным треугольником называют треугольник, у которого две стороны равны.
Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника.
Если треугольник является равнобедренным треугольником, то углы при его основании равны.
Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником.
Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным
Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным
Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Равнобедренный треугольник | 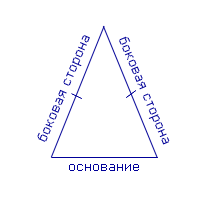 |
|
| Свойство | Углы при основании равнобедренного треугольника | 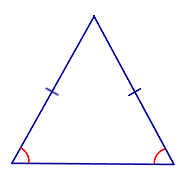 |
|
| Признак | Два равных угла треугольника | ||
| Свойство | Медиана, биссектриса и высота, проведённые к основанию равнобедренного треугольника | 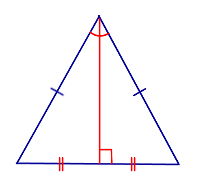 |
В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают. |
| Признак | Высота треугольника, совпадающая с медианой | 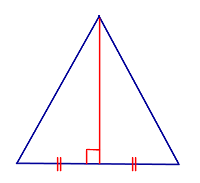 |
|
| Признак | Высота треугольника, совпадающая с биссектрисой | 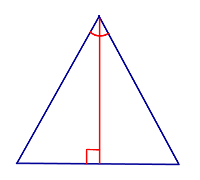 |
|
| Признак | Биссектриса треугольника, совпадающая с медианой | 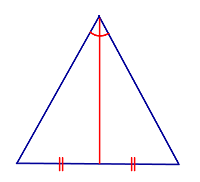 |
Равнобедренным треугольником называют треугольник, у которого две стороны равны.
Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника.
Если треугольник является равнобедренным треугольником, то углы при его основании равны.
Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником.
Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным
Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным
Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным
| Определение: равнобедренный треугольник | |
 |
|
| Свойство: углы при основании равнобедренного треугольника | |
 |
|
| Признак: два равных угла треугольника | |
 |
|
| Свойство: медиана, биссектриса и высота, проведённые к основанию равнобедренного треугольника | |
 |
В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают. |
| Признак: высота треугольника, совпадающая с медианой | |
 |
|
| Признак: высота треугольника, совпадающая с биссектрисой | |
 |
|
| Признак: биссектриса треугольника, совпадающая с медианой | |
 |
| Определение равнобедренного треугольника |
 |
Равнобедренным треугольником называют треугольник, у которого две стороны равны.
Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника.
Свойство углов при основании равнобедренного треугольника
Если треугольник является равнобедренным треугольником, то углы при его основании равны.
Признак равнобедренного треуголька: два равных угла треугольника
Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником.
Свойство медианы, биссектрисы и высоты, проведённых к основанию равнобедренного треугольника
В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают.
Признак равнобедренного треугольника: высота треугольника, совпадающая с медианой
Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным
Признак равнобедренного треугольника: высота треугольника, совпадающая с биссектрисой
Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным
Признак равнобедренного треугольника: биссектриса треугольника, совпадающая с медианой
Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным
источники:
http://examer.ru/ege_po_matematike/teoriya/ravnobedrennye_treugolniki
http://www.resolventa.ru/demo/eng/diagege.htm
Равнобедренным треугольником называют треугольник, у которого две равные стороны. Эти стороны называют боковыми сторонами, третью сторону называют основанием. Если в задаче дан равнобедренный треугольник, то пользуются его свойствами.
1. В равнобедренном треугольнике углы при основании равны.
2. Высота, проведённая к основанию равнобедренного треугольника (между равными сторонами), является медианой и биссектрисой.
Посмотрим на рисунок 1. В треугольнике основание
, боковые стороны
, угол
равен углу
, высота
делит
на равные отрезки
и угол
на два равных угла.
Рис. 1.
Задача 1. В треугольнике
,
,
. Найдите высоту
.
Решение.
В треугольнике стороны
, значит, он равнобедренный. Высота
, проведённая к основанию равнобедренного треугольника, делит
пополам, поэтому
. Рассмотрим прямоугольный треугольник
с прямым углом
и катетами
и
.
,
. Найдём
. Косинусом угла называют отношение прилежащего катета к гипотенузе.
По теореме Пифагора
Ответ: 16.
Задача 2. В треугольнике
, высота
равна 6,
(см. рис. 2). Найдите тангенс угла
.
Рис. 2.
Решение.
В равнобедренном треугольнике углы при основании равны. В данном треугольнике , основание
, равны углы
и
. Следовательно, можно вместо тангенса угла
найти тангенс угла
. Рассмотрим прямоугольный треугольник
с гипотенузой
и катетами
и
. Длину катета
можно найти по теореме Пифагора.
Тангенсом угла называют отношение противолежащего катета к прилежащему. Для нашего треугольника
Ответ: 0,5.
Задача 3. В треугольнике
,
. Найдите
.
Решение.
Рис. 3.
В равнобедренном треугольнике высота
является медианой, значит,
(см. рис. 3). Рассмотрим прямоугольный треугольник
с гипотенузой
и катетами
и
. В данном треугольнике
, тогда
Катет ) можно найти по теореме Пифагора:
в два раза больше
,
.
Ответ: 12.
Задача 4. В треугольнике
,
. Найдите
.
Решение.
Рис. 4.
Проведём высоту , тогда
. Рассмотрим прямоугольный треугольник
(см. рис. 4). Катет
можно найти по теореме Пифагора.
Ответ: 0,35.