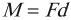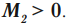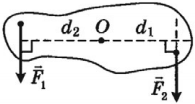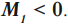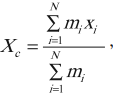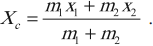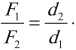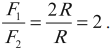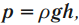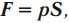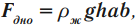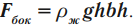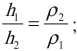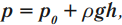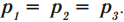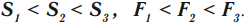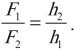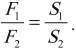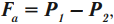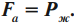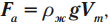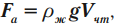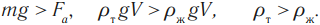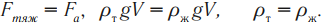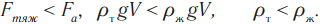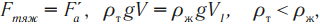Теория по статике для егэ

Статика твёрдого тела.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: момент силы, условия равновесия твёрдого тела.

Статика изучает равновесие тел под действием приложенных к ним сил. Равновесие — это состояние тела, при котором каждая его точка остаётся всё время неподвижной в некоторой инерциальной системе отсчёта.

Условием равновесия материальной точки является равенство нулю равнодействующей (т. е. векторной суммы) всех сил, приложенных к точке. В этом случае наша точка будет двигаться равномерно и прямолинейно в произвольной инерциальной системе отсчёта. Значит, система отсчёта, связанная с точкой, также будет инерциальной, и в ней точка будет покоиться.

В случае твёрдого тела ситуация сложнее. Прежде всего, важно учитывать точку приложения каждой силы.

-Сила тяжести приложена в центре тяжести тела. Для тела простой формы центр тяжести совпадает с центром симметрии.

-Силы упругости и трения приложены в точке или в плоскости контакта тела с соприкасающимся телом.

Прямая линия, проходящая через точку приложения вдоль вектора силы, называется линией действия силы. Оказывается, точку приложения силы можно переносить вдоль линии её действия — от этого механическое состояние тела не изменится (в частности, равновесие не нарушится).

Для равновесия твёрдого тела недостаточно потребовать равенства нулю векторной суммы всех приложенных к телу сил.

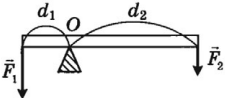
В качестве примера рассмотрим пару сил — так называются две равные по модулю противоположно направленные силы, линии действия которых не совпадают. Пусть пара сил и приложена к твёрдому стержню (рис. 1).

Рис. 1. Пара сил

Векторная сумма этих сил равна нулю. Но стержень покоиться не будет: он начнёт вращаться. В данном случае не выполнено второе условие равновесия твёрдого тела. Чтобы его сформулировать, нужно ввести понятие момента силы.

Как должна быть направлена линия действия силы, чтобы тело стало вращаться вокруг неподвижной оси? Для начала заметим следующее.

— Если линия действия силы параллельна данной оси, то вращения не будет.
— Если линия действия силы пересекает данную ось, то вращения не будет.

В каждом из этих случаев действие силы вызывает лишь деформацию твёрдого тела.

Чтобы началось вращение, линия действия силы и ось вращения должны быть скрещивающимися прямыми.

Без ограничения общности можно считать эти прямые перпендикулярными друг другу. Мы всегда можем этого добиться, разложив силу на две составляющие — параллельную и перпендикулярную оси вращения — и отбросив параллельную составляющую как не вызывающую вращения. Поэтому везде далее мы считаем, что все силы, действующие на тело, перпендикулярны оси вращения.

Момент силы.

Плечо силы — это расстояние от оси вращения до линия действия силы (т. е. длина общего перпендикуляра к двум этим прямым).

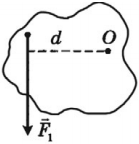
В качестве примера на рис. 2 изображён диск, к которому приложена сила . Ось вращения перпендикулярна плоскости чертежа и проходит через точку . Плечом силы является величина , где — основание перпендикуляра, опущенного из точки на линию действия
силы.

Рис. 2. Плечо силы

Момент силы относительно оси вращения — это произведение силы на плечо:

.

Чтобы учесть также направление вращения, вызываемого действием силы, моменту силы приписывают знак. Именно, момент силы считается положительным, если сила стремится поворачивать тело против часовой стрелки, и отрицательным, если по часовой стрелке.

Условия равновесия.

Если тело имеет неподвижную ось вращения и если алгебраическая сумма моментов всех сил относительно этой оси обращается в нуль, то тело будет находиться в равновесии. Это так называемое правило моментов . Оказывается, что в этом случае обращается в нуль алгебраическая сумма моментов всех сил относительно любой другой оси, параллельной оси вращения.

В общем случае, когда твёрдое тело может совершать как поступательное, так и вращательное движение, мы имеем два условия равновесия.

1. Равна нулю векторная сумма всех сил, приложенных к телу.
2. Равна нулю алгебраическая сумма моментов всех сил, приложенных к телу, относительно данной оси вращения или любой другой оси, параллельной данной.

Так, в примере на рис. 1 алгебраическая сумма моментов пары сил не обращается нуль (оба момента положительны). Поэтому стержень не находится в равновесии.

При решении задач удобно использовать сформулированные выше условия равновесия в следующем виде.

1′. Силы уравновешены вдоль любой оси.
2′. Суммарный момент сил, вращающих тело в одну сторону, равен суммарному моменту сил, вращающих тело в другую сторону.

Сейчас мы разберём одну достаточно содержательную задачу по статике и посмотрим, как работают наши условия равновесия.

Задача. Однородная лестница опирается на гладкую вертикальную стену, образуя с ней угол . При каком максимальном значении лестница будет покоиться? Коэффициент трения между лестницей и полом равен .

Решение. Пусть лестница опирается о пол и стену в точках и соответственно (рис. 3). Расставим силы, действующие на лестницу.

Рис. 3. К задаче

Поскольку лестница однородная, сила тяжести приложена в середине лестницы. Сила упругости пола и сила трения приложены в точке . На рис. 3 точка приложения этих сил немного смещена от точки внутрь лестницы; тем самым мы однозначно указываем, что силы приложены именно к лестнице (а не к полу).

Точно так же сила упругости стены приложена в точке . Поскольку стена гладкая, сила трения между стеной и лестницей отсутствует.
Воспользуемся условием 1′. Вдоль горизонтальной оси силы уравновешены:

. (1)

Вдоль вертикальной оси силы также уравновешены:

. (2)

Теперь переходим к правилу моментов — условию 2′. Какую ось вращения выбрать? Удобнее всего взять ось, проходящую через точку (перпендикулярно плоскости рисунка). В таком случае моменты сразу двух сил и обратятся в нуль — ведь плечи этих сил относительно точки равны нулю (поскольку линии действия сил проходят через эту точку). Ненулевые моменты относительно точки имеют силы и , которые стремятся вращать лестницу в разные стороны; стало быть, моменты данных сил должны быть равны друг другу.

Плечо силы — это длина перпендикуляра , опущенного из точки на линию действия силы . Плечо силы — это длина перпендикуляра , опущенного из точки на линию действия силы . Согласно правилу моментов имеем:

Пусть длина лестницы равна . Тогда . Подставляем эти соотношения в равенство моментов:

откуда

(3)

С учётом равенства (1) имеем вместо (3):

(4)

Вспомним теперь, что в условии спрашивается максимальное значение . При максимальном угле лестница пока ещё стоит, но уже находится на грани проскальзывания. Это означает, что сила трения достигла своего максимального значения, равного силе трения скольжения:

.

Теперь из (4) получаем:

,

а с учётом равенства (2):

.

Отсюда получаем искомую максимальную величину :

.

Оглавление:

• Основные теоретические сведения
  • Основы статики
  • Момент силы. Правило моментов
  • Рычаги и блоки
  • Центр тяжести тела

Основные теоретические сведения

Основы статики

К оглавлению…

Статикой называется раздел механики, изучающий условия равновесия тел. Равновесием называют такое состояние тела или системы тел, в котором оно не движется в данной системе отсчета. Различают три вида равновесия:

• Устойчивое равновесие. Если систему вывести из состояния устойчивого равновесия, то она самопроизвольно в него вернется, то есть при выведении из положения равновесия возникает сила, возвращающая систему к равновесию. Для этого необходимо, чтобы потенциальная энергия системы в состоянии устойчивого равновесия имела минимальное значение. Любая физическая система стремится к состоянию устойчивого равновесия. Это значит, что любой самопроизвольный процесс всегда проходит с уменьшением потенциальной энергии.
• Неустойчивое равновесие. В данном случае при выведении из состояния равновесия возникают силы, уводящие систему от равновесия, и система самопроизвольно не может в него вернуться. В состоянии неустойчивого равновесия потенциальная энергия системы имеет максимальное значение.
• Безразличное равновесие. При выведении из состояния равновесия в системе не возникает ни возвращающих, ни уводящих в сторону сил.

Из второго закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к невращающемуся телу, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение (действительно, ведь ускорение тела при этом равно нулю). В этом случае принято говорить, что силы, приложенные к телу, уравновешивают друг друга. При вычислении равнодействующей силы все силы, действующие на тело, можно прикладывать к центру масс. Центр масс (или центр тяжести) – точка к которой приложена сила тяжести, действующая на тело.

Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю. Иными словами, векторная сумма всех сил, приложенных к телу должна быть равна нолю:

Момент силы. Правило моментов

К оглавлению…

Если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил. Вращающее действие силы зависит не только от ее величины, но и от расстояния между линией действия силы и осью вращения. Длина перпендикуляра, проведенного от оси вращения до линии действия силы, называется плечом силы.

Для описания причин вызывающих вращения и условия равновесия тела в статике вводится новое понятие — момент силы. Произведение модуля силы F на плечо d и называется моментом силы M. Таким образом момент силы в статике вычисляется по формуле:

Обычно в физике используется следующее правило знаков: если сила поворачивает тело по часовой стрелке, то ее момент считается положительным, а если против – то отрицательным. Момент силы может и равняться нулю, если сила проходит (сама или продолжением) через ось. Обратите внимание: если Вы перепутаете, и возьмете знаки моментов наоборот (по часовой стрелке со знаком минус, а против часовой со знаком плюс), то ничего страшного не произойдет. Поэтому, важно запомнить, что моменты сил, вращающих тело в различных направлениях относительно часовой стрелки, берутся с различными знаками.

Обратите внимание, что момент силы зависит не только от величины силы, но и от ее плеча. Следовательно, одно и то же значение момента можно получить двумя способами: взять большую силу и малое плечо или взять малую силу и большое плечо. Вывод: чем больше плечо, тем меньшую силу необходимо прилагать для получения одного и того же результата.

Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:

При записи этого условия в ходе решения конкретной задачи по статике моменты сил необходимо записывать с учётом их знаков. В Международной системе единиц (СИ) моменты сил измеряются в ньютоно-метрах (Н∙м).

Обратите внимание: в общем случае, когда тело может двигаться поступательно и вращаться, для равновесия необходимо выполнение обоих условий: равенство нулю равнодействующей силы и равенство нулю суммы всех моментов.

Алгоритм решения задач на правило моментов (задач по статике):

1. Нарисовать рисунок. Следует помнить, что сила тяжести, действующая на тело изображается один раз. Если же в задаче идет речь об изломанной палочке, то удобнее рисовать отдельно силы тяжести, действующие на каждую часть палочки, считая массы частей пропорциональными их длинам. В отличие от динамики, где силы изображаются из одной точки, в статике важно точно указать точку приложения силы.
2. Выбрать ось вращения в точке приложения самой ненужной в задаче силы или сил (той силы, которую определять не надо и не хочется из-за природного чувства лени). При этом плечо (и, следовательно, момент) этой силы обратится в нуль независимо от ее величины, и в дальнейших вычислениях эту силу можно не учитывать совсем.
3. Записать правило моментов относительно данной оси, на забывая про правило знаков.
4. При необходимости записать также условие согласно которому равнодействующая сила равна нолю.
5. Выразить искомую силу.

Рычаги и блоки

К оглавлению…

Как вы знаете из практики, иногда необходимо изменить направление силы, увеличить или уменьшить ее величину. Этой цели служат простые механизмы: устройства, преобразующие величину или направление силы с помощью механических явлений. Для всех простых механизмов справедливо золотое правило механики: выиграл в силе – проиграл в перемещении (или наоборот). Это значит, что при увеличении силы за счет некоторого механизма неизбежно будет уменьшено и перемещение. Рассмотрим основные типы простых механизмов изучаемых в школьной физике:

• Равноплечий рычаг (весы). Рычаг, ось вращения которого проходит через его геометрический центр.
• Неравноплечий рычаг. Рычаг ось вращения которого проходит через произвольную точку.
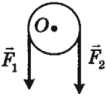
• Неподвижный блок. Это диск с закрепленной осью, через который переброшена нить. Неподвижный блок используется для изменения направления приложения силы. Если трение в блоке отсутствует, нить невесома, то сила ее натяжения до и после блока не изменяется. Таким образом, неподвижный блок не дает ни выигрыша в силе, ни проигрыша в перемещении.
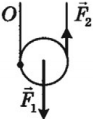
• Подвижный блок. Это диск, ось которого может двигаться поступательно. Подвижный блок позволяет уменьшить силу в два раза, одновременно с этим вдвое увеличивая перемещение.
• Наклонная плоскость. Это устройство применяется для поднятия тяжестей. При достаточно малых значениях угла наклона и небольшом коэффициенте трения сила, которую необходимо приложить чтобы поднимать некоторое тело вдоль наклонной плоскости может быть значительно меньше веса тела. Таким образом, подъем становится легче. Естественно, при этом в полном соответствии с «золотым правилом» увеличивается перемещение тела.

Центр тяжести тела

К оглавлению…

Центр масс (или центр тяжести) – точка к которой приложена сила тяжести, действующая на тело. В общем случае центр тяжести может и не лежать внутри тела, а выходить за его пределы (например, различные изогнутые длинные предметы, кольца, полукольца и так далее).

Рассмотрим основные методы определения положения центра масс тел для некоторых конкретных случаев, возникающих при решении задач по статике:

1. У однородных тел правильной формы (шары, прямоугольники, стержни) центр тяжести совпадает с геометрическим центром. Следует запомнить, что центр тяжести однородной треугольной пластины лежит в точке пересечения ее медиан. Для однородных симметричных тел центр тяжести всегда расположен на оси симметрии.

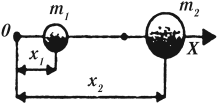
2. Определение положения центра тяжести системы из двух тел с известными центрами тяжести. Здесь можно использовать замечательное свойство центра тяжести. Подперев центр тяжести, мы обеспечим равновесие тела. Таким образом, центр тяжести системы из двух тел лежит на отрезке, соединяющем их центры тяжести, и делит его в отношении, обратном отношению масс тел:

где: l₁ – расстояние от центра масс до тела с массой m₁, а l₂ – до тела с массой m₂.

3. Определение положения центра тяжести любой системы тел с известными положениями центров тяжести. Необходимо ввести систему координат (естественно, начало координат выбрать в точке, относительно которой необходимо рассчитать положение центра тяжести), определить в ней координаты центров тяжести всех тел и найти координаты центра тяжести системы по формуле:

Аналогичные уравнения получаются для остальных координатных осей, если таковые необходимо рассматривать в задаче (просто переменная x меняется на y или z соответственно).

4. Однородное тело правильной формы с вырезом правильной формы. Проще всего свести задачу к обратной: мысленно вставить вырез обратно и получить тело правильной формы с известным положением центра тяжести. Далее представить его в виде двух тел: страшного с вырезом и самого выреза. А теперь все просто. У одного из тел (выреза) мы знаем положения центра тяжести. У другого – нет. Зато знаем положение центра тяжести системы двух тел. Составив уравнение для определения общего центра тяжести получим выражение с одной неизвестной – центром тяжести тела с вырезом. Решив уравнение получим искомый ответ.

5. Теорема Паппа. Применяется для определения положения центра тяжести плоской пластины, которая при вращении вокруг некоторой оси образует тело с легко вычисляемым объемом. Необходимо мысленно повернуть пластину на один оборот, нарисовать рисунок и применить теорему:

Формулировка теоремы: объем тела, полученного при вращении пластины, равен произведению ее площади на путь, пройденный центром тяжести при вращении:

Полная теория по Статике и Гидростатике, теория и практика ЕГЭ по физике

30.09.2013

Полный материал по физике на тему: Статика и Гидростатика.

Материал содержит в себе необходимую теорию по теме, а также множество различных практических заданий и тестов, ориентированных на ЕГЭ.

Вместе с этим материалом вы сможете максимально качественно изучить раздел физики «Статика и Гидростатика» для ЕГЭ.

Смотреть в PDF:

Или прямо сейчас: Скачайте в pdf файле.

Добавить комментарий

Комментарии без регистрации. Несодержательные сообщения удаляются.

СТАТИКА И ГИДРОСТАТИКА
Теория и формулы (кратко)

Статика — раздел механики, изучаю­щий условия равновесия тел.

Условия рав­новесия  тела:

а) Поступательно движущееся тело на­ходится в состоянии равновесия (покоится или движется прямолинейно и равномерно),    если 

б) Вращающееся    тело,   имеющее   непо­движную ось вращения, находится в покое или равномерно вращается, если         М₁ + М₂ + М₃ + … + M_N = 0,  где М — момент силы —  произведение силы на её плечо.

---

Виды равновесия.

1. Виды равновесия тела с закрепленной осью вращения:

а) если ось проходит через центр масс, то тело находится в безразличном равновесии при любом положении тела (а);

б) ось выше точки центра тяжести — ус­тойчивое равновесие (б);

в) ось ниже точки центра тяжести — неус­тойчивое равновесие( в).

1. Виды равновесия тела, имеющего точ­ку опоры:

а) если равнодействующая всех сил направлена к положению равновесия, то тело нахо­дится в устойчивом положении (рис. а);

б)    если равнодействующая всех сил направлена от положения равновесия, то тело находится в неустойчивом  равновесии (рис. б);

в)    если Σ  = 0, — равновесие безразличное (рис. в).

1. Виды равновесия тела, имеющего пло­щадь опоры.

Если вертикаль, проведенная через центр тяжести тела, пересекает площадь его опоры, то равновесие тела устойчивое. Если не пересекает, то тело падает, — равновесие не­устойчивое.

Простые механизмы и блоки

Простые механизмы — приспособления, которые служат для преобразования силы. К ним относятся:  рычаг (блок, ворот) и наклонная плоскость (клин, винт). Они применяются для получения выигрыша в силе.

F₂/F₁ – выигрыш в силе.      F₁l₁=F₂l₂ — условие равновесия рычага для двух сил.

Золотое правило механики: все простые механизмы, не дают выигрыша в работе — во сколько раз мы выигрываем в силе, во столько же раз мы проигрываем в расстоянии.

Гидростатика.

Давление — скалярная физическая величина, равная отношению модуля силы, действующей перпендикулярно поверхности, к площади её поверхности.   

Гидростатическое давление — давление, обусловленное весом столба жидкости. Манометр — прибор для измерения давления в жидкости или газа. 

p = ρ_жgh   — давление на произвольной глубине несжимаемой жидкости            

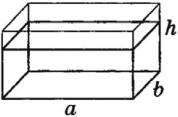
F = pS = ρ_жghS_дна  — сила давления на дно сосуда         

---

 На одном и том же уровне давление одинаково во всех направлениях.

Давление р на произвольной глубине h сжимаемой поршнем жидкости определяется давлением поршня и давлением столба жидкости           р = р_порш. + ρ_жgh

---

---

 Атмосферное давление – давление, которое производит воздушная оболочка Земли.

Опыт Торричелли (1634 г.) свидетельствует: атмосферное  давление  равно давлению столба ртути в трубке.

Нормальное атмосферное давление:  1 атм = 760 мм.рт.ст. = 1 01325 Па ≈ 10⁵ Па (при 0ºС);     1 мм.рт.ст.=133,3 Па

Оно может изменяться от места к месту и во времени (циклоны и антициклоны) и убывает с увеличением высоты над уровнем моря (на каждые 12 м подъёма  оно уменьшается на 1 мм. рт. ст.).

Барометры — приборы для измерения атмосферного давления. Существуют 1) жидкостный;  2) барометр — анероид (металлический).

Закон Паскаля (1653 г.) —  жидкости и газы передают производимое на них давление во все стороны одинаково. 

 Сообщающимися называются сосуды, соединённые между собой каналом с жидкостью.

---

Закон Архимеда: на тело, погруженное в покоящуюся жидкость (или газ), действует выталкивающая сила, направленная  вертикально верх и равная весу жидкости, вытесненной телом.

F_A =ρ_жgV_пчт                        F_A = Р_ж,выт.= m_ж,выт g,

F_A = Р_воз — Р_жид.    V_пчт – объём погруженной части тела.    ρ_ж — плотность жидкости или газа.

Условие плавания тел:

а) F_A > mg, ρ_т > ρ_ж — тело всплывает;  

б) F_A < mg, ρ_т < ρ_ж — тело тонет;      

в) F_A = mg, ρ_т = ρ_ж — тело находится в равновесии на любой глубине.  

Условие плавания тела на поверхности  F_A = mg

Если тело будет плавать частично погрузившись в жидкость, то ρ_ж/ρ_т=V_т/V_пчт

На этом основано применение ареометра- прибора для определения плотности жидкости.

---

Конспект урока «Статика и гидростатика. Теория и формулы для ЕГЭ» + шпаргалка.

Еще конспекты для 10-11 классов:

Статика

Статика – это раздел механики, изучающий условия равновесия тел.

Виды равновесия тел

• Устойчивое равновесие – это равновесие, при котором тело, выведенное из положения равновесия и предоставленное самому себе, возвращается в прежнее положение.

• Неустойчивое равновесие – это равновесие, при котором тело, выведенное из положения равновесия и предоставленное самому себе, будет еще больше отклоняться от положения равновесия.

• Безразличное равновесие – это равновесие, при котором тело, выведенное из положения равновесия и предоставленное самому себе, не меняет своего положения.

Момент силы

Момент силы – это физическая величина, равная произведению модуля силы на ее плечо.

Обозначение – ​( M )​, единицы измерения – Н·м.

где ​( d )​ – плечо силы ​( F )​.

Плечо силы – это кратчайшее расстояние (перпендикуляр) от оси вращения до прямой, вдоль которой действует сила.
Обозначение – ​( d )​ или ​( l )​, единицы измерения – м.

Знак момента силы

Если сила, приложенная к телу, вращает его по часовой стрелке, то момент силы положителен (​( M )​ > 0):

Если сила, приложенная к телу, вращает его против часовой стрелки, то момент силы отрицателен (( M ) < 0):

Момент силы равен нулю, если плечо силы, приложенной к телу, равно нулю.

Условия равновесия тел

Тело находится в равновесии, если

1. векторная сумма всех сил, действующих на тело, равна нулю;
2. алгебраическая сумма всех моментов сил, вращающих тело по часовой стрелке, равна алгебраической сумме моментов сил, вращающих его против часовой стрелки:

Центр тяжести – это точка внутри тела или вне его, относительно которой сумма моментов сил тяжести, действующих на отдельные его части, равна нулю.
Центр масс – геометрическая точка, положение которой характеризует распределение масс в теле:

Важно!
Для твердого тела центр тяжести совпадает с центром масс.

Простые механизмы

Простые механизмы – это приспособления, служащие для преобразования силы.

Рычаг – это простейшее механическое устройство, представляющее собой твердое тело (перекладину), вращающееся вокруг точки опоры.

Рычаг дает выигрыш в силе:

Блок — простое механическое устройство, представляющее собой колесо с желобом по окружности, вращающееся вокруг своей оси. Желоб предназначен для каната, цепи, ремня и т. п.
Блок бывает подвижный и неподвижный.

Неподвижный блок – это блок, ось которого закреплена.

Неподвижный блок не дает выигрыша в силе, он используется для изменения направления действия силы.

Подвижный блок – это блок, имеющий свободную ось.

Подвижный блок дает выигрыш в силе в 2 раза:

«Золотое правило» механики

При использовании простых механизмов во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии, т. е. простые механизмы выигрыша в работе не дают.

Давление жидкости

Давление жидкости – это величина, равная произведению плотности жидкости на модуль ускорения свободного падения и на высоту столба жидкости.

где ​( rho )​ – плотность жидкости,
​( h )​ – высота столба жидкости.

Сила давления жидкости – это сила, равная произведению давления жидкости на площадь поверхности:

• на дно сосуда:

• на боковую стенку:

Сообщающиеся сосуды

Сообщающиеся сосуды – это сосуды, соединенные между собой ниже уровня жидкости.

Закон сообщающихся сосудов:
в неподвижных и открытых сообщающихся сосудах любой формы давление жидкости на любом горизонтальном уровне одинаково.

Следствия из закона сообщающихся сосудов:

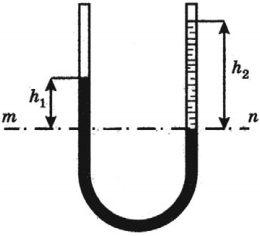
• в неподвижных и открытых сообщающихся сосудах высоты столбов жидкостей, отсчитываемых от уровня, ниже которого жидкость однородна (уровня mn), обратно пропорциональны плотностям этих жидкостей:

• в неподвижных и открытых сообщающихся сосудах однородная жидкость всегда устанавливается на одинаковом уровне независимо от формы сосудов.

Важно!
Давление, которое создает жидкость, находящаяся в равновесии при действии на нее силы тяжести, называют гидростатическим. Гидростатическое давление определяется формулой ​( p=rho gh )​.
Давление внутри жидкости на любой глубине складывается из атмосферного давления, или внешнего давления на жидкость, и гидростатического давления:

где ​( p_0 )​ – атмосферное давление.

Закон Паскаля

Закон Паскаля
Давление, производимое на жидкость или газ, передается по всем направлениям одинаково.

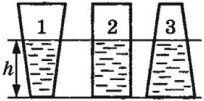
Следствие из закона Паскаля — гидростатический парадокс: давление, производимое на дно сосуда, зависит только от высоты столба жидкости:

Сила давления жидкости на дно разная, т.к. она зависит от площади дна:

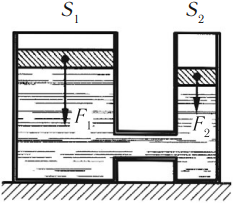
Гидравлический пресс – два сообщающихся сосуда, заполненные жидкостью и закрытые поршнями различной площади.
Гидравлический пресс дает выигрыш в силе, но проигрыш в длине пути поршня:

Силы, действующие на поршни гидравлического пресса, пропорциональны площадям этих поршней:

Атмосферное давление – это давление, которое оказывает атмосфера на все находящиеся в ней предметы.
Атмосферное давление уменьшается с увеличением высоты подъема над Землей.

Нормальное атмосферное давление: ​( p_0 )​ = 10⁵ Па.

Приборы для измерения давления:

• барометры – приборы, предназначенные для измерения атмосферного давления (ртутный барометр, барометр-анероид);
• манометры – приборы, предназначенные для измерения давлений жидкостей и газов.

Закон Архимеда

Архимедова сила – это выталкивающая сила, действующая на тело, погруженное в жидкость или газ.

Причина возникновения выталкивающей силы – разница давлений жидкости или газа на верхнюю и нижнюю грани.
Архимедова сила всегда направлена перпендикулярно поверхности жидкости.
Архимедова сила равна разности веса тела в воздухе и веса тела в жидкости или газе:

где ​( P_1 )​ – вес тела в воздухе,
​( P_2 )​ – вес тела в жидкости или газе.

Закон Архимеда
На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу жидкости или газа, вытесненных телом:

Если тело полностью погружено в жидкость, то

где ​( V_m )​ – объем тела, погруженного в жидкость.

Если тело не полностью погружено в жидкость, то

где ​( V_{чm} )​ – объем части тела, погруженной в жидкость.

Условия плавания тел

На любое тело, погруженное в жидкость или газ, действуют две силы, направленные в противоположные стороны, – это сила тяжести и архимедова сила. Направление движения тела зависит от того, какая из этих сил больше по модулю.

Условия плавания тел

• Тело тонет:

• Тело плавает внутри жидкости:

• Тело всплывает:

• Тело плавает на поверхности жидкости:

где ​( V_1 )​ – объем части тела, погруженной в жидкость.

Важно!
Выталкивающая сила действует на тела в жидкостях и газах, потому что сжаты силой притяжения к Земле. В состоянии невесомости эта сила не действует.

Основные формулы по теме «Статика»

Статика и гидростатика (теория)

Статика — раздел механики, изучаю­щий условия равновесия тел.

Условия рав­новесиятела:

а) Поступательно движущееся тело на­ходится в состоянии равновесия (покоится или движется прямолинейно и равномерно),если ,( = 0).

б) Вращающеесятело,имеющее непо­движную ось вращения, находится в покое или равномерно вращается, еслиМ2 + М3 + … + MN = 0,где

М — момент силы — произведение силы на её плечо.

М = Fl = Frsinα, где

l- плечо силы — кратчайшее рас­стояние от оси

вращения до линиидействия силы.r- расстояние от

оси вращения до точки приложения силы;α — угол

между r и F.[М] = Н·м.

М >0, если F,М <0, если F(условно)

Центр масс системы.

l1l2

m1 m2

В большинстве случаев центр тяжести сов­падает с центром масс (например, когда раз­меры тела много меньше радиуса Земли) — воображаемая точка тела при опоре на которую тело находится в равновесии.

Виды равновесия.

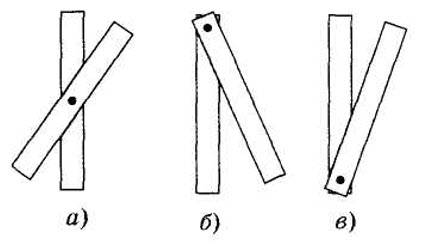
1. Виды равновесия тела с закрепленной осью вращения:

а) если ось проходит через центр масс, то тело

находится в безразличном равновесии при любом

положении тела ( а);

б) ось выше точки центра тяжести — ус­тойчивое равновесие (б);

в) ось ниже точки центра тяжести — неус­тойчивое равновесие( в).

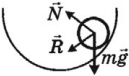
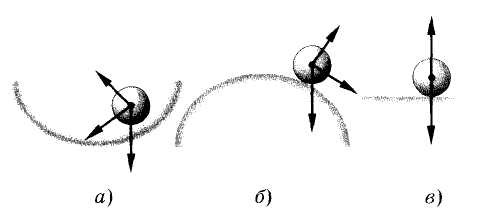
2. Виды равновесия тела, имеющего точ­ку опоры:

а) если равнодействующая всех сил направлена

к положению равновесия, то тело нахо­дится в

устойчивом положении (рис. а);

б)если равнодействующая всех сил направлена

от положения равновесия, то тело находится в

неустойчивомравновесии (рис. б);

в)если Σ = 0, — равновесие безразличное (рис. в).

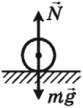
3. Виды равновесия тела, имеющего пло­щадь опоры.

Если вертикаль, проведенная через центр тяжести тела, пересекает

площадь его опоры, то равновесие тела устойчивое. Если не

пересекает, то тело падает, — равновесие не­устойчивое.

Простые механизмы — приспособления, которые служат для преобразования силы. К ним относятся:рычаг (блок, ворот) и наклонная плоскость (клин, винт). Они применяются для получения выигрыша в силе.

F2/F1 – выигрыш в силе

Bl1Ol2AF1l1=F2l2 — условие равновесия рычага для двух сил.

т.е.

Блоки.

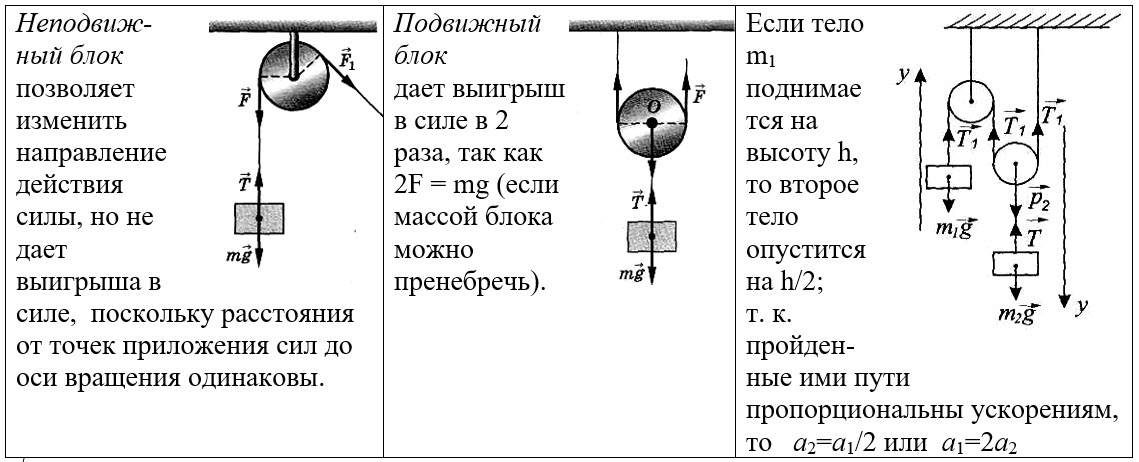
Неподвижный блок позволяет изменить направлениедействия силы, но не дает выигрыша в силе,поскольку расстояния от точек приложения сил дооси вращения одинаковы.

Подвижный блок

дает вы­игрыш в силе в 2 раза, так как 2F = mg (ес­ли массой блока можнопренебречь).

Если тело m1 поднимается на высоту h, то второе тело опустится на h/2;т. к. пройденные ими пути пропорциональны ускорениям, тоa2=a1/2 илиa1=2a2

Золотое правило механики: все простые механизмы, не дают выигрыша в работе — во сколько раз мы выигрываем в силе, во столько же раз мы проигрываем в расстоянии.

Гидростатика.

Давление — скалярная физическая величина, равная отношению модуля силы, действующей перпендикулярно поверхности, к площади её поверхности.[р] = 1 Па =1

Гидростатическое давление — давление, обусловленное весом столба жидкости. Манометр — прибор для измерения давления в жидкости или газа.

p = ρжgh— давление на произвольной глубине несжимаемой жидкости

F = pS = ρжghSдна— сила давления на дно сосуда

—среднее давление жидкости на боковую стенку высотой h

F = pS = ρжghSстен -сила давления жидкости на стенку сосуда

На одном и том же уровне давление одинаково во всех направлениях.

Давление р на произвольной глубине h сжимаемой поршнем жидкости определяется давлением поршня и давлением столба жидкости р = рρжgh

Атмосферное давление – давление, которое производит воздушная оболочка Земли.

Опыт Торричелли (1634 г.) свидетельствует: атмосферное давление равно давлению столба ртути в трубке.

Нормальное атмосферное давление:1атм = 760 мм.рт.ст. =1 01325 Па ≈ 10

1мм.рт.ст.=133,3 Па

Оно может изменяться от места к месту и во времени (циклоны и антициклоны) и убывает с увеличением высоты над уровнем моря (на каждые 12 м подъёмаоно уменьшается на 1мм. рт. ст.).

Барометры — приборы для измерения атмосферного давления.

1) жидкостный;2) барометр — анероид (металлический).

Закон Паскаля (1653 г.) —жидкости и газы передают производимое на них давление во все стороны одинаково.

Сообщающимися называются сосуды, соединённые между собой каналом с жидкостью.

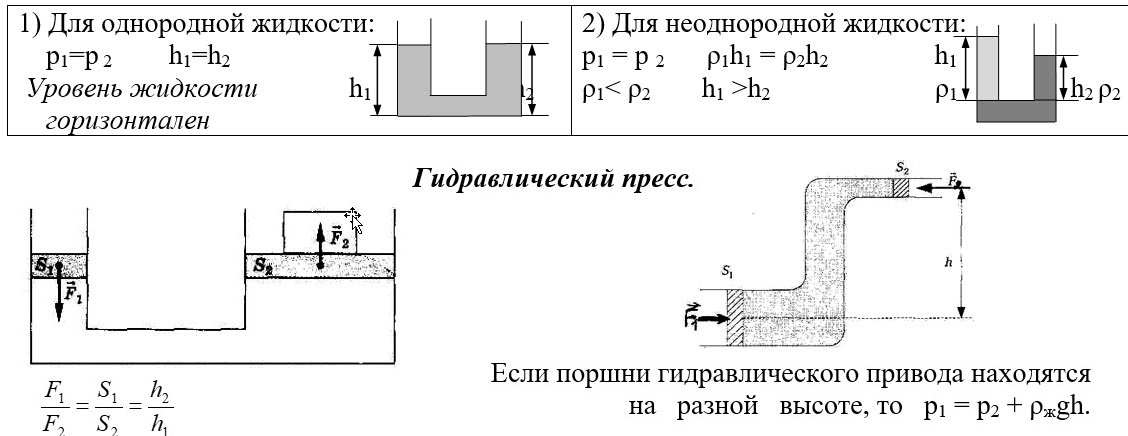
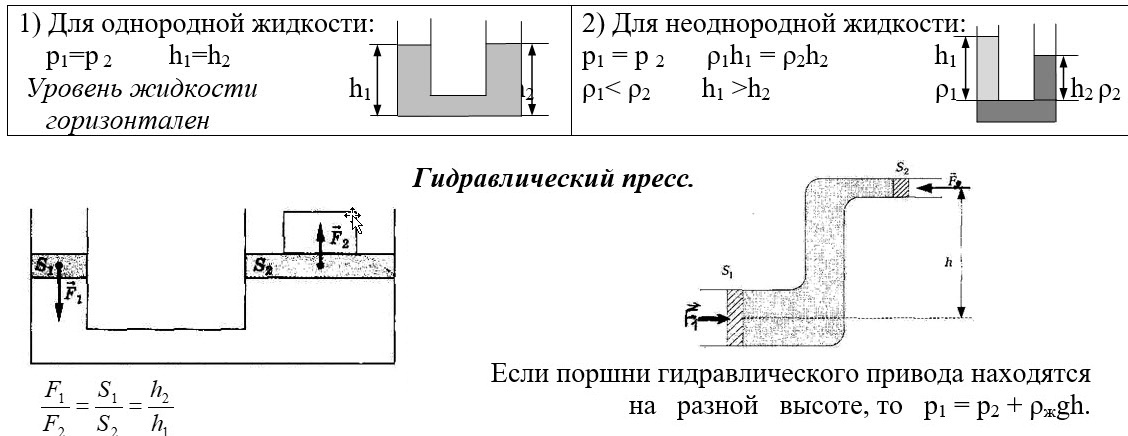
1) Для однородной жидкости:

р 2 h1=h2

Уровень жидкостиh1h2

горизонтален

2) Для неоднородной жидкости:

р2ρ1h1 = ρ2h2 h1

ρ1< ρ h1 >h2 ρ1h2 ρ2

Гидравлический пресс.

Если поршни гидравлического привода находятся

наразнойвысоте, тор2 + ρжgh.

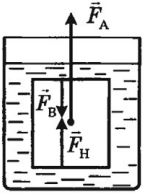
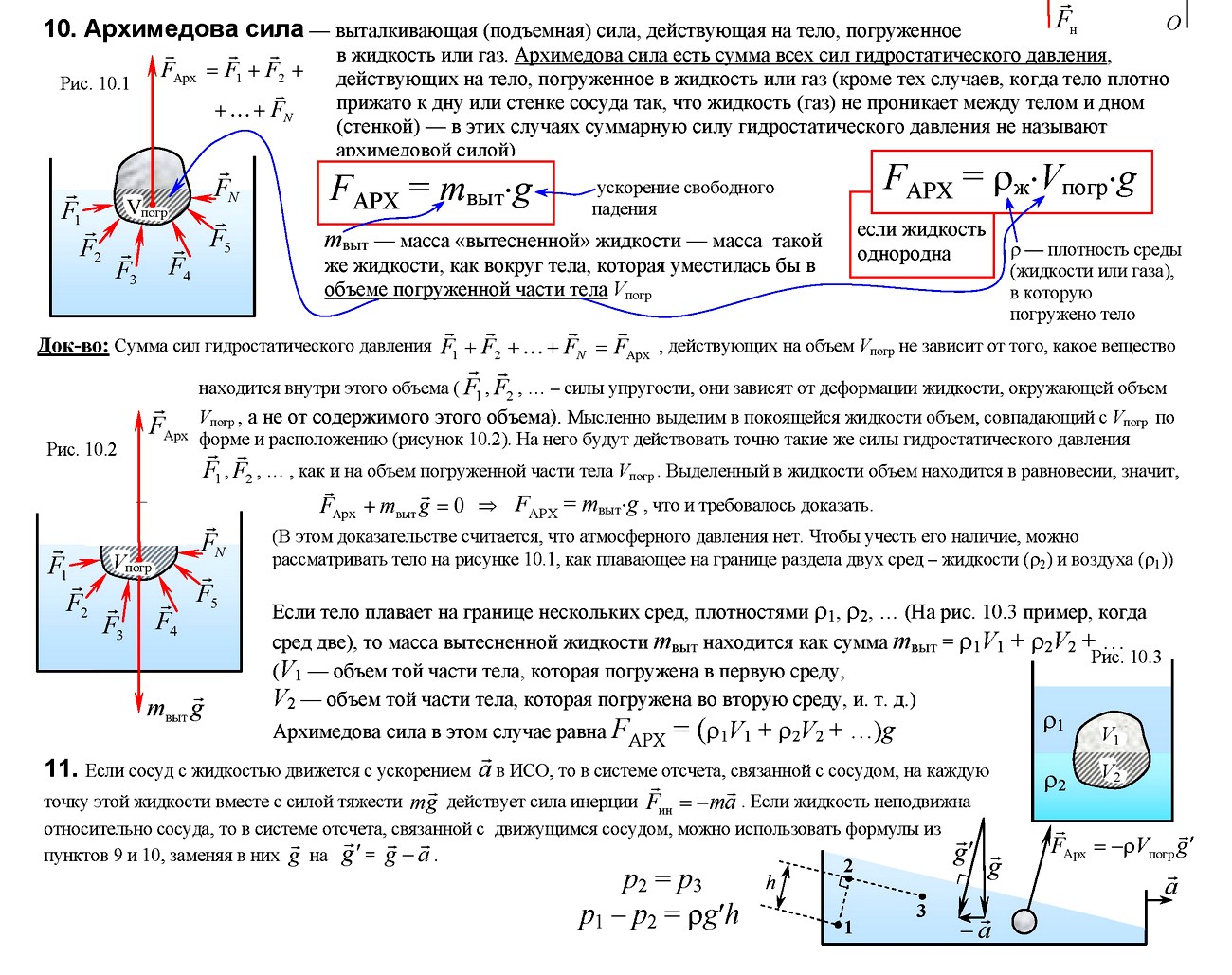
Закон Архимеда: на тело, погруженное в покоящуюся жидкость (или газ), действует выталкивающая сила, направленная вертикально верх и равная весу жидкости, вытесненной телом.

F =ρжgVпчтFA = Рж,выт.= mж,выт g,FA

F = Рвоз — Ржид.Vпчт – объём погруженной части тела.

ρFA

Условие плавания тел:mg

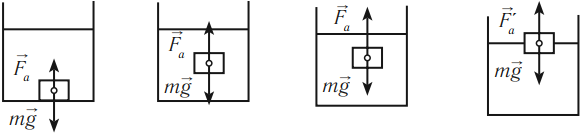
а) F > mg, ρт > ρж — тело всплывает; FA

б) F < mg, ρт < ρж — тело тонет;mgFA=0

в) F = mg, ρт = ρж — тело находится в равновесии

на любой глубине.mg mg

Условие плавания тела на поверхностиF = mg

Если тело будет плавать частично погрузившись в жидкость, то ρт=Vт/Vпчт

На этом основано применение ареометра- прибора для определения плотности жидкости.

Далее вы найдете различные задания по теме «Статика и гидростатика»