Теория по теории вероятности для егэ профиль 2022 - Помощь в подготовке к экзаменам и поступлению

Автор материала — Анна Малкова

На этой странице – решения новых задач из Открытого Банка заданий, из которого формируется Банк заданий ФИПИ. Вы знаете, что в Проекте ЕГЭ-2022 в варианте Профильного ЕГЭ по математике не одна задача на теорию вероятностей, а две, причем вторая – повышенной сложности. Покажем, какие задачи могут вам встретиться на ЕГЭ-2022. Проект пока не утвержден, возможны изменения, но ясно одно – теория вероятностей на ЕГЭ будет на более серьезном уровне, чем раньше. Раздел будет дополняться, так что заходите на наш сайт почаще!

1. Игральный кубик бросают дважды. Известно, что в сумме выпало 8 очков. Найдите вероятность того, что во второй раз выпало 3 очка.

Решение:

Выпишем возможные варианты получения 8 очков в сумме:

Подходит только вариант 5; 3. Вероятность этого события равна 1 : 5 = 0,2 (один случай из 5 возможных).

Ответ: 0,2.

2. В ящике 4 красных и 2 синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер появится третьим по счету?

Решение:

Благоприятными будут следующие исходы:

Первый раз – вытащили красный фломастер,

И второй раз – красный,

А третий раз – синий.

Вероятность вытащить красный фломастер (которых в ящике 4) равна $displaystyle frac{4}{6}=frac{2}{3}.$

После этого в ящике остается 5 фломастеров, из них 3 красных, вероятность вытащить красный равна $displaystyle frac{3}{5}.$

Наконец, когда осталось 4 фломастера и из них 2 синих, вероятность вытащить синий равна $displaystyle frac{1}{2}.$

Вероятность события {красный – красный – синий } равна произведению этих вероятностей, то есть $displaystyle frac{2}{3}cdot frac{3}{5}cdot frac{1}{2}=frac{1}{5}=0,2.$

Ответ: 0,2.

3. В коробке 10 синих, 9 красных и 6 зеленых фломастеров. Случайным образом выбирают 2 фломастера. Какова вероятность того, что окажутся выбраны один синий и один красный фломастер?

Решение:

Всего в коробке 25 фломастеров.
В условии не сказано, какой из фломастеров вытащили первым – красный или синий.

Предположим, что первым вытащили красный фломастер. Вероятность этого $displaystyle frac{9}{25},$ в коробке остается 24 фломастера, и вероятность вытащить вторым синий равна $displaystyle frac{10}{24}.$ Вероятность того, что первым вытащили красный, а вторым синий, равна $displaystyle frac{9}{25} cdot frac{10}{24} = frac{3}{5} cdot frac{1}{4} = frac{3}{20}.$

А если первым вытащили синий фломастер? Вероятность этого события равна $displaystyle frac{10}{25}=frac{2}{5}.$ Вероятность после этого вытащить красный равна $displaystyle frac{9}{24}=frac{3}{8},$ вероятность того, что синий и красный вытащили один за другим, равна $displaystyle frac{2}{5}cdot frac{3}{8} = frac{3}{20}.$

Значит, вероятность вытащить первым красный, вторым синий или первым синий, вторым красный равна $displaystyle frac{3}{20} + frac{3}{20} =0,3.$

А если их доставали из коробки не один за другим, а одновременно? Вероятность остается такой же: 0,3. Потому что она не зависит от того, вытащили мы фломастеры один за другим, или с интервалом в 2 секунды, или с интервалом в 0,5 секунды… или одновременно!
Ответ: 0,3.

4. При подозрение на наличие некоторого заболевания пациента отправляют на ПЦР-тест. Если заболевание действительно есть, то тест подтверждает его в 86 % случаев. Если заболевания нет, то тест выявляет отсутствие заболевания в среднем в 94% случаев.

Известно, что в среднем тест оказывается положительным у 10% пациентов, направленных на тестирование. При обследовании некоторого пациента врач направил его на ПЦР-тест, который оказался положительным. Какова вероятность того, что пациент действительно имеет это заболевание?

Решение:

Задача похожа на уже знакомую тем, кто готовится к ЕГЭ (про гепатит), однако вопрос здесь другой.
Уточним условие: «Какова вероятность того, что пациент, ПЦР-тест которого положителен, действительно имеет это заболевание?». В такой формулировке множество возможных исходов — это число пациентов с положительным результатом ПЦР-теста, причем только часть из них действительно заболевшие.

Пациент приходит к врачу и делает ПЦР-тест. Он может быть болен этим заболеванием – с вероятностью х. Тогда с вероятностью 1 – х он этим заболеванием не болен.

Анализ пациента может быть положительным по двум причинам:
а) пациент болеет заболеванием, которое нельзя называть, его анализ верен; событие А,
б) пациент не болен этим заболеванием, его анализ ложно-положительный, событие В.
Это несовместные события, и вероятность их суммы равна сумме вероятностей этих событий.

Имеем:

Мы составили уравнение, решив которое, найдем вероятность

Что такое вероятность х? Это вероятность того, что пациент, пришедший к доктору, действительно болен. Здесь множество возможных исходов — это количество всех пациентов, пришедших к доктору.

Нам же нужно найти вероятность z того, что пациент, ПЦР-тест которого положителен, действительно имеет это заболевание. Вероятность этого события равна (пациент болен и ПЦР-тест выявил заболевание, произведение событий). С другой стороны, эта вероятность равна (у пациента положительный результат ПЦР-теста, и при выполнении этого условия он действительно болен).

Получим: отсюда z = 0,43.
Ответ: 0,43.

Вероятность того, что пациент с положительным результатом ПЦР-теста действительно болен, меньше половины!
Кстати, это реальная проблема для диагностики в медицине, то есть в задаче отражена вполне жизненная ситуация.

5. Телефон передает sms-сообщение. В случае неудачи телефон делает следующую попытку. Вероятность того, что сообщение удастся передать без ошибок в каждой следующей попытке, равна 0,4. Найдите вероятность того, что для передачи сообщения потребуется не больше 2 попыток.

Решение:

Здесь все просто. Либо сообщение удалось передать с первой попытки, либо со второй.
Вероятность того, что сообщение удалось передать с первой попытки, равна 0,4.
С вероятностью 0,6 с первой попытки передать не получилось. Если при этом получилось со второй, то вероятность этого события равна
Значит, вероятность того, что для передачи сообщения потребовалось не более 2 попыток, равна

Ответ: 0,64.

6. Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?

Решение:

А это более сложная задача. Можно, как и в предыдущих, пользоваться определением вероятности и понятиями суммы и произведения событий. А можно применить формулу Бернулли.

Формула Бернулли:

– Вероятность P_n^m того, что в независимых испытаниях некоторое случайное событие наступит ровно раз, равна:

$P_n^m=C_n^m p^m q^{n-m},$ где:

– вероятность появления события в каждом испытании;
q=1-p – вероятность непоявления события в каждом испытании.

Коэффициент C_n^m часто называют биномиальным коэффициентом.

О том, что это такое, расскажем с следующих статьях на нашем сайте. Чтобы не пропустить – подписывайтесь на нашу рассылку.

А пока скажем просто, как их вычислять.

$displaystyle C_n^m=frac{n!}{m!(n-m)!}$

Нет, это не заклинание. Не нужно громко кричать: Эн!!!! Поделить на эм! И на эн минус эм! 🙂 То, что вы видите в формуле, – это не восклицательные знаки. Это факториалы.
На самом деле все просто: n! (читается: эн факториал) – это произведение натуральных чисел от 1 до n. Например,

Пусть вероятность выпадения орла при одном броске монеты равна $displaystyle frac{1}{2},$ вероятность решки тоже $displaystyle frac{1}{2}.$ Давайте посчитаем вероятность того, что из 10 бросков монеты выпадет ровно 5 орлов.

$displaystyle P_1=C_{10}^5 cdot left ( frac{1}{2} right )^5 cdot left ( frac{1}{2} right )^5 =frac{10!}{5!cdot 5!}cdot frac{1}{2^{10}}.$

Вероятность выпадения ровно 4 орлов равна

$displaystyle P_2=C_{10}^4 cdot left ( frac{1}{2} right )^4 cdot left ( frac{1}{2} right )^6 =frac{10!}{4!cdot 6!}cdot frac{1}{2^{10}}.$

Найдем, во сколько раз P_1 больше, чем P_2.

$displaystyle frac{P_1}{P_2}=frac{10!cdot 4!cdot 6!cdot 2^{10}}{5!cdot 5!cdot 2^{10}cdot 10!}=frac{4!}{5!}=frac{1cdot 2cdot 3cdot 4cdot 1cdot 2cdot 3 cdot 4cdot 5cdot 6}{1cdot 2cdot 3cdot 4cdot 5 cdot 1cdot 2cdot 3 cdot 4cdot 5}=$

$displaystyle =frac{6}{5}=1,2.$

Ответ: 1,2.

7. Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень дается не более двух выстрелов, и известно, что вероятность поразить мишень каждым отдельным выстрелом равна 0,6. Во сколько раз вероятность события «стрелок поразит ровно 5 мишеней» больше вероятности события «стрелок поразит ровно 4 мишени»?

Решение:

Стрелок поражает мишень с первого или со второго выстрела.

Вероятность поразить мишень равна

Вероятность поразить 5 мишеней из 5 равна

Вероятность поразить 4 мишени из 5 находим по формуле Бернулли:

$displaystyle P_2={C_5}^4 cdot 0,84^4 cdot 0,16 = frac{5!}{4!}cdot 0,84^4 cdot 0,16 = 5cdot 0,84^4 cdot 0,16 ;$

$displaystyle frac{P_1}{P_2}=frac{0,84^5}{5cdot 0,84^4 cdot 0,16} = frac{0,84}{0,8} = 1,05.$

8. В одном ресторане в г. Тамбове администратор предлагает гостям сыграть в «Шеш-беш»: гость бросает одновременно 2 игральные кости. Если он выбросит комбинацию 5 и 6 очков хотя бы один раз из двух попыток, то получит комплимент от ресторана: чашку кофе или десерт бесплатно. Какова вероятность получить комплимент? Результат округлите до сотых.

Решение:

Ресторан «Шеш-Беш» должен сказать составителям задачи спасибо: теперь популярность вырастет во много раз
Заметим, что условие не вполне корректно. Например, я бросаю кости и при первом броске получаю 5 и 6 очков. Надо ли мне бросать второй раз? Могу ли я получить 2 десерта, если дважды выброшу комбинацию из 5 и 6 очков?

Поэтому уточним условие. Если при первом броске получилась комбинация из 5 и 6 очков, то больше кости я не бросаю и забираю свой десерт (или кофе).

Если первый раз не получилось – у меня есть вторая попытка.

Решим задачу с учетом этих условий.

При броске одной игральной кости возможны 6 исходов, при броске 2 костей – 36 исходов. Только два из них благоприятны: это 5; 6 и 6; 5, вероятность каждого из них равна $displaystyle frac{1}{36}.$ Вероятность выбросить 5 и 6 при первом броске равна $displaystyle frac{1}{36} + frac{1}{36}=frac{2}{36}=frac{1}{18}.$

Вероятность того, что с первой попытки не получилось, равна $displaystyle 1- frac{1}{18}=frac{17}{18}.$

Если в первый раз не получилось выбросить 5 и 6, а во второй раз получилось – вероятность этого события равна $displaystyle frac{17}{18}cdot frac{1}{18}.$

Вероятность выбросить 5 и 6 с первой или со второй попытки равна $displaystyle frac{1}{18}+ frac{1}{18} cdot frac{17}{18}= frac{1}{18} cdot frac{35}{18} = frac{35}{324}approx 0,11.$

9. Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 4. Какова вероятность того, что был сделан один бросок? Ответ округлите до сотых.

Решение:

Рассмотрим возможные варианты. Игральную кость могли бросить:
1 раз, выпало 4 очка. Вероятность этого события равна $displaystyle frac{1}{6}$ (1 благоприятный исход из 6 возможных). При этом, если получили 4 очка, кость больше не бросаем.

2 раза, выпало 3 и 1 или 1 и 3 или 2 и 2. При этом, если получили 4 очка, больше не бросаем кость. Для 2 бросков: всего 36 возможны исходов, из них 3 благоприятных, вероятность получить 4 очка равна $displaystyle frac{3}{36}.$

3 раза, выпало 1, 1, 2 или 1, 2, 1 или 2, 1, 1. Если получили 4 очка – больше не бросаем кость. Для 3 бросков: всего возможны исходов, из них 3 благоприятных, вероятность получить 4 очка равна $displaystyle frac{3}{216}.$

4 раза, каждый раз по 1 очку. Вероятность этого события равна $displaystyle frac{1}{6^4}.$

Вероятность получить 4 очка равна

$displaystyle P=frac{1}{6}+frac{3}{6^2}+frac{3}{6^3}+frac{1}{6^4}=frac{1}{6}left ( 1+frac{3}{6}+frac{3}{6^2}+frac{1}{6^3} right )=$

$displaystyle =frac{1}{6}left ( 1+frac{1}{6} right )^3=frac{1}{6}cdot frac{7^3}{6^3}=frac{7^3}{6^4}.$

Воспользуемся формулой условной вероятности.

Пусть P_1 — вероятность получить 4 очка, сделав 1 бросок; $displaystyle P_1=frac{1}{6}$ (для одного броска: 6 возможных исходов, 1 благоприятный);

— вероятность получить 4 очка с одной или нескольких попыток, $displaystyle P=frac{7^3}{6^4};$

P_2 — вероятность, что при этом был сделан только один бросок;

$displaystyle frac{1}{6}=frac{1}{6}cdot frac{7^3}{6^3}cdot P_2;$

$displaystyle P_2=frac{6^3}{7^3}=frac{216}{343}approx 0,63.$

Ответ: 0,63.

10. В викторине участвуют 6 команд. Все команды разной силы, и в каждой встрече выигрывает та команда, которая сильнее. В первом раунде встречаются две случайно выбранные команды.

Ничья невозможна. Проигравшая команда выбывает из викторины, а победившая команда играет со следующим случайно выбранным соперником. Известно, что в первых трех играх победила команда А. Какова вероятность того, что эта команда выиграет следующий раунд?

Решение:

Пусть силы команд равны 1, 2, 3, 4, 5 и 6.
В трех раундах участвуют 4 команды, то есть выбирается 4 числа из 6 и среди этих четырех находится наибольшее.
Выпишем в порядке возрастания, какие 4 команды могли участвовать в первых трех раундах:

1234, 1235, 1236, 1245, 1246, 1256, 1345, 1346, 1356, 1456, 2345, 2346, 2356, 2456, 3456 — всего 15 вариантов.

Среди этих 15 групп есть только одна, в которой 4 — наибольшее число. Это группа 1234. Однако, если команда 4 победила команды 1, 2 и 3, то у нее нет шансов выиграть в следующем раунде у команды 5 или 6.

Есть также 4 группы, в которых 5 — наибольшее число. Вероятность того, что команда 5 победила в трех первых раундах, равна $displaystyle frac{4}{15}.$ В следующем туре команда 5 встретится либо с командой 6 (и проиграет), либо с командой 1, 2, 3 или 4 и выиграет, то есть в четвертом раунде команда 5 побеждает с вероятностью $displaystyle frac{1}{2}.$

Есть также 10 групп, где 6 — наибольшее число. Вероятность того, что команда 6 победила в трех первых раундах, равна $displaystyle frac{10}{15}.$ В четвертом туре команда 6 побеждает с вероятностью 1 (она самая сильная). Соответственно, в следующем туре команда 6 побеждает с вероятностью 1.
Получается $displaystyle frac{4}{15} cdot frac{1}{2} + frac{10}{15} cdot 1 = frac{12}{15} = frac{4}{5}$ — вероятность команды, победившей в 3 первых турах, победить в четвертном.

Ответ: $displaystyle frac{4}{5}.$

И наконец, хитроумная задача, совсем не похожая на школьную теорию вероятностей. В математике ее называют «задачей о разорении игрока». Это уже крутейший теорвер! Будем надеяться, что в варианты ЕГЭ ее все-таки включать не будут.

11. Первый член последовательности целых чисел равен 0. Каждый следующий член последовательности с вероятностью р = 0,8 на единицу больше предыдущего и с вероятностью 1 – р меньше предыдущего. Какова вероятность того, что какой-то член этой последовательности окажется равен – 1?

Решение:

Кошмар, что и говорить, и точно не задача из Части 1 ЕГЭ. Будем разбираться.
Вначале мы находимся в точке 0, из нее можем попасть в точку с координатой 1 или в точку с координатой -1. Дальше возможно увеличение или уменьшение координаты на каждом шаге, а найти надо вероятность того, что когда-либо попадем в точку -1.

Обозначим P_1 – вероятность когда-либо попасть в точку -1, если сейчас мы находимся в точке 0,
P_i – вероятность когда-либо попасть в точку -1, если сейчас мы находимся в точке i.

Из точки 0 можно пойти вверх или вниз. Если мы идем вниз (с вероятностью q=1 – р) – мы сразу попадаем в точку -1.

Поскольку из точки 0 можно пойти вверх или вниз, и эти события несовместны, получим:

где P_2 – вероятность попасть когда-нибудь в точку -1, находясь в данный момент в точке 1.
А из точки 1 в точку – 1 можно попасть следующим образом: сначала в точку 0, потом в точку – 1; вероятность каждого из этих событий равна P_1.
Да, это сложно воспринять! Но давайте вернемся к обозначениям: Р1 – вероятность когда-либо попасть в точку -1, если сейчас мы находимся в точке 0. И она точно такая же, как вероятность когда-либо попасть в точку 0, если сейчас мы находимся в точке 1.
Значит, вероятность попадания из точки 1 в точку – 1 равна ${P_1}^2 .$ Мы получаем квадратное уравнение: $P_1 = q +p cdot {P_1}^2 .$

По условию, Тогда $0,8cdot{P_1}^2 - P_1 + 0,2 = 0;$
$4 cdot {P_1}^2 - 5P_1 + 1 = 0.$ Корни этого уравнения: или $displaystyle P_1 = frac{1}{4} = frac{q}{p}.$

Какой из этих корней выбрать? Оказывается, если по условию $displaystyle frac{q}{p} textgreater 1,$ то в ответе получится 1 (всегда попадем в точку -1).
А если, как в нашем случае, $displaystyle frac{q}{p} textless 1,$ то ответ $displaystyle frac{q}{p} ,$ то есть 0,25.
Ответ: 0,25.

А теперь представим себе, что будет, если эту задачи все-таки включат в курс подготовки к ЕГЭ. Учителя будут говорить ученикам: если тебе надо попасть из 0 в точку – 1, вероятность перехода вверх равна р, вероятность перехода вниз равна q, и если то в ответе будет $displaystyle frac{q}{p},$ а если то в ответе будет 1. Бессмысленная зубрежка, короче говоря.

Задачи, разобранные в этой статье, взяты из Открытого Банка заданий ЕГЭ по математике: mathege.ru

Будут ли эти задачи — и особенно последние — на ЕГЭ-2022? Вот официальный ответ ФИПИ:

«Открытость и прозрачность ЕГЭ, наличие открытых банков, дает возможность развивать различные ресурсы, способствующие повышению качества образования.

При этом вся официальная информация, спецификации, демонстрационные варианты, открытые банки, содержатся только на сайте ФИПИ. Типы заданий, которые будут включены в ЕГЭ по математике в 2022 году прошли широкое обсуждение и апробацию в регионах, соответствуют ФГОС.

ФИПИ не комментирует содержание других ресурсов».
Ждем, когда на сайте ФИПИ появятся подборки задач №10 ЕГЭ-2022.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Новые задачи по теории вероятностей из Открытого Банка заданий ЕГЭ, 2021-2022 год» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Вероятностью события $А$ называется отношение числа благоприятных для $А$ исходов к числу всех
равновозможных исходов

$P(A)={m}/{n}$, где $n$ – общее количество возможных исходов, а $m$ – количество исходов, благоприятствующих событию
$А$.

Вероятность события — это число из отрезка $[0; 1]$

В фирме такси в наличии $50$ легковых автомобилей. $35$ из них чёрные, остальные — жёлтые.
Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета.

Решение:

Найдем количество желтых автомобилей:

$50-35=15$

Всего имеется $50$ автомобилей, то есть на вызов приедет одна из пятидесяти. Желтых автомобилей $15$,
следовательно, вероятность приезда именно желтого автомобиля равна ${15}/{50}={3}/{10}=0,3$

Ответ:$0,3$

Противоположные события

Два события называются противоположными, если в данном испытании они несовместимы и одно из них обязательно
происходит. Вероятности противоположных событий в сумме дают 1.Событие, противоположное событию $А$, записывают
${(А)}↖{-}$.

$Р(А)+Р{(А)}↖{-}=1$

Независимые события

Два события $А$ и $В$ называются независимыми, если вероятность появления каждого из них не зависит от того,
появилось другое событие или нет. В противном случае события называются зависимыми.

Вероятность произведения двух независимых событий $A$ и $B$ равна произведению этих
вероятностей:

$Р(А·В)=Р(А)·Р(В)$

Иван Иванович купил два различных лотерейных билета. Вероятность того, что выиграет первый
лотерейный билет, равна $0,15$. Вероятность того, что выиграет второй лотерейный билет, равна $0,12$. Иван Иванович
участвует в обоих розыгрышах. Считая, что розыгрыши проводятся независимо друг от друга, найдите вероятность того,
что Иван Иванович выиграет в обоих розыгрышах.

Решения:

Вероятность $Р(А)$ — выиграет первый билет.

Вероятность $Р(В)$ — выиграет второй билет.

События $А$ и $В$ – это независимые события. То есть, чтобы найти вероятность того, что они произойдут оба
события, нужно найти произведение вероятностей

$Р(А·В)=Р(А)·Р(В)$

$Р=0,15·0,12=0,018$

Ответ: $0,018$

Несовместные события

Два события $А$ и $В$ называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию
$А$, так и событию $В$. (События, которые не могут произойти одновременно)

Вероятность суммы двух несовместных событий $A$ и $B$ равна сумме вероятностей этих
событий:

$Р(А+В)=Р(А)+Р(В)$

На экзамене по алгебре школьнику достается один вопрос их всех экзаменационных. Вероятность
того, что это вопрос на тему «Квадратные уравнения», равна $0,3$. Вероятность того, что это вопрос на тему
«Иррациональные уравнения», равна $0,18$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите
вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Решение:

Данные события называются несовместные, так как школьнику достанется вопрос ЛИБО по теме «Квадратные уравнения»,
ЛИБО по теме «Иррациональные уравнения». Одновременно темы не могут попасться. Вероятность суммы двух
несовместных событий $A$ и $B$ равна сумме вероятностей этих событий:

$Р(А+В)=Р(А)+Р(В)$

$Р = 0,3+0,18=0,48$

Ответ: $0,48$

Совместные события

Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же
испытании. В противном случае события называются несовместными.

Вероятность суммы двух совместных событий $A$ и $B$ равна сумме вероятностей этих событий минус
вероятность их произведения:

$Р(А+В)=Р(А)+Р(В)-Р(А·В)$

В холле кинотеатра два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится
кофе, равна $0,6$. Вероятность того, что кофе закончится в обоих автоматах, равна $0,32$. Найдите вероятность того,
что к концу дня кофе закончится хотя бы в одном из автоматов.

Решение:

Обозначим события, пусть:

$А$ = кофе закончится в первом автомате,

$В$ = кофе закончится во втором автомате.

Тогда,

$A·B =$ кофе закончится в обоих автоматах,

$A + B =$ кофе закончится хотя бы в одном автомате.

По условию, $P(A) = P(B) = 0,6; P(A·B) = 0,32$.

События $A$ и $B$ совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий,
уменьшенной на вероятность их произведения:

$P(A + B) = P(A) + P(B) − P(A·B) = 0,6 + 0,6 − 0,32 = 0,88$

Ответ: $0,88$

Источник

Уважаемый посетитель!

Если у вас есть вопрос, предложение или жалоба, пожалуйста, заполните короткую форму и изложите суть обращения в текстовом поле ниже. Мы обязательно с ним ознакомимся и в 30-дневный срок ответим на указанный вами адрес электронной почты

Статус Абитуриент Студент Родитель Соискатель Сотрудник Другое

Филиал Абакан Актобе Алагир Алматы Алушта Анапа Ангарск Архангельск Армавир Асбест Астана Астрахань Атырау Баку Балхаш Барановичи Барнаул Белая Калитва Белгород Бельцы Берлин Бишкек Благовещенск Бобров Бобруйск Борисов Боровичи Бронницы Брянск Бузулук Чехов Челябинск Череповец Черкесск Дамаск Дербент Димитровград Дмитров Долгопрудный Домодедово Дубай Дубна Душанбе Екатеринбург Электросталь Елец Элиста Ереван Евпатория Гана Гомель Гродно Грозный Хабаровск Ханты-Мансийск Хива Худжанд Иркутск Истра Иваново Ижевск Калининград Карабулак Караганда Каракол Кашира Казань Кемерово Киев Кинешма Киров Кизляр Королев Кострома Красноармейск Краснодар Красногорск Красноярск Краснознаменск Курган Курск Кызыл Липецк Лобня Магадан Махачкала Майкоп Минеральные Воды Минск Могилев Москва Моздок Мозырь Мурманск Набережные Челны Нальчик Наро-Фоминск Нижневартовск Нижний Новгород Нижний Тагил Ногинск Норильск Новокузнецк Новосибирск Новоуральск Ноябрьск Обнинск Одинцово Омск Орехово-Зуево Орел Оренбург Ош Озёры Павлодар Пенза Пермь Петропавловск Подольск Полоцк Псков Пушкино Пятигорск Радужный Ростов-на-Дону Рязань Рыбинск Ржев Сальск Самара Самарканд Санкт-Петербург Саратов Сергиев Посад Серпухов Севастополь Северодвинск Щербинка Шымкент Слоним Смоленск Солигорск Солнечногорск Ставрополь Сургут Светлогорск Сыктывкар Сызрань Тамбов Ташкент Тбилиси Терек Тихорецк Тобольск Тольятти Томск Троицк Тула Тверь Тюмень Уфа Ухта Улан-Удэ Ульяновск Ургенч Усть-Каменогорск Вёшенская Видное Владимир Владивосток Волгодонск Волгоград Волжск Воркута Воронеж Якутск Ярославль Юдино Жлобин Жуковский Златоуст Зубова Поляна Звенигород

Тип обращения Вопрос Предложение Благодарность Жалоба

Тема обращения Поступление Трудоустройство Обучение Оплата Кадровый резерв Внеучебная деятельность Работа автоматических сервисов университета Другое

* Все поля обязательны для заполнения

Я даю согласие на обработку персональных данных, согласен на получение информационных рассылок от Университета «Синергия» и соглашаюсь c политикой конфиденциальности

Источник

Теория вероятностней ЕГЭ по математике

07.01.2020

Полная подборка теории и заданий для подготовки к заданиями ЕГЭ, связанным с теорией вероятности. Конечно же, этот тип заданий встречается именно в профильной математике.

Этот тип заданий встречается в ЕГЭ по математике за всего года и времена Поэтому материал актуален (задание может лишь менять порядковый номер, но суть одна).

Сборник заданий с ответами по теории вероятностей

Документы

Сборник теории от А до Я про задания ЕГЭ по теории вероятности PDF
Супер-мега ШПАРГАЛКА по теории вероятности именно для ЕГЭ (Школа Пифагора, картинка)

Все основы теории вероятностей видеоурок

Смотреть в PDF:

Или прямо сейчас: cкачать в pdf файле.

Источник

Рассмотрим решение новых задач по теории вероятностей, которые появятся в ЕГЭ по математике в 2022 году.

Вы можете попробовать решить задачи самостоятельно, а потом сверить свое решение с предложенным.

1. № 508755

Игральный кубик бросают дважды. Известно, что в сумме выпало 8 очков. Найдите вероятность того, что в первый раз выпало 6 очков.

Решение. показать

2. № 508769

Игральную кость бросили два раза. Известно, что три очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 8».

Решение. показать

3. № 508781

Симметричную монету бросают 11 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?

Решение. показать

4. № 508791

В одном ресторане в г. Тамбове администратор предлагает гостям сыграть в «Шеш-беш»: гость бросает одновременно две игральные кости. Если он выбросит комбинацию 5 и 6 очков хотя бы один раз из двух попыток, то получит комплимент от ресторана: чашку кофе или десерт бесплатно. Какова вероятность получить комплимент? Результат округлите до сотых.

Решение. показать

5. № 508793

Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 4. Какова вероятность того, что потребовалось сделать три броска? Результат округлите до сотых.

Решение. показать

6. № 508798

Игральную кость бросали до тех пор, пока сумма выпавших очков не превысила число 3. Какова вероятность того, что для этого потребовалось 3 броска? Ответ округлите до сотых.

Решение. показать

7. № 508809

Телефон передает SMS-сообщение. В случае неудачи телефон делает следующую попытку. Вероятность того, что сообщение удастся передать без ошибок в каждой отдельной попытке, равна 0,2. Найдите вероятность того, что для передачи сообщения потребуется не больше двух попыток.

Решение. показать

8. № 508820

При подозрении на наличие некоторого заболевания пациента отправляют на ПЦР-тест. Если заболевание действительно есть, то тест подтверждает его в 91% случаев. Если заболевание нет, то тест выявляет отсутствие заболевания в среднем в 93% случаев. Известно, что в среднем тест оказывается положительным у 10% пациентов, направленных на тестирование. При обследовании некоторого пациента врач направил его на ПЦР-тест, который оказался положительным. Какова вероятность того, что пациент действительно имеет это заболевание? Результат округлите до сотых.

Решение. показать

9. № 508831

Стрелок в тире стреляет по мишени до тех пор, пока не поразит ее. Известно, что он попадает в цель с вероятностью 0,2 при каждом отдельном выстреле. Сколько патронов нужно дать стрелку, чтобы он поразил цель с вероятностью не менее 0,5?

Решение. показать

10. № 508843

В ящике три красных и три синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что в первый раз синий фломастер появится третьим по счету?

Решение. показать

11. №508851

Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень дается не более двух выстрелов, и известно, что вероятность поразить мишень каждым отдельным выстрелом равна 0,6. Во сколько раз вероятность события «стрелок поразит ровно три мишени» больше вероятность события «стрелок поразит ровно две мишени».

Решение. показать

12. № 508868

В викторине участвуют 10 команд. Все команды разной силы, и в каждой встрече выигрывает та команда, которая сильнее. В первом раунде встречаются две случайно выбранные команды. Ничья невозможна. Проигравшая команда выбывает из викторины, а победившая команда играет со следующим случайно выбранным соперником. Известно, что в первых шести играх победила команда А. Какова вероятность, что эта команда выиграет седьмой раунд.

Решение. показать

13. № 508871

Турнир по настольному теннису проводится по олимпийской системе: игроки случайным образом разбиваются на пары; проигравший в каждой паре выбывает из турнира, а победитель выходит в следующий тур, где встречается со следующим противником, который определен жребием. Всего в турнире 8 игроков, все они играют одинаково хорошо, поэтому в каждой встрече вероятность выигрыша и поражения у каждого игрока равна 0,5. Среди игроков два друга — Иван и Алексей. Какова вероятность того, что этим двоим в каком-то туре придется сыграть друг с другом?

Решение. показать

14. № 508887

Первый игральный кубик обычный, а на гранях второго кубика нет четных чисел, а нечетные числа встречаются по два раза. В остальном кубики одинаковые. Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 3 и 5 очков. Какова вероятность, что бросали второй кубик?

Решение. показать

15. № 509078

Маша коллекционирует принцесс из Киндер-сюрпризов. Всего в коллекции 10 разных принцесс, и они равномерно распределены, то есть в каждом Киндер-сюрпризе может с равными вероятностями оказаться любая из 10 принцесс. У Маши есть две разные принцессы из коллекции. Какова вероятность того, что для получения следующей принцессы Маше придется купить еще 2 или 3 шоколадных яйца?

Решение. показать

15. № 508885

Первый член последовательности целых чисел равен 0. Каждый следующий член последовательности с вероятность на единицу больше предыдущего и с вероятность на единицу меньше предыдущего. Какова вероятность того, что какой-то член этой последовательности окажется равен -1?

Решение. показать

И.В. Фельдман, репетитор по математике

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

ЕГЭ Профиль №2. Теоремы о вероятностях событий

ЕГЭ Профиль №2. Теоремы о вероятностях событийadmin2022-07-23T12:34:42+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №2. Теоремы о вероятностях событий

Задача 1. На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Задача 2. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

Задача 3. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из не пристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.

Задача 4. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.

Задача 5. При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?

Задача 6. Вероятность того, что на тесте по биологии учащийся О. верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач.

Задача 7. Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание. Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5. Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.

Задача 8. Чтобы поступить в институт на специальность «Международные отношения» абитуриент должен набрать на ЕГЭ не менее 67 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Менеджмент» нужно набрать не менее 67 баллов по каждому из трёх предметов — математика, русский язык и обществознание. Вероятность того, что абитуриент Т. получит не менее 67 баллов по математике — равна 0,6, по русскому языку — 0,5, по иностранному языку — 0,8 и по обществознанию — 0,9. Найдите вероятность того, что Т. сможет поступить на одну из двух упомянутых специальностей.

Задача 9. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 20 пассажиров, равна 0,94. Вероятность того, что окажется меньше 15 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 15 до 19. Ответ ОТВЕТ: 0,38.
Задача 10. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода. Ответ ОТВЕТ: 0,392.
Задача 11. Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным. Ответ ОТВЕТ: 0,0545.
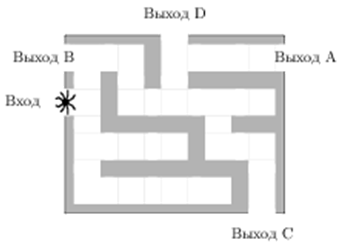
Задача 12. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу D. Ответ ОТВЕТ: 0,0625.
Задача 13. Какова вероятность того, что последние три цифры номера случайно выбранного паспорта различны? Ответ ОТВЕТ: 0,72.
Задача 14. Какова вероятность того, что в случайном телефонном номере три последние цифры одинаковые? Ответ ОТВЕТ: 0,01.
Задача 15. При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше 810 г, равна 0,96. Вероятность того, что масса окажется больше 790 г, равна 0,82. Найдите вероятность того, что масса буханки больше 790 г, но меньше 810 г. Ответ ОТВЕТ: 0,78.
Задача 16. При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше 810 г, равна 0,98. Вероятность того, что масса окажется больше 790 г, равна 0,83. Найдите вероятность того, что масса буханки больше 790 г, но меньше 810 г. Ответ ОТВЕТ: 0,81.

Источник

Теория вероятности – подробнее

Что такое вероятность?

Рассмотрим пример. Допустим, мы бросаем игральную кость. Что это за кость такая, знаешь? Так называют кубик с цифрами на гранях. Сколько граней, столько и цифр: от ( 1) до ( 6).

Итак, мы бросаем кость и хотим, чтобы выпало ( 5) или ( 6). И нам выпадает ( 5).

В теории вероятностей говорят, что произошло благоприятное событие.

Если бы выпало ( 6), событие тоже было бы благоприятным. Итого может произойти всего два благоприятных события.

А сколько неблагоприятных?

Раз всего возможных событий ( 6), значит, неблагоприятных из них ( 6-2=4) события (это если выпадет ( 1,text{ }2,text{ }3) или ( 4)).

Вероятностью называется отношение количества благоприятных событий к количеству всех возможных событий.

То есть вероятность показывает, какая доля из всех возможных событий приходится на благоприятные.

Обозначают вероятность латинской буквой ( p) (видимо, от английского слова probability – вероятность).

Принято измерять вероятность в процентах (см. темы “Дроби, рациональные числа” и “Проценты”).

Для этого значение вероятности нужно умножать на ( 100%).

В примере с игральной костью вероятность ( p=frac{благоприятных}{всего}=frac{2}{6}=frac{1}{3}).

А в процентах: ( p=frac{1}{3}cdot 100%=frac{100}{3}%approx 33,3%).

И еще события бывают зависимыми друг от друга и независимыми. Начнем с зависимых событий.

Зависимые события

Например, ты решил зайти к знакомому, помнишь подъезд и даже этаж на котором он живет. А вот номер и расположение квартиры забыл. И вот стоишь ты на лестничной клетке, а перед тобой ( 3) двери на выбор.

Каков шанс (вероятность) того, что если ты позвонишь в первую дверь, тебе откроет твой друг? Всего квартиры ( 3), а друг живет только за одной из них. С равным шансом мы можем выбрать любую дверь.

Но каков этот шанс?

Дверей ( 3), нужная дверь ( 1). Вероятность угадать, позвонив в первую дверь: ( frac{1}{3}). То есть один раз из трех ты точно угадаешь.

Мы хотим узнать, позвонив ( 1) раз, как часто мы будем угадывать дверь? Давай рассмотри все варианты:

1. Ты позвонил в 1-ю дверь
2. Ты позвонил в 2-ю дверь
3. Ты позвонил в 3-ю дверь

А теперь рассмотрим все варианты, где может находиться друг:

а. За 1ой дверью
б. За 2ой дверью
в. За 3ей дверью

Сопоставим все варианты в виде таблицы. Галочкой обозначены варианты, когда твой выбор совпадает с местоположением друга, крестиком – когда не совпадает.

Как видишь, всего возможно ( 9) вариантов местоположения друга и твоего выбора, в какую дверь звонить.

А благоприятных исходов всего ( 3). То есть ( 3) раза из ( 9) ты угадаешь, позвонив в дверь ( 1) раз, т.е. ( frac{3}{9}=frac{1}{3}).

Это и есть вероятность – отношение благоприятного исхода (когда твой выбор совпал с местоположение друга) к количеству возможных событий.

Определение – это и есть формула. Вероятность принято обозначать p, поэтому:

( displaystyle p=frac{text{благоприятных}}{всего})

Такую формулу писать не очень удобно, поэтому примем за ( displaystyle {{N}_{б}}) – количество благоприятных исходов, а за ( N) – общее количество исходов.

( displaystyle p=frac{{{N}_{б}}}{N})

Вероятность можно записывать в процентах, для этого нужно умножить получившийся результат на ( 100%):

( displaystyle p=frac{{{N}_{б}}}{N}cdot 100%)

Наверное, тебе бросилось в глаза слово «исходы».

Поскольку математики называют различные действия (у нас такое действие – это звонок в дверь) экспериментами, то результатом таких экспериментов принято называть исход.

Ну а исходы бывают благоприятные и неблагоприятные.

Давай вернемся к нашему примеру. Допустим, мы позвонили в одну из дверей, но нам открыл незнакомый человек. Мы не угадали. Какова вероятность, что если позвоним в одну из оставшихся дверей, нам откроет наш друг?

Если ты подумал, что ( displaystyle frac{1}{3}), то это ошибка. Давай разбираться.

У нас осталось две двери. Таким образом, у нас есть возможные шаги:

1. Позвонить в 1-ую дверь
2. Позвонить во 2-ую дверь

Друг, при всем этом, точно находится за одной из них (ведь за той, в которую мы звонили, его не оказалось):

а. Друг за 1-ой дверью
б. Друг за 2-ой дверью

Давай снова нарисуем таблицу:

Как видишь, всего есть ( 4) варианта, ( 2) из которых – благоприятны. То есть вероятность равна ( displaystyle frac{2}{4}=frac{1}{2}).

А почему не ( displaystyle frac{1}{3})?

Рассмотренная нами ситуация – пример зависимых событий. Первое событие – это первый звонок в дверь, второе событие – это второй звонок в дверь.

А зависимыми они называются потому что влияют на следующие действия. Ведь если бы после первого звонка в дверь нам открыл друг, то какова была бы вероятность того, что он находится за одной из двух других?

Правильно, ( 0%).

Но если есть зависимые события, то должны быть и независимые? Верно, бывают.

Независимые события

Два события независимы, если при наступлении одного вероятность наступления другого не изменяется.

Хрестоматийный пример – бросание монетки.

Бросаем монетку ( 1) раз. Какова вероятность того, что выпадет, например, орел?

Правильно: ( displaystyle frac{1}{2}), ведь вариантов всего ( 2) (либо орел, либо решка, пренебрежем вероятностью монетки встать на ребро), а устраивает нас только ( 1).

Но выпала решка. Ладно, бросаем еще раз. Какова сейчас вероятность выпадения орла? Ничего не изменилось, все так же ( displaystyle frac{1}{2}).

Сколько вариантов? Два. А сколько нас устраивает? Один.

И пусть хоть тысячу раз подряд будет выпадать решка. Вероятность выпадения орла на ( displaystyle 1001-й) раз будет все также ( displaystyle frac{1}{2}).

Вариантов всегда ( 2), а благоприятных – ( 1).

Отличить зависимые события от независимых легко:

Если эксперимент проводится ( 1) раз (( 1) раз бросают монетку, 1 раз звонят в дверь и т.д.), то события всегда независимые.

Если эксперимент проводится несколько раз (монетку бросают ( 5) раз, в дверь звонят несколько раз), то первое событие всегда независимое. А дальше, если количество благоприятных или количество всех исходов меняется, то события зависимые, а если нет – независимые.

Ошибка игрока или ложный вывод Монте-Карло

Знаешь, то, что я описал сверху, очень хорошо отражает явление под названием ложный вывод Монте-Карло.

Попробуй придумать и записать на листочке результаты подбрасывания монетки.

А потом попробуй действительно подбрасывать монетку и записывать результат.

Спорим, я без труда определю, какую последовательность ты выдумал?

В реальной последовательности может абсолютно спокойно выпасть 18 решек подряд. А вот ты, составляя последовательность, когда-нибудь точно подумаешь: “Так, что-то многовато решек уже, пора бы и орлу появиться”

В этом и заключается ложный вывод Монте-Карло. В знаменитом казино Монте-Карло люди часто думают, что следующее событие как-то связано с предыдущим, например, ставят на красное, если ранее много раз выпало черное.

В действительности это не так.

А теперь давай немного потренируемся определять вероятность.

Решение:

Давай посчитаем количество благоприятных исходов.

НЕ красный фломастер, это значит зеленый, синий, желтый или черный.

Всего их ( 3+2+2+1=8). ( displaystyle {{N}_{б}}=8).

( displaystyle p=frac{{{N}_{б}}}{N}=frac{8}{10}=0,8)

Так мы учились считать раньше, но сейчас, зная что такое полная вероятность, можно поступить немного проще.

Вероятность всех событий ( 1). А вероятность событий, которые мы считаем неблагоприятными (когда вытащим красный фломастер) – ( displaystyle frac{2}{10}) .

Таким образом, вероятность вытащить НЕ красный фломастер – ( displaystyle 1-frac{2}{10}=0,8).

Ответ: ( displaystyle 0,8)

Запомни:

Вероятность того, что событие НЕ произойдет, равна ( displaystyle 1) минус вероятность того, что событие произойдет.

Правило умножения вероятностей независимых событий

Что такое независимые события ты уже знаешь.

А если нужно найти вероятность того, что два (или больше) независимых события произойдут подряд?

Можно конечно посчитать, но есть способ проще.

Допустим мы хотим знать, какова вероятность того, что бросая монетку ( 2) раза, мы два раза увидим орла?

Мы уже считали: ( p=0,25).

А если бросаем монетку ( 3) раза? Какова вероятность увидеть орла ( 3) раза подряд?

Всего возможных вариантов ( 8):

Орел-орел-орел
Орел-орел-решка
Орел-решка-орел
Орел-решка-решка
Решка-орел-орел
Решка-орел-решка
Решка-решка-орел
Решка-решка-решка

Не знаю, как ты, но я ( 3) раза ошибся, составляя этот список. Ух! А подходит нам только ( 1) вариант (первый).

( displaystyle p=frac{{{N}_{б}}}{N}=frac{1}{8})

Для 5 бросков можешь составить список возможных исходов сам. Но математики не столь трудолюбивы, как ты.

Поэтому они сначала заметили, а потом доказали, что вероятность определенной последовательности независимых событий каждый раз уменьшается на вероятность одного события.

Другими словами,

Вероятность определенной последовательности независимых событий равна произведению вероятностей каждого из событий

Рассмотрим на примере все той же, злосчастной, монетки.

Вероятность выпадения орла в ( 1) испытании? ( displaystyle frac{1}{2}). Теперь мы бросаем монетку ( 5) раз.

Какова вероятность выпадения ( 5) раз подряд орла?

( displaystyle p=frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}={{left( frac{1}{2} right)}^{5}}=frac{1}{32})

Это правило работает не только, если нас просят найти вероятность того, что произойдет одно и то же событие несколько раз подряд.

Если бы мы хотели найти последовательность РЕШКА-ОРЕЛ-РЕШКА, при ( 3) бросках подряд, мы поступили бы также.

Вероятность выпадения решка – ( displaystyle frac{1}{2}), орла – ( displaystyle frac{1}{2}).

Вероятность выпадения последовательности РЕШКА-ОРЕЛ-РЕШКА-РЕШКА:

( displaystyle p=frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}={{left( frac{1}{2} right)}^{4}}=frac{1}{16})

Можешь проверить сам, составив таблицу.

Правило сложения вероятностей несовместных событий

Так стоп! Новое определение.

Несовместными называются события, которые никак не могут произойти одновременно в результате эксперимента.

Ряд несовместных событий образуют полную группу событий.

Давай разбираться. Возьмем нашу изношенную монетку и бросим её ( 3) раза. Возможные варианты:

Орел-орел-орел
Орел-орел-решка
Орел-решка-орел
Орел-решка-решка
Решка-орел-орел
Решка-орел-решка
Решка-решка-орел
Решка-решка-решка

Так вот, несовместные события – это определенная, заданная последовательность событий. ( 1),text{ }2),text{ }3),text{ }4)ldots text{ }8)) – это несовместные события.

Вероятности несовместных событий складываются.

Если мы хотим определить, какова вероятность двух (или больше) несовместных событий, то мы складываем вероятности этих событий.

Нужно понять, что выпадение орла или решки – это два независимых события.

Если мы хотим определить, какова вероятность выпадения последовательности ( 1)) (или любой другой), то мы пользуемся правилом умножения вероятностей.

Какова вероятность выпадения при первом броске орла, а при втором и третьем решки?

( displaystyle p=frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}=frac{1}{8})

Но если мы хотим узнать, какова вероятность выпадения одной из нескольких последовательностей, например, когда орел выпадет ровно ( 1) раз, т.е. варианты ( 4),text{ }6)) и ( 7)), то мы должны сложить вероятности этих последовательностей.

Всего вариантов ( 8), нам подходит ( 3).

( displaystyle p=frac{{{N}_{б}}}{N}=frac{3}{8})

То же самое мы можем получить, сложив вероятности появления каждой последовательности:

( displaystyle p={{p}_{4}}+{{p}_{6}}+{{p}_{7}}=frac{1}{8}+frac{1}{8}+frac{1}{8}=frac{3}{8})

Таким образом, мы складываем вероятности, когда хотим определить вероятность некоторых, несовместных, последовательностей событий.

Правило, помогающее не запутаться, когда умножать, а когда складывать:

Опишите, что должно произойти, используя союзы «И» или «ИЛИ». Затем вместо «И» ставим знак умножения, а вместо «ИЛИ» – сложения.

Возвратимся к примеру, когда мы подбросили монетку ( 3) раза, и хотим узнать вероятность увидеть орла ( 1) раз.

Что должно произойти?

Должны выпасть:

(орел И решка И решка) ИЛИ (решка И орел И решка) ИЛИ (решка И решка И орел).

Вот и получается:

( displaystyle left( frac{1}{2}cdot frac{1}{2}cdot frac{1}{2} right)+left( frac{1}{2}cdot frac{1}{2}cdot frac{1}{2} right)+left( frac{1}{2}cdot frac{1}{2}cdot frac{1}{2} right)=frac{1}{8}+frac{1}{8}+frac{1}{8}=frac{3}{8})

Давай рассмотрим несколько примеров.

Задачи смешанного типа

Пример 16.

Монетку бросают два раза. Какова вероятность того, что результат бросков будет разный?

Решение.

Имеется в виду, что если первым выпал орел, второй должна быть решка, и наоборот. Получается, что здесь две пары независимых событий, и эти пары друг с другом несовместны. Как бы не запутаться, где умножать, а где складывать.

Есть простое правило для таких ситуаций.

Попробуй описать, что должно произойти, соединяя события союзами «И» или «ИЛИ».

Например, в данном случае:

Должны выпасть (орел и решка) или (решка и орел).

Там где стоит союз «и», будет умножение, а там где «или» – сложение:

( p=left( frac{1}{2}cdot frac{1}{2} right)+left( frac{1}{2}cdot frac{1}{2} right)=frac{1}{4}+frac{1}{4}=frac{1}{2}=0,5).

Попробуй сам:

С какой вероятностью при двух бросаниях монетки оба раза выпадет одно и та же сторона?
Игральную кость бросают дважды. Какова вероятность, что в сумме выпадет ( 10) очков?
Бросаем монетку ( 3) раза. Какова вероятность, что хотя-бы один раз выпадет орел?

Решения:

Источник