[{Large{text{Основные сведения}}}]
Определения
Угол – это геометрическая фигура, состоящая из точки и двух лучей, выходящих из этой точки. Градусная мера угла может принимать значения от (0^circ) до (180^circ) включительно.
Угол (alpha) называется острым, если (0^circ<alpha<90^circ), прямым – если (alpha=90^circ), тупым – если (90^circ<alpha<180^circ), и развернутым – если (alpha=180^circ).
Биссектриса угла – это луч, выходящий из вершины угла и делящий угол пополам.
Смежные углы – это два угла, у которых общая вершина и одна общая сторона, а две другие стороны образуют прямую.
Вертикальные углы – это два угла, образованные пересечением двух прямых и не являющиеся смежными.
Теорема
Смежные углы (alpha) и (beta) в сумме дают (180^circ).
Вертикальные углы равны: (alpha=gamma).
Определения
Треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой (называемых вершинами треугольника), и отрезков, соединяющих эти точки (называемых сторонами треугольника). Треугольник со своей внутренностью будем сокращенно называть также треугольником.
Угол (внутренний) треугольника – угол, образованный вершиной треугольника и двумя его сторонами.
Теоремы: признаки равенства треугольников
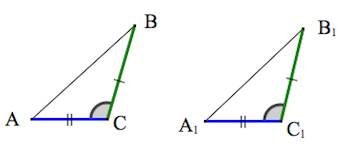
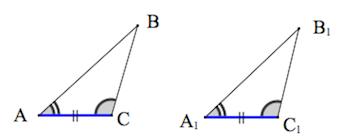
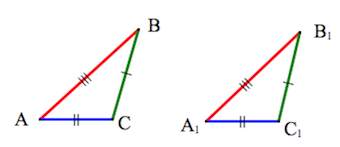
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2. Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.
3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Определение
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Две прямые называются перпендикулярными, если угол между ними равен (90^circ).
Перпендикуляр из точки к прямой – это отрезок, соединяющий данную точку с точкой на прямой, проведенный под углом (90^circ).
Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
Замечание
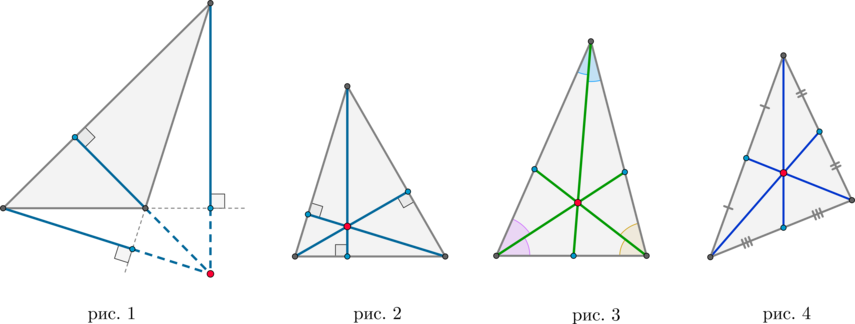
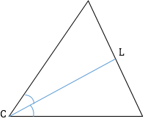
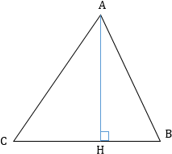
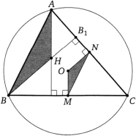
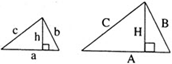
Если в треугольнике один угол тупой, то высоты, опущенные из вершин острых углов, упадут не на сторону, а на продолжение стороны (рис. 1).
Теорема
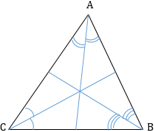
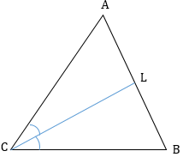
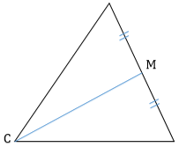
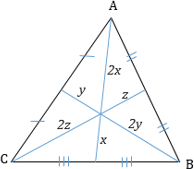
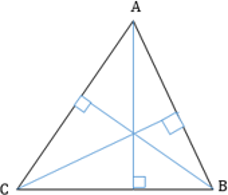
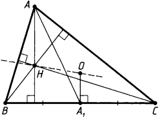
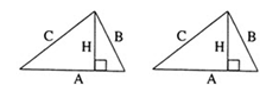
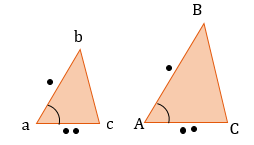
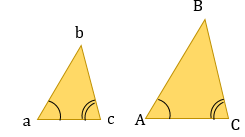
В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).
[{Large{text{Параллельные прямые}}}]
Определение
Две различные прямые на плоскости называются параллельными, если они не пересекаются.
Замечание
Заметим, что на плоскости существует три вида взаимного расположения прямых: совпадают, пересекаются и параллельны.
Аксиома параллельных прямых
Через точку, не лежащую на данной прямой, проходит единственная прямая, параллельная данной.
Следствия из аксиомы
1. Если прямая пересекает одну из параллельных прямых, то она пересекает и другую прямую.
2. Две прямые, параллельные третьей прямой, параллельны.
Теоремы: признаки параллельности прямых
1. Если при пересечении двух прямых (a) и (b) секущей (c) накрест лежащие углы равны: (angle 1=angle 2), то такие прямые параллельны.
2. Если при пересечении двух прямых (a) и (b) секущей (c) сумма односторонних углов (angle 1) и (angle 3) равна (180^circ), то такие прямые параллельны.
3. Если при пересечении двух прямых (a) и (b) секущей (c) соответственные углы равны: (angle 1=angle 4), то такие прямые параллельны.
Теоремы: свойства параллельных прямых
1. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
2. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна (180^circ).
3. Если две параллельные прямые пересечены секущей, то соответственные углы равны.
[{Large{text{Углы треугольника}}}]
Определения
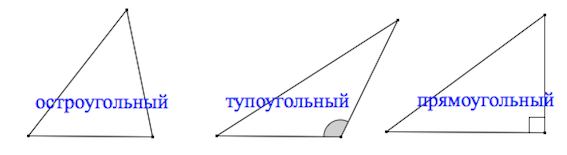
Треугольник называется остроугольным, если все его углы острые.
Треугольник называется тупоугольным, если один его угол тупой (остальные — острые).
Треугольник называется прямоугольным, если один его угол прямой (остальные — острые).
Теорема
Сумма внутренних углов треугольника равна (180^circ).
Доказательство
Рассмотрим произвольный треугольник (ABC) и покажем, что (angle A +
angle B + angle C = 180^circ).
Проведём через вершину (B) прямую (a), параллельную стороне (AC).
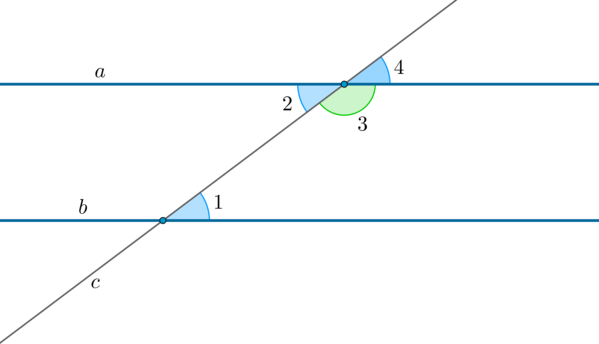
Углы (1) и (4) являются накрест лежащими углами при пересечении параллельных прямых (a) и (AC) секущей (AB), а углы (3) и (5) – накрест лежащими углами при пересечении тех же параллельных прямых секущей (BC). Поэтому [begin{aligned}
&angle 4 = angle 1, angle 5 = angle 3. qquad qquad qquad
(1)
end{aligned}]
Очевидно, сумма углов (4, 2) и (5) равна развёрнутому углу с вершиной (B), то есть (angle 4 + angle 2 + angle 5 = 180^circ). Отсюда, учитывая равенства ((1)), получаем: (angle 1 + angle 2 + angle 3 = 180^circ).
Определение
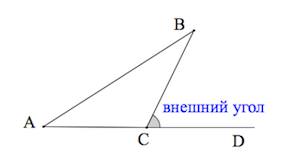
Внешний угол треугольника – это угол, смежный с каким-нибудь внутренним углом треугольника.
Теорема
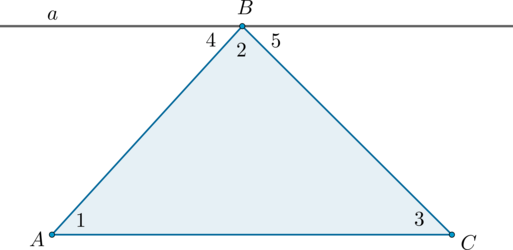
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним: (angle BCD=angle BAC+angle ABC).
Доказательство
Рассмотрим рисунок.
Угол (4) – внешний угол треугольника, смежный с углом (3). Так как (angle 4 + angle 3 = 180^circ), а по теореме о сумме углов треугольника (angle 1 + angle 2 + angle 3 = 180^circ), то (angle 4 = angle 1 + angle 2), что и требовалось доказать.
[{Large{text{Равнобедренный треугольник}}}]
Определения
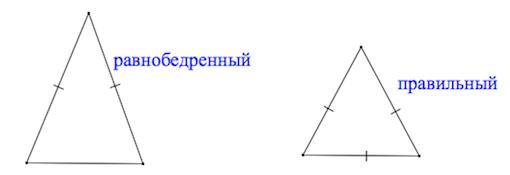
Треугольник называется равнобедренным, если две его стороны равны.
Эти стороны называются боковыми сторонами треугольника, а третья сторона — основанием.
Треугольник называется равносторонним, если все его стороны равны.
Равносторонний треугольник, очевидно, является и равнобедренным.
Теорема
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Доказательство
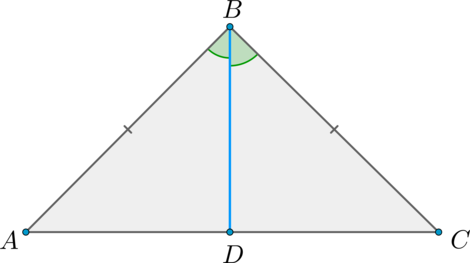
Пусть (ABC) – равнобедренный треугольник, (AB = BC), (BD) – биссектриса (проведённая к основанию).
Рассмотрим треугольники (ABD) и (BCD): (AB = BC), (angle ABD =
angle CBD), (BD) – общая. Таким образом, (triangle ABD =
triangle BCD) по двум сторонам и углу между ними.
Из равенства этих треугольников следует, что (AD = DC), следовательно, (BD) – медиана.
Кроме того, в равных треугольниках против равных сторон лежат равные углы, а (AB = BC), следовательно, [begin{aligned}
&angle ADB = angle CDB, qquad qquad qquad (2)
end{aligned}] но (angle ADB + angle CDB = angle ADC) – развёрнутый, следовательно, (angle ADB + angle CDB = 180^circ), откуда при учёте ((2)): (angle ADB = 90^circ = angle CDB), то есть (BD) – высота.
Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема
В равнобедренном треугольнике углы при основании равны.
Доказательство
Проведем биссектрису (BD) (см. рисунок из предыдущей теоремы). Тогда (triangle ABD=triangle CBD) по первому признаку, следовательно, (angle A=angle C).
Теоремы: признаки равнобедренного треугольника
1. Если в треугольнике два угла равны, то треугольник равнобедренный.
2. Если в треугольнике высота является медианой или биссектрисой, то треугольник равнобедренный.
Теорема о соотношении между сторонами и углами треугольника
В треугольнике против большей стороны лежит больший угол.
В треугольнике против большего угла лежит большая сторона.
Теорема: неравенство треугольника
В треугольнике сумма любых двух сторон больше третьей стороны.
Другая формулировка: в треугольнике разность любых двух сторон меньше третьей стороны.
[{Large{text{Прямоугольный треугольник}}}]
Определения
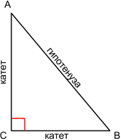
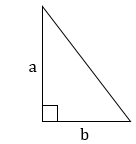
В прямоугольном треугольнике большая сторона (то есть сторона, лежащая напротив прямого угла) называется гипотенузой.
Две другие стороны называются катетами.
Теоремы: свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна (90^circ).
2. В прямоугольном треугольнике катет, лежащий против угла (30^circ), равен половине гипотенузы.
Верно и обратное: если катет равен половине гипотенузы, то он лежит против угла (30^circ).
-
Треугольники
Треугольник— это геометрическая фигура, состоящая из трех точек плоскости, не лежащих на одной прямой и трех отрезков, попарно соединяющих эти точки.
Теорема об углах треугольника: Сумма углов треугольника равна 1800
Внешний угол треугольника: это угол смежный с любым углом треугольника Свойство: Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним
Неравенство треугольника: Любая сторона треугольника меньше суммы двух других сторон и больше их разности
Периметр треугольника: PABC = AB + BC + AC (сумма дин все сторон)
Площадь треугольника: 


Теорема синусов

Теорема косинусов
Признаки равенства треугольников
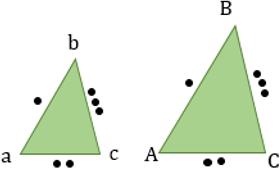
- Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны (по двум сторонам и углу между ними)
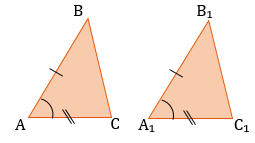
- Если сторона и два, прилежащих к ней угла одного треугольника соответственно равны стороне и и двум, прилежащим к ней углам другого треугольника, то треугольники равны (по стороне и двум углам, прилежащим к ней)
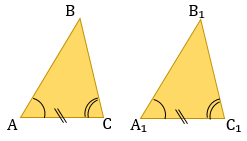
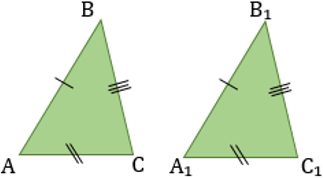
- Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то треугольники равны ( по трем сторонам)
Основные элементы треугольника
- Высота — перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противоположную сторону.
- Медиана — отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Основные свойства медианы:
а) Медиана разбивает треугольник на два треугольника одинаковой площади.
б) Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины.
- Биссектриса — отрезок биссектрисы угла треугольника, соединяющий вершину с точкой, находящейся на противолежащей стороне. Свойства:
а) Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам
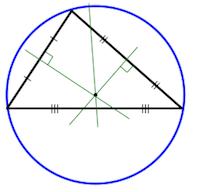
б) Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в этот треугольник.
в) Биссектрисы внутреннего и внешнего углов треугольника перпендикулярны.
г) От любой точки, лежащей на биссектрисе угла, расстояния до сторон угла равны.
- Серединный перпендикуляр — прямая проходящая через середину стороны и перпендикулярна ей.
- Средняя линия — отрезок, соединяющий середины двух сторон. Свойства:
а) равна половине длины стороны треугольника и параллельна ей;
б) средняя линия отсекает треугольник, который подобен данному, а его площадь равна одной четвёртой площади исходного треугольника
Виды треугольников:
1. равнобедренный — треугольник, у которого две стороны равны (стороны, которые равны называются боковыми, третья называется основанием) Свойства: 1) углы при основании равны; 2) биссектриса(медиана,высота), проведенная к основанию является медианой (биссектрисой, высотой);
2. равносторонний — треугольник, у которого все стороны равны. Свойства: 1) все углы равны 600.
3. разносторонний — треугольник, у которого все стороны разные
4. остроугольные — треугольник, у которого все углы острые (меньше 900)
5. тупоугольные — треугольник, у которого один из углов тупой (больше 900)
6. прямоугольные — треугольник, у которого один из углов прямой (равен 900).
Свойства прямоугольного треугольника
1) сумма острых углов равна 900;
2) катет, лежащий против угла в 300, равен половине гипотенузы;
3) если катет равен половине гипотенузы, то он лежит напротив угла в 300)
4) медиана проведенная к гипотенузе равна ее половине
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов (с2=a2+b2)
Соотношения, связывающие пропорциональные отрезки в прямоугольном треугольнике
1. 
2. 
3. 
4
Отношение сторон прямоугольного треугольника (синус, косинус, тангенс)
Синус — отношение противолежащего катета к гипотенузе
Косинус — отношение прилежащего катета к гипотенузе
Тангенс -отношение противолежащего катета к прилежащему
Основное тригонометрическое тождество
Подобные треугольники
Треугольники, углы у которых соответственно равны, а стороны соответственно пропорциональны.
Коэффициентом подобия называют число k, равное отношению соответственных сторон подобных треугольников.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Отношение периметров подобных треугольников равно коэффициенту подобия.
Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.
Признаки подобия треугольников
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами равны, то такие треугольники подобны.( по двум сторонам и углу между ними)
- Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. (по двум углам)
- Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны ( по трем сторонам)
Теорема Менелая
Если на сторонах AB и BC треугольника ABC взяты соответственно точки C1 и A1, а точка B1 взята на продолжении стороны AC за точку C (рис.1), то точки C1, A1 и B1 лежат на одной прямой тогда и только тогда, когда выполнено равенство
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
СВОЙСТВА ТРЕУГОЛЬНИКА:
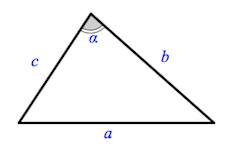
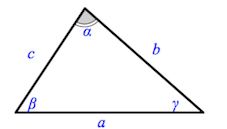
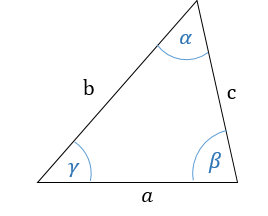
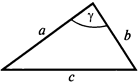
1. Сумма углов в треугольнике равна α + β + γ = 180°.
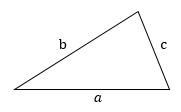
2. Против большей стороны находится больший угол; против меньшего угла находится меньшая сторона. Отсюда следует, что если:
a < b < c, то α < β < γ и наоборот.
3. Сумма длин двух любых сторон треугольника всегда больше длины третьей стороны:
a + b > c.
Если это правило не выполняется — треугольник не существует.
4. Формулы площади треугольника:
|
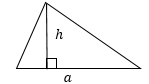
1 (через высоту) |
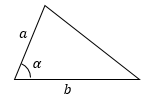
2 (через две стороны и синус угла между ними) |
3 (формула Герона) |
|
|
|
|
|
|
|
|
|
Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне. |
Площадь треугольника равна половине произведения его сторон на синус угла между ними. |
Площадь треугольника равна квадратному корню из произведения его полупериметра на разности полупериметра и каждой из его сторон. |
5. Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
с² = а² + b² – 2ab · cosγ
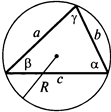
6. Теорема синусов: Отношения сторон треугольника к синусам противоположных им углов равны. Это отношение равно 2R, где R — радиус описанной окружности.
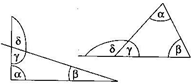
7. Внешний угол треугольника — δ, является смежным с одним из внутренних углов (сумма = 180°). Из этого следует, что внешний угол равен сумме двух внутренних, но не смежных с ним, углов треугольника (α + β = δ).
ВИДЫ ТРЕУГОЛЬНИКОВ:
Треугольники бывают:
- остроугольными (если все его углы острые),
- тупоугольными (если один из его углов тупой),
- прямоугольными (если один из его углов прямой).
Треугольник называется:
- равнобедренным, если две его стороны равны;
- равносторонним, если все три стороны равны;
- разносторонним, если все его стороны разные.
ЭЛЕМЕНТЫ ТРЕУГОЛЬНИКА:
БИССЕКТРИСА
Биссектриса ― луч, который соединяет вершину треугольника с противоположной стороной, при этом разделяя угол на две равные части.
Свойства биссектрисы треугольника:
1. Все три биссектрисы треугольника пересекаются в одной точке. Эта точка — центр вписанной в треугольник окружности.
2. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам.
3. Формулы для биссектрисы треугольника. Если а и b — стороны треугольника, γ — угол между ними, l — биссектриса треугольника, проведённая из вершины этого угла, а а’ и b’ — отрезки, на которые биссектриса делит третью сторону треугольника, то
МЕДИАНА
Медиана ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Свойства медианы треугольника:
1. Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и точкой пересечения делятся в отношении 2 к 1, считая от вершины.
- Медиана разбивает треугольник на два равновеликих (по площади) треугольника.
- Треугольник делится тремя медианами на шесть равновеликих треугольников.
- В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.
- Формула для медианы треугольника. Если стороны треугольника a и b, mc — медиана треугольника, проведённая к стороне c, то
ВЫСОТА
Высота — перпендикуляр, опущенный из вершины треугольника на противоположную сторону (точнее, на прямую, содержащую противоположную сторону).
В зависимости от типа треугольника высота может содержаться:
- внутри треугольника (для остроугольного треугольника),
- совпадать с его стороной (являться катетом прямоугольного треугольника),
- проходить вне треугольника (для тупоугольного треугольника).
Свойства высоты треугольника:
1. Все три высоты треугольника пересекаются в одной точке, которая называется ортоцентром.
2. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.
3. Если в треугольнике две высоты равны, то треугольник — равнобедренный.
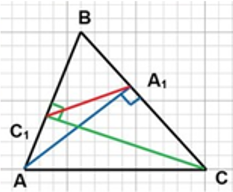
4. Если CC₁ и АА₁ — высоты треугольника АВС, то треугольник ВА₁С₁ подобен треугольнику АВС, причём коэффициент подобия равен cos B.
Сложные теоремы:
5. Если Н — точка пересечения высот треугольника AВС, а О — центр его описанной окружности, то отрезок АН вдвое больше расстояния от точки О до середины стороны ВС. То есть AH = 2OM.
6. Если Н — точка пересечения высот треугольника AВС, М — точка пересечения медиан треугольника AВС, а О — центр его описанной окружности, то точки О, H и М лежат на одной прямой (прямая Эйлера), причём точка М лежит на отрезке ОН и ОМ : МН = 1 : 2.
СРЕДИННЫЙ ПЕРПЕНДИКУЛЯР
Срединный перпендикуляр треугольника — прямая, перпендикулярная стороне треугольника и проходящая через его середину.
Все три срединных перпендикуляра треугольника пересекаются в одной точке, которая является центром описанной около треугольника окружности.
СРЕДНЯЯ ЛИНИЯ
Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника
Свойства средней линии треугольника:
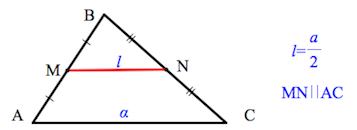
- Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине:
MN||BC,MN = 1/2 BC
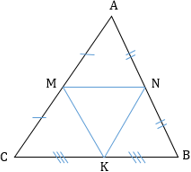
- В любом треугольнике три средних линии, при пересечении которых образуются 4 равных треугольника, подобных исходному с коэффициентом 1/2.
ПОДОБИЕ И РАВЕНСТВО ТРЕУГОЛЬНИКОВ
|
Подобные треугольники |
Равные треугольники |
|
Треугольники подобны, если их углы равны. В подобных фигурах сохраняется отношение между соответствующими сторонами и другими линейными величинами (высоты, медианы, биссектрисы и периметры): Также сохраняется внутреннее отношение длин: |
Два треугольника равны, если у них соответствующие стороны равны и соответствующие углы равны (треугольники равны, если их можно совместить наложением). |
|
Признаки подобия треугольников: 1. По двум пропорциональным сторонам и углу между ними: 2. 3. По двум равным углам (тогда и третьи тоже будут равны) 4. 5. По трем пропорциональным сторонам: |
Признаки равенства треугольников: 1. По двум сторонам и углу между ними: 2. По стороне и двум прилежащим к ней углам. 3. По трем сторонам. |
ОСОБЫЕ ТРЕУГОЛЬНИКИ И ИХ СВОЙСТВА:
«Особенными», то есть обладающими какими — то дополнительными свойствами, считаются:
- равнобедренный,
- равносторонний
- прямоугольный треугольники.
РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК
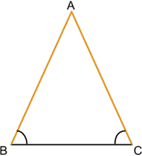
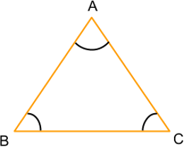
Равнобедренный треугольник ― это треугольник, у которого две стороны равны (АВ = АС).
Равные стороны (АВ и АС) в таком треугольнике называются боковыми, а оставшаяся третья сторона (ВС) ― основанием.
Свойства равнобедренного треугольника:
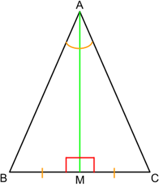
1. Углы при основании равны (∠АВС = ∠АСВ).
2. Медиана, проведённая к основанию, является биссектрисой и высотой. То есть она не только делит противолежащую сторону пополам (ВМ = МС), но и падает на неё под углом 90°, а кроме того делит угол, из которого выходит, пополам (∠ВАМ = ∠МАС).
Посмотрим на пример конкретной задачи. В равнобедренном треугольнике внешний угол равен 80°, необходимо найти все углы треугольника. Сразу возникает вопрос ― внешний угол при каком угле треугольника? Предположим, что это внешний угол при угле В (с нашего первого рисунка). Но в таком случае выходит, что сам ∠В = 100° (по сумме смежных углов). Значит, и ∠С = 100°, так как треугольник равнобедренный. Но тогда сумма только двух углов получается 200°, чего быть никак не может. Значит, речь идёт о внешнем угле при угле А треугольника. Тогда ∠А = 100°, а ∠В = ∠С = 40°.
РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК
Равносторонний треугольник ― треугольник, у которого все три стороны равны
Свойства равностороннего треугольника:
1. Кроме равенства сторон в таком треугольнике равны и все углы (каждый из которых по 60° ― так как 180°/3 = 60°).
2. Медиана, проведённая из любого угла, будет являться биссектрисой и высотой (другими словами, равносторонний треугольник с любой стороны является равнобедренным).
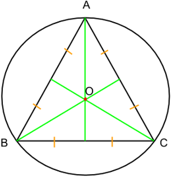
1. Центры вписанной и описанной окружностей совпадают.
2. Формулы 2 и 3 для площади треугольника превращаются в одну формулу:
— Через синус (так как все стороны равны и каждый угол равен 60°):
— Формула Герона (так как все стороны равны):
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Прямоугольный треугольник ― треугольник, у которого один угол равен 90° (собственно, это и есть прямой угол, дающий название всему треугольнику). Сторона, лежащая против такого угла, называется гипотенузой (АВ), а две другие стороны ― катетами (АС и ВС).
Свойства прямоугольного треугольника:
1. В любом прямоугольном треугольнике гипотенуза всегда больше катета (против большего угла лежит большая сторона, и наоборот).
2. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов
АВ2 = АС2 + ВС2
Теорема, обратная теореме Пифагора: Если для сторон произвольного треугольника выполняется отношение АВ2= АС2 + ВС2, то треугольник является прямоугольным.
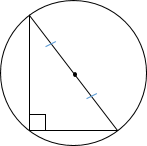
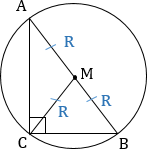
3. Центр описанной вокруг прямоугольного треугольника окружности всегда лежит на середине гипотенузы (доказательство: прямой ∠С становится вписанным, а против вписанного угла в 90° всегда лежит диаметр ― значит, гипотенуза является диаметром).
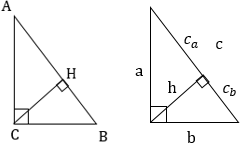
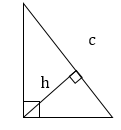
Высота, проведенная к гипотенузе, разбивает треугольник на два подобных прямоугольных треугольника, каждый из которых подобен исходному треугольнику
4. Высота, проведенная к гипотенузе, равна:
- Произведению катетов, деленному на гипотенузу
- Среднему геометрическому из произведений отрезков, на которые гипотенуза делится высотой
5. Медиана, проведенная к гипотенузе равна половине гипотенузы, то есть радиусу описанной около треугольника окружности.
6. Формулы площади прямоугольного треугольника:
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
Площадь прямоугольного треугольника равна половине произведения его катетов. |
Площадь прямоугольного треугольника равна половине произведения гипотенузы на опущенную к ней высоту. |
Площадь прямоугольного треугольника равна половине произведения его катета, гипотенузы и синуса угла между ними. |
ЗОЛОТОЙ И СЕРЕБРЯНЫЙ ТРЕУГОЛЬНИКИ:
|
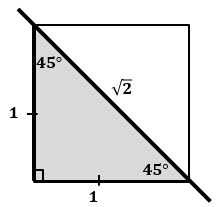
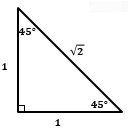
Серебряный треугольник — треугольник с углами 45°, 45° и 90° (разрубленный по диагонали квадрат) Отношение сторон в серебряном треугольнике: |
— треугольник с углами 30°, 60° и 90°. Отношение сторон в золотом треугольнике: |
Сумма углов треугольника. Внутренние и внешние углы
Внутренние углы треугольника
Сумма внутренних углов любого треугольника равна ( displaystyle 180{}^circ ).
Единственное, что тебя может смущать в нашей формулировке – это слово «внутренних».
Зачем оно тут? А вот именно затем, чтобы подчеркнуть, что речь идёт об углах, которые внутри треугольника.
А что, разве бывают ещё какие-то углы снаружи? Вот представь себе, бывают.
У треугольника ещё бывают внешние углы.
И самое главное следствие из того факта, что сумма внутренних углов треугольника равна ( displaystyle 180{}^circ ), касается как раз внешнего треугольника.
Внешние углы треугольника
Так что давай выясним, что же такое этот внешний угол треугольника.
Смотри на картинку: берём треугольник и одну сторону (скажем ( displaystyle AC)) продолжаем.
Видишь, получился новый угол, ( displaystyle angle BCE)?
Этот угол образован одной стороной (( displaystyle BC)) треугольника и продолжением другой стороны (( displaystyle AC)).
Вот он и называется внешним углом треугольника ( displaystyle ABC) при вершине ( displaystyle C).
Конечно, мы бы могли оставить сторону ( displaystyle AC), а продолжить сторону ( displaystyle BC). Вот так:
Тогда ( displaystyle angle ACK) тоже будет внешним углом при вершине ( displaystyle C), да и к тому же он будет равен углу ( displaystyle BCE).
Смотри:
Углы ( displaystyle BCE) и ( displaystyle ACK) – равны как вертикальные, и оба они имеют право называться внешним углом при вершине ( displaystyle C).
А вот про угол ( displaystyle ECK) такого сказать ни в коем случае нельзя!
Он образован пересечением двух продолжений сторон!
Угол ( displaystyle ECK) вообще равен внутреннему ( displaystyle angle C) треугольника ( displaystyle ABC).
Так что не каждый угол снаружи треугольника имеет право называется внешним углом, а только тот, который образован одной стороной и продолжением другой стороны.
Так что же мы должны знать про внешний угол?
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
Смотри, на нашем рисунке это означает, что ( angle 4=angle 1+angle 2).
Как же это связано с суммой углов треугольника?
Давай разберёмся. Сумма внутренних углов равна ( displaystyle 180{}^circ Rightarrow )
( angle 1+angle 2+angle 3=180{}^circ ),
но ( angle 4+angle 3=180{}^circ ) – потому, что ( angle 3) и ( angle 4) – смежные.
Ну вот и получается: ( angle 4=angle 1+angle 2).
Видишь как просто?! Но очень важно. Так что запоминай:
Сумма внутренних углов треугольника равна ( 180{}^circ ), а внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
Неравенство треугольника
Следующий факт касается не углов, а сторон треугольника.
Сумма любых двух сторон треугольника больше его третьей стороны.
Это означает, что:
- ( a+b>c)
- ( a+c>b)
- ( b+c>a)
Ты уже догадался, почему этот факт называется неравенством треугольника?
Ну вот, а где же это неравенство треугольника может оказаться полезным?
А представь, что у тебя есть три друга: Коля, Петя и Сергей.
И вот, Коля говорит: «От моего дома до Петиного ( 100) м по прямой». А Петя: «От моего дома до дома Сергея ( 200) метров по прямой». А Сергей: «Вам хорошо, а от моего дома до Колиного аж ( 500) м по прямой».
Ну, тут уже ты должен сказать: «Стоп, стоп! Кто – то из вас говорит неправду!»
Так не может быть!
Почему?
Да потому что если от Коли до Пети ( 100) м, а от Пети до Сергея ( 200) м, то от Коли до Сергея точно должно быть меньше ( 300) (( =100+200)) метров – иначе и нарушается то самое неравенство треугольника.
Ну и здравый смысл точно, естественно, нарушается: ведь всякому с детства неизвестно, что путь до прямой (( КС)) должен быть короче, чем путь с заходом в точку ( П). (( К-П-С)).
Так что неравенство треугольника просто отражает этот общеизвестный факт. Ну вот, ты теперь знаешь, как отвечать на такой, скажем, вопрос:
Бывает ли треугольник со сторонами ( 1,3,7)?
Ты должен проверить, правда ли, что любые два числа из этих трёх в сумме больше третьего. Проверяем: ( 1+3<7), значит, треугольника со сторонами ( 1,3) и ( 7) не бывает! А вот со сторонами ( 2,4,5) – бывает, потому что
- ( 2+5>4)
- ( 2+4>5)
- ( 4+5>2)
Равенство треугольников
Ну вот, а если не один, а два или больше треугольников. Как проверишь, равны ли они? Вообще-то по определению:
Два треугольника равны, если они совпадают при наложении.
Но…это ужасно неудобное определение! Как, скажите на милость, накладывать два треугольника хотя бы даже в тетради?!
Но на наше счастье есть признаки равенства треугольников, которые позволяют действовать умом, не подвергая риску тетрадки.
Да и к тому же, отбросив легкомысленные шуточки, открою тебе секрет: для математика слово «наложить треугольники» означает вовсе не вырезать их и наложить, а сказать много-много-много слов, которые будeт доказывать, что два треугольника совпадут при наложении.
Так что ни в коем случае нельзя в работе писать «я проверил – треугольники совпадают при наложении» – тебе это не засчитают, и будут правы, потому что никто не гарантирует, что ты при наложении не ошибся, скажем, на четверть миллиметра.
Итак, какие-то математики сказали кучу слов, мы за ними эти слова повторять не будем (разве что в последнем уровне теории), а будем активно пользоваться тремя признаками равенства треугольников.
Бонусы: Вебинары из нашего курса по подготовке к ЕГЭ по математике
В этом разделе вы найдете несколько вебинаров из нашего курса по подготовке к ЕГЭ по математике.
От самого простого (но важного!) на площадь фигур на клетчатой бумаге, до сложного 16 задания ЕГЭ на доказательство подобия треугольников (по которому максимальный балл получают менее 1% учеников!
Выбирайте вебинар по силам и учитесь решать задачи!
ЕГЭ 3. Площадь фигур на клетчатой бумаге
Клетчатая бумага очень удобная для геометрии. В основном тем, что на ней очень легко рисовать прямые углы.
А если прямой угол достроить к какому-то отрезку, то получится прямоугольный треугольник. А для прямоугольного треугольника можно записать теорему Пифагора – и вот уже мы определили длину нашего отрезка.
И хотя в 2021 году задача на геометрию на клечатой бумаге не будет входить в ЕГЭ, она очень полезна для того, чтобы начать изучать геометрию, для понимания планиметрии.
ЕГЭ 6. Прямоугольный треугольник: свойства, теорема Пифагора, тригонометрия
Подавляющее большинство задач в планиметрии решается через прямоугольные треугольники.
Как это так? Ведь далеко не в каждой задаче речь идёт о треугольниках вообще, не то что прямоугольных. Но на уроках этой темы мы убедимся, что это действительно так.
Дело в том, что редкая сложная задача решается какой-то одной теоремой – почти всегда она разбивается на несколько задач поменьше. И в итоге мы имеем дело с треугольниками, зачастую – прямоугольными.
В этом видео мы научимся решать задачи о прямоугольных треугольниках из ЕГЭ, выучим все необходимые теоремы и затронем основы тригонометрии.
ЕГЭ 6. Равнобедренный треугольник, произвольный треугольник
В этом видео мы вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ.
Очень часто все “проблемы” с решением задач на равнобедренный треугольник решаются построением высоты.
Также мы научимся решать и “обычные” треугольники. Убедимся в достоверности утверждении из прошлого урока о прямоугольных треугольниках https://youtu.be/ZKGTVfaiGe8) – очень часто решение задач сводится к нескольким прямоугольным треугольникам.
ЕГЭ 6, 14, 16. Теорема косинусов и синусов
Универсальный инструмент при решении треугольников – это теоремы косинусов и синусов. Они подходят для любых треугольников, а не только для прямых (как теорема Пифагора).
А как мы уже знаем, почти любая задача в планиметрии сводится именно к треугольникам.
На этом уроке мы выучим сами теоремы и научимся применять их при решении задач первой части.
ЕГЭ 16. Подобие треугольников. Задачи на доказательство
Это одна из самых сложных задачи в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников!
Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства.
Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы.
В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение.
Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем.
Вы научитесь также применять подобие треугольников для расчетных задач (не только для доказательств).
Треугольник
Треугольник произвольный
Треугольник – это многоугольник с тремя сторонами (тремя углами).
Виды треугольников :+ показать
Остроугольный треугольник – треугольник, у которого все углы острые (то есть меньше 90˚).
Тупоугольный треугольник – треугольник, у которого один из углов тупой (больше 90˚).
Прямоугольный треугольник – треугольник, у которого один из углов прямой (равен 90˚).
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми , третья сторона называется основанием .
Равносторонний (правильный) треугольник – треугольник, у которого все три стороны равны.
Свойства
1. Против большей стороны лежит больший угол, и наоборот.
2. Против равных сторон лежат равные углы, и наоборот.
3. Сумма углов треугольника равна 180 º .
4. Внешний угол треугольника равен сумме внутренних углов,
не смежных с ним:
(Внешний угол образуется в результате продолжения одной из сторон треугольника).
5. Любая сторона треугольника меньше суммы двух других сторон.
Признаки равенства треугольников
1. Треугольники равны, если у них соответственно равны две стороны и угол между ними.
2 . Треугольники равны, если у них соответственно равны два угла и прилегающая к ним сторона.
3. Треугольники равны, если у них соответственно равны три стороны.
Биссектриса, высота, медиана
Здесь подробно о биссектрисе, высоте, медиане треугольника.
Средняя линия треугольника
Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника.
Средняя линия треугольника параллельна третьей стороне и равна ее половине.
Вписанная окружность
Центр вписанной окружности – точка пересечения биссектрис треугольника.
Описанная окружность
Центр описанной окружности – точка пересечения серединных перпендикуляров.
Соотношение сторон в произвольном треугольнике
Теорема косинусов:
Теорема синусов:
Площадь треугольника
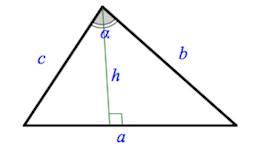
Через две стороны и угол между ними
Через радиус описанной окружности
Через радиус вписанной окружности
, где
– полупериметр
, где
– полупериметр
Смотрите также площадь треугольника здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Есть пара ошибок в формулах. В частности в формуле вычисления площади через 2 стороны и угол между ними, в теореме Синусов, в разделе “свойства”.
А вообще отличные статьи, очень выручают, всё понятно и доступно, премного благодарен 😉
Анатолий, спасибо!
В разделе “свойства” ошибок не нашла…
В теореме синусов, – да… не пропечаталась буква гамма. Подправила.
В формуле площади треугольника, вы правы – картинка не соответствовала формуле. Исправила.
К сожалению, ошибки сразу не всегда замечаются.
Благодарю еще раз!
В разделе свойства:
Да, не хватало значка «» у А. Спасибо! 😉
Здраствуйте! Мне нужна ваша помощь!
Задача: ВЕРШИНЫ ТРЕУГОЛЬНИКА ДЕЛЯТ ОПИСАННУЮ ОКОЛО НЕГО ОКРУЖНОСТЬ НА ТРИ ДУГИ, ДЛИНЫ КОТОРЫХ ОТНОСЯТСЯ КАК 6:7:33. НАЙДИТЕ РАДИУС ОКРУЖНОСТИ, ЕСЛИ МЕНЬШАЯ ИЗ СТОРОН РАВНА 11.
Подозреваю, у вас опечатка в условии…
Если длины дуг (а значит и их градусные меры) находятся в отношении , то выходим на уравнение
Откуда
Значит угол треугольника, что напротив меньшей стороны, есть
Применяем теорему синусов: , откуда
спасибо я так и думал а то не могу решить и всё
СПАСИБО!
Здравствуйте. Пожалуйста, объясните, как решить задачу:
Вписанная в теругольник ABC окружность касается сторон AB, BC и AC в точках K,L и М соответственно.Найдите KL, если AM=2, МС=3 и угол С=π/3
Очевидно,
Примите за
.
Примените к треугольнику теорему косинусов:
Найдете , далее можно найти угол
и из треугольника
найти
Спасибо большое за ваш сайт. Очень радует, тот факт, что когда люди не понимают какую-нибудь задачу, вы помогаете решить. Спасибо. Побольше бы таких сайтов, всё понятно и доступно
Основные факты о треугольниках
Определения
Угол – это геометрическая фигура, состоящая из точки и двух лучей, выходящих из этой точки. Градусная мера угла может принимать значения от (0^circ) до (180^circ) включительно.
Угол (alpha) называется острым, если (0^circ , прямым – если (alpha=90^circ) , тупым – если (90^circ , и развернутым – если (alpha=180^circ) .
Биссектриса угла – это луч, выходящий из вершины угла и делящий угол пополам.
Смежные углы – это два угла, у которых общая вершина и одна общая сторона, а две другие стороны образуют прямую.
Вертикальные углы – это два угла, образованные пересечением двух прямых и не являющиеся смежными.
Теорема
Смежные углы (alpha) и (beta) в сумме дают (180^circ) .
Вертикальные углы равны: (alpha=gamma) .
Определения
Треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой (называемых вершинами треугольника), и отрезков, соединяющих эти точки (называемых сторонами треугольника). Треугольник со своей внутренностью будем сокращенно называть также треугольником.
Угол (внутренний) треугольника – угол, образованный вершиной треугольника и двумя его сторонами.
Теоремы: признаки равенства треугольников
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2. Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.
3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Определение
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Две прямые называются перпендикулярными, если угол между ними равен (90^circ) .
Перпендикуляр из точки к прямой – это отрезок, соединяющий данную точку с точкой на прямой, проведенный под углом (90^circ) .
Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
Замечание
Если в треугольнике один угол тупой, то высоты, опущенные из вершин острых углов, упадут не на сторону, а на продолжение стороны (рис. 1).
Теорема
В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).
Определение
Две различные прямые на плоскости называются параллельными, если они не пересекаются.
Замечание
Заметим, что на плоскости существует три вида взаимного расположения прямых: совпадают, пересекаются и параллельны.
Аксиома параллельных прямых
Через точку, не лежащую на данной прямой, проходит единственная прямая, параллельная данной.
Следствия из аксиомы
1. Если прямая пересекает одну из параллельных прямых, то она пересекает и другую прямую.
2. Две прямые, параллельные третьей прямой, параллельны.
Теоремы: признаки параллельности прямых
1. Если при пересечении двух прямых (a) и (b) секущей (c) накрест лежащие углы равны: (angle 1=angle 2) , то такие прямые параллельны.
2. Если при пересечении двух прямых (a) и (b) секущей (c) сумма односторонних углов (angle 1) и (angle 3) равна (180^circ) , то такие прямые параллельны.
3. Если при пересечении двух прямых (a) и (b) секущей (c) соответственные углы равны: (angle 1=angle 4) , то такие прямые параллельны.
Теоремы: свойства параллельных прямых
1. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
2. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна (180^circ) .
3. Если две параллельные прямые пересечены секущей, то соответственные углы равны.
Определения
Треугольник называется остроугольным, если все его углы острые.
Треугольник называется тупоугольным, если один его угол тупой (остальные — острые).
Треугольник называется прямоугольным, если один его угол прямой (остальные — острые).
Теорема
Сумма внутренних углов треугольника равна (180^circ) .
Доказательство
Рассмотрим произвольный треугольник (ABC) и покажем, что (angle A + angle B + angle C = 180^circ) .
Проведём через вершину (B) прямую (a) , параллельную стороне (AC) .
Углы (1) и (4) являются накрест лежащими углами при пересечении параллельных прямых (a) и (AC) секущей (AB) , а углы (3) и (5) – накрест лежащими углами при пересечении тех же параллельных прямых секущей (BC) . Поэтому [begin &angle 4 = angle 1, angle 5 = angle 3. qquad qquad qquad (1) end]
Очевидно, сумма углов (4, 2) и (5) равна развёрнутому углу с вершиной (B) , то есть (angle 4 + angle 2 + angle 5 = 180^circ) . Отсюда, учитывая равенства ((1)) , получаем: (angle 1 + angle 2 + angle 3 = 180^circ) .
Определение
Внешний угол треугольника – это угол, смежный с каким-нибудь внутренним углом треугольника.
Теорема
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним: (angle BCD=angle BAC+angle ABC) .
Доказательство
Угол (4) – внешний угол треугольника, смежный с углом (3) . Так как (angle 4 + angle 3 = 180^circ) , а по теореме о сумме углов треугольника (angle 1 + angle 2 + angle 3 = 180^circ) , то (angle 4 = angle 1 + angle 2) , что и требовалось доказать.
Определения
Треугольник называется равнобедренным, если две его стороны равны.
Эти стороны называются боковыми сторонами треугольника, а третья сторона — основанием.
Треугольник называется равносторонним, если все его стороны равны.
Равносторонний треугольник, очевидно, является и равнобедренным.
Теорема
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Доказательство
Пусть (ABC) – равнобедренный треугольник, (AB = BC) , (BD) – биссектриса (проведённая к основанию).
Рассмотрим треугольники (ABD) и (BCD) : (AB = BC) , (angle ABD = angle CBD) , (BD) – общая. Таким образом, (triangle ABD = triangle BCD) по двум сторонам и углу между ними.
Из равенства этих треугольников следует, что (AD = DC) , следовательно, (BD) – медиана.
Кроме того, в равных треугольниках против равных сторон лежат равные углы, а (AB = BC) , следовательно, [begin &angle ADB = angle CDB, qquad qquad qquad (2) end] но (angle ADB + angle CDB = angle ADC) – развёрнутый, следовательно, (angle ADB + angle CDB = 180^circ) , откуда при учёте ((2)) : (angle ADB = 90^circ = angle CDB) , то есть (BD) – высота.
Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема
В равнобедренном треугольнике углы при основании равны.
Доказательство
Проведем биссектрису (BD) (см. рисунок из предыдущей теоремы). Тогда (triangle ABD=triangle CBD) по первому признаку, следовательно, (angle A=angle C) .
Теоремы: признаки равнобедренного треугольника
1. Если в треугольнике два угла равны, то треугольник равнобедренный.
2. Если в треугольнике высота является медианой или биссектрисой, то треугольник равнобедренный.
Теорема о соотношении между сторонами и углами треугольника
В треугольнике против большей стороны лежит больший угол.
В треугольнике против большего угла лежит большая сторона.
Теорема: неравенство треугольника
В треугольнике сумма любых двух сторон больше третьей стороны.
Другая формулировка: в треугольнике разность любых двух сторон меньше третьей стороны.
Определения
В прямоугольном треугольнике большая сторона (то есть сторона, лежащая напротив прямого угла) называется гипотенузой.
Две другие стороны называются катетами.
Теоремы: свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна (90^circ) .
2. В прямоугольном треугольнике катет, лежащий против угла (30^circ) , равен половине гипотенузы.
Верно и обратное: если катет равен половине гипотенузы, то он лежит против угла (30^circ) .
Подготовка выпускников к сдаче ЕГЭ, как правило, начинается с повторения базовой теории по планиметрии, в том числе и по теме «Треугольники». Знакомство учащихся с этим разделом геометрии начинается еще в средней школе. Неудивительно, что потребность в повторении основных правил и теории по теме «Треугольник» возникает у многих выпускников. При этом решать планиметрические задачи обязательно должны уметь все учащиеся. Подобные задания включены как в базовый, так и в профильный уровень аттестационного испытания. Разобравшись с теорией и практическими упражнениями, в том числе и на вычисление вертикальных углов треугольника, старшеклассники смогут решать задачи с любым количеством действий и рассчитывать на получение конкурентных баллов по итогам сдачи ЕГЭ.
Готовьтесь к экзамену вместе с образовательным порталом «Школково»
Занимаясь перед сдачей ЕГЭ, многие учащиеся сталкиваются с проблемой поиска базовой теории по геометрии о треугольниках. Школьных учебников в нужный момент может просто не оказаться под рукой. А найти необходимые формулы иногда оказывается достаточно сложно даже в Интернете.
Вместе с образовательным порталом «Школково» выпускники смогут качественно подготовиться к сдаче аттестационного испытания. Вся базовая теория о равнобедренных и прямоугольных треугольниках систематизирована и изложена нашими специалистами с учетом богатого опыта в максимально доступной форме. Изучив представленную информацию, школьники смогут вспомнить материал, который вызывает определенные затруднения.
Чтобы хорошо подготовиться к экзамену, учащимся, проживающим в Москве и других городах России, необходимо не только повторить теорию о прямоугольных и равнобедренных треугольниках, но и попрактиковаться в выполнении соответствующих упражнений. Задачи по данной теме вы можете найти в разделе «Каталог». Для каждого задания наши специалисты прописали подробный ход решения и указали правильный ответ. Последовательно выполняя простые и более сложные упражнения по данной теме, учащиеся смогут научиться применять на практике теоремы равенства треугольников и другую теорию, которую необходимо усвоить при подготовке к ЕГЭ. Перечень заданий в соответствующем разделе постоянно дополняется и обновляется.
Попрактиковаться в решении задач, в которых применяется теория смежных углов и другие теоремы, школьники могут в режиме онлайн.
По желанию учащегося любое упражнение можно сохранить в «Избранное». Еще раз повторив базовую теорию о прямоугольных и равнобедренных треугольниках, выпускник может в дальнейшем вернуться к заданию, которое вызвало затруднения, и обсудить алгоритм его решения с преподавателем.
Все, что нужно знать о треугольнике

- Сделать чертеж. Чертеж должен максимально соответствовать условию задачи, так его основная задача помочь найти ход решения
- Нанести все данные из условия задачи на чертеж
- Выписать все геометрические понятия, которые встречаются в задаче
- Вспомнить все теоремы, которые относятся к этим понятию
- Нанести на чертеж все соотношения между элементами геометрической фигуры, которые следуют из этих теорем
Например, если в задаче встречается слова биссектриса угла треугольника, нужно вспомнить определение и свойства биссектрисы и обозначить на чертеже равные или пропорциональные отрезки и углы.
В этой статье вы найдете основные свойства треугольника, которые необходимо знать для успешного решения задач.
ТРЕУГОЛЬНИК.
Площадь треугольника.
1. 
здесь 

2. 
здесь 

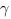
3. Формула Герона:
— здесь 

4. 
здесь 

Пусть 
Тогда формулу Герона можно записать в таком виде:
5.
6. 
здесь 

Если на стороне треугольника взята точка, которая делит эту сторону в отношении m:n, то отрезок, соединяющий эту точку с вершиной противолежащего угла делит треугольник на два треугольника, площади которых относятся как m:n:
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Медиана треугольника
— это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины.
Точка пересечения медиан правильного треугольника делит медиану на два отрезка, меньший из которых равен радиусу вписанной окружности, а больший — радиусу описанной окружности.

Длина медианы произвольного треугольника вычисляется по формуле:

здесь 


Биссектриса треугольника
— это отрезок биссектрисы любого угла треугольника, соединяющий вершину этого угла с противоположной стороной.
Биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам:
Биссектрисы треугольника пересекаются в одной точке, которая является центром вписанной окружности.
Все точки биссектрисы угла равноудалены от сторон угла.
Высота треугольника
— это отрезок перпендикуляра, опущенный из вершины треугольника на противоположную сторону, или ее продолжение. В тупоугольном треугольнике высота, проведенная из вершины острого угла лежит вне треугольника.
Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
Чтобы найти высоту треугольника, проведенную к стороне 
Центр окружности, описанной около треугольника, лежит в точке пересечения серединных перпендикуляров, проведенных к сторонам треугольника.
Радиус описанной окружности треугольника можно найти по таким формулам:
— здесь 


где 

Неравенство треугольника
Каждая сторона треугольника меньше суммы и больше разности двух других.
Сумма длин любых двух сторон всегда больше длины третьей стороны:

Напротив большей стороны лежит больший угол; напротив большего угла лежит большая сторона:
Если 


Теорема синусов:
стороны треугольника пропорциональны синусам противолежащих углов:
Теорема косинусов:
квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними:
Прямоугольный треугольник
— это треугольник, один из углов которого равен 90°.
Сумма острых углов прямоугольного треугольника равна 90°.
Гипотенуза — это сторона, которая лежит против угла 90°. Гипотенуза является наибольшей стороной.
Теорема Пифагора:
квадрат гипотенузы равен сумме квадратов катетов:
Радиус окружности, вписанной в прямоугольный треугольник, равен

здесь 

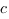
Центр окружности, описанной около прямоугольного треугольника лежит в середине гипотенузы:
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.
Определение синуса, косинуса , тангенса и котангенса прямоугольного треугольника смотрите здесь.
Соотношение элементов в прямоугольном треугольнике:
Квадрат высоты прямоугольного треугольника, проведенной из вершины прямого угла, равен произведению проекций катетов на гипотенузу:
Квадрат катета равен произведению гипотенузы на проекцию катета на гипотенузу:

Катет, лежащий против угла 
Равнобедренный треугольник.
Биссектриса равнобедренного треугольника, проведенная к основанию является медианой и высотой.
В равнобедренном треугольнике углы при основании равны.






Внимание! Высота, биссектриса и медиана, проведенные к боковой стороне не совпадают.
Правильный треугольник
(или равносторонний треугольник ) — это треугольник, все стороны и углы которого равны между собой.
Площадь правильного треугольника равна

где 
Центр окружности, вписанной в правильный треугольник, совпадает с центром окружности, описанной около правильного треугольника и лежит в точке пересечения медиан.
Точка пересечения медиан правильного треугольника делит медиану на два отрезка, меньший из которых равен радиусу вписанной окружности, а больший — радиусу описанной окружности.
Если один из углов равнобедренного треугольника равен 60°, то этот треугольник правильный.
Средняя линия треугольника
— это отрезок, соединяющий середины двух сторон.
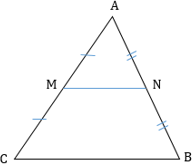
На рисунке DE — средняя линия треугольника ABC.
Средняя линия треугольника параллельна третьей стороне и равна ее половине: DE||AC, AC=2DE
Внешний угол треугольника
— это угол, смежный какому либо углу треугольника.
Внешний угол треугольника равен сумме двух углов, не смежных с ним.
Тригонометрические функции внешнего угла:
Признаки равенства треугольников:
1 . Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2 . Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
3 Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Важно: поскольку в прямоугольном треугольнике два угла заведомо равны, то для равенства двух прямоугольных треугольников требуется равенство всего двух элементов: двух сторон, или стороны и острого угла.
Признаки подобия треугольников:
1 . Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, заключенные между этими сторонами равны, то эти треугольники подобны.
2 . Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то эти треугольники подобны.
3 . Если два угла одного треугольника равны двум углам другого треугольника, то эти треугольники подобны.
Важно: в подобных треугольниках сходственные стороны лежат против равных углов.
Теорема Менелая
Пусть прямая пересекает треугольник 


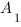

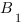

источники:
http://shkolkovo.net/theory/65
http://ege-ok.ru/2012/05/04/vse-chto-nuzhno-znat-o-treugolnike
Треугольник, подготовка к ЕГЭ по математике
- 22.12.2017
Таблицы с теорией на тему: «Треугольник» для подготовки к ЕГЭ по математике. В кратком содержании изложена вся необходимая теория для этой темы.
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Сохранить ссылку:
Комментарии (0)
Добавить комментарий
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Имя (обязательное)
E-Mail
Подписаться на уведомления о новых комментариях
Отправить








































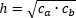
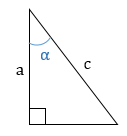




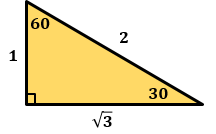 Золотой треугольник
Золотой треугольник