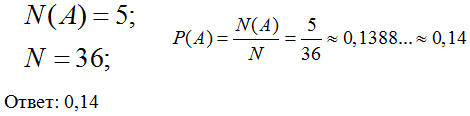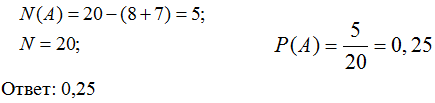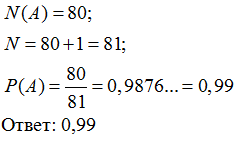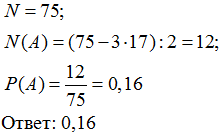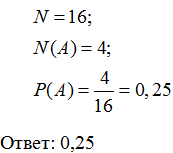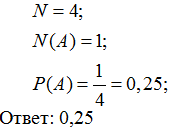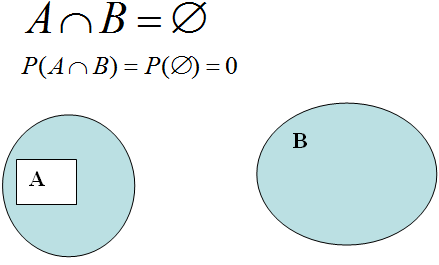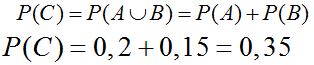Главная » ЕГЭ » Математика. Подготовка к ЕГЭ-2014. Теория вероятностей — Иванов С.О., Коннова Е.Г. и др.
Пособие предназначено для формирования устойчивых навыков в решении задач по теории вероятностей. Представленный материал охватывает все темы заданий по теории вероятностей из открытого банка ЕГЭ, имеющиеся на момент выпуска книги. Книга разделена на 3 модуля в соответствии со степенью трудности предлагаемых задач. Каждый модуль содержит диагностическую работу, теоретический материал, задачи с разобранными решениями, варианты для самостоятельной работы. Пособие является частью учебно-методического комплекса «Математика. Подготовка к ЕГЭ», включающего такие книги, как «Математика. ЕГЭ-2014. Учебно-тренировочные тесты», «Математика. Повышенный уровень ЕГЭ-2014 (Cl, C3). Тематические тесты. Уравнения, неравенства, системы» и др.
- Рубрика: ЕГЭ / ЕГЭ по математике / Учебные пособия ЕГЭ
- Автор: Иванов С.О., Коннова Е.Г. и др.
- Год: 2013
- Для учеников: 11 класс
- Язык учебника: Русский
- Формат: PDF
- Страниц: 64
скачать учебник Математика. Подготовка к ЕГЭ-2014. Теория вероятностей — Иванов С.О., Коннова Е.Г. и др.
Решение задач В6.
(Теория вероятностей.)
Презентация. Слайд 1.
В случайном эксперименте бросают две игральные кости. Найдите вероятность
того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Прототип задания В6 (№282853).
Решение:
Благоприятные события (2;6) (6;2) (3;5) (5;3) (4;4)
Слайд 2.
В случайном эксперименте симметричную монету бросают дважды. Найдите
вероятность того, что орёл выпадет ровно один раз.
Прототип задания В6 (№282854).
Слайд 3.
В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США,
остальные – из Китая. Порядок, в котором выступают гимнастки, определяется
жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется
из Китая.
Прототип задания В6 (№282855).
Слайд 4.
В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают.
Найдите вероятность того, что один случайно выбранный для контроля насос не
подтекает.
Прототип задания В6 (№282856).
Слайд 5.
Фабрика выпускает сумки. В среднем на 80 качественных сумок приходится одна
сумка со скрытыми дефектами. Найдите вероятность того, что купленная сумка
окажется качественной. Результат округлите до сотых.
Прототип задания В6 (№283631)
Решение: A = {Купленная сумка – качественная}
Слайд 6.
Научная конференция проводится в 5 дней. Всего запланировано 75 докладов –
первые три дня по 17 докладов, остальные распределены поровну между четвертым и
пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что
доклад профессора М. окажется запланированным на последний день конференции?
Прототип задания В6 (№285922)
Решение: A = {доклад М.запланирован на последний день}
Слайд 7.
В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на
четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с
номерами групп:
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда
России окажется во второй группе?
Прототип задания В6 (№320170)
Решение: A = {Команда России окажется во второй группе}
Слайд 8.
Вася, Петя, Коля и Лёша бросили жребий – кому начинать игру. Найдите
вероятность того, что начинать игру должен будет Петя.
Прототип задания В6 (№320169)
Решение: A = {Игру начинает Петя}
Слайд 9.
Если события А и В не имеют общих благоприятных элементарных событий, то они
не могут наступить одновременно в ходе одного и того же опыта. Такие события
называют несовместными.
Важным свойством несовместных событий является то, что для них справедливо
правило сложения вероятностей.
Слайд 10.
На экзамене по геометрии школьнику достаётся один вопрос из списка
экзаменационных вопросов. Вероятность того, что это вопрос на тему “Вписанная
окружность”, равна 0,2. Вероятность того, что это вопрос на тему
“Параллелограмм”, равна 0,15. Вопросов, которые одновременно относятся к этим
двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется
вопрос по одной из этих двух тем.
Прототип задания В6 (№320171)
Решение: A = {вопрос о вписанной окружности};
В = {вопрос о параллелограмме};
В условии задачи сказано, что нет вопросов, которые одновременно относятся и
к А и к В. События А и В являются несовместными.
Событие С ={вопрос по одной из этих двух тем} является объединением этих
событий и находится по формуле
Ответ: 0,35
Слайд 11.
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика
выпускает 45 % этих стекол, вторая – 55% . Первая фабрика выпускает 3%
бракованных стекол, а вторая – 1% . Найдите вероятность того, что случайно
купленное в магазине стекло окажется бракованным.
Прототип задания В6 (№319353)
Решение: A = {Стекло выпущено на первой фабрике}
В = {Стекло выпущено на второй фабрике}
С = {Стекло бракованное}
Воспользуемся правилом умножения и сложения вероятностей.
Вероятность того, что куплено стекло первой фабрики и оно браковано:
Вероятность того, что куплено стекло второй фабрики и оно браковано:
По формуле полной вероятности, вероятность того , что случайно купленное в
магазине стекло окажется бракованным:
Ответ: 0,019
Слайд 12.
Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с
вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью
0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют
цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Прототип задания В6 (№319355)
Решение: Н = {А.играет белыми и выигрывает};
К = {А.играет чёрными и выигрывает}
С = {А. выиграет оба раза}
Возможность выиграть в первой и во второй партии не зависят друг от друга.
События Н и К независимые события. Вероятность события С равна произведению
их вероятностей.
Приложение.
Литература
- Ю.Н.Тюрин, А.А.Макаров, И.Р.Высоцкий, И.В.Ященко “Теория
вероятностей и статистика”, из-во МЦНМО ОАО “Московские учебники”, М.2008. - “Математика №1.2012” методическая газета для учителей математики.
- Открытый банк задач ЕГЭ по математике. ЕГЭ 2014.
- Интернет ресурсы, находящиеся в открытом доступе (Картинки, задачи,
рисунки).
У нас вы найдете много учебных материалов: решебники, ГДЗ, тестовые задания, видео уроки, генераторы задач, решения упражнений гиа и егэ.
Расскажи друзьям
Ищи САЙТ в Яндексе и Google по слову:
vpr-klass или впр-класс
Сохрани сайт в закладки — нажми Ctrl+D
Интересно
ГИА (ОГЭ) по математике
Много разных решений
Тесты ГИА онлайн.
Видео — ГИА 2013: геометрия
Видео — ГИА 2012
Видео — Демо-вариант 2012.
Решение Демо-варианта 2013 года (2014 года).
Задача №1, Вычислить.
Задача №2, Числа и прямая.
Задача №3, Сравнение чисел.
Задача №4, Уравнения.
Задача №5, Графики и формулы.
Задача №6, Прогрессии.
Задача №7, Упростить выражение.
Задача №8, Неравенства, системы неравенств.
Задача №9, Задания по геометрии.
Генератор вариантов ГИА 2014
ЕГЭ по математике
Много разных решений.
Онлайн тесты.
Видео уроки ЕГЭ по математике.
Генератор вариантов ЕГЭ 2014
Книги, справочники
Решение демо варианта ЕГЭ по математике 2014
Задания B1, задача.
Задания B2, диаграммы.
Задания B5, уравнения.
Задания B8, производная.
Задания B10, вероятность.
ОГЭ по информатике
Видео уроки
Copyright © 2017 vpr-klass.com | Если какой-либо из материалов нарушает ваши авторские права, просим немедленно связаться с Администрацией!!! Наш e-mail: [email protected] | Правообладателям |
sitemap.xml
- Математика ЕГЭ
- Математика ОГЭ
- Биология ОГЭ
- Биология ЕГЭ
- Физика ОГЭ
- Физика ЕГЭ
- Химия ЕГЭ
- Химия ОГЭ
- Русский язык ОГЭ
- Русский язык ЕГЭ
- Английский язык ОГЭ
- Английский язык ЕГЭ
- Литература ЕГЭ
- Литература ОГЭ
- История ЕГЭ
- История ОГЭ
- Информатика ЕГЭ
- Информатика ОГЭ
- География ЕГЭ
- География ОГЭ
Вы здесь: ✔️ Главная сайта ГДЗ 

👀 Просмотров: 3501
Инфо
Предмет теста: Математика.
Класс заданий: 11 класс.
Автор подготовки: Иванов С.О., Коннова Е.Г. и др.
Категория: Теория вероятностей.
Объем книги (скачать): 0.798 мб.
Год теста: 2014
Опубликован тест: 12.03.2014
Кем разработано: рекомендовано «РРФ»
Страниц заданий: 64.
Издатель теста: «Легион»
Читать онлайн: ЕГЭ 2014. Иванов Теория вероятностей или скачать незамедлительно:
Самые популярные статьи:
- ЕГЭ 2015. Ященко Математика. 36 вариантов.
- Лысенко, Калабухова ЕГЭ-2019 профильный уровень 40 тренировочных вариантов математика
- Ященко ЕГЭ-2019 36 типовых экзаменационных вариантов профильный уровень математика
- Подготовка к ЕГЭ-2016. Математика. 40 тренировочных вариантов по демоверсии на 2016 год. Профильный уровень. Лысенко Ф.Ф., Кулабухов С.Ю.
- Ященко ЕГЭ-2019 50 вариантов заданий профильный уровень математика
Новые материалы для вашего класса:
- ЕГЭ 2015. Математика. 30 вариантов. Ященко И.В.
- ЕГЭ 2015. Математика. Ященко 2 части
- ЕГЭ 2015. Математика. Ященко И.В. Типовые тестовые задания.
- ЕГЭ 2015. Семенова и Ященко. Математика.
< НазадВперёд >
Вам это пригодится
Барашкова английский язык на каникулах н…
Узорова английский язык в схемах и табл…
Державина английский язык для начальной …
Барашкова английский язык на каникулах н…
Карачаева 100 тестов по лексике и грамма…
Мордкович учебник алгебра углубленный ур…
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
К сожалению, на данный момент у нас невозможно бесплатно скачать полный вариант книги.
Но вы можете попробовать скачать полный вариант, купив у наших партнеров электронную книгу здесь, если она у них есть наличии в данный момент.
Также можно купить бумажную версию книги здесь.
Математика, Подготовка к ЕГЭ 2014, Теория вероятностей, Иванов С.О., Лысенко Ф.Ф., Кулабухов С.Ю., 2013.
Пособие предназначено для формирования устойчивых навыков в решении задач по теории вероятностей. Представленный материал охватывает все темы заданий по теории вероятностей из открытого банка ЕГЭ, имеющиеся на момент выпуска книги. Книга разделена на 3 модуля в соответствии со степенью трудности предлагаемых задач. Каждый модуль содержит диагностическую работу, теоретический материал, задачи с разобранными решениями, варианты для самостоятельной работы.
Примеры.
На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной и больше 5?
Решение.
Исходом здесь является нажатие определённой клавиши, поэтому всего имеется 10 равновозможных исходов. Указанному событию благоприятствуют исходы, означающие нажатие клавиши 6 или 8. Таких исходов два. Искомая вероятность равна 2/10 = 0,2.
Ответ: 0,2.
Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию «сумма очков равна 8»?
Решение.
Исходом будем считать пару чисел: очки при первом и втором броске. Тогда указанному событию благоприятствуют следующие исходы: 2-6, 3-5, 4-4, 5-3, 6-2. Их количество равно 5.
Ответ: 5.
Оглавление
От авторов 4
Модуль 1. Простые задачи 6
Диагностическая работа 6
Теоретическая часть 7
Задачи о выборе объектов из набора 9
Задачи о подбрасывании монеты 16
Задачи о бросках кубика 18
Варианты для самостоятельного решения 20
Модуль 2. Задачи средней трудности 26
Диагностическая работа 26
Теоретическая часть 27
Задачи о пересечении независимых событий 30
Задачи об объединении несовместных событий 34
Задачи об объединении пересечений событий 36
Задачи о частоте 41
Варианты для самостоятельного решения 41
Модуль 3. Трудные задачи 48
Диагностическая работа 48
Теоретическая часть 49
Задачи о зависимых событиях 50
Задачи на проценты 52
Разные задачи 53
Варианты для самостоятельного решения 58
Ответы 63.
Купить книгу Математика, Подготовка к ЕГЭ 2014, Теория вероятностей, Иванов С.О., Лысенко Ф.Ф., Кулабухов С.Ю., 2013
.
По кнопкам выше и ниже «Купить бумажную книгу» и по ссылке «Купить» можно купить эту книгу с доставкой по всей России и похожие книги по самой лучшей цене в бумажном виде на сайтах официальных интернет магазинов Лабиринт, Озон, Буквоед, Читай-город, Литрес, My-shop, Book24, Books.ru.
По кнопке «Купить и скачать электронную книгу» можно купить эту книгу в электронном виде в официальном интернет магазине «ЛитРес», и потом ее скачать на сайте Литреса.
По кнопке «Найти похожие материалы на других сайтах» можно найти похожие материалы на других сайтах.
On the buttons above and below you can buy the book in official online stores Labirint, Ozon and others. Also you can search related and similar materials on other sites.
Дата публикации: 10.04.2014 05:11 UTC
Теги:
ЕГЭ по математике :: математика :: Иванов :: Лысенко :: Кулабухов
Следующие учебники и книги:
- Математика, Подготовка к ЕГЭ 2014, Решебник, Часть 2, Войта Е.А., Лысенко Ф.Ф., Кулабухов С.Ю., 2013
- Математика, Подготовка к ЕГЭ 2014, Решебник, Часть 1, Войта Е.А., Лысенко Ф.Ф., Кулабухов С.Ю., 2013
- Математика, Подготовка к ЕГЭ 2014, Учебно-тренировочные тесты по новой спецификации, B1-B15, C1-C6, Войта Е.А., Лысенко Ф.Ф., Кулабухов С.Ю.
- Математика, Подготовка к ЕГЭ, Секреты оценки заданий части С, Решения и комментарии, Васильева Е.Н., 2013
Предыдущие статьи:
- ЕГЭ 2014, Математика, Базовый уровень, Пособие для «чайников», Часть 3, Геометрия, Коннова Е.Г., Лысенко Ф.Ф., Кулабухов С.Ю., 2013
- ЕГЭ 2014, Математика, Базовый уровень, Пособие для «чайников», Часть 2, Алгебра и начала анализа, Коннова Е.Г., Лысенко Ф.Ф., Кулабухов С.Ю., 2013
- ЕГЭ 2014, Математика, Базовый уровень, Пособие для «чайников», Часть 1, Арифметика и алгебра, Коннова Е.Г., Лысенко Ф.Ф., Кулабухов С.Ю., 2013
- ЕГЭ, Математика, Тематическая рабочая тетрадь, Ященко, Шестаков, Трепалин, 2012
<< Назад
Пособие предназначено для формирования устойчивых навыков в решении задач по теории вероятностей. Представленный материал охватывает все темы заданий по теории вероятностей из открытого банка ЕГЭ, имеющиеся на момент выпуска книги. Книга разделена на 3 модуля в соответствии со степенью трудности предлагаемых задач. Каждый модуль содержит диагностическую работу, теоретический материал, задачи с разобранными решениями, варианты для самостоятельной работы. Пособие является частью учебно-методического комплекса «Математика. Подготовка к ЕГЭ», включающего такие книги, как «Математика. ЕГЭ-2014. Учебно-тренировочные тесты», «Математика. Повышенный уровень ЕГЭ-2014 (Cl, C3). Тематические тесты. Уравнения, неравенства, системы» и др.
math/ege-exam14/14.pdf
Год издания: 2014
Файл книги удален из-за претензий издательства
Почему файл удалён? Об этом вы можете узнать задав вопрос в Форме обратной связи.
|
|
Для просмотра файлов формата PDF вам нужна программа Adobe Reader. Её вы всегда можете скачать на официальном сайте Adobe. |
Если хотите пожаловаться на книгу, то оставьте сообщение в форме обратной связи
<< Назад