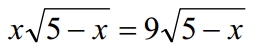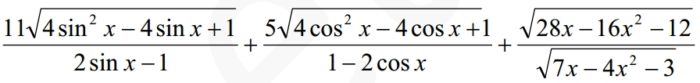Теория вероятности егэ ларин - Помощь в подготовке к экзаменам и поступлению

Задание 4

Трое охотников одновременно стреляют по кабану, каждый по одному выстрелу.
Вероятности попадания охотников в цель равны: 0,7 – для первого, 0,75 – для второго и 0,8 – для третьего. Оказалось, что в кабана попали ровно две пули. Найдите вероятность того, что это пули второго и третьего охотников. Ответ округлите до сотых.

Ответ: 0,42

Скрыть

Тут задача на условную вероятность.

Если бы в задаче не было оговорки про попадание 2 пуль. А просто посчитать из всех возможных вариантов. То тогда, раз события независимы (попадание каждого), то итоговая вероятность считается умножением вероятностей событий. То есть событие: (первый не попал; второй попал; третий попал) = $$P(не1)cdot P(2)cdot P(3) = 0,3cdot0,75cdot0,8 = 0,18$$

Но в задаче вводят дополнительное условие: «известно, что попали ровно 2 пули».

А это меняет условие: Надо посчитать вероятность, при условии, что попали 2 пули.

По определению: Вероятность События A при условии события B равна отношению вероятности (пересечения A и B) ко всем возможным событиям B.

По простому: Надо посчитать все возможные вероятности, когда попали ровно 2 раза — это знаменатель. И из них выбрать вероятность, когда попали только 2-й и 3-й

Считаем: попали ровно 2 раза

$$P(B) = P(1)cdot P(2)cdot P(не3) + P(1)cdot P(3)cdot P(не2) + P(2)cdot P(3)cdot P(не1)$$

$$P(B) = 0,7cdot0,75cdot0,2 + 0,7cdot0,8cdot0,25 + 0,75cdot0,8cdot0,3$$

$$= 0,105 + 0,14 + 0,18 = 0,425$$

А вероятность $$P(Acap B)$$ — это пересечение, что 2 и3 попали и попало только двое (значит первый не попал) — это уже посчитано $$= 0,3cdot0,75cdot0,8 = 0,18$$

Таким образом требуемая условная вероятность

$$P(frac{A}{B}) = frac{P(Acap B)}{P(B)}$$

$$P(frac{A}{B}) = frac{0,18}{0,425}approx 0,42$$

Источник


3655	Площадь трапеции ABCD равна 30. Точка Р – середина боковой стороны АВ. Точка R на боковой стороне CD выбрана так, что 2CD=3RD. Прямые AR и PD пересекаются в точке Q , AD=2BC. a) Докажите, что точка Q – середина отрезка AR б) Найдите площадь треугольника APQ Решение	Площадь трапеции ABCD равна 30. Точка Р – середина боковой стороны АВ. Точка R на боковой стороне CD выбрана так, что 2CD=3RD ! Тренировочный вариант 221 от Ларина Задание 16 # Решение пункта Б

3471	а) Решите уравнение cos(3x)/(2sin(x)+sqrt(2))=sin(x)/(2sin(x)+sqrt(2)) б) Найдите все корни уравнения, принадлежащие отрезку [0; pi]. Решение График	а) Решите уравнение cos3x /(2sinx + sqrt2 = sinx /2sinx +sqrt2 ! Тренировочный вариант 399 от Ларина Задание 12

3470	В основании пирамиды лежит параллелограмм со сторонами 8 и 10, а его большая диагональ равна 2sqrt73. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 4. а) Докажите, что две боковые грани являются прямоугольными треугольниками. б) Найдите площади двух других боковых граней Решение	В основании пирамиды лежит параллелограмм со сторонами 8 и 10, а его большая диагональ равна 2sqrt73 ! Тренировочный вариант 399 от Ларина Задание 13

3469	Решите неравенство 64^x/(36^x-27^x)+(4(16^x-12^x))/(16^x-2*12^x+9^x). <= 16^(x+0.5)/(12^x-9^x). Решение График	Решите неравенство 64^x / 36^x -27^x +4(16^x-12^x) /16^x -2*12^x+9^x <= 16^ x+0,5 / 12^x-9^x ! Тренировочный вариант 399 от Ларина Задание 14

3468	На сторонах АВ, ВС и АD квадрата ABCD взяты соответственно точки М, К и N, такие, что АМ : МВ = 3 : 1, ВК : КС = 2 : 1 и АN : ND = 1 : 2. а) Докажите, что площадь четырехугольника МКСN составляет 11/24 площади квадрата ABCD. б) Найдите синус угла между диагоналями четырехугольника МКCN Решение	На сторонах АВ, ВС и АD квадрата ABCD взяты соответственно точки М, К и N, такие, что АМ : МВ = 3 : 1, ВК : КС = 2 : 1 и АN : ND = 1 : 2 ! Тренировочный вариант 399 от Ларина Задание 16

3467	В трапеции АВСD боковая сторона CD перпендикулярна основаниям AD и ВС. В эту трапецию вписали окружность с центром О. Прямая АО пересекает продолжение отрезка ВС в точке Е а) Докажите, что AD=CE+CD б) Найдите площадь трапеции ABCD, если АЕ=10, /_BAD=60^@ Решение	В трапеции АВСD боковая сторона CD перпендикулярна основаниям AD и ВС ! Тренировочный вариант 398 от Ларина Задание 16

3466	Найдите значение выражения ((root(4)(3)-root(4)(27))^2+7)((root(4)(3)+root(4)(27))^2-7) Решение	Найдите значение выражения ((root(4)(3) -root(4)(27))2 +7 ((root(4)(3)+root(4)(27))2 -7) ! Тренировочный вариант 398 от Ларина Задание 6

3465	Имеются два сплава, состоящие из цинка, меди и олова. Известно, что первый сплав содержит 40% олова, а второй ‐ 25% меди. Процентное содержание цинка в первом и втором сплавах одинаково. Соединив 150 кг первого сплава и 250 кг второго, получили новый сплав, в котором оказалось 30% цинка. Сколько килограммов олова содержится в получившемся сплаве? Решение	Имеются два сплава, состоящие из цинка, меди и олова ! Тренировочный вариант 398 от Ларина Задание 9

3464	а) Решите уравнение sqrt(2sin(x)+sqrt(2))*log_{4}(2cos(x))=0 б) Найдите все корни уравнения, принадлежащие отрезку [-(5pi)/2; -pi]. Решение График	а) Решите уравнение sqrt(2sinx +sqrt2) log4 2cosx = 0 ! Тренировочный вариант 398 от Ларина Задание 12

3463	SMNK – правильный тетраэдр. На ребре SK отмечена точка Р такая, что КР:PS=1:3, точка L – середина ребра MN. а) Доказать, что плоскости SLK и MPN перпендикулярны б) Найдите длину отрезка PL, если длина ребра MN равна 4 Решение	SMNK – правильный тетраэдр ! Тренировочный вариант 398 от Ларина Задание 13

Показана страница 1 из 89

Источник

28 февраля прошел Главный Мастер-класс 2016 года !

Два лучших репетитора страны Анна Малкова и Александр Ларин рассказали все секреты ЕГЭ-2016 по математике.

Во время трансляции ребятам было рассказано:

— Как оформлять решения части 2 на ЕГЭ по математике,
— За что снижают баллы в оформлении части 2,
— Что все-таки будет на ЕГЭ-2016?
— На что обращать внимание при подготовке?
— Стоит ли покупать ответы на ЕГЭ-2016?

Прямая трансляция, эмоции и много интересного увидели более 3700 человек, зарегистрированных на этот мастер-класс.
Александр Ларин прокомментировал решение каждого задания из предложенного к разбору варианта. Было показано несколько вариантов решения одних и тех же задач. Секреты раскрыты!
Ждите видео на ютубе, заходите на наш сайт и не прогадаете. До ЕГЭ осталось совсем чуть чуть, а у нас самая полезная и, главное, новая информация.

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Александр Ларин и Анна Малкова» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из Рубрики: Новости.

Публикация обновлена:
08.03.2023

Мы используем файлы cookie, чтобы персонализировать контент, адаптировать и оценивать результативность рекламы, а также обеспечить безопасность. Перейдя на сайт, вы соглашаетесь с использованием файлов cookie.

Источник

03
Окт 2019

Категория: 17 (С6) Параметры*ПараметрТ/P A. Ларина

Елена Репина
2019-10-03
2019-10-10

Смотрите также №14 Т/Р №281

18. При каких значениях параметра уравнение $6cdot (frac{x}{x^2+1})^2-frac{(6a+1)x}{x^2+1}-12a^2+8a-1=0$ имеет ровно корня?

Решение:

ВНИМАНИЕ! На 7-й минуте при решении системы есть небольшой “косяк”! Однако это не повлияло на ответ чудеснейшим образом)))

вместо следует читать !

Ответ: $(0;frac{1}{6})cup(frac{1}{6};frac{5}{18})cup (frac{5}{18};frac{5}{12}).$

Автор: egeMax |

Нет комментариев

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Печать страницы

Добавить комментарий

Материалы для подготовки к ЕГЭ
Рубрики
- 01 Геометрия (13)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (78)
- 13 (С2) Стереометр. задачи (94)
- 14 (С3) Неравенства (89)
- 15 (С4) Практич. задачи (71)
- 16 (С5) Планиметр. задачи (86)
- 17 (С6) Параметры* (79)
- 18 (С7) Числа, их свойства (38)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (60)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина
ЕгэТренер – О. Себедаш
Математика?Легко!
Егэ? Ок! – И. Фельдман
Свежие записи
- Тест «Гиперболы»
- Тест. Графики функций. Комбинированные задачи
- 10. Графики функций. Комбинированные задачи
- Тест. Тригонометрические функции
- 10. Тригонометрическая функция
- Тест. Кусочно-линейная функция
- 10. Кусочно-линейная функция
Архивы Архивы

Источник

Решение и ответы заданий № 1–12 варианта №334 Александра Ларина. Разбор ЕГЭ 2021 по математике (профильный уровень).

Задание 1.
За год стипендия студента увеличилась на 32%. В первом полугодии стипендия увеличилась на 10%. Определите, на сколько процентов увеличилась стипендия во втором полугодии.

Задание 2.
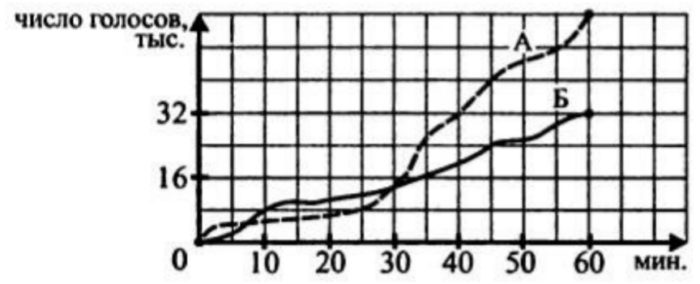
На рисунке изображены графики, показывающие, как во время телевизионных дебатов между кандидатами А и Б, длившихся ровно 1 час, телезрители голосовали за каждого из них: по горизонтальной оси откладывается время с начала голосования, по вертикальной – число голосов (в тыс.), поданных за это время. Какой процент голосов телезрителей был у кандидата А через 45 минут после начала теледебатов?

Задание 3.
Найдите площадь пятиугольника АВСDЕ с вершинами в точках А (‐1;0), В (2;5), С (5;3), D(10;6), Е (13;0).

Задание 4.
В шкатулке лежат 6 шаров, 4 из которых – красные. Наугад взяты 3 шара. Какова вероятность того, что все выбранные шары красные?

Задание 5.
Решите уравнение, указав в ответе корень уравнения или сумму корней, если их несколько:

Задание 6.
В треугольнике ABC длины сторон и его площадь связаны соотношением 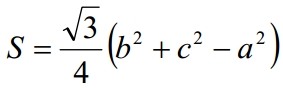Найдите градусную меру угла А.

Задание 7.
Для четной функции f(x) и нечетной функции g(x) для всех действительных значений аргумента выполнено равенство f(x) + g(x) = x² + 3x – 2. Найдите значения выражения f′(2) – 4g′(3)

Задание 8.
Высота правильной треугольной пирамиды в три раза меньше высоты основания пирамиды. Найдите угол между плоскостью боковой грани и плоскостью основания пирамиды. Ответ дайте в градусах.

Задание 9.
Найдите значение выражения:

Задание 10.
Вратарь выбросил мяч в поле, направив его под углом 45º к поверхности поля. Пока мяч не упал, высота, на которой он находится, описывается формулой h(t) = –5t² + 12t + 1,25 (h – высота в метрах, t – время в секундах, прошедшее с момента удара). Пренебрегая сопротивлением воздуха, считаем, что горизонтальная составляющая скорости мяча не меняется в полете. Определите, на каком расстоянии от вратаря в метрах мяч приземлится на поле.

Задание 11.
Гекльберри Финн может покрасить весь забор за 3 часа, а Том Сойер покрасил бы за это время треть забора. Друзья начали работу вместе, но через некоторое время Том Сойер убежал к Бекки. В результате Гекльберри Финн закончил работу один, и весь забор был покрашен за 2 часа 54 минуты. Найдите количество минут, затраченных на работу Томом Сойером.

Задание 12.
Найдите наибольшее значение функции: у = 4(12sin²x + 15cosx – 4cos³x)

Источник варианта: alexlarin.net

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 0 / 5. Количество оценок: 0

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник