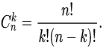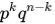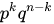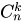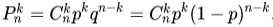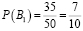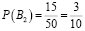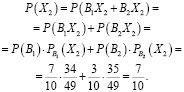Теория вероятности вероятность сдать экзамен на баллов

Задание 3. Теория вероятностей на ЕГЭ по математике.

Мы начнем с простых задач и основных понятий теории вероятностей.
Случайным называется событие, которое нельзя точно предсказать заранее. Оно может либо произойти, либо нет.
Вы выиграли в лотерею — случайное событие. Пригласили друзей отпраздновать выигрыш, а они по дороге к вам застряли в лифте — тоже случайное событие. Правда, мастер оказался поблизости и освободил всю компанию через десять минут — и это тоже можно считать счастливой случайностью…

Наша жизнь полна случайных событий. О каждом из них можно сказать, что оно произойдет с некоторой вероятностью. Скорее всего, вы интуитивно знакомы с этим понятием. Теперь мы дадим математическое определение вероятности.

Начнем с самого простого примера. Вы бросаете монетку. Орел или решка?

Такое действие, которое может привести к одному из нескольких результатов, в теории вероятностей называют испытанием.

Орел и решка — два возможных исхода испытания.

Орел выпадет в одном случае из двух возможных. Говорят, что вероятность того, что монетка упадет орлом, равна 1/2 .

Бросим игральную кость. У кубика шесть граней, поэтому возможных исходов тоже шесть.

Например, вы загадали, что выпадет три очка. Это один исход из шести возможных. В теории вероятностей он будет называться благоприятным исходом.

Вероятность выпадения тройки равна 1/6 (один благоприятный исход из шести возможных).

Вероятность четверки — тоже 1/6 .

А вот вероятность появления семерки равна нулю. Ведь грани с семью точками на кубике нет.

Вероятность события равна отношению числа благоприятных исходов к общему числу исходов.

Очевидно, что вероятность не может быть больше единицы.

Вот другой пример. В пакете яблок, из них — красные, остальные — зеленые. Ни формой, ни размером яблоки не отличаются. Вы запускаете в пакет руку и наугад вынимаете яблоко. Вероятность вытащить красное яблоко равна 8/25 , а зеленое — 17/25 .

Вероятность достать красное или зеленое яблоко равна .

БЕСПЛАТНЫЙ МИНИ-КУРС ПО ТЕОРВЕРУ

Определение вероятности. Простые задачи из вариантов ЕГЭ.

Разберем задачи по теории вероятностей, входящие в сборники для подготовки к ЕГЭ.

В фирме такси в данный момент свободно машин: красных, желтых и зеленых. По вызову выехала одна из машин, случайно оказавшихся ближе всего к заказчице. Найдите вероятность того, что к ней приедет желтое такси.

Всего имеется машин, то есть к заказчице приедет одна из пятнадцати. Желтых — девять, и значит, вероятность приезда именно желтой машины равна 9/15 , то есть 0,6 .

В сборнике билетов по биологии всего билетов, в двух из них встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет. Найдите вероятность того, что в этом билете не будет вопроса о грибах.

Очевидно, вероятность вытащить билет без вопроса о грибах равна 23/25 , то есть 0,92 .

Родительский комитет закупил пазлов для подарков детям на окончание учебного года, из них с картинами известных художников и с изображениями животных. Подарки распределяются случайным образом. Найдите вероятность того, что Вовочке достанется пазл с животным.

Задача решается аналогично.

Ответ: 0,6 .

В чемпионате по гимнастике участвуют спортсменок: — из России, — из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая последней, окажется из Китая.

Давайте представим, что все спортсменки одновременно подошли к шляпе и вытянули из нее бумажки с номерами. Кому-то из них достанется двадцатый номер. Вероятность того, что его вытянет китайская спортсменка, равен 5/20 (поскольку из Китая — спортсменок). Ответ: 0,25 .

Ученика попросили назвать число от до . Какова вероятность того, что он назовет число кратное пяти?

Каждое пятое число из данного множества делится на . Значит, вероятность равна 1/5 .

Брошена игральная кость. Найдите вероятность того, что выпадет нечетное число очков.

1, 3, 5 — нечетные числа; 2,4,6 — четные. Вероятность нечетного числа очков равна 1/2 .

Ответ: 0,5 .

Монета брошена три раза. Какова вероятность двух «орлов» и одной «решки»?

Заметим, что задачу можно сформулировать по-другому: бросили три монеты одновременно. На решение это не повлияет.

Как вы думаете, сколько здесь возможных исходов?

Бросаем монету. У этого действия два возможных исхода: орел и решка.

Две монеты — уже четыре исхода:

орел	орел
орел	решка
решка	орел
решка	решка

Три монеты? Правильно, исходов, так как .

Вот они:

орел	орел	орел
орел	орел	решка
орел	решка	орел
решка	орел	орел
орел	решка	решка
решка	орел	решка
решка	решка	орел
решка	решка	решка

Два орла и одна решка выпадают в трех случаях из восьми.

Ответ: 3/8 .

В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет очков. Результат округлите до сотых.

Бросаем первую кость — шесть исходов. И для каждого из них возможны еще шесть — когда мы бросаем вторую кость.

Получаем, что у данного действия — бросания двух игральных костей — всего возможных исходов, так как 6^2=36 .

А теперь — благоприятные исходы:

Вероятность выпадения восьми очков равна .

Стрелок попадает в цель с вероятностью . Найдите вероятность того, что он попадёт в цель четыре выстрела подряд.

Если вероятность попадания равна 0,9 — следовательно, вероятность промаха 0,1 . Рассуждаем так же, как и в предыдущей задаче. Вероятность двух попадания подряд равна . А вероятность четырех попаданий подряд равна .

Лень разбираться самому?
Присоединяйся к мини-курсу по теории вероятностей

ПОДРОБНЕЕ

Вероятность: логика перебора.

10. В кармане у Пети было монеты по рублей и монеты по рублей. Петя не глядя переложил какие-то монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.

Мы знаем, что вероятность события равна отношению числа благоприятных исходов к общему числу исходов. Но как посчитать все эти исходы?

Можно, конечно, обозначить пятирублевые монеты цифрами , а десятирублевые цифрами — а затем посчитать, сколькими способами можно выбрать три элемента из набора .

Однако есть более простое решение:

Кодируем монеты числами: , (это пятирублёвые), (это десятирублёвые). Условие задачи можно теперь сформулировать так:

Есть шесть фишек с номерами от до . Сколькими способами можно разложить их по двум карманам поровну, так чтобы фишки с номерами и не оказались вместе?

Давайте запишем, что у нас в первом кармане.

Для этого составим все возможные комбинации из набора . Набор из трёх фишек будет трёхзначным числом. Очевидно, что в наших условиях 1 2 3 и 2 3 1 — это один и тот же набор фишек. Чтобы ничего не пропустить и не повториться, располагаем соответствующие трехзначные числа по возрастанию:

…

А дальше? Мы же говорили, что располагаем числа по возрастанию. Значит, следующее — 134 , а затем:

Все! Мы перебрали все возможные комбинации, начинающиеся на . Продолжаем:

Всего возможных исходов.

У нас есть условие — фишки с номерами и не должны оказаться вместе. Это значит, например, что комбинация 356 нам не подходит — она означает, что фишки и обе оказались не в первом, а во втором кармане. Благоприятные для нас исходы — такие, где есть либо только , либо только . Вот они:

134, 135, 136, 145, 146, 156, 234, 235, 236, 245, 246, 256 – всего благоприятных исходов.

Тогда искомая вероятность равна 12/20 .

Ответ: 0,6 .

Сумма событий, произведение событий и их комбинации

Вероятность того, что новый электрический чайник прослужит больше года, равна 0,93. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

Проработав год, чайник может либо сломаться на второй год, либо благополучно служить и после 2 лет работы.
Пусть – вероятность того, что чайник прослужил больше года.

p_1 – вероятность того, что он сломается на второй год, p_2 – вероятность того, что он прослужит больше двух лет.

Очевидно,

Тогда

Ответ: 0,06.

События, взаимоисключающие друг друга в рамках данной задачи, называются несовместными. Появление одного из несовместных событий исключает появление других.

Сумма двух событий – термин, означающий, что произошло или первое событие, или второе, или оба сразу.

Вероятность суммы несовместных событий равна сумме их вероятностей.

В нашей задаче события «чайник сломался на второй год работы» и «чайник работает больше двух лет» — несовместные. Чайник или сломался, или остается в рабочем состоянии.

На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук выйдет через выход А.

Пронумеруем развилки, на которых паук может случайным образом свернуть в ту или другую сторону.

Он может либо выйти в выход D, и вероятность этого события равна $frac{1}{2}.$ Либо уйти дальше в лабиринт. На второй развилке он может либо свернуть в тупик, либо выйти в выход В (с вероятностью $frac{1}{2}cdot frac{1}{2}=frac{1}{4}).$ На каждой развилке вероятность свернуть в ту или другую сторону равна $frac{1}{2},$ а поскольку развилок пять, вероятность выбраться через выход А равна $frac{1}{32},$ то есть 0,03125.

События А и В называют независимыми, если вероятность появления события А не меняет вероятности появления события В.

В нашей задаче так и есть: неразумный паук сворачивает налево или направо случайным образом, независимо от того, что он делал до этого.

Для нескольких независимых событий вероятность того, что все они произойдут, равна произведению вероятностей.

(А) Два грузовика, работая совместно, вывозят снег с улицы Нижняя Подгорная, причем первый грузовик должен сделать три рейса с грузом снега, а второй — два. Вероятность застрять с грузом снега при подъеме в горку равна 0,2 для первого грузовика и 0,25 — для второго. С какой вероятностью грузовики вывезут снег с улицы Нижняя Подгорная, ни разу не застряв на горке?

Вероятность для первого грузовика благополучно одолеть горку Для второго Поскольку первый грузовик должен сделать 3 рейса, а второй – два, грузовики ни разу не застрянут на горке с вероятностью

Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

Нарисуем все возможные исходы ситуации. Покупатель пришел в магазин, который принадлежит агрофирме, и купил яйцо. Надо найти вероятность того, что это яйцо из первого хозяйства.

Яйца могут быть только или из первого домашнего хозяйства, или из второго, причем эти два события несовместны. Других яиц в этот магазин не поступает.

Пусть вероятность того, что купленное яйцо из первого хозяйства, равна . Тогда вероятность того, что яйцо из второго хозяйства (противоположного события), равна 1-x .

Яйца могут быть высшей категории и не высшей.
В первом хозяйстве 40% яиц имеют высшую категорию, а 60% — не высшую. Это значит, что случайно выбранное яйцо из первого хозяйства с вероятностью 40% будет высшей категории.

Во втором хозяйстве 20% яиц высшей категории, а 80% — не высшей.

Пусть случайно выбранное в магазине яйцо — из первого хозяйства и высшей категории. Вероятность этого события равна произведению вероятностей: 0,4 x.

Вероятность того, что яйцо из второго хозяйства и высшей категории, равна

Если мы сложим эти две вероятности, мы получим вероятность того, что яйцо имеет высшую категорию. По условию, высшую категорию имеют 35% яиц, значит, эта вероятность равна 0,35.

Мы получили уравнение:

Решаем это уравнение и находим, что – вероятность того, что яйцо, купленное у этой агрофирмы, оказалось из первого хозяйства.

15. Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.

С чем пришел пациент в клинику? – С подозрением на гепатит. Возможно, он действительно болен гепатитом, а возможно, у его плохого самочувствия другая причина. Может быть, он просто съел что-нибудь. Вероятность того, что он болен гепатитом, равна 0,05 (то есть 5%). Вероятность того, что он здоров, равна 0,95 (то есть 95%).

Пациенту делают анализ. Покажем на схеме все возможные исходы:

Если он болен гепатитом, анализ дает положительный результат с вероятностью 0,9. То есть анализ покажет: «есть гепатит».
Заметим, что анализ не во всех случаях выявляет гепатит у того, кто действительно им болен. С вероятностью 0,1 анализ не распознает гепатит у больного.

Более того. Анализ может ошибочно дать положительный результат у того, кто не болеет гепатитом. Вероятность такого ложного положительного результата 0,01. Тогда с вероятностью 0,99 анализ даст отрицательный результат, если человек здоров.

Найдем вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.

Благоприятные для этой ситуации исходы: человек болен, и анализ положительный (вероятность одновременного наступления этих двух событий равна ), или человек здоров, и анализ ложный положительный (вероятность одновременного наступления этих двух событий равна ). Так как события «человек болен» и «человек не болен» несовместны, то вероятность того, что результат анализа будет положительным, равна

Ответ: 0,0545.

16. Чтобы поступить в институт на специальность «Лингвистика», абитуриент З. должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание.

Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5.
Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.

Заметим, что в задаче не спрашивается, будет ли абитуриент по фамилии З. учиться и лингвистике, и коммерции сразу и получать два диплома. Здесь надо найти вероятность того, что З. сможет поступить хотя бы на одну из двух данных специальностей – то есть наберет необходимое количество баллов.
Для того чтобы поступить хотя бы на одну из двух специальностей, З. должен набрать не менее 70 баллов по математике. И по русскому. И еще – обществознание или иностранный.
Вероятность набрать 70 баллов по математике для него равна 0,6.
Вероятность набрать баллы по математике и русскому равна

Разберемся с иностранным и обществознанием. Нам подходят варианты, когда абитуриент набрал баллы по обществознанию, по иностранному или по обоим. Не подходит вариант, когда ни по языку, ни по «обществу» он не набрал баллов. Значит, вероятность сдать обществознание или иностранный не ниже чем на 70 баллов равна

В результате вероятность сдать математику, русский и обществознание или иностранный равна Это ответ.

Чтобы полностью освоить тему, смотрите видеокурс по теории вероятностей. Это бесплатно.

Еще задачи ЕГЭ по теме «Теория вероятностей».

Смотрите также: парадокс Монти Холла.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 3. Теория вероятностей на ЕГЭ по математике.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Библиографическое описание:

Петров, Р. С. Вероятность сдачи ЕГЭ методом угадывания правильного ответа / Р. С. Петров, Б. З. Назримадов, Н. Н. Романова. — Текст : непосредственный // Юный ученый. — 2020. — № 4 (34). — С. 67-70. — URL: https://moluch.ru/young/archive/34/1985/ (дата обращения: 12.03.2023).

Единый государственный экзамен (ЕГЭ) — это один из видов государственной итоговой аттестации по образовательным программам среднего общего образования (ГИА), которую пишут все без исключения выпускники одиннадцатых классов российских средних учебных заведений. Первая часть экзамена — это тест, т. е. выбор правильного(-ых) варианта(-ов) ответа(-ов) из нескольких предложенных. Если вы не знаете ответа, вам остаётся положиться на свою интуицию… Однако реально ли получить высокий балл, попросту расставляя ответы наобум?

Ключевые слова:

ЕГЭ, теория вероятностей, вероятность сдачи ЕГЭ, экзамен, тест.

Актуальность исследования:

данное исследование будет актуально в основном для учащихся 11-х классов, так как оно даст ответ на довольно важный вопрос: насколько хорошо можно написать ЕГЭ, не готовясь к нему? Кажется, как можно «предвидеть» наступление такого случайного события, как правильно данный ответ? Оно ведь может произойти, а может и нет… Но математика нашла способы оценивать вероятность наступления таких событий.

Цель

: определить вероятность сдачи ЕГЭ при помощи угадывания правильного ответа, применяя теорию вероятностей

Объект исследования:

теория вероятностей

Предмет исследования

: практическое применение теории вероятностей

Задачи

:

Изучить задания первой части (теста) из ЕГЭ

Выявить вероятность сдачи ЕГЭ методом угадывания ответов

Гипотеза

: предположим, что невозможно сдать ЕГЭ, просто расставляя ответы в первой части «наугад»

Методы исследования

:

Изучение литературы и других источников информации

Анализ и синтез

Идеализация

Изучение и обобщение

Единый государственный экзамен

Основные сведения о

ЕГЭ

Единый государственный экзамен (ЕГЭ) является одним из видов государственной итоговой аттестации (ГИА) по образовательным программам среднего общего образования.

При проведении ЕГЭ используются контрольные измерительные материалы (КИМ), представляющие собой наборы из заданий стандартизированной формы, а также специальные бланки для оформления ответов на задания.

Чтобы получить аттестат, выпускникам необходимо сдать ЕГЭ по двум обязательным предметам — русскому языку и математике (базового или профильного уровня). ЕГЭ по остальным учебным предметам они сдают по своему выбору.

Структура ЕГЭ

Задания ЕГЭ (КИМы) разрабатываются

Федеральным институтом педагогических измерений

[6].

Примерная структура, форма и содержание КИМов предопределены и не могут быть изменены произвольным образом, а регламентируется они тремя документами, утверждаемыми Рособрнадзором каждую осень: кодификаторами, спецификациями и демоверсиями экзаменов. КИМы включают в себя задания с кратким и развернутым ответами.

В экзаменах по математике базового и профильного уровней нет заданий с выбором ответа: следовательно, для сдачи данных экзаменов способ расстановки ответов «наугад» не подходит меньше всего.

При проведении ЕГЭ по иностранным языкам в состав экзамена входит раздел «говорение», устные ответы на задания которого записываются на аудионосители.

Теория вероятностей

Теория вероятностей — это раздел математики, который изучает числовые характеристики вероятности появления некоторого случайного события в конкретных условиях, которые могут быть многократно воссозданы (как, например, сдача ЕГЭ).

Для событий, вероятность которых находиться по формуле классической вероятности, может быть применён статистический подход. Это было обосновано ещё швейцарским математиком Якобом Бернулли (1655–1705).

Являясь математической основой статистики, теория вероятностей имеет большое значение для множества видов деятельности человека, включающих количественный анализ данных, таких как: социологические исследования, экономический анализ и др.

За последние десятилетия теория вероятностей стала развивающейся наукой со множеством возможных направлений применения.

Вероятность события

В так называемых

случайных

^[1]
явлениях существуют определённые закономерности. Задачей теории вероятности является установление таких закономерностей.

Классическое определение вероятности: вероятность события А (обозначается Р(А)) равна отношению числа благоприятствующих исходов к числу всех возможных исходов. Т. е. вероятность события А вычисляется по формуле: Р(А)=n/m, где n ≤ m и n, m є N, из чего следует, что 0 ≤ Р(А) ≤ 1. В данной формуле: n — число благоприятствующих исходов, m — число всех исходов испытания.

Однако в нашей жизни встречаются ситуации, где без практики определить число благоприятных исходов очень трудно, а то и вовсе невозможно.

Например, не подбрасывая кнопку много раз, трудно определить, равновозможны ли ее падения на плоскую часть или на иглу. В подобных случаях и используется статистическое определение вероятности.

Статистическая вероятность

Статистическая вероятность — это числовое выражение степени возможности наступления некоторого события (или того, что данное событие не наступит). Одним из способов, помогающих её рассчитать, является использование формулы Бернулли, позволяющей найти вероятность появления события A при нескольких независимых испытаниях.

Чтобы найти, каков шанс наступления события А при помощи формулы Бернулли, нам надо:

– найти общее количество исходов рассматриваемой ситуации;

– найти количество всех возможных исходов, при которых произойдёт событие А;

– найти, какую часть составляют возможные исходы, при которых произойдёт событие А, от общего количества исходов

Определение вероятности сдачи ЕГЭ

Вероятность сдачи ЕГЭ

Согласно нашим наблюдениям, у учащихся старших классов часто возникают мысли, что можно выбрать ответ наугад и при этом получить высокий балл за экзамен. Но так ли это?

Ответить на этот вопрос мы планируем, используя методы из теории вероятностей. А в качестве объекта для анализа мы решили выбрать ЕГЭ по истории, который сдаём сами.

По данному предмету экзамен включает 14 заданий с выбором ответа. Чтобы сдать экзамен, нужно набрать больше или ровно 32 балла.

Определить вероятность сдачи экзамена (о получении «высокого балла» для поступления в вуз, как мы понимаем, речи не идёт) можно по формуле Бернулли.

Если проводится n независимых испытаний, в результате каждого из которых событие A наступает с вероятностью P(A)=p и не наступает с вероятностью q (q=P(А)=1-p). Вероятность того, что в результате n независимых испытаний событие A наступит ровно k раз равна количеству сочетаний из n по k:

При этом все испытания независимы, а их исходы несовместимы (событие A либо наступает, либо нет). Из этого следует, что вероятность получения удовлетворяющей комбинации будет равна:

Чтобы найти вероятность того, что в n испытаниях событие A наступит k раз, нужно сложить вероятности получения всех удовлетворяющих комбинаций

(они одинаковы и равны).

Тогда количество комбинаций равно

. Получим, что:

— это и есть формула Бернулли.

В итоге мы имеем 14 вопросов. Вероятность угадывания правильного ответа на отдельный вопрос одинакова и равна 1/4 = 0.25 (количество удовлетворяющих исходов (дан правильный ответ) ко всем возможным (всего 4 варианта ответа)). Получаем:

P = P(14) = C
¹⁴
₁₄
*0.25
¹⁴
*0.75
⁰
= 0,0000000037252902984619140625‬ — данное число и является числовым выражением вероятности сдачи ЕГЭ методом угадывания правильного ответа.

Заключение

Как мы можем видеть, вероятность сдать ЕГЭ по истории методом случайной расстановки ответов практически равна нулю. Судя по количеству тестовых заданий в ЕГЭ по другим предметам, утверждение, что сдать его методом угадывания правильного ответа невозможно, справедливо для всех предметов, которые доступны для сдачи выпускниками 11-х классов.

Литература:

Аджиева А. А., Кибишева А. Р. Формула Бернулли // Вестник научных конференций. — ООО Консалтинговая компания Юком, 2016. — №. 4–3. — С. 17–18.

Википедия [электронный ресурс] // Единый государственный экзамен URL:

https

://

ru

.

wikipedia

.

org

/

wiki

/

Единый

_

государственный

_

экзамен

Википедия [электронный ресурс] // Формула Бернулли URL:

https

://

ru

.

wikipedia

.

org

/

wiki

/

Формула

_

Бернулли

Википедия [электронный ресурс] // Бернулли, Якоб URL:

https

://

ru

.

wikipedia

.

org

/

wiki

/

Бернулли

,_

Якоб

4ege [электронный ресурс] // Шкала перевода баллов ЕГЭ 2020 URL:

https

://4

ege

.

ru

/

novosti

—

ege

/4023-

shkala

—

perevoda

—

ballov

—

ege

.

html

О нас // Федеральный институт педагогических измерений. URL: http://www.fipi.ru/about (дата обращения: 21.03.2020).

^[1]
Событие называют случайным, если оно либо происходит, либо не происходит

Основные термины (генерируются автоматически): теория вероятностей, правильный ответ, вероятность сдачи ЕГЭ, ЕГЭ, единый государственный экзамен, вероятность, задание, исход, ответ, событие.

Мы, не раз слышали или сами говорили “это возможно”, “это не возможно”, это обязательно случится”, “это маловероятно”. Такие выражения обычно употребляют, когда говорят о возможности наступления события, которое в одних и тех же условиях может произойти, а может и не произойти.

Цель моего исследования: выявить вероятность успешной сдачи экзамена обучающимися 9 класса путем угадывания правильного ответа, применяя теорию вероятностей.

Для реализации целей я поставила перед собой задачи:

1) собрать, изучить и систематизировать материал о теории вероятностей, воспользовавшись различными источниками информации;

2) рассмотреть использование теории вероятности в различных сферах жизнедеятельности;

3) провести исследование по определению вероятности получения положительной оценки при сдаче ОГЭ путем угадывания правильного ответа.

Я выдвинула гипотезу: с помощью теории вероятностей можно с большой степенью уверенности предсказать события, происходящие в нашей жизни.

Объект исследования – теория вероятностей.

Предмет исследования: практическое применение теории вероятностей.

Методы исследования:1) анализ,2) синтез, 3) сбор информации, 4) работа с печатными материалами, 5) анкетирование, 6) эксперимент.

Я считаю, что вопрос, исследованный в моей работе, является актуальным по ряду причин:

Случай, случайность – с ними мы встречаемся повседневно. Кажется, как можно «предвидеть» наступление случайного события? Ведь оно может произойти, а может и не сбыться! Но математика нашла способы оценивать вероятность наступления случайных событий. Они позволяют человеку уверенно чувствовать себя при встрече со случайными событиями.
Серьёзный шаг в жизни каждого выпускника – Единый государственный экзамен. Мне тоже предстоит на следующий год сдавать экзамены. Успешная его сдача — это дело случая или нет?

Глава 1.Теория вероятностей.

История

Корни теории вероятностей уходят далеко вглубь веков. Известно, что в древнейших государствах Китае, Индии, Египте, Греции уже использовались некоторые элементы вероятностных рассуждений для переписи населения, и даже определения численности войска неприятеля.

Первые работы по теории вероятности, принадлежащие французским учёным Б. Паскалю и П. Ферма, голландскому учёному X. Гюйгенсу, появились в связи с подсчётом различных вероятностей в азартных играх. Крупный успех теории вероятностей связан с именем швейцарского математика Я. Бернулли (1654-1705гг.). Он открыл знаменитый закон больших чисел: дал возможность установить связь между вероятностью какого-либо случайного события и частотой его появления, наблюдаемой непосредственно из опыта. Следующий период истории теории вероятностей (XVIII в. и начало ХIХ в.) связан с именами А. Муавра, П. Лапласа, К. Гаусса и С. Пуассона. В этот период теория вероятностей находит ряд применений в естествознании и технике.

Третий период истории теории вероятностей, (вторая половина XIX в.) связан в основном с именами русских математиков П. Л. Чебышева, А. М. Ляпунова. Наиболее распространённая в настоящее время логическая схема построения основ теории вероятностей разработана в 1933 году математиком А. Н. Колмогоровым.

Определение и основные формулы

Итак, насколько эта теория полезна в прогнозировании и насколько она точна? Каковы ее основные тезисы? Какие полезные наблюдения можно вынести из текущей теории вероятностей?

Основным понятием теории вероятностей является вероятность. Это слово достаточно часто применяется в повседневной жизни. Думаю, каждому знакомы фразы: «Завтра, вероятно, выпадет снег», или «вероятнее всего в выходные я поеду на природу». В словаре С.И.Ожегова дается толкование слова вероятность как «возможности осуществления чего-нибудь». И здесь же дается определение понятию теории вероятностей как «разделу математики, изучающей закономерности, основанные на взаимодействии большого числа случайных явлений».

В учебнике «Алгебра и начала анализа» для 10-11 классов под редакцией Ш.А.Алимова дается следующее определение: теория вероятностей — раздел математики, который «занимается исследованием закономерностей в массовых явлениях».

При изучении явлений, мы проводим эксперименты, в ходе которых происходят различные события, среди которых различают: достоверные, случайные, невозможные, равновероятные.

Событие U называют достоверным по отношению к некоторому испытанию, если в ходе этого испытания событие U обязательно произойдет. Например, достоверным будет появление одного из шести чисел 1,2,3,4,5,6 при одном бросании игральной кости. Событие называют случайным по отношению к некоторому испытанию, если в ходе этого испытания оно может произойти, а может и не произойти. Например, при однократном бросании игральной кости может выпасть число 1 или не выпасть, т.е. событие является случайным, потому что оно может произойти, а может и не произойти. Событие V называют невозможным по отношению к некоторому испытанию, если в ходе этого испытания событие V не произойдет. Например, невозможным является выпадение числа 7 при бросании игрального кубика. Равновероятные события – это события, которые при данных условиях имеют одинаковые шансы для наступления.

А как подсчитать вероятность случайного события? Ведь если случайное, значит, не подчиняется закономерностям, алгоритмам. Оказывается, и в мире случайного действуют определенные законы, позволяющие вычислять вероятности.

Принято вероятность события А обозначать буквой Р(А),тогда формула для вычисления вероятности записывается так:

Р(А)=, где m ≤n(1)

Вероятностью Р(А) события А в испытании с равновозможными элементарными исходами называется отношение числа исходов m, благоприятствующих событию А, к числу исходов n всех исходов испытания. Из формулы (1) следует, что

0≤ Р(А)≤ 1.

Данное определение принято называть классическим определением вероятности. Оно применяется, когда теоретически удается выявить все равновозможные исходы испытания и определить благоприятствующие исследуемому испытанию исходы. Однако на практике часто встречаются испытания, число возможных исходов которых очень велико. Например, без многократного подбрасывания кнопки трудно определить, равновозможны ли ее падения «на плоскость» или на «острие». Поэтому используется и статистическое определение вероятности. Статистической вероятностью называют число, около которого колеблется относительная частота события (W(A)– отношение числа испытаний М, в которых это событие произошло, к числу всех проведенных испытаний N) при большом числе испытаний.

Также я познакомилась с формулой Бернулли — это формула в теории вероятностей, позволяющая находить вероятность появления события A при независимых испытаниях. Названа в честь выдающегося швейцарского математика Якоба Бернулли, выведшего формулу:

P(m)=

Чтобы найти каковы шансы наступления события А в данной ситуации, необходимо:

найти общее количество исходов этой ситуации;
найти количество возможных исходов, при которых произойдёт событие А;
найти, какую часть составляют возможные исходы от общего количества исходов.

Теория вероятностей в жизни.

В развитии теории вероятностей весьма большую роль играли задачи, связанные с азартными играми, в первую очередь с игрой в кости.

Игры в кости

Инструментом для игры являются кубики (кости) в количестве от одного до пяти в зависимости от вида игры. Суть игры состоит в выбрасывании кубиков и дальнейшем подсчёте очков, количество которых и определяет победителя. Основной принцип игры в кости — каждый игрок по очереди бросает некоторое количество игральных костей (от одной до пяти), после чего результат броска (сумма выпавших очков; в некоторых вариантах используются очки каждой кости по отдельности) используется для определения победителя или проигравшего.

Лотерея

Лотерея — организованная игра, при которой распределение выгод и убытков зависит от случайного извлечения того или иного билета или номера (жребия, лота).

Карточные игры

Карточная игра — игра с применением игральных карт, характеризуется случайным начальным состоянием, для определения которого используется набор (колода).

Важным принципом практически всех карточных игр является случайность порядка карт в колоде.

Игровые автоматы

Известно, что в игровых автоматах скорость вращения барабанов зависит от работы микропроцессора, повлиять на который нельзя. Но можно вычислить вероятность выигрыша на игровом автомате, в зависимости от количества символов на нем, числа барабанов и других условий. Однако выиграть это знание вряд ли поможет. В наше время наука о случайном очень важна. Она применяется в селекции при разведении ценных сортов растений, при приемке промышленной продукции, при расчете графика разгрузки вагонов и т.д.

Глава II. ОГЭ как пример использования теории вероятностей жизни

2.1. Единый государственный экзамен

Я обучаюсь в 9 классе, и мне предстоит сдавать экзамены.

Среди нерадивых учеников возник вопрос: «А нельзя ли выбрать наугад ответ и при этом получить положительную оценку за экзамен?» Я провел опрос среди обучающихся: можно ли практически угадать 7 заданий, т.е. сдать ОГЭ по математике без подготовки. Результаты такие: 50% учащихся считают, что смогут сдать экзамен указанным выше способом.

Я решил проверить, правы ли они? Ответить на этот вопрос можно путем использования элементов теории вероятностей. Я хочу проверить это на примере предметов, обязательных для сдачи экзаменов: математика и русский язык и на примере наиболее предпочитаемых предметов в 9 классе.

А) Русский язык. По данному предмету тест включает 14 заданий из которых 11 заданий с выбором ответа из предложенных. Для того, чтобы пройти порог на экзамене в 2018 году достаточно правильно выполнить заданий. Каждое задание имеет несколько вариантов ответов, один из которых правильный. Определить вероятность получения положительной оценки на экзамене можно по формуле Бернулли: P(m)=

Обществознание

Первая часть демонстрационного варианта ОГЭ 2018 года по обществознанию содержит 20 заданий с выбором ответа, из которых только один верный. Определим вероятность получения положительной оценки. Рособрнадзором установлен минимальный первичный балл по обществознанию – 19.

Вероятность получения положительной оценки:

= =15504

0,000003*100%=0,0003%

Таким образом, вероятность благополучного исхода примерно равна 0,0003%!

Я попросила обучающихся 11 класса угадать ответы по обществознанию. Средний балл составил 4,2 балла. Самый высокий балл -7, самый низкий- 1. Таким образом, ни один обучающийся не смог набрать нужное количество баллов по обществознанию. (Приложение I)

Математика

В 2018 году демонстрационный вариант КИМ ОГЭ по МАТЕМАТИКЕ содержит 20 заданий. Для успешной сдачи экзамена необходимо было решить не менее 7 заданий. Применим формулу Бернулли.

(8)=* *; ==9; (8)=9**=0,000102996;

0,0001*100%=0,01%

Вывод: вероятность получения положительной оценки составляет 0,01%.

Эксперимент, проведенный, среди моих одноклассников показал, что самое большое количество совпадений — 3, средний балл составил 1,7 балла.

Экспериментальная часть

Анкетирование

Анкетирование проводилось среди обучающихся 9 класса. Им было предложено ответить на следующий вопрос:

1.Можно ли сдать экзамены без подготовки, угадывая ответ в заданиях?

Результаты проведенного опроса отражены в диаграммах. (Приложение II)

Эксперимент

1.Среди обучающихся 11 класса на примере демонстрационного варианта контрольно-измерительных материалов ЕГЭ-2016 провела эксперимент с угадыванием ответа по русскому языку и обществознанию. Результаты отражены в таблице 1 (Приложение I) .

2.Своим одноклассникам и одноклассницам предложила угадать ответ в демонстрационном варианте по математике за 2018 год, результаты также представлены в приложении I.

В результате проведенного эксперимента и применяя формулу Бернулли, я доказала, что сдать экзамены путем угадывания ответа невозможно. Только планомерная, вдумчивая и добросовестная учеба в школе позволит выпускнику хорошо подготовиться к участию в ОГЭ, и успешно решить судьбоносную проблему при переходе на более высокий уровень обучения в вуз.

Заключение

В результате проделанной мной работы, я добилась реализации поставленных перед собой задач:

во-первых, поняла, что теория вероятностей — это огромный раздел науки математики и изучить его в один заход невозможно;

во-вторых, перебрав множество фактов из жизни, и проведя эксперименты, я поняла, что действительно с помощью теории вероятностей можно предсказать события, происходящие в различных сферах жизнедеятельности;

в-третьих, исследовав вероятность успешной сдачи обучающимися 9 класса ОГЭ по математике, я пришла к выводу, что только планомерная, вдумчивая и добросовестная учеба в школе позволит выпускнику хорошо подготовиться к участию в ОГЭ. Таким образом, выдвинутая мной гипотеза подтвердилась, с помощью теории вероятностей я доказала, что к экзаменам надо готовиться, а не рассчитывать на авось.

На примере моей работы можно сделать и более общие выводы: подальше держаться от всяких лотерей, казино, карт, азартных игр вообще. Всегда надо подумать, оценить степень риска, выбрать наилучший из возможных вариантов – это, я думаю, пригодится мне в дальнейшей жизни.

Литература

Макарычев Ю.Н. Алгебра: элементы статистики и теории вероятностей: учеб. пособие для учащихся 7-9 кл. общеобразоват. учреждений-М.:Просвещение,2007.
Ожегов С.И. Словарь русского языка:.М.:Рус.яз.,1989.
Федосеев В.Н .Элементы теории вероятностей для VII-IX классов средней школы.//Математика в школе.-2002.-№4,5.

Ресурсы:

http://www.blagodeteleva-vovk.com/theory/never.htm
http://habrahabr.ru/blogs/gtd/101695
http://www.prosto.ws/2010/03/02/ot-teorii-veroyatnosti-k-teorii-vsego
http://www.mathematics.ru/courses/algebra/content/chapter4/section3/paragraph1/theory.html
http://ru.wikipedia.org/wiki
www.fipi.ru

Приложение 1.

Таблица 1.

№	ФИО	Русский	Общество
1.	Долгова Анастасия	4	—
2.	Зыков Данил	3	1
3.	Зыкова Светлана	5	—
4.	Лиховидова Галина	10	5
5.	Магомедов Гасан	3	3
6.	Овчаров Роман	5	4
7.	Пахомова Людмила	11	7
8.	Софина Яна	15	5
	среднее	7	4,2

Таблица 2.

№	ФИО	Математика
1.	Алексеева Катерина	0
2.	Дьяченко Александр	1
3.	Линник Дмитрий	1
4.	Магомедова Рукият	2
5.	Макарова Татьяна	2
6.	Суковатова Ирина	3
7.	Шведова Марина	3
	среднее	1,7

Приложение II.

1.Можно ли сдать экзамены без подготовки, угадывая ответ в заданиях?

Результаты проведенного опроса отражены в диаграммах.

9 класс.

Источник

Вероятностью события $А$ называется отношение числа благоприятных для $А$ исходов к числу всех
равновозможных исходов

$P(A)={m}/{n}$, где $n$ – общее количество возможных исходов, а $m$ – количество исходов, благоприятствующих событию
$А$.

Вероятность события — это число из отрезка $[0; 1]$

В фирме такси в наличии $50$ легковых автомобилей. $35$ из них чёрные, остальные — жёлтые.
Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета.

Решение:

Найдем количество желтых автомобилей:

$50-35=15$

Всего имеется $50$ автомобилей, то есть на вызов приедет одна из пятидесяти. Желтых автомобилей $15$,
следовательно, вероятность приезда именно желтого автомобиля равна ${15}/{50}={3}/{10}=0,3$

Ответ:$0,3$

Противоположные события

Два события называются противоположными, если в данном испытании они несовместимы и одно из них обязательно
происходит. Вероятности противоположных событий в сумме дают 1.Событие, противоположное событию $А$, записывают
${(А)}↖{-}$.

$Р(А)+Р{(А)}↖{-}=1$

Независимые события

Два события $А$ и $В$ называются независимыми, если вероятность появления каждого из них не зависит от того,
появилось другое событие или нет. В противном случае события называются зависимыми.

Вероятность произведения двух независимых событий $A$ и $B$ равна произведению этих
вероятностей:

$Р(А·В)=Р(А)·Р(В)$

Иван Иванович купил два различных лотерейных билета. Вероятность того, что выиграет первый
лотерейный билет, равна $0,15$. Вероятность того, что выиграет второй лотерейный билет, равна $0,12$. Иван Иванович
участвует в обоих розыгрышах. Считая, что розыгрыши проводятся независимо друг от друга, найдите вероятность того,
что Иван Иванович выиграет в обоих розыгрышах.

Решения:

Вероятность $Р(А)$ — выиграет первый билет.

Вероятность $Р(В)$ — выиграет второй билет.

События $А$ и $В$ – это независимые события. То есть, чтобы найти вероятность того, что они произойдут оба
события, нужно найти произведение вероятностей

$Р(А·В)=Р(А)·Р(В)$

$Р=0,15·0,12=0,018$

Ответ: $0,018$

Несовместные события

Два события $А$ и $В$ называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию
$А$, так и событию $В$. (События, которые не могут произойти одновременно)

Вероятность суммы двух несовместных событий $A$ и $B$ равна сумме вероятностей этих
событий:

$Р(А+В)=Р(А)+Р(В)$

На экзамене по алгебре школьнику достается один вопрос их всех экзаменационных. Вероятность
того, что это вопрос на тему «Квадратные уравнения», равна $0,3$. Вероятность того, что это вопрос на тему
«Иррациональные уравнения», равна $0,18$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите
вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Решение:

Данные события называются несовместные, так как школьнику достанется вопрос ЛИБО по теме «Квадратные уравнения»,
ЛИБО по теме «Иррациональные уравнения». Одновременно темы не могут попасться. Вероятность суммы двух
несовместных событий $A$ и $B$ равна сумме вероятностей этих событий:

$Р(А+В)=Р(А)+Р(В)$

$Р = 0,3+0,18=0,48$

Ответ: $0,48$

Совместные события

Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же
испытании. В противном случае события называются несовместными.

Вероятность суммы двух совместных событий $A$ и $B$ равна сумме вероятностей этих событий минус
вероятность их произведения:

$Р(А+В)=Р(А)+Р(В)-Р(А·В)$

В холле кинотеатра два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится
кофе, равна $0,6$. Вероятность того, что кофе закончится в обоих автоматах, равна $0,32$. Найдите вероятность того,
что к концу дня кофе закончится хотя бы в одном из автоматов.

Решение:

Обозначим события, пусть:

$А$ = кофе закончится в первом автомате,

$В$ = кофе закончится во втором автомате.

Тогда,

$A·B =$ кофе закончится в обоих автоматах,

$A + B =$ кофе закончится хотя бы в одном автомате.

По условию, $P(A) = P(B) = 0,6; P(A·B) = 0,32$.

События $A$ и $B$ совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий,
уменьшенной на вероятность их произведения:

$P(A + B) = P(A) + P(B) − P(A·B) = 0,6 + 0,6 − 0,32 = 0,88$

Ответ: $0,88$

Источник

Расчёт вероятности получения положительной отметки при решении тестовых заданий по математике

Авторы
Руководители
Файлы работы
Наградные документы

Кокорев Е.Э. 1

1МБОУ «Плотавская СОШ»

Левшина О.Н. 1

1МБОУ «Плотавская СОШ»

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Расчёт вероятности получения положительной отметки

при решении тестовых заданий по математике

Высшее назначение математики…состоит в том,

чтобы находить скрытый порядок в хаосе, который нас окружает

Н.Винер

Введение

Однажды при подготовке к контрольной работе учитель математики задала на дом пять задач по геометрии. Четыре я решил, пятая же не получилась. Я понадеялся, что учитель спросит кого-либо другого, а если и меня, то попадется одна из четырех решенных мной задач. Но учитель вызвала именно меня и спросила как раз пятую задачу. Случайность! И на этот раз не очень-то приятная! Кажется, как можно «предвидеть» наступление случайного события? Ведь оно может произойти, а может и не сбыться!

При решении самостоятельной или контрольной работы в тестовой форме, особенно по математике, информатике, физике большинство моих одноклассников надеются, что за работу можно будет получить хорошую оценку, выбирая правильные варианты ответов интуитивно, без теоретических знаний. Поэтому я решил оценить, насколько данный метод обеспечит положительную оценку, и как результаты моего исследования по теории вероятностей можно будет практически применить при тестировании.

Актуальность

Тестирование в образовании – современный подход к оценке знаний учащихся. Тестовая форма контроля на сегодняшний день является самой востребованной: она используется на ГИА и ЕГЭ. А потому, чем раньше мы начнем приобщаться к такой форме проверки знаний, тем лучше будем подготовлены к итоговой аттестации и различного рода испытаниям в тестовой форме.

Гипотеза:

Вероятность угадать верные ответы при тестировании очень мала, а значит практически невозможно получить положительную оценку без подготовки.

Цель:

Определить вероятность получения положительной отметки при написании тестов по математике путем угадывания правильного ответа.

Для реализации цели были поставлены следующие задачи:

2) провести статистический эксперимент;

3) проанализировать результаты тестовых работ с применением теории вероятности.

Объект исследования: теория вероятности.

Предмет исследования: тесты по математике.

Методы исследования: анализ, синтез, сбор информации, анкетирование работа с литературой, эксперимент.

Практическая значимость данной работы состоит в том, что она нацелена помочь обучающимся осознать важность учения, так как согласно проведенному исследованию получить положительную отметку за тестовую работу путем угадывания мало вероятна.

Теоретическая часть

Глава 1. Теория вероятностей

История возникновения.

Теория вероятностей — раздел математики, изучающий случайность. Теория вероятностей используется в таких разделах математики как математическая статистика, теория случайных процессов, теория массового обслуживания. Она находит применение в физике, в анализе азартных игр, в страховании и в расчете пенсионных схем. На теории вероятностей основана разработка, применение и анализ вероятностных алгоритмов [1].

Как наука, теория вероятностей зародилась в середине XVII века с появлением азартных игр, таких как карты и кости, когда начали применять в них количественные подсчеты и прогнозирование шансов на успех. А зарождение теории вероятностей началось с того, что придворный французского короля, шевалье (кавалер) де Мерэ (1607-1648г. г. ), сам азартный игрок, обратился к французскому физику, математику и философу Блезу Паскалю (1623-1662г. г.) с вопросами к задаче об очках. (см. главы «Формулировки и основные понятия», «Примеры и решения практических задач на вероятность»). Паскаль обратился к математику Пьеру Ферма (1601-1665г. г.) и переписывался с ним по поводу этих задач. Они вдвоем установили некоторые основные положения теории вероятностей, в частности пришли к понятию математического ожидания и теоремам сложения и умножения вероятностей.

Другим толчком для развития теории вероятностей послужило страховое дело, а именно с конца XVII века на научной основе стало производиться страхование от несчастных случаев и стихийных бедствий. В XVI-XVII веках во всех странах Западной Европы получило распространение страхование судов и страхование от пожаров. В XVII веке были созданы многочисленные страховые компании и лотереи в Италии, Фландрии, Нидерландах. Затем методы теории вероятностей стали широко применять в демографии, например, при ведении статистики рождения и смерти.

Первооткрывателями теории вероятностей считаются французские ученые Б. Паскаль и П. Ферма и голландский ученый Х. Гюйгенс (1629-1695г. г.). Стала зарождаться новая наука, вырисовываться ее специфика и методология: определения, теоремы, методы. Также теория вероятностей связана с именами известных математиков: швейцарца Якоба Бернулли (1654-1705г.г.), француза П. С. Лапласа, англичанина А. Муавра (1667-1754г. г. ) и др. Вклад в развитие теории вероятностей внесли русские и советские ученые П. Л. Чебышев, А. А. Марков, А. М Ляпунов и многие другие [2].

В XX веке выяснилось, что эта, казалось бы, легкомысленная наука играет важную роль в познании фундаментальных процессов, протекающих в микромире. Была создана современная теория вероятностей [3].

Основные понятия теории вероятностей

Основными понятиями в теории вероятностей являются испытание, событие и вероятность.

Испытание — это эксперимент, проводимый над объектом в комплексе определенных условий.

Событие — это случай или факт, который произошел или не произошел в результате испытания.

Вероятность — это численная мера степени объективной возможности наступления события.

Вероятностью события А называется отношение числа случаев наступления этого события к общему числу случаев:

, P(A) – вероятность события A, m – число случаев наступления события А, n – общее число случаев, m , 0. Данное определение принято называть классическим определением вероятности. Оно применяется, когда теоретически удается выявить все равновозможные исходы испытания и определить благоприятствующие исследуемому испытанию исходы.

Событие U называют достоверным по отношению к некоторому испытанию, если в ходе этого испытания событие U обязательно произойдет. Например, достоверным будет появление одного из шести чисел 1,2,3,4,5,6 при одном бросании игральной кости.

Событие называют случайным по отношению к некоторому испытанию, если в ходе этого испытания оно может произойти, а может и не произойти. Событие V называют невозможным по отношению к некоторому испытанию, если в ходе этого испытания событие V не произойдет.

Равновероятные события – это события, которые при данных условиях имеют одинаковые шансы для наступления.

Но встречаются случаи, когда без практики определить число благоприятных исходов невозможно. В таких случаях используется статистическое определение вероятности.

Статистическая вероятность (частота, относительная частота) –это отношение числа испытаний, в которых событие появилось к общему числу фактически произведенных испытаний. Определяется следующей формулой для события: P(A) = , где n – общее число фактически проведенных испытаний, m – число появлений событий. Другими словами, статистическая вероятность – это вероятность события, рассчитанная опытным путем.

Формула Бернулли — это формула в теории вероятностей, позволяющая находить вероятность появления события A при независимых испытаниях. Формула названа в честь выдающегося швейцарского математика Якоба Бернулли [4].

Теория вероятности в жизни

Людей всегда интересовало будущее. Человечество во все времена искало способ его предугадать, или спланировать. В разное время разными способами. В жизни мы часто сталкиваемся со случайными явлениями. Чем обусловлена их случайность – нашим незнанием истинных причин происходящего или случайность лежит в основе многих явлений? Случайным ли образом возникают мутации, насколько зависит историческое развитие от отдельной личности, можно ли считать Вселенную случайным отклонением от законов сохранения? [2]

Примеров реального использования теории вероятности в жизни множество. Практически вся современная экономика базируется на ней. Невозможно представить без теории вероятности жизнь брокеров на мировых рынках. Предсказывание денежного курса на денежных опционах дает возможность зарабатывать на данной теории серьезные деньги.

Теория вероятности имеет значение в начале практически любой деятельности, а также ее регулирования. Благодаря оценке шансов той или иной неполадки (например, космического корабля), мы знаем, какие усилия нам нужно приложить, что именно проверить, что вообще ожидать в тысячи километров от Земли. Возможности теракта в метрополитене, экономического кризиса или ядерной войны – все это можно выразить в процентах.

Таким образом, теорию вероятностей нельзя не применять в нашей жизни. Она имеет разные области применения такие как: биологические и химические процессы, история, экономика, кораблестроение и машиностроение, медицина и большинство различной деятельности человека. Люди применяют её как сознательно, так и подсознательно, что проявляется в обычных повседневных фразах и действиях. Разумный человек должен стремиться мыслить, исходя из законов вероятностей. Теория вероятностей – это одна из составляющих частей успеха. Если стремиться учитывать законы вероятностей и, в том случае, если вероятность неблагоприятная, предпринимать соответствующие контрдействия, то можно упростить себе жизнь в разы и сэкономить своё время, которое так ценно для каждого из нас [5].

Вероятностно–статистические методы играют важную роль в практической деятельности — это контроль качества продукции, техническая диагностика оборудования, технология производства, обеспечения надежности оборудования, организация массового обслуживания, военное дело (стрельба, бомбометание, тактика, теория боеприпасов), получение достоверных результатов измерений, астрономические наблюдения и многое другое.

Глава 2. Практическая часть

2.1 Исследование

Сейчас обучение в любом классе начинается с входного тестирования, сопровождается текущим контролем с помощью заданий в тестовой форме и заканчивается объективным тестированием учебных достижений.

Кроме того, тесты позволяют наладить самоконтроль — самую полезную для обучения и гуманную форму контроля знаний, а также организовать рейтинг — эффективное средство повышения учебной мотивации.

Мы провели социологический опрос среди учащихся 7-9 классов. В связи малой накаляемостью учащихся в классах нашей школы (5-6 учащихся – средняя накаляемость класса), в анкетировании принимали участие 15 человек. Учащимся предложили ответить на вопросы:

можно ли сдать тест, экзамен без подготовки методом угадывания?

можно ли угадать, например, 6 заданий из 10, таким образом, решив тестовое задание по математике без подготовки?

По первому вопросу из 15 респондентов 9 человек (60%) ответили «да», 6 человек ( 40%) ответили «нет», т. е. считают, что таким способом сдать экзамен или решить тест нельзя.

По второму вопросу результаты такие: 80% учащихся 7 класса считают, что можно угадать 6 заданий из 10, 8кл. — 60%, 9кл. — 33%.

Вывод: чем старше класс, тем меньше веры в случай. (Приложение 1)

2.2 Теоретический расчет успешного решения тестового задания

Определить вероятность угадывания верного ответа можно по формуле Бернулли.

Пусть событие А – это правильно выбранный ответ из четырех предложенных в одном задании теста. Вероятность события А определена как отношение числа случаев, благоприятствующих этому событию (т.е. правильно угаданный ответ, а таких случаев 1), к числу всех случаев (таких случаев 4).

Тогда p=1/4, а q=1-p=3/4.

Вероятность получения положительной оценки:

Р₁₀(7)= С₁₀⁵р⁵q^10-5 , где

= = 2 3 7 = 252

Р₁₀(5)=252 = 0,0583991 0,058

То есть, вероятность благополучного исхода очень низкая, примерно 5,8%

Вывод: мало шансов решить тест или сдать экзамен на положительную оценку без подготовки. Из 10000 человек только 5- 6 могут получить положительную оценку.

2.3 Эксперимент: расчет вероятности получения положительной отметки по алгебре

Для подтверждения гипотезы исследования в 7-9 классах мы воспользовались материалами сайта «Контроль знаний» [6]. Учащимся предложили решить тесты по алгебре по следующим темам¹:

Тест по алгебре 7 класс: Степень и её свойства (10 вопросов)²

Тест по алгебре 8 класс: «Решение неравенств с одной переменной» (10 вопросов)³.

Алгебра 9: Квадратный трехчлен(10 вопросов)⁴.

В каждом тесте 10 заданий с выбором ответа по алгебре. Один ответ из четырех верный. Чтобы получить положительную оценку необходимо правильно угадать 6 ответов (60%).

Результаты эксперимента показывают, что угадал 6 ответов только один ученик (Приложение 2).

Произведем расчеты по формуле.

Пусть событие А– это правильно выбранный ответ из четырех предложенных в одном задании. Вероятность события Аопределена как отношение числа случаев, благоприятствующих этому событию (то есть правильно угаданный ответ, а таких случаев 1), к числу всех случаев (таких случаев 4). Тогда p = P(A)=1/4.

Вероятность противоположного события q = P(Ā)=1- p = 3/4.

Вероятность получения положительной отметки вычислим по формуле Бернулли, где n = 10, m = 6.

Вероятность получения положительной оценки:

Р₁₀(6)= С₁₀⁶р⁴q^10-6 , где

= = 10 3 7= 210

Р₁₀(6) = 210 = 0,016222 0,02

Таким образом, максимальное количество правильно угаданных ответов

равно 4, что не позволяет ученику получить положительную отметку за тест по алгебре. Это же подтверждают теоретические вычисления – вероятность угадывания правильных ответов – достаточно мала, в данном случае только 0,02.. Процент правильно угаданных ответов — 13,3% (Приложение 2).

2.4 Эксперимент: расчет вероятности получения положительной отметки по геометрии

При повторном эксперименте учащимся предложили решить тесты по геометрии по следующим темам:

Геометрия 7 класс. Свойства параллельных прямых⁵.

Геометрия 8. Признаки подобия треугольников⁶

Геометрия 9. Треугольники⁷

В каждом тесте 12 заданий с выбором ответа по геометрии. Один ответ из четырех верный. Чтобы получить положительную оценку необходимо правильно угадать не менее 50% от всего теста, т.е. угадать не менее 6 ответов.

Вероятность получения положительной отметки вычислим по формуле Бернулли, где n = 12, m = 6.

Вероятность получения положительной оценки:

Р₁₂(6)= С₁₂⁶р⁶q^12-6 , где

= = 11 3 = 924

Р₁₂(6) = 924 = 0,0401494 0,04. Вероятность угадывания правильных ответов выше, чем в первом эксперименте. Процент правильно угаданных ответов 17% (Приложение 3).

Вывод: данные теории вероятностей и результаты эксперимента показывают, что способом угадывания правильного ответа в тестовом задании по алгебре и геометрии получить положительную отметку почти невозможно.

Заключение

В результате проделанной работы, были достигнуты поставленные задачи:

была изучена научная литература по теме «Теория вероятностей» — это огромный раздел науки математики;

в ходе работы был проведен эксперимент, позволяющий определить вероятность успешного выполнения тестов по математике обучающимися 7-9 классов путем угадывания правильного ответа, применяя теорию вероятностей.

При проведении эксперимента наибольший процент правильно угаданных ответов был получен при написании тестовой работы по геометрии. Это, возможно, связано с тем, что обучающиеся использовали те знания, которые они получили на уроках и в повседневной жизни. Им было легче сориентироваться при выборе ответа, на уровне подсознания.

Таким образом, ранее выдвинутая гипотеза нашла свое подтверждение в проведенном исследовании. Полученные данные позволяют сделать вывод, что только планомерная, вдумчивая и добросовестная учеба в школе позволит учащимся успешно писать тестовые контрольные работы, хорошо подготовиться к участию в ГИА и успешно решить судьбоносную проблему при переходе на более высокий уровень обучения в ВУЗ.

С результатами данного исследования можно ознакомить будущих выпускников во время проведения классных часов, внеклассных мероприятий, с целью пропаганды подготовки их к экзаменам.

Вывод

Результаты практических экспериментов и их теоретическое обоснование подтверждают правильность выдвинутой гипотезы.

Литература

Савельева Р. Ю. Основы теории вероятностей и математической статистики [Электронный ресурс]. – Режим доступа: http://открытыйурок.рф/статьи/526665/ (дата обращения – 24.01.2018)

Гатауллина Л. Теория вероятности в жизни [Электронный ресурс]. – Режим доступа: https://nsportal.ru/ap/library/nauchno-tekhnicheskoe-tvorchestvo/2012/01/07/teoriya-veroyatnosti-v-zhizni (дата обращения — 6.02.2018)

Кибзун А. И. Теория вероятностей и математическая статистика. Базовый курс с примерами и задачами [Текст]: учебное пособие/А. И. Кибзун, Е. Р. Горяинова, А. В. Наумов, А. Н. Сиротин. – Москва: ФИЗМАТЛИТ, 2002. – 224 с.

Теория вероятностей и основные понятия теории [Электронный ресурс]. – Режим доступа: https://bookmaker-ratings.ru/wiki/teoriya-veroyatnostej-i-osnovny-e-ponyatiya-teorii/ (дата обращения 24.01.2018)

Вишня Ю. Теория вероятности в жизни [Электронный ресурс]. – Режим доступа: https://allowwonder.com/teoriya-veroyatnosti-v-zhizni/ (дата обращения – 6.02.2018)

http://контрользнаний.рф/geometriya-7-test-za-ii-chetvert/

Приложение 1

Анкетирование

Можно ли сдать тест, экзамен без подготовки методом угадывания?

Рис. 1. Результаты анкетирования респондентов

Можно ли угадать, например, 6 заданий из 10, таким образом, решив тестовое задание по математике без подготовки?

Приложение 2

Результаты статистического эксперимента: выбор учащимися 7-9 классов правильного ответа в тесте по алгебре

Класс	К-во уч-ся	Количество угаданных ответов
0	1	2	3	4	5	6	7 и более
7	3	1	1	2	1	0	0	0	0
8	5	1	0	3	1	1	0	1	0
9	7	0	1	4	1	1	1	0	0
Всего	15	2	2	9	3	2	1	1	0

Выбор правильных ответов по алгебре

Приложение 3.

Результаты статистического эксперимента: выбор учащимися 7-9 классов правильного ответа в тесте по геометрии

Класс	К-во уч-ся	Количество угаданных ответов
0	1	2	3	4	5	6	7	8 и более
7	3	1	1	2	1	0	0	0	0	0
8	5	1	0	3	1	1	1	1	1	0
9	7	1	1	4	2	2	1	1	0	0
Всего	15	2	2	9	4	3	2	2	1	0

Выбор правильных ответов по геометрии

1 http://контроль-знаний.рф/

2 http://контроль-знаний.рф/stepen-i-eyo-svoystva/

3 http://контроль-знаний.рф/reshenie-neravenstv-s-odnoy-peremen/

4 http://контроль-знаний.рф/kvadratnyy-trekhchlen/

5 http://контроль-знаний.рф/svoystva-parallelnykh-pryamykh/

6 http://контроль-знаний.рф/priznaki-podobiya-treugolnikov/

7 https://testedu.ru/test/matematika/9-klass/treugolniki.html

Просмотров работы: 1386

Источник

Авторы
Резюме
Файлы
Ключевые слова
Литература

Ревегук Ю.А.

1

Рудикова Е.С.

1 ФГБОУ ВО «Ставропольский государственный аграрный университет»

Вокруг нас происходит так много вещей и событий, которые, несмотря на уровень развития науки, трудно спрогнозировать. Сложно предугадать с каким номером выпадет бочонок при игре в лото или сколько будет солнечных дней в году. Но при этом, имея дополнительные сведения, возможно прогнозировать и вычислять вероятность таких событий. В данной статье идет речь о теории вероятности, составлен алгоритм решения задач по этой теме, а так же приведены примеры, с помощью которых возможно вычислить вероятность выпадения «счастливого» билета на экзамене. Теория вероятности – это отличный помощник, при предсказании наступления определенного события, в том числе выпадения «счастливого» билета на экзамене. Простые формулы позволяют провести расчеты любому человеку.

теория вероятности

«счастливый» билет

задачи

1. Бондаренко В.А., Цыплакова О.Н. Задачи с экономическим содержанием на занятиях по дифференциальному исчислению // Актуальные вопросы теории и практики бухгалтерского учета, анализа и аудита: ежегодная 75-я научно-практическая конференция / Редколлегия: В.З. Мазлоев, А.В. Ткач, И.С. Санду, И.Ю. Скляров, Е.И. Костюкова, ответственный за выпуск А.Н. Бобрышев, 2011. – С. 124–127.

2. Гулай Т.А., Жукова В.А., Мелешко С.В., Невидомская И.А. Математика: рабочая тетрадь. – Ставрополь, 2015.

3. Литвин Д.Б., Гулай Т.А., Жукова В.А., Мамаев И.И. Модель экономического роста с распределенным запаздыванием в инвестиционной сфере // Вестник АПК Ставрополья. – 2017. – № 2 (26). – С. 225–228.

4. Математика. Теория вероятностей и случайные величины: рабочая тетр.; учеб. пособие для студентов вузов по направлениям: 38.03.04 – «Гос. муницип. упр.», 38.03.05 – «Бизнес-информатика» / Т.А. Гулай, В.А. Жукова, С.В. Мелешко, И.А. Невидомская; СтГАУ. – Ставрополь: Сервисшкола, 2016.

5. Элементы теории вероятностей случайных событий: Рабочая тетрадь / И.А. Невидомская, С.В. Мелешко, Т.А. Гулай. – Ставрополь: Сервисшкола, 2015.

6. Теория вероятностей для экономических специальностей на базе Excel (практикум) / А.Ф. Долгополова, О.В. Морозова, Е.В. Долгих, Р.В. Крон, Н.Н. Тынянко, С.В. Попова, Н.Б. Смирнова // Международный журнал экспериментального образования. – 2009. – № S4. – С. 19.

Каждый человек в той или иной мере применяет теорию вероятности для анализа произошедших в его жизни событий. Люди обращают внимание на вероятность вещей и прогнозируют свое дальнейшие поведение. Но к большому сожалению, не всегда возможны точно определить вероятность того или иного события [1, 3].

Примеров реального использования теории вероятности в жизни огромное множество. Так, практически вся современная экономика базируется на ней. В общем, можно сказать, что теория вероятности будет иметь большое значение в начале практически любой деятельности, а так же в её регулировании. Она дает возможность оценить шансы той или иной неполадки, позволяет нам понять, что нужно проверить и какие усилия необходимо предпринять, исходя из полученных данных [5].

Любую деятельность любой сферы можно проанализировать, используя статистику, рассчитать благодаря теории вероятности и заметно улучшить.

Попробуем составить собственный алгоритм для решения задач по теории вероятности [2, 4]:

1. Необходимо ознакомится с условием задачи и понять какие действия, с какими предметами выполняются.

2. Определить ключевой вопрос задачи и обозначить событие, вероятность которого необходимо вычислить.

3. Чтобы выбрать дальнейшую последовательность действий следует конкретизировать тип задачи и выяснить, какие формулы будут использоваться в дальнейшем для её решения.

4. Исходя из ответов на приведенные вопросы, выбрать формулы и подставить в них данные задачи.

5. Готово, вероятность найдена.

Одно из важных событий в жизни любого студента – это сессия. Это то время, когда нервничают все, включая отличников. Ведь всегда существует вероятность не сдать экзамен. Чтобы этого не произошло необходимо соблюдать десятки различных примет, можно даже обратиться к нумерологии. Но один из простых способов вытянуть счастливый билет – рассчитать вероятность его выпадения.

Составим и решим несколько простыхзадач, на примере которых каждый студент может вычислить вероятность выпадения счастливого билета на экзамене [6].

Задача 1. «На экзамене по математике шесть студентов второго курса факультета агробиологии и земельных ресурсов друг за другом вытягивают билеты. Тридцать билетов включают в себя четыре простых вопроса. Необходимо вычислить вероятность, что хотя бы одному студенту попадется билет с простыми вопросами».

Решение. В первую очередь, определим ключевой вопрос задачи – вычислить вероятность, что хотя бы одному студенту попадется билет с простыми вопросами.

Далее пойдем от обратного, найдем вероятность того, что никому из студентов не попадется простой билет.

Эта вероятность будет равна

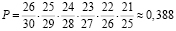
Первая дробь 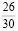показывает вероятность того, что билет со сложным вопросом достался первому студенту.

Вторая дробь 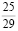показывает вероятность того, что билет со сложным вопросом достался второму студенту. Третья дробь показывает вероятность того, что билет со сложным вопрос достался третьему студенту и так далее до шестого студента. Так как в задаче требуется одновременное выполнение условий, то вероятности следует перемножить.

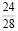
Для того, чтобы найти искомую вероятность, надо вычесть полученную выше вероятность из единицы.

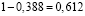
Задача 2. Леша, студент второго курса факультета механизации сельского хозяйства, сдаёт экзамен по теоретической механике, при этом из 50 билетов 35 он знает хорошо, а 15 плохо. Допустим, группа сдаёт экзамен по частям. В первый день 15 человек, включая Алексея. В каком случае Леше достанется с большей вероятностью «счастливый» билет – если он пойдет на экзамен в числе первых, в середине или же будет тянуть билет последним? Когда ему лучше зайти в кабинет?

Для начала рассмотрим случай, при котором Леша сохраняет свои шансы постоянными, то есть он не знает какие билеты вытянули однокурсники и не учит вопросы, которые знает плохо.

Пусть Алексей зайдет в аудиторию первым и вытянет «счастливый» билет, обозначим это событие 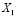. По классическому определению вероятности:

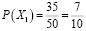
Может ли измениться вероятность извлечения нужного билета, если пропустить вперед отличника Жору? В этом случае станут возможными две несовместимые гипотезы:

– Жора вытянет «счастливый» (для Леши) билет;

– Жора вытянет «несчастливый» билет, таким образом, увеличивая шансы Леши.

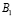
Событие , при котором Леша зайдет вторым и вытянет «счастливый» билет становится зависимым.

1) Можно предположить, что Жора с вероятностью

забрал у Леши «удачный» билет. Тогда останется всего 49 билетов, среди которых 34 «Счастливых». По классическому определению вероятности:

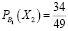
2) Допустим, что Жора с вероятностью

«спас» Лешу от одного сложного билета. В этом случае останется 49 билетов, 35 из которых «счастливые». Тогда по классическому определению вероятности:

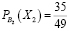
Воспользовавшись теоремами сложения вероятностей несовместных и умножение вероятностей зависимых событий, определим вероятность, что Леша вытянет «счастливый» билет, будучи вторым в очереди:

Вероятность не изменилась.

Рассмотрим следующее событие 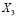, при котором Леша пойдет третьим, пропустив перед собой Жору и Леру, и вытянет «счастливый» билет.

В данном событии гипотез будет больше: однокурсники могут забрать два удачных билета или же два неудачных, так же вытянуть один «счастливый» билет и один «несчастливый» билет. Проведем аналогичные рассуждения, воспользуемся теми же теоремами и получим значение вероятности

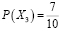
И так далее.

Следовательно, не важно, когда идти – первоначальные вероятности останутся неизменными. Но нужно помнить, что это лишь усредненная теоретическая оценка. Если Леша пойдет последним на экзамен, то это не значит, что ему достанутся на выбор 17 «счастливых» билетов и 19 «несчастливых» билетов в соответствии с его изначальными шансами. Это соотношение может изменяться, как в лучшую, так и в худшую сторону. Однако, маловероятно, что среди билетов останутся одни «счастливые» или же наоборот – «несчастливые».

Математика и «чистый эксперимент» – это хорошо, но чего следует придерживаться в реальных условиях? Нужно принять во внимание субъективные факторы, такие как дополнительный балл для «храбрецов» или же усталость преподавателя в конце экзамена. Часто они могут решающими факторами.

В случае, если вы хорошо подготовились к экзамену, то лучше идти в числе первых, так как есть полный комплект билетов, постулат «мало возможные события не происходят» работает в большей степени.

Если же студент готов к экзамену достаточно хорошо, но пробелы в знаниях всё-таки есть, то будет целесообразно пропустить вперед несколько человек и ожидать подходящего момента вне аудитории. Здесь нужно действовать по ситуации, когда начнет поступать информация о вытянутых билетах, и можно будет учить и повторять оставшиеся билеты, повышая первоначальную вероятность своего успеха.

В случае, если вы готовы неважно или плохо, то лучше идти в последнюю очередь. Существует небольшая вероятность, что останутся «счастливые» для вас билеты, вы можете изучить материал за время экзамена или же (в крайнем случае) сделать «шпаргалку».

Никогда невозможно точно предугадать, что произойдет с нами через день, два. Ведь событий связанных с нами в каждый момент невероятно много. Безусловно, мало кто будет высчитывать по формулам вероятность появления событий, но иногда бывает интересно проверить совпадает ли «эмпирический анализ» с математическим. Теория вероятности позволяет предугадать лишь однотипные события. Именно поэтому её применение связанно с большим количеством условий и ограничений, существуют такие задачи, вычисления в которых можно провести лишь с использованием компьютера.

Библиографическая ссылка

Ревегук Ю.А., Рудикова Е.С. ВЕРОЯТНОСТЬ ВЫПАДЕНИЯ «СЧАСТЛИВОГО» БИЛЕТА НА ЭКЗАМЕНЕ // Международный студенческий научный вестник. – 2018. – № 3-1.
;

URL: https://eduherald.ru/ru/article/view?id=18220 (дата обращения: 12.03.2023).

Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»

(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)

Источник

ВЕРОЯТНОСТЬ УСПЕШНОЙ СДАЧИ ЭКЗАМЕНА

Эта задача встает практически перед каждым студентом по крайней мере дважды в год. Мало кто выучивает все экзаменационные вопросы. И часто бывает, что хочется узнать свои шансы, достаточно ли уже выучил, чтобы почти наверняка получить четверку? Конечно, учить надо все вопросы, предмет нужно знать. Но обстоятельства бывают разные… Итак!

Перед экзаменом Вы получили список из N вопросов. Известно, что в билете будет содержаться B вопросов, но распределение их по билетам заранее неизвестно. К экзамену Вы успели выучить только M вопросов. Какова вероятность P того, что во взятом Вами билете Вы будете знать T вопросов? (Все числа должны быть реальные и осмысленные!)

Введите общее число вопросов N:
Введите число выученных вопросов M:
Введите число вопросов в билете B:

Для получения результата нажмите кнопку

Источник

Задание 3. Теория вероятностей на ЕГЭ по математике.

Определение вероятности. Простые задачи из вариантов ЕГЭ.

Вероятность: логика перебора.

Сумма событий, произведение событий и их комбинации

Библиографическое описание:

Похожие статьи

Взаимосвязь теории вероятности и случайных событий

Особенности решения текстовых задач в вариантах ЕГЭ по…

Конструирование электронных учебных материалов по…

Типология текстовых задач в Едином государственном экзамене…

Об автоматизации процедуры проведения единого…

Единый государственный экзамен: достоинства и недостатки

Некоторые факты об успешной подготовке к ЕГЭ

Внеклассное мероприятие «Акция «100 баллов для Победы»

Три основных действия с процентами. Математика вокруг нас

Я считаю, что вопрос, исследованный в моей работе, является актуальным по ряду причин:

Р(А)=, где m ≤n(1)

Теория вероятностей в жизни.

Игры в кости

Лотерея — организованная игра, при которой распределение выгод и убытков зависит от случайного извлечения того или иного билета или номера (жребия, лота).

В результате проделанной мной работы, я добилась реализации поставленных перед собой задач:

во-первых, поняла, что теория вероятностей — это огромный раздел науки математики и изучить его в один заход невозможно;

www.fipi.ru

Противоположные события

Независимые события

Несовместные события

Совместные события

Расчёт вероятности получения положительной отметки при решении тестовых заданий по математике

Библиографическая ссылка

ВЕРОЯТНОСТЬ УСПЕШНОЙ СДАЧИ ЭКЗАМЕНА

Задание 3. Теория вероятностей на ЕГЭ по математике.

Определение вероятности. Простые задачи из вариантов ЕГЭ.

Вероятность: логика перебора.

Сумма событий, произведение событий и их комбинации

Библиографическое описание:

Похожие статьи

Взаимосвязь теории вероятности и случайных событий

Особенности решения текстовых задач в вариантах ЕГЭ по…

Конструирование электронных учебных материалов по…

Типология текстовых задач в Едином государственном экзамене…

Об автоматизации процедуры проведения единого…

Единый государственный экзамен: достоинства и недостатки

Некоторые факты об успешной подготовке к ЕГЭ

Внеклассное мероприятие «Акция «100 баллов для Победы»

Три основных действия с процентами. Математика вокруг нас

Я считаю, что вопрос, исследованный в моей работе, является актуальным по ряду причин:

Р(А)=<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://nsportal.ru/sites/default/files/docpreview_image/2020/09/14/ivanov_proekt_1.docx_image1.jpg" />, где m ≤n(1)

Теория вероятностей в жизни.

Игры в кости

Лотерея — организованная игра, при которой распределение выгод и убытков зависит от случайного извлечения того или иного билета или номера (жребия, лота).

В результате проделанной мной работы, я добилась реализации поставленных перед собой задач:

во-первых, поняла, что теория вероятностей — это огромный раздел науки математики и изучить его в один заход невозможно;

www.fipi.ru

Противоположные события

Независимые события

Несовместные события

Совместные события

Расчёт вероятности получения положительной отметки при решении тестовых заданий по математике

Библиографическая ссылка

ВЕРОЯТНОСТЬ УСПЕШНОЙ СДАЧИ ЭКЗАМЕНА

Р(А)=, где m ≤n(1)