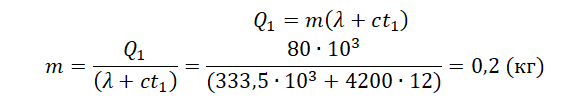В калориметр поместили m = 200 г льда при температуре t1 = −18 ºC, затем сообщили льду количество теплоты Q = 120 кДж и добавили в калориметр еще М = 102 г льда при температуре t2 = 0 ºC. Какая температура t3 установилась в калориметре в состоянии равновесия? Теплообменом содержимого калориметра с окружающей средой и теплоемкостью калориметра можно пренебречь.
Спрятать решение
Решение.
Удельная теплоемкость льда равна сл = 2100 Дж/(кг·К), удельная теплоемкость воды равна св = 4200 Дж/(кг·К), удельная теплота плавления льда равна λ = 330 000 Дж/кг.
Вначале вычислим количество теплоты, необходимое для нагревания начальной массы m льда от −18 ºC до 0 ºC и плавления всей массы льда (m + M) при 0 ºC:
так что оставшееся количество теплоты пойдёт на нагревание полученной воды:
Отсюда
Ответ: t3 ≈ +10 °C.
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
|
Приведено полное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае – уравнение теплового баланса и выражения для количества теплоты, необходимого для нагревания льда, плавления льда и нагревания воды); II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, и обозначений величин, используемых в условии задачи); III) проведены необходимые математические преобразования, приводящие к правильному ответу; IV) представлен правильный ответ |
3 |
|
Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования. Но имеются следующие недостатки. Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. ИЛИ В решении лишние записи, не входящие в решение (возможно, неверные), не отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.). ИЛИ В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) преобразования/вычисления не доведены до конца. ИЛИ Отсутствует пункт IV или в нём допущена ошибка |
2 |
|
Представлены записи, соответствующие одному из следующих случаев. Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения задачи, без каких-либо преобразований с их использованием, направленных на решение задачи и получение ответа. ИЛИ В решении отсутствует одна из исходных формул, необходимая для решения задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. ИЛИ В одной из исходных формул, необходимых для решения задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи |
1 |
| Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла. | 0 |
| Максимальный балл | 3 |
Количество теплоты
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: количество теплоты, удельная теплоёмкость вещества, уравнение теплового баланса.
Как мы знаем, одним из способов изменения внутренней энергии является теплопередача (теплообмен). Предположим, что тело участвует в теплообмене с другими телами, и при этом не совершается механическая работа — ни самим телом, ни другими телами над этим телом.
Если в процессе теплообмена внутренняя энергия тела изменилась на величину , то говорят, что тело получило соответствующее количество теплоты:
.
Если при этом величина отрицательна, т.е. тело отдавало энергию, то говорят также, что тело отдавало тепло. Например, вместо формально верной, но несколько нелепой фразы «тело получило —5 Дж тепла» мы скажем: «тело отдало 5 Дж тепла».
Удельная теплоёмкость вещества
Предположим, что в процессе теплообмена агрегатное состояние вещества тела не изменяется (не происходит плавление, кристаллизация, парообразование или конденсация). Начальную температуру тела обозначим , конечную температуру —
.
Опыт показывает, что количество теплоты, полученное телом, прямо пропорционально массе тела и разности конечной и начальной температур:
Коэффициент пропорциональности c называется удельной теплоёмкостью вещества тела. Удельная теплоёмкость не зависит от формы и размеров тела. Удельные теплоёмкости различных веществ можно найти в таблицах.
Введя обозначение , получим также:
Чтобы понять физический смысл удельной теплоёмкости, выразим её из последней формулы:
Мы видим, что удельная теплоёмкость численно равна количеству теплоты, которое необходимо для нагревания 1кг данного вещества на (или, что то же самое, на
). Измеряется удельная теплоёмкость в Дж/(кг·
C) или в Дж/(кг·K).
Чем больше удельная теплоёмкость вещества, тем большее количество теплоты требуется для нагревания тела данной массы на заданное количество градусов.
В задачах часто фигурируют вода и лёд. Их удельные теплоёмкости желательно помнить.
Вода: Дж/(кг·
C).
Лёд: Дж/(кг·
C).
Произведение удельной теплоёмкости вещества на массу тела называется теплоёмкостью тела и обозначается :
Соответственно, для количества теплоты имеем:
Уравнение теплового баланса
Рассмотрим два тела (обозначим их 1 и 2), которые образуют замкнутую систему. Это означает, что данные тела могут обмениваться энергией только друг с другом, но не с другими телами. Считаем также, что механическая работа не совершается — внутренняя энергия тел меняется только в процессе теплообмена.
Имеется фундаментальный закон природы, подтверждаемый всевозможными экспериментами — закон сохранения энергии. Он гласит, что полная энергия замкнутой системы тел не меняется со временем.
В данном случае закон сохранения энергии утверждает, что внутренняя энергия нашей системы будет оставаться одной и той же: . Если изменение внутренней энергии первого тела равно
, а изменение внутренней энергии второго тела равно
, то суммарное изменение внутренней энергии будет равно нулю:
Но — количество теплоты, полученное первым телом в процессе теплообмена; аналогично
— количество теплоты, полученное вторым телом в процессе теплообмена. Стало быть,
(1)
Попросту говоря, сколько джоулей тепла отдало одно тело, ровно столько же джоулей получило второе тело. Так как система замкнута, ни один джоуль наружу не вышел. Соотношение (1) называется уравнением теплового баланса. В общем случае, когда тел образуют замкнутую систему и обмениваются энергией только с помощью теплопередачи, из закона сохранения энергии с помощью тех же рассуждений получаем общее уравнение теплового баланса:
(2)
В качестве простого примера применения уравнения теплового баланса рассмотрим следующую задачу.
Смешали г воды при температуре
и
г воды при температуре
. Найти установившуюся температуру смеси.
Обозначим искомую установившуюся температуру через . Запишем уравнение теплового баланса (1):
где — удельная теплоёмкость воды. Раскрываем скобки и находим:
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Количество теплоты» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Кусок льда, имеющий температуру 0°С, помещён в калориметр с электронагревателем. Чтобы превратить этот лёд в воду с температурой 12°С, требуется количество теплоты 80 кДж. Какая температура установится внутри калориметра, если лёд получит от нагревателя количество теплоты 60 кДж? Теплоёмкостью калориметра и теплообменом с внешней средой пренебречь.
Ответ:
а) 0°С
б) 4°С
в) 6°С
г) 9°С
📜Теория для решения:
Фазовые переходы и уравнение теплового баланса
Посмотреть решение
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать уравнение теплового баланса для первого случая.
Решение
Запишем исходные данные:
• Начальная температура льда: t0 = 0 oC.
• Конечная температура воды в первом случае: t1 = 12 oC.
• Количество теплоты, выделенное электронагревателем в первом случае: Q1 = 80 кДж.
• Количество теплоты, выделенное электронагревателем во втором случае: Q2 = 60 кДж.
Составим уравнение теплового баланса для первого случая:
Q1=λm+cmt1
Внимание! Вместо разности температур используется значение только конечной температуры, так как начальная температура равна 0.
Найдем массу льда из уравнения теплового баланса для первого случая. Учтем что:
• Удельная теплоемкость воды: c = 4200 Дж/(кг∙К).
• Удельная теплота плавления льда: λ = 333,5 кДж/(кг∙К).
Отсюда:
Чтобы расплавить кусок льда массой 0,5 кг, нужно затратить следующее количество теплоты:
Лед не расплавится весь, так как ему будет сообщено лишь 60 кДж теплоты. Поэтому в калориметре температура будет равна 0 оС.
Ответ: а
Алиса Никитина | Просмотров: 886
Плотность, теплопроводность и теплоемкость льда в зависимости от температуры
В таблице приведены значения плотности, теплопроводности, удельной теплоемкости льда в зависимости от температуры в интервале от 0 до -100°С.
По данным таблицы видно, что с понижением температуры удельная теплоемкость льда уменьшается, а теплопроводность и плотность льда, напротив, растут. Например, при температуре 0°С плотность льда имеет значение 916,2 кг/м3, а при температуре минус 100°С его плотность становится равной 925,7 кг/м3.
Значение удельной теплоемкости льда при 0°С составляет 2050 Дж/(кг·град). При снижении температуры льда с -5 до -100°С его удельная теплоемкость снижается в 1,45 раза. Теплоемкость льда в два раза меньше значения этой величины у воды.
Теплопроводность льда при понижении его температуры с 0 до минус 100°С увеличивается с 2,22 до 3,48 Вт/(м·град). Лед более теплопроводен, чем вода — он может проводить в 4 раза больше тепла при одинаковых граничных условиях.
Следует отметить, что плотность льда меньше плотности воды, однако с понижением температуры плотность льда растет и при приближении к абсолютному нулю температуры плотность льда становится близка к величине плотности воды.
| Температура, °С | Плотность, кг/м3 | Теплопроводность, Вт/(м·град) | Теплоемкость, Дж/(кг·град) |
|---|---|---|---|
| 0.01 (Вода) | 999,8 | 0,56 | 4212 |
| 0 | 916,2 | 2,22 | 2050 |
| -5 | 917,5 | 2,25 | 2027 |
| -10 | 918,9 | 2,30 | 2000 |
| -15 | 919,4 | 2,34 | 1972 |
| -20 | 919,4 | 2,39 | 1943 |
| -25 | 919,6 | 2,45 | 1913 |
| -30 | 920,0 | 2,50 | 1882 |
| -35 | 920,4 | 2,57 | 1851 |
| -40 | 920,8 | 2,63 | 1818 |
| -50 | 921,6 | 2,76 | 1751 |
| -60 | 922,4 | 2,90 | 1681 |
| -70 | 923,3 | 3,05 | 1609 |
| -80 | 924,1 | 3,19 | 1536 |
| -90 | 924,9 | 3,34 | 1463 |
| -100 | 925,7 | 3,48 | 1389 |
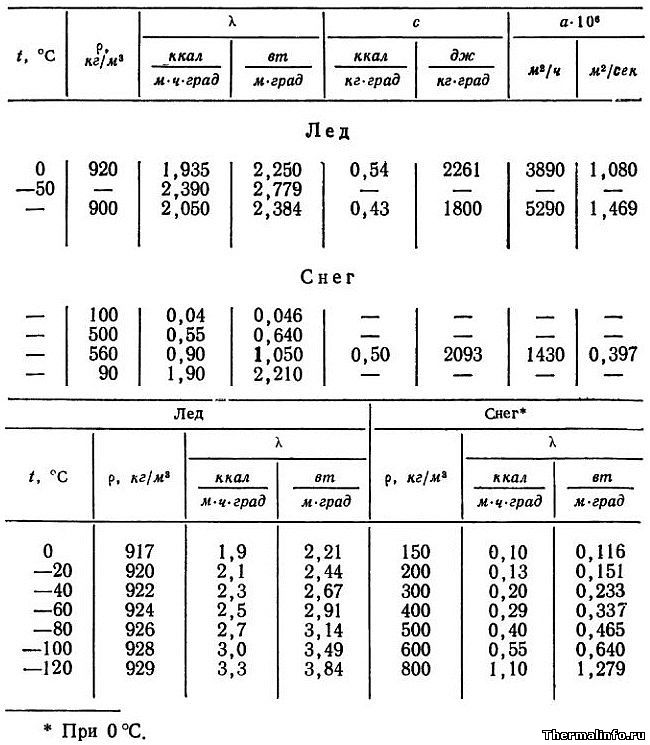
Теплофизические свойства льда и снега
В таблице представлены следующие свойства льда и снега:
- плотность льда, кг/м3;
- теплопроводность льда и снега, ккал/(м·час·град) и Вт/(м·град);
- удельная массовая теплоемкость льда, ккал/(кг·град) и Дж/кг·град);
- коэффициент температуропроводности, м2/час и м2/сек.
Свойства льда и снега представлены в зависимости от температуры в интервале: для льда от 0 до -120°С; для снега от 0 до -50°С в зависимости от уплотненности (плотности). Температуропроводность льда и снега в таблице приведена с множителем 106. Например, температуропроводность льда при температуре 0°С равна 1,08·10-6 м2/с.
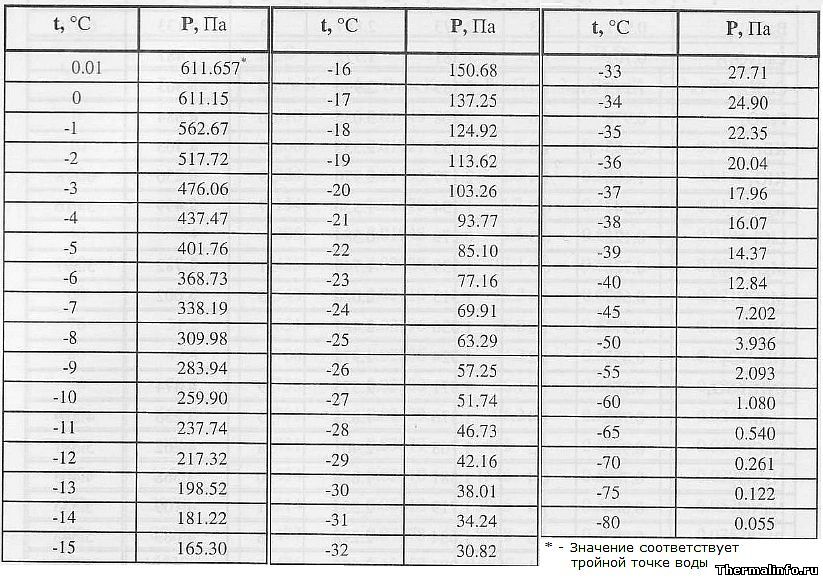
Давление насыщенного пара льда
В таблице приведены значения давления насыщенного пара льда при сублимации (переход льда в пар, миную жидкую фазу) в зависимости от температуры в интервале от 0,01 до -80°С. Из таблицы видно, что с понижением температуры льда давление его насыщенного пара снижается.
Источники:
- Чубик И. А., Маслов А. М. Справочник по теплофизическим характеристикам пищевых продуктов и полуфабрикатов. М.: Пищевая промышленность, 1970 — 184 с.
- Волков. А.И., Жарский. И.М. Большой химический справочник. — М: Советская школа, 2005. — 608 с.
Тип 0 № 1328
В калориметр с воды при температуре
поместили три кубика льда массой
каждый, имеющих температуры
и
Какая температура установится в калориметре после теплообмена? Теплоемкостью калориметра и потерями тепла можно пренебречь. Удельная теплоемкость воды
удельная теплоемкость льда
удельная теплота кристаллизации воды
Спрятать решение
Решение.
Определим — количество теплоты, необходимое для нагревания до 0 °C и плавления всего льда:
Составим уравнение теплового баланса для льда и остывающей воды:
Отсюда
Спрятать критерии
Критерии проверки:
?
Московская олимпиада школьников, 9 класс, 1 тур (отборочный) 2 этап
Классификатор: МКТ и термодинамика. Теплообмен
Насыщенные и ненасыщенные пары
Насыщенный пар
При испарении одновременно с переходом молекул из жидкости в пар происходит и обратный процесс. Беспорядочно двигаясь над поверхностью жидкости, часть молекул, покинувших ее, снова возвращается в жидкость.
Если испарение происходит в закрытом сосуде, то сначала число молекул, вылетевших из жидкости, будет больше числа молекул, возвратившихся обратно в жидкость. Поэтому плотность пара в сосуде будет постепенно увеличиваться. С увеличением плотности пара увеличивается и число молекул, возвращающихся в жидкость. Довольно скоро число молекул, вылетающих из жидкости, станет равным числу молекул пара, возвращающихся обратно в жидкость. С этого момента число молекул пара над жидкостью будет постоянным. Для воды при комнатной температуре это число приблизительно равно $10^{22}$ молекул за $1с$ на $1см^2$ площади поверхности. Наступает так называемое динамическое равновесие между паром и жидкостью.
Пар, находящийся в динамическом равновесии со своей жидкостью, называется насыщенным паром.
Это означает, что в данном объеме при данной температуре не может находиться большее количество пара.
При динамическом равновесии масса жидкости в закрытом сосуде не изменяется, хотя жидкость продолжает испаряться. Точно так же не изменяется и масса насыщенного пара над этой жидкостью, хотя пар продолжает конденсироваться.
Давление насыщенного пара. При сжатии насыщенного пара, температура которого поддерживается постоянной, равновесие сначала начнет нарушаться: плотность пара возрастет, и вследствие этого из газа в жидкость будет переходить больше молекул, чем из жидкости в газ; продолжаться это будет до тех пор, пока концентрация пара в новом объеме не станет прежней, соответствующей концентрации насыщенного пара при данной температуре (и равновесие восстановится). Объясняется это тем, что число молекул, покидающих жидкость за единицу времени, зависит только от температуры.
Итак, концентрация молекул насыщенного пара при постоянной температуре не зависит от его объема.
Поскольку давление газа пропорционально концентрации его молекул, то и давление насыщенного пара не зависит от занимаемого им объема. Давление $р_0$, при котором жидкость находится в равновесии со своим паром, называют давлением насыщенного пара.
При сжатии насыщенного пара большая его часть переходит в жидкое состояние. Жидкость занимает меньший объем, чем пар той же массы. В результате объем пара при неизменной его плотности уменьшается.
Зависимость давления насыщенного пара от температуры. Для идеального газа справедлива линейная зависимость давления от температуры при постоянном объеме. Применительно к насыщенному пару с давлением $р_0$ эта зависимость выражается равенством:
$p_0=nkT$
Так как давление насыщенного пара не зависит от объема, то, следовательно, оно зависит только от температуры.
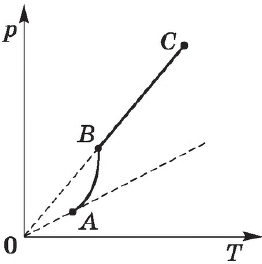
Экспериментально определенная зависимость $Р_0(Т)$ отличается от зависимости $p_0=nkT$ для идеального газа. С увеличением температуры давление насыщенного пара растет быстрее, чем давление идеального газа (участок кривой $АВ$). Это становится особенно очевидным, если провести изохору через точку $А$ (пунктирная прямая). Происходит это потому, что при нагревании жидкости часть ее превращается в пар, и плотность пара растет.
Поэтому, согласно формуле $p_0=nkT$, давление насыщенного пара растет не только в результате повышения температуры жидкости, но и вследствие увеличения концентрации молекул (плотности) пара. Главное различие в поведении идеального газа и насыщенного пара заключается в изменении массы пара при изменении температуры при неизменном объеме (в закрытом сосуде) или при изменении объема при постоянной температуре. С идеальным газом ничего подобного происходить не может (МКТ идеального газа не предусматривает фазового перехода газа в жидкость).
После испарения всей жидкости поведение пара будет соответствовать поведению идеального газа (участок $ВС$ кривой).
Ненасыщенный пар
Если в пространстве, содержащем пары какой-либо жидкости, может происходить дальнейшее испарение этой жидкости, то пар, находящийся в этом пространстве, является ненасыщенным.
Пар, не находящийся в состоянии равновесия со своей жидкостью, называется ненасыщенным.
Ненасыщенный пар можно простым сжатием превратить в жидкость. Как только это превращение началось, пар, находящийся в равновесии с жидкостью, становится насыщенным.
Влажность воздуха
Влажность воздуха — это содержание в воздухе водяного пара.
Окружающий нас атмосферный воздух вследствие непрерывного испарения воды с поверхности океанов, морей, водоемов, влажной почвы и растений всегда содержит в себе водяные пары. Чем больше водяных паров находится в определенном объеме воздуха, тем ближе пар к состоянию насыщения. С другой стороны, чем выше температура воздуха, тем большее количество водяных паров требуется для его насыщения.
В зависимости от количества водяных паров, находящихся при данной температуре в атмосфере, воздух бывает различной степени влажности.
Количественная оценка влажности
Для того чтобы количественно оценить влажность воздуха, пользуются, в частности, понятиями абсолютной и относительной влажности.
Абсолютная влажность — это количество граммов водяного пара, содержащееся в $1м^3$ воздуха при данных условиях, т. е. это плотность водяного пара $р$, выраженная в г/$м^3$.
Относительная влажность воздуха $φ$ — это отношение абсолютной влажности воздуха $р$ к плотности $р_0$ насыщенного пара при той же температуре.
Относительную влажность выражают в процентах:
$φ=({p}/{p_0})·100%$
Концентрация пара связана с давлением ($p_0=nkT$), поэтому относительную влажность можно определить как процентное отношение парциального давления $р$ пара в воздухе к давлению $р_0$ насыщенного пара при той же температуре:
$φ=({p}/{p_0})·100%$
Под парциальным давлением понимают давление водяного пара, которое он производил бы, если бы все другие газы в атмосферном воздухе отсутствовали.
Если влажный воздух охлаждать, то при некоторой температуре находящийся в нем пар можно довести до насыщения. При дальнейшем охлаждении водяной пар начнет конденсироваться в виде росы.
Точка росы
Точка росы — это температура, до которой должен охладиться воздух, чтобы находящийся в нем водяной пар достиг состояния насыщения при постоянном давлении и данной влажности воздуха. При достижении точки росы в воздухе или на предметах, с которыми он соприкасается, начинается конденсация водяного пара. Точка росы может быть вычислена по значениям температуры и влажности воздуха или определена непосредственно конденсационным гигрометром. При относительной влажности воздуха $φ = 100%$ точка росы совпадает с температурой воздуха. При $φ < 100%$ точка росы всегда ниже температуры воздуха. Так, при температуре воздуха $15°$С и относительной влажности $(%) 100, 80, 60, 40$ точка росы оказывается равной $15.0; 11.6; 7.3; 1.5°$С.