Диагностические и тренировочные варианты СтатГрад ЕГЭ Профиль по математике с ответами
Расписание СтатГрад 11 класс ЕГЭ 2022
22.09.2016
10109-22.09.2016
10110-22.09.2016
10111-22.09.2016
10112-22.09.2016
20.12.2016
10209-20.12.2016
10210-20.12.2016
10211-20.12.2016
10212-20.12.2016
26.01.2017
10309-26.01.2017
10310-26.01.2017
10311-26.01.2017
10312-26.01.2017
06.03.2017
10609-06.03.2017
10610-06.03.2017
10611-06.03.2017
10612-06.03.2017
21.04.2017
10709-21.04.2017
10710-21.04.2017
10711-21.04.2017
10712-21.04.2017
21.09.2017
10109-21.09.2017
10110-21.09.2017
10111-21.09.2017
10112-21.09.2017
21.12.2017
10209-21.12.2017
10210-21.12.2017
10211-21.12.2017
10212-21.12.2017
25.01.2018
10309-25.01.2018
10310-25.01.2018
10311-25.01.2018
10312-25.01.2018
06.03.2018
10409-06.03.2018
10410-06.03.2018
10411-06.03.2018
10412-06.03.2018
18.04.2018
10509-18.04.2018
10510-18.04.2018
10511-18.04.2018
10512-18.04.2018
20.09.2018
10109-20.09.2018
10110-20.09.2018
10111-20.09.2018
10112-20.09.2018
20.12.2018
10209-20.12.2018
10210-20.12.2018
10211-20.12.2018
10212-20.12.2018
24.01.2019
10309-24.01.2019
10310-24.01.2019
10311-24.01.2019
10312-24.01.2019
06.02.2019 (10 класс)
00309-06.02.2019
00310-06.02.2019
13.03.2019
10409-13.03.2019
10410-13.03.2019
10411-13.03.2019
10412-13.03.2019
19.04.2019
10509-19.04.2019
10510-19.04.2019
10511-19.04.2019
10512-19.04.2019
24.04.2019 (Итоговая контрольная работа Профильный уровень 10 класс)
00403-24.04.2019
00404-24.04.2019
17.05.2019 (10-11 класс)
00509-17.05.2019
00510-17.05.2019
00511-17.05.2019
00512-17.05.2019
25.09.2019
1910109-25.09.2019
1910110-25.09.2019
1910111-25.09.2019
1910112-25.09.2019
18.12.2019
1910209-18.12.2019
1910210-18.12.2019
1910211-18.12.2019
1910212-18.12.2019
29.01.2020
1910309-29.01.2020
1910310-29.01.2020
1910311-29.01.2020
1910312-29.01.2020
06.02.2020 (10 класс)
1900209-06.02.2020
1900210-06.02.2020
12.02.2020 (10 класс Тригонометрия)
1900403-12.02.2020
1900404-12.02.2020
11.03.2020
1910409-11.03.2020
1910410-11.03.2020
1910411-11.03.2020
1910412-11.03.2020
02.04.2020 (10 класс Теория вероятностей и статистика)
1900503-02.04.2020
1900504-02.04.2020
15.04.2020 (10 класс Итоговая уровневая работа)
1900603-15.04.2020
1900604-15.04.2020
22.04.2020
1910509-22.04.2020
1910510-22.04.2020
1910511-22.04.2020
1910512-22.04.2020
15.05.2020
1900709-15.05.2020
1900710-15.05.2020
30.09.2020
2010109-30.09.2020
2010110-30.09.2020
2010111-30.09.2020
2010112-30.09.2020
16.12.2020
2010209-16.12.2020
2010210-16.12.2020
2010211-16.12.2020
2010212-16.12.2020
28.01.2021 (10 класс)
2000309-28.01.2021
2000310-28.01.2021
10.02.2021
2010309-10.02.2021 [с видео-разбором]
2010310-10.02.2021
2010311-10.02.2021
2010312-10.02.2021
16.03.2021
2010409-16.03.2021
2010410-16.03.2021
2010411-16.03.2021
2010412-16.03.2021
29.04.2021
2010509-29.04.2021 [с видео-разбором]
2010510-29.04.2021
2010511-29.04.2021
2010512-29.04.2021
13.05.2021
2000709-13.05.2021
2000710-13.05.2021
28.09.2021
2110109-28.09.2021
2110110-28.09.2021
2110111-28.09.2021
2110112-28.09.2021
15.12.2021
2110209-15.12.2021
2110210-15.12.2021
2110211-15.12.2021
2110212-15.12.2021
27.01.2022 (10-11 класс)
2100109-27.01.2022
2100110-27.01.2022
16.02.2022
2110309-16.02.2022
2110310-16.02.2022
2110311-16.02.2022
2110312-16.02.2022
15.03.2022
2110409-15.03.2022
2110410-15.03.2022
2110411-15.03.2022
2110412-15.03.2022
28.04.2022
2110509-28.04.2022
2110510-28.04.2022
2110511-28.04.2022
2110512-28.04.2022
18.05.2022
2100309-18.05.2022
2100310-18.05.2022
28.09.2022
2210109-28.09.2022
2210110-28.09.2022
2210111-28.09.2022
2210112-28.09.2022
13.12.2022
2210209-13.12.2022
2210210-13.12.2022
2210211-13.12.2022
2210212-13.12.2022
08.02.2023 (10 класс)
2200109-08.02.2023
2200110-08.02.2023
28.02.2023
2210309-28.02.2023
2210310-28.02.2023
2210311-28.02.2023
2210312-28.02.2023
Сборники тренировочных тестов по математике профильного уровня для ЕГЭ в 2023 году и для ЕГЭ прошлых лет. Все тренировочные варианты/пробники содержат ответы и решения ко 2-й части кима. Обсудить решение и задания каждого варианта вы можете в комментариях под ними. РЕШАТЬ ТЕСТЫ
Обращайте внимание на уровень пробника — здесь только профильный! Базовый уровень смотрите здесь.
- Всё про ЕГЭ 2023
- Демоверсия 2023 + изменения 2023
Что почитать?
- Из актуального: рекомендации от ФИПИ по профильной математике
Что изменилось в ЕГЭ 2023 по математике
Представляете — ничего 
Теория для подготовки к ЕГЭ 2023 по математике
Для теории у нас создан особый раздел «Теория для ЕГЭ по математике». Отдельно может порекомендовать посмотреть сборник шпаргалок для ЕГЭ по математике и на проекте ЕГЭ100Баллов целая ветка, посвященная шпаргалкам.
Что можно брать с собой на ЕГЭ по профильной математике?
На ЕГЭ по математике как всегда с собой можно взять только линейку. Никаких калькуляторов и мобильных телефонов, конечно же. Вода и шоколадка разрешаются 
Выбирайте вариант, сверяйте с ответами, оставляйте комментарии НИЖЕ
Критерии
Оценивание
| № задания | 1-11 | 12, 14, 15 | 13, 16 | 17, 18 | Всего |
|---|---|---|---|---|---|
| Баллы | 1 | 2 | 3 | 4 | 31 |
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–11 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться справочными материалами, выдаваемыми вместе с работой.
Разрешается использовать только линейку, но можно сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене не используются.
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
| № задания | 1-11 | 12, 14, 15 | 13, 16 | 17, 18 | Всего |
|---|---|---|---|---|---|
| Баллы | 1 | 2 | 3 | 4 | 31 |
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–11 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться справочными материалами, выдаваемыми вместе с работой.
Разрешается использовать только линейку, но можно сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене не используются.
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |
5 новых тренировочных работ статград по математике 11 класс в формате реального ЕГЭ 2022 год база и профиль. Тренировочные варианты с ответами ЕГЭ статград за 2022 учебный год. Каждая работа по математике состоит из вариантов базового и профильного уровня.
Тренировочная работа №1 статград ЕГЭ 2022 по математике 11 класс варианты МА2110101-МА2110112
Тренировочная работа №1 ЕГЭ 2022 статград по математике 10-11 класс варианты МА2100101-МА2100110
Тренировочная работа №2 статград ЕГЭ 2022 по математике 11 класс варианты МА2110201-МА2110212
Тренировочная работа №3 статград ЕГЭ 2022 по математике 11 класс варианты МА2110301-МА2110312
Тренировочная работа №4 статград ЕГЭ 2022 по математике 11 класс варианты МА2110401-МА2110412
Тренировочная работа №5 статград ЕГЭ 2022 по математике 11 класс варианты МА2110501-МА2110512
18.05.2022 (18 мая) Тренировочная работа №2 статград по математике 10-11 класс ответы и задания для вариантов
Решите данные пробники и вам будет легче на ЕГЭ 2022 по математике, который пройдёт 2-3 июня, а также можете посмотреть:
Вариант с досрочного ЕГЭ 2022 по математике профильный уровень
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Тренировочная работа №5 статград ЕГЭ 2022 по математике 11 класс задания и ответы для тренировочных вариантов МА2110501-МА2110512 базового и профильного уровня. Официальная дата проведения работы: 28 апреля 2022 год.
Скачать варианты базового уровня
Скачать варианты профильного уровня
Все ответы (решения) и задания (без водяного знака)
Тренировочные варианты статград математика 11 класс ЕГЭ 2022 профильный уровень МА2110509-МА2110512
Тренировочные варианты статград математика 11 класс ЕГЭ 2022 базовый уровень МА2110501-МА2110508
Задания и ответы варианта МА2110501 статграда:
2)Мотоциклист проехал 14 километров за 21 минуту. Сколько километров он проедет за 30 минут, если будет ехать с той же скоростью?
4)На рисунке показано изменение атмосферного давления в течение трёх суток. По горизонтали указаны дни недели и время, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Определите по рисунку значение атмосферного давления в среду в 6:00. Ответ дайте в миллиметрах ртутного столба.
5)План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.
6)В период распродажи магазин снижал цены дважды: в первый раз на 10 %, во второй — на 25 %. Сколько рублей стал стоить чайник после второго снижения цен, если до начала распродажи он стоил 1600 рублей?
10)Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота перил h1 равна 1 м, а наибольшая высота h2 равна 2 м. Ответ дайте в метрах.
11)В фирме такси в наличии 20 легковых автомобилей: 7 из них чёрного цвета с жёлтыми надписями на боках, остальные — жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.
13)Однородный шар диаметром 3 см весит 162 грамма. Сколько граммов весит шар диаметром 2 см, изготовленный из того же материала?
15)В треугольнике ABC проведена биссектриса AL, угол ALC равен 160° , угол ABC равен 148° . Найдите угол ACB . Ответ дайте в градусах.
18)Во дворе школы растут всего три дерева: берёза, клён и дуб. Берёза выше клёна на 1 метр, но ниже дуба на 3 метра. Выберите утверждения, которые верны при указанных условиях. 1) Среди указанных деревьев не найдётся двух одной высоты. 2) Берёза, растущая во дворе школы, выше дуба, растущего там же. 3) Любое дерево, помимо указанных, которое ниже берёзы, растущей во дворе школы, также ниже клёна, растущего там же. 4) Любое дерево, помимо указанных, которое ниже клёна, растущего во дворе школы, также ниже берёзы, растущей там же.
19)Найдите четырёхзначное число, большее 1000, но меньшее 1700, которое делится на 45 и сумма цифр которого равна 18. В ответе укажите какое-нибудь одно такое число.
20)Теплоход, скорость которого в неподвижной воде равна 24 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 4 км/ч, стоянка длится 3 часа, а в исходный пункт теплоход возвращается через 36 часов после отправления из него. Сколько километров проходит теплоход за весь рейс?
21)Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 254, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?
Задания и ответы варианта МА2110502 статграда:
2)За 20 минут автобус проехал 23 километра. Сколько километров он проедет за 35 минут, если будет ехать с той же скоростью?
4)На рисунке показано изменение атмосферного давления в течение трёх суток. По горизонтали указаны дни недели и время, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Определите по рисунку значение атмосферного давления в четверг в 12:00. Ответ дайте в миллиметрах ртутного столба.
5)План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.
6)В период распродажи магазин снижал цены дважды: в первый раз на 15 %, во второй — на 25 %. Сколько рублей стал стоить чайник после второго снижения цен, если до начала распродажи он стоил 2000 рублей?
10)Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота перил h1 равна 0,7 м, а наибольшая высота h2 равна 1,5 м. Ответ дайте в метрах.
11)В фирме такси в наличии 15 легковых автомобилей: 3 из них чёрного цвета с жёлтыми надписями на боках, остальные — жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.
13)Однородный шар диаметром 3 см весит 189 грамм. Сколько граммов весит шар диаметром 4 см, изготовленный из того же материала?
15)В треугольнике ABC проведена биссектриса AL, угол ALC равен 41° , угол ABC равен 26° . Найдите угол ACB . Ответ дайте в градусах.
18)Кошка Китти весит на 3 килограмма больше кошки Машки, а кошка Лада на полтора килограмма легче кошки Машки. Выберите утверждения, которые верны при указанных условиях. 1) Любая кошка, помимо указанных, которая весит меньше Лады, весит также меньше Китти. 2) Любая кошка, помимо указанных, которая весит меньше Китти, весит также меньше Лады. 3) Среди указанных кошек нет кошек тяжелее Китти. 4) Машка весит меньше Лады.
19)Найдите четырёхзначное число, большее 1500, но меньшее 2000, которое делится на 24 и сумма цифр которого равна 21. В ответе укажите какоенибудь одно такое число.
20)Теплоход, скорость которого в неподвижной воде равна 15 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 3 км/ч, стоянка длится 7 часов, а в исходный пункт теплоход возвращается через 37 часов после отправления из него. Сколько километров проходит теплоход за весь рейс?
21)Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 496, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?
Задания и ответы варианта МА2110505 статграда:
2)Принтер печатает одну страницу за 8 секунд. Какое наибольшее количество страниц можно напечатать на этом принтере за 14 минут?
4)На рисунке показано изменение атмосферного давления в течение трёх суток. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Определите по рисунку наименьшее значение атмосферного давления (в миллиметрах ртутного столба) в четверг.
6)Банк начисляет на срочный вклад 8 % годовых. Вкладчик положил на счёт 7000 рублей. Сколько рублей будет на этом счёте через год, если никаких операций, кроме начисления процентов, со счётом проводиться не будет?
10)Столб подпирает детскую горку посередине. Найдите высоту l этого столба, если высота горки h равна 3,9 м. Ответ дайте в метрах.
11)На экзамене будет 50 билетов, Серёжа не выучил 11 из них. Найдите вероятность того, что ему попадётся выученный билет.
13)Две кружки имеют форму цилиндра. Первая кружка в полтора раза ниже второй, а вторая вдвое шире первой. Во сколько раз объём первой кружки меньше объёма второй?
14)На рисунке точками показан годовой объём добычи угля в России открытым способом в период с 2001 по 2010 год. По горизонтали указывается год, по вертикали — объём добычи угля в миллионах тонн. Для наглядности точки соединены ломаной линией.
16)В основании прямой призмы лежит прямоугольный треугольник, катеты которого равны 3 и 16. Найдите объём призмы, если её высота равна 3.
18)Двадцать выпускников одного из одиннадцатых классов сдавали ЕГЭ по русскому языку. Самый низкий балл, полученный в этом классе, был равен 28, а самый высокий — 83. Выберите утверждения, которые верны при указанных условиях. 1) Среди этих выпускников есть человек, который получил 83 балла за ЕГЭ по русскому языку. 2) Среди этих выпускников есть двадцать человек с равными баллами за ЕГЭ по русскому языку. 3) Среди этих выпускников есть человек, получивший 100 баллов за ЕГЭ по русскому языку. 4) Баллы за ЕГЭ по русскому языку любого из этих двадцати человек не ниже 27.
19)Найдите четырёхзначное число, большее 2000, но меньшее 4000, которое делится на 18 и каждая следующая цифра которого больше предыдущей. В ответе укажите какое-нибудь одно такое число.
20)Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 19 км. Путь из А в В занял у туриста 5 часов, из которых 4 часа ушло на спуск. Найдите скорость туриста на спуске, если она больше скорости на подъёме на 1 км/ч. Ответ дайте в км/ч.
21)Список заданий викторины состоял из 50 вопросов. За каждый правильный ответ ученик получал 9 очков, за неправильный ответ с него списывали 16 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 171 очко, если известно, что по крайней мере один раз он ошибся?
Задания и ответы варианта МА2110506 статграда:
2)Принтер печатает одну страницу за 9 секунд. Какое наибольшее количество страниц можно напечатать на этом принтере за 12 минут?
4)На рисунке показано изменение атмосферного давления в течение трёх суток. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Определите по рисунку наименьшее значение атмосферного давления (в миллиметрах ртутного столба) во вторник.
5)План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.
6)Банк начисляет на срочный вклад 12 % годовых. Вкладчик положил на счёт 3000 рублей. Сколько рублей будет на этом счёте через год, если никаких операций, кроме начисления процентов, со счётом проводиться не будет?
10)Столб подпирает детскую горку посередине. Найдите высоту l этого столба, если высота горки h равна 3,2 м. Ответ дайте в метрах.
11)На экзамене будет 40 билетов, Яша не выучил 4 из них. Найдите вероятность того, что ему попадётся выученный билет.
13)Даны две кружки цилиндрической формы. Первая кружка в четыре с половиной раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой кружки меньше объёма второй?
14)На рисунке точками показан прирост населения Китая в период с 2004 по 2013 год. По горизонтали указывается год, по вертикали — прирост населения в процентах (увеличение численности населения относительно прошлого года). Для наглядности точки соединены ломаной линией.
16)В основании прямой призмы лежит прямоугольный треугольник, катеты которого равны 13 и 4. Найдите объём призмы, если её высота равна 5.
18)В посёлке городского типа всего 17 жилых домов. Высота каждого дома меньше 25 метров, но не меньше 5 метров. Выберите утверждения, которые верны при указанных условиях. 1) В посёлке есть жилой дом высотой 25 метров. 2) Разница в высоте любых двух жилых домов посёлка больше 6 метров. 3) В посёлке нет жилого дома высотой 4 метра. 4) Высота любого жилого дома в посёлке не меньше 3 метров.
19)Найдите четырёхзначное число, большее 6000, но меньшее 7000, которое делится на 12 и каждая следующая цифра которого меньше предыдущей. В ответе укажите какое-нибудь одно такое число.2
20)Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 14 км. Путь из А в В занял у туриста 3 часа, из которых 1 час ушёл на спуск. Найдите скорость туриста на спуске, если она больше скорости на подъёме на 2 км/ч. Ответ дайте в км/ч.
21)Список заданий викторины состоял из 25 вопросов. За каждый правильный ответ ученик получал 5 очков, за неправильный ответ с него списывали 7 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 60 очков, если известно, что по крайней мере один раз он ошибся?
Задания и ответы варианта МА2110509 статграда:
2)В среднем из 75 морозильников, поступивших в продажу, 6 имеют скрытый дефект. Найдите вероятность того, что один случайно выбранный для контроля морозильник не имеет дефекта.
3)В четырёхугольник ABCD , периметр которого равен 56, вписана окружность, AB =12. Найдите длину стороны CD .
5)Шар, объём которого равен 29π , вписан в куб. Найдите объём куба.
8)Из городов A и B одновременно навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 4 часа раньше, чем велосипедист приехал в A, а встретились они через 1 час 30 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
10)По отзывам покупателей Пётр Петрович оценил надёжность двух интернетмагазинов. Вероятность того, что нужный товар доставят из магазина А вовремя, равна 0,84. Вероятность того, что товар доставят вовремя из магазина Б, равна 0,9. Пётр Петрович заказал товары одновременно в двух магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар вовремя.
13)Радиус основания конуса равен 8, высота равна 4. Сечение конуса плоскостью α , проходящей через его вершину, отсекает от окружности основания дугу в 60° . а) Докажите, что величина угла между плоскостью α и плоскостью основания конуса равна 30° . б) Найдите расстояние от центра основания конуса до плоскости сечения.
15)15 августа планируется взять кредит в банке на 16 месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца (r — целое число); — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма денег, которую нужно выплатить банку за весь срок кредитования, на 51 % больше, чем сумма, взятая в кредит. Найдите r.
16)Дана равнобедренная трапеция ABCD с основаниями AD и BC , причём AD BC = 2 . а) Докажите, что высота CH трапеции разбивает основание AD на отрезки, один из которых втрое больше другого. б) Пусть O — точка пересечения диагоналей трапеции. Найдите расстояние от вершины C до середины отрезка OD , если AB =13 и BC =10 .
Задания и ответы варианта МА2110510 статграда:
2)В среднем из 80 морозильников, поступивших в продажу, 4 имеют скрытый дефект. Найдите вероятность того, что один случайно выбранный для контроля морозильник не имеет дефекта.
3)В четырёхугольник ABCD , периметр которого равен 48, вписана окружность, AB =14. Найдите длину стороны CD .
5)Шар, объём которого равен 23π, вписан в куб. Найдите объём куба.
8)Из городов A и B одновременно навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 2 часа раньше, чем велосипедист приехал в A, а встретились они через 1 час 20 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
10)По отзывам покупателей Пётр Петрович оценил надёжность двух интернетмагазинов. Вероятность того, что нужный товар доставят из магазина А вовремя, равна 0,85. Вероятность того, что товар доставят вовремя из магазина Б, равна 0,86. Пётр Петрович заказал товары одновременно в двух магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар вовремя.
13)Радиус основания конуса равен 4, высота равна 6. Сечение конуса плоскостью α , проходящей через его вершину, отсекает от окружности основания дугу в 60° . а) Докажите, что величина угла между плоскостью α и плоскостью основания конуса равна 60° . б) Найдите расстояние от центра основания конуса до плоскости сечения.
15)15 августа планируется взять кредит в банке на 18 месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца (r — целое число); — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма денег, которую нужно выплатить банку за весь срок кредитования, на 38 % больше, чем сумма, взятая в кредит. Найдите r.
16)Дана равнобедренная трапеция ABCD с основаниями AD и BC , причём AD BC = 2 . а) Докажите, что высота CH трапеции разбивает основание AD на отрезки, один из которых втрое больше другого. б) Пусть O — точка пересечения диагоналей трапеции. Найдите расстояние от вершины C до середины отрезка OD , если AB =17 и BC =16 .
Задания и ответы варианта МА2110511 статграда:
2)Вероятность того, что новому ноутбуку в течение года потребуется ремонт, равна 0,051. Из 1000 проданных ноутбуков в течение года ремонт потребовался 45 ноутбукам. На сколько отличается частота события «в течение года потребуется ремонт» от вероятности этого события?
3)Два угла вписанного в окружность четырёхугольника равны 101° и 99° . Найдите величину большего из оставшихся углов. Ответ дайте в градусах.
5)Один цилиндрический сосуд вчетверо выше второго, зато второй втрое шире первого. Во сколько раз объём второго сосуда больше объёма первого?
8)Имеется два сплава. Первый содержит 10 % никеля, второй — 35 % никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 25 % никеля. На сколько килограммов масса первого сплава была меньше массы второго?
10)Биатлонист 5 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние три промахнулся. Результат округлите до сотых.
15)15 августа планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца (r — целое число); — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма денег, которую нужно выплатить банку за весь срок кредитования, на 56 % больше, чем сумма, взятая в кредит. Найдите r.
16)Дана равнобедренная трапеция ABCD с основаниями AD и BC , причём AD BC = 2 . а) Докажите, что высота CH трапеции разбивает основание AD на отрезки, один из которых втрое больше другого. б) Пусть O — точка пересечения диагоналей трапеции. Найдите расстояние от вершины C до середины отрезка OD , если AB =15 и BC =18 .
Другие тренировочные варианты статград ЕГЭ по математике 11 класс:
Работы СТАТГРАД по математике задания и ответы
Варианты МА2110401-МА2110412 ЕГЭ 2022 работа статград математика 11 класс с ответами
Share the post «Варианты база и профиль ЕГЭ 2022 работа статград математика 11 класс с ответами»
- VKontakte
Метки: ЕГЭ 2022заданияматематика 11 классответыстатградтренировочная работа
Тренировочная работа №1 статград ЕГЭ 2022 по математике 11 класс задания и ответы для вариантов базового и профильного уровня, официальная дата проведения: 28.09.2021 (28 сентября 2021 год).
Варианты базового уровня (МА2110101-МА2110108): скачать
Варианты профильного уровня (МА2110109-МА2110112): скачать
Все ответы, задания (без водяного знака) и критерии: скачать
Тренировочная работа №1 статград ЕГЭ 2022 по математике 11 класс задания и ответы:
Задания и ответы варианта МА2110101:
2)Поезд Хабаровск–Благовещенск отправляется в 13:57, а прибывает в 2:57 на следующий день (время московское). Сколько часов поезд находится в пути?
Ответ: 13
4)На рисунке жирными точками показана цена золота, установленная Центробанком РФ во все рабочие дни в октябре 2008 года. По горизонтали указываются числа месяца, по вертикали — цена золота в рублях за грамм. Для наглядности жирные точки на рисунке соединены линиями.
Ответ: 967,5
5)План местности разбит на клетки. Каждая клетка является квадратом размером 1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.
Ответ: 35
6)В технических вузах собираются учиться 49 выпускников школы. Они составляют 49 % от числа выпускников. Сколько в школе выпускников?
Ответ: 100
8)Работа постоянного тока (в джоулях) вычисляется по формуле 2 A I Rt = , где I — сила тока (в амперах), R — сопротивление (в омах), t — время (в секундах). Пользуясь этой формулой, найдите A (в джоулях), если t = 4 c, I = 7 А и R = 5 Ом.
Ответ: 980
10)Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 35 м и 75 м. Найдите длину забора (в метрах), которым нужно огородить участок, предусмотрев проезд шириной 4 м.
Ответ: 216
11)Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений — по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день запланировано 32 выступления, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность того, что выступление исполнителя из России состоится в третий день конкурса?
Ответ: 0,15
12)Строительный подрядчик планирует купить 20 тонн облицовочного кирпича у одного из трёх поставщиков. Один кирпич весит 5 кг. Цена кирпича и условия доставки всей покупки приведены в таблице.
13)В бак, имеющий форму правильной четырёхугольной призмы со стороной основания 80 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 5 см. Ответ дайте в кубических сантиметрах.
14)На рисунке точками показан прирост населения Китая в период с 2004 по 2013 год. По горизонтали указывается год, по вертикали — прирост населения в процентах (увеличение численности населения относительно прошлого года). Для наглядности точки соединены линией.
16)Два ребра прямоугольного параллелепипеда равны 8 и 5, а объём параллелепипеда равен 280. Найдите площадь поверхности этого параллелепипеда.
18)Перед футбольным турниром измерили рост игроков футбольной команды города N. Оказалось, что рост каждого из футболистов этой команды больше 170 см и меньше 190 см. Выберите утверждения, которые верны при указанных условиях. 1) В футбольной команде города N обязательно есть игрок, рост которого равен 160 см. 2) В футбольной команде города N нет игроков с ростом 169 см. 3) Рост любого футболиста этой команды меньше 190 см. 4) Разница в росте любых двух игроков футбольной команды города N составляет более 20 см.
19)Найдите четырёхзначное число, большее 1000, но меньшее 1300, которое делится на 18 и сумма цифр которого равна 18. В ответе укажите какое-нибудь одно такое число.
20)Товарный поезд каждую минуту проезжает на 200 метров меньше, чем скорый, и на путь в 240 км тратит времени на 1 час больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
21)Клетки таблицы 7 5 × раскрашены в чёрный и белый цвета так, что получилось 27 пар соседних клеток разного цвета и 21 пара соседних клеток чёрного цвета. (Клетки считаются соседними, если у них есть общая сторона.) Сколько пар соседних клеток белого цвета?
Задания и ответы варианта МА2110102:
2)Поезд Благовещенск–Тында отправляется в 13:02, а прибывает в 5:02 на следующий день (время московское). Сколько часов поезд находится в пути?
Ответ: 16
4)На рисунке жирными точками показана цена никеля на момент закрытия биржевых торгов во все рабочие дни с 10 по 26 ноября 2008 года. По горизонтали указаны числа месяца, по вертикали — цена никеля в долларах США за тонну. Для наглядности жирные точки на рисунке соединены линиями.
Ответ: 10000
5)План местности разбит на клетки. Каждая клетка является квадратом размером 1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.
Ответ: 7
6)В технических вузах собираются учиться 20 выпускников школы. Они составляют 25 % от числа всех выпускников. Сколько в школе выпускников?
Ответ: 80
10)Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 25 м и 50 м. Найдите длину забора (в метрах), которым нужно огородить участок, предусмотрев проезд шириной 3 м.
Ответ: 147
11)Конкурс исполнителей проводится в 5 дней. Всего заявлено 50 выступлений — по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день запланировано 14 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность того, что выступление исполнителя из России состоится в третий день конкурса?
Ответ: 0,18
12)Строительный подрядчик планирует купить 6 тонн облицовочного кирпича у одного из трёх поставщиков. Один кирпич весит 5 кг. Цена кирпича и условия доставки всей покупки приведены в таблице.
13)В бак, имеющий форму правильной четырёхугольной призмы со стороной основания 20 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 20 см. Ответ дайте в кубических сантиметрах.
14)На рисунке точками показан годовой объём добычи угля в России открытым способом в период с 2001 по 2010 год. По горизонтали указывается год, по вертикали — объём добычи угля в миллионах тонн. Для наглядности точки соединены линиями.
16)Два ребра прямоугольного параллелепипеда равны 1 и 2, а объём параллелепипеда равен 6. Найдите площадь поверхности этого параллелепипеда.
18)В зоомагазине в один из аквариумов запустили 20 рыбок. Длина каждой рыбки больше 3 см, но не превышает 13 см. Выберите утверждения, которые верны при указанных условиях. 1) Десять рыбок в этом аквариуме меньше 3 см. 2) В этом аквариуме нет рыбки длиной 14 см. 3) Разница в длине любых двух рыбок не больше 10 см. 4) Длина каждой рыбки больше 13 см.
19)Найдите четырёхзначное число, большее 2000, но меньшее 3000, которое делится на 60 и сумма цифр которого равна 12. В ответе укажите какое-нибудь одно такое число.
20)Товарный поезд каждую минуту проезжает на 200 метров меньше, чем скорый, и на путь в 360 км тратит времени на 1 час больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
21)Клетки таблицы 6 6 × раскрашены в чёрный и белый цвета так, что получилось 30 пар соседних клеток разного цвета и 16 пар соседних клеток чёрного цвета. (Клетки считаются соседними, если у них есть общая сторона.) Сколько пар соседних клеток белого цвета?
Задания и ответы варианта МА2110105:
2)Бегун пробежал 180 м за 24 секунды. Найдите среднюю скорость бегуна на дистанции. Ответ дайте в километрах в час.
Ответ: 27
4)На рисунке жирными точками показана цена золота на момент закрытия биржевых торгов во все рабочие дни с 11 по 27 июля 2000 года. По горизонтали указываются числа месяца, по вертикали — цена унции золота в долларах США. Для наглядности жирные точки на рисунке соединены линиями.
Ответ: 21
5)План местности разбит на клетки. Каждая клетка является квадратом размером 1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.
Ответ: 30
6)В школе французский язык изучают 165 учащихся, что составляет 30 % от числа всех учащихся школы. Сколько учащихся в школе?
Ответ: 550
10)Участок земли для строительства дачи имеет форму прямоугольника, стороны которого равны 50 м и 40 м. Одна из больших сторон участка идёт вдоль реки, а три остальные стороны нужно огородить забором. Найдите длину этого забора. Ответ дайте в метрах.
Ответ: 130
11)В соревнованиях по толканию ядра участвуют 6 спортсменов из Великобритании, 3 спортсмена из Франции, 6 спортсменов из Германии и 10 — из Италии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Франции.
Ответ: 0,12
12)Для транспортировки 44 тонн груза на 1300 км можно воспользоваться услугами одной из трёх фирм-перевозчиков. Стоимость перевозки и грузоподъёмность автомобилей каждого перевозчика указаны в таблице.
13)В бак, имеющий форму правильной четырёхугольной призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке увеличился в 1,4 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
14)На графике изображена зависимость скорости движения рейсового автобуса от времени. На вертикальной оси отмечена скорость автобуса в км/ч, на горизонтальной — время в минутах, прошедшее с начала движения автобуса.
15)Четырёхугольник ABCD вписан в окружность. Угол ABC равен 132° , угол CAD равен 80°. Найдите угол ABD. Ответ дайте в градусах.
16)Два ребра прямоугольного параллелепипеда равны 9 и 3, а объём параллелепипеда равен 189. Найдите площадь поверхности этого параллелепипеда.
18)Перед волейбольным турниром измерили рост игроков волейбольной команды города N. Оказалось, что рост каждого из волейболистов этой команды больше 190 см и меньше 210 см. Выберите утверждения, которые верны при указанных условиях. 1) В волейбольной команде города N обязательно есть игрок, рост которого равен 220 см. 2) В волейбольной команде города N нет игроков с ростом 189 см. 3) Рост любого волейболиста этой команды меньше 210 см. 4) Разница в росте любых двух игроков волейбольной команды города N составляет более 20 см.
19)Найдите четырёхзначное число, большее 6000, но меньшее 7000, которое делится на 12 и каждая следующая цифра которого меньше предыдущей. В ответе укажите какое-нибудь одно такое число.
20)По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 80 км/ч и 70 км/ч. Длина пассажирского поезда равна 150 метрам. Найдите длину скорого поезда, если время, за которое он прошёл мимо пассажирского поезда, равно 12 секундам. Ответ дайте в метрах.
21)В магазине квас на разлив можно купить в бутылках, причём стоимость кваса в бутылке складывается из стоимости самой бутылки и кваса, налитого в неё. Цена бутылки не зависит от её объёма. Бутылка кваса объёмом 1 литр стоит 35 рублей, объёмом 2 литра — 65 рублей. Сколько рублей будет стоить бутылка кваса объёмом 1,5 литра?
Задания и ответы варианта МА2110109:
2)В соревнованиях по толканию ядра участвуют спортсмены из четырёх стран: 5 из Чехии, 4 из Словакии, 8 из Австрии и 8 из Швейцарии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, окажется из Чехии.
Ответ: 0,2
3)В треугольнике ABC угол C равен 32° , AD — биссектриса, угол BAD равен 23° . Найдите угол ADB. Ответ дайте в градусах.
Ответ: 55
5)Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 10 и 24, и боковым ребром, равным 19.
Ответ: 1228
8)Моторная лодка прошла против течения реки 112 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 3 км/ч. Ответ дайте в км/ч.
Ответ: 11
10)В коробке 8 синих, 6 красных и 11 зелёных фломастеров. Случайным образом выбирают два фломастера. Какова вероятность того, что окажутся выбраны один синий и один красный фломастер?
15)В июле планируется взять кредит на сумму 800 800 рублей. Условия его возврата таковы: — каждый январь долг возрастает на 20 % по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить некоторую часть долга. На сколько рублей больше придётся отдать в случае, если кредит будет полностью погашен тремя равными платежами (то есть за 3 года), по сравнению со случаем, если кредит будет полностью погашен двумя равными платежами (то есть за 2 года)?
16)Около окружности с центром O описана трапеция ABCD с основаниями AD и BC . а) Докажите, что AB — диаметр окружности, описанной около треугольника AOB. б) Найдите отношение площади четырёхугольника, вершины которого — точки касания окружности со сторонами трапеции, к площади самой трапеции ABCD , если известно, что AB CD = , а основания трапеции относятся как 1: 2 .
Задания и ответы варианта МА2110111:
2)В чемпионате по гимнастике участвуют 50 спортсменок: 9 из России, 18 из США, остальные из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
Ответ: 0,46
3)В треугольнике ABC угол C равен 56° , AD — биссектриса, угол CAD равен 38° . Найдите угол B . Ответ дайте в градусах.
Ответ: 48
5)Если каждое ребро куба увеличить на 1, то площадь его поверхности увеличится на 42. Найдите ребро куба.
Ответ: 3
8)Моторная лодка прошла против течения реки 96 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 10 км/ч. Ответ дайте в км/ч.
Ответ: 2
10)Стрелок в тире стреляет по мишени до тех пор, пока не поразит её. Известно, что он попадает в цель с вероятностью 0,6 при каждом отдельном выстреле. Сколько патронов нужно дать стрелку, чтобы он поразил цель с вероятностью не менее 0,9?
Ответ: 3
15)В июле планируется взять кредит на сумму 800 800 рублей. Условия его возврата таковы: — каждый январь долг возрастает на 20 % по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить некоторую часть долга. На сколько рублей больше придётся отдать в случае, если кредит будет полностью погашен тремя равными платежами (то есть за 3 года), по сравнению со случаем, если кредит будет полностью погашен двумя равными платежами (то есть за 2 года)?
16)Около окружности с центром O описана трапеция ABCD с основаниями AD и BC . а) Докажите, что AB — диаметр окружности, описанной около треугольника AOB. б) Найдите отношение площади четырёхугольника, вершины которого — точки касания окружности со сторонами трапеции, к площади самой трапеции ABCD , если известно, что AB CD = , а основания трапеции относятся как 1: 2 .
Другие тренировочные варианты ЕГЭ 2022 по математике 11 класс:
Работы СТАТГРАД по математике задания и ответы
Математика 10-11 класс варианты МА2000701-МА2000710 статград ответы и задания ЕГЭ 2021
Метки: ЕГЭ 2022заданияматематика 11 классответыстатград
Решение и ответы заданий варианта 2210209 СтатГрад 13 декабря ЕГЭ 2023 по математике (профильный уровень). ГДЗ профиль для 11 класса. +Задания №1, №4, №6 из варианта 2210211.


Задание 1.
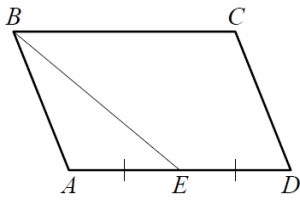
Площадь параллелограмма ABCD равна 96. Точка Е – середина стороны AD. Найдите площадь треугольника ABE.
Задание 1 из варианта 2210211.
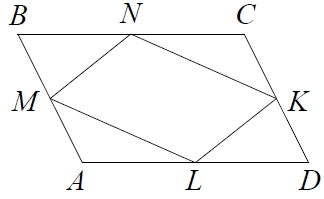
Площадь параллелограмма ABCD равна 26. Найдите площадь параллелограмма MNKL , вершинами которого являются середины сторон данного параллелограмма.
Задание 2.
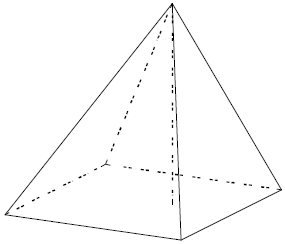
Основанием пирамиды является прямоугольник со сторонами 2 и 7. Её объём равен 14. Найдите высоту этой пирамиды.
Задание 3.
На чемпионате по прыжкам в воду выступают 30 спортсменов, среди них 3 прыгуна из Польши и 4 прыгуна из Дании. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что четвёртым будет выступать прыгун из Польши.
Задание 4.
Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 4. Какова вероятность того, что был сделан один бросок? Ответ округлите до сотых.
Задание 4 из варианта 2210211.
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 4. Какова вероятность того, что для этого потребовалось два броска?
Задание 5.
Решите уравнение sqrt{-35-12x}=-x. Если уравнение имеет больше одного корня, в ответе запишите больший из корней.
Задание 6.
Найдите значение 13cos(frac{pi}{2} − α), если cosα = −frac{12}{13} и α∈ (frac{pi}{2}; π).
Задание 6 из варианта 2210211.
Найдите значение frac{4cos(–pi–beta)+3sin(frac{3pi}{2}+beta)}{cos(beta+3pi)}.
Задание 7.
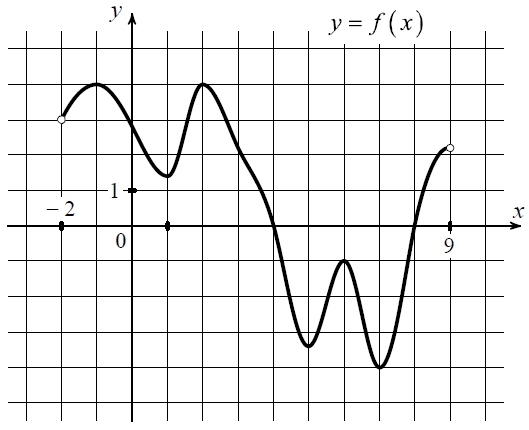
На рисунке изображён график функции y = f(x), определённой на интервале (−2; 9). Определите количество точек, в которых производная функции f(x) равна 0.
Задание 8.
Если достаточно быстро вращать ведёрко с водой на верёвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведёрка сила давления воды на дно не остаётся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила её давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна P=m(frac{v^{2}}{L}-g), где m – масса воды в килограммах, v – скорость движения ведёрка в м/с, L – длина верёвки в метрах, g – ускорение свободного падения (считайте g = 10 м/с2). С какой наименьшей скоростью надо вращать ведёрко, чтобы вода не выливалась, если длина верёвки равна 90 см? Ответ дайте в м/с.
Задание 9.
Первый садовый насос перекачивает 6 литров воды за 2 минуты, второй насос перекачивает тот же объём воды за 3 минуты. Сколько минут эти два насоса должны работать одновременно, чтобы перекачать 5 литров воды?
Задание 10.
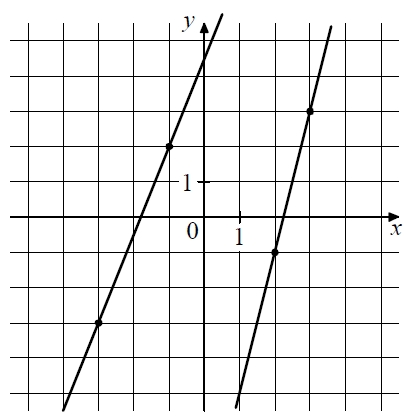
На рисунке изображены графики линейных функций, которые пересекаются в точке A. Найдите абсциссу точки A.
Задание 11.
Найдите наименьшее значение функции y = 10x − 10ln(x + 4) + 23 на отрезке [−3,5; 0].
Задание 12.
а) Решите уравнение 15sinx = 3sinx·5–cosx.
б) Найдите все корни этого уравнения, принадлежащие отрезку [frac{3pi}{2};3pi].
Задание 13.
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB = 5 и BC = √23 . Длины боковых рёбер пирамиды SA = 2√15, SB = √85, SD = √83.
а) Докажите, что SA – высота пирамиды SABCD.
б) Найдите угол между прямыми SC и BD.
Задание 14.
Решите неравенство
(3x3 – 18x2 + 27x)·(x – 3)–1 – (6x3 – 11x2 – 44x – 30)·(2x + 3)–1 ≤ 11.
Задание 15.
15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 3 % по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо оплатить часть долга одним платежом;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Какую сумму следует взять в кредит, чтобы общая сумма платежей после полного погашения равнялась 4,6 млн рублей?
Задание 16.
Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H.
а) Докажите, что ∠BB1C1 = ∠BAH.
б) Найдите расстояние от центра окружности, описанной около треугольника ABC, до стороны BC, если B1C1 = 9 и ∠BAC = 60°.
Задание 17.
Найдите все значения a, при каждом из которых уравнение
2sqrt{x^{4}+(a-3)^{4}}=|x+a-3|+|x-a+3|
имеет единственное решение.
Задание 18.
Сначала Маша написала на доске 15 натуральных чисел (необязательно различных), каждое из которых не превосходит 30. Затем вместо некоторых из чисел (возможно, одного) она написала на доске числа, меньшие первоначальных на единицу. Числа, которые после этого оказались равными 0, она с доски стёрла.
а) Могло ли оказаться так, что среднее арифметическое чисел на доске увеличилось?
б) Среднее арифметическое первоначально написанных чисел равнялось 25. Могло ли среднее арифметическое оставшихся на доске чисел оказаться равным 32?
в) Среднее арифметическое первоначально написанных чисел равнялось 25. Найдите наибольшее возможное значение среднего арифметического чисел, которые остались на доске.
Источник варианта: СтатГрад/statgrad.org.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.4 / 5. Количество оценок: 7
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.