- 31.10.2020
Ответы к сборнику «30 типовых экзаменационных вариантов ЕГЭ 2021 по математике базового уровня» под редакцией Ященко. Все варианты сборника составлены на основе официальных демоверсий ФИПИ 2021 года для 11 классов.
- Тренировочные варианты ЕГЭ 2021 по базовой математике
- Всё про ЕГЭ в 2021 году
Кратко о пособии
Выполнение заданий типовых экзаменационных вариантов предоставляет обучающимся возможность самостоятельно подготовиться к государственной итоговой аттестации в форме ЕГЭ, а также объективно оценить уровень своей подготовки к экзамену.
Учителя могут использовать типовые экзаменационные варианты для организации контроля результатов освоения школьниками образовательных программ среднего общего образования и интенсивной подготовки обучающихся к ЕГЭ.
Его можно приобрести https://www.labirint.ru/books/762486/
Выберите свой номер варианта теста:
1 / 2 / 3 / 4 / 5 / 6 / 7 / 8 / 9 / 10 / 11 / 12 / 13 / 14 / 15 / 16 / 17 / 18 / 19 / 20 / 21 / 22 / 23 / 24 / 25 / 26 / 27 / 28 / 29 / 30
Вариант 1
1) -1,5
2) 0,5
3) 108
4) 0,2
5) 0,5
6) 520
7) -3

9) 4123
10) 0,25
11) 757
12) 738
13) 96
14) 3412
15) 16,5
16) 4
17) 2413
18) 13 или 31
19) 53535 или 97575 или 57975 или 42420 или 13575
20) 35
Вариант 2
1) -2,8
2) 0,2
3) 75
4) 0,3
5) 0,2
6) 330
7) -1,8

9) 2431
10) 0,125
11) 755
12) 336
13) 84
14) 2314
15) 78
16) 540
17) 4312
18) 24
19) 63030 или 69630 или 69696
20) 20
Вариант 3
1) 1,25
2) 334,4
3) 1240
4) 50
5) 3,5
6) 105
7) 3,5

9) 2143
10) 0,02
11) 4,5
12) 17540
13) 1024
14) 1423
15) 17
16) 9
17) 1432
18) 13
19) 120 или 180 или 240 или 360 или 420 или 480 или 840
20) 10
Вариант 4
1) 1,65
2) 544,3
3) 950
4) 90
5) 3,5
6) 36
7) 3

9) 4123
10) 0,03
11) 500
12) 17220
13) 7000
14) 4132
15) 12,5
16) 4
17) 3124
18) 24
19) 240 или 280 или 640 или 680
20) 8
Вариант 5
1) -7
2) 60
3) 476
4) 208
5) 9
6) 62,5
7) -0,6

9) 1432
10) 0,45
11) 26
12) 3780
13) 21150
14) 3412
15) 83
16) 175
17) 2143
18) 13
19) 11125 или 11215 или 12115 или 21115
20) 38
Вариант 6
1) -3
2) 0,9
3) 744
4) 5
5) 15
6) 75
7) -5

9) 3241
10) 0,65
11) 84
12) 3590
13) 18525
14) 2413
15) 110
16) 18
17) 4213
18) 23
19) 1125 или 1215 или 2115
20) 26
Вариант 7
1) 19,2
2) 625
3) 30
4) 3
5) -150
6) 28
7) -7,5

9) 4123
10) 0,2
11) 5
12) 0,76
13) 45
14) 4123
15) 75
16) 130
17) 1432
18) 14
19) 1395 или 1935 или 3195 или 3915 или 9135 или 9315
20) 9
Вариант 8
1) 18,2
2) 81
3) 21
4) 6
5) -18
6) 373
7) -9,2

9) 3214
10) 0,6
11) 3
12) 7
13) 1200
14) 1324
15) 72
16) 54
17) 3124
18) 34
19) 2640 или 8624 или 6248
20) 12
Вариант 9
1) 2,9
2) 0,8
3) 200
4) 0,0098
5) 0,5
6) 12
7) -5

9) 4132
10) 0,45
11) 34
12) 15 или 51 или 236 или 263 или 326 или 362 или 623 или 632
13) 8
14) 3241
15) 0,96
16) 10
17) 4123
18) 23
19) 816 или 824 или 864 или 936
20) 15
Вариант 10
1) 1,8
2) 48
3) 150
4) 0,0225
5) 0,2
6) 30
7) -4

9) 4231
10) 0,36
11) 31,8
12) 35 или 53 или 124 или 142 или 214 или 241 или 412 или 421
13) 2
14) 1432
15) 0,28
16) 9
17) 3421
18) 12
19) 1236 или 1248 или 1296 или 1326
20) 35
Вариант 11
1) 0,4
2) 512
3) 24000
4) 8
5) 2
6) 6
7) -8

9) 3241
10) 0,3
11) 4
12) 10900
13) 6
14) 2431
15) 67
16) 222
17) 2314
18) 14
19) 421 или 541 или 721 или 841 или 961
20) 23
Вариант 12
1) 0,3
2) 27
3) 27000
4) 3
5) 3
6) 4
7) 9

9) 1423
10) 0,68
11) 10
12) 12600
13) 4
14) 3241
15) 123
16) 370
17) 4132
18) 23
19) 721 или 631 или 541
20) 20
Вариант 13
1) 4,8
2) 900
3) 918
4) 4
5) 20
6) 305
7) -4

9) 1324
10) 0,3
11) 19
12) 52500
13) 76,25
14) 3412
15) 2
16) 16
17) 3142
18) 13
19) 201 или 243 или 402 или 444
20) 13
Вариант 14
1) 1,2
2) 80
3) 1275
4) 14
5) 24
6) 650
7) -12

9) 2143
10) 0,45
11) 16
12) 59100
13) 1675
14) 4213
15) 3
16) 4
17) 4231
18) 23
19) 321 или 404 или 642 или 963
20) 10
Вариант 15
1) -1,3
2) 0,0004
3) 450
4) 4
5) 3
6) 20,4
7) 2

9) 3421
10) 0,4
11) 10
12) 422400
13) 8400
14) 3124
15) 20
16) 36
17) 2341
18) 13
19) 897 или 798 или 699
20) 18
Вариант 16
1) -1,84
2) 0,0005
3) 525
4) 10
5) 5
6) 40,25
7) 8

9) 3241
10) 0,35
11) 5
12) 312000
13) 13800
14) 1342
15) 64
16) 84
17) 1432
18) 14
19) 357 или 366 или 389
20) 14
Вариант 17
1) 2,44
2) 330
3) 18
4) 29
5) 2
6) 7
7) 4,75

9) 1432
10) 0,35
11) 94,6
12) 17220
13) 12500
14) 1432
15) 85
16) 4,5
17) 4123
18) 13
19) 7705 или 7815 или 7925
20) 27
Вариант 18
1) 3,75
2) 410
3) 24
4) 37
5) 3
6) 10
7) 16,8

9) 4321
10) 0,26
11) 94,4
12) 17540
13) 40500
14) 4231
15) 47
16) 1,5
17) 3214
18) 23
19) 9705 или 9815 или 9925
20) 5
Вариант 19
1) 2,7
2) 25
3) 1323
4) 1190
5) 2
6) 12
7) -0,25

9) 3241
10) 0,138
11) 38
12) 5
13) 1423
14) 20
15) 45
16) 2431
17) 23
18) 2304 или 5625
19) 34
Вариант 20
1) 2,28
2) 1
3) 2240
4) 850
5) 1
6) 24
7) -2

9) 4213
10) 0,06
11) 3
12) 13
13) 6
14) 3241
15) 34
16) 21
17) 4312
18) 14
19) 3267 или 7744
20) 9
Вариант 21
1) -2,8
2) 16
3) 64
4) 205
5) 180
6) 15
7) 64

9) 3142
10) 0,75
11) 745
12) 11220
13) 375
14) 2143
15) 12
16) 20,25
17) 3412
18) 23
19) 1112112 или 2111112 или 1211112 или 1121112
20) 23
Вариант 22
1) -16,3
2) 125
3) 450
4) 0,2
5) 0,25
6) 7
7) 4,8

9) 3124
10) 0,2
11) 8
12) 3170
13) 24
14) 4312
15) 9
16) 0,75
17) 4213
18) 34
19) 116616 или 161616 или 611616
20) 19
Вариант 23
1) -2,95
2) 9
3) 50
4) 1,5
5) 5
6) 12
7) 0,5

9) 3241
10) 0,85
11) 747
12) 153000
13) 14,7
14) 2341
15) 30
16) 1,5
17) 3214
18) 13
19) 2749 или 2947 или 2974 или 4297 или 4729 или 4792 или 4927
20) 22
Вариант 24
1) -7
2) 36
3) 13
4) 10
5) 9
6) 7625
7) -12

9) 4312
10) 0,9
11) 30
12) 156000
13) 6,8
14) 4231
15) 32
16) 3,5
17) 2314
18) 14
19) 3849 или 3948 или 4398 или 4839 или 4938
20) 13
Вариант 25
1) -0,8
2) 16
3) 11
4) 19
5) 3
6) 3
7) 4

9) 3214
10) 0,4
11) 8
12) 5600
13) 1125
14) 3412
15) 118
16) 4,5
17) 4312
18) 24
19) 3312 или 3132 или 1332
20) 340
Вариант 26
1) 0,4
2) 2
3) 221
4) 4500
5) 32
6) 3
7) -2

9) 1243
10) 0,25
11) 3
12) 4830
13) 3125
14) 4123
15) 53
16) 10,5
17) 1432
18) 13
19) 3222 или 2322 или 2232
20) 304
Вариант 27
1) 36,4
2) 162
3) 480
4) 75
5) 25
6) 12
7) 3,5

9) 3214
10) 0,02
11) 57
12) 23
13) 92
14) 2431
15) 23
16) 252
17) 2413
18) 13
19) 2134 или 3124 или 1342 или 4312
20) 28
Вариант 28
1) 8,25
2) 88
3) 23
4) 2642
5) 12
6) 11
7) -5

9) 2314
10) 0,56
11) 2
12) 2
13) 146
14) 1324
15) 12
16) 126
17) 3124
18) 23
19) 1452 или 1518 или 5412 или 1254 или 5214
20) 24
Вариант 29
1) 1,04
2) 90,23
3) 133
4) 14
5) 0,4
6) 465,3
7) 0,25

9) 3241
10) 231
11) 60
12) 345 или 354 или 435 или 453 или 534 или 543
13) 9
14) 4312
15) 2,5
16) 126
17) 2431
18) 34
19) 65835 или 26835 или 26535
20) 175
Вариант 30
1) 2,15
2) 70,56
3) 122,4
4) 5
5) 6
6) 1720,8
7) 4

9) 2314
10) 213
11) 6
12) 145
13) 8
14) 2431
15) 3
16) 112
17) 2143
18) 14
19) 87648 или 78648 или 78768
20) 166
Задание 1
Показания счётчика электроэнергии 1 января составляли 53848 кВт*ч, а 1 февраля — 54107 кВт*ч. Сколько нужно заплатить за электроэнергию за январь, если 1 кВт*ч электроэнергии стоит 2 руб. 80 коп.? Ответ дайте в рублях.
Ответ: 725,2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Разница в кВт*ч: $$54107-53848=259$$.
Стоимость: $$259cdot 2,8=725,2$$ рубля.
Задание 2
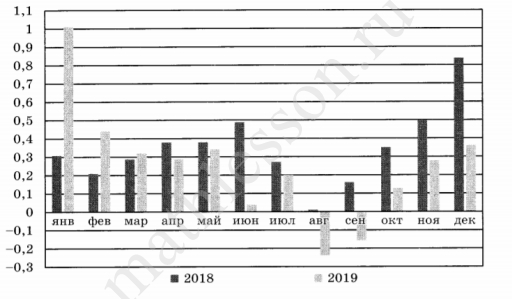
На диаграмме показан уровень инфляции в России в 2018 и 2019 годах. По горизонтали указаны месяцы, по вертикали — уровень инфляции (в процентах) за каждый месяц соответствующего года. Определите количество месяцев, когда инфляция в 2019 году была ниже, чем инфляция в соответствующем месяце 2018 года.
Ответ: 9
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Это месяцы с апреля по декабрь: 9 месяцев.
Задание 3
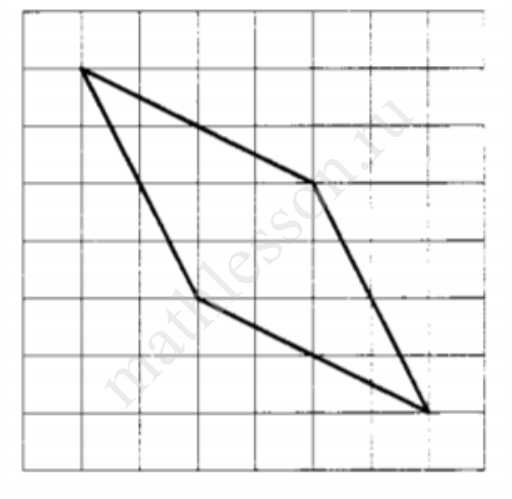
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите его площадь.
Ответ: 12
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Найдем диагонали по теореме Пифагора $$d_1=sqrt{2^2+2^2}=2sqrt{2}; d_2=sqrt{6^2+6^2}=6sqrt{2}$$. $$S=frac{1}{2} d_1cdot d_2=frac{1}{2} cdot 2sqrt{2} cdot 6sqrt{2}=12$$
Задание 4
В гонке с раздельным стартом участвуют 25 лыжников, среди которых 7 спортсменов из Норвегии. Порядок старта определяется с помощью жребия случайным образом. Один из норвежских лыжников получил стартовый номер «5». Найдите вероятность, что он будет стартовать за своим соотечественником.
Ответ: 0,25
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Вероятность, что 4-ый будет из Норвегии: $$Pleft(Aright)=frac{6}{24}$$ (т.к. после того, как один получит номер «5» лыжников из Норвегии осталось 6, а всего лыжников 24). Т.е. 0,25.
Задание 5
Найдите корень уравнения $$frac{1}{2x-3}=frac{1}{8}$$.
Ответ: 5,5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$frac{1}{2x+3}=frac{1}{8}leftrightarrow 2x-3=8leftrightarrow 2x=11leftrightarrow x=5,5$$
Задание 6
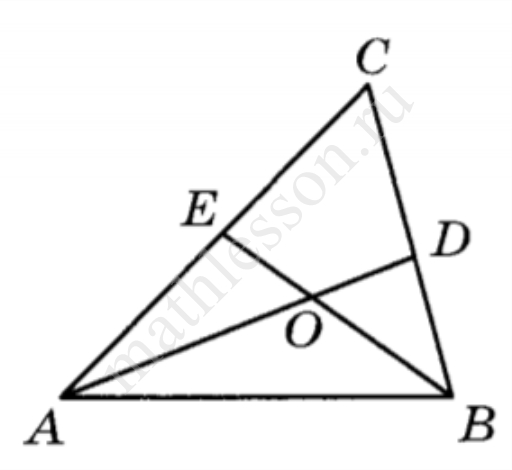
В треугольнике АВС угол С равен $$46{}^circ $$, AD и BE — биссектрисы, пересекающиеся в точке О. Найдите угол АОВ. Ответ дайте в градусах.
Ответ: 113
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$angle A+angle B=180{}^circ -angle C=134{}^circ to frac{angle A}{2}+frac{angle B}{2}=frac{134}{2}=67{}^circ to$$ $$to angle AOB=180-67=113{}^circ $$
Задание 7
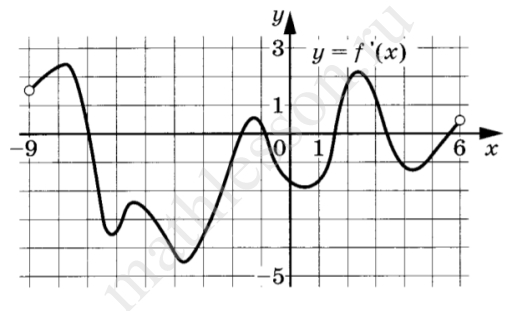
На рисунке изображён график $$у = f'(x)$$ — производной функции $$f(x)$$, определённой на интервале (-9; 6). Найдите количество точек минимума функции $$f(x)$$, принадлежащих отрезку $$[-8; 5].$$
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Точка минимума там, где $$f’left(xright)=0$$ при возрастании $$f’left(xright)$$, т.е. $$approx -1,8; approx 1,5; approx 5,6$$. Но на $$xin [-8;5]$$ их 2 точки.
Задание 8
В кубе $$ABCDA_1B_1C_1D_1$$ найдите угол между прямыми $$DC_1$$ и $$BD$$. Ответ дайте в градусах.
Ответ: 60
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Рассмотрим $$triangle BC_1D:BC_1=DC_1=BC_1=BD$$ (диагонали равных квадратов)$$to triangle BC_1D$$ — равносторонний $$to angle BDC_1=60{}^circ $$.
Задание 9
Найдите значение выражения $$4^{1-2{{log }_{0,5} 3 }}$$
Ответ: 324
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$4^{1-2{{log }_{0,5} 3 }}=frac{4^1}{4^{2{{log }_{0,5} 3 }}}=frac{4^1}{{(2^2)}^{{{log }_{2^{-1}} 3 }}}=frac{4}{2^{-2{{log }_2 9 }}}=frac{4}{2^{{{log }_2 frac{1}{81} }}}=frac{4}{frac{1}{81}}=324$$
Задание 10
Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением $$a$$ в км/ч$${}^{2}$$. Скорость $$v$$ (в км/ч) вычисляется по формуле $$v=sqrt{2la}$$, где $$l$$ — пройденный автомобилем путь (в км). Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав 0,8 км, приобрести скорость 100 км/ч. Ответ дайте в км/ч$${}^{2}$$.
Ответ: 6250
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Подставим известные в формулу: $$100=sqrt{2cdot 0,8cdot a}leftrightarrow 10000=1,6aleftrightarrow a=6250$$.
Задание 11
Катер в 8:40 вышел из пунтка А в пункт В, расположенный в 48 км от А. Пробыв 40 минут в пункте В, катер отправился назад и вернулся в пункт А в 16:20 того же дня. Найдите собственную скорость катера (в км/ч), если известно, что скорость течения реки 2 км/ч.
Ответ: 14
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Прошло времени: 7 часов 40 минут. При этом 40 минут стоял, т.е. в движении 5 часов. Пусть $$x$$ км/ч — собственная скорость катера.
Тогда: $$frac{48}{x+2}+frac{48}{x-2}=7leftrightarrow 48x-96+48x+96=7x^2-28leftrightarrow 7x^2-96x-28=0to $$ $$to frac{D}{4}=2304+196=2500to left[ begin{array}{c}
x_1=frac{48+50}{7} \
x_2<0 end{array}
right.leftrightarrow x=14$$
Задание 12
Найдите наименьшее значение функции $$y=4{sin x }-6x+7$$ на отрезке $$left[-frac{3pi }{2};0right]$$
Ответ: 7
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Найдем производную: $$y’=4{cos x }-6$$. Т.к. $$left|{cos x }right|le 1$$, то $$y'<0$$ при любом $$x$$, тогда функция убывает на всем $$Dleft(xright)to y_{min}=y(0)$$. $$yleft(0right)=4{sin 0 }-6cdot 0+7=7$$
Задание 13
а) Решите уравнение $$2{{sin }^{{rm 2}} (frac{pi }{2}-x) }+{sin 2x }=0$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[3pi ;frac{9pi }{2}]$$
Ответ: а)$$frac{pi }{2}+pi n,nin Z$$; $$-frac{pi }{4}+pi n,nin Z$$ б) $$1)3pi +frac{pi }{2}=frac{7pi }{2};2)4pi +frac{pi }{2}=frac{9pi }{2} ;3)4pi -frac{pi }{4}=frac{15pi }{4} $$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
а) $$2{{sin }^{{rm 2}} (frac{pi }{2}-x) }+{sin 2x }=0leftrightarrow 2{{cos }^{{rm 2}} x }+2{sin x }{cos x }=0leftrightarrow$$ $$leftrightarrow 2{cos x }left({cos x }+{sin x }right)=0leftrightarrow left[ begin{array}{c} {cos x=0 } \ {cos x }+{sin x }=0 end{array} right.leftrightarrow left[ begin{array}{c} {cos x=0 } \ 1+{tan x }=0 end{array} right.leftrightarrow$$ $$leftrightarrow left[ begin{array}{c} x=frac{pi }{2}+pi n,nin Z \ x=-frac{pi }{4}+pi n,nin Z end{array} right.$$
б) С помощью единичной окружности отберем корни на $$left[3pi ;frac{9pi }{2}right]:1)3pi +frac{pi }{2}=frac{7pi }{2};2)4pi +frac{pi }{2}=frac{9pi }{2} ;3)4pi -frac{pi }{4}=frac{15pi }{4} $$
Задание 14
В правильной шестиугольной пирамиде SABCDEF сторона основания АВ равна 2, а боковое ребро SA равно 8. Точка М — середина ребра АВ. Плоскость $$alpha $$ перпендикулярна плоскости АВС и содержит точки М и D. Прямая SC пересекает плоскость $$alpha $$ в точке К.
а) Докажите, что KM = KD.
б) Найдите объём пирамиды CDKM.
Ответ: $$frac{3sqrt{5}}{4}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
А) 1) Пусть $$FCcap DM=L$$. Т.к. $$alpha bot ABC$$, то ч/з L пойдет $$LKbot ABC$$. Пусть $$CBcap DM=H$$, $$KHcap SB=Rto left(DKRMright)$$ — искомая плоскость.
2) FC равноудалена от ED и AB $$to $$ т.к. $$EDparallel AB$$, то $$angle XDL=angle LZB$$ (накрест лежащие) $$to triangle XDL=triangle LMZto DL=LMto KL$$ — высота и медиана $$to $$ $$triangle DKM$$ — равнобедренный $$to KM=KD$$.
Б) 1) $$V_{CDKM}=frac{1}{3}S_{CDKM}cdot KL$$. $$S_{ABCDEF}=6S_{AOB}=6cdot frac{1}{2}cdot 2cdot 2cdot frac{sqrt{3}}{2}=6sqrt{3}to S_{MNDCB}=3sqrt{3}.$$ $$S_{MND}=frac{1}{2}MNcdot ND=frac{1}{2}cdot 2cdot 2cdot frac{sqrt{3}}{2}=6sqrt{3}.$$ $$S_{MBC}=frac{1}{2}MBcdot BC{sin angle B }=frac{1}{2}cdot 1cdot 2cdot frac{sqrt{3}}{2}=frac{sqrt{3}}{2}to S_{CDM}=3sqrt{3}-sqrt{3}-frac{sqrt{3}}{2}=$$ $$=frac{3sqrt{3}}{2}.$$
2) $$NX=OLto LC=2-frac{1}{2}=frac{3}{2}to frac{KL}{SO}=frac{LC}{OC}=frac{frac{3}{2}}{2}=frac{3}{4}$$ (т.к. $$triangle SOCsim triangle KLC$$ по острому углу) — $$SO=sqrt{SB^2-OB^2}=sqrt{8^2-2^2}=sqrt{60}=2sqrt{15}to KL=frac{3sqrt{15}}{2}to$$ $$to V_{CDKM}=frac{1}{3}cdot frac{3sqrt{3}}{2}cdot frac{3sqrt{15}}{2}=frac{3sqrt{5}}{4}$$.
Задание 15
Решите неравенство $$x^2{{log }_{64} (3-2x) }ge {{log }_2 left(4x^2-12x+9right) }$$
Ответ: $$xin left(-infty ;-sqrt{12}right];[1;1,5)$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$x^2{{log }_{64} (3-2x) }ge {{log }_2 left(4x^2-12x+9right) }leftrightarrow frac{x^2}{6}{{log }_2 left(3-2xright) }-{{log }_{64} {left(2x-3right)}^2 }ge 0leftrightarrow $$ $$leftrightarrow $$ т.к. $$3-2x>0$$, то: $$frac{x^2}{6}{{log }_2 left(3-2xright) }-2{{log }_2 left(3-2xright) }ge 0leftrightarrow (x^2-12)({{log }_2 (3-2x) })ge 0leftrightarrow $$ $$leftrightarrow left{ begin{array}{c}
3-2x>0 \
(x^2-12)(3-2x-1)ge 0 end{array}
right.leftrightarrow left{ begin{array}{c}
x<1,5 \
(x-sqrt{12})(x+sqrt{12})(x-1)le 0 end{array}
right.$$.
$$xin left(-infty ;-sqrt{12}right];[1;1,5)$$
Задание 16
Две окружности касаются внутренним образом в точке С. Вершины А и В равнобедренного прямоугольного треугольника АВС с прямым углом С лежат на меньшей и большей окружностях соответственно. Прямая АС вторично пересекает большую окружность в точке Е, а прямая ВС вторично пересекает меньшую окружность в точке D.
а) Докажите, что прямые AD и BE параллельны.
б) Найдите АС, если радиусы окружностей равны 3 и 4.
Ответ: 4,8
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
а) По т.о. касательной и хорде $$angle LCD=angle CAD$$ (для меньшей) и $$angle LCD=angle CED$$ (для большей) $$to angle CAD=angle CED$$, а они накрест лежащие $$to ADparallel BE$$.
б) $$angle CDA$$ и $$angle EBE$$ — прямоугольные, $$angle CAD=angle CEDto triangle CDAsim triangle CBEto frac{CD}{CB}=frac{CA}{CE}=frac{AD}{BE}$$. При этом AD и BE — диаметры ($$angle C$$ — вписан и прямой) $$to AD=6;BE=8to frac{CD}{CB}=frac{3}{4}$$. Пусть $$CA=CB=xto CD=frac{3}{4}x$$. Из $$triangle ADC:AD^2=CD^2+CA^2to 36=x^2+frac{9x^2}{16}to x^2=frac{36cdot 16}{25}to x=4,8$$.
Задание 17
В июле 2022 года планируется взять кредит на пять лет в размере 1050 тыс. рублей. Условия его возврата таковы:
— каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— в июле 2023, 2024 и 2025 годов долг остаётся равным 1050 тыс. рублей;
— выплаты в 2026 и 2027 годах равны;
— к июлю 2027 года долг будет выплачен полностью.
На сколько рублей последняя выплата будет больше первой?
Ответ: 500 т.р.
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Раз первые 3 года долг не менялся, то платили только проценты, т.е. $$1050cdot 0,1=105$$ т.р. Пусть крайние 2 выплаты по $$x$$ т.р. Тогда: $$left(1050cdot 1,1-xright)cdot 1,1-x=0leftrightarrow 1270,5-2,1x=0to x=605$$ т.р. Тогда разница: $$605-105=500$$ т.р.
Задание 18
Найдите все значения $$a$$, при каждом из которых система уравнений $$left{ begin{array}{c} sqrt{16-y^2}=sqrt{16-a^2x^2} \ x^2+y^2=8x+4y end{array} right.$$ имеет ровно два различных решения.
Ответ: $$ain left(-infty ;-2right);(-2;+infty )$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$left{ begin{array}{c} sqrt{16-y^2}=sqrt{16-a^2x^2} \ x^2+y^2=8x+4y end{array} right.leftrightarrow left{ begin{array}{c} 16-y^2ge 0 \ 16-y^2=16-{left(axright)}^2 \ x^2+y^2-8x-4y=0 end{array} right.leftrightarrow$$ $$leftrightarrow left{ begin{array}{c} yin [-4;4] \ y=ax \ y=-ax \ x^2+y^2-8x-4y=0 end{array} right.$$
При $$y=ax:x^2+{a^2x}^2-8x-4ax=0leftrightarrow xleft(x+a^2x-8-4aright)=0leftrightarrow left[ begin{array}{c} x=0 \ x=frac{4a+8}{a^2+1} end{array} right.leftrightarrow $$ $$leftrightarrow left[ begin{array}{c} y=0 \ y=frac{4a^2+8a}{a^2+1} end{array} right.$$.
При $$y=-ax: x^2+{a^2x}^2-8x+4ax=0leftrightarrow left[ begin{array}{c} x=0 \ x=frac{-4a+8}{a^2+1} end{array} right.leftrightarrow left[ begin{array}{c} y=0 \ y=frac{4a^2-8a}{a^2+1} end{array} right.$$.
Получим: $$left(0:0right):left(frac{4a+8}{a^2+1};frac{4a^2+8a}{a^2+1}right);(frac{8-4a}{a^2+1};frac{4a^2-8a}{a^2+1})$$.
При этом $$left(0:0right)$$ всегда, т.к. $$yin [-4;4]$$ выполняется.
Вторая пара существует при: $$-4le frac{4a^2+8a}{a^2+1}le 4to left{ begin{array}{c} 4a^2+8age -4a^2-4 \ 4a^2+8ale 4a^2+4 end{array} right.leftrightarrow left{ begin{array}{c} 8a^2+8a+4ge 0 \ ale frac{1}{2} end{array} right.leftrightarrow ale frac{1}{2}$$.
Третья пара существует при: $$-4le frac{4a^2-8a}{a^2+1}le 4to left{ begin{array}{c} 4a^2-8age -4a^2-4 \ 4a^2-8age 4a^2+4 end{array} right.$$$$leftrightarrow left{ begin{array}{c} 8a^2-8a+4ge 0 \ age -frac{1}{2} end{array} right.leftrightarrow age -frac{1}{2}$$.
При этом первая и вторая совпадают при $$frac{4a+8}{a^2+1}=0to a=-2.$$
Первая и третья: $$frac{8-4a}{a^2+1}=0to a=2$$.
Вторая и третья: $$frac{4a+8}{a^2+1}=frac{8-4a}{a^2+1}to a=0$$. т.е. должно быть только 2: $$ain left(-infty ;-2right);(-2;+infty )$$.
Задание 19
На доске было написано несколько различных натуральных чисел. Эти числа разбили на три группы, в каждой из которых оказалось хотя бы одно число. К каждому числу из первой группы приписали справа цифру 3, к каждому числу из второй группы — цифру 7, а числа из третьей группы оставили без изменений.
а) Могла ли сумма всех этих чисел увеличиться в 8 раз?
б) Могла ли сумма всех этих чисел увеличиться в 17 раз?
в) В какое наибольшее число раз могла увеличиться сумма всех этих чисел?
Ответ: а)да б)нет в)$$frac{232}{21}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
А) Пусть было три числа $$A,B,Cin N,Ane Bne Cle 9$$. Получим $$Ato 10A+3;Bto 10B+7$$. Следовательно, $$frac{10A+3+10B+7+C}{A+B+C}=8to 2A+2B+10-7C=0$$. Пусть $$A=2,B=8,C=4to $$ Да, могла.
Б) Пусть в 1-ой группе $$x$$ чисел, их сумма $$A$$, во 2-ой $$y$$ чисел, сумма $$B$$, в 3-ей $$Z$$ чисел, сумма $$C$$. Тогда $$frac{10A+3x+10B+7y+C}{A+B+C}=17to 3x+7y=7A+7B+16C.$$ При этом $$Age x,Bge y$$, тогда $$3x+7y<7A+7Bto $$ равенство невозможно.
В) Пусть в 1,2 и 3 группах x, y и 7 чисел соответственно, их сумма $$A,B,C$$. Тогда $$frac{10A+3x+10B+7y+C}{A+B+C}=Qto frac{10left(A+B+Cright)+3x+7y-9C}{A+B+C}=Qto$$ $$to Q=10+frac{3x+7y-9c}{A+B+C}$$ т.к. при переносе чисел из первой или третьей группы во вторую $$A+B+C$$ не меняется, но $$3x+7y-9C$$ увеличивается, то и Q увеличится. Следовательно, $$Qto max$$, при $$xto min$$. А $$x_{min}=1$$. $$Cto min$$, т.е. $$Zto min, Z=1(C=1)$$. При этом общее число чисел тогда $$y+2$$. Получим: $$Q=10+frac{3x+7y-9c}{A+B+C}$$. Т.к. числа разные натуральные, то $$A+B+Cge 2+1+frac{2cdot 3+1left(y-1right)}{2}cdot y$$ (т.к. минимальная сумма будет у подряд идущих натуральных чисел с единицы). Т.е. $$A+B+Cge 3+frac{left(5+yright)y}{2}$$ или $$A+B+Cge frac{y^2+5y+6}{2}=frac{left(y+2right)left(y+3right)}{2}$$. Тогда: $$Q=10+frac{left(7y-6right)cdot 2}{(y+2)(y+3)}$$. Найдем максимальное значение $$frac{14y-12}{(y+2)(y+3)}=f(y)$$ при $$yin N$$. $$f’left(yright)=frac{14left(y^2+5y+6right)-left(14y-12right)left(2y+5right)}{{left((y+2)(y+3)right)}^2}=0to $$ $$to 14y^2+70y+84-28y^2-70y+24y+60=0$$. $$-14y^2+24y+144=0to -7y^2+12y+72=0to frac{D}{4}=540in ({23}^2;{24}^2)$$. $$left[ begin{array}{c} y_1=frac{-6+sqrt{540}}{-7} \ y_2=frac{-6-sqrt{540}}{-7}-max end{array} right..$$
При этом $$y_2=frac{6+sqrt{540}}{7}approx frac{6+23}{7}approx frac{29}{7}to y=4$$ или $$y=5$$. При $$y=4:fleft(4right)=frac{14cdot 4-12}{6cdot 7}=frac{44}{6cdot 7}=frac{22}{21}$$.
При $$y=5:fleft(5right)=frac{14cdot 5-12}{7cdot 8}=frac{58}{7cdot 8}=frac{29}{28}$$. $$fleft(4right)>fleft(5right)to Q_{max}=10+frac{22}{21}=frac{232}{21}.$$
Ответы к 36 вариантам профильного ЕГЭ по математике. Сборник ЕГЭ-2023 «Типовые экзаменационные варианты».
Вариант 1
1) 5,5
2) 2048
3) 0,06
4) 0,89
5) -0,2
6) 0,5
7) 5

9) 2
10) -4
11) -2910
Вариант 2
1) 7,5
2) 4
3) 0,12
4) 0,91
5) -0,9
6) 0,2
7) 1

9) 16
10) -8
11) 12,25
Вариант 3
1) 2,5
2) 30
3) 0,37
4) 0,375
5) -2,5
6) 4
7) 2

9) 14
10) 32
11) 204
Вариант 4
1) 1,5
2) 12
3) 0,24
4) 0,125.
5) 0,375
6) 125
7) 8

9) 18
10) -56
11) -10,9
Вариант 5
1) 99,5
2) 12
3) 0,004 /или/ -0,004
4) 0,9409
5) -0,5
6) 2
7) -19

9) 17
10) 16
11) -52
Вариант 6
1) 55
2) 18
3) 0,006 /или/ -0,006
4) 0,8464
5) -5,5
6) 3
7) -4

9) 24
10) -1
11) -6
Вариант 7
1) 0,2
2) 10
3) 0,2
4) 0,56
5) -0,4
6) -1
7) 9

9) 55
10) 6
11) 0,5
Вариант 8
1) 0,4
2) 5
3) 0,125
4) 0,46
5) -7
6) -1
7) 7

9) 11
10) 0,25
11) 17
Вариант 9
1) 3
2) 15 625
3) 0,01
4) 0,28
5) -12
6) 144
7) -1

9) 20
10) -3
11) 9
Вариант 10
1) 0,6
2) 150
3) 0,28
4) 0,17
5) -2,6
6) 625
7) -18

9) 9
10) 253
11) -23,25
Вариант 11
1) -0,7
2) 72
3) 0,25
4) 0,043
5) -0,2
6) -5
7) -1

9) 17,5
10) 78
11) 6,75
Вариант 12
1) 0,75
2) 24
3) 0,55
4) 0,02
5) -1,5
6) -4
7) 4

9) 13,5
10) -23
11) 6,25
Вариант 13
1) 8
2) 48
3) 0,4
4) 0,6
5) -9
6) 0,5
7) 4

9) 9
10) -0,5
11) 77
Вариант 14
1) 14
2) 40,5
3) 0,28
4) 0,78
5) -2
6) 0,04
7) 39

9) 24
10) 0,4
11) 37
Вариант 15
1) 11,55
2) 432
3) 0,014
4) 0,06
5) -9
6) 0,25
7) 2

9) 3
10) 2,5
11) 208
Вариант 16
1) 12
2) 192
3) 0,29
4) 0,02
5) -8
6) 0,125
7) 4

9) 1
10) -15
11) 5
Вариант 17
1) 10
2) 80
3) 0,08
4) 0,2
5) -2,5
6) 216
7) -2

9) 18
10) 16
11) -24
Вариант 18
1) 35
2) 10
3) 0,2
4) 0,24
5) -0,2
6) 3,5
7) 28

9) 21
10) 2,25
11) -15
Вариант 19
1) 2,5
2) 7,28
3) 0,25
4) 0,22
5) -1,5
6) 1
7) 0,2

9) 135
10) 2
11) -34
Вариант 20
1) 6
2) 7,68
3) 0,75
4) 0,27
5) -4,5
6) 10
7) -0,25

9) 52
10) 27
11) 0
Вариант 21
1) 113
2) 60
3) 0,2
4) 0,973
5) 5,5
6) 324
7) 2

9) 14
10) 15
11) 7
Вариант 22
1) 0,75
2) 45
3) 0,3
4) 0,9744
5) 11
6) -7,5
7) 7

9) 5
10) 3,4
11) 1,2
Вариант 23
1) 62
2) 25
3) 0,25
4) 0,3
5) -2
6) 80
7) 6

9) 75
10) 28
11) 18
Вариант 24
1) 78
2) 20
3) 0,2
4) 0,82
5) 0
6) 28
7) 6

9) 10
10) -28
11) -2
Вариант 25
1) 37
2) 135
3) 0,18
4) 3
5) 0,8
6) 0,4
7) -0,2

9) 1 35
10) -0,4
11) 14
Вариант 26
1) 53
2) 72
3) 0,38
4) 5
5) -4
6) -0,3
7) -0,75

9) 28
10) -13
11) 1
Вариант 27
1) 29
2) 315
3) 0,14
4) 0,03
5) 4
6) 2,72
7) 6

9) 77
10) 76
11) -3
Вариант 28
1) 6
2) 176
3) 0,375
4) 0,012
5) -1
6) -3
7) -3

9) 6
10) -5
11) 38
Вариант 29
1) 60
2) 18
3) 0,24
4) 0,2
5) 3
6) 4
7) 4

9) 6,4
10) 67
11) -21
Вариант 30
1) 64
2) 4
3) 0,28
4) 0,6
5) 4
6) 8
7) 14

9) 22
10) 3
11) -8
Вариант 31
1) 6,5
2) 54
3) 0,98
4) 0,2
5) 2
6) -10
7) 2

9) 54
10) -7
11) 8
Вариант 32
1) 30
2) 27
3) 0,024
4) 0,15
5) -2
6) 91
7) 3

9) 12
10) 13
11) -9
Вариант 33
1) 72,5
2) 47
3) 0,28
4) 0,097
5) -5
6) 65
7) 3

9) 48
10) -2,5
11) 26
Вариант 34
1) 68
2) 76
3) 0,16
4) 0,068
5) 6
6) 16
7) 6

9) 64
10) -0,25
11) -1
Вариант 35
1) 21
2) 200
3) 0,56
4) 0,9
5) -2
6) 7,5
7) 0,5

9) 20
10) 0,75
11) 9
Вариант 36
1) 35
2) 88
3) 0,12
4) 12
5) -5
6) 2,5
7) 5,5

9) 756
10) -0,5
11) 30
Барашкова английский язык на каникулах н…
Узорова английский язык в схемах и табл…
Державина английский язык для начальной …
Барашкова английский язык на каникулах н…
Карачаева 100 тестов по лексике и грамма…
Мордкович учебник алгебра углубленный ур…