ЕГЭ Профильный уровень. Задание №12
Тренажер № 4 «ВСЕ ТИПЫ ФУНКЦИЙ»
1. Найдите наибольшее значение функции на отрезке [−4,5; 0].
2. Найдите точку минимума функции
3. Найдите наименьшее значение функции .
4. Найдите наименьшее значение функции на отрезке
5. Найдите точку максимума функции .
6. Найдите точку минимума функции .
7. Найдите наибольшее значение функции на отрезке
8. Найдите точку минимума функции .
9. Найдите наибольшее значение функции на отрезке
.
10. Найдите наименьшее значение функции на отрезке
.
11. Найдите наименьшее значение функции на отрезке
.
12. Найдите наименьшее значение функции на отрезке
.
13. Найдите точку минимума функции .
14. Найдите наименьшее значение функции на отрезке [9; 36].
15. Найдите наименьшее значение функции на отрезке
.
16. Найдите наименьшее значение функции на отрезке
.
17. Найдите наибольшее значение функции на отрезке .
18. Найдите наименьшее значение функции на отрезке
19. Найдите точку минимума функции .
20. Найдите наибольшее значение функции на отрезке .
21. Найдите точку максимума функции
22. Найдите наибольшее значение функции на отрезке .
23. Найдите точку минимума функции .
24. Найдите наибольшее значение функции на отрезке
25. Найдите точку максимума функции .
26. Найдите наименьшее значение функции на отрезке .
27. Найдите точку минимума функции .
28. Найдите точку минимума функции .
29. Найдите наибольшее значение функции на отрезке .
30. Найдите точку минимума функции
31. Найдите наибольшее значение функции на отрезке .
32. Найдите наименьшее значение функции на отрезке .
33. Найдите наибольшее значение функции на отрезке .
34. Найдите наибольшее значение функции на отрезке .
35. Найдите наибольшее значение функции на отрезке .
36. Найдите наименьшее значение функции на отрезке .
37. Найдите точку минимума функции
38. Найдите точку минимума функции .
39. Найдите точку минимума функции .
40. Найдите наибольшее значение функции на отрезке .
41. Найдите наибольшее значение функции на отрезке
42. Найдите наименьшее значение функции на отрезке .
43. Найдите наибольшее значение функции на отрезке
44. Найдите наибольшее значение функции на отрезке .
45. Найдите точку максимума функции .
46. Найдите точку минимума функции
47. Найдите наименьшее значение функции на отрезке .
48. Найдите точку максимума функции .
49. Найдите наибольшее значение функции на отрезке .
50. Найдите наименьшее значение функции на отрезке .
ОТВЕТЫ:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
20 |
-13 |
9 |
3 |
-4 |
1 |
29 |
9 |
5 |
-54 |
6 |
20 |
2 |
-77 |
-14 |
73 |
17 |
-13 |
|
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
|
2 |
263 |
3 |
7 |
-3 |
48 |
0 |
3 |
2 |
196 |
1 |
0 |
-33 |
16 |
15 |
-6 |
7 |
-1 |
|
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
|
-7.75 |
-2 |
8 |
139 |
10 |
-27 |
15 |
43 |
0 |
4 |
-607.5 |
-1 |
295 |
19 |
2 балла
Обоснованно получены верные ответы в обоих пунктах (решение уравнения и указание корней)
1 балл
Обоснованно получен верный ответ в пункте а
ИЛИ
получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов: пункта а и пункта б
0 баллов
Решение не соответствует ни одному из критериев, перечисленных выше
Классы
- 11 класс
- 10 класс
- 9 класс
- 8 класс
- 7 класс
- 6 класс
- 5 класс
- 4 класс
- 3 класс
- 2 класс
- 1 класс
Предметы
- Русский
- Общество
- История
- Математика
- Физика
- Литература
- Английский
- Информатика
- Химия
- Биология
- География
Онлайн-школы
- Умскул
- Учи Дома
- Фоксфорд
- Тетрика
- Skypro
Репетиторы по предметам
- Русский
- Общество
- История
- Математика
- Физика
- Литература
- Английский
- Информатика
- Химия
- Биология
ЕГЭ Профильный уровень. Задание №12
Тренажер № 4 «ВСЕ ТИПЫ ФУНКЦИЙ»
1. Найдите наибольшее значение функции на отрезке [−4,5; 0].
2. Найдите точку минимума функции
3. Найдите наименьшее значение функции .
4. Найдите наименьшее значение функции на отрезке
5. Найдите точку максимума функции .
6. Найдите точку минимума функции .
7. Найдите наибольшее значение функции на отрезке
8. Найдите точку минимума функции .
9. Найдите наибольшее значение функции на отрезке
.
10. Найдите наименьшее значение функции на отрезке
.
11. Найдите наименьшее значение функции на отрезке
.
12. Найдите наименьшее значение функции на отрезке
.
13. Найдите точку минимума функции .
14. Найдите наименьшее значение функции на отрезке [9; 36].
15. Найдите наименьшее значение функции на отрезке
.
16. Найдите наименьшее значение функции на отрезке
.
17. Найдите наибольшее значение функции на отрезке .
18. Найдите наименьшее значение функции на отрезке
19. Найдите точку минимума функции .
20. Найдите наибольшее значение функции на отрезке .
21. Найдите точку максимума функции
22. Найдите наибольшее значение функции на отрезке .
23. Найдите точку минимума функции .
24. Найдите наибольшее значение функции на отрезке
25. Найдите точку максимума функции .
26. Найдите наименьшее значение функции на отрезке .
27. Найдите точку минимума функции .
28. Найдите точку минимума функции .
29. Найдите наибольшее значение функции на отрезке .
30. Найдите точку минимума функции
31. Найдите наибольшее значение функции на отрезке .
32. Найдите наименьшее значение функции на отрезке .
33. Найдите наибольшее значение функции на отрезке .
34. Найдите наибольшее значение функции на отрезке .
35. Найдите наибольшее значение функции на отрезке .
36. Найдите наименьшее значение функции на отрезке .
37. Найдите точку минимума функции
38. Найдите точку минимума функции .
39. Найдите точку минимума функции .
40. Найдите наибольшее значение функции на отрезке .
41. Найдите наибольшее значение функции на отрезке
42. Найдите наименьшее значение функции на отрезке .
43. Найдите наибольшее значение функции на отрезке
44. Найдите наибольшее значение функции на отрезке .
45. Найдите точку максимума функции .
46. Найдите точку минимума функции
47. Найдите наименьшее значение функции на отрезке .
48. Найдите точку максимума функции .
49. Найдите наибольшее значение функции на отрезке .
50. Найдите наименьшее значение функции на отрезке .
ОТВЕТЫ:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
20 |
-13 |
9 |
3 |
-4 |
1 |
29 |
9 |
5 |
-54 |
6 |
20 |
2 |
-77 |
-14 |
73 |
17 |
-13 |
|
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
|
2 |
263 |
3 |
7 |
-3 |
48 |
3 |
2 |
196 |
1 |
-33 |
16 |
15 |
-6 |
7 |
-1 |
|
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
|
-7.75 |
-2 |
8 |
139 |
10 |
-27 |
15 |
43 |
4 |
-607.5 |
-1 |
295 |
19 |
СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий
Задания 12. Уравнения. Тригонометрические уравнения
Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 12 № 507595
а) Решите уравнение
б) Найдите корни этого уравнения, принадлежащие промежутку
Аналоги к заданию № 507595: 500917 501709 Все
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, сводимые к целым на синус или косинус
Методы алгебры: Формулы двойного угла, Формулы приведения
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
2
Тип 12 № 510018
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие промежутку
Источник: Демонстрационная версия ЕГЭ—2016 по математике. Профильный уровень.
Классификатор алгебры: Тригонометрические уравнения
Методы алгебры: Формулы двойного угла, Формулы приведения
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
1 комментарий · Сообщить об ошибке · Помощь
3
Тип 12 № 504543
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Аналоги к заданию № 504543: 504564 507292 510671 Все
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Группировка
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
2 комментария · Сообщить об ошибке · Помощь
4
Тип 12 № 500366
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Аналоги к заданию № 500366: 500587 501482 514505 Все
Классификатор алгебры: Тригонометрические уравнения
Методы алгебры: Формулы двойного угла
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
4 комментария · Сообщить об ошибке · Помощь
5
Тип 12 № 509579
а) Решите уравнение
б) Найдите все корни уравнения, принадлежащие отрезку
Аналоги к заданию № 509579: 509926 509947 509968 515762 519665 Все
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, сводимые к целым на синус или косинус
Методы алгебры: Формулы двойного угла
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
- ЕГЭ по математике профиль
Прототипы задания №12 ЕГЭ по математике профильного уровня — уравнения. Практический материал для подготовки к экзамену в 11 классе.
Для успешного выполнения задания №12 необходимо уметь решать уравнения и неравенства.
Практика
Коды проверяемых элементов содержания (по кодификатору) — 2.1, 2.2
Уровень сложности задания — повышенный.
Максимальный балл за выполнение задания — 2
Примерное время выполнения задания выпускником, изучавшим математику на профильном уровне (в мин.) — 10
Связанные страницы:
Всё варианты 12 задания математика ЕГЭ Профиль 2022
Скачать задания в формате pdf.
Задания 12 ЕГЭ по математике профильного уровня 2022 год (уравнения)
1) (28.03.2022 досрочная волна) а) Решите уравнение ({4^{sin x}} + {4^{sin left( {pi + x} right)}} = frac{5}{2}.)
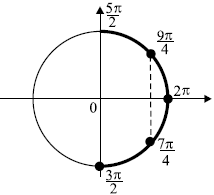
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{5}}pi }}{2};;4pi } right]).
ОТВЕТ: а) ( pm frac{pi }{6} + pi k;;;k in Z;) б) (frac{{17pi }}{6};,,,,,frac{{19pi }}{6};,,,,,frac{{{text{23}}pi }}{6}.)
2) (28.03.2022 досрочная волна) а) Решите уравнение ({81^{cos x}} — 12 cdot {9^{cos x}} + 27 = 0.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — ,4pi ;,,, — frac{{{text{5}}pi }}{2}} right]).
ОТВЕТ: а) ( pm frac{pi }{3} + 2pi k;;;2pi k;;;k in Z;) б) ( — frac{{11pi }}{3};,,,, — 4pi .)
3) (28.03.2022 досрочная волна) а) Решите уравнение ({16^{sin x}} — 1,5 cdot {4^{sin x + 1}} + 8 = 0.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — ,5pi ;,,, — frac{{{text{7}}pi }}{2}} right]).
ОТВЕТ: а) (frac{pi }{6} + 2pi k;,,;frac{{{text{5}}pi }}{6} + 2pi k;;;frac{pi }{2} + 2pi k;;;k in Z;) б) ( — frac{{{text{23}}pi }}{6};,,,, — frac{{7pi }}{2}.)
4) (02.06.2022 основная волна) а) Решите уравнение (2{sin ^2}x — cos left( { — x} right) — 1 = 0.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — ,pi ;,,,frac{pi }{2}} right]).
ОТВЕТ: а) ( pm frac{pi }{3} + 2pi k;,,;pi + 2pi k;;;k in Z;) б) ( — pi ;,,, — frac{pi }{3};,,,,frac{pi }{3}.)
5) (06.2022 основная волна) а) Решите уравнение (2{cos ^2}x — 3sinleft( { — x} right) — 3 = 0.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{5}}pi }}{2};,,4pi } right]).
ОТВЕТ: а) (frac{pi }{6} + 2pi k;,,;frac{{{text{5}}pi }}{6} + 2pi k;;;frac{pi }{2} + 2pi k;;;k in Z;) б) (frac{{{text{17}}pi }}{6};,,,,frac{{{text{5}}pi }}{2}.)
6) (06.2022 основная волна) а) Решите уравнение (cos 2x + sinleft( { — x} right) — 1 = 0.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{pi }{2};,,2pi } right]).
ОТВЕТ: а) ( — frac{pi }{6} + 2pi k;,,; — frac{{{text{5}}pi }}{6} + 2pi k;;;pi k;;;k in Z;) б) (pi ;,,,,frac{{{text{7}}pi }}{6};,,,,frac{{{text{11}}pi }}{6};,,,2pi .)
7) (06.2022 основная волна) а) Решите уравнение (cos 2x + 3sinleft( { — x} right) — 2 = 0.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{3}}pi }}{2};,,3pi } right]).
ОТВЕТ: а) ( — frac{pi }{6} + 2pi k;,,; — frac{{{text{5}}pi }}{6} + 2pi k;;; — frac{pi }{{text{2}}}{text{ + 2}}pi k;;;k in Z;) б) (frac{{{text{3}}pi }}{2};,,,,frac{{{text{11}}pi }}{6}.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {{text{3}}pi ;,,frac{{{text{9}}pi }}{2}} right]).
ОТВЕТ: а) ( — frac{pi }{2} + 2pi k;,,;2pi k;;;;k in Z;) б) (frac{{{text{7}}pi }}{2};,,,4pi .)
9) (06.2022 основная волна) а) Решите уравнение (sin 2x + 2sin left( { — x} right) + cos left( { — x} right) — 1 = 0.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {{text{2}}pi ;,,frac{{{text{7}}pi }}{2}} right]).
ОТВЕТ: а) ( — frac{pi }{6} + 2pi k;,,; — frac{{{text{5}}pi }}{6} + 2pi k;;;2pi k;;;k in Z;) б) (frac{{{text{19}}pi }}{6};,,,2pi .)
10) (27.06.2022 резервная волна) а) Решите уравнение ({log _{11}}left( {2{{sin }^2}x + 7sqrt 3 sin x — 11} right) = 0.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{3}}pi }}{2};,,3pi } right]).
ОТВЕТ: а) (frac{pi }{3} + 2pi k;,,;frac{{{text{2}}pi }}{3} + 2pi k;;;k in Z;) б) (frac{{{text{7}}pi }}{3};,,,frac{{{text{8}}pi }}{3}.)
11) (27.06.2022 резервная волна) а) Решите уравнение ({log _9}left( {sqrt 2 sin x + sin 2x + 9} right) = 1.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — frac{{{text{7}}pi }}{2};,, — 2pi } right]).
ОТВЕТ: а) ( pm frac{{{text{3}}pi }}{4} + 2pi k;,,;;pi k;;;k in Z;) б) ( — frac{{{text{13}}pi }}{4};,, — 3pi ;,,, — frac{{{text{11}}pi }}{4};,, — 2pi .)
1 вариант.
1. Найдите точку минимума функции .
2. Найдите точку максимума функции .
3. Найдите наименьшее значение функции на отрезке
.
4. Найдите наибольшее значение функции на отрезке
.
5. Найдите наибольшее значение функции на отрезке
.
2 вариант.
1. Найдите точку минимума функции
2. Найдите точку минимума функции .
3. Найдите наибольшее значение функции на отрезке
.
4. Найдите наименьшее значение функции на отрезке
.
5. Найдите наименьшее значение функции на отрезке
.
3 вариант.
1.
Найдите наибольшее значение функции .
2. Найдите точку максимума функции .
3. Найдите наибольшее значение функции
4. Найдите точку минимума функции ,
принадлежащую промежутку .
5. Найдите наименьшее значение функции на отрезке
.
4 вариант.
1. Найдите точку максимума функции .
2. Найдите точку минимума функции .
3. Найдите точку максимума функции .
4. Найдите наибольшее значение функции на отрезке
5. Найдите точку минимума функции .
5 вариант.
1. Найдите точку максимума функции .
2. Найдите точку минимума функции .
3. Найдите точку максимума функции
4. Найдите наименьшее значение функции на отрезке
.
5. Найдите точку максимума функции .
6 вариант.
1. Найдите точку максимума функции .
2. Найдите точку минимума функции .
3. Найдите точку максимума функции .
4. Найдите наименьшее значение функции на отрезке
.
5. Найдите наименьшее значение функции на отрезке
.
Ответы:
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
4 |
100 |
-18 |
101 |
1 |
|
2 |
-2 |
2,25 |
51 |
-41 |
0 |
|
3 вариант |
4 |
-9 |
-1 |
0,5 |
-6 |
|
4 вариант |
-10 |
3 |
-7 |
-12 |
2 |
|
5 вариант |
3 |
256 |
-5 |
2 |
-4 |
|
6 вариант |
2 |
-6 |
-3,25 |
6 |
0 |
За это задание ты можешь получить 2 балла. На решение дается около 10 минут. Уровень сложности: повышенный.
Средний процент выполнения: 45.3%
Ответом к заданию 12 по математике (профильной) может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
а) Решите уравнение $11cos 2x=7sin (x-{π} / {2})-9$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[-π;0]$.
Решение
а) $11cos 2x=7sin (x-{π} / {2})-9$,
$11(2cos^2 x-1)=-7cos x-9$,
$22cos^2 x -11+7cos x +9=0$,
$22cos^2 x+7cos x -2=0$.
Обозначим $cos x=t$, $|t|⩽1$.
Тогда уравнение примет вид: $22t^2+7t-2=0$.
Решим его. $22t^2+7t-2=0$,
$D=49+2⋅ 4⋅ 22=225$. $t_{1,2}={-7±15} / {44}$,
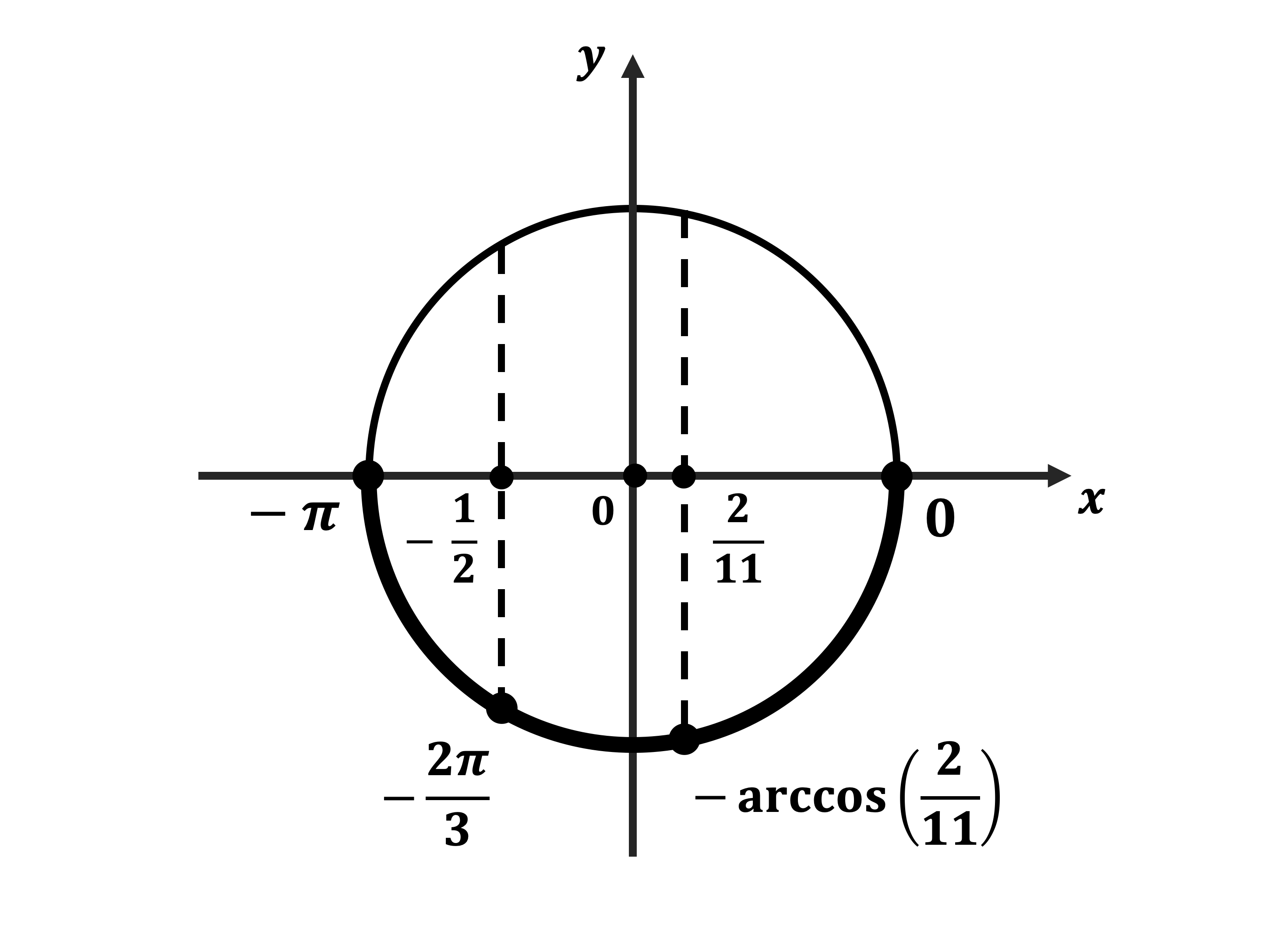
$t_1=-{1} / {2}$, $t_2={8} / {44}={2} / {11}$.
$1$. $cos x=-{1} / {2}$, $x=±(π-{π} / {3})+2π n$;
$x=± {2π} / {3}+2π n$, $n∈ Z$.
$2$. $cos x={2} / {11}$, $x=± arccos {2} / {11}+2π k$, $k∈ Z$.
б) Найдём корни этого уравнения, принадлежащие промежутку $[-π;0]$.
$x_1=-π+{π} / {3}=-{2π} / {3}$
$x_2=-arccos {2} / {11}$.
Ответ: а)$± {2π} / {3}+2πn, n∈ Z; ± arccos {2} / {11}+2π k, k∈ Z;б)-{2π}/{3}, -arccos{2}/{11}$
Задача 2
а) Решите уравнение $2 sin^2 x — 7 cos(x + {π}/{2})- 4 = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[-2π;-{π}/{2}]$.
Решение
а) Преобразуем уравнение, согласно формуле приведения:
$cos(x+{π}/{2})=-sinx,$
$2sin^2x + 7sinx -4 = 0$
Обозначим $sin x = t, −1 ≤ t ≤ 1$, получим
$2t^2 + 7t -4 = 0.$
$t_1 = {−7 − 9}/{2·2} = −4$ — не удовлетворяет условию $−1 ≤ t ≤ 1. $
$t_2 = {−7 + 9}/{2·2} = {1}/{2}$.
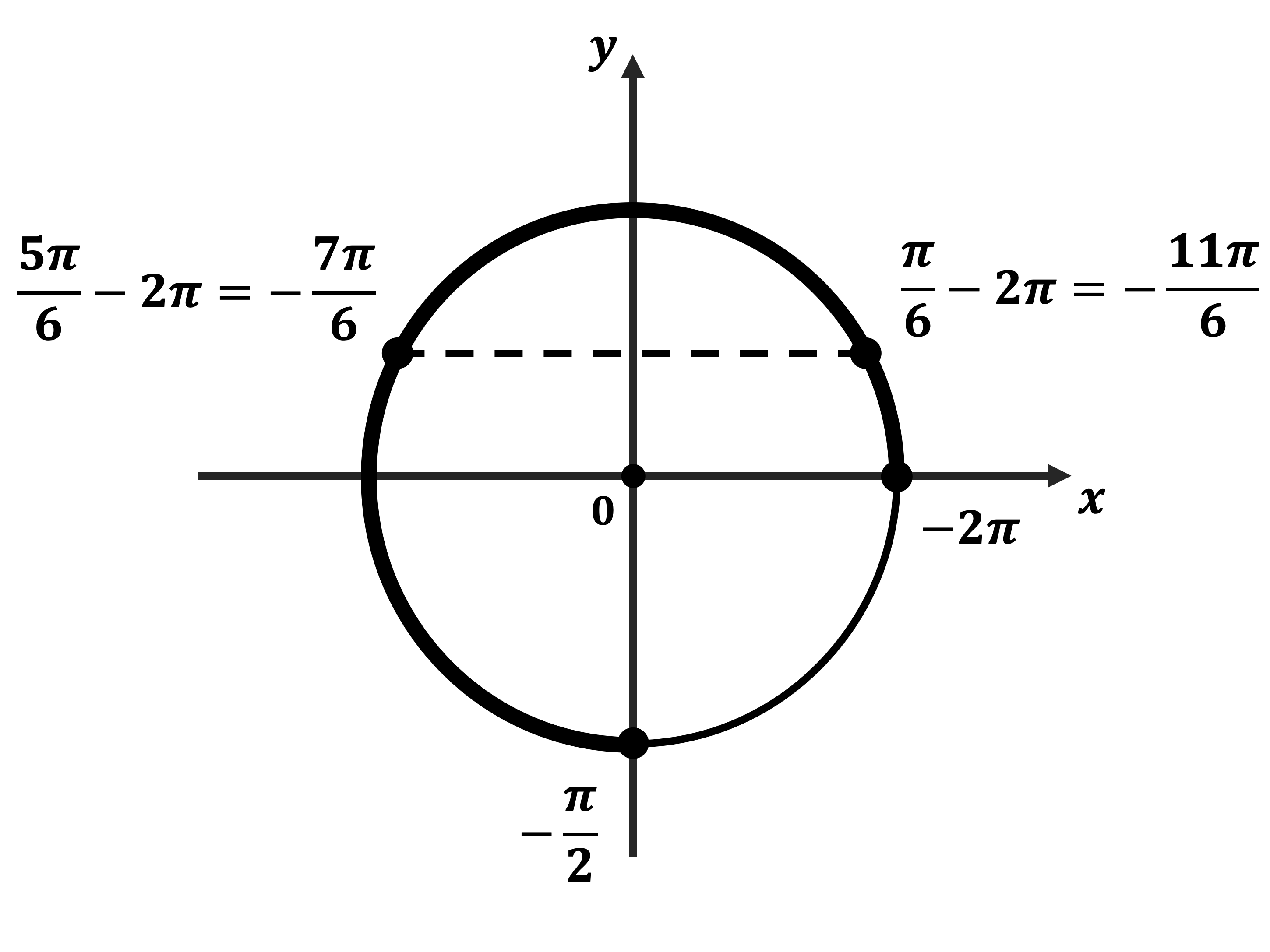
Вернёмся к исходной переменной:
$sinx ={1}/{2}$,
$x = {π}/{6} + 2πn, n ∈ Z$
$x = {5π}/{6} + 2πk, k ∈ Z$
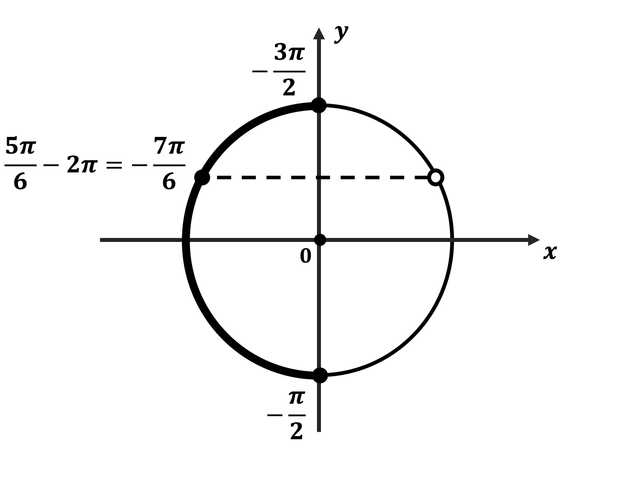
б) Корни, принадлежащие отрезку $[-2π; -{π}/{2}]$, найдём с помощью единичной окружности. Получим: ${π}/{6}-2π=-{11π}/{6}; {5π}/{6}-2π=-{7π}/{6}$.
Ответ: а) $ {π}/{6} + 2πn, n ∈ Z$; $ {5π}/{6} + 2πk, k ∈ Z$ б) $-{11π}/{6};-{7π}/{6}$
Задача 3
а) Решите уравнение $2 cos^2 x — 5 sin(x + {3π}/{2})+ 2 = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[{π}/{2};{3π}/{2}]$.
Решение
а) Преобразуем уравнение, согласно формуле приведения:
$sin(x+{3π}/{2})=-cosx,$
$2cos^2x + 5 cos x + 2 = 0$
Обозначим $cos x = t, −1 ≤ t ≤ 1$, получим $2t^2 + 5t + 2 = 0. t_1 = {−5 − 3}/{2·2} = −2$ — не удовлетворяет условию $−1 ≤ t ≤ 1. t_2 = {−5 + 3}/{2· 2} = −{1}/{2}$.
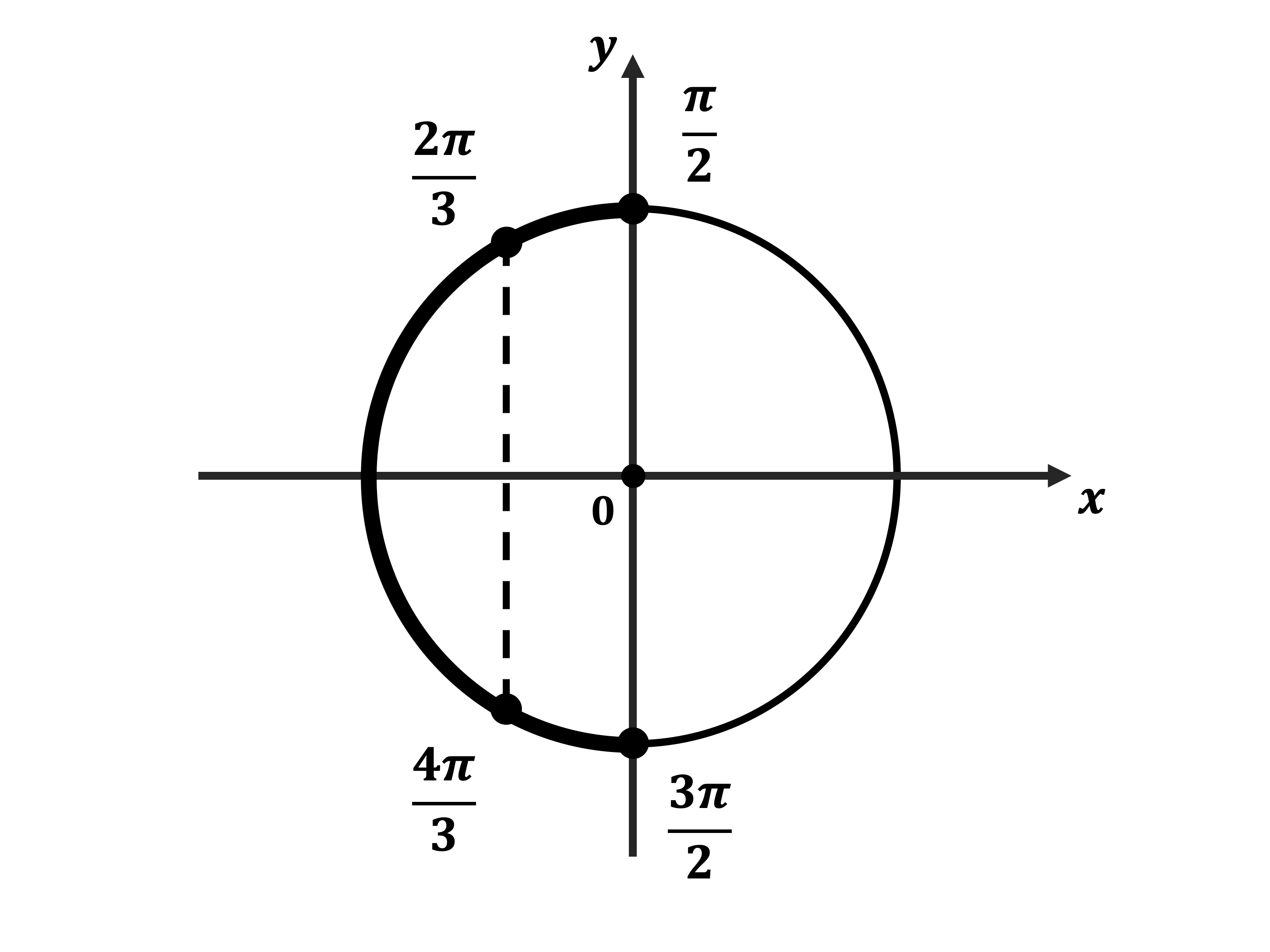
Вернёмся к исходной переменной: $cos x = − {1}/{2}$,
$x = ±(π − {π}/{3}) + 2πn, n ∈ Z , x = ±{2π}/{3} + 2πn, n ∈ Z.$
б) Корни, принадлежащие отрезку $[{π}/{2}; {3π}/{2}]$, найдём с помощью единичной окружности. Получим числа ${2π}/{3}; {4π}/{3}$.
Ответ: а)$±{2π}/{3}+2πn,n∈Z;$ б) ${2π}/{3};{4π}/{3}$
Задача 4
а) Решите уравнение $cos(x — {3π}/{2})= sin 2x$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[-{3π}/{2};0]$.
Решение
а) Преобразуем уравнение:
$−sin x = sin 2x,$
$sinx + 2 sin x cos x = 0,$
$sinx(1 + 2 cos x) = 0,$
$sin x = 0;x = πn, n ∈ Z,$
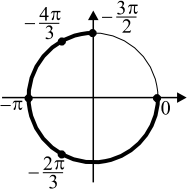
$cosx = -{1}/{2}; x = ±{2π}/{3} + 2πk, k ∈ Z .,$
б) Корни, принадлежащие отрезку $[-{3π}/{2};0]$, найдём с помощью единичной окружности. Получим числа $−{4π}/{3}; −π; −{2π}/{3}; 0$.
Ответ: а) $x=±{2π}/{3}+2πk;x=πn,k,n∈Z$ б) $-{4π}/{3};-π;-{2π}/{3};0$.
Задача 5
а) Решите уравнение $sin({π}/{2}+ x)= sin (-2x)$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[0; π]$.
Решение
а) Преобразуем уравнение:
$cos x = − sin 2x,$
$cos x + 2 sin x cos x = 0,$
$cos x(1 + 2 sin x) = 0,$
$cos x = 0;$
$x = {π}/{2} + πn, n ∈ Z$
$sin x = −{1}/{2},$
$x = (−1)^{k+1}·{π}/{6} + πk, k ∈ Z$
б) Корни, принадлежащие отрезку $[0; π]$, найдём с помощью единичной окружности.
Указанному промежутку принадлежит единственное число ${π}/{2}$.
Ответ: а) ${π}/{2}+πn,n∈Z;(-1)^{k+1}{π}/{6}+πk,k∈Z$; б) ${π}/{2}$
Задача 6
а) Решите уравнение $sin x(2 sin x — 1) + √3 sin x + sin {4π}/{3}= 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[-{π}/{2};π]$.
Решение
а) Решим уравнение $sinx(2sinx-1) +√3sinx + sin{4π}/{3} = 0$.
Так как $sin{4π}/{3} = sin(π +{π}/{3}) = − sin{π}/{3} = −{√3}/{2}$, то уравнение примет вид $sin x(2 sin x-1) +√3 sin x-{√3}/{2} = 0$. Отсюда $2 sin x(sin x-{1}/{2})+ √3(sin x-{1}/{2}) = 0; (2sinx+√3)(sin x-{1}/{2}) = 0$.
Тогда $sin x = {1}/{2}; x = (−1)^n{π}/{6} + πn$ или $sin x = −{√3}/{2}; x = (−1)^{n+1}{π}/{3} + πn$, где $n ∈ Z.$
б) Корни, принадлежащие промежутку $[−{π}/{2}; π]$, найдём с помощью числовой окружности: $−{π}/{3}; {π}/{6}; {5π}/{6}$.
Ответ: а)$(-1)^{n}{π}/{6}+πn;(-1)^{n+1}{π}/{3}+πn,n∈Z$; б) $-{π}/{3};{π}/{6};{5π}/{6}$
Задача 7
а) Решите уравнение $4cos^{2}x = 3cos2x + 1$.
б) Найдите корни уравнения, принадлежащие отрезку $[-4π;-{5π}/{4})$.
Решение
a) $4cos^{2}x = 3cos2x+1$,
$4cos^{2}x = 3(2cos^{2}x-1)+1$,
$4cos^{2}x=6cos^{2}x-3+1$,
$cos^{2}x=1, [tablecosx=1; cosx=-1;$ $[tablex=2πn, n ∈ Z; x=π+2πk, k ∈ Z;$ $x=πk, k ∈ Z$
б) Корни, принадлежащие промежутку $[-4π;-{5π}/{4})$, найдем из неравенства $-4π ≤ πk < -{5π}/{4}; k=-4, -3, -2$
$x_1=-4π, x_2=-3π, x_3=-2π$.
Ответ: а)$πn,n∈Z$;б)$-4π;-3π;-π$
Задача 8
а) Решите уравнение $cos (2x) + 3 sin x — 2 = 0$.
б) Найдите корни уравнения, принадлежащие отрезку $[-3π;-π]$.
Решение
a) $cos(2x) + 3sinx-2=0$,
$1 — 2sin^{2}x + 3 sin x -2 = 0$,
$2 sin^{2}x — 3sin x +1 = 0$,
Пусть $sin x = y, |sinx| ≤ 1$, уравнение примет вид
$2y^2 — 3y + 1 = 0$,
$y_{1,2} = {3±√{9-8}}/{4} = {3±1}/{4};$
$ y_1=1, y_2={1}/{2}$.
$sin x = 1, x = {π}/{2}+2πn, n ∈ Z; sinx={1}/{2}, x=(-1)^{k}{π}/{6} + πk, k ∈ Z$.
б) Найдём корни уравнения на отрезке $[-3π;-π]$.
С помощью числовой окружности отберём корни уравнения, принадлежащие $[-3π;-π]$.
Это числа $-{11π}/{6}, -{3π}/{2}, -{7π}/{6}$.
Ответ: а)${π}/{2}+2πn,n∈Z;(-1)^{k}{π}/{6}+πk,k∈Z$;б)$-{11π}/{6};-{3π}/{2};-{7π}/{6}$
Задача 9
а) Решите уравнение $2 cos^2 x + 19 sin x + 8 = 0$.
б) Найдите корни уравнения, принадлежащие отрезку $[-π;{π}/{2}]$.
Решение
a) $2 cos^{2}x + 19sinx+8=0$,
$2(1 — sin^{2}x) + 19 sin x +8 = 0$,
$-2 sin^{2}x + 19 sin x +10 = 0$,
$2 sin^{2}x — 19 sin x -10 = 0$.
Пусть $sin x = y, |y| ≤ 1$, уравнение примет вид $2y^2 — 19y -10 = 0$, решим его: $y_{1,2} = {19±√{361 + 80}}/{4} = {19±21}/{4}$.
$y_1 = 10$ или $y_2 = -{1}/{2}$. $y_1=10$ не удовлетворяет условию $|y| ≤ 1$. $sin x = -{1}/{2}, x = (-1)^{n+1}{π}/{6} + πn, n ∈ Z$.
б) Найдём корни уравнения на отрезке $[-π;{π}/{2}]$.
Это числа $-{5π}/{6}$ и $-{π}/{6}$.
Ответ: а)$(-1)^{n+1}{π}/{6}+πn,n∈Z$; б) $-{5π}/{6},-{π}/{6}$
Задача 10
а) Решите уравнение $8sin x + 4 cos^2 x = 7$.
б) Найдите корни уравнения, принадлежащие отрезку $[-{3π}/{2};-{π}/{2}]$.
Решение
a) $8 sin x + 4 cos^{2} x = 7$,
$4(1 — sin^{2}x) + 8 sin x — 7 = 0$,
$-4 sin^{2}x + 8 sin x — 3 = 0$,
$4 sin^{2}x — 8 sin x + 3 = 0$.
Пусть $sin x = t, |t| ≤ 1$, уравнение примет вид $4t^2 — 8t + 3 = 0$, решим его: $t_{1,2} = {8±√{64 — 48}}/{8} = {8±√{16}}/{8} = {8±4}/{8} = 1±{1}/{2}$.
$t_1 = {1}/{2}$ или $t_2 = {3}/{2}$. $t_2$ не удовлетворяет условию $|t| ≤ 1$. $sin x = {1}/{2}, x = (-1)^{n}{π}/{6} + πn, n ∈ Z$.
б) Найдём корни уравнения на отрезке $[-{3π}/{2};-{π}/{2}]$.
Это число ${5π}/{6} — 2π = -{7π}/{6}$.
Ответ: а)$(-1)^{n}{π}/{6}+πn,n∈Z$;б)$-{7π}/{6}$
Задача 11
а) Решите уравнение ${sin 2x}/{sin({3π}/{2}+ x)}= 1$.
б) Укажите корни этого уравнения, принадлежащие промежутку $(3π;{9π}/{2})$.
Решение
а) ${{sin2x}/{sin({3π}/{2} + x)} = 1$.
Зная, что $sin2x = 2sinxcosx$ и $sin({3π}/{2}+ x)= −cosx$, получим: ${2sinxcosx}/{−cosx}= 1$, где $cosx≠0, x≠{π}/{2}+ πm, m ∈ Z$.
$−2sinx = 1, sinx =−{1}/{2}$.
$x=−{π}/{6}+2πn, n ∈ Z;$
$x=-{5π}/{6}+ 2πk, k ∈ Z$.
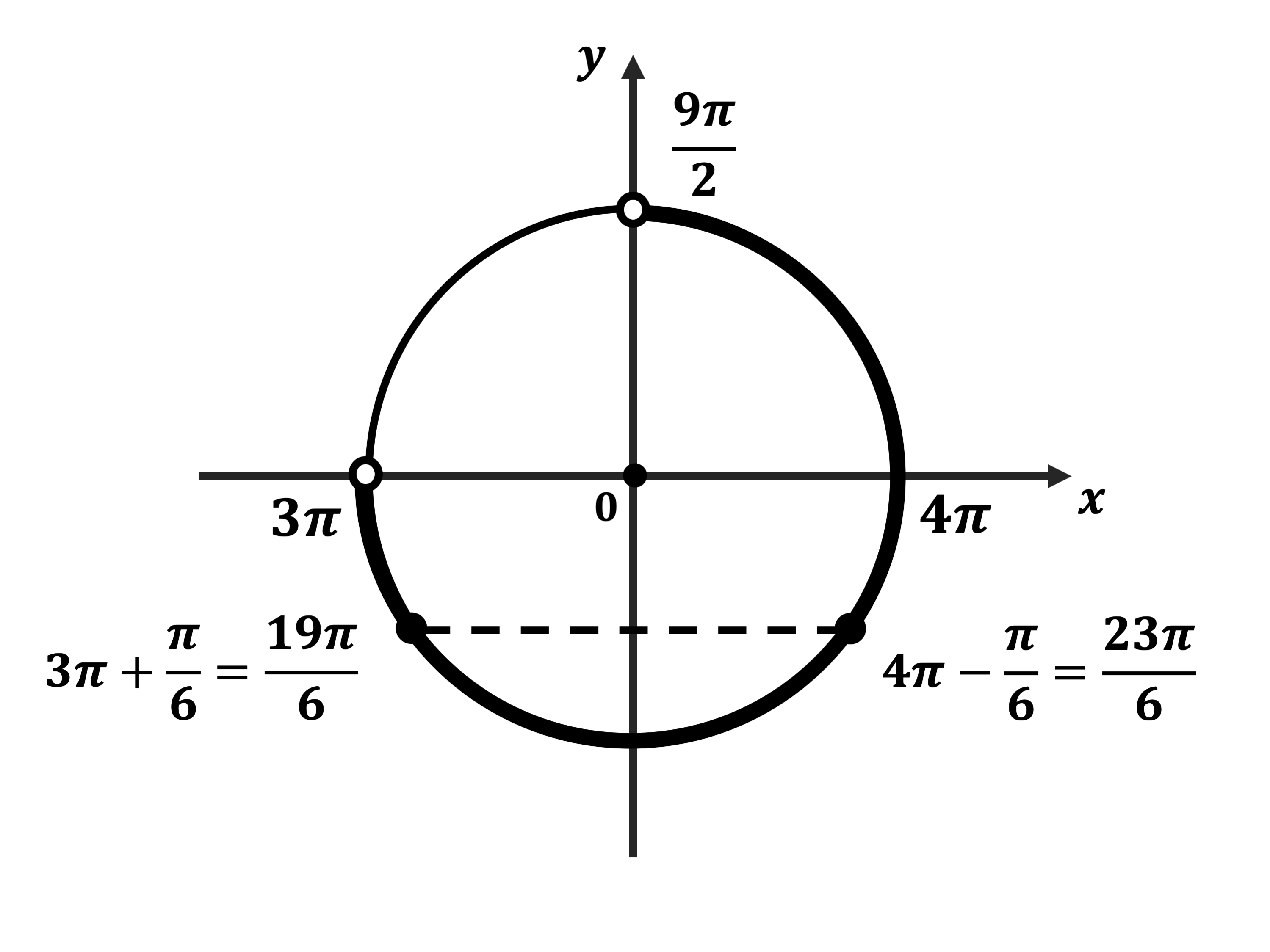
б) Отберём корни уравнения, принадлежащие промежутку $(3π; {9π}/{2})$,с помощью числовой окружности.
$x_1=3π+{π}/{6}={19π}/{6}$,
$x_2=4π−{π}/{6}={23π}/{6}$.
Ответ: а)$-{π}/{6}+2πn,-{5π}/{6}+2πk,n,k∈Z$;б)${19π}/{6};{23π}/{6}$
Задача 12
а) Решите уравнение ${sin 2x}/{sin(π — x)}= √2$.
б) Укажите корни этого уравнения, принадлежащие промежутку $[-{5π}/{2};-π)$.
Решение
а)${sin2x}/{sin(π — x)}=√2$.
а) Применим формулу синуса двойного аргумента $sin2x = 2sinxcosx$ и формулу приведения $sin(π — x) = sin x$.
Уравнение примет вид: ${2sinxcosx}/{sinx} = √2$.
Учитывая, что $sinx≠0, x≠πn, n∈Z$, получим:
$2cosx=√2$,
$cosx = {√2}/{2}$,
$x = ±{π}/{4} + 2πk, k∈Z$;
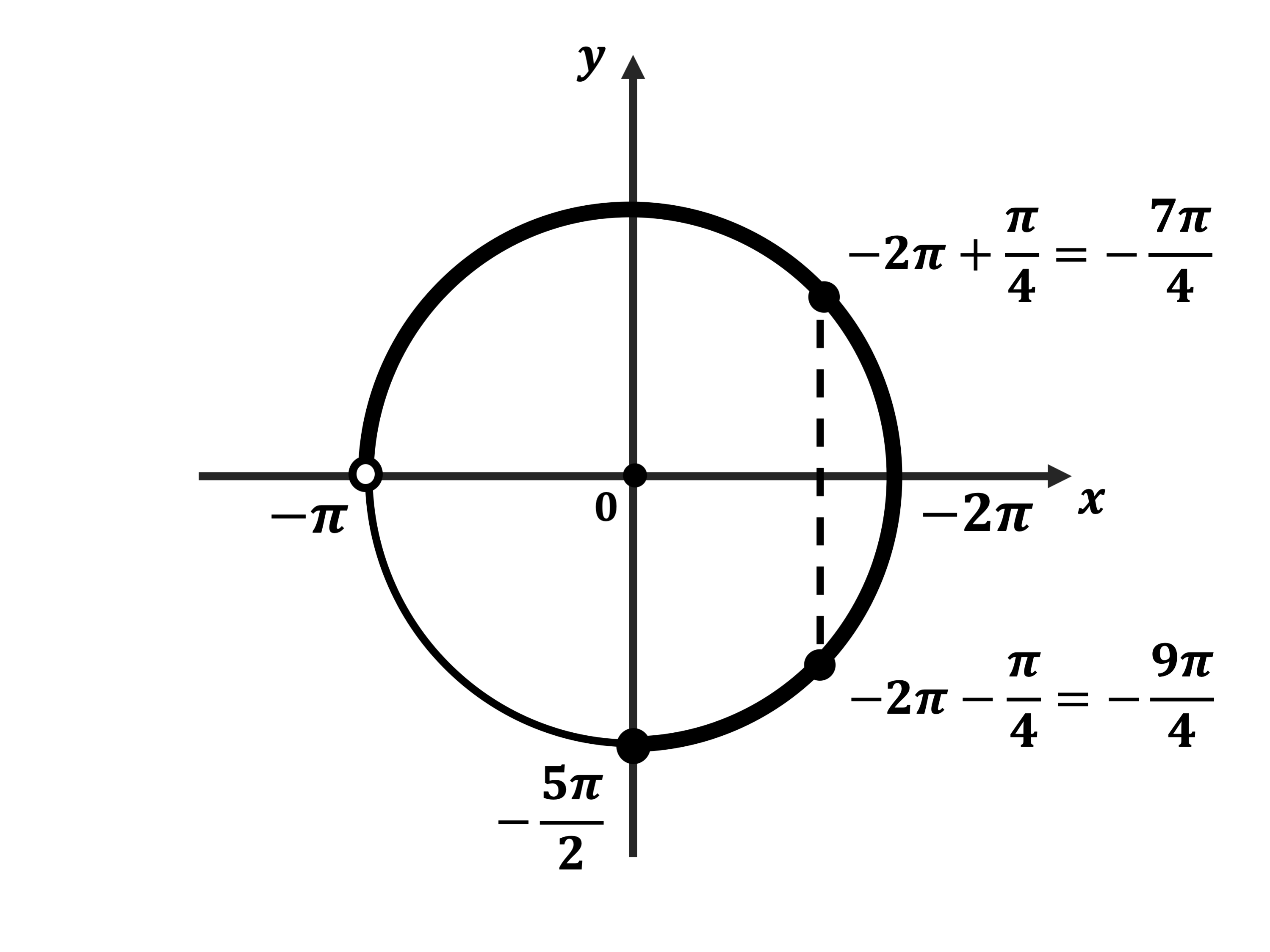
б) Отберём корни уравнения, принадлежащие промежутку $[-{5π}/{2};-π)$, с помощью окружности.
$x_1=-2π+{π}/{4}=-{7π}/{4}$
$x_2=-2π-{π}/{4}=-{9π}/{4}$
Ответ: а)$±{π}/{4}+2πk,k∈Z$;б)$-{9π}/{4};-{7π}/{4}$
Задача 13
а) Решите уравнение ${sin 2x}/{cos(π + x)}= -√2$.
б) Укажите корни этого уравнения, принадлежащие промежутку $(-2π;-{π}/{2})$.
Решение
а)${sin2x}/{cos(π + x)}=-√2$.
Зная, что $sin2x = 2sinxcosx, cos(π + x)=-cosx$, получим: ${2sinxcosx}/{-cosx}=-√2$.
Учитывая, что $cosx≠0, x≠{π}/{2} + πm, m∈Z$, имеем:
$2sinx=√2$,
$sinx = {√2}/{2}$,
$x = {π}/{4} + 2πn, n∈Z$;
$x = {3π}/{4} + 2πk, k∈Z$.
б) Отберём корни уравнения, принадлежащие промежутку $(-2π;-{π}/{2})$.
1. $x = {π}/{4} + 2πn, n∈Z$.
$-2π < {π}/{4} + 2πn < -{π}/{2},$
$-2 < {1}/{4} + 2n < -{1}/{2},$
$-2-{1}/{4} < 2n < -{1}/{2}-{1}/{4},$
$-{9}/{4} < 2n < -{3}/{4},$
$-{9}/{8} < n < -{3}/{8},$
$n = -1$.
При $n =-1$
$x = {π}/{4}-2π=-{7π}/{4}$.
2. $x = {3π}/{4} + 2πk, k∈Z$.
$-2π < {3π}/{4} + 2πk < -{π}/{2}$,
$-2 < {3}/{4} + 2k < -{1}/{2}$,
$-2-{3}/{4} < 2k < -{1}/{2}-{3}/{4}$,
$-{11}/{4} < 2k < -{5}/{4}$,
$-{11}/{8} < k < -{5}/{8}$,
$k = -1$.
При $k = -1$
$x = {3π}/{4}-2π = -{5π}/{4}$.
Ответ: а)${π}/{4}+2πn,{3π}/{4}+2πk,n,k∈Z$;б)$-{7π}/{4};-{5π}/{4}$
Задача 14
а) Решите уравнение $9·3^{2 cos x} — 10√3·3^{cos x} + 3 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[{3π}/{2};4π]$.
Решение
а) После замены $t = 3^{cosx}$ исходное уравнение примет вид $9t^2 — 10√3t + 3 = 0$. Корни этого уравнения $t = √3; t = {√3}/{9}$. Возвращаясь к переменной $x$, получим
$[table3^{cosx}=√3; 3^{cosx}={√3}/{9};$ $[table3^{cosx}=3^{{1}/{2}}; 3^{cosx}=3^{-{3}/{2}};$ $[tablecosx={1}/{2}; cosx=-{3}/{2};$
Второе уравнение совокупности не имеет корней. Решая первое уравнение, получим $x =±{π}/{3} + 2πn; n ∈ Z$.
б) Запишем решение уравнения в виде $x =-{π}/{3} + 2πn; n ∈ Z$ или $x ={π}/{3} + 2πk; k ∈ Z$ и выясним, для каких целых значений $n$ и $k$ справедливы неравенства ${3π}/{2}≤-{π}/{3}+2πn≤4π$ и ${3π}/{2}≤{π}/{3}+2πk≤4π$.
Получим ${11}/{12} ≤ n ≤ {26}/{12}$ и ${7}/{12} ≤ k ≤{22}/{12}$.
Откуда следует, что два целых значения $n = 1$ и $n = 2$ удовлетворяют неравенству ${11}/{12} ≤ n ≤ {26}/{12}; k = 1$ — единственное целое $k$, удовлетворяющее неравенству ${7}/{12} ≤ k ≤{22}/{12}$.
При $n = 1$ $x = -{π}/{3} + 2π·1 = {5π}/{3}$.
При $n = 2$ $x = -{π}/{3} + 2π·2 = {11π}/{3}$.
При $k = 1$ $x = {π}/{3} + 2π·1 = {7π}/{3}$. Итак, ${5π}/{3}; {7π}/{3}; {11π}/{3}$ — корни уравнения, принадлежащие промежутку $[{3π}/{2};4π]$.
Ответ: а)$x=±{π}/{3}+2πn,n∈Z$;б)${5π}/{3};{7π}/{3};{11π}/{3}$
Задача 15
а) Решите уравнение $log_2^2(2 sin x + 1) — 17 log_2(2 sin x + 1) + 16 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[{π}/{4};2π]$.
Решение
а) После замены $t = log_2(2 sin x+1)$ исходное уравнение примет вид $t^2-17t+16 = 0$. Корни этого уравнения $t = 1, t = 16$. Возвращаясь к переменной $x$, получим:
$[tablelog_2(2 sin x + 1) = 1; log_2(2 sin x + 1) = 16;$ $[table2 sin x + 1 = 2;; 2sin x + 1 = 2^{16};$
Второе уравнение совокупности не имеет корней. Решая первое уравнение, получим: $sin x = {1}/{2}; x = (-1)^n{π}/{6} + πn; n ∈ Z$.
б) Запишем решение уравнения в виде $x = {π}/{6} + 2πn; n ∈ Z$ или $x = {5π}/{6} + 2πk; k ∈ Z$ и выясним, для каких целых значений $n$ и $k$ справедливы неравенства ${π}/{4}≤{π}/{6}+2πn≤2π$ и ${π}/{4}≤{5π}/{6}+2πk≤2π$.
Получим: ${1}/{24}≤n≤{11}/{12}$ и $-{7}/{24}≤k≤{7}/{12}$, откуда следует, что нет целых значений $n$, удовлетворяющих неравенству ${1}/{24}≤n≤{11}/{12}; k = 0$ — единственное целое $k$, удовлетворяющее неравенству $-{7}/{24}≤k≤{7}/{12}$.
При $k = 0$ $x = {5π}/{6} + 2π·0 = {5π}/{6}$. Итак, ${5π}/{6}$ — корень уравнения, принадлежащий отрезку $[{π}/{4};2π]$.
Ответ: а)$(-1)^{n}{π}/{6}+πn,n∈Z$;б)${5π}/{6}$
Задача 16
а) Решите уравнение $6 log_2^2(2 cos x) — 9 log_2(2 cos x) + 3 = 0$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $[-{π}/{2};π]$.
Решение
а) Решим уравнение $6log_2^2(2 cos x)-9 log_2(2 cos x)+3 = 0$. Обозначим $log_2(2 cos x) = t$ и решим получившееся квадратное уравнение.
$6t^2 — 9t + 3 = 0, t = {9±3}/{12}; t_1 = {1}/{2}; t_2 = 1$.
$[tablelog_2(2 cos x) ={1}/{2}; log_2(2 cos x) = 1;$ $[table2 cos x = √2; 2 cos x = 2;$
$[tablecos x = {√2}/{2}; cos x= 1;$ $[tablex = ±{π}/{4}+ 2π n; n ∊ Z; x = 2πk; k ∊ Z;$
б) Корни, принадлежащие отрезку $[-{π}/{2};π]$, найдём с помощью числовой окружности:
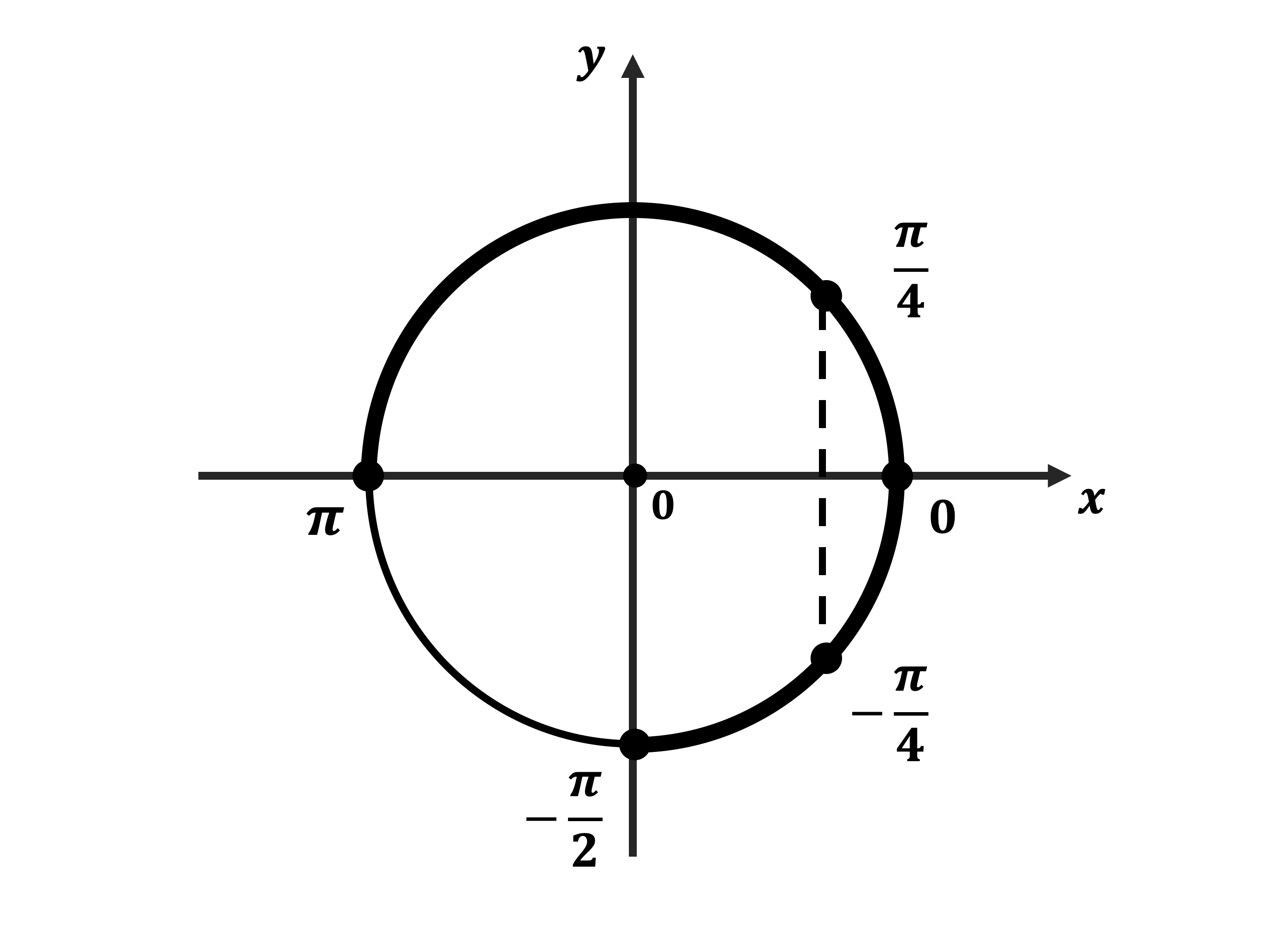
$x_1 = -{π}/{4}; x_2 = 0; x_3 ={π}/{4}$.
Ответ: а)$±{π}/{4}+2πn,n∈Z;2πk,k∈Z$;б)$-{π}/{4};0;{π}/{4}$
Задача 17
а) Решите уравнение $2log_2^2(2 sin x) — 3 log_2(2 sin x) + 1 = 0$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $[{3π}/{2}; 3π]$.
Решение
а) Решим уравнение $2log_2^2(2 sin x) — 3 log_2(2 sin x) + 1 = 0$. Обозначим $log_2(2 sin x) = t$ и решим получившееся уравнение. $2t^2 — 3t + 1 = 0, t = {3±1}/{4}; t_1 = 1; t_2 ={1}/{2}$
$[tablelog_2(2 sin x) = 1; log_2(2 sin x) ={1}/{2};$ $[table2 sin x = 2; 2 sin x=√2;$
$[tablesin x = 1; sin x = {√2}/{2};$ $[tablex={π}/{2}+2πn; x=(-1)^k{π}/{4}+πk;$ $n,k∈Z$
б) Корни, принадлежащие отрезку $[{3π}/{2}; 3π]$, найдём с помощью числовой окружности:
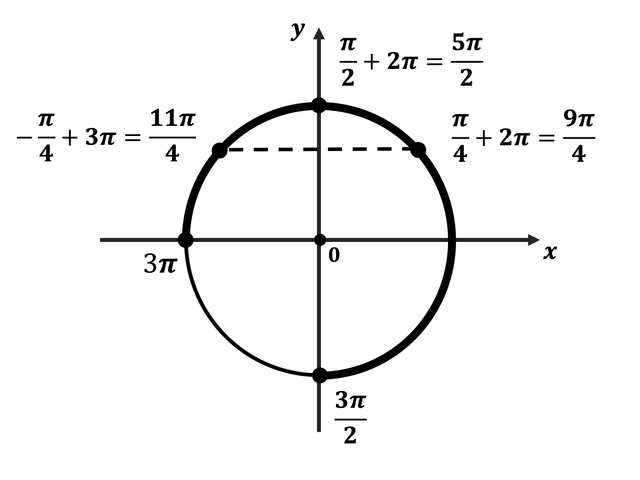
$x_1 = 2π + {π}/{4} = {9π}/{4}; x_2 = 2π + {π}/{2} ={5π}/{2}; x_3 = 3π -{π}/{4} = {11π}/{4}$.
Ответ: а)${π}/{2}+2πn,n∈Z;(-1)^k{π}/{4}+πk,k∈Z$;б)${9π}/{4};{5π}/{2};{11π}/{4}$
Задача 18
а) Решите уравнение $27^{x} — 5·9^{x} — 3^{x+4} + 405 = 0$.
б) Укажите все корни этого уравнения, принадлежащие отрезку $[log_{3}6; log_{3}10]$.
Решение
а) Преобразуем исходное уравнение и разложим на множители его левую часть.
$3^{3x} — 5·3^{2x} — 81·3^x + 405 = 0$,
$3^{2x}(3^x — 5) — 81(3^x — 5) = 0$,
$(3^{2x} — 81)(3^x — 5) = 0$.
Получаем: $3^{2x} -81 = 0$ или $3^x -5 = 0$. Значит, $3^{2x} = 81$, откуда $x = 2$ или $3^x = 5$, откуда $x = log_{3}5$.
б) Нам нужно выбрать те корни уравнения, которые принадлежат отрезку $[log_{3}6; log_{3}10]$. Заметим, что $2 = log_{3}9$. Тогда $log_{3}5 < log_{3}6 < 2 < log_{3}10$. Значит, указанному отрезку принадлежит корень $x = 2$.
Ответ: а)$2;log_{3}5$; б)$2$
Задача 19
а) Решите уравнение $3√{2}sin({π}/{2}+x)-2=2cos^{2}x$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[{3π}/{2};{5π}/{2}]$.
Решение
а) Запишем исходное уравнение в виде $2 cos^2 x — 3√2 cos x + 2 = 0$.
Решая это уравнение как квадратное относительно $cos x$, получим $(cos x)_{1,2} ={3√2±√{18 — 16}}/{4}={3√2± √2}/{4}$.
Значит, $(cos x)_1 = {√2}/{2}$, откуда $x =π/4 + 2πn, n ∈ Z$ или $x =-π/4 + 2πn, n ∈ Z$.
Уравнение $(cosx)_2 = √2$ корней не имеет.
б) Отберём корни, принадлежащие отрезку $[{3π}/{2};{5π}/{2}]$ с помощью числовой окружности.
Получим числа
$2π -{π}/{4} ={7π}/{4}$;
$2π + {π}/{4} = {9π}/{4}$.
Ответ: а)$±{π}/{4}+2πn,n∈Z$;б)${7π}/{4},{9π}/{4}$
Задача 20
а) Решите уравнение $3√{3}cos({3π}/{2}+x)-3=2sin^{2}x$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[2π; 3π]$.
Решение
а) Запишем исходное уравнение в виде $2sin^2 x — 3√3 sin x + 3 = 0$.
Решая это уравнение как квадратное относительно $sin x$, получим $(sin x)_{1,2} = {3√3±√{27-24}}/{4}= {3√3±√3}/{4}$.
Значит,$(sin x)_1 ={√3}/{2}$, откуда $x ={π}/{3} +2πn, n ∈ Z$ или $x ={2π}/{3}+2πm, m ∈ Z$.
Уравнение $(sin x)_2 = √3$ корней не имеет.
б) С помощью числовой окружности отберём корни, принадлежащие отрезку: $[2π; 3π]$
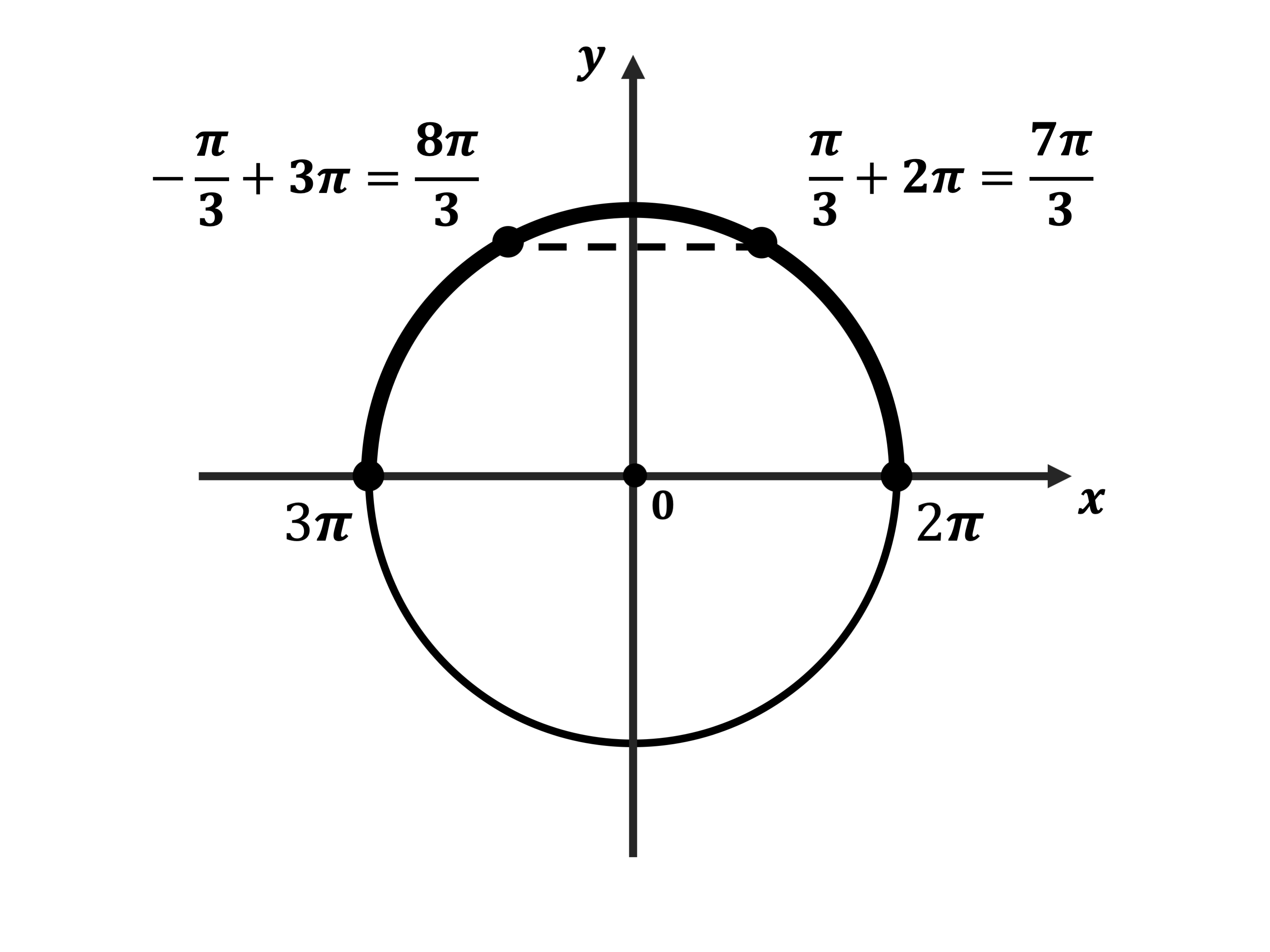
Получим числа:
$2π +{π}/{3}={7π}/{3}$;
$3π -{π}/{3}={8π}/{3}$.
Ответ: а)${π}/{3}+2πn,n∈Z;{2π}/{3}+2πm,m∈Z$;б)${7π}/{3},{8π}/{3}$