ЕГЭ математика — База 2021. Открытый банк заданий с ответами.
Критерии
Оценивание
| № задания | 1-20 | Всего |
|---|---|---|
| Баллы | 1 | 20 |
На выполнение работы отводится 3 часа (180 минут).
Экзаменационная работа состоит из одной части, включающей 20 заданий с кратким ответом базового уровня сложности.
Ответом к каждому из заданий 1–20 является целое число или конечная десятичная дробь, или последовательность цифр.
| № задания | 1-21 | Всего |
|---|---|---|
| Баллы | 1 | 21 |
На выполнение работы отводится 3 часа (180 минут).
Экзаменационная работа состоит из одной части, включающей 21 заданий с кратким ответом базового уровня сложности. Все задания направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.
Ответом к каждому из заданий 1–21 является целое число или конечная десятичная дробь, или последовательность цифр. Задание с кратким ответом считается выполненным, если верный ответ записан в бланке ответов №1 в той форме, которая предусмотрена инструкцией по выполнению задания.
При выполнении работы Вы можете воспользоваться справочными материалами, содержащими основные формулы курса математики, выдаваемыми вместе с работой.
Разрешается использовать только линейку, но можно сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене не используются.
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
Шкалирование
| Балл / Оценка | 0-6 / «2» | 7-11 / «3» | 12-16 / «4» | 17-20 / «5» |
|---|
Мы знаем в чем причина низких баллов в 2022 году.
МЫ ЗНАЕМ КАК ИСПРАВИТЬ ЭТО В 2023 ГОДУ!
Подготовка к ЕГЭ/ОГЭ от Университета «Синергия»
Информцентр образования
Собрал необходимые материалы по всем предметам и уже разделили их по блокам, вопросам, вариантам и типам заданий на экзамене. В разделах есть официальная информация к изучению — кодификатор, спецификация ФИПИ, демоверсии, КИМ (пробные варианты) и многое другое.
Теория
Для удобства информация распределена по номерам заданий демоверсий 2023 года. Материал изложен полно, но кратко. Простым языком. Есть наглядные примеры для понимания, схемы, таблицы для запоминания.
Практика
Это удобное пособие для быстрой подготовки к экзаменам: просто выбирайте задание, которое вызвало больше всего затруднений или вопросов, и тренируйтесь. В каждом листе есть список заданий, которые вы можете пройти самостоятельно, также правильные ответы с пояснениями (обоснованиями).
Осипов НикитаПодготовка к ЕГЭ/ОГЭ по математике
Образование:
- Призер математических олимпиад «Физтех» и «Звезда»
- Автор более 10 электронных курсов по подготовке к ЕГЭ и ОГЭ
- Преподавательский опыт более 5 лет в центрах подготовки к ЕГЭ и ОГЭ, на онлайн-платформах
Дополнительно:
Эксперт ЕГЭ по математике
Достижения:
Моя философия проста. Я ориентируюсь на умение, а не на запоминание. Я стремлюсь к тому, чтобы каждый учащийся осваивал концепции, суть математических явлений, почему что-то так или иначе, а не просто запомнил схему.
В «Синергии» отвечает за:
- Разработку учебно-методических пособий, дидактических и наглядных материалов по математике, и их оперативной корректировке;
- Организацию проведения методических экспериментов, внедрение в учебный процесс методических достижений и новых технологий обучения.
Наверх
Сборник ЕГЭ 2021 по математике 11 класс базовый уровень 30 примерных тренировочных вариантов в формате ЕГЭ 2021 года с ответами, авторы: Семёнов А.В, Ященко И.В, Высоцкий И.Р и другие.
Ссылка для скачивания сборника ЕГЭ 2021 по математике: скачать в PDF
ЕГЭ 2021 Семёнов А.В Ященко математика базовый уровень 30 вариантов в формате ЕГЭ с ответами онлайн:
Данное пособие предназначено для подготовки к Единому государственному экзамену по математике базового уровня. Издание включает типовые задания по всем содержательным линиям экзаменационной работы, а также 30 примерных вариантов в формате ЕГЭ 2021 года.
Пособие поможет школьникам проверить свои знания и умения по предмету, а учителям — оценить степень достижения требований образовательных стандартов отдельными учащимися и обеспечить их целенаправленную подготовку к экзамену.
Другие сборники ЕГЭ 2021 по математике:
ЕГЭ 2021 математика Лысенко, Кулабухов 40 тренировочных вариантов с ответами
https://100ballnik.com/%d0%b5%d0%b3%d1%8d-2021-%d1%8f%d1%89%d0%b5%d0%bd%d0%ba%d0%be-%d0%b8-%d0%b2-36-%d0%b2%d0%b0%d1%80%d0%b8%d0%b0%d0%bd%d1%82%d0%be%d0%b2-%d0%bc%d0%b0%d1%82%d0%b5%d0%bc%d0%b0%d1%82%d0%b8%d0%ba%d0%b0-11/
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Ниже Вы можете бесплатно скачать электронные книги и учебники и читать статьи и уроки к разделу ЕГЭ по математике 2023, 2022, 2021, 2020:
У нас Вы можете скачать реальные задания ЕГЭ по математике 2023, 2022, 2021, 2020, 2019, 2018, 2017, 2016, 2015, 2014, 2013, демоверсию ЕГЭ, реальные и демонстрационные варианты, официальные варианты.
Специально для всех абитуриентов в данной категории собраны все необходимые материалы для подготовки к Единому Государственному Экзамену по математике следующих авторов: Колесникова С.И., Семёнов А.Л., Ященко И.В., Кочагин В.В., Кочагина М.Н., Лысенко Ф.Ф., Кулабухова С.Ю., И.В, Шестаков С.А, Захаров П.И., Сергеев И.Н., Дорофеев Г.В., Титаренко А.М., Третьяк Т.М, Виноградова Т.М., Рязановский А.Р., Попов М.А., Клово А.Г., Мальцев Д.А., Абзелилова Л.И., Глазков Ю.А., Корешкова Т.А., Мирошин В.В., Шевелева Н.В., Гордин Р.К., Смирнов В.А., Гущин Д.Д., Высоцкий И.Р. и др.
По опросу всех учащихся математика — один из самых сложных предметов, изучаемых в школе. Тем более, что он подразделяется на алгебру и геометрию. Следовательно, сдать ЕГЭ по математике на отлично невероятно трудно. Нужно готовиться, решать экзаменационные варианты, проходить интенсивный курс подготовки, решать сборник тренировочных работ и заданий, тематические тесты, искать репетиторов.
Не забудьте просмотреть задания открытого бланка, почитать методические указания, практикум по выполнению типовых тестовых заданий ЕГЭ, ознакомиться с решением сложных задач, скачать справочник, учебно-методическое пособие для подготовки к экзамену, рабочую тетрадь, диагностические работы по математике в формате ЕГЭ 2023, 2022, 2021, 2020, 2019, 2018, 2017, 2016, 2015, 2014, 2013, 2012, 2011, 2010, 2009.
Готовьтесь по книгам, вариантам и сборникам тестов, решайте реальные задания, используйте КИМ — контрольно измерительные материалы, смотрите демонстрационные варианты ниже к подготовке к сдаче экзамена Единый государственный экзамен по математике, и у Вас получится успешно сдать его, ответить на все вопросы и тесты к экзамену по математике.
В 2011 и 2010 тест ЕГЭ по математике состоял из 18 заданий.
С 2010 года группа заданий А отсутствует в ЕГЭ по математике.
В 2012 и 2013 году тест ЕГЭ по математике состоял из 20 заданий.
В 2014 году тест ЕГЭ по математике состоит из 20 заданий, которые по уровню сложности и типу ответов на задачи можно разделить следующим образом:
Вариант № 1 база
1. Найдите значение выражения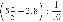 
2. Найдите значение выражения 
3.
Студент получил свой первый гонорар в размере 800 рублей за выполненный перевод. Он решил на все полученные деньги купить букет роз для своей учительницы английского языка. Какое наибольшее количество роз сможет купить студент, если удержанный у него налог на доходы составляет 13% гонорара, розы стоят 100 рублей за штуку и букет должен состоять из нечетного числа цветов?
4. Среднее гармоническое трёх чисел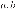 
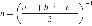
и 
вычисляется по формуле 
.
Найдите среднее гармоническое чисел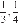 
и 
.
5. Найдите значение выражения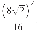 
6. В общежитии института в каждой комнате можно поселить четырех человек. Какое наименьшее количество комнат необходимо для поселения 83 иногородних студентов?
7. Найдите корень уравнения 
8. 
Два садовода, имеющие прямоугольные участки размерами 20 м на 30 м с общей границей, договорились и сделали общий круглый пруд площадью 140 квадратных метров (см. чертёж), причём граница участков проходит точно через центр пруда. Какова площадь (в квадратных метрах) оставшейся части участка каждого садовода?
9. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
|
ВЕЛИЧИНЫ |
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ |
|
А) площадь футбольного поля Б) площадь купюры достоинством 100 рублей В) площадь трёхкомнатной квартиры Г) площадь территории России |
1) 97,5 кв. см 2) 0,7 га 3) 17,1 млн кв. км 4) 100 кв. м |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
A |
Б |
В |
Г |
10. Научная конференция проводится в 4 дня. Всего запланировано 60 докладов: первые два дня — по 12 докладов, остальные распределены поровну между третьим и четвёртым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
11. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Определите по рисунку наибольшее значение атмосферного давления во вторник (в мм рт. ст.).
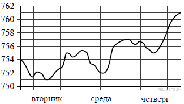
12. В первом банке один фунт стерлингов можно купить за 47,4 рубля. Во втором банке 30 фунтов — за 1446 рублей. В третьем банке 12 фунтов стоят 561 рубль. Какую наименьшую сумму (в рублях) придется заплатить за 10 фунтов стерлингов?
13.
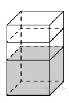
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 40 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 15 см. Ответ дайте в кубических сантиметрах.
14. На рисунках изображены графики функций вида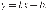 
Установите соответствие между графиками функций и знаками коэффициентов k и b.
ФУНКЦИИ
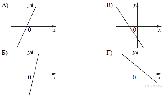
КОЭФФИЦИЕНТЫ
1) 
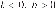
2) 
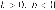
3) 
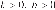
4) 
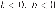
В таблице под каждой буквой укажите соответствующий номер.
|
A |
Б |
В |
Г |
15. 
Сторона правильного треугольника равна 
. Найдите радиус окружности, описанной около этого треугольника.
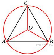
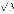
16. 
В основании пирамиды SABC лежит правильный треугольник ABC со стороной 6, а боковое ребро SA перпендикулярно основанию и равно 
Найдите объём пирамиды SABC.
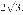
17. На координатной прямой отмечено число 
Каждому из четырёх чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.
|
ТОЧКИ |
ЧИСЛА |
|
|
А) Б) В) Г) |
1) [0;1] 2) [1; 2] 3) [2; 3] 4) [4; 5] |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
A |
Б |
В |
Г |
18. В классе учится 30 человек, из них 20 человек посещают кружок по истории, а 16 человек — кружок по математике. Выберите утверждения, которые следуют из приведённых данных. В этом классе
1) найдутся хотя бы два человека, которые посещают оба кружка
2) если ученик не ходит на кружок по истории, то он обязательно ходит на кружок по математике
3) нет ученика, который не посещает ни кружок по истории, ни кружок по математике
4) не найдётся 17 человек, которые посещают оба кружка
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
19. Приведите пример четырёхзначного числа А, обладающего следующими свойствами:
1) сумма цифр числа А делится на 8;
2) сумма цифр числа (А + 2) также делится на 8;
3) число А меньше 3000.
В ответе укажите ровно одно такое число.
20. Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника.
Вариант № 2 база
1. Вычислите
2. Найдите сумму чисел и
.
3. В школе французский язык изучают 117 учащихся, что составляет 26% от числа всех учащихся школы. Сколько учащихся в школе?
4. Площадь трапеции вычисляется по формуле где a и b — длины оснований трапеции, h — ее высота. Пользуясь этой формулой, найдите площадь S, если a = 6, b = 4, h = 6.
5. Найдите , если
.
6. Баночка йогурта стоит 14 рублей 60 копеек. Какое наибольшее количество баночек йогурта можно купить на 100 рублей?
7. Найдите корень уравнения
8.
Дачный участок имеет форму прямоугольника со сторонами 35 метров и 20 метров. Хозяин отгородил на участке квадратный вольер со стороной 10 метров (см. рисунок). Найдите площадь оставшейся части участка. Ответ дайте в квадратных метрах.
9. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
|
ВЕЛИЧИНЫ |
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ |
|
А) масса человека Б) масса железнодорожного состава В) масса шариковой ручки Г) масса автомобиля |
1) 80 кг 2) 460 т 3) 1,3 т 4) 10 г |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
A |
Б |
В |
Г |
10. На чемпионате по прыжкам в воду выступают 50 спортсменов, среди них 9 прыгунов из России и 12 прыгунов из Китая. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что третьим будет выступать прыгун из Китая.
11. На диаграмме показано количество посетителей сайта РИА «Новости» в течение каждого часа 8 декабря 2009 года. По горизонтали указывается час, по вертикали — количество посетителей сайта на протяжении этого часа. Определите по диаграмме, в течение какого часа на сайте РИА «Новости» побывало максимальное количество посетителей.
12. Для обслуживания международного семинара необходимо собрать группу переводчиков. Сведения о кандидатах представлены в таблице.
|
Переводчики |
Языки |
Стоимость услуг (рублей в день) |
|
1 |
Немецкий |
4000 |
|
2 |
Испанский |
2050 |
|
3 |
Французский |
3000 |
|
4 |
Французский, английский |
5900 |
|
5 |
Английский, немецкий |
6900 |
|
6 |
Французский, испанский |
5900 |
Пользуясь таблицей, соберите хотя бы одну группу, в которой переводчики вместе владеют всеми четырьмя языками: английским, немецким, испанским и французским, а суммарная стоимость их услуг не превышает 12 000 рублей в день. В ответе укажите ровно один набор номеров переводчиков без пробелов, запятых и других дополнительных символов. Перечисляйте в порядке возрастания номеров.
13. Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.
14. На рисунке изображен график функции y = f(x). Точки a, b, c, d и e задают на оси Ox интервалы. Пользуясь графиком, поставьте в соответствие каждому интервалу характеристику функции или её производной.
|
ТОЧКИ |
ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
|
|
А) (a; b) Б) (b; c) В) (c; d) Г) (d; e) |
1) значения производной функции положительны в каждой точке интервала 2) значения производной функции отрицательны в каждой точке интервала 3) значения функции отрицательны в каждой точке интервала 4) значения функции положительны в каждой точке интервала |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
Г |
15. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной
16. Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30 . В ответе укажите
.
17. На координатной прямой отмечены точки A, B, C, и D.
Число m равно .
Установите соответствие между указанными точками и числами из правого столбца, которые им соответствуют.
Установите соответствие между указанными точками и числами из правого столбца, которые им соответствуют.
|
ТОЧКИ |
ЧИСЛА |
|
A B C D |
1) 2) 3) 4) |
В таблице под каждой буквой укажите соответствующий номер.
|
A |
B |
C |
D |
18. Среди сотрудников фирмы А некоторые летом 2013 года отдыхали в Греции, а некоторые — в Испании. Все те сотрудники, которые отдыхали в Испании, не отдыхали в Греции. Выберите утверждения, которые следуют из приведённых данных.
1) Сотрудник фирмы А, который летом 2013 года не отдыхал в Греции, обязательно отдыхал в Испании.
2) Каждый сотрудник фирмы А отдыхал за лето 2013 года хоть где-то.
3) Среди тех сотрудников, которые не отдыхали в Испании летом 2013 года, есть хотя бы один сотрудник, который отдыхал в Греции.
4) Нет ни одного сотрудника фирмы А, который за лето 2013 года отдыхал и в Греции, и в Испании.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
19. Найдите пятизначное число, кратное 15, произведение цифр которого равно 60. В ответе укажите какое-нибудь одно такое число.
Укажите наименьшее такое число.
20. Врач прописал пациенту принимать лекарство по такой схеме: в первый день он должен принять 3 капли, а в каждый следующий день — на 3 капли больше, чем в предыдущий. Приняв 30 капель, он ещё 3 дня пьёт по 30 капель лекарства, а потом ежедневно уменьшает приём на 3 капли. Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится 20 мл лекарства (что составляет 250 капель)?
Вариант № 3 база
1. Найдите значение выражения
2. Найдите значение выражения .
3. В магазине вся мебель продаётся в разобранном виде. Покупатель может заказать сборку мебели на дому, стоимость которой составляет 10 % от стоимости купленной мебели. Шкаф стоит 3100 рублей. Во сколько рублей обойдётся покупка этого шкафа вместе со сборкой?
4. Сумма углов правильного выпуклого многоугольника вычисляется по формуле где n — количество его углов. Пользуясь этой формулой, найдите n, если
= 15π.
5. Найдите , если
и
.
6. В летнем лагере 172 ребёнка и 24 воспитателя. В одном автобусе можно перевозить не более 30 пассажиров. Какое наименьшее количество таких автобусов понадобится, чтобы за один раз перевезти всех из лагеря в город?
7. Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.
8. Строители огораживают место для проведения работ забором. Забор имеет форму прямоугольника со сторонами 18 м и 16 м. Причём необходимо оставить проёмы в заборе для проезда машин. Проездов четыре, каждый шириной 2 м. Найдите общую длину забора.
9. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
|
ВЕЛИЧИНЫ |
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ |
|
А) масса кухонного холодильника Б) масса трамвая В) масса новорожденного ребенка Г) масса карандаша |
1) 3500 г 2) 15 г 3) 12 т 4) 38 кг |
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
|
А |
Б |
В |
Г |
10. На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.
11. На рисунке показано изменение атмосферного давления в течение трёх суток. По горизонтали указаны дни недели и время, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Определите по рисунку значение атмосферного давления в среду в 6:00. Ответ дайте в миллиметрах ртутного столба.
12. От дома до дачи можно доехать на автобусе, на электричке или на маршрутном такси. В таблице показано время, которое нужно затратить на каждый участок пути. Какое наименьшее время потребуется на дорогу? Ответ дайте в часах.
|
1 |
2 |
3 |
|
|
Автобусом |
От дома до автобусной |
Автобус в пути: |
От остановки автобуса |
|
Электричкой |
От дома до станции железной |
Электричка в пути: |
От станции до дачи |
|
Маршрутным такси |
От дома до остановки маршрутного |
Маршрутное такси в дороге: |
От остановки маршрутного такси |
13. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 23,5. Найдите объем исходной призмы.
14. На рисунке точками показаны объёмы месячных продаж холодильников в магазине бытовой техники. По горизонтали указываются месяцы, по вертикали — количество проданных холодильников. Для наглядности точки соединены линией.
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику продаж холодильников.
|
ПЕРИОДЫ ВРЕМЕНИ |
ХАРАКТЕРИСТИКИ |
|
А) январь–март Б) апрель–июнь В) июль–сентябрь Г) октябрь–декабрь |
1) Продажи за первый и второй месяцы квартала совпадают. 2) Ежемесячный объём продаж достигает максимума за весь период. 3) За этот период ежемесячный объём продаж увеличился на 300 холодильников. 4) За последний месяц периода было продано меньше 200 холодильников. |
В таблице под каждой буквой укажите соответствующий номер.
|
А |
Б |
В |
Г |
15. Диагонали ромба равны 12 и 16. Найдите длину вектора
.
16. Два ребра прямоугольного параллелепипеда равны 8 и 5, а объём параллелепипеда равен 280. Найдите площадь поверхности этого параллелепипеда.
17. На координатной прямой отмечено число
Расположите в порядке убывания числа:
|
1) |
2) |
3) |
4) |
В ответе укажите номера выбранных чисел в порядке убывания.
18. Когда учитель математики Иван Петрович ведёт урок, он обязательно отключает свой телефон. Выберите утверждения, которые верны при приведённом условии.
1) Если телефон Ивана Петровича включён, значит, он не ведёт урок.
2) Если телефон Ивана Петровича включён, значит, он ведёт урок.
3) Если Иван Петрович проводит контрольную работу по математике, значит, его телефон выключен.
4) Если Иван Петрович ведёт урок математики, значит, его телефон включён.
19. Найдите трёхзначное натуральное число, большее 500, которое при делении на 8 и на 5 даёт равные ненулевые остатки и средняя цифра которого является средним арифметическим крайних цифр. В ответе укажите какое-
нибудь одно такое число.
20. Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 1 м. Высота дерева 13 м. За сколько дней улитка впервые доползёт до вершины дерева?
Вариант № 4 база
1. Найдите значение выражения
2. Найдите значение выражения .
3. Число посетителей сайта увеличилось за месяц впятеро. На сколько процентов увеличилось число посетителей сайта за этот месяц?
4. Площадь поверхности прямоугольного параллелепипеда с рёбрами 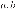и вычисляется по формуле
. Найдите площадь поверхности прямоугольного параллелепипеда с рёбрами
и
.
5.
Найдите значение выражения .
6. В доме, в котором живет Петя, один подъезд. На каждом этаже находится по 6 квартир. Петя живет в квартире № 50. На каком этаже живет Петя?
7.Найдите корень уравнения: Если уравнение имеет более одного корня, в ответе укажите меньший из них.
8. Какой наименьший угол (в градусах) образуют минутная и часовая стрелки в четыре часа утра?
9. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
|
ВЕЛИЧИНЫ |
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ |
|
А) объём ведра воды Б) объём товарного вагона В) объём лёгких взрослого человека Г) объём ванны |
1) 120 м3 2) 250 л 3) 15 л 4) 4 л |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
A |
Б |
В |
Г |
10. Конкурс исполнителей проводится в 5 дней. Всего заявлено 60 выступлений — по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. Все выступления поровну распределены между конкурсными днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность того, что выступление исполнителя из России состоится в третий день конкурса?
11.
На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат — температура двигателя в градусах Цельсия.
Определите по графику, сколько минут двигатель нагревался до температуры .
12. Независимая экспертная лаборатория определяет рейтинг бытовых приборов на основе коэффициента ценности, равного 0,01 средней цены
, показателей функциональности
, качества
и дизайна
. Каждый из показателей оценивается целым числом от 0 до 4. Итоговый рейтинг вычисляется по формуле
В таблице даны средняя цена и оценки каждого показателя для нескольких моделей электрических мясорубок. Определите наивысший рейтинг представленных в таблице моделей электрических мясорубок.
|
Модель мясорубки |
Средняя цена |
Функциональность |
Качество |
Дизайн |
|
А |
4600 |
2 |
0 |
2 |
|
Б |
5500 |
4 |
3 |
1 |
|
В |
4800 |
4 |
4 |
4 |
|
Г |
4700 |
2 |
1 |
4 |
13. Найдите объем многогранника, вершинами которого являются точки
параллелепипеда
, у которого
,
,
.
14. На рисунке изображён график функции y = f(x) . Точки a, b, c, d и e задают на оси Oxинтервалы. Пользуясь графиком, поставьте в соответствие каждому интервалу характеристику функции или её производной.
|
ИНТЕРВАЛЫ ВРЕМЕНИ |
ХАРАКТЕРИСТИКИ |
|
А) (a; b) Б) (b; c) В) (c; d) Г) (d; e) |
1) Значения функции положительны в каждой точке интервала. 2) Значения производной функции положительны в каждой точке интервала. 3) Значения функции отрицательны в каждой точке интервала. 4) Значения производной функции отрицательны в каждой точке интервала. |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
Г |
15. На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 11. Найдите площадь заштрихованной фигуры.
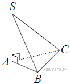
16. В правильной четырёхугольной пирамиде SABCD высота SO равна 13, диагональ основания BD равна 8. Точки К и М — середины ребер CD и ВС соответственно. Найдите тангенс угла между плоскостью SMK и плоскостью основания AВС.
17. На координатной прямой отмечены точки ,
,
и
.
Число m равно
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами. Впишите в приведённую в ответе таблицу под каждой буквой соответствующий числу номер.
|
ТОЧКИ |
ЧИСЛА |
|
|
А) A Б) B В) C Г) D |
1) 2) 3) 4) |
18. Некоторые сотрудники фирмы летом 2014 года отдыхали на даче, а некоторые — на море. Все сотрудники, которые не отдыхали на море, отдыхали на даче. Выберите утверждения, которые верны при указанных условиях.
1) Каждый сотрудник этой фирмы отдыхал летом 2014 года или на даче, или на море, или и там, и там.
2) Сотрудник этой фирмы, который летом 2014 года не отдыхал на море, не отдыхал и на даче.
3) Если Фаина не отдыхала летом 2014 года ни на даче, ни на море, то она является сотрудником этой фирмы.
4) Если сотрудник этой фирмы не отдыхал на море летом 2014 года, то он отдыхал на даче.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
19. Приведите пример четырёхзначного числа, кратного 12, произведение цифр которого больше 40, но меньше 45. В ответе укажите ровно одно такое число.
20. Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 12 прыжков, начиная прыгать из начала координат?
Вариант № 5 база
1. Найдите значение выражения .
2. Найдите значение выражения 7,9 · 10-2 + 4,5 · 10-1.
3. Рост Билла 5 футов 11 дюймов. Выразите рост Билла в сантиметрах, если 1 фут равен 0,305 м, а 1 дюйм равен 2,54 см. Результат округлите до целого числа сантиметров.
4. Среднее геометрическое трёх чисел
и
вычисляется по формуле
. Вычислите среднее геометрическое чисел
и
.
5. Найдите значение выражения .
6. В летнем лагере на каждого участника полагается 60 г сахара в день. В лагере 127 человек. Какое наименьшее количество килограммовых упаковок сахара нужно на весь лагерь на 9 дней?
7. Найдите отрицательный корень уравнения
8. Масштаб карты такой, что в одном сантиметре 1,5 км. Чему равно расстояние между городами A и B (в км), если на карте оно составляет 16 см?
9. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
|
ВЕЛИЧИНЫ |
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ |
|
А) рост новорожденного ребёнка Б) длина Енисея В) толщина лезвия бритвы Г) высота Эльбруса |
1) 4300 км 2) 50 см 3) 5642 м 4) 0,08 мм |
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
|
A |
Б |
В |
Г |
10. Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже 36,8°С, равна 0,71. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8°С или выше.
11. На диаграмме показана среднемесячная температура в Нижнем Новгороде (Горьком) за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в 1994 году. Ответ дайте в градусах Цельсия.
12. Клиент хочет арендовать автомобиль на сутки для поездки протяжённостью 700 км. В таблице приведены характеристики трёх автомобилей и стоимость их аренды.
|
Автомобиль |
Топливо |
Расход топлива |
Арендная плата |
|
А |
Дизельное |
5 |
4200 |
|
Б |
Бензин |
11 |
2700 |
|
В |
Газ |
16 |
3000 |
Помимо аренды, клиент обязан оплатить топливо для автомобиля на всю поездку. Цена дизельного топлива — 30 рублей за литр, бензина — 35 рублей за литр, газа — 20 рублей за литр. Сколько рублей заплатит клиент за аренду и топливо, если выберет самый дешёвый вариант?
13. В правильной четырехугольной пирамиде точка
– центр основания,
– вершина,
Найдите длину отрезка
.
14. На рисунке изображён график функции y = f(x) и отмечены точки A, B, C и D на оси x. Пользуясь графиком, поставьте в соответствие каждой точке характеристику функции и её производной.
Ниже указаны значения производной в данных точках. Пользуясь графиком, поставьте в соответствие каждой точке значение производной в ней.
|
ТОЧКИ |
ХАРАКТЕРИСТИКИ ФУНКЦИИ ИЛИ ПРОИЗВОДНОЙ |
|
А) A Б) B В) C Г) D |
1) Функция положительна, производная равна 0. 2) Производная отрицательна, функция равна 0. 3) Производная положительна, функция положительна. 4) Функция отрицательна, производная отрицательна. |
В таблице под каждой буквой укажите соответствующий номер.
|
А |
Б |
В |
Г |
15. В треугольнике
,
. Найдите
.
16. Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на .
17. Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого столбца. Установите соответствие между неравенствами и множествами их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
А) Б) В) Г) |
Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
|
А |
Б |
В |
Г |
18. В зоомагазине в один из аквариумов запустили 20 рыбок. Длина каждой рыбки больше 3 см, но не превышает 13 см. Выберите утверждения, которые следуют из данной информации.
1) Десять рыбок в этом аквариуме меньше 8 см.
2) В этом аквариуме нет рыбки длиной 14 см.
3) Разница в длине любых двух рыбок не больше 10 см.
4) Длина каждой рыбки больше 10 см.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
19. Найдите четырёхзначное натуральное число, кратное 19, сумма цифр которого на 1 больше их произведения.
20. При демонстрации летней одежды наряды каждой манекенщицы отличаются хотя бы одним из трёх элементов: блузкой, юбкой и туфлями. Всего модельер приготовил для демонстрации 5 видов блузок, 3 вида юбок и 4 вида туфель. Сколько различных нарядов будет показано на этой демонстрации?
Вариант № 6952166(1)
|
№ |
Номер |
Тип |
Ответ |
|
1 |
513746 |
1 |
24 |
|
2 |
511935 |
2 |
9001 |
|
3 |
83785 |
3 |
5 |
|
4 |
506507 |
4 |
0,2 |
|
5 |
512513 |
5 |
8 |
|
6 |
77338 |
6 |
21 |
|
7 |
509961 |
7 |
7 |
|
8 |
509773 |
8 |
530 |
|
9 |
509634 |
9 |
2143 |
|
10 |
509615 |
10 |
0,3 |
|
11 |
508043 |
11 |
755 |
|
12 |
77358 |
12 |
467,5 |
|
13 |
511677 |
13 |
24000 |
|
14 |
513883 |
14 |
3241 |
|
15 |
27892 |
15 |
1 |
|
16 |
513783 |
16 |
18 |
|
17 |
512209 |
17 |
4312 |
|
18 |
506624 |
18 |
14 |
|
19 |
506291 |
19 |
1698│2598│1599│2499 |
|
20 |
511016 |
20 |
12 |
Вариант № 6952204(2)
|
№ |
Номер |
Тип |
Ответ |
|
1 |
511431 |
1 |
49 |
|
2 |
506755 |
2 |
9620 |
|
3 |
510956 |
3 |
450 |
|
4 |
511897 |
4 |
30 |
|
5 |
26788 |
5 |
-9 |
|
6 |
509959 |
6 |
6 |
|
7 |
512435 |
7 |
-4 |
|
8 |
512516 |
8 |
600 |
|
9 |
509714 |
9 |
1243 |
|
10 |
512362 |
10 |
0,24 |
|
11 |
509776 |
11 |
13 |
|
12 |
506720 |
12 |
235 |
|
13 |
284359 |
13 |
6 |
|
14 |
511907 |
14 |
2314 |
|
15 |
53629 |
15 |
147 |
|
16 |
27093 |
16 |
1 |
|
17 |
512545 |
17 |
2314 |
|
18 |
506341 |
18 |
34 |
|
19 |
509624 |
19 |
11265 |
|
20 |
507074 |
20 |
2 |
Вариант № 6952294(3)
|
№ |
Номер |
Тип |
Ответ |
|
1 |
512549 |
1 |
-2,32 |
|
2 |
26738 |
2 |
5 |
|
3 |
510234 |
3 |
3410 |
|
4 |
512452 |
4 |
17 |
|
5 |
506611 |
5 |
1 |
|
6 |
511730 |
6 |
7 |
|
7 |
13377 |
7 |
-0,5 |
|
8 |
506527 |
8 |
60 |
|
9 |
506615 |
9 |
4312 |
|
10 |
320186 |
10 |
0,33 |
|
11 |
513015 |
11 |
756 |
|
12 |
282829 |
12 |
2,25 |
|
13 |
74789 |
13 |
94 |
|
14 |
510265 |
14 |
1324 |
|
15 |
27713 |
15 |
10 |
|
16 |
510227 |
16 |
262 |
|
17 |
506310 |
17 |
4312 |
|
18 |
510991 |
18 |
13 |
|
19 |
510972 |
19 |
642│963 |
|
20 |
506793 |
20 |
4 |
Вариант № 6952318(4)
|
№ |
Номер |
Тип |
Ответ |
|
1 |
506120 |
1 |
2,65 |
|
2 |
26747 |
2 |
2 |
|
3 |
510699 |
3 |
400 |
|
4 |
511688 |
4 |
126 |
|
5 |
66871 |
5 |
8 |
|
6 |
77350 |
6 |
9 |
|
7 |
11149 |
7 |
-3 |
|
8 |
508409 |
8 |
120 |
|
9 |
507048 |
9 |
3142 |
|
10 |
512587 |
10 |
0,2 |
|
11 |
263983 |
11 |
8 |
|
12 |
316048 |
12 |
32 |
|
13 |
264511 |
13 |
120 |
|
14 |
509699 |
14 |
1432 |
|
15 |
509640 |
15 |
33 |
|
16 |
501189 |
16 |
6,5 |
|
17 |
513131 |
17 |
1432 |
|
18 |
510249 |
18 |
14 |
|
19 |
506502 |
19 |
1176│1716│7116 |
|
20 |
508401 |
20 |
13 |
Вариант № 6955039(5)
|
№ |
Номер |
Тип |
Ответ |
|
1 |
506876 |
1 |
-1,05 |
|
2 |
509687 |
2 |
0,529 |
|
3 |
318741 |
3 |
180 |
|
4 |
506799 |
4 |
12 |
|
5 |
26795 |
5 |
11 |
|
6 |
512583 |
6 |
69 |
|
7 |
509963 |
7 |
-2 |
|
8 |
513855 |
8 |
24 |
|
9 |
506884 |
9 |
2143 |
|
10 |
506743 |
10 |
0,29 |
|
11 |
27511 |
11 |
-14 |
|
12 |
510708 |
12 |
5240 |
|
13 |
912 |
13 |
5 |
|
14 |
508082 |
14 |
1243 |
|
15 |
27290 |
15 |
0,6 |
|
16 |
27120 |
16 |
128 |
|
17 |
506480 |
17 |
3124 |
|
18 |
506873 |
18 |
23 |
|
19 |
507054 |
19 |
3211 |
|
20 |
507082 |
20 |
60 |