Тренировочный вариант №8 профильного ЕГЭ

Материалы и статьи
Распечатай и реши ЕГЭ 2023 база по математике 11 класс новый тренировочный вариант в формате реального экзамена №7 и вариант №8 с ответами и решением по новой демоверсии ФИПИ, варианты опубликованы на сайте 9 января 2023 года.
Скачать варианты и ответы
Распечатай и реши ЕГЭ 2023 база математика вариант №7, №8
1. Установка двух счётчиков воды (холодной и горячей) стоит 3200 рублей. До установки счётчиков за воду платили 1700 рублей ежемесячно. После установки счётчиков ежемесячная оплата воды стала составлять 1100 рублей. Через какое наименьшее количество месяцев экономия по оплате воды превысит затраты на установку счётчиков, если тарифы на воду не изменятся?
2. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
3. В таблице показано расписание пригородных электропоездов по направлению Москва Октябрьская – Тверь. Какой из электропоездов Москва Октябрьская – Тверь проводит в пути меньше всего времени? В ответе укажите номер этого электропоезда.
5. На семинар приехали 7 учёных из Норвегии, 6 из России и 2 из Испании. Каждый учёный подготовил один доклад. Порядок докладов определяется случайным образом. Найдите вероятность того, что восьмым окажется доклад учёного из России.
6. В городском парке работает 5 аттракционов: карусель, колесо обозрения, автодром, «Ромашка» и «Весёлый тир». В кассах продаётся 6 видов билетов, каждый из которых на один или два аттракциона. Сведения о стоимости билетов представлены в таблице. Какие билеты должен купить Андрей, чтобы посетить все пять аттракционов и затратить не более 950 рублей? В ответе укажите какой-нибудь один набор номеров билетов без пробелов, запятых и других дополнительных символов.
7. На графике изображена зависимость частоты пульса гимнаста от времени в течение и после его выступления в вольных упражнениях. На горизонтальной оси отмечено время (в минутах), прошедшее с начала выступления гимнаста, на вертикальной оси – частота пульса (в ударах в минуту). Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику пульса гимнаста на этом интервале.
8. Тане на день рождения подарили 15 шариков, 8 из которых жёлтые, а остальные зелёные. Таня хочет на трёх случайных шариках нарисовать рисунки маркером, чтобы подарить маме, папе и брату. Выберите все утверждения, которые будут верны при указанных условиях независимо от того, на каких шариках Таня нарисует рисунки.
- 1) Найдётся 2 зелёных шарика без рисунков.
- 2) Не найдётся 5 жёлтых шариков с рисунками.
- 3) Если шарик жёлтый, то на нём Таня нарисует рисунок.
- 4) Найдётся 3 жёлтых шарика с рисунками.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
9. План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.
10. Квартира состоит из комнаты, кухни, коридора и санузла (смотрите чертёж). Кухня имеет размеры 3 м × 4 м, санузел – 2 м × 2 м, длина комнаты 4,5 м. Найдите площадь коридора (в квадратных метрах).
11. Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
13. Стороны основания правильной шестиугольной пирамиды равны 24, боковые рёбра равны 37. Найдите площадь боковой поверхности этой пирамиды.
15. В школе французский язык изучают 121 учащихся, что составляет 22% от числа всех учащихся школы. Сколько учащихся в школе?
19. Найдите трёхзначное натуральное число, большее 400, которое при делении и на 6, и на 5 даёт равные ненулевые остатки и первая цифра в записи которого является средним арифметическим двух других цифр. В ответе укажите какое-нибудь одно такое число.
20. Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 18 км. Путь из А в В занял у туриста 6 часов, из которых 2 часа ушло на спуск. Найдите скорость туриста на спуске, если она больше скорости на подъёме на 3 км/ч. Ответ дайте в км/ч.
21. На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 11 кусков, если по жёлтым – 6 кусков, а если по зелёным – 7 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
Вам будет интересно:
Тренировочный вариант №3, №4 по профильной математике ЕГЭ 2023 (задания и ответы).
Метки: 11 класс варианты и ответы ЕГЭ математика
Школьный портал
→
ЕГЭ
→
ЕГЭ по математике
→
Тренировочный вариант ЕГЭ 2021 по математике № 8 (база)

Пробный вариант № 8 ЕГЭ по математике базового уровня на 2021 год составлен в соответствии с кодификатором ФИПИ и официальными демоверсиями.
Файл в формате pdf содержит задания, решения и ответы.
Скачать вариант в формате pdf — СКАЧАТЬ.
Вариант составлен авторами: Школа Пифагора.
Смотрите также:
- ЕГЭ по математике
- Расписание ЕГЭ 2021
- Шкала перевода баллов ЕГЭ
Одноклассники
Вконтакте
Мой мир
Задание 1
В треугольнике $$ABC$$ известно, что $$AC=BC$$, высота $$AH$$ равна 8, $$BH=20$$. Найдите $$tg BAC$$.
Ответ: 0,4
Скрыть
Задание 2
Найдите объём многогранника, вершинами которого являются точки $$A_1$$, $$B_1$$, $$F_1$$, $$E$$ правильной шестиугольной призмы $$ABCDEFA_1B_1C_1D_1E_1F_1$$, площадь основания которой равна 10, а боковое ребро равно 9.
Ответ: 5
Скрыть
Задание 3
В группе туристов 32 человека. Их вертолётом доставляют в труднодоступный район, перевозя по 4 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист Г. полетит четвёртым рейсом вертолёта.
Ответ: 0,125
Скрыть
Задание 4
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 9. Какова вероятность того, что для этого потребовалось три броска? Ответ округлите до сотых.
Ответ: 0,46
Скрыть
Задание 5
Найдите корень уравнения $$(frac{1}{9})^{x+4}=729$$
Ответ: -7
Скрыть
Задание 6
Найдите значение выражения $$log_{6}1,25cdot log_{0,8}6$$
Ответ: -1
Скрыть
Задание 7
На рисунке изображён график функции $$y=f(x)$$, определённой на интервале (-11; 2). Найдите количество точек, в которых касательная к графику функции $$y=f(x)$$ параллельна прямой $$y=-4$$.
Ответ: 7
Скрыть
Задание 8
Высота над землёй подброшенного вверх мяча меняется по закону $$h(t)=1+11t-5t^{2}$$, где $$h$$ — высота в метрах, $$t$$ — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?
Ответ: 1,8
Скрыть
Задание 9
Имеется два сосуда. Первый содержит 25 кг, а второй — 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 52 % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 53 % кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Ответ: 11
Скрыть
Задание 10
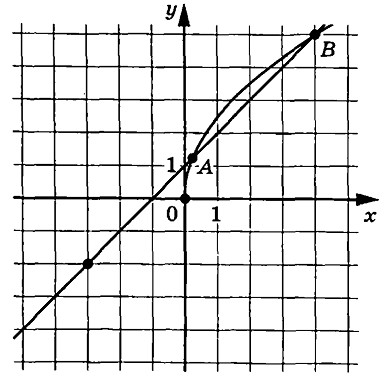
На рисунке изображены графики функций $$f(x)=asqrt{x}$$ и $$g(x)=kx+b$$, которые пересекаются в точках $$A$$ и $$B$$. Найдите абсциссу точки $$A$$.
Ответ: 0,25
Скрыть
Задание 11
Найдите наименьшее значение функции $$y=6x-sin x+17$$ на отрезке $$[0;frac{pi}{2}]$$
Ответ: 17
Скрыть
Задание 12
а) Решите уравнение $$log^{2}_{2}(8x^{2})-log_{4}(2x)-1=0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку [0,4; 0,8].
Ответ: а)$$0,5;frac{sqrt[8]{2}}{4}$$; б)$$0,5$$
Скрыть
Задание 13
Сторона основания правильной четырёхугольной пирамиды $$SABCD$$ относится к боковому ребру как $$1:sqrt{2}$$ . Через вершину $$D$$ проведена плоскость $$alpha$$, перпендикулярная боковому ребру $$SB$$ и пересекающая его в точке $$M$$.
а) Докажите, что сечение пирамиды $$SABCD$$ плоскостью $$alpha$$ — это четырёхугольник, диагонали которого перпендикулярны.
б) Найдите площадь этого сечения, если боковое ребро пирамиды равно 6.
Ответ: $$6sqrt{3}$$
Скрыть
Задание 14
Решите неравенство $$frac{sqrt{x-2}(4-3^{x-1})}{2^{1-x^{2}}-3}geq 0$$
Ответ: $$2;[log_{3}12;+infty)$$
Скрыть
Задание 15
15 июня 2025 года Данила Сергеевич планирует взять кредит в банке на 4 года в размере целого числа миллионов рублей. Условия его возврата таковы:
— в январе каждого года действия кредита долг увеличивается на 15 % от суммы долга на конец предыдущего года;
— в период с февраля по июнь в каждый из 2026 и 2027 годов необходимо выплатить только начисленные в январе проценты по кредиту;
— в период с февраля по июнь в каждый из 2028 и 2029 годов выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.
Найдите наибольший размер кредита, при котором общая сумма выплат по кредиту не превысит 20 млн рублей.
Ответ: 13 млн. руб.
Скрыть
Задание 16
Окружность с центром в точке $$C$$ касается гипотенузы $$AB$$ прямоугольного треугольника $$ABC$$ и пересекает его катеты $$AC$$ и $$BC$$ в точках $$E$$ и $$F$$. Точка $$D$$ — основание высоты, опущенной на $$AB$$. $$I$$ и $$J$$ — центры окружностей, вписанных в треугольники $$BCD$$ и $$ACD$$.
а) Докажите, что точки $$E$$ и $$F$$ лежат на прямой $$IJ$$.
б) Найдите расстояние от точки $$C$$ до прямой $$IJ$$, если $$AC=2sqrt{3}$$, $$BC=2$$.
Ответ: $$frac{sqrt{6}}{2}$$
Скрыть
Задание 17
Найдите все значения $$a$$, при каждом из которых оба уравнения $$a+frac{x}{3}=|x|$$ и $$2a+x=sqrt{2a^{2}+4ax-x^{2}+12}$$ имеют ровно по 2 различных корня, и строго между корнями каждого из уравнений лежит корень другого уравнения.
Ответ: $$(frac{2sqrt{6}}{sqrt{13}};frac{4sqrt{6}}{5})$$
Скрыть
Задание 18
Трёхзначное число, меньшее 700, поделили на сумму его цифр и получили натуральное число $$n$$.
а) Может ли $$n$$ равняться 64?
б) Может ли $$n$$ равняться 78?
в) Какое наибольшее значение может принимать $$n$$, если все цифры ненулевые?
Ответ: а)да б)нет в)73
Скрыть
А. Ларин: Тренировочный вариант № 8.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Дано уравнение
а) Решите уравнение.
б) Найдите все корни на промежутке
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
Ребро куба ABCDA1B1C1D1 равно 1. Найдите расстояние между прямыми AD1 и A1C1.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите систему
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
Четырехугольник KLMN вписан в окружность, его диагонали KM и LN пересекаются в точке F, причем KL = 8, MN = 4, периметр треугольника MNF равен 9, площадь треугольника KLF равна Найдите радиус окружности, описанной около треугольника KNF.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
Найдите наименьшее значение a, при котором имеет решение система
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Лужков и Батурина поворачивают с Рублевки на МКАД в разные стороны — Лужков — налево, Батурина — направо. За сколько минут каждый из них проезжает полный круг по МКАД, если известно, что Лужков тратит на 12 минут меньше Батуриной, при этом проезжая круг не быстрее 31 минуты. Время проезда одного круга измеряется целым числом минут и их седьмая встреча произошла снова на Рублёвке.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
- 02.01.2021
Вариант №8 по математике (профильного уровня) в формате ЕГЭ (11 класс) в 2021 году от проекта «ЕГЭ 100 БАЛЛОВ» https://vk.com/ege100ballov
Работа проводилась 26 октября 2020 года в добровольном порядке. Вариант полностью соответствует официальной демоверсии ФИПИ ЕГЭ 2021 по математике.
- Другие варианты ЕГЭ по профильной математике
Ответы ко всем заданиям представлены в конце документа, а также есть подробные критерии решения заданий второй части теста.
Есть вопросы по решениям? Пишите в комментариях ниже!
Дополнительно:
- Демоверсия ЕГЭ 2021 по математике — профиль
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.