Диагностический вариант СтатГрад ЕГЭ Профиль по математике 2210309-28.02.2023 с ответами и критериями
Варианты и ответы для тренировочной работы №1 статград ЕГЭ 2023 по математике 11 класс, тренировочные варианты базового и профильного уровня с ответами и решением, официальная дата проведения работы 28 сентября 2022 год.
Скачать варианты базового уровня
Скачать варианты профильного уровня
Скачать ответы и решения для вариантов
Статград математика 11 класс ЕГЭ 2023 база 8 вариантов
МА2210101-МА2210108-база-статград
Работа по математике включает в себя 21 задание (варианты МА2210101, МА2210102, МА2210103, МА2210104, МА2210105, МА2210106, МА2210107, МА2210108).
На выполнение работы отводится 3 часа (180 минут). Ответы к заданиям записываются в виде числа или последовательности цифр в поле ответа в тексте работы.
Статград математика 11 класс ЕГЭ 2023 профиль 4 варианта
МА2210109-МА2210112-профиль-статград
Работа по математике состоит из двух частей, включающих в себя 18 заданий (варианты МА2210109, МА2210110, МА2210111, МА2210112) . Часть 1 содержит 11 заданий с кратким ответом базового и повышенного уровней сложности. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Вариант МА2210101
1)В школе есть двухместные туристические палатки. Какое наименьшее число палаток нужно взять в поход, в котором участвует 21 человек?
2)Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) рост новорождённого ребёнка Б) длина реки Енисей В) толщина лезвия бритвы Г) высота горы Эльбрус.
3)Результаты соревнований по метанию молота представлены в таблице. Места распределяются по результату лучшей попытки каждого спортсмена: чем дальше он метнул молот, тем лучше. Каков результат лучшей попытки (в метрах) спортсмена, занявшего третье место?
4)Скорость камня (в м/с), падающего с высоты h (в м), в момент удара о землю можно найти по формуле v gh = 2 . Найдите скорость (в м/с), с которой ударится о землю камень, падающий с высоты 0,9 м. Считайте, что ускорение свободного падения g равно 2 9,8 м/с .
5)Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд будет владеть мячом в начале матча. Команда «Физик» играет два матча с разными командами. Найдите вероятность того, что «Физик» хотя бы один раз выиграет мяч.
6)Турист подбирает экскурсии. Сведения об экскурсиях представлены в таблице. Пользуясь таблицей, подберите набор экскурсий так, чтобы турист посетил четыре объекта: крепость, загородный дворец, парк и музей живописи, а суммарная стоимость экскурсий не превышала 650 рублей. В ответе укажите какой-нибудь один набор номеров экскурсий без пробелов, запятых и других дополнительных символов.
7)На графике изображена зависимость скорости движения рейсового автобуса от времени. На вертикальной оси отмечена скорость автобуса в км/ч, на горизонтальной — время в минутах, прошедшее с начала движения автобуса. Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику движения автобуса на этом интервале.
8)Во дворе школы растут всего три дерева: берёза, клён и дуб. Берёза выше клёна на 1 метр, но ниже дуба на 3 метра. Выберите утверждения, которые верны при указанных условиях.
- 1) Среди указанных деревьев не найдётся двух одной высоты.
- 2) Берёза, растущая во дворе школы, выше дуба, растущего там же.
- 3) Любое дерево, помимо указанных, которое ниже берёзы, растущей во дворе школы, также ниже клёна, растущего там же.
- 4) Любое дерево, помимо указанных, которое ниже клёна, растущего во дворе школы, также ниже берёзы, растущей там же.
9)План местности разбит на клетки. Каждая клетка обозначает квадрат 1м×1м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
10)Дачный участок имеет форму прямоугольника со сторонами 30 метров и 20 метров. Хозяин планирует обнести его изгородью и отгородить такой же изгородью квадратный участок со стороной 12 метров (см. рисунок). Найдите суммарную длину изгороди в метрах.
11)Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Цифры на рисунке обозначают длины рёбер в сантиметрах. Найдите площадь поверхности этой детали. Ответ дайте в квадратных сантиметрах.
15)Тетрадь стоит 21 рубль. Сколько рублей заплатит покупатель за 70 тетрадей, если при покупке больше 50 тетрадей магазин делает скидку 10 % от стоимости всей покупки?
19)Четырёхзначное число A состоит из цифр 3, 4, 8, 9, а четырёхзначное число B — из цифр 6, 7, 8, 9. Известно, что B A = 2 . Найдите число A. В ответе укажите какое-нибудь одно такое число, большее 3500.
20)Расстояние между городами A и B равно 500 км. Из города A в город B выехал первый автомобиль, а через час после этого навстречу ему из городе B выехал со скоростью 80 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 260 км от города A. Ответ дайте в км/ч.
21)Клетки таблицы 6*5 раскрашены в чёрный и белый цвета так, что получилось 26 пар соседних клеток разного цвета и 6 пар соседних клеток чёрного цвета. (Клетки считаются соседними, если у них есть общая сторона.) Сколько пар соседних клеток белого цвета?
Вариант МА2210105
1)Выпускники 11 «А» класса покупают букеты цветов для последнего звонка: из 7 роз каждому учителю и из 11 роз классному руководителю и директору. Они собираются подарить букеты 20 учителям (включая директора и классного руководителя), розы покупаются по оптовой цене 35 рублей за штуку. Сколько рублей стоят все розы?
2)Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) диаметр монеты Б) рост жирафа В) высота Эйфелевой башни Г) радиус Земли.
3)Результаты соревнований по метанию молота представлены в таблице. Места распределяются по результату лучшей попытки каждого спортсмена: чем дальше он метнул молот, тем лучше. Какое место занял спортсмен Арнюк?
5)В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что оба раза выпадет решка.
6)В городском парке работает пять аттракционов: карусель, колесо обозрения, автодром, «Ромашка» и «Весёлый тир». В кассах продаётся шесть видов билетов, каждый из которых позволяет посетить один или два аттракциона. Сведения о стоимости билетов представлены в таблице. Какие билеты должен купить Андрей, чтобы посетить все пять аттракционов и затратить не более 900 рублей? В ответе укажите какой-нибудь один набор номеров билетов без пробелов, запятых и других дополнительных символов.
7)На рисунке точками показано атмосферное давление в некотором городе на протяжении трёх суток с 4 по 6 апреля 2013 года. В течение суток давление измеряется 4 раза: в 00:00, в 06:00, в 12:00 и в 18:00. По горизонтали указывается время и дата, по вертикали — давление в миллиметрах ртутного столба. Для наглядности точки соединены ломаной линией. Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику атмосферного давления в этом городе в течение этого периода.
8)Во дворе школы растут всего три дерева: берёза, клён и дуб. Берёза выше клёна на 1 метр, но ниже дуба на 3 метра. Выберите утверждения, которые верны при указанных условиях.
- 1) Среди указанных деревьев не найдётся двух одной высоты.
- 2) Берёза, растущая во дворе школы, выше дуба, растущего там же.
- 3) Любое дерево, помимо указанных, которое ниже берёзы, растущей во дворе школы, также ниже клёна, растущего там же.
- 4) Любое дерево, помимо указанных, которое ниже клёна, растущего во дворе школы, также ниже берёзы, растущей там же.
10)Дачный участок имеет форму прямоугольника со сторонами 30 метров и 20 метров. Хозяин отгородил на участке квадратный вольер со стороной 12 метров (см. рисунок). Найдите периметр оставшейся части участка.
11)Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
13)Два ребра прямоугольного параллелепипеда равны 10 и 7, а объём параллелепипеда равен 420. Найдите площадь поверхности этого параллелепипеда.
15)В спортивном магазине любой свитер стоит 320 рублей. Сейчас магазин проводит акцию: при покупке двух свитеров делается скидка на второй свитер 25 %. Сколько рублей придётся заплатить за покупку двух свитеров в период действия акции?
19)Найдите число A, обладающее всеми следующими свойствами: • сумма цифр числа A делится на 7; • сумма цифр числа A + 2 делится на 7; • число A больше 300 и меньше 350. В ответе укажите какое-нибудь одно такое число.
20)Два человека отправляются из одного дома на прогулку до опушки леса, находящейся в 6,3 км от дома. Один идёт со скоростью 2,5 км/ч, а другой — со скоростью 3,8 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от дома произойдёт их встреча? Ответ дайте в километрах.
21)В таблице три столбца и несколько строк. В каждую клетку таблицы вписали по натуральному числу так, что сумма всех чисел в первом столбце равна 148, во втором — 108, в третьем — 70, а сумма чисел в каждой строке больше 26, но меньше 29. Сколько всего строк в таблице?
Вариант МА2210109
2)Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 7 и 4. Объём параллелепипеда равен 140. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
3)При производстве в среднем из 2000 насосов 4 неисправных. Найдите вероятность того, что случайно выбранный насос окажется неисправным.
4)Игральную кость бросили два раза. Известно, что четыре очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 11».
9)Расстояние между пристанями A и B равно 60 км. Из A в B по течению реки отправился плот, а через 3 часа вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот проплыл 44 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч.
15)15 января планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 40 % больше суммы, взятой в кредит. Найдите r.
18)На сайте проводится опрос, кого из 156 футболистов посетители сайта считают лучшим по итогам сезона. Каждый посетитель голосует за одного футболиста. На сайте отображается рейтинг каждого футболиста — доля голосов, отданных за него, в процентах, округлённая до целого числа. Например, числа 9,3, 10,5 и 12,7 округляются до 9, 11 и 13 соответственно.
- а) Всего проголосовало 11 посетителей сайта, и рейтинг первого футболиста стал равен 45. Увидев это, Вася отдал свой голос за другого футболиста. Чему теперь равен рейтинг первого футболиста?
- б) Вася проголосовал за некоторого футболиста. Могла ли после этого сумма рейтингов всех футболистов уменьшиться на 150 или больше?
- в) Какое наибольшее значение может принимать сумма рейтингов всех футболистов?
Вариант МА2210110
2)Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 12 и 5. Объём параллелепипеда равен 540. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
3)При производстве в среднем из 2000 насосов 10 неисправных. Найдите вероятность того, что случайно выбранный насос окажется неисправным.
4)Игральную кость бросили два раза. Известно, что два очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 12».
9)Расстояние между пристанями A и B равно 168 км. Из A в B по течению реки отправился плот, а через 3 часа вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот проплыл 32 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.
15)15 января планируется взять кредит в банке на 11 месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 27 % больше суммы, взятой в кредит. Найдите r.
18)На сайте проводится опрос, кого из 146 футболистов посетители сайта считают лучшим по итогам сезона. Каждый посетитель голосует за одного футболиста. На сайте отображается рейтинг каждого футболиста — доля голосов, отданных за него, в процентах, округлённая до целого числа. Например, числа 9,3, 10,5 и 12,7 округляются до 9, 11 и 13 соответственно. а) Всего проголосовало 13 посетителей сайта, и рейтинг первого футболиста стал равен 31. Увидев это, Вася отдал свой голос за другого футболиста. Чему теперь равен рейтинг первого футболиста? б) Вася проголосовал за некоторого футболиста. Могла ли после этого сумма рейтингов всех футболистов уменьшиться на 140 или больше? в) Какое наибольшее значение может принимать сумма рейтингов всех футболистов?
Вариант МА2210111
2)Во сколько раз увеличится объём куба, если все его рёбра увеличить в четырнадцать раз?
3)Фабрика выпускает сумки. В среднем 14 сумок из 130 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без скрытых дефектов. Результат округлите до сотых.
4)Биатлонист 5 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,7. Найдите вероятность того, что биатлонист первые 4 раза попал в мишени, а последний раз промахнулся. Результат округлите до сотых.
9)Теплоход, скорость которого в неподвижной воде равна 15 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 1 км/ч, стоянка длится 5 часов, а в исходный пункт теплоход возвращается через 65 часов. Сколько километров прошёл теплоход за весь рейс?
15)15 января планируется взять кредит в банке на 13 месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 28 % больше суммы, взятой в кредит. Найдите r.
16)Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M . Окружность с центром O и диаметром CM касается гипотенузы в точке N . а) Докажите, что прямые MN и BO параллельны. б) Найдите площадь четырёхугольника BOMN , если CN 5 и AM MC : 1: 24 .
18)На сайте проводится опрос, кого из 156 футболистов посетители сайта считают лучшим по итогам сезона. Каждый посетитель голосует за одного футболиста. На сайте отображается рейтинг каждого футболиста — доля голосов, отданных за него, в процентах, округлённая до целого числа. Например, числа 9,3, 10,5 и 12,7 округляются до 9, 11 и 13 соответственно. а) Всего проголосовало 12 посетителей сайта, и рейтинг первого футболиста стал равен 58. Увидев это, Вася отдал свой голос за другого футболиста. Чему теперь равен рейтинг первого футболиста? б) Вася проголосовал за некоторого футболиста. Могла ли после этого сумма рейтингов всех футболистов уменьшиться на 170 или больше? в) Какое наибольшее значение может принимать сумма рейтингов всех футболистов?
Вариант МА2210112
2)Во сколько раз увеличится объём куба, если все его рёбра увеличить в двенадцать раз?
3)Фабрика выпускает сумки. В среднем 20 сумок из 200 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без скрытых дефектов.
4)Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
9)Теплоход, скорость которого в неподвижной воде равна 18 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 2 км/ч, стоянка длится 2 часа, а в исходный пункт теплоход возвращается через 38 часов. Сколько километров прошёл теплоход за весь рейс?
15)15 января планируется взять кредит в банке на 17 месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 54 % больше суммы, взятой в кредит. Найдите r.
18)На сайте проводится опрос, кого из 164 футболистов посетители сайта считают лучшим по итогам сезона. Каждый посетитель голосует за одного футболиста. На сайте отображается рейтинг каждого футболиста — доля голосов, отданных за него, в процентах, округлённая до целого числа. Например, числа 9,3, 10,5 и 12,7 округляются до 9, 11 и 13 соответственно. а) Всего проголосовало 14 посетителей сайта, и рейтинг первого футболиста стал равен 36. Увидев это, Вася отдал свой голос за другого футболиста. Чему теперь равен рейтинг первого футболиста? б) Вася проголосовал за некоторого футболиста. Могла ли после этого сумма рейтингов всех футболистов уменьшиться на 160 или больше? в) Какое наибольшее значение может принимать сумма рейтингов всех футболистов?
Тренировочные варианты ЕГЭ по математике
Тренировочный вариант №2 ЕГЭ 2023 по математике профиль с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2023 из различных источников.
Варианты составлены в соответствии с демоверсией 2023 года
Тренировочные варианты ЕГЭ 2023 по математике (профиль)
| vk.com/pezhirovschool | |
| Вариант 1 | решения |
| Вариант 2 | решения |
| Вариант 3 | решения |
| Вариант 4 | решения |
| Вариант 5 (с ответами) | |
| Вариант 6 (с ответами) | |
| Вариант 7 (с ответами) | |
| Вариант 8 (с ответами) | |
| egemath.ru | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| вариант 12 | скачать |
| вариант 13 | скачать |
| вариант 14 | скачать |
| вариант 15 | скачать |
| вариант 16 | скачать |
| вариант 17 | скачать |
| вариант 18 | скачать |
| вариант 19 | скачать |
| вариант 20 | скачать |
| time4math.ru | |
| вариант 1-2 | ответы |
| вариант 3-4 | ответы |
| вариант 5-6 | ответы |
| вариант 7-8 | |
| yagubov.ru | |
| вариант 33 (сентябрь) | ege2023-yagubov-prof-var33 |
| вариант 34 (октябрь) | ege2023-yagubov-prof-var34 |
| вариант 35 (ноябрь) | ege2023-yagubov-prof-var35 |
| вариант 36 (декабрь) | ege2023-yagubov-prof-var36 |
| вариант 37 (январь) | ege2023-yagubov-prof-var37 |
| вариант 38 (февраль) | ege2023-yagubov-prof-var38 |
| math100.ru (с ответами) | |
| variant 179 | скачать |
| variant 180 | скачать |
| variant 181 | скачать |
| variant 182 | скачать |
| variant 183 | скачать |
| variant 184 | скачать |
| variant 185 | скачать |
| variant 186 | скачать |
| variant 187 | скачать |
| variant 188 | скачать |
| variant 189 | скачать |
| variant 190 | скачать |
| variant 191 | скачать |
| variant 192 | скачать |
| variant 193 | скачать |
| variant 194 | скачать |
| variant 195 | скачать |
| variant 196 | скачать |
| variant 197 | скачать |
| variant 198 | скачать |
| variant 199 | скачать |
| variant 200 | скачать |
| variant 201 | скачать |
| variant 202 | скачать |
| variant 203 | скачать |
| variant 204 | скачать |
| variant 205 | скачать |
| alexlarin.net | |
| Вариант 397 | проверить ответы |
| Вариант 398 | проверить ответы |
| Вариант 399 | проверить ответы |
| Вариант 400 | проверить ответы |
| Вариант 401 | проверить ответы |
| Вариант 402 | проверить ответы |
| Вариант 403 | проверить ответы |
| Вариант 404 | проверить ответы |
| Вариант 405 | проверить ответы |
| Вариант 406 | проверить ответы |
| Вариант 407 | проверить ответы |
| Вариант 408 | проверить ответы |
| Вариант 409 | проверить ответы |
| Вариант 410 | проверить ответы |
| Вариант 411 | проверить ответы |
| Вариант 412 | проверить ответы |
| Вариант 413 | проверить ответы |
| vk.com/ege100ballov | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| vk.com/math.studying | |
| Вариант 1 | ответы |
| vk.com/marsel_tutor | |
| Вариант 1 | разбор |
| Вариант 2 | конспект / разбор |
| Вариант 3 | конспект / разбор |
| Вариант 4 | конспект / разбор |
| Вариант 5 | конспект / разбор |
| Вариант 6 | разбор |
| vk.com/shkolkovo_easy_math | |
| Вариант 1 | решение |
| Вариант 2 | решение |
| Вариант 3 | решение |
| Вариант 5 | решение |
| Вариант 6 | решение |
| vk.com/mathlearn_ru | |
| вариант 1 | разбор |
| vk.com/ekaterina_chekmareva | |
| Вариант 1 | ответы |
| Вариант 2 | ответы |
| Вариант 3 | ответы |
| Вариант 4 | ответы |
| Вариант 5 | ответы |
| Вариант 6 | ответы |
| Вариант 7 | ответы |
| Вариант 8 | ответы |
Структура варианта КИМ ЕГЭ 2023 по математике профильного уровня
Экзаменационная работа состоит из двух частей и включает в себя 18 заданий, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях. Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Задания части 1 предназначены для определения математических компетентностей выпускников образовательных организаций, реализующих программы среднего (полного) общего образования на базовом уровне. Задание с кратким ответом (1–11) считается выполненным, если в бланке ответов № 1 зафиксирован верный ответ в виде целого числа или конечной десятичной дроби.
Задания 12–18 с развёрнутым ответом, в числе которых 5 заданий повышенного уровня и 2 задания высокого уровня сложности, предназначены для более точной дифференциации абитуриентов вузов.
Примеры заданий:
1. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 22 спортсмена из России, в том числе Игорь Чаев. Найдите вероятность того, что в первом туре Игорь Чаев будет играть с каким-либо бадминтонистом из России.
2. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу
3. На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 363. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71).
а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 4 раза больше, чем сумма исходных чисел.
б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел?
в) Найдите наибольшее возможное значение суммы получившихся чисел.
Смотрите также:
Сборники тренировочных тестов по математике профильного уровня для ЕГЭ в 2023 году и для ЕГЭ прошлых лет. Все тренировочные варианты/пробники содержат ответы и решения ко 2-й части кима. Обсудить решение и задания каждого варианта вы можете в комментариях под ними. РЕШАТЬ ТЕСТЫ
Обращайте внимание на уровень пробника — здесь только профильный! Базовый уровень смотрите здесь.
- Всё про ЕГЭ 2023
- Демоверсия 2023 + изменения 2023
Что почитать?
- Из актуального: рекомендации от ФИПИ по профильной математике
Что изменилось в ЕГЭ 2023 по математике
Представляете — ничего 
Теория для подготовки к ЕГЭ 2023 по математике
Для теории у нас создан особый раздел «Теория для ЕГЭ по математике». Отдельно может порекомендовать посмотреть сборник шпаргалок для ЕГЭ по математике и на проекте ЕГЭ100Баллов целая ветка, посвященная шпаргалкам.
Что можно брать с собой на ЕГЭ по профильной математике?
На ЕГЭ по математике как всегда с собой можно взять только линейку. Никаких калькуляторов и мобильных телефонов, конечно же. Вода и шоколадка разрешаются 
Выбирайте вариант, сверяйте с ответами, оставляйте комментарии НИЖЕ
Тренировочная работа №1 статград пробный ЕГЭ 2023 по математике 10-11 класс 10 тренировочных варианта МА2200101-МА2200110 с ответами и решением. Официальная дата проведения работы: 8 февраля 2023 года.
Скачать ответы и решени для вариантов
Статград математика ЕГЭ 2023 варианты базового уровня
Статград математика ЕГЭ 2023 варианты профильного уровня
Вариант МА2200101 ответы
1. Бегун пробежал 400 метров за 40 секунд. Найдите среднюю скорость бегуна на дистанции. Ответ дайте в километрах в час.
2. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
- А) время одного оборота Земли вокруг Солнца
- Б) длительность полнометражного художественного фильма
- В) длительность звучания одной песни
- Г) продолжительность вспышки фотоаппарата
- 1) 3,5 минуты
- 2) 105 минут
- 3) 365 суток
- 4) 0,1 секунды
3. На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены ломаной линией. Определите по рисунку, какого числа в Казани выпало наибольшее количество осадков за данный период.
5. Вероятность того, что новая шариковая ручка пишет плохо или вовсе не пишет, равна 0,14. Покупатель не глядя берёт одну шариковую ручку из коробки. Найдите вероятность того, что эта ручка пишет хорошо.
7. На рисунке точками показано атмосферное давление в некотором городе на протяжении трёх суток с 4 по 6 апреля 2013 года. В течение суток давление измеряется 4 раза: в 0:00, в 6:00, в 12:00 и в 18:00. По горизонтали указываются время и дата, по вертикали — давление в миллиметрах ртутного столба. Для наглядности точки соединены ломаной линией. Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику атмосферного давления в этом городе в течение этого периода.
8. Двадцать выпускников одного из одиннадцатых классов сдавали ЕГЭ по обществознанию. Самый низкий балл, полученный в этом классе, был равен 36, а самый высокий — 75. Выберите утверждения, которые верны при указанных условиях.
- 1) Среди этих выпускников есть человек, который получил 75 баллов за ЕГЭ по обществознанию.
- 2) Среди этих выпускников есть двадцать человек с равными баллами за ЕГЭ по обществознанию.
- 3) Среди этих выпускников есть человек, получивший 20 баллов за ЕГЭ по обществознанию.
- 4) Баллы за ЕГЭ по обществознанию любого из этих двадцати человек не ниже 35.
9. План местности разбит на клетки. Каждая клетка обозначает квадрат 1м×1м . Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
10. Пол в комнате, имеющей форму прямоугольника со сторонами 7 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 20 см. Какое минимальное количество таких дощечек потребуется?
11. Плоскость, проходящая через точки A, B и C (см. рисунок), разбивает правильную треугольную призму на два многогранника. Сколько граней у получившегося многогранника с меньшим числом рёбер?
12. В прямоугольнике одна из сторон равна 48, а диагональ равна 50. Найдите площадь этого прямоугольника.
15. Число посетителей сайта увеличилось за месяц впятеро. На сколько процентов увеличилось число посетителей сайта за этот месяц?
19. Четырёхзначное число A состоит из цифр 1, 3, 6, 8, а четырёхзначное число B — из цифр 2, 3, 6, 7. Известно, что B A = 2 . В ответе укажите какое-нибудь одно такое число А, большее 1500.
20. Первую треть трассы автомобиль ехал со скоростью 30 км/ч, вторую треть — со скоростью 80 км/ч, а последнюю — со скоростью 60 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
21. Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 21, 11 и 4. Найдите периметр четвёртого прямоугольника.
Вариант МА2200105 ответы
1. Поезд Новосибирск – Красноярск отправляется в 15:20, а прибывает в 4:20 на следующий день (время московское). Сколько часов согласно расписанию поезд находится в пути?
2. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
- А) время одного оборота Меркурия вокруг Солнца
- Б) длительность эпизода драматического сериала
- В) длительность прямого авиаперелёта Москва – Южно-Сахалинск
- Г) продолжительность взмаха крыла колибри
3. На рисунке жирными точками показана цена палладия, установленная Центробанком РФ во все рабочие дни в октябре 2009 года. По горизонтали указываются числа месяца, по вертикали — цена палладия в рублях за грамм. Для наглядности жирные точки на рисунке соединены ломаной линией. Определите по рисунку наименьшую цену палладия в период с 14 по 26 октября. Ответ дайте в рублях за грамм.
5. Вероятность того, что стекло мобильного телефона разобьётся при падении на твёрдую поверхность, равна 0,84. Найдите вероятность того, что при падении на твёрдую поверхность стекло мобильного телефона не разобьётся.
7. На рисунке точками показано атмосферное давление в некотором городе на протяжении трёх суток с 4 по 6 апреля 2013 года. В течение суток давление измеряется 4 раза: в 0:00, в 6:00, в 12:00 и в 18:00. По горизонтали указываются время и дата, по вертикали — давление в миллиметрах ртутного столба. Для наглядности точки соединены ломаной линией. Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику атмосферного давления в этом городе в течение этого периода.
8. Перед футбольным турниром измерили рост игроков футбольной команды города N. Оказалось, что рост каждого из футболистов этой команды больше 170 см и меньше 190 см. Выберите утверждения, которые верны при указанных условиях.
- 1) В футбольной команде города N обязательно есть игрок, рост которого равен 160 см.
- 2) В футбольной команде города N нет игроков с ростом 169 см.
- 3) Рост любого футболиста этой команды меньше 190 см.
- 4) Разница в росте любых двух игроков футбольной команды города N составляет более 20 см.
9. План местности разбит на клетки. Каждая клетка обозначает квадрат 1м×1м . Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
10. Масштаб карты такой, что в одном сантиметре 2,5 км. Чему равно расстояние между городами А и В (в км), если на карте оно составляет 12 см?
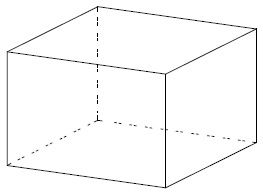
11. Плоскость, проходящая через точки A, B и C (см. рисунок), разбивает куб на два многогранника. Сколько граней у получившегося многогранника с бóльшим числом рёбер?
12. Площадь прямоугольника равна 12, а одна из сторон равна 4. Найдите диагональ этого прямоугольника.
13. Сторона основания правильной шестиугольной пирамиды равна 10, боковое ребро равно 13. Найдите площадь боковой поверхности этой пирамиды.
15. Длины двух рек относятся как 4:7, при этом одна из них длиннее другой на 30 км. Найдите длину большей реки. Ответ дайте в километрах.
19. Найдите четырёхзначное число, которое в 3 раза меньше четвёртой степени некоторого натурального числа. В ответе укажите какое-нибудь одно такое число.
20. Петя и Ваня выполняют одинаковый тест. Петя отвечает за час на 18 вопросов теста, а Ваня — на 30. Они одновременно начали отвечать на вопросы теста, и Петя закончил свой тест позже Вани на 56 минут. Сколько вопросов содержит тест?
21. Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Площади трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 12, 15 и 30. Найдите площадь четвёртого прямоугольника.
Вариант МА2200109 ответы
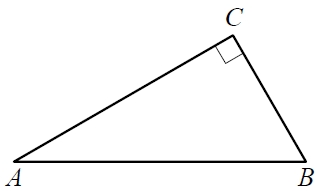
1. В треугольнике ABC угол C равен 90° , BC=6, tg A= 0,75.Найдите длину стороны AC .
2. Стороны основания правильной четырёхугольной пирамиды равны 12, боковые рёбра равны 10. Найдите площадь поверхности этой пирамиды.
3. Вероятность того, что на тестировании по биологии учащийся У. верно решит больше 9 задач, равна 0,61. Вероятность того, что У. верно решит больше 8 задач, равна 0,73. Найдите вероятность того, что У. верно решит ровно 9 задач.
4. В викторине участвуют 10 команд. Все команды разной силы, и в каждой встрече выигрывает та команда, которая сильнее. В первом раунде встречаются две случайно выбранные команды. Ничья невозможна. Проигравшая команда выбывает из викторины, а победившая команда играет со следующим случайно выбранным соперником. Известно, что в первых шести играх победила команда А. Какова вероятность того, что эта команда выиграет седьмой раунд?
9. Плиточник должен уложить 240 2 м плитки. Если он будет укладывать на 3 2 м в день больше, чем запланировал, то закончит работу на 4 дня раньше. Сколько квадратных метров плитки в день планирует укладывать плиточник?
15. В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы: — каждый январь долг возрастает на 20 % по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга. Известно, что кредит будет полностью погашен четырьмя равными платежами (то есть за четыре года). Каждый из четырёх платежей составит 2,592 млн рублей. Сколько рублей будет взято в банке?
16. Четырёхугольник ABCD вписан в окружность, причём диаметром окружности является его диагональ AC . Также известно, что в четырёхугольник ABCD можно вписать окружность. а) Докажите, что отрезки AC и BD перпендикулярны. б) Найдите радиус окружности, вписанной в четырёхугольник ABCD , если AC = 50 и BD =14.
Вариант МА2200110 ответы
1. Найдите площадь квадрата, если его диагональ равна 8.
2. Стороны основания правильной четырёхугольной пирамиды равны 16, боковые рёбра равны 17. Найдите площадь поверхности этой пирамиды.
3. Вероятность того, что на тестировании по истории учащийся Д. верно решит больше 11 задач, равна 0,64. Вероятность того, что Д. верно решит больше 10 задач, равна 0,7. Найдите вероятность того, что Д. верно решит ровно 11 задач.
4. В викторине участвуют 15 команд. Все команды разной силы, и в каждой встрече выигрывает та команда, которая сильнее. В первом раунде встречаются две случайно выбранные команды. Ничья невозможна. Проигравшая команда выбывает из викторины, а победившая команда играет со следующим случайно выбранным соперником. Известно, что в первых 8 играх победила команда А. Какова вероятность того, что эта команда выиграет девятый раунд?
9. Плиточник должен уложить 221 2 м плитки. Если он будет укладывать на 4 в день больше, чем запланировал, то закончит работу на 4 дня раньше. Сколько квадратных метров плитки в день планирует укладывать плиточник?
15. В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы: — каждый январь долг возрастает на 10 % по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга. Известно, что кредит будет полностью погашен четырьмя равными платежами (то есть за четыре года). Каждый из четырёх платежей составит 2,9282 млн рублей. Сколько рублей будет взято в банке?
16. Четырёхугольник ABCD вписан в окружность, причём диаметром окружности является его диагональ AC . Также известно, что в четырёхугольник ABCD можно вписать окружность. а) Докажите, что отрезки AC и BD перпендикулярны. б) Найдите радиус окружности, вписанной в четырёхугольник ABCD , если AC = 34 и BD =16.
Статград работы по математике ЕГЭ ОГЭ для 9 и 11 класса
Share the post «8 февраля 2023 статград математика 10-11 класс ЕГЭ 2023 база и профиль варианты»
- VKontakte
Метки: ЕГЭ 2023заданияматематика 11 классответыстатградтренировочная работа
Решение и ответы заданий варианта 2210109 СтатГрад 28 сентября ЕГЭ 2023 по математике (профильный уровень). ГДЗ профиль для 11 класса.


Задание 1.
В треугольнике ABC угол C равен 90°, AB = 4, sinA=frac{sqrt{19}}{10}. Найдите AC.
Задание 2.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 7 и 4. Объём параллелепипеда равен 140. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
Задание 3.
При производстве в среднем из 2000 насосов 4 неисправных. Найдите вероятность того, что случайно выбранный насос окажется неисправным.
Задание 4.
Игральную кость бросили два раза. Известно, что четыре очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 11».
Задание 5.
Найдите корень уравнения sqrt{frac{7x+13}{19}}=5.
Задание 6.
Найдите значение выражения frac{a^{-1}b^{-1}}{(2a)^{2}b^{-3}}cdot frac{11}{a^{-3}b^{2}}.
Задание 7.
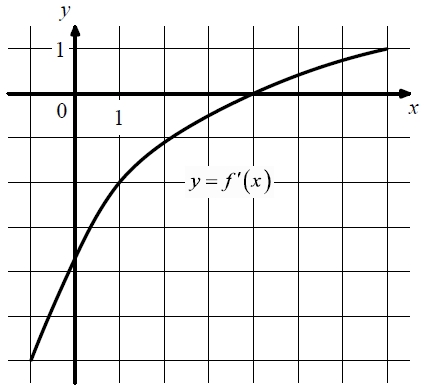
На рисунке изображён график функции y = f ‘(x) – производной функции f(x). Найдите абсциссу точки, в которой касательная к графику функции y = f(x) параллельна прямой y = 6 − 2x или совпадает с ней.
Задание 8.
Рейтинг R интернет-магазина вычисляется по формуле , R=r_{пок}–frac{r_{пок}–r_{экс}}{(K+1)^{m}}, где m=frac{0,02K}{r_{пок}+0,1}, rпок – средняя оценка магазина покупателями, rэкс – оценка магазина, данная экспертами, K – число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оценивших магазин, равно 15, их средняя оценка равна 0,5, а оценка экспертов равна 0,22.
Задание 9.
Расстояние между пристанями A и B равно 60 км. Из A в B по течению реки отправился плот, а через 3 часа вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот проплыл 44 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч.
Задание 10.
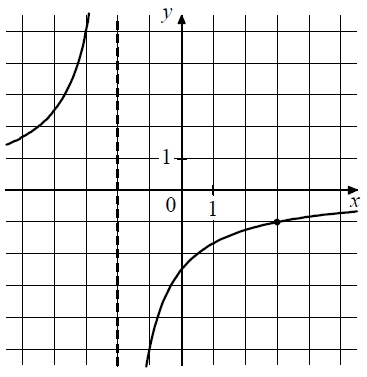
На рисунке изображён график функции вида f(x)=frac{k}{x+a}. Найдите значение x, при котором f(x) = –0,125.
Задание 11.
Найдите точку минимума функции y = x3 − 6x2 + 15.
Задание 12.
а) Решите уравнение cos2 x − cos2x = 0,75.
б) Найдите все корни этого уравнения, принадлежащие отрезку [frac{3pi}{2};3pi].
Задание 13.
Ребро куба ABCDA1B1C1D1 равно 2. На ребре BB1 отмечена точка K так, что KB = 1,6. Через точки K и C1 проведена плоскость α , параллельная прямой BD1.
а) Докажите, что A1P : PB1 = 3:1, где P – точка пересечения плоскости α с ребром A1B1.
б) Найдите угол между плоскостями α и BB1C1.
Задание 14.
Решите неравенство frac{(3x–4)^{2}}{x–3}ge frac{16–24x+9x^{2}}{15–8x+x^{2}}.
Задание 15.
15 января планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 40 % больше суммы, взятой в кредит. Найдите r.
Задание 16.
Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M. Окружность с центром O и диаметром CM касается гипотенузы в точке N.
а) Докажите, что прямые MN и BO параллельны.
б) Найдите площадь четырёхугольника BOMN, если CN = 9 и AM:MC = 1:8.
Задание 17.
Найдите все значения a, при каждом из которых уравнение
(|x + 2| + |x – a|)2 – 4(|x + 2| + |x – a|) + 3a(4 – 3a) = 0
имеет ровно два решения.
Задание 18.
На сайте проводится опрос, кого из 156 футболистов посетители сайта считают лучшим по итогам сезона. Каждый посетитель голосует за одного футболиста. На сайте отображается рейтинг каждого футболиста – доля голосов, отданных за него, в процентах, округлённая до целого числа. Например, числа 9,3, 10,5 и 12,7 округляются до 9, 11 и 13 соответственно.
а) Всего проголосовало 11 посетителей сайта, и рейтинг первого футболиста стал равен 45. Увидев это, Вася отдал свой голос за другого футболиста. Чему теперь равен рейтинг первого футболиста?
б) Вася проголосовал за некоторого футболиста. Могла ли после этого сумма рейтингов всех футболистов уменьшиться на 150 или больше?
в) Какое наибольшее значение может принимать сумма рейтингов всех футболистов?
Источник варианта: СтатГрад/statgrad.org.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3.2 / 5. Количество оценок: 10
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Пробники ЕГЭ ↓
Математика,
Физика,
Информатика,
Химия,
Русский,
Обществознание,
Литература,
История,
Иностранные языки,
География,
Биология
1 ноября 2022
В закладки
Обсудить
Жалоба
Пять пробных вариантов ЕГЭ по профильной математике + видеоразбор + конспект.
Разбор пробного варианта ЕГЭ по профильной математике №1
Файл с вариантом: probnyi-variant-1.pdf
Разбор пробного варианта ЕГЭ по профильной математике №2
Файл с вариантом: probnik-2.pdf
Конспект с разбором: konspekt-variant-2.pdf
Разбор пробного варианта ЕГЭ по профильной математике №3
Файл с вариантом: probnik-3.pdf
Конспект с разбором: konspekt-variant-3.pdf
Разбор пробного варианта ЕГЭ по профильной математике №4
Файл с вариантом: probnik-4.pdf
Конспект с разбором: konspekt-razbora-4.pdf
Разбор пробного варианта ЕГЭ по профильной математике №5
Файл с вариантом: probnik_5.pdf
Конспект с разбором: 5_konspekt-s-razborom.pdf
Автор: Марсель Нуртдинов.
Источник: vk.com/marsel_tutor