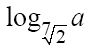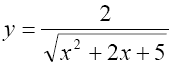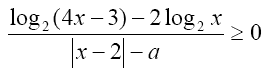Тренировочный вариант 184 профильного егэ

Skip to content

Ответы на тренировочный вариант №184 профильного ЕГЭ

Ответы на тренировочный вариант №184 профильного ЕГЭadmin2022-10-15T12:45:17+03:00

Источник

А. Ларин: Тренировочный вариант № 184.

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Версия для печати и копирования в MS Word

1

а)  Решите уравнение: корень из логарифм по основанию левая круглая скобка корень из x правая круглая скобка левая круглая скобка 5x правая круглая скобка умножить на логарифм по основанию 5 x = минус 2.

б)  Найти натуральное число n такое, что x_0 принадлежит левая круглая скобка дробь: числитель: lg2, знаменатель: n плюс 1 конец дроби ; дробь: числитель: lg2, знаменатель: n конец дроби правая круглая скобка ,гдеx_0   — корень уравнения.

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

2

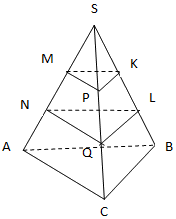
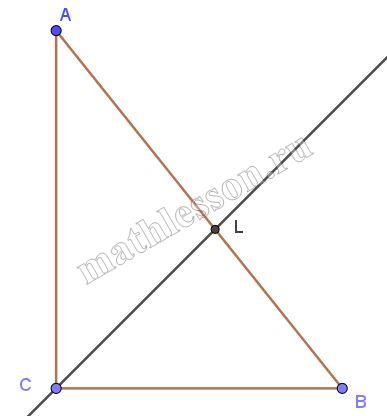
В правильной треугольной пирамиде SABC, точки P, Q, R лежат на боковых ребрах AS, CS и BS, причем дробь: числитель: SP, знаменатель: AP конец дроби = дробь: числитель: CQ, знаменатель: QS конец дроби = дробь: числитель: SR, знаменатель: RB конец дроби =2.

а)  Доказать, что объемы пирамид SPRQ и SABC относятся как 4 : 27.

б)  Найти объем пирамиды CPQR, если AB  =   2 и SA  =   3.

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

3

Решите неравенство: 3 корень из x в квадрате плюс 6x плюс 9 минус левая круглая скобка корень из 3x плюс 7 правая круглая скобка в квадрате минус 2|x минус 1| меньше или равно 0.

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

4

В остроугольном треугольнике АВС из вершин А и С опущены высоты АР и CQ на стороны ВС и АВ. Известно, что площадь треугольника АВС равна 18,площадь треугольника BPQ равна 2, а длина отрезка РQ равна2 корень из 2 .

а)  Доказать, что треугольники QBP и СВА подобны.

б)  Вычислить радиус окружности, описанной около треугольника АВС.

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

5

Для увеличения выпуска продукции решено расширить производство за счет использования имеющейся свободной площади в 70 кв. м, на которой предполагается установить оборудование двух видов общей стоимостью не более 100 млн.руб. Каждый комплект оборудования вида А занимает 20 кв. м, стоит 10 млн руб. и позволяет получить за смену 40 ед. продукции, а каждый комплект оборудования вида В занимает 10 кв. м, стоит 30 млн руб. и позволяет получить за смену 80 ед. продукции. Определить значение максимально возможного прироста выпуска продукции за смену.

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

6

При каждом значении параметра «a» решить неравенство

дробь: числитель: логарифм по основанию 2 левая круглая скобка 4x минус 3 правая круглая скобка минус 2 логарифм по основанию 2 x, знаменатель: |x минус 2| минус a конец дроби больше или равно 0.

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

7

Последовательные нечетные числа сгруппированы следующим образом: (1); (3;5); (7;9;11);(13;15;17;19)…

а)  Найти сумму чисел в десятой группе;

б)  Найти сумму чисел в сотой группе;

в)  Определить среди первых ста групп количество групп, в которых сумма чисел делится на 3.

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

Завершить тестирование, свериться с ответами, увидеть решения.

Источник

Вопрос B1 #3388

Билет на электричку стоит 62р 50коп. Проездной на 60 поездок (срок действия 3 месяца) стоит 3300 руб. Гражданин купил проездной и за 3 месяца совершил 56 поездок. Сколько рублей сэкономил гражданин, купив проездной.

Вопрос B2 #3389

На диаграмме отображены показания электросчетчика в киловаттах на первое число каждого месяца

Сколько рублей необходимо заплатить за 3 весенних месяца при стоимости 4.88 руб/киловатт.

Вопрос B3 #3390

Найти площадь треугольника АВС, если площадь треугольника PRT равна 7, где P, R, T – середины сторон треугольника АВС.

Вопрос B4 #3391

Бросили два игральных кубика. Найти вероятность того, что выпал дубль (на обоих кубиках одинаковое число очков). Ответ округлить до сотых.

Вопрос B5 #3392

Решить уравнение

Вопрос B6 #3393

Найти сторону равностороннего треугольника, площадь которого равна площади трапеции с основаниями (sqrt{3}) и (3 sqrt{3}) и высотой (8).

Вопрос B7 #3394

На рисунке изображён график (y = {f}'(x)) — производной функции (f(x)), определённой на отрезке ((-11; 2)). Найдите абсциссу точки, в которой касательная к графику функции (y = f(x)) параллельна оси абсцисс или совпадает с ней.

Вопрос B8 #3395

В треугольной пирамиде SABC точки N и M, P и Q, K и L делят соответствующие боковые ребра на 3 равные части. Объем многогранника NLQMKP равен 21. Найти объем пирамиды SABC.

Вопрос B9 #3396

Найдите

Если (log_{a}8a=8)

Вопрос B10 #3397

Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону (U=U_{0}cos(omega t + varphi )) , где (t) — время в секундах, амплитуда (U_{0} = 2B), частота ( omega = 200 ^{circ} /{C}) , фаза (varphi =-120^{circ}) . Датчик настроен так, что если напряжение в нем не ниже, чем (1B), загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?

Вопрос B11 #3398

Василий ведет машину со скоростью 40 км/ч. Он хочет проезжать каждый километр на 1 минуту быстрее. На сколько ему надо увеличить скорость? (Ответ дать в км/ч)

Вопрос B12 #3399

Найти наибольшее значение функции

на промежутке [-2;2]

Вопрос B13 #3400

а) Решить уравнение (sqrt{log_{sqrt{x}}(5x)} cdot log_{5}x=-2)
б) Найти натуральное числ (n), что (x_{0} in left( frac{lg2}{n+1}; frac{lg2}{n} right)), где (x_{0}) — корень уравнения

Вопрос B14 #3401

В правильной треугольной пирамиде (SABC), точки (P, Q, R) лежат на боковых ребрах (AS, CS) и (BS), причем (frac{SP}{AP}=frac{CQ}{QS}=frac{SR}{RB}=2)

а) Доказать, что объемы пирамид (SPRQ) и (SABC) относятся как (4:27).
б) Найти объем пирамиды (CPQR), если (AB = 2) и (SA = 3).

Вопрос B15 #3402

Решите неравенство: (3 sqrt{x^{2}+6x+9} — (sqrt{3x+7})^{2}-2|x-1| leq 0)

Вопрос B16 #3403

В остроугольном треугольнике (ABC) из вершин (A) и (C) опущены высоты (AP) и (CQ) на стороны (BC) и (AB). Известно, что площадь треугольника (ABC) равна (18), площадь треугольника (BPQ) равна (2), а длина отрезка (PQ) равна (2sqrt{2}) .
а) Доказать, что треугольники (QBP )и (CBA) подобны.
б) Вычислить радиус окружности, описанной около треугольника (ABC).

Вопрос B17 #3404

Для увеличения выпуска продукции решено расширить производство за счет использования имеющейся свободной площади в 70 кв.м, на которой предполагается установить оборудование двух видов общей стоимостью не более 100 млн.руб. Каждый комплект оборудования вида А занимает 20 кв.м, стоит 10 млн.руб. и позволяет получить за смену 40 ед. продукции, а каждый комплект оборудования вида В занимает 10 кв.м, стоит 30 млн.руб. и позволяет получить за смену 80 ед. продукции. Определить значение максимально возможного прироста выпуска продукции за смену.

Вопрос B18 #3405

При каждом значении параметра «a» решить неравенство 

Вопрос B19 #3406

Последовательные нечетные числа сгруппированы следующим образом: (1); (3;5); (7;9;11);(13;15;17;19)…
а) Найти сумму чисел в десятой группе;
б) Найти сумму чисел в сотой группе;
в) Определить среди первых ста групп количество групп, в которых сумма чисел делится на 3.

Источник

16
Фев 2017

Категория: 12 (С1) УравненияТ/P A. Ларина

Елена Репина
2017-02-16
2017-03-15

Смотрите также  №14; №15; №16; №17; №18; №19  Тренировочной работы №184 А. Ларина

13. Дано уравнение sqrt{log_{sqrt x}5x}cdot log_5x=-2.

а) Решите уравнение.

б) Найдите натуральное число n, такое, что  x_0in (frac{lg2}{n+1};frac{lg2}{n}),  где x_0 – корень уравнения.

Решение:

а)

sqrt{log_{sqrt x}5x}cdot log_5x=-2;

sqrt{2(log_{x}5+log_xx)}cdot log_5x=-2;

sqrt{log_{x}5+1}cdot log_5x=-sqrt 2;

sqrt{log_{x}5+1}=-sqrt 2log_x5;

log_{x}5+1=2log_x^25 при условии log_x5< 0;

2log_x5^2-log_{x}5-1=0 при условии log_x5< 0;

(log_x5-1)(log_x5+frac{1}{2})=0 при условии log_x5< 0;

log_x5=-frac{1}{2};

x=frac{1}{25}.

б) Найдем натуральное число n, такое, что  frac{1}{25}in (frac{lg2}{n+1};frac{lg2}{n}).

frac{lg2}{n+1}<frac{1}{25}<frac{lg2}{n};

25lg2-1<n<25lg2;

lgfrac{2^{25}}{10}<n<lg2^{25};

frac{2^{25}}{10}<10^n<2^{25};

Так как

2^{25}=2cdot (2^{12})^2=2cdot 4096^2=33554432=3,3cdot 10^7.

и, с другой стороны,

2^{25}=(2^{10})^2cdot 2^5=1024^2cdot 32>10^6cdot 32=3,2cdot 10^7,

(то есть 3,2cdot 10^6<frac{2^{25}}{10}),

то

3,2cdot 10^6<10^n<3,3cdot 10^7;

n=7.

Ответ: а) frac{1}{25}; б) 7.

Автор: egeMax |

комментариев 9

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Печать страницы

комментариев 9

  1. Kirill

    2017-02-18 в 18:44

    Откуда во 2ой строке сверху взялась двойка под корнем? Формула перехода к новому основанию?

    [ Ответить ]

    • egeMax

      2017-02-18 в 19:03

      Прежде был вынесен вперёд логарифма показатель x. То есть 1/2, перевернувшись, превратилась в 2-ку. А уже затем перешли к сумме логарифмов.

      [ Ответить ]

  2. Татьяна

    2017-02-18 в 20:58

    Добрый вечер! Не поняла переход в части б) от1/25 к n. Спасибо.

    [ Ответить ]

    • egeMax

      2017-02-18 в 21:08

      Татьяна, если вы имеете ввиду вторую строку? Двойное неравенство предыдущей строки рассмотрите как систему двух неравенств. Выразите из каждого неравенства n. Появится возможность опять вернуться к двойному неравенству, но уже в серединке – n.

      [ Ответить ]

      • Татьяна

        2017-02-18 в 21:12

        Спасибо

        [ Ответить ]

  3. Александр

    2017-03-02 в 13:52

    В части б) – предпоследняя строчка [ 3,2*10^6 < 10^n < 2*10^8 ] подходит n = 7 и n = 8. подскажите пожалуйста, почему взяли именно n = 7?

    [ Ответить ]

    • egeMax

      2017-03-02 в 14:31

      Подправила, – сделана более точная оценка. Спасибо!

      [ Ответить ]

  4. Dimitry

    2017-03-15 в 11:22

    Как произошёл переход от пятой строчки к шестой?

    [ Ответить ]

    • egeMax

      2017-03-15 в 11:39

      Там опечатка была, – квадрат перебежал не туда… Подправила, – думаю, теперь вопросы отпадут.

      [ Ответить ]

Добавить комментарий

  • Материалы для подготовки к ЕГЭ

  •    

  • Рубрики
    • 01 Геометрия (13)
    • 02 Стереометрия (9)
    • 03 Теория вероятностей ч.1 (1)
    • 04 Теория вероятностей ч.2 (1)
    • 05 Простейшие уравнения (5)
    • 06 Вычисления (5)
    • 07 Производная, ПО (4)
    • 08 «Прикладные» задачи (5)
    • 09 Текстовые задачи (7)
    • 10 Графики функций (7)
    • 11 Исследование функции (2)
    • 12 (С1) Уравнения (78)
    • 13 (С2) Стереометр. задачи (94)
    • 14 (С3) Неравенства (89)
    • 15 (С4) Практич. задачи (71)
    • 16 (С5) Планиметр. задачи (86)
    • 17 (С6) Параметры* (79)
    • 18 (С7) Числа, их свойства (38)
    • A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
    • A2 Читаем графики (нет в ЕГЭ-22) (1)
    • Видеоуроки (44)
    • ГИА (11)
      • II часть (11)
    • ЕГЭ (диагностич. работы) (70)
    • Иррациональные выражения, уравнения и неравенства (15)
    • Логарифмы (39)
    • МГУ (12)
    • Метод интервалов (4)
    • Метод рационализации (18)
    • Модуль (9)
    • Параметр (40)
    • Переменка (5)
    • Планиметрия (60)
    • Показательные выражения, уравнения и неравенства (8)
    • Разложение на множители (1)
    • Рациональные выражения, уравнения и неравенства (10)
    • Справочные материалы (92)
    • Стереометрия (52)
    • Т/P A. Ларина (443)
    • Текстовые задачи (12)
    • Теория чисел (2)
    • Тесты по темам (80)
    • Тригонометрические выражения, уравнения и неравенства (43)
    • Функции и графики (10)
  • Дружественные сайты

    Сайт А. Ларина
    ЕгэТренер – О. Себедаш
    Математика?Легко!
    Егэ? Ок! – И. Фельдман

  • Свежие записи
    • Тест «Гиперболы»
    • Тест. Графики функций. Комбинированные задачи
    • 10. Графики функций. Комбинированные задачи
    • Тест. Тригонометрические функции
    • 10. Тригонометрическая функция
    • Тест. Кусочно-линейная функция
    • 10. Кусочно-линейная функция
  • Архивы Архивы

Источник

Найденные материалы, документы, бумажные и электронные книги и файлы:

Ниже показаны результаты поиска поисковой системы Яндекс. В результатах могут быть показаны как эта книга, так и похожие на нее по названию или автору.

Search results:

  1. Ответы на тренировочный вариант №184 профильного ЕГЭ

    ГВЭ 11 класс. ВПР. ВПР 4 класс.

    math100.ru

  2. Единый государственный экзамен по МАТЕМАТИКЕ…

    Часть 2 содержит 7 заданий с развѐрнутым ответом повышенного и высокого уровней сложности. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут). Ответы к заданиям 1–11 записываются по приведѐнному ниже образцу в виде целого числа или конечной десятичной дроби.

    Ответом к заданиям 1‐11 является целое число или конечная десятичная дробь. Запишите число в поле ответа в тексте работы, затем перенесите его в БЛАНК ОТВЕТОВ №1 справа от номера соответствующего задания, начиная с первой клеточки.

    vpr-ege.ru

  4. Канцтовары

    Купить книгу в интернет магазине My-shop

    Канцтовары: бумага, ручки, карандаши, тетради.
    Ранцы, рюкзаки, сумки.
    И многое другое.

    my-shop.ru

  6. Единый государственный экзамен по МАТЕМАТИКЕ

    На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут). Ответы к заданиям 1–12 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1.

    © alexlarin.net 2017 Разрешается свободное копирование, распространение и использование в образовательных некоммерческих целях. Единый государственный экзамен, 2017 г. Математика, 11 класс Тренировочный вариант № 184.

    alexlarin.net

  7. Тренировочный вариант №184 ЕГЭ — 2017

    Тренировочный вариант №184. Варианты публикуются еженедельно в субботу ответы — в пятницу. Скачать документ в формате pdf. Обсуждение задач…

    9. 10. 11. 12. Обсуждение задач…

    alexlarin.net

  8. Тренировочный вариант № 184 математика ЕГЭ Ларин А.

    …Экзамены, ЕГЭ, ОГЭ, 11 класс, Варианты ЕГЭ с сайта А.Ларина, Тренировочный вариант № 184 математика ЕГЭ Ларин А.

    Просмотр содержимого документа «Тренировочный вариант № 184 математика ЕГЭ Ларин А.» Алгебра 11 класc. Электронная тетрадь по алгебре 7 класс…

    multiurok.ru

  9. ЕГЭ–2023, математика: задания, ответы, решения

    А. Ларин: Тренировочный вариант № 184. При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр.

    Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом.

    math-ege.sdamgia.ru

  10. Тренировочные варианты профильного ЕГЭ 2023 по математике…

    Важно не просто прорешать все возможные варианты с ФИПИ и Решу ЕГЭ, важно иметь полное системное представление о математике. Данные тренировочные варианты помогут вам проверить свои знания на практике, получить представление о трудностях на экзамене. Тренировочные варианты содержат задания разных уровней сложности: 1) 12 номеров с кратким вариантов ответа; 2) 7 номеров с развернутым вариантом ответа, из которых 2 последних задачи олимпиадного уровня.

    math100.ru

  11. Тренировочные варианты ЕГЭ 2023 по математике профильного…

    Структура варианта КИМ ЕГЭ 2023 по математике профильного уровня. Экзаменационная работа состоит из двух частей и включает в себя 18 заданий, которые различаются по содержанию, сложности и количеству заданий: – часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби; – часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).

    vpr-ege.ru

  12. Пробные варианты ЕГЭ 2023 по математике профильного уровня

    Пробные варианты по математике профильного уровня в формате ЕГЭ 2023 из различных источников. Варианты составлены в соответствии с демоверсией 2023 года.

    Задание 10 по профильной математике — новые задачи по теории вероятностей в ЕГЭ-2022. Тест по теме «Производная» 11 класс алгебра с ответами. Основные тригонометрические тождества и формулы. Тренировочные варианты ОГЭ

    prooge.ru

  13. ЕГЭ–2023: задания, ответы, решения | Вариант учителя

    Образовательный портал для подготовки к экзаменам. Математика профильного уровня.

    Все варианты А. ЛаринаАлександра Ларинас 2013 года. Для тех, кто ищет варианты посложнее, чем обычно предлагают на ЕГЭ, публикуем задания с развернутым ответом из тренировочных вариантов А. А. Ларина. Новые условия по субботам, решения по пятницам.

    math-ege.sdamgia.ru

  14. Тренировочные варианты ЕГЭ 2022 по математике (профиль)

    Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2022 из различных источников.

    Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и количеству заданий: – часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби; – часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).

    vpr-ege.ru

  15. Тренировочные варианты ЕГЭ 2021 по математике (профиль)

    Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2021 из различных источников.

    Реальный вариант (по материалам из открытых источников). скачать.

    Вариант 11. скачать.

    Разбор задания 13 ЕГЭ по математике (профильный уровень).

    vpr-ege.ru

  16. ВАРИАНТЫ ЕГЭ 2023 (ПРОФИЛЬ) | ВКонтакте

    ВАРИАНТЫ ЕГЭ 2023 (ПРОФИЛЬ). Школа Пифагора ЕГЭ и ОГЭ по математике 25 авг 2022 в 15:50. #Варианты_ЕГЭ_профиль_2023_Школа_Пифагора. 35. Нравится Показать список оценивших.

    vk.com

  17. Тренировочные варианты ЕГЭ 2023 по математике 11 класс…

    Официальные тренировочные варианты математике 11 класс задания с ответами для подготовки к ЕГЭ (новые варианты ниже): 21.09.2017 Тренировочная работа статград.

    100ballnik.com

  18. Пробные варианты ЕГЭ по математике

    Тренировочные варианты профильного уровня по материалам открытого банка ФИПИ.

    ВПР в 11 классе. Новости вузов.

    Шкала ЕГЭ Видеоуроки Пробники Демоверсии ЕГЭ 2023 ОГЭ 2023.

    4ege.ru

  19. Математика 11 класс ЕГЭ 2023 варианты база и профиль работа…

    Новая тренировочная работа №1 ЕГЭ 2023 по математике 11 класс базовый и профильный уровень варианты, ответы и решения для работы статград, официальная дата.

    Вариант МА2210105. 1)Выпускники 11 «А» класса покупают букеты цветов для последнего звонка: из 7 роз каждому учителю и из 11 роз классному руководителю и директору. Они собираются подарить букеты 20 учителям (включая директора и классного руководителя), розы покупаются по оптовой цене 35 рублей за штуку.

    myotveti.ru

  20. Ященко егэ 2022 математика профильный уровень 36 вариантов…

    Сборник предназначен для подготовки к единому государственному экзамену по математике и содержит 36 полных вариантов, составленных в соответствии с проектом демоверсии КИМ ЕГЭ по математике профильного уровня. Варианты подготовлены специалистами федеральной комиссии разработчиков контрольных измерительных материалов ЕГЭ. В соответствии с документами, регламентирующими ЕГЭ по математике профильного уровня в 2022 году, каждый вариант содержит 18 заданий.

    100ballnik.com

  21. Пробник ЕГЭ по математике формата 2023

    По материалам открытого банка ФИПИ и заданий прошлых лет. Соответствует новому порядку заданий. → Вариант: → Ответы

    → Вариант: v1-m23.pdf → Ответы: otvety.pdf.

    4ege.ru

  22. Тренировочные варианты ЕГЭ 2023 по математике базового…

    Структура варианта КИМ ЕГЭ 2023 по математике базового уровня. Экзаменационная работа включает в себя 21 задание с кратким ответом базового уровня сложности. Все задания направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.

    vpr-ege.ru

  23. ЕГЭ по математике — Профиль 2023. Открытый… — math100.ru

    Демо вариант ЕГЭ Профиль 2023. Шкала перевода баллов ЕГЭ Профиль 2023.

    11. Наибольшее и наименьшее значение функций. Степенные, иррациональные и дробные функции.

    math100.ru

  24. Тренировочные варианты ЕГЭ 2021 по математике (база)

    Вариант 11. скачать. Разные.

    Разбор задания 17 ЕГЭ по профильной математике — Финансовая математика в задачах ЕГЭ.

    Решение задачи №19 ЕГЭ по профильной математике.

    vpr-ege.ru

  25. Пробные варианты ЕГЭ 2023 по математике базового уровня

    Сборник задач по стереометрии для 10-11 классов. Задание 10 по профильной математике — новые задачи по теории вероятностей в ЕГЭ-2022. Тест по теме «Производная» 11 класс алгебра с ответами. Основные тригонометрические тождества и формулы. Тренировочные варианты ОГЭ: Математика. Русский язык. Досрочные варианты ЕГЭ

    prooge.ru

  26. ЕГЭ 2023 математика база и профиль тренировочные варианты…

    Новые тренировочные варианты ЕГЭ 2023 по математике базовый и профильный уровень с ответами и решением для 10 и 11 класса, больше 100 вариантов в формате реального экзамена ФИПИ вы можете решать онлайн или скачать.

    100ballnik.com

  27. ЕГЭ 2023 по математике профиль: ФИПИ тренировочные…

    ЕГЭ по математике: тренировочные тесты, пробные и реальные варианты ЕГЭ по математике.

    16.12.2021 Тренировочная работа Статград ЕГЭ 2022 №2 по математике от 15.12.2021 (21243). 28.11.2021 Тренировочный вариант №4 ЕГЭ 2022 по профильной математике с ответами (15302).

    ctege.info

  28. Пять пробников ЕГЭ по профильной математике 2023

    Пять пробных вариантов ЕГЭ по профильной математике + видеоразбор + конспект.

    Разбор пробного варианта ЕГЭ по профильной математике №5. Файл с вариантом: probnik_5.pdf Конспект с разбором: 5_konspekt-s-razborom.pdf.

    4ege.ru

  29. Реальные (официальные) варианты ЕГЭ 2021 по математике…

    Варианты составлены из реальных заданий ЕГЭ 2021 по математике от 7 июня. Все задания взяты из открытых источников В конце варианта приведены правильные ответы ко всем заданиям. Вы можете свериться с ними и найти у себя ошибки. Скачать 1 вариант: Скачать Скачать 2 вариант: Скачать Смотреть 1 вариант онлайн: Смотреть 2 вариант онлайн

    co8a.ru

  30. Диагностические и тренировочные варианты СтатГрад ЕГЭ База…

    ГВЭ 11 класс.

    ВПР 4 класс.

    Варианты 2016-2017 учебного года.

    math100.ru

  31. ЕГЭ 2021 математика профильный уровень 40 вариантов…

    Пособие предназначено для эффективной подготовки к единому го­ сударственному экзамену по математике на профильном уровне. Книга будет поЛезна выпускникам, учителям, а также тем, кто собирается сда­ вать ЕГЭ после перерыва в обучении. .,.. Если сдача ЕГЭ по математике нужна вам только для получе­ ния аттестата, а не для поступления в вуз, то сдавайте базовый уро­ вень. Рекомендуем воспользоваться пособием «Математика. Подготовка к ЕГЭ-202 1 . Базовый уровень.

    100ballnik.com

  32. Варианты ЕГЭ 2023 | ВКонтакте

    Распечатай и реши: математика ОГЭ/ЕГЭ 2023.

    vk.com

  33. ЕГЭ–2023: задания, ответы, решения | Варианты

    Тысячи заданий с решениями для подготовки к ЕГЭ–2023 по всем предметам.

    Справочник по банковским задачам для ЕГЭ по профильной математике. Скачать.

    Варианты О. А. Иванова. 2022—2023 УЧЕБНЫЙ ГОД. Демонстрационная версия ЕГЭ по математике 2023 года с решениями.

    184. 185. 186.

    ege.sdamgia.ru

  34. ЕГЭ 2023 по математике база: ФИПИ тренировочные и реальные…

    Сборники тренировочных (пробных) и реальных тестов ЕГЭ по математике базового уровня за 2023 год. Все пробники составлены на основе реальных заданий или демоверсии и спецификации ФИПИ по базовой математике. А также варианты прошлых лет.

    ctege.info

  35. Диагностические и тренировочные варианты СтатГрад ЕГЭ…

    ГВЭ 11 класс.

    Расписание СтатГрад 11 класс ЕГЭ 2022.

    math100.ru

На данной странице Вы можете найти лучшие результаты поиска для чтения, скачивания и покупки на интернет сайтах материалов, документов, бумажных и электронных книг и файлов похожих на материал «ЕГЭ по математике, Вариант № 184, 11 класс, 2010»

Для формирования результатов поиска документов использован сервис Яндекс.XML.

Нашлось 20 млн ответов. Показаны первые 32 результата(ов).

Дата генерации страницы: суббота, 25 февраля 2023 г., 22:36:34 GMT

Источник

Сборники тренировочных тестов по математике профильного уровня для ЕГЭ в 2023 году и для ЕГЭ прошлых лет. Все тренировочные варианты/пробники содержат ответы и решения ко 2-й части кима. Обсудить решение и задания каждого варианта вы можете в комментариях под ними. РЕШАТЬ ТЕСТЫ

Обращайте внимание на уровень пробника — здесь только профильный! Базовый уровень смотрите здесь.

  • Всё про ЕГЭ 2023
  • Демоверсия 2023 + изменения 2023

Что почитать?

  • Из актуального: рекомендации от ФИПИ по профильной математике

Что изменилось в ЕГЭ 2023 по математике

Представляете — ничего :) Изменения в 2023 году отсутствуют — официальные данные от ФИПИ. А значит вы можете смело использовать материалы и тесты прошлых лет. Особенно это актуально для тренировочных работ Статграда: за 2022 год работы здесь, за 2023 год работы здесь.

Теория для подготовки к ЕГЭ 2023 по математике

Для теории у нас создан особый раздел «Теория для ЕГЭ по математике». Отдельно может порекомендовать посмотреть сборник шпаргалок для ЕГЭ по математике и на проекте ЕГЭ100Баллов целая ветка, посвященная шпаргалкам.

Что можно брать с собой на ЕГЭ по профильной математике?

На ЕГЭ по математике как всегда с собой можно взять только линейку. Никаких калькуляторов и мобильных телефонов, конечно же. Вода и шоколадка разрешаются :)

Выбирайте вариант, сверяйте с ответами, оставляйте комментарии НИЖЕ

Источник

Задание 1

Найдите значение выражения $$frac{0,25*7,5}{0,3-0,5*0,3}$$

Ответ: 12,5

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

$$frac{0,25*7,5}{0,3-0,5*0,3}=$$$$frac{frac{25}{100}*frac{75}{10}}{0,3(1-0,5)}=$$$$frac{frac{1}{4}*frac{15}{2}}{frac{3}{10}*frac{1}{2}}=$$$$frac{15*10*2}{4*3*2}=12,5$$

Задание 2

В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.

Вещество Дети от 1 года до 14 лет Мужчины Женщины
Жиры 40-97 70-154 60-102
Белки 36-87 65-117 58-87
Углеводы 170-420 257-586 257-586

Какой вывод о суточном потреблении жиров, белков и углеводов 13-летним мальчиком можно сделать, если по подсчётам диетолога в среднем за сутки он потребляет 90 г жиров, 90 г белков и 359 г углеводов?

В ответе укажите номера верных утверждений.

1. Потребление жиров в норме.

2. Потребление белков в норме.

3. Потребление углеводов в норме

Ответ: 13

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

1. Потребление жиров в норме — верно

2. Потребление белков в норме — неверно

3. Потребление углеводов в норме — верно

Следовательно, ответом будет 13

Задание 3

На координатной прямой отмечены числа x и y

Какое из следующих утверждений об этих числах верно?

Варианты ответа

1) x<y и |x|<|y|

2)x>y и |x|>|y|

3) x<y и |x|>|y|

4) x>y и |x|<|y|

Ответ: 1

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Модуль — это расстояние от начала координат до числа, как видим по рисунку, расстояние оу больше, чем ох, следовательно: |x|<|y|. С другой стороны число х левее, чем число у, следовательно, x

Задание 4

Найдите значение выражения $$sqrt{0,48}*frac{1}{sqrt{12}}$$ Варианты ответа 1)0,6 2)$$sqrt{3}$$ 3)0,2 4)$$frac{sqrt{3}}{4}$$

Ответ: 3

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

$$sqrt{0,48}*frac{1}{sqrt{12}}=$$$$sqrt{frac{48}{100*12}}=$$$$sqrt{frac{4}{100}}=frac{2}{10}=0,2$$. Что соответствует 3 варианту ответа

Задание 5

На рисунке изображена зависимость температуры (в градусах Цельсия) от высоты (в метрах) над уровнем моря. Определите по графику, на сколько градусов Цельсия температура на высоте 250 метров выше, чем на высоте 650 метров.

Ответ: 2

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

250 метров — 9 градусов, 650 метров — 7 градусов. Тогда разница составит : 9-7=2

Задание 6

Решите уравнение $$5-frac{2x-7}{4}=-5x$$

Ответ: -1,5

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

$$5-frac{2x-7}{4}=-5xLeftrightarrow $$$$20-2x+7=-20xLeftrightarrow $$$$-2x+20x=-20-7Leftrightarrow $$$$18x=-27|:18Leftrightarrow x=-1,5$$

Задание 7

В городе 90000 жителей, причём 32% — это пенсионеры. Сколько примерно человек составляет эта категория жителей? Ответ округлите до тысяч.

Ответ: 29

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Пусть х — количество пенсионеров, тогда : 90000 — 100% x — 32% Тогда: $$x=frac{90000*32}{100}=28800$$ человек. Тогда вы тысячах человек это будет примерно 29.

Задание 8

На диаграмме показан возрастной состав населения России. Определите по диаграмме, какая из возрастных категорий самая малочисленная.

Варианты ответа

1) 0 – 14 лет

2) 15 – 50 лет

3) 51 – 64 лет

4) 65 лет и более

Ответ: 4

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Наименьший сегмент составляет возрастная группа 65 лет и более, что соответствует 4 варианту ответа.

Задание 9

На экзамене 60 билетов, Василий не выучил 12 из них. Найдите вероятность того, что ему попадется выученный билет.

Ответ: 0,8

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Вероятность того, что попадется не выученный: $$P=frac{12}{60}=0,2$$. Тогда вероятность противоположного события (выученный) будет равна: $$1-P=1-0,2=0,8$$

Задание 10

На рисунке изображены графики функций вида $$y=ax^{2}+bx+c$$ . Установите соответствие между графиками функций и знаками коэффициентов a и c.

КОЭФФИЦИЕНТЫ

1) a>0, c>0

2)a<0, c>0

3) a>0, c>0

Ответ: 321

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Коэффициент а отвечает за направление ветвей параболы, если а > 0, то ветви вверх, если а < 0, то ветви вниз. Коэффициент с показывает ординату точки пересечения графиком оси оУ, если с > 0, то пересекает над осью оХ, если c < 0, то под осью оХ. Тогда получаем:

A)a > 0, c > 0 — 3 вариант ответа

Б)a < 0, c > 0 — 2 вариант ответа

В)a > 0, c < 0 — 1 вариант ответа

Задание 11

Последовательность $$a_{n}$$ задана условиями $$a_{1}=-3, a_{n+1}=a_{n}-3$$. Найдите $$a_{21}$$

Ответ: -63

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Найдем разность арифметической прогрессии: $$d=a_{n+1}-a_{n}=a_{n}-3-a_{n}=-3$$. Найдем 21 член прогрессии: $$a_{n}=a_{1}+d(n-1)$$ Тогда $$a_{21}=-3-3*(21-1)=-63$$

Задание 12

Найдите значение выражения $$frac{1}{a}-frac{3a+b}{ab}$$, при $$a=sqrt{5} ; b = frac{1}{5}$$

Ответ: -15

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

$$frac{1}{a}-frac{3a+b}{ab}=$$$$frac{b-3a-b}{ab}=$$$$-frac{3a}{ab}=$$$$-frac{3}{b}=$$$$-frac{3}{frac{1}{5}}=-15$$

Задание 13

В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) рассчитывается по формуле $$C=150+11cdot(t-5)$$, где t — длительность поездки, выраженная в минутах (t>5). Пользуясь этой формулой, рассчитайте стоимость 24-минутной поездки. Ответ укажите в рублях.

Ответ: 359

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

$$C=150+11cdot(24-5)=359$$

Задание 14

Укажите неравенство, которое не имеет решений

1)$$x^{2}-169geq 0$$

2)$$x^{2}+169geq 0$$

3)$$x^{2}-169leq0$$

4)$$x^{2}+169leq0$$

Ответ: 4

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Если можно найти какой-либо корень уравнения в данном случае, то неравенства будут иметь решения, то есть $$x^{2}-169=0 Leftrightarrow$$$$x=pm 13$$. Следовательно, оба неравенства, где слева стоит данное выражения будут иметь решения. $$x^{2}+169$$ всегда принимает положительные значения, так как это сумма неотрицательного и положительного. Следовательно, $$x^{2}+169geq 0$$ — имеет решением любое число, тогда $$x^{2}+169leq0$$ вообще не имеет решений

Задание 15

На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 4 м?

Ответ: 11

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Пусть х — расстояние от человека до фонаря, тогда из подобия треугольников ABC и A1B1C: $$frac{AB}{A_{1}B_{1}}=frac{BC}{B_{1}C} Leftrightarrow$$ $$frac{4}{1,8}=frac{x+9}{9} |*9 Leftrightarrow$$$$frac{4}{0,2}=x+9 Leftrightarrow$$$$x=20-9=11$$

Задание 16

Прямые m и n параллельны. Найдите $$angle 1$$, если $$angle 2 = 52^{circ}, angle 3 = 48^{circ}$$. Ответ дайте в градусах.

Ответ: 80

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Угол 2 равен углу 4 как накрестлежащие, но сумма углов 3,4,1 равна 180, тогда $$angle 1=180 — 52 — 48 = 80$$

Задание 17

Основания трапеции равны 5 и 14. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Ответ: 7

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

В треугольнике ABD HM — средняя линия, тогда: $$HM = frac{1}{2}AB=2,5$$

В треугольнике BDC ML — средняя линия, тогда: $$ML=frac{1}{2}DC=7$$

Задание 18

Боковая сторона равнобедренного треугольника равна 26, а основание равно 10. Найдите площадь этого треугольника.

Ответ: $$5sqrt{651}$$

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Высота треугольника : $$h = sqrt{26^{2}-5^{2}}=sqrt{651}$$. Тогда его площадь $$S=frac{1}{2}h*10=5sqrt{651}$$

Задание 19

В треугольнике ABC угол C равен 90°, СН – высота, AВ = 16, sin A = 3/4 . Найдите BН

Ответ: 9

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Из треугольника ABC : $$CB=ABsin A = 16*frac{3}{4}=12$$. $$angle A = angle HCB$$ из подобия треугольников при проведении высоты в прямоугольном треугольнике. Из треугольника CHB: $$HB=CB sin HCB = 12* frac{3}{4}=9$$

Задание 20

Какие из следующих утверждений верны?

1. Если в четырёхугольнике две стороны параллельны, то этот четырёхугольник — параллелограмм.

2. Через любые три точки плоскости, не лежащие на одной прямой, проходит единственная окружность.

3. Любые два равнобедренных прямоугольных треугольника подобны.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов

Ответ: 23

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

1) Неверно, так как это трапеция 2) Верно 3) Верно

Задание 21

Решите уравнение $$(x+2)(x^{2}-6x+9)=-4(x-3)$$

Ответ: -1 ; 2 ; 3

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

$$(x+2)(x^{2}-6x+9)=-4(x-3) Leftrightarrow$$$$(x+2)(x^-3)^{2}+4(x-3)=0 Leftrightarrow$$$$(x-3)((x+2)(x-3)+4)=0$$ Произведение равно нулю, когда один из множителей равен нулю: $$left [ begin{matrix}x-3=0\ (x+2)(x-3)+4=0end{matrix}right.Leftrightarrow $$$$left [ begin{matrix}x=3\ x^{2}-x-2=0end{matrix}right.Leftrightarrow $$$$left [ begin{matrix}x=3\ x=2\ x=-1end{matrix}right.$$

Задание 22

Двое рабочих могут вместе выполнить 2/3 некоторой работы за 4 дня. За сколько дней каждый рабочий может выполнить всю работу, если один из них может сделать это на 5 дней раньше, чем второй.

Ответ: 10 и 15

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Пусть х — производительность первого в день, y — производительность второго в день. Объем всей работы равен 1. Тогда: $$x+y=frac{frac{2}{3}}{4}=frac{1}{6}$$ (объем работы поделили на количество дней и получили суммарную производительность). Отсюда $$x=frac{1-6y}{6}$$. Пусть первый работает медленнее, тогда $$frac{1}{x}-frac{1}{y}=5$$. Подставим в это уравнение выраженное значение х через у: $$frac{1}{frac{1-6y}{6}}-frac{1}{y}=5 Leftrightarrow$$$$frac{6}{1-6y}-frac{1}{y}=5Leftrightarrow$$$$6y-1+6y=5y-30y^{2}Leftrightarrow$$$$30y^{2}+7y-1=0$$. Отсюда $$y_{1}=frac{1}{10}$$ ; $$y_{2}$$ меньше нуля. Следовательно, время второго $$t=frac{1}{frac{1}{10}}=10$$, тогда время первого на пять дней больше, то есть 15

Задание 23

Постройте график функции $$y=frac{(x-4)(x^{2}-4)}{x^{2}-6x+8}$$ и определите, при каких значениях k построенный график не будет иметь общих точек с прямой у=kx

Ответ: 1 ; 1,5 ; 2

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Найдем область определения заданной функции: $$x^{2}-6x+8 neq 0 Leftrightarrow $$$$x_{1} neq 2 ; 4$$

Преобразуем данную функцию с учетом полученной области определения: $$frac{(x-4)(x^{2}-4)}{x^{2}-6x+8}=$$$$frac{(x-4)(x-2)(x+2)}{(x-4)(x-2)}=x+2$$. То есть график функции $$y=x+2$$ совпадает с графиком начальной функции при наличии области ее определения.

Получаем, что точки (2;4) и (4;6) пустые, следовательно, чтобы прямая y=kx не имела с графиком пересечений, она должна пройти через эти точки. Подставим их координаты в уравнение прямой, чтобы найти k:

$$4=2k Leftrightarrow$$$$k=2$$

$$6=4k Leftrightarrow$$$$k=1,5$$

Так же прямая не будет иметь пересечений, если она будет параллельна графику начальной функции. Две прямые $$y_{1}=k_{1}x+b_{1}$$ и $$y_{2}=k_{2}x+b_{2}$$ параллельны в том случае, если коэффициенты при х у них одинаковы ($$k_{1}=k_{2}$$, а свободные — разные ($$b_{1} neq b_{2}$$). То есть k=1 тоже будет ответом.

Задание 24

Найдите площадь прямоугольного треугольника, если биссектриса прямого угла делит гипотенузу на отрезки длины 15 и 20 см.

Ответ: 294

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

1)$$frac{AC}{CB}=frac{AL}{LB}=frac{3}{4}$$ по свойству биссектрисы. Тогда, пусть AC=3x ; CB=4x

2)Из треугольника ABC по теореме Пифагора: $$AC^{2}+CB^{2}=AB^{2} Leftrightarrow$$$$(3x)^{2}+(4x)^{2}=35^{2}$$. Отсюда x=7. Тогда AC=21 ; CB = 28.

3)$$S_{ABC}=frac{1}{2}AC*CB=frac{1}{2}*21*28=294$$

Задание 25

На стороне BC квадрата ABCD взята точка М. Докажите, что площадь треугольника AМD равна половине площади квадрата.

Ответ:

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

1)Пусть $$MH perp AD$$ , тогда ABMH — прямоугольник и MH=AB

2)$$S_{AMD}=frac{1}{2}AD*MH$$, или $$S_{AMD}=frac{1}{2}AD*AB=frac{1}{2}S_{ABCD}$$

Задание 26

Диагонали вписанного в окружность четырехугольника ABCD пересекаются в точке Е, причем AD·СЕ = DС·АЕ, BD = 6, $$angle ADB = 22,5^{circ}$$. Найдите площадь четырехугольника ABCD

Ответ: $$9sqrt{2}$$

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

1) AD*CE=CD*AE, тогда $$frac{AD}{CD}=frac{AE}{CE} Leftrightarrow$$ DB — биссектриса в треугольнике ADC. Тогда $$angle BDA = angle CDB$$ , но $$angle BDA = angle BCA$$ и $$angle CDB = angle BAC$$ (как вписанные), следовательно $$angle BCA = angle BAC$$ , тогда треугольник ABC — равнобедренный

2)Построим продолжение DС за точка C и отложим из B отрезок BF = DB так, что $$F in DC$$. Тогда треугольник DBF — равнобедренный. Так как AB = BC, DB = BF и из равнобедренности DBF $$angle BDF = angle BFD$$, но и $$angle BDA = angle CDB$$, тогда $$angle BDA=angle BFD$$. $$angle BAD + angle DCB = 180$$ по свойству вписанного четырехугольника, но и $$angle BCF + angle DCB = 180$$ по свойству смежных углов, тогда $$angle BAD = angle BCF$$ и, следовательно, треугольники ABD и BCF равны, следовательно, $$S_{ADF}=S_{ABCD}$$

3)$$angle DBF = 180 — 2*22.5 = 135$$ (из треугольника DBF), $$S_{DBF}=frac{1}{2}DB*DF*sin DBF$$, то есть $$S_{DBF}=0,5*6*6*frac{sqrt{2}}{2}=9sqrt{2}$$

Источник

Понравилась статья? Поделить с друзьями:
  • Тренировочный вариант егэ по истории онлайн
  • Тренировочный вариант егэ математика профиль 144
  • Тренировочный вариант 180 егэ математика
  • Тренировочный вариант егэ по истории 2023 с ответами
  • Тренировочный вариант егэ математика 211011