Ответы на тренировочный вариант №200 профильного ЕГЭ
Задание 1
В лицее 750 учеников, из них 20% − ученики начальных классов. Среди учеников средних и старших классов 20% изучают немецкий язык. Сколько учеников в лицее изучают немецкий язык, если в начальных классах немецкий язык не изучается?
Ответ: 120
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 2
На графике показано изменение температуры воздуха на протяжении трех суток, начиная с 0 часов вторника. На оси абсцисс отмечается время суток в часах, на оси ординат – значение температуры в градусах. Определите по графику наибольшую температуру воздуха в четверг.
Ответ: 18
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 3
Найдите площадь треугольника, изображенного на рисунке.
Ответ: 2,5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 4
Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,8. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,03. Известно, что 70% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
Ответ: 0,569
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 5
Угол при вершине А, противолежащей основанию ВС равнобедренного треугольника АВС, равен 30°. Найдите боковую сторону треугольника, если его площадь равна 81.
Ответ: 18
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 6
На рисунке изображен график функции у = f (х), определенной на интервале (−5; 5). Определите количество целых точек этого интервала, в которых производная функции f (х) положительна.
Ответ: 36
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 7
Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен $$sqrt{3}$$, а высота равна 3.
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 8
Найдите $$f(x)$$, если $$f(x)=(x-frac{9}{x})cdot (frac{1}{x}-9x)$$, где $$xneq 0$$.
Ответ: 0
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 9
Автомобиль, масса которого равна m=1125 кг, начинает двигаться с ускорением, которое в течение t секунд остается неизменным, и проходит за это время путь S = 400 метров. Значение силы (в ньютонах), приложенной в это время к автомобилю, равно $$F=frac{2mS}{t^{2}}$$ . Определите наибольшее время после начала движения автомобиля, за которое он пройдет указанный путь, если известно, что сила $$F$$, приложенная к автомобилю, не меньше 4 кН. Ответ выразите в секундах.
Ответ: 15
Задание 10
Первая труба наполняет бассейн на 9 часов дольше, чем вторая труба наполняет половину бассейна. За какое время наполнит бассейн первая труба, если первая и вторая трубы вместе могут наполнить его за 2 часа 56 минут? Ответ дайте в часах.
Ответ: 11
Задание 11
Найдите точку максимума функции $$f(x)=-frac{x}{x^{2}+196}$$
Ответ: -14
Задание 12
Дано уравнение $$tg 2x+ctg x=8cos^{2}x$$
А) Решите уравнение.
Б) Найдите его корни, принадлежащие отрезку $$[frac{11pi}{2};4pi]$$
Ответ: А)$$frac{pi}{2}+pi k; (-1)^{n}frac{pi}{24}+frac{pi n}{4}, k,n in Z$$ Б)$$frac{73pi}{2};frac{77pi}{24};frac{85pi}{24};frac{89pi}{24}$$
Задание 13
В прямоугольном параллелепипеде $$ABCDA_{1}B_{1}C_{1}D_{1}$$ на ребре $$BB_{1}$$ отмечена точка $$K$$ так, что $$BK:B_{1}K=1:2$$. Через точку $$K$$ параллельно $$(BDA_{1})$$ проведена плоскость $$beta$$.
А) Докажите, что плоскость $$beta$$ пересекает ребро $$CD$$ в такой точке $$M$$, что $$CM=2MD$$.
Б) Найдите площадь сечения параллелепипеда плоскостью $$beta$$, если известно, что $$AB=6$$, $$BC=8$$, $$BB_{1}=12$$.
Ответ: $$frac{52sqrt{29}}{3}$$
Задание 14
Решите неравенство $$frac{1}{3x+6-sqrt{2x^{2}+3x}}geq frac{1}{x+12}$$
Ответ: $$[-3;-2);(-frac{12}{7};-frac{3}{2}];[0;+infty)$$
Задание 15
В треугольнике $$ABC$$ сторона $$AC$$ больше стороны $$BC$$. Биссектриса $$CL$$ пересекает описанную около треугольника $$ABC$$ окружность в точке $$K$$. На стороне $$AC$$ отмечена точка $$P$$ так, что $$angle ALK=angle CLP$$ .
А) Докажите, что точки $$A, P, L, K$$ лежат на одной окружности.
Б) Найдите площадь четырехугольника $$APLK$$, если $$BC=4$$, $$AB=5$$, $$AC=6$$.
Ответ: $$frac{3sqrt{7}}{2}$$
Задание 16
Фонд «Божий Дар» владеет ценными бумагами, которые стоят t2 млн. рублей в конце года t (t=1; 2; 3…). В конце любого года фонд может продать ценные бумаги и положить деньги в банк «Пятёрочка» под 20% годовых. В конце какого года фонд должен продать ценные бумаги, чтобы через 15 лет сумма на его счету была наибольшей? Сколько рублей составит эта сумма?
Ответ: 11 лет ; 250 905 600 руб.
Задание 17
Найдите все значения параметра $$a$$, при каждом из которых уравнение
$$(16x^2-4(a+1)(x^3+x)+a(x^2+1)^2)cdot((a-1)x^{2}+2x+a+1)=0$$
имеет ровно четыре корня.
Ответ: $$frac{1}{2};frac{2}{3};2;(-2;0]$$
Задание 18
а) Можно ли число 2016 представить в виде суммы шести последовательных нечётных натуральных чисел?
б) Можно ли число 2016 представить в виде суммы шести последовательных чётных натуральных чисел?
в) Представьте число 2016 в виде суммы наибольшего количества последовательных чётных натуральных чисел.
Ответ: А)да, $$331+333+335+337+339+341$$ Б)нет В)$$32+34+36+…+92+94$$
А. Ларин: Тренировочный вариант № 200.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
В треугольнике ABC сторона AC больше стороны BC. Биссектриса CL пересекает описанную около треугольника ABC окружность в точке K. На стороне AC отмечена точка P так, что
а) Докажите, что точки A, P, L, K лежат на одной окружности.
б) Найдите площадь четырехугольника APLK, если
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
Фонд «Божий Дар» владеет ценными бумагами, которые стоят t2 млн рублей в конце года В конце любого года фонд может продать ценные бумаги и положить деньги в банк «Пятёрочка» под 20% годовых. В конце какого года фонд должен продать ценные бумаги, чтобы через 15 лет сумма на его счету была наибольшей? Сколько рублей составит эта сумма?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра а, при каждом из которых уравнение
имеет ровно четыре корня.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
а) Можно ли число 2016 представить в виде суммы шести последовательных нечётных натуральных чисел?
б) Можно ли число 2016 представить в виде суммы шести последовательных чётных натуральных чисел?
в) Представьте число 2016 в виде суммы наибольшего количества последовательных чётных натуральных чисел.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Регистрация Форум Текущее время: 12 мар 2023, 22:12 Сообщения без ответов | Активные темы Страница 1 из 20 [ Сообщений: 194 ] На страницу 1, 2, 3, 4, 5 … 20 След. Начать новую тему»> Ответить Тренировочный вариант №200
Тренировочный вариант №200
Страница 1 из 20 [ Сообщений: 194 ] На страницу 1, 2, 3, 4, 5 … 20 След. Текущее время: 12 мар 2023, 22:12 | Часовой пояс: UTC + 3 часа Удалить cookies форума | Наша команда | Вернуться наверх Кто сейчас на форуме
|
31 мая 2017
В закладки
Обсудить
Жалоба
Разбор тренировочного варианта по математике
Решение заданий тренировочного варианта №200 от Александра Ларина.
Сам вариант: trvar200.pdf
Contents
- 1 Задание №1. Решение варианта №200 ОГЭ по математике Ларин
- 1.1 Решение
- 2 Задание №2. Решение варианта №200 ОГЭ по математике Ларин
- 2.1 Решение
- 3 Задание №3
- 3.1 Решение
- 4 Задание №4
- 4.1 Решение
- 5 Задание №5
- 5.1 Решение
- 6 Задание №6
- 6.1 Решение
- 7 Задание №7. Решение варианта №200 ОГЭ по математике Ларин
- 7.1 Решение
- 8 Задание №8
- 8.1 Решение
- 9 Задание №9. Решение варианта №200 ОГЭ по математике Ларин
- 9.1 Решение
- 10 Задание №10. Решение варианта №200 ОГЭ по математике Ларин
- 10.1 Решение
- 11 Задание №11. Решение варианта №200 ОГЭ по математике Ларин
- 11.1 Решение
- 12 Задание №12
- 12.1 Решение
- 13 Задание №13
- 13.1 Решение
- 14 Задание №14
- 14.1 Решение
- 15 Задание №15. Решение варианта №200 ОГЭ по математике. Ларин
- 15.1 Решение
- 16 Задание №16
- 16.1 Решение
- 17 Задание №17
- 17.1 Решение
- 18 Задание №18
- 18.1 Решение
- 19 Задание №19
- 19.1 Решение
- 20 Задание №20. Решение варианта №200 ОГЭ по математике. Ларин
- 20.1 Решение
- 21 Задание №21
- 21.1 Решение
- 22 Задание №22
- 22.1 Решение
- 23 Задание №23
- 23.1 Решение
- 24 Задание №24
- 24.1 Решение
- 25 Задание №25
- 25.1 Решение
- 25.2
- 26 Задание №26. Решение варианта №200 ОГЭ по математике. Ларин
- 26.1 Решение
- 26.2
- 27 Видео: Решение Варианта ОГЭ Ларина №200 (№1-20)
- 28 Видео: Решение Варианта ОГЭ Ларина №200 (№21-26)
Найдите значение выражения:
Решение
Ответ: -0,15625.
Задание №2. Решение варианта №200 ОГЭ по математике Ларин
В таблице приведены нормативы по прыжкам с места для учеников 11 класса.
| Мальчики | Девочки | |||||
| Отметка | «5» | «4» | «3» | «5» | «4» | «3» |
| Расстояние, см | 230 | 220 | 200 | 185 | 170 | 155 |
Какую оценку получит девочка, прыгнувшая на 177 см?
Решение
177 см больше 170 см, но меньше 185 см, следовательно, оценка будет 4
Ответ: 4.
Задание №3
Известно, что число m отрицательное. На каком из рисунков точки с координатами 0, m, 2m, m2 расположены на координатной прямой в правильном порядке?
Решение
Пусть m = -2,
тогда 2m = -4;
m² = 4.
Следовательно, в порядке возрастания 2m; m; 0; , что соответствует 3 варианту ответа.
Ответ: 3.
Задание №4
Какое из данных чисел:
√ является рациональным?
Варианты ответа:
- ни одного.
Решение
Следовательно, 3 вариант ответа.
Ответ: 3.
Задание №5
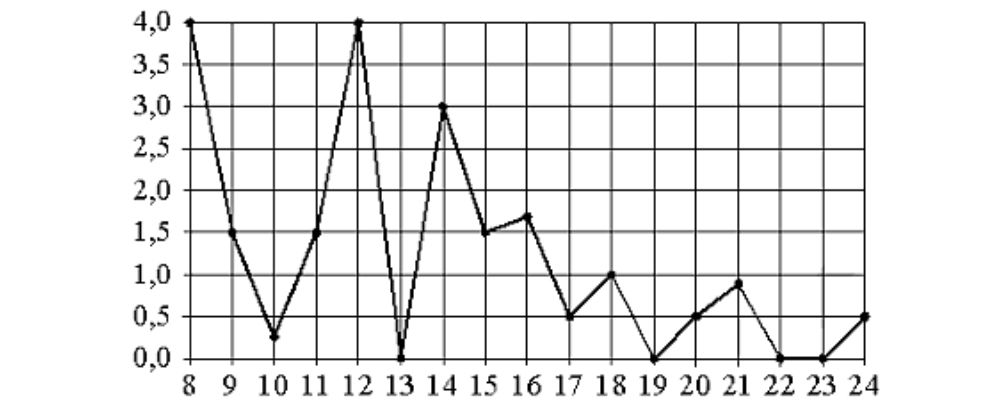
На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2015 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа в Томске выпало ровно 1 миллиметр осадков.
Решение
1 мл выпал 18 числа
Задание №6
Решите уравнение:
Решение
Ответ: -2
Задание №7. Решение варианта №200 ОГЭ по математике Ларин
Катя прочитала 85 страниц книги, после чего ей осталось прочитать еще 60 страниц. Сколько страниц в книге?
Решение
В книге всего:
Ответ 145.
Задание №8
На диаграмме показан возрастной состав населения России.
Определите по диаграмме, какая из возрастных категорий самая малочисленная. Варианты ответа:
- 1) 0 — 14 лет.
- 2) 15 — 50 лет.
- 3) 51 — 64 лет.
- 4) 65 лет и более.
Решение
Самый маленький сегмент составляет 65 лет и более, что соответствует 4 варианту ответа.
Ответ: 4.
Задание №9. Решение варианта №200 ОГЭ по математике Ларин
В каждом двадцать пятом пакете сока согласно условиям акции под крышкой есть приз. Призы распределены случайно. Маша покупает пакет сока. Найдите вероятность того, что Маша не найдёт приз в своём пакете.
Решение
Ответ 0.96.
Задание №10. Решение варианта №200 ОГЭ по математике Ларин
На рисунке изображён график функции у = ax2+bx+c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
УТВЕРЖДЕНИЯ
- А)Функция возрастает на промежутке.
- Б) Функция убывает на промежутке.
ПРОМЕЖУТКИ
- 1) [-3;3]
- 2) [0;3]
- 3) [-3;-1]
- 4) [-3;0]
Решение
Функция возрастает , что соответствует 2 варианту , убывает на , что соответствует 3 варианту.
Ответ: 2, 3.
Задание №11. Решение варианта №200 ОГЭ по математике Ларин
Дана геометрическая прогрессия 12, 48, 192, … Какое число стоит в этой последовательности на 6-м месте?
Решение
Ответ 12288.
Задание №12
Найдите значение выражения:
при
, b = √
Решение
Ответ: -95.
Задание №13
Из формулы радиуса окружности:
r = (a*b)/(a + b + c),
вписанной в прямоугольный треугольник, выразите и вычислите катет a, если катет b=7,2, гипотенуза c=7,8 и радиус вписанной окружности r=1,2.
Решение
Ответ: 3.
Задание №14
На каком рисунке изображено множество решений неравенства 13 — 3x ≥ 6 — x?
Решение
2 вариант.
Ответ: 2.
Задание №15. Решение варианта №200 ОГЭ по математике. Ларин
Пол комнаты, имеющей форму прямоугольника со сторонами 6 м и 7 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 25 см. Сколько потребуется таких дощечек?
Решение
Задание №16
Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла В треугольника ABC, если угол AOС равен 140. Ответ дайте в градусах .
Решение
(свойство вписанного угла).
ABC = ½*140 = 70.
Ответ: 70.
Задание №17
Сторона ромба равна 17, а диагональ равна 16. Найдите площадь ромба.
Решение
Ответ 240.
Задание №18
В треугольнике ABC AC= √5 , BC=√11 , угол C равен 90º. Найдите радиус окружности, описанной около этого треугольника.
Решение
Радиус описанной окружности около прямоугольного треугольника равен половине его гипотенузы:
R = ½
Ответ: 2.
Задание №19
Найдите угол ABC. Ответ дайте в градусах.
Решение
Ответ 67.5.
Задание №20. Решение варианта №200 ОГЭ по математике. Ларин
Какие из следующих утверждений верны?
- 1. Если диагонали четырёхугольника делят его углы пополам, то этот четырёхугольник — ромб.
- 2. Центром окружности, описанной около треугольника, является точка пересечения его высот.
- 3. Треугольник, стороны которого равны 7, 24, 25 является прямоугольным.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
Решение
- да.
- нет — серединных перпендикуляров.
- да (выполняется теорема Пифагора).
Ответ: 3.
Задание №21
Решите систему уравнений:
Решение
Ответ: (1;2); (2;1).
Задание №22
Мастеру на выполнение заказа потребуется на 5 дней меньше, чем его ученику, но при совместной работе они выполнят заказ на 4 дня быстрее, чем мастер, работающий в одиночку. За сколько дней выполнит заказ мастер, работая в одиночку?
Решение
Пусть x-производительность мастера в день, y-ученика , 1-объем работы . Тогда:
Ответ: 10.
Задание №23
Постройте график функции и найдите все значения k, при которых прямая у = kх имеет с графиком данной функции ровно одну общую точку.
Решение
Рассмотрим раскрытие модулей:
Построим график данной функции:
Одна точка пересечения у графика будет в случае:
Ответ:
Задание №24
В прямоугольной трапеции с острым углом 45, большая боковая сторона равна 16√2см, а меньшая диагональ равна 20см. Найдите площадь трапеции.
Решение
Ответ: 320
Задание №25
Докажите, что сумма квадратов медиан прямоугольного треугольника в 1,5 раза больше квадрата гипотенузы.
Решение
Задание №26. Решение варианта №200 ОГЭ по математике. Ларин
Диагонали с длинами √7 и 4 делят четырёхугольник на части, площади которых образуют арифметическую прогрессию. Найдите площадь четырёхугольника, зная, что угол между большей диагональю и меньшей из сторон равен 30.
Решение
Ответ: √3.





 Для печати
Для печати
 Предыдущая тема | Следующая тема
Предыдущая тема | Следующая тема