А. Ларин. Тренировочный вариант № 331. (часть C).
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие промежутку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
Точка M середина ребра AB правильного тетраэдра DABC.
а) Докажите, что ортогональная проекция точки M на плоскость ACD лежит на медиане AP грани ACD.
б) Найдите угол между прямой DM и плоскостью ACD.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
В треугольнике ABC AB = 3, Хорда KN окружности, описанной около треугольника ABC, пересекает отрезки AC и BC в точках M и L соответственно. Известно, что
площадь четырёхугольника ABLM равна 2, LM = 1.
а) Докажите, что треугольник KNC равнобедренный.
б) Найдите площадь треугольника KNC.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
Первичная информация разделяется по серверам 1 и 2 и обрабатывается на них. С сервера 1 при объёме t2 Гбайт входящей в него информации выходит 30t Гбайт, а с сервера 2 при объёме t2 Гбайт входящей в него информации выходит 36t Гбайт обработанной информации при условии, что Каков наибольший общий объём выходящей информации при общем объёме входящей информации в 3904 Гбайт?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите наименьшее целое значение параметра а, при котором уравнение
имеет ровно четыре корня.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
На психологический тренинг пришли m человек. В начале работы психолог попросил каждого пришедшего написать записку с вопросом к любому одному из других участников. После этого в группу А были отобраны те, кто получил не более 1 вопроса.
а) Какое наибольшее число участников могло оказаться в группе А, если m = 100?
б) Какое наименьшее число участников могло оказаться в группе А, если m = 144?
в) Какое наименьшее число участников могло оказаться в группе А, если m = 97, а в группу А вошли те, кто не получил ни одного вопроса, и половина тех, кто получил ровно один вопрос? (Если ровно один вопрос получило нечетное число человек, то берется наибольшее число, не превосходящее половину.)
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Решение и ответы заданий № 1–12 варианта №331 Александра Ларина. Разбор ЕГЭ 2021 по математике (профильный уровень).
Задание 1.
В ящике с шоколадками шоколадок содержит орехи, а
изюм. Сколько процентов шоколадок содержит и орехи, и изюм, если каждая шоколадка содержит хотя бы одну из добавок?
Задание 2.
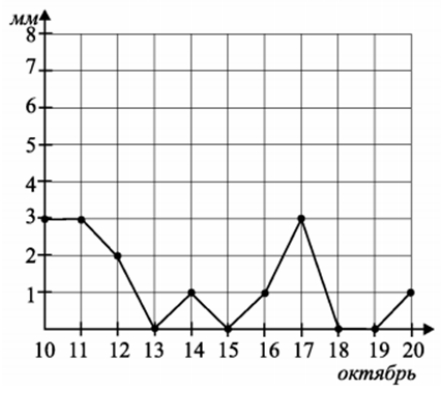
На рисунке показано суточное количество осадков, выпадавших с 10 по 20 октября. По горизонтали указываются числа месяца, по вертикали – количество осадков в миллиметрах, выпавших в соответствующий день. Для наглядности точки на рисунке соединены линией. Определите по рисунку, сколько дней указанного периода не было осадков.
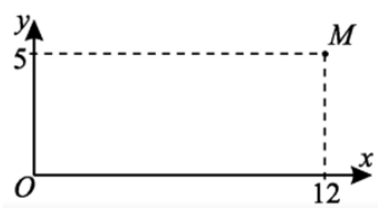
Задание 3.
Окружность с центром в начале координат проходит через точку М(12;5). Найдите ее радиус.
Задание 4.
В магазине на полке стоят DVD‐диски с фильмами, среди которых 130 детективов, 160 боевиков, 92 фильма в жанре «вестерн» и 218 мелодрам. Какова вероятность, что взятый наугад диск будет содержать либо боевик, либо фильм в жанре «вестерн»?
Задание 5.
Решить уравнение: Если уравнение имеет более одного корня, то в ответе запишите наибольший из корней.
Задание 6.
В параллелограмме ABCD диагональ BD перпендикулярна AD, а угол A равен 60º. Найдите сторону AD, если площадь параллелограмма равна 16√3.
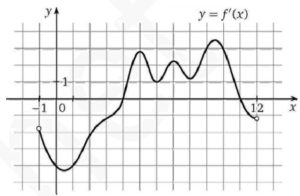
Задание 7.
На рисунке изображен график функции y = f′(x), где f′(x) производная функции y = f(x), определенной на интервале (–1;12) . Значение какой из сумм:
будет наименьшим? В ответе укажите номер этой суммы.
Задание 8.
Радиус основания цилиндра равен 5, а высота равна 8. Отрезки AB и CD диаметры одного из оснований цилиндра, а отрезок AA1 его образующая. Найдите косинус угла между прямыми A1C и BD, если синус угла CAB равен 0,8.
Задание 9.
Вычислите |sin 15º| + |sin 15º – 5|
Задание 10.
Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f = 80 см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 70 до 120 см, а расстояние d2 от линзы до экрана – в пределах от 300 до 400 см. Изображение на экране будет четким, если выполнено соотношение . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы ее изображение на экране было чётким. Ответ выразите в сантиметрах.
Задание 11.
Из пункта A в пункт B, расположенный в 24 км от A, одновременно отправились велосипедист и пешеход. Велосипедист прибыл в B на 4 ч раньше пешехода. Если бы велосипедист ехал со скоростью, меньшей на 4 км/ч, то на путь из A в B он затратил бы вдвое меньше времени, чем пешеход. Найдите скорость пешехода.
Задание 12.
Найдите наименьшее значение функции 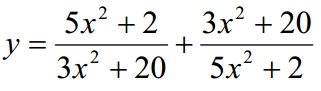
Источник варианта: alexlarin.net
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 0 / 5. Количество оценок: 0
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
| 2626 | Найдите наименьшее целое значение параметра а, при котором уравнение abs((7-abs(x))/(abs(x)-2))=a. имеет ровно четыре корня |
Найдите наименьшее целое значение параметра а, при котором уравнение abs((7-abs(x)) / (abs(x)-2))= a имеет ровно четыре корня ! Тренировочный вариант 331 от Ларина Задание 18 # Два способа решения. 1 Решение — Кирилла Колокольцева. 2 Решение — Елены Ильиничны Хажинской | |
| 2619 | а) Решите уравнение sin(3x)cos(4x)=1 б) Укажите корни этого уравнения, принадлежащие промежутку (-pi/2; (7pi)/2]. |
Решите уравнение sin 3x cos 4x =1 ! Тренировочный вариант 331 от Ларина Задание 13 ЕГЭ | |
| 2618 | Точка M середина ребра AB правильного тетраэдра DABC. а) Докажите, что ортогональная проекция точки M на плоскость ACD лежит на медиане AP грани ACD. б) Найдите угол между прямой DM и плоскостью ACD |
Точка M середина ребра AB правильного тетраэдра DABC ! Тренировочный вариант 331 от Ларина Задание 14 | |
| 2617 | Решите неравенство (2(log_{x-2}((x^2-4x+4)/(10-3x)))^2)/(4-2log_{x-2}(16x-20-3x^2)-log_{x-2}(9x^2-60x+100)) <=3. |
Тренировочный вариант 331 от Ларина Задание 15 | |
| 2616 | В треугольнике АВС АВ=3, /_ACB=arcsin(3/5). Хорда KN окружности, описанной около треугольника АВС, пересекает отрезки АС и ВC в точках M и L соответственно. Известно, что /_ABC=/_CML, площадь четырехугольника ABLM равна 2, а LM=1. a) Докажите, что треугольник KNC равнобедренный. б) Найдите площадь треугольника KNC |
В треугольнике АВС АВ=3 ! Тренировочный вариант 331 от Ларина Задание 16 #Задача-аналог 1489 | |
| Clear |
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №331
|
||||
|
http://alexlarin.net/ege/2021/trvar331.html |
|||
  |
||||
|
|
||||
|
Kirill Kolokolcev |
Заголовок сообщения: Re: Тренировочный вариант №331
|
|||
|
Спасибо за интересный вариант! Подробности: 17 Подробности: 18 Подробности: Последний раз редактировалось Kirill Kolokolcev 14 ноя 2020, 18:16, всего редактировалось 1 раз. |
|||
  |
||||
|
khazh |
Заголовок сообщения: Re: Тренировочный вариант №331
|
|||
|
Ответ к №18 не соответствует заданию. |
|||
  |
||||
|
Kirill Kolokolcev |
Заголовок сообщения: Re: Тренировочный вариант №331
|
|||
|
khazh писал(а): Ответ к №18 не соответствует заданию. Елена Ильинична, спасибо! Прочитал «найдите все значения `a`, при которых система имеет 4 решения» Подробности: |
|||
  |
||||
|
Kirill Kolokolcev |
Заголовок сообщения: Re: Тренировочный вариант №331
|
|||
|
19 Подробности: |
|||
  |
||||
|
Raisa |
Заголовок сообщения: Re: Тренировочный вариант №331
|
|||
|
В 16, 18 так же, в 14-м sqrt(7)/3? |
|||
  |
||||
|
hpbhpb |
Заголовок сообщения: Re: Тренировочный вариант №331
|
|||
|
Raisa писал(а): В 16, 18 так же, в 14-мsqrt(7)/3? Здравствуйте, Раиса Трофимовна! Да, `arccos((sqrt(7))/(3))`. |
|||
  |
||||
|
JUTA |
Заголовок сообщения: Re: Тренировочный вариант №331
|
|||
|
Kirill Kolokolcev писал(а): 17 Подробности: В 17 такой же ответ. |
|||
  |
||||
|
An_na |
Заголовок сообщения: Re: Тренировочный вариант №331
|
|||
|
13 Подробности: 15 Подробности: |
|||
  |
||||
|
netka |
Заголовок сообщения: Re: Тренировочный вариант №331
|
|||
|
An_na писал(а): 13; 15 такие же ответы |
|||
  |
||||
| Показать сообщения за: Сортировать по: |
Кто сейчас на форуме
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 1 |
|
Вы не можете начинать темы |
|
|
На чтение 1 мин Просмотров 2 Опубликовано 5 марта, 2023
Решение варианта Ларина №331 ЕГЭ Решение и ответы на задачи на официальном сайте источника онлайн.
Решение и ответы заданий № 1–12 варианта №331 Александра Ларина. Разбор ЕГЭ 2021 по математике (профильный уровень).
Варианты ответов и решение задачи ТУТ: https://ege314.ru/ege-varianty-larina/reshenie-varianta-larina-331-ege/
Ответы и решение задачи онлайн
Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.
Тренировочный вариант №331 Алекса Ларина ОГЭ 2023 по математике 9 класс с ответами и решением, который вышел на сайте 5 октября 2022 года, по новой демоверсии ОГЭ 2023 года ФИПИ.
Скачать 2 варианта с ответами
Пробный вариант ОГЭ 2023 состоит из двух модулей: «Алгебра» и «Геометрия». Всего в работе 25 заданий. Модуль «Алгебра» содержит семнадцать заданий: в части 1 — четырнадцать заданий; в части 2 — три задания. Модуль «Геометрия» содержит восемь заданий: в части 1 — пять заданий; в части 2 — три задания.
Тренировочный вариант 331 Ларина ОГЭ 2023 по математике 9 класс
вариант-331-ларин-огэ2023
Задания и ответы
На графике (см. выше) точками изображено количество минут, потраченных на исходящие вызовы, и количество гигабайтов мобильного интернета, израсходованных абонентом в процессе пользования смартфоном, за каждый месяц 2018 года. Для удобства точки, соответствующие минутам и гигабайтам, соединены сплошными и пунктирными линиями соответственно.
В течение года абонент пользовался тарифом «Стандартный», абонентская плата по которому составляет 400 рублей в месяц. При условии нахождения абонента на территории РФ в абонентскую плату тарифа «Стандартный» входит: – пакет минут, включающий 350 минут исходящих вызовов на номера, зарегистрированные на территории РФ;
- – пакет интернета, включающий 2,8 гигабайта мобильного интернета;
- – пакет SMS, включающий 150 SMS в месяц;
- – безлимитные бесплатные входящие вызовы.
Стоимость минут, интернета и SMS сверх пакета указана в таблице (см. ниже). Абонент не пользовался услугами связи в роуминге и не звонил на номера, зарегистрированные за рубежом. За весь год абонент отправил 140 SMS.
1.Определите, какие месяцы соответствуют указанному в таблице количеству израсходованных минут. Заполните таблицу. В ответе запишите последовательность четырёх чисел без пробелов, запятых и других разделительных символов.
Ответ: 5624
2.Сколько рублей потратил абонент на услуги связи в ноябре?
Ответ: 565
3.Сколько месяцев в 2018 году абонент превышал лимит по пакету мобильного интернета?
Ответ: 4
4.Сколько месяцев в 2018 году абонент превышал лимит либо по пакету минут, либо по пакету мобильного интернета?
Ответ: 5
5.В конце 2018 года оператор связи предложил абоненту перейти на новый тариф. Его условия приведены в таблице.
Ответ: 400
10.В среднем из каждых 70 поступивших в продажу аккумуляторов 61 аккумулятор заряжен. Найдите вероятность того, что купленный аккумулятор не заряжен. Результат округлите до тысячных.
Ответ: 0,129
14.Рихарду необходимо разобрать 315 квадратных уравнений. Ежедневно он разбирает на одно и то же количество уравнений больше по сравнению с предыдущим днём. Известно, что за первый день Рихард разобрал 11 квадратных уравнений, а справился со всеми он за 9 дней. Сколько уравнений Рихард разберёт в последний день?
Ответ: 59
21.На изготовление 231 детали ученик тратит на 11 часов больше, чем мастер на изготовление 462 таких же деталей. Известно, что ученик за час делает на 4 детали меньше, чем мастер. Сколько деталей в час делает ученик?
Ответ: 3
24.Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.
25.Через середину AC 56 . K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P . Найдите отношении площади треугольника е ABC к площади четырёхугольника KPCM .
Ответ: 2,4
Варианты в формате ОГЭ 2023 по математике 9 класс



 ?
?