Тренировочный вариант №361 Алекса Ларина ЕГЭ 2022 по математике профильный уровень 11 класс с ответами и решением по новой демоверсии ЕГЭ 2022 года для подготовки к экзамену, дата выхода варианта: 25.09.2021 (25 сентября 2021 года)
Тренировочный вариант №361 ЕГЭ 2022: скачать (ответы)
Решать тренировочный вариант Ларина №361 ЕГЭ 2022 по математике:
Ответы:
Сложные задания и ответы с варианта:
2)В коробке 10 синих, 9 красных и 6 зеленых фломастеров. Случайным образом выбирают 2 фломастера. Какова вероятность того, что окажутся выбраны один синий и один красный фломастер?
Ответ: 0,3
3)На сторонах AB и BC треугольника ABC выбраны соответственно точки M и Q, а на стороне AC —точки P, K, N (именно в таком порядке, считая от A) таким образом, что MN || BC, PQ || AB и KB проходит через точку пересечения MN и PQ. Известно, что AP =4, PK =5 и KN =6. Найдите NC.
Ответ: 4,8
5)Объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен 25. Найдите объём куба.
Ответ: 200
8)Из пункта А круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через полчаса после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
Ответ: 80
10)При подозрении на наличие некоторого заболевания пациента отправляют на ПЦР‐тест. Если заболевание действительно есть, то тест подтверждает его в 86 % случаев. Если заболевания нет, то тест выявляет отсутствие заболевания в среднем в 94% случаев. Известно, что в среднем тест оказывается положительным у 10% пациентов, направленных на тестирование. При обследовании некоторого пациента врач направил его на ПЦР‐тест, который оказался положительным. Какова вероятность того, что пациент действительно имеет это заболевание?
Ответ: 0,43
13)В правильной треугольной пирамиде МАВС с основанием АВС стороны основания равны 6, а боковые ребра равны 5. На ребре АС находится точка D, на ребре АВ находится точка Е, а на ребре АМ – точка L. Известно, что AD=AE=AL=4. А) Докажите, что отрезок DE содержит центр основания пирамиды Б) Найдите угол между плоскостью основания и плоскостью, проходящей через точки E, D и L.
15)Вкладчик разместил в банке 32 тысячи рублей. Несколько лет он получал то 5%, то 10% годовых, а за последний год получил 25% годовых. При этом проценты начислялись в конце каждого года и добавлялись к сумме вклада. В результате его вклад стал равным 53 361 рублю. Сколько лет пролежал вклад?
Ответ: 5
16)Дан треугольник АВС со сторонами АВ=4, ВС=5 и АС=6. А) Докажите, что прямая, проходящая через точку пересечения медиан и центр вписанной окружности, параллельна стороне ВС. Б) Найдите длину биссектрисы треугольника АВС, проведенной из вершины А.
18)Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 16 произвольно делят на три группы так, чтобы в каждой группе было хотя бы одно число. Затем вычисляют значение среднего арифметического чисел в каждой из групп (для группы из единственного числа среднее арифметическое равно этому числу). А) Могут ли быть одинаковыми два из этих трех значений средних арифметических в группах из разного количества чисел? Б) Могут ли быть одинаковыми все три значения средних арифметических? В) Найдите наименьшее возможное значение наибольшего из получаемых трех средних арифметических.
Видео разбор варианта
Смотрите также другие варианты ЕГЭ 2022 Ларина:
Тренировочный вариант Ларина №360 ЕГЭ 2022 по математике с ответами
Тренировочный вариант Ларина №359 ЕГЭ 2022 по математике с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Задание 1
Решите уравнение $$sqrt{x^2+6x+8}=sqrt{x+2}$$. Если уравнение имеет более одного корня, в ответе запишите меньший из них.
Ответ: -2
Скрыть
ОДЗ:
$$x+2geq0$$ (можно написать и на первое ОДЗ, но это будет лишним)
Возводим все в квадрат.
$$x^2+6x+8=x+2$$
$$x^2+5x+6=0$$
$$x=−3$$ – не подходит под ОДЗ
$$x=−2$$
Задание 2
В коробке 10 синих, 9 красных и 6 зеленых фломастеров. Случайным образом выбирают 2 фломастера. Какова вероятность того, что окажутся выбраны один синий и один красный фломастер?
Ответ: 0,3
Скрыть
Всего два возможных благоприятных событий ($$A$$) – в первый раз достали красный ($$A_1$$), потом синий и наоборот ($$A_2$$). (эти события несовместные!)
$$P(A_1)=frac{9}{25}cdotfrac{10}{24}$$
$$P(A_2)=frac{10}{25}cdotfrac{9}{24}$$
$$P(A)=P(A_1+A_2)=P(A_1)+P(A_2)=0,3$$
Задание 3
На сторонах AB и BC треугольника ABC выбраны соответственно точки M и Q, а на стороне AC — точки P, K, N (именно в таком порядке, считая от A) таким образом, что MN || BC, PQ || AB и KB проходит через точку пересечения MN и PQ. Известно, что AP = 4, PK = 5 и KN = 6. Найдите NC.
Ответ: 4,8
Скрыть
Параллельные прямые делят стороны угла на пропорциональные отрезки, значит
$$frac{AP}{PK}=frac{BO}{OK}$$ и $$frac{KN}{NC}=frac{OK}{BO}$$
Запишем
$$frac{KN}{NC}=frac{5}{4}=frac{6}{NC}$$
$$NC=4,8$$
Задание 4
Найдите значение выражения $$-frac{22}{cos^2 34^{circ}cos^2 124^{circ}}$$
Ответ: -22
Скрыть
$$cos^2 124^{circ}=cos^2(90^{circ}+34^{circ})=sin^2 34^{circ}$$
$$-frac{22}{cos^2 34^{circ}+sin^2 34^{circ}}=-frac{22}{1}=-22$$
Задание 5
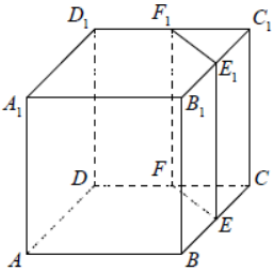
Объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен 25. Найдите объём куба.
Ответ: 200
Скрыть
Пусть ребро куба $$a$$, тогда
$$V_{F_1C_1E_1FCE}=hcdot S_{осн}=C_1Ccdot S_{C_1F_1E_1}=acdot0,5cdotfrac{a}{2}cdotfrac{a}{2}=25$$
$$a^3=25cdot8=200$$
$$V_{куб}=a^3=200$$
Задание 6
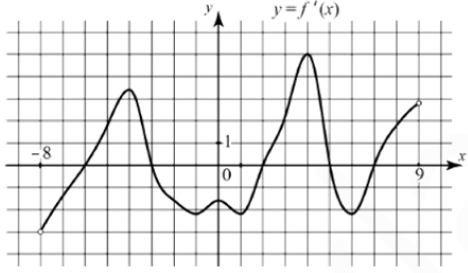
На рисунке изображён график производной $$y=f'(x)$$ функции $$f(x)$$, определённой на интервале $$(-8; 9)$$. Найдите количество точек минимума функции $$f(x)$$, принадлежащих отрезку $$[-2; 8]$$.
Ответ: 2
Скрыть
Точка минимума (неформально) – где функция меняет знак с “-“ (убывает) на “+” (возрастает).
Таких точек на отрезке [-2;8] – 2
Задание 7
Автомобиль, движущийся в начальный момент времени со скоростью $$v_0 = 17$$ м/с, начал торможение с постоянным ускорением $$a = 2$$ м/с2. За $$t$$ секунд после начала торможения он прошёл путь $$S=v_0t-frac{at^2}{2}$$ (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 60 метров. Ответ выразите в секундах.
Ответ: 5
Скрыть
$$17t−t^2=60$$
$$t=5$$ – через это время автомобиль проедет 60 метров
$$t=12$$ – через это время автомобиль остановится, поедет назад и снова пересечет ту же точку
Задание 8
Из пункта А круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через полчаса после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
Ответ: 80
Скрыть
Составляем два уравнения:
$$t_1=frac{1}{6}$$ ч
$$t=0,5$$ ч
$$V_мcdot t_1−V_вcdot t_1=V_вcdot t$$
$$V_м−V_в=3V_в$$
$$V_м=4V_в$$
Составляем второе уравнение, нам известно что “еще через 30 минут после этого догнал его во второй раз”
$$0,5V_м−0,5V_в=30$$
$$V_в=V_м−60$$
вспоминаем первое уравнение
$$V_в=4V_в−60$$
$$V_в=20$$
значит $$V_м=80$$
Задание 9
На рисунке изображен график функции $$f(x) = frac{kx+a}{x+b}$$. Найдите $$k$$.
Ответ: 1
Скрыть
График проходит через (1;2); (-3;6) и (-5;-4).
Получим:
$$left{begin{matrix} 2=frac{k+a}{1+b}\ 6=frac{-3k+a}{-3+b}\ -4=frac{-5k+a}{-5+b} end{matrix}right.Leftrightarrowleft{begin{matrix} 2+2b=k+a\ -18+6b=-3k+a\ 20-4b=-5k+a end{matrix}right.Leftrightarrowleft{begin{matrix} a=2b+2-k\ -18+6b=-3k+2b+2-k\ 20-4b=-5k+2b+2-k end{matrix}right.Leftrightarrow$$
$$Leftrightarrowleft{begin{matrix} a=2b+2-k\ b=-k+5\ b=k+3 end{matrix}right.Leftrightarrowleft{begin{matrix} a=9\ b=4\ k=1 end{matrix}right.$$
Задание 10
При подозрении на наличие некоторого заболевания пациента отправляют на ПЦР-тест. Если заболевание действительно есть, то тест подтверждает его в 86 % случаев. Если заболевания нет, то тест выявляет отсутствие заболевания в среднем в 94% случаев.
Известно, что в среднем тест оказывается положительным у 10% пациентов, направленных на тестирование. При обследовании некоторого пациента врач направил его на ПЦР-тест, который оказался положительным. Какова вероятность того, что пациент действительно имеет это заболевание?
Ответ: 0,43
Скрыть
Пусть $$P(A)=x$$ – вероятность, что человек болен
Пусть $$P(C)$$ – тест положительный
$$P(B_1)$$ – тест положительный, если человек болен
$$P(B_2)$$ – тест положительный, если человек не болен
Пусть $$P(C)$$ – вероятность, что тест положительный
$$P(C)=P(B_1)+P(B_2)=xcdot0,86+(1−x)cdot(1−0,94)=0,1$$
Откуда $$x=0,05$$
Нам нужно найти условную вероятность, что человек болен и получил положительный тест
По формуле Байеса
$$P_{иск}=P(A|C)=frac{P(C|A)cdot P(A)}{P(C)}=frac{0,86cdot0,05}{0,1}=0,43$$
Задание 11
Найдите наибольшее значение функции $$y = 15 + 12x -x^3$$ на отрезке $$[-2;2]$$
Ответ: 31
Скрыть
$$y’=12−3x^2$$
Найдем критические точки $$y’=0$$
$$x^2=4$$
$$x=−2$$ – точка min
$$x=2$$ – точка max
$$y(2)=31$$
Задание 12
А) Решите уравнение $$(frac{4}{9})^{cos x}+2cdot(frac{2}{3})^{cos x}-3=0$$
Б) Найдите все корни уравнения, принадлежащие отрезку $$[pi;4pi]$$
Ответ: А)$$frac{pi}{2}+pi n,nin Z$$ Б)$$frac{3pi}{2};frac{5pi}{2};frac{7pi}{2}$$
Задание 13
В правильной треугольной пирамиде МАВС с основанием АВС стороны основания равны 6, а боковые ребра равны 5. На ребре АС находится точка D, на ребре АВ находится точка Е, а на ребре АМ — точка L. Известно, что AD=AE=AL=4.
А) Докажите, что отрезок DE содержит центр основания пирамиды
Б) Найдите угол между плоскостью основания и плоскостью, проходящей через точки E, D и L.
Ответ: $$arctgfrac{2sqrt{39}}{3}$$
Задание 14
Решите неравенство: $$frac{sqrt{x^2-2x}-sqrt{x^2-5x+6}}{x^2-3x-4}leq0$$
Ответ: $$(-infty;-1),left{2right},[3;4)$$
Задание 15
Вкладчик разместил в банке 32 тысячи рублей. Несколько лет он получал то 5%, то 10% годовых, а за последний год получил 25% годовых. При этом проценты начислялись в конце каждого года и добавлялись к сумме вклада. В результате его вклад стал равным 53 361 рублю. Сколько лет пролежал вклад?
Ответ: 5
Задание 16
Дан треугольник АВС со сторонами АВ=4, ВС=5 и АС=6.
А) Докажите, что прямая, проходящая через точку пересечения медиан и центр вписанной окружности, параллельна стороне ВС.
Б) Найдите длину биссектрисы треугольника АВС, проведенной из вершины А.
Ответ: $$3sqrt{2}$$
Задание 17
Найдите все значения параметра $$a$$, при каждом из которых система
$$left{begin{matrix}
|x^2-5x+4|-9x^2-5x+4+10x|x|=0\
x^2-2(a-1)x+a(a-2)=0
end{matrix}right.$$
имеет единственное решение.
Ответ: $$left{-1right},(1;3),(4;6]$$
Задание 18
Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 16 произвольно делят на три группы так, чтобы в каждой группе было хотя бы одно число. Затем вычисляют значение среднего арифметического чисел в каждой из групп (для группы из единственного числа среднее арифметическое равно этому числу).
А) Могут ли быть одинаковыми два из этих трех значений средних арифметических в группах из разного количества чисел?
Б) Могут ли быть одинаковыми все три значения средних арифметических?
В) Найдите наименьшее возможное значение наибольшего из получаемых трех средних арифметических.
Ответ: А) да, Б) нет, В) $$6frac{1}{7}$$
А. Ларин. Тренировочный вариант № 361.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
В правильной треугольной пирамиде MABC с основанием ABC стороны основания равны 6, а боковые ребра равны 5. На ребре AC находится точка D, на ребре AB находится точка E, а на ребре AM — точка L. Известно, что AD = AE = AL = 4.
а) Докажите, что отрезок DE содержит центр основания пирамиды.
б) Найдите угол между плоскостью основания и плоскостью, проходящей через точки E, D и L.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
Вкладчик разместил в банке 32 тысячи рублей. Несколько лет он получал то 5%, то 10% годовых, а за последний год получил 25% годовых. При этом проценты начислялись в конце каждого года и добавлялись к сумме вклада. В результате его вклад стал равным 53 361 рублю. Сколько лет пролежал вклад?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
Дан треугольник ABC со сторонами AB = 4, BC = 5 и AC = 6.
а) Докажите, что прямая, проходящая через точку пересечения медиан и центр вписанной окружности, параллельна стороне BC.
б) Найдите длину биссектрисы треугольника ABC, проведенной из вершины A.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра a, при каждом из которых система уравнений
имеет единственное решение.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 16 произвольно делят на три группы так, чтобы в каждой группе было хотя бы одно число. Затем вычисляют значение среднего арифметического чисел в каждой из групп (для группы из единственного числа среднее арифметическое равно этому числу).
а) Могут ли быть одинаковыми два из этих трех значений средних арифметических в группах из разного количества чисел?
б) Могут ли быть одинаковыми все три значения средних арифметических?
в) Найдите наименьшее возможное значение наибольшего из получаемых трех средних арифметических
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
| 2974 | В коробке 10 синих, 9 красных и 6 зеленых фломастеров. Случайным образом выбирают 2 фломастера. Какова вероятность того, что окажутся выбраны один синий и один красный фломастер? |
В коробке 10 синих, 9 красных и 6 зеленых фломастеров !Тренировочный вариант 361 от Ларина Задание 2 (4) # Два способа решения. Задача-аналог 2980 | |
| 2973 | Из пункта А круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через полчаса после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч |
Из пункта А круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист ! Тренировочный вариант 361 от Ларина Задание 8 (11) ЕГЭ | |
| 2972 | Найдите значение выражения -22/(cos^2(34^@)+cos^2(124^@)) |
Тренировочный вариант 361 от Ларина Задание 4 (9) | |
| 2971 | Найдите наибольшее значение функции y=15+12x-x^3 на отрезке [-2; 2] |
Найдите наибольшее значение функции y=15+12x-x3 ! Тренировочный вариант 361 от Ларина Задание 11 (12) ЕГЭ | |
| 2970 | а) Решите уравнение (4/9)^cos(x)+2*(2/3)^cos(x)-3=0 б) Найдите все корни уравнения, принадлежащие отрезку [pi; 4pi]. |
Тренировочный вариант 361 от Ларина Задание 12 (13) ЕГЭ | |
| 2969 | Решите неравенство (sqrt(x^2-2x)-sqrt(x^2-5x+6))/(x^2-3x-4) <= 0 |
Тренировочный вариант 361 от Ларина Задание 14 (15) | |
| 2724 | Объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из той же вершины, равен 25. Найдите объём куба |
Объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер ! 36 вариантов ФИПИ Ященко 2022 Вариант 25 Задание 5 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 15 Задание 8 # ! Тренировочный вариант 361 от Ларина Задание 5 (8) | |
| 796 | Дан треугольник ABC. AB=4, BC=6, AC=8. а) Докажите, что прямая, проходящая через точку пересечения медиан и центр вписанной в треугольник окружности параллельна BC. б) Найти длину биссектрисы треугольника ABC, проведённой из вершины A |
Дан треугольник ABC со сторонами AB=4, BC=6, AC=8 ! Ященко ЕГЭ 2017 30 вариантов Вариант 5 задача 16 # Аналог решения для Задания 16 Варианта № 361 Ларина | |
| 443 | В правильной треугольной пирамиде стороны основания 6, боковые рёбра 5. Точка D лежит на AC, точка E лежит на AB , точка L лежит на AM, AD=AE=AL=4. Доказать, что DE содержит центр основания пирамиды. Найти угол между плоскостью основания и плоскостью, проходящей через точки D, L, E |
В правильной треугольной пирамиде МАВС с основанием АВС стороны основания равны 6, а боковые ребра равны 5 ! Тренировочный вариант 361 от Ларина Задание 13 (14) | |
На чтение 1 мин Просмотров 1 Опубликовано 5 марта, 2023
Тренировочный вариант Ларина №361 ЕГЭ 2022 по математике с ответами Решение и ответы на задачи на официальном сайте источника онлайн.
Тренировочный вариант №361 Алекса Ларина ЕГЭ 2022 по математике профильный уровень 11 класс с ответами и решением по новой демоверсии
Варианты ответов и решение задачи ТУТ: https://100ballnik.com/%d1%82%d1%80%d0%b5%d0%bd%d0%b8%d1%80%d0%be%d0%b2%d0%be%d1%87%d0%bd%d1%8b%d0%b9-%d0%b2%d0%b0%d1%80%d0%b8%d0%b0%d0%bd%d1%82-%d0%bb%d0%b0%d1%80%d0%b8%d0%bd%d0%b0-%e2%84%96361-%d0%b5%d0%b3%d1%8d-2022/
Ответы и решение задачи онлайн
Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.
Вариант 361 ларин егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
А. Ларин. Тренировочный вариант № 361.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
В правильной треугольной пирамиде MABC с основанием ABC стороны основания равны 6, а боковые ребра равны 5. На ребре AC находится точка D, на ребре AB находится точка E, а на ребре AM — точка L. Известно, что AD = AE = AL = 4.
А) Докажите, что отрезок DE содержит центр основания пирамиды.
Б) Найдите угол между плоскостью основания и плоскостью, проходящей через точки E, D и L.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
—>
На ребре AC находится точка D, на ребре AB находится точка E, а на ребре AM точка L.
Math-ege. sdamgia. ru
09.08.2018 16:17:49
2018-08-09 16:17:49
Источники:
Https://math-ege. sdamgia. ru/test? id=41029568
Тренировочный вариант Ларина №362 ЕГЭ 2022 по математике с ответами | ЕГЭ ОГЭ СТАТГРАД ВПР 100 баллов » /> » /> .keyword { color: red; } Вариант 361 ларин егэ математика
Тренировочный вариант Ларина №362 ЕГЭ 2022 по математике с ответами
Тренировочный вариант Ларина №362 ЕГЭ 2022 по математике с ответами
Тренировочный вариант №362 Алекса Ларина ЕГЭ 2022 по математике профильный уровень 11 класс с ответами и решением по новой демоверсии ЕГЭ 2022 года для подготовки к экзамену, дата выхода варианта: 02.10.2021 (2 октября 2021 года)
Задания варианта №362 ЕГЭ 2022: скачать
Ответы для варианта: скачать
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий с кратким ответом базового и повышенного уровней сложности.
Часть 2 cодержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
Решать тренировочный вариант Ларина №362 ЕГЭ 2022 по математике:
Ответы для варианта
Сложные задания и ответы с варианта:
2)Найдите вероятность того, что случайно выбранное трехзначное число делится на 34.
Ответ: 0,03
3)Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 4 : 7 : 9. Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 338.
Ответ: 117
5)В основании пирамиды лежит прямоугольник. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы 300 и 450. Найдите диагональ прямоугольника, если высота пирамиды равна 4.
Ответ: 8
8)Готовясь к олимпиаде по математике, школьник за 10 недель прорешал 700 задач. Приобретая опыт, он в каждую последующую неделю, начиная со второй, решал на 10 задач больше, чем в предыдущую. Какое количество задач успеет прорешать школьник за остающиеся до олимпиады 4 недели, если будет увеличивать количество еженедельно решаемых задач прежним образом?
Ответ: 560
10)Васе нужно забить в дубовую доску гвоздь. Если гвоздь стальной, то он согнется с вероятностью 0,1, а если гвоздь медный, то он согнется с вероятностью 0,3. На столе вперемешку лежат 6 стальных и 4 медных гвоздя. Вася берет первый попавшийся гвоздь со стола и пытается забить его в доску. Найдите вероятность того, что этот гвоздь не согнется.
Ответ: 0,82
15)Билл несколько лет назад вложил деньги в акции некоего предприятия. Ежегодно он получал прибыль по акциям сначала 1 9 % в год, потом в год и, наконец, 11 37,5% 2 6 % 3 в год и сразу же вкладывал деньги в те же акции. Известно, что одинаковые процентные ставки сохранялись равное число лет, в результате стоимость акций увеличилась на 156% . Определите, сколько лет Билл получал прибыль по акциям.
Ответ: 6
18)Натуральные числа от 1 до в порядке возрастания записаны в строчку. Под ними записаны те же числа в другом порядке. Можно ли добиться того, что сумма каждого числа и записанного под ним была бы точным квадратом: n n Проверьте, чтобы каждый ответ был записан рядом с номером соответствующего задания. а) при = 7; б) при n = 12; в) при n = 2015?
Решать тренировочный вариант Ларина №362 ЕГЭ 2022 по математике:
2)Найдите вероятность того, что случайно выбранное трехзначное число делится на 34.
Ответ: 0,03
3)Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 4 : 7 : 9. Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 338.
Ответ: 117
5)В основании пирамиды лежит прямоугольник. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы 300 и 450. Найдите диагональ прямоугольника, если высота пирамиды равна 4.
Ответ: 8
8)Готовясь к олимпиаде по математике, школьник за 10 недель прорешал 700 задач. Приобретая опыт, он в каждую последующую неделю, начиная со второй, решал на 10 задач больше, чем в предыдущую. Какое количество задач успеет прорешать школьник за остающиеся до олимпиады 4 недели, если будет увеличивать количество еженедельно решаемых задач прежним образом?
Ответ: 560
10)Васе нужно забить в дубовую доску гвоздь. Если гвоздь стальной, то он согнется с вероятностью 0,1, а если гвоздь медный, то он согнется с вероятностью 0,3. На столе вперемешку лежат 6 стальных и 4 медных гвоздя. Вася берет первый попавшийся гвоздь со стола и пытается забить его в доску. Найдите вероятность того, что этот гвоздь не согнется.
Ответ: 0,82
15)Билл несколько лет назад вложил деньги в акции некоего предприятия. Ежегодно он получал прибыль по акциям сначала 1 9 % в год, потом в год и, наконец, 11 37,5% 2 6 % 3 в год и сразу же вкладывал деньги в те же акции. Известно, что одинаковые процентные ставки сохранялись равное число лет, в результате стоимость акций увеличилась на 156% . Определите, сколько лет Билл получал прибыль по акциям.
Ответ: 6
18)Натуральные числа от 1 до в порядке возрастания записаны в строчку. Под ними записаны те же числа в другом порядке. Можно ли добиться того, что сумма каждого числа и записанного под ним была бы точным квадратом: n n Проверьте, чтобы каждый ответ был записан рядом с номером соответствующего задания. а) при = 7; б) при n = 12; в) при n = 2015?
Ответы для варианта.
100ballnik. com
05.04.2018 22:17:57
2018-04-05 22:17:57
Источники:
Https://100ballnik. com/%D1%82%D1%80%D0%B5%D0%BD%D0%B8%D1%80%D0%BE%D0%B2%D0%BE%D1%87%D0%BD%D1%8B%D0%B9-%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82-%D0%BB%D0%B0%D1%80%D0%B8%D0%BD%D0%B0-%E2%84%96362-%D0%B5%D0%B3%D1%8D-2022/
Ларин А. А. ЕГЭ (профильного уровня) по математике — Архив файлов » /> » /> .keyword { color: red; } Вариант 361 ларин егэ математика
ЕГЭ (профильного уровня) → Ларин А. А. 521
ЕГЭ (профильного уровня) → Ларин А. А. [521]
Экзаменационная работа состоит из Двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–11 записываются В виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться Справочными материалами, выдаваемыми вместе с работой. Разрешается использовать только линейку, но можно Сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене Не используются.
На экзамене при себе надо иметь документ удостоверяющий личность (Паспорт), Пропуск и капиллярную или Гелевую ручку с черными чернилами! Разрешают брать с собой Воду (в прозрачной бутылке) и Еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
№ задания
Всего
31
| 1-11 | 12, 14, 16 | 13, 15 | 17-18 |
| 1 | 2 | 3 | 4 |
Баллы
Экзаменационная работа состоит из Двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–11 записываются В виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться Справочными материалами, выдаваемыми вместе с работой. Разрешается использовать только линейку, но можно Сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене Не используются.
На экзамене при себе надо иметь документ удостоверяющий личность (Паспорт), Пропуск и капиллярную или Гелевую ручку с черными чернилами! Разрешают брать с собой Воду (в прозрачной бутылке) и Еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий.
Yagubov. ru
20.10.2019 20:12:22
2019-10-20 20:12:22
Источники:
Https://yagubov. ru/ege/larin
Тренировочные варианты профильного ЕГЭ 2023 по математике с ответами.