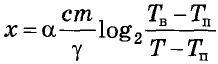Тренировочный вариант №4 ЕГЭ 2023 по математике профильный уровень с ответами и решением по новой демоверсии ЕГЭ 2023 года от ФИПИ для подготовки на 100 баллов в новом формате, задания взяты из банка заданий ФИПИ и с экзамена прошлых лет.
Скачать вариант с ответами
Скачать решение каждого задания
Скачать удобный формат решения
Вариант состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий с кратким ответом базового и повышенного уровней сложности. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
Решать вариант №4 ЕГЭ 2023 по математике профиль с ответами
егэ2023-профиль-математика-вариант4-ответы
Решение каждого задания
решение-задания-вариант4-егэ2023
1.Две стороны треугольника равны 21 и 28. Высота, опущенная на большую из этих сторон, равна 15. Найдите высоту, опущенную на меньшую из этих сторон треугольника.
Ответ: 20
2.Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 57.
Ответ: 171
3.На конференцию приехали 2 учёных из Дании, 7 из Польши и 3 из Венгрии. Каждый из них делает на конференции один доклад. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что четвёртым окажется доклад учёного из Венгрии.
Ответ: 0,25
4.В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в первом автомате закончится кофе, равна 0,1. Вероятность того, что кофе закончится во втором автомате, такая же. Вероятность того, что кофе закончится в двух автоматах, равна 0,03. Найдите вероятность того, что к концу дня кофе останется в двух автоматах.
Ответ: 0,83
5.Найдите корень уравнения log7 (1 − 𝑥) = log7 5.
Ответ: -4
7.На рисунке изображён график дифференцируемой функции 𝑦 = 𝑓(𝑥) и отмечены семь точек на оси абсцисс: 𝑥1, 𝑥2, 𝑥3, 𝑥4, 𝑥5, 𝑥6, 𝑥7. В скольких из этих точек производная функции 𝑓(𝑥) положительна?
Ответ: 3
9.Дорога между пунктами A и B состоит из подъёма и спуска, а её длина равна 25 км. Путь из A в B занял у туриста 6 часов, из которых 1 час ушёл на спуск. Найдите скорость туриста на спуске, если она больше скорости на подъёме на 1 км/ч. Ответ дайте в км/ч.
Ответ: 5
10.На рисунке изображён график функции вида 𝑓(𝑥) = 𝑎 𝑥 . Найдите значение 𝑓(3).
Ответ: 8
11.Найдите наименьшее значение функции 𝑦 = 𝑒 2𝑥 − 5𝑒 𝑥 − 2 на отрезке [−2; 1].
Ответ: -8, 25
12.а) Решите уравнение √2sin3𝑥 − √2 sin 𝑥 + cos2𝑥 = 0. б) Найдите все корни этого уравнения, принадлежащие отрезку.
13.В правильной четырёхугольной пирамиде 𝑆𝐴𝐵𝐶𝐷 сторона основания 𝐴𝐵 равна боковому ребру 𝑆𝐴. Медианы треугольника 𝑆𝐵𝐶 пересекаются в точке 𝑀. а) Докажите, что 𝐴𝑀 = 𝐴𝐷. б) Точка 𝑁 − середина 𝐴𝑀. Найдите 𝑆𝑁, если 𝐴𝐷 = 6.
Ответ: √15
15.15-го марта в банке был взят кредит на некоторую сумму на 31 месяц. Условия его возврата таковы: – 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца; – со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; – 15-го числа каждого месяца с 1-го по 30-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца; – 15-го числа 30-го месяца долг составит 100 тысяч рублей; – к 15-му числу 31-го месяца кредит должен быть полностью погашен. Какая сумма была взята в кредит, если общая сумма выплат после его погашения составила 555 тысяч рублей?
Ответ: 400 тыс.
16.Дан прямоугольный треугольник 𝐴𝐵𝐶 с прямым углом 𝐶. На катете 𝐴𝐶 взята точка 𝑀. Окружность с центром 𝑂 и диаметром 𝐶𝑀 касается гипотенузы в точке 𝑁. а) Докажите, что прямые 𝑀𝑁 и 𝐵𝑂 параллельны. б) Найдите площадь четырёхугольника 𝐵𝑂𝑀𝑁, если 𝐶𝑁 = 4 и 𝐴𝑀: 𝑀𝐶 = 1: 3.
Ответ: 7
17.Найдите все значения 𝑎, при каждом из которых уравнение (5𝑥 − 2) ∙ ln(𝑥 + 𝑎) = (5𝑥 − 2) ∙ ln(2𝑥 − 𝑎) имеет ровно один корень на отрезке [0; 1].
Ответ: (−0,4; 0] ∪ {0,2} ∪ (0,5; 0,8)
18.На доске написано несколько (более одного) различных натуральных чисел, причём любые два из них отличаются не более чем в три раза. а) Может ли на доске быть 5 чисел, сумма которых равна 47? б) Может ли на доске быть 10 чисел, сумма которых равна 94? в) Сколько может быть чисел на доске, если их произведение равно 8000?
Ответ: а) да, например 7 8 9 10 13 б) нет в) 2; 3
Статград математика 11 класс ЕГЭ 2023
28 сентября 2022 Статград математика 11 класс ЕГЭ 2023 варианты и ответы
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Решение и ответы заданий Варианта №4 из сборника ЕГЭ 2022 по математике (профильный уровень) И.В. Ященко. ГДЗ Решебник профиль для 11 класса. Полный разбор. Ответы с решением.
Задание 1.
Решите уравнение frac{7x}{3x^{2}–26}=1. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Задание 2.
Из множества натуральных чисел от 56 до 80 (включительно) наудачу выбирают одно число. Какова вероятность того, что оно делится на 4?
Задание 3.
Боковая сторона равнобедренной трапеции равна её меньшему основанию, угол при основании равен 60°, большее основание равно 28. Найдите радиус описанной окружности этой трапеции.
Задание 4.
Найдите значение выражения 5√3–4·51+3√3:54√3–1.
Задание 5.
Сторона основания правильной шестиугольной пирамиды равна 3, боковое ребро равно 6. Найдите объём пирамиды.
Задание 6.
Материальная точка движется прямолинейно по закону
x(t) = –frac{1}{2}t4 + 4t3 – t2 – t + 14,
где х – расстояние от точки отсчёта в метрах, t – время в секундах, прошедшее с начала движения. Найдите её скорость (в метрах в секунду) в момент времени t = 5 с.
Задание 7.
Для обогрева помещения, температура в котором поддерживается на уровне Тп = 15 °C, через радиатор отопления пропускают горячую воду. Расход проходящей через трубу радиатора воды m = 0,5 кг/с. Проходя по трубе расстояние х, вода охлаждается от начальной температуры Тв = 79 °C до температуры Т, причём
где с = 4200 Вт·с/кг·°C – теплоёмкость воды, γ = 63 Вт/м·°C – коэффициент теплообмена, а α = 1,3 – постоянная. Найдите, до какой температуры (в градусах Цельсия) охладится вода, если длина трубы радиатора равна 130 м.
Задание 8.
Имеется два сплава. Первый сплав содержит 5 % никеля, второй – 14 % никеля. Масса второго сплава больше массы первого на 8 кг. Из этих двух сплавов получили третий сплав, содержащий 11 % никеля. Найдите массу третьего сплава. Ответ дайте в килограммах.
Задание 9.
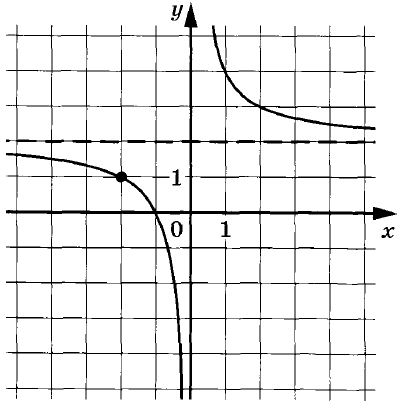
На рисунке изображён график функции f(х) = frac{k}{x} + а. Найдите, при каком значении х значение функции равно 7.
Задание 10.
В торговом центре два одинаковых автомата продают чай. Вероятность того, что к концу дня в автомате закончится чай, равна 0,2. Вероятность того, что чай закончится в обоих автоматах, равна 0,18. Найдите вероятность того, что к концу дня чай останется в обоих автоматах.
Задание 11.
Найдите наименьшее значение функции y = 49x – 46sinx + 37 на отрезке [-frac{pi}{2}; 0].
Задание 12.
а) Решите уравнение 25x–0,5 – 13·10x–1 + 4x+0,5 = 0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [-frac{pi}{2}; π].
Задание 13.
В правильной треугольной призме АВСА1В1С1 на рёбрах АС и ВС отмечены соответственно точки М и N так, что AM:МС = CN:BN = 2:1. Точка К – середина ребра A1C1.
а) Докажите, что плоскость MNK проходит через вершину В1.
б) Найдите расстояние от точки С до плоскости KMN, если АВ = 6, АА1 = 2,4.
Задание 14.
Решите неравенство 8lg(–1 – х) ≤ (х2 – 1)lg2.
Задание 15.
По вкладу «А» банк в конце каждого года увеличивает на 10 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» – увеличивает эту сумму на 14 % в течение каждого из первых двух лет. Найдите наименьшее натуральное число процентов, начисленное за третий год по вкладу «Б», при котором за все три года этот вклад будет более выгоден, чем вклад «А».
Задание 16.
В параллелограмме ABCD тангенс угла А равен 1,5. На продолжениях сторон АВ и ВС параллелограмма за точку В выбраны точки N и М соответственно, причём BC = CN и АВ = AM.
а) Докажите, что DN = DM.
б) Найдите MN, если АС = √13.
Задание 17.
Найдите все положительные значения а, при каждом из которых корни уравнения 5а2х – 2·4х + 9·(2а)x = 0 принадлежат отрезку [–3; 1].
Задание 18.
Известно, что а, b, с, d, е и f – это различные, расставленные в некотором, возможно ином, порядке числа 2, 3, 4, 6, 7 и 16.
а) Может ли выполняться равенство frac{a}{b}+frac{c}{d}+frac{e}{f}=11?
б) Может ли выполняться равенство frac{a}{b}+frac{c}{d}+frac{e}{f}=frac{1345}{336}?
в) Какое наибольшее значение может принимать сумма frac{a}{b}+frac{c}{d}+frac{e}{f}?
Источник варианта: Сборник ЕГЭ 2022. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4 / 5. Количество оценок: 4
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
- 21.11.2022
Четвертый тестовый вариант по математике профильного уровня в формате ЕГЭ 2023 года для 11 класса. Данный тест составлен на основе демоверсии ФИПИ ЕГЭ 2023, с учетом кодификатора и спецификации текущего года. Вариант составлен волонтерским проектом ЕГЭ100БАЛЛОВ https://vk.com/ege100ballov
Скачать PDF вариант вы можете по ссылке ниже. В конце документа содержатся ответы к первой части и подробный разбор и решение с критериями проверки для второй части теста.
- Другие тестовые варианты ЕГЭ по профильной математике
Работа проводилась 3 октября 2022 года.
Есть вопросы? Задавайте их ниже в комментариях!
Некоторые задания из варианта №4
Задание 4
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в первом автомате закончится кофе, равна 0,1. Вероятность того, что кофе закончится во втором автомате, такая же. Вероятность того, что кофе закончится в двух автоматах, равна 0,03. Найдите вероятность того, что к концу дня кофе останется в двух автоматах.
Задание 9
Дорога между пунктами A и B состоит из подъёма и спуска, а её длина равна 25 км. Путь из A в B занял у туриста 6 часов, из которых 1 час ушёл на спуск. Найдите скорость туриста на спуске, если она больше скорости на подъёме на 1 км/ч. Ответ дайте в км/ч.
Задание 13
В правильной четырёхугольной пирамиде 𝑆𝐴𝐵𝐶𝐷 сторона основания 𝐴𝐵 равна боковому ребру 𝑆𝐴. Медианы треугольника 𝑆𝐵𝐶 пересекаются в точке 𝑀.
а) Докажите, что 𝐴𝑀=𝐴𝐷.
б) Точка 𝑁− середина 𝐴𝑀. Найдите 𝑆𝑁, если 𝐴𝐷=6.
Задание 18
На доске написано несколько (более одного) различных натуральных чисел, причём любые два из них отличаются не более чем в три раза.
а) Может ли на доске быть 5 чисел, сумма которых равна 47?
б) Может ли на доске быть 10 чисел, сумма которых равна 94?
в) Сколько может быть чисел на доске, если их произведение равно 8000?
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
А. Ларин: Тренировочный вариант № 4*.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Найдите все корни на промежутке
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
На стороне CD квадрата ABCD построен равносторонний треугольник CPD. Найдите высоту треугольника ADP, проведённую из вершины D, если известно, что сторона квадрата равна 1.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
Найдите все значения а, при которых система уравнений
имеет ровно три решения?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
А, И, Б сидели на трубе. К ним стали по очереди подсаживаться другие буквы так, что порядковый номер очередной буквы в русском алфавите равнялся сумме цифр порядковых номеров двух предыдущих букв. Оказалось, что начиная с некоторого момента буквы стали циклически повторяться.
а) Какая буква (из числа циклически повторяющихся) встречается наиболее часто?
б) Может ли циклически повторяющийся набор состоять из одной буквы? Если да, указать эту букву.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Тренировочный вариант ЕГЭ 2023 по математике (профиль) №4 с ответами «ЕГЭ 100 БАЛЛОВ». Пробные варианты ЕГЭ по математике профиль 2023. ЕГЭ МАТЕМАТИКА Профильный уровень.
https://vk.com/ege100ballov
https://vk.com/math_100
скачать
Примеры некоторых заданий из варианта
Смотрите также: