- 30.10.2020
Четвёртый пробный вариант ЕГЭ по математике профильного уровня для учащихся 11 классов в формате демоверсии ФИПИ для 2021 года.
Работа проходила 28 сентября 2020 года. Вариант создан участниками проекта https://vk.com/ege100ballov
- Другие тренировочные варианты ЕГЭ по профильной математике
- Тренировочные работы СтатГрад 2020-2021
В конце варианта по математике приведены ответы ко всем заданиями, а также ОЧЕНЬ подробное решение для всех заданий второй части.
Есть вопросы? Пишите в комментариях ниже!
Подробный разбор варианта №4 с решениями и ответами
Продолжение разбора
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.

Пробный вариант № 4 ЕГЭ по математике профильного уровня на 2021 год составлен в соответствии с кодификатором ФИПИ и официальными демоверсиями.
Файл в формате pdf содержит задания, решения и ответы.
Скачать вариант в формате pdf — СКАЧАТЬ.
Вариант составлен авторами: Школа Пифагора.
Смотрите также:
- ЕГЭ по математике
- Расписание ЕГЭ 2021
- Шкала перевода баллов ЕГЭ
Одноклассники
Вконтакте
Мой мир
Пробный вариант ЕГЭ 2021 по математике (профиль) №4 с ответами «ЕГЭ 100 БАЛЛОВ». Тренировочные варианты ЕГЭ 2021 по математике (профиль) с ответами. ЕГЭ МАТЕМАТИКА Профильный уровень.
https://vk.com/ege100ballov
https://vk.com/math_100
Смотрите также:
Пробный вариант ЕГЭ 2021 по математике (профиль) №3 с ответами
Тренировочный вариант №4 КИМ №210927 ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки на 100 баллов от 27 сентября 2021 года.
Вариант с ответами: скачать
Решение каждого задания: скачать
Данный вариант составлен по новой демоверсии ФИПИ экзамена ЕГЭ 2022 года, к тренировочным заданиям прилагаются решения и правильные ответы.
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий с кратким ответом базового и повышенного уровней сложности.
Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
Решу ЕГЭ 2022 по математике профиль вариант 100 баллов №210927:
Сложные задания и ответы с варианта
1)Найдите корень уравнения log27 3 5𝑥+5 = 2.
Ответ: 0,2
2)В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 7. Результат округлите до тысячных.
Ответ: 0,167
3)В треугольнике 𝐴𝐵𝐶 𝐶𝐷 − медиана, угол 𝐶 равен 90°, угол 𝐵 равен 35°. Найдите угол 𝐴𝐶𝐷. Ответ дайте в градусах.
Ответ: 55
5)Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 37. Найдите площадь боковой поверхности исходной призмы.
Ответ: 74
6)На рисунке изображены график функции 𝑦 = 𝑓(𝑥) и касательная к нему в точке с абсциссой 𝑥0 . Найдите значение производной функции 𝑓(𝑥) в точке 𝑥0 .
Ответ: 3
7)Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объём и давление связаны соотношением 𝑝1𝑉1 1,4 = 𝑝2𝑉2 1,4 , где 𝑝1 и 𝑝2 − давление газа (в атмосферах) в начальном и конечном состояниях, 𝑉1 и 𝑉2 − объём газа (в литрах) в начальном и конечном состояниях. Изначально объём газа равен 294,4 л, а давление газа равно одной атмосфере. До какого объёма нужно сжать газ, чтобы давление в сосуде стало 128 атмосфер? Ответ дайте в литрах.
Ответ: 9,2
8)Первый час автомобиль ехал со скоростью 115 км/ч, следующие три часа – со скоростью 45 км/ч, а затем два часа – со скоростью 40 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Ответ: 55
9)На рисунке изображён график функции 𝑓(𝑥) = 𝑘 𝑥 +𝑎. Найдите 𝑓(−12).
Ответ: 0,75
10)Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,02. Известно, что 77% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
Ответ: 0,6976
13)В основании прямой треугольной призмы 𝐴𝐵𝐶𝐴1𝐵1𝐶1 лежит равнобедренный (𝐴𝐵 = 𝐵𝐶) треугольник 𝐴𝐵𝐶. Точка 𝐾 − середина ребра 𝐴1𝐵1 , а точка 𝑀 делит ребро 𝐴𝐶 в отношении 𝐴𝑀: 𝑀𝐶 = 1: 3. а) Докажите, что 𝐾𝑀 ⊥ 𝐴𝐶. б) Найдите угол между прямой 𝐾𝑀 и плоскостью 𝐴𝐵𝐵1 , если 𝐴𝐵 = 6, 𝐴𝐶 = 8 и 𝐴𝐴1 = 3.
15)15-го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы: – 1-го числа каждого месяца долг возрастает на 𝑟% по сравнению с концом предыдущего месяца; – со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; – 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите 𝑟.
Ответ: 3
16)В трапеции 𝐴𝐵𝐶𝐷 основание 𝐴𝐷 в два раза меньше основания 𝐵𝐶. Внутри трапеции взяли точку 𝑀 так, что углы 𝐵𝐴𝑀 и 𝐶𝐷𝑀 прямые. а) Докажите, что 𝐵𝑀 = 𝐶𝑀. б) Найдите угол 𝐴𝐵𝐶, если угол 𝐵𝐶𝐷 равен 64°, а расстояние от точки 𝑀 до прямой 𝐵𝐶 равно стороне 𝐴𝐷.
Ответ: 71
18)Каждый из группы учащихся сходил в кино или в театр, при этом возможно, что кто-то из них мог сходить и в кино, и в театр. Известно, что в театре мальчиков было не более 2 11 от общего числа учащихся группы, посетивших театр, а в кино мальчиков было не более 2 5 от общего числа учащихся группы, посетивших кино.
- а) Могло ли быть в группе 9 мальчиков, если дополнительно известно, что всего в группе было 20 учащихся?
- б) Какое наибольшее количество мальчиков могло быть в группе, если дополнительно известно, что всего в группе было 20 учащихся?
- в) Какую наименьшую долю могли составлять девочки от общего числа учащихся в группе без дополнительного условия пунктов а и б?
Ответ: а) да б) 9 в) 9/17
Другие тренировочные варианты ЕГЭ по математике:
28.09.2021 Математика 11 класс МА2110101-МА2110112 ЕГЭ 2022 работа статград ответы и задания
Тренировочный вариант №143 ЕГЭ 2022 по математике 11 класс профильный уровень с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Решение и ответы заданий № 1–12 варианта №4 из сборника ЕГЭ 2021 по математике (профильный уровень) И.В. Ященко. ГДЗ профиль для 11 класса.
Задание 1.
В летнем лагере 220 детей и 24 воспитателя. Автобус рассчитан не более чем на 38 пассажиров. Какое наименьшее количество автобусов понадобится, чтобы за один раз перевезти всех из лагеря в город?
Задание 2.
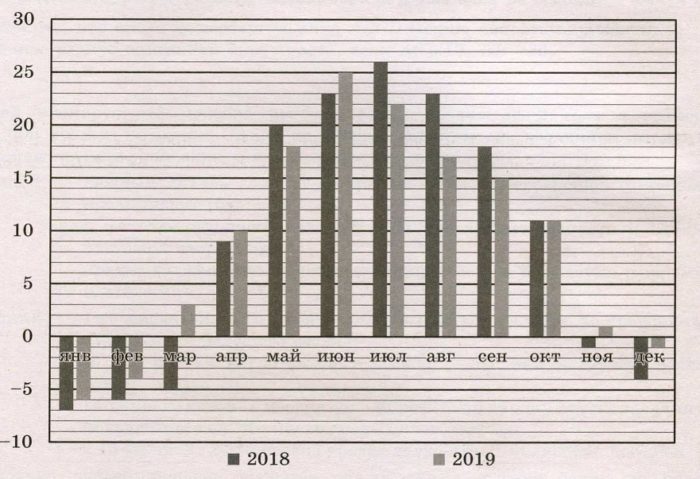
На диаграмме показано изменение средней температуры за каждый месяц в 2018 и 2019 годах в Волгограде. По горизонтали указаны месяцы, по вертикали – значение температуры в градусах Цельсия. Определите разницу между наибольшей и наименьшей среднемесячными температурами в Волгограде в 2019 году. Ответ дайте в градусах Цельсия.
Задание 3.
На клетчатой бумаге с размером клетки 1 х 1 изображён квадрат. Найдите радиус вписанной в него окружности.
Задание 4.
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей – 1 очко, если проигрывает – 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований, если вероятности выигрыша и проигрыша в каждой игре одинаковы и равны 0,4.
Задание 5.
Найдите корень уравнения log0,5(x+5) = log20,2
Задание 6.
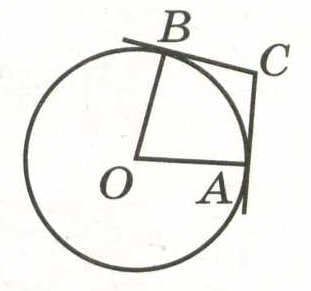
Через концы А и В дуги окружности с центром О проведены касательные СА и СВ. Угол САВ равен 39°. Найдите угол АОВ. Ответ дайте в градусах.
Задание 7.
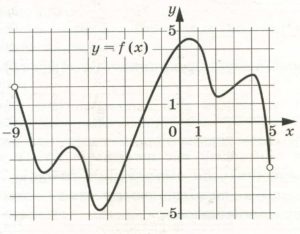
На рисунке изображён график функции у = f(x), определённой на интервале (–9; 5). Найдите количество точек, в которых производная функции f(x) равна 0.
Задание 8.
Объём параллелепипеда АВСDА1В1С1D1 равен 60. Найдите объём треугольной пирамиды АСВ1D1.
Задание 9.
Найдите значение выражения
Задание 10.
Мяч бросили под острым углом α к плоской горизонтальной поверхности земли. Время полёта мяча (в секундах) определяется по формуле . При каком значении угла α (в градусах) время полёта составит 1,4 секунды, если мяч бросают с начальной скоростью v0 = 14 м/с2. Считайте, что ускорение свободного падения g = 10 м/с2.
Задание 11.
Смешали 3 кг 24-процентного раствора, 4 кг 32-процентного раствора и некоторое количество 48-процентного раствора одного и того же вещества. Сколько килограммов 48-процентного раствора использовали, если в результате получили 40-процентный раствор вещества?
Задание 12.
Найдите точку минимума функции y = (x + 4)2(x + 1) + 9
Источник варианта: Сборник ЕГЭ 2021 по математике профильный уровень. Типовые экзаменационные варианты. 36 вариантов. Под редакцией И.В. Ященко.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.2 / 5. Количество оценок: 5
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Тренировочные варианты профильного ЕГЭ 2023 по математике с ответами.
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |