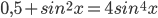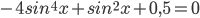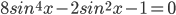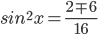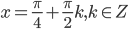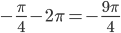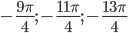Ответы на тренировочный вариант №199 профильного ЕГЭ
Задание 1
Показания счетчика электроэнергии 1 мая составляли 37142 кВт∙ч, а 1 июня — 37292 кВт∙ч. Сколько нужно заплатить за электроэнергию за май, если известно, что цена 1 кВт∙ч электроэнергии составляет: 3 руб. 50 коп., если ее расход не превышает социальной нормы 120 кВт∙ч; 4 руб. 20 коп. – сверх социальной нормы ? Ответ дайте в рублях.
Ответ: 630
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Наработка элетроэнергии за май : 37292 — 37142 = 150
Расход превышает соцнорму, поэтому тариф повышенный: 4.2*150=630
Задание 2
На диаграмме показана температура воздуха (в градусах Цельсия) за 31 день мая (по горизонтальной оси откладываются дни месяца, по вертикальной – температура в градусах Цельсия). Определите, сколько дней в течение мая температура не превышала 15 C .
Ответ: 20
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
| Найдем количество месяцев, где превышает ( над черной линией ). Их 11. Значит дней, когда не превышает 31 — 11 = 20 |  |
Задание 3
Каждая клетка имеет размер 1х1. Найдите длину отрезка АВ.
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Треугольники MKL и AOL подобны, поэтому LO/LK=AO/MK. То есть AO = 1/4.
Аналогично из треугольников RQB и RHZ QB = 3/4.
Тогда AB = 1/4 + 2 + 3/4 = 3
Задание 4
Вероятность попасть в мишень равна 0,7. Произведено три выстрела. Какова вероятность, что мишень была поражена ровно два раза?
Ответ: 0,441
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Вероятность промаха равна 1 — 0,7 = 0,3. Чтобы выполнялось условие двух попаданий, один выстрел должен быть промахом. Тогда, если попадание это «+», а промах это «-» , получаем следующие случаи
+ + — = 0,7*0,7*0,3=0,147
+ — + = 0,7*0,3*0,7=0,147
— + + = 0,3*0,7*0,7=0,147
В итоге будет 0,147+0,147+0,147=0,441
Задание 5
В треугольнике АВС угол С равен 90º. Площади квадратов АВРК и АСЕМ равны 16 и 12 соответственно. Найдите площадь квадрата СВNT.
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Из площадей квадратов получим:
$$AB = sqrt{16}$$
$$AC = sqrt{12}$$
Из треугольника ABC:
$$CB = sqrt{(sqrt{16})^{2}-(sqrt{12})^{2}}=2$$
Тогда площадь CBNT : $$S = 2^{2}=4$$
Задание 6
На рисунке изображён график функции y=F(x) − одной из первообразных некоторой функции f(x), определённой на интервале (‐7;4). Пользуясь рисунком, определите значение функции f(x) в точке х=1.
Ответ: 0
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Нам дана первообразная F, нам необходимо найти значение функции f в точке. При подобном задании можно рассматривать следующую ситуацию, вместо F — рассматривается функция g, вместо функции f — производная g’. То есть нам дан график функции g(x), а надо найти значение производной g'(x) в точке x = 1. Как видим на графике, данная точка — точка минимум, значит значение производной и ответ — 0
Задание 7
Цилиндр описан около шара. Найдите объем шара, если известно, что объем цилиндра равен 60.
Ответ: 40
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Высота цилиндра у нас равна двум радиусам вписанного шара. Обозначим радиус шара ( в таком случае и радиус основания цилиндра ) за R, объем цилиндра $$V_{1}$$, а объем шара V. Тогда :
$$V_{1}=Sh=pi R^{2}*2R=2pi R^{3}=60$$
$$R^{3}=frac{30}{pi} $$
Тогда объем шара будет:
$$V=frac{4}{3}pi R^{3}=frac{4}{3}pi * frac{30}{pi}=40$$
Задание 8
Найдите значение выражения $$frac{log_{25} 2}{log_{125} 2}$$
Ответ: 1.5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$frac{log_{25} 2}{log_{125} 2}=frac{log_{5^{2}} 2}{log_{5^{3}} 2}=$$ $$frac{frac{1}{2}log_{5} 2}{frac{1}{3}log_{5} 2}=frac{frac{1}{2}}{frac{1}{3}}=1.5$$
Задание 9
Максимальная высота подъёма тела, брошенного под углом к горизонту, вычисляется по формуле $$h=frac{(vsin alpha)^{2} }{2g}$$ , где v (м/c) – начальная скорость тела, α – угол, под которым тело брошено к горизонту, g – ускорение свободного падения (считать, что g=10 м/с2). С какой скоростью необходимо бросить мяч под углом 30º к горизонту, чтобы он поднялся на высоту 4 м 5 см?
Ответ: 18
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Подставим имеющиеся значения, предварительно представив высоту в метрах:
$$4.05=frac{(vsin 30)^{2} }{2*10}$$
$$81=(v * frac{1}{2})^{2}$$
$$81*4=v^{2}$$
$$v=18$$
Задание 10
Одна бригада может убрать поле за 12 дней, а другая выполняет ту же работу за 75% времени, необходимого первой бригаде. После того как в течение 5 дней работала первая бригада, к ней присоединилась вторая и они вместе закончили работу. Сколько дней бригады работали вместе?
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Время работы второй бригады будет равно 12 * 0,75 = 9 дней. Пусть все поле равно 1. Тогда ежедневно первая бригада убирает 1/12 этого поля, а вторая 1/9. Тогда, если они работали вместе x дней: $$5 * frac{1}{12} + x (frac{1}{12} + frac{1}{9} )= 1$$ $$x (frac{3}{36} + frac{4}{36}) = frac{7}{12}$$ $$x * frac {7}{36} = frac{7}{12}$$ $$x = 3$$
Задание 11
Найдите точку минимума функции $$f(x) =x^{2}-3.75x- ln (x+2)$$
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Найдем производную этой функции и приравняем к нулю:
$$f'(x) =2x-3.75- frac{1}{x+2}=0 $$
$$frac{2x^{2}+4x-3.75x-7.5-1}{x+2}=0$$
$$2x^{2}+0.25x-8.5=0 $$
$$x_{1}=frac{-34}{16}$$
$$x_{2}=2 $$
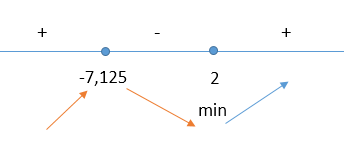
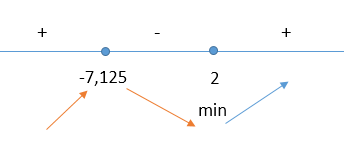
Начертим координатную прямую и посмотрим какие знаки принимает производная на полученных интервалах и получим, что точка 2 — точка минимума
Задание 12
Дано уравнение $$sqrt{0,5+sin^{2}x}+cos 2x=1$$
a) Решите уравнение.
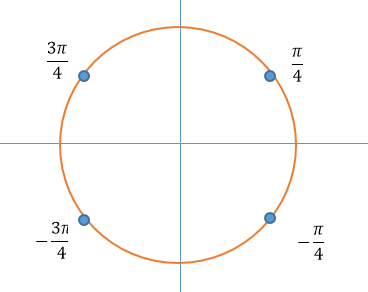
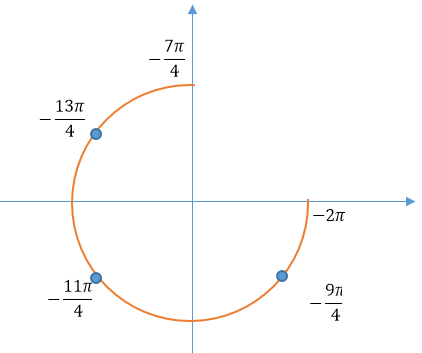
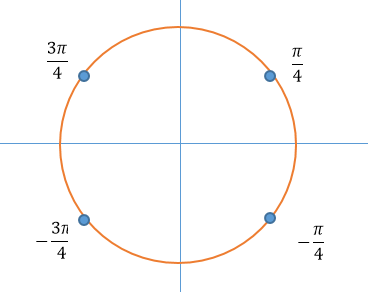
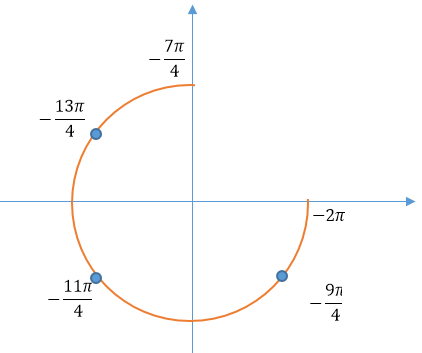
б) Найдите его корни, принадлежащие отрезку $$[-frac{7pi}{2};-2pi]$$
Ответ: А)$$frac{pi}{4}+frac{pi n}{2}, nin Z$$ Б)$$-frac{13pi}{4};-frac{11pi}{4};-frac{9pi}{4}$$
Задание 13
В основании прямой призмы $$ABCA_{1}B_{1}C_{1}$$ лежит прямоугольный треугольник $$ABC$$ с гипотенузой $$AB$$, причем $$AB=AA_{1}$$. Через точку $$B_{1}$$ перпендикулярно $$CA_{1}$$ проведена плоскость $$alpha$$.
а) Докажите, что сечением призмы плоскостью $$alpha$$ является прямоугольный треугольник.
б) Найдите объем большей части призмы, на которые ее делит плоскость $$alpha$$, если известно, что $$AC=8$$, $$BC=6$$.
Ответ: 188,8
Задание 14
Решите неравенство $$frac{1}{log_{2}(x^4-8x^2+16)-log_{2}^{2}(4-x^{2})}leq 1$$
Ответ: $$(-2;-sqrt{3});pm sqrt{2};(sqrt{3};2)$$
Задание 15
На стороне $$AC$$ треугольника $$ABC$$ отметили точку $$D$$ так, что $$BC=sqrt{ACcdot CD}$$
а) Докажите, что углы $$BAD$$ и $$CBD$$ равны.
б) Найдите отношение отрезков биссектрисы $$CL$$ треугольника $$ABC$$, на которые ее делит прямая $$BD$$, если известно, что $$BC=6$$, $$AC=9$$.
Ответ: 2
Задание 16
1 июня планируется взять кредит в банке на сумму 6 млн. рублей на срок 12 месяцев. Условия возврата таковы:
— 15 числа каждого месяца долг возрастает на r % (r – целое число) по сравнению с началом текущего месяца;
— с 16 по 28 число необходимо выплатить часть долга так, чтобы на начало каждого следующего месяца долг уменьшался на одну и ту же сумму по сравнению с предыдущим месяцем.
Найдите наименьшую возможную ставку r, если известно, что в декабре банку будет выплачено более, чем на 100 тыс. руб. больше, нежели в марте.
Ответ: 7
Задание 17
Найдите все значения параметра $$a$$, при каждом из которых уравнение $$4^{|x|}+acdot 2^{|x|}-2^{|x|+2}=6a^{2}-13a+5$$ имеет ровно два корня.
Ответ: $$(-infty;1);1;2;(frac{4}{3};+infty)$$
Задание 18
Известно, что $$a, b, c, d$$ – попарно различные натуральные числа, большие 1.
А) Может ли выполняться равенство $$frac{1}{a}+frac{1}{b}=frac{1}{c}+frac{1}{d}$$ ?
Б) Может ли выполняться равенство $$frac{1}{a}+frac{1}{b}+frac{1}{c}+frac{1}{d}=1,26$$
В) Найдите наименьшее и наибольшее значение суммы $$S=frac{1}{a}+frac{1}{b}+frac{1}{c}+frac{1}{d}$$ , если известно, что $$1,2 < S < 1,3$$.
Ответ: А)да Б)нет В)$$1frac{5}{24};1frac{17}{60}$$
А. Ларин: Тренировочный вариант № 199.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
В основании прямой призмы лежит прямоугольный треугольник ABC с гипотенузой AB, причем
Через точку
перпендикулярно
проведена плоскость α.
а) Докажите, что сечением призмы плоскостью α является прямоугольный треугольник.
б) Найдите объем большей части призмы, на которые ее делит плоскость α, если известно, что
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
На стороне AC треугольника ABC отметили точку D так, что
а) Докажите, что углы BAD и СВD равны.
б) Найдите отношение отрезков биссектрисы CL треугольника ABC, на которые ее делит прямая BD, если известно, что
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
1 июня планируется взять кредит в банке на сумму 6 млн рублей на срок 12 месяцев. Условия возврата таковы:
— 15 числа каждого месяца долг возрастает на r% (r — целое число) по сравнению с началом текущего месяца;
— с 16 по 28 число необходимо выплатить часть долга так, чтобы на начало каждого следующего месяца долг уменьшался на одну и ту же сумму по сравнению с предыдущим месяцем.
Найдите наименьшую возможную ставку r, если известно, что в декабре банку будет выплачено более, чем на 100 тыс. руб. больше, нежели в марте.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра а, при каждом из которых уравнение
имеет ровно два корня.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
Известно, что a, b, c, d — попарно различные натуральные числа, большие 1.
а) Может ли выполняться равенство ?
б) Может ли выполняться равенство ?
в) Найдите наименьшее и наибольшее значение суммы если известно, что
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Ответы и решение – Тренировочный вариант № 199 Alexlarin.net
Данный вариант взят с сайта alexlarin.net
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 546 | 20 | 3 | 0,441 | -1,5 | 4 | 0 | 40 | 1,5 | 18 | 3 | 2 |
1. 37292-37142=150
120.3,5=420
30.4,2=126
420+126=546
2. 31-11=20
3.
4. P=3.0,7.0,7.(1-0,7)=0,441
5.
6. 16=12+x ⇒ x=4
7. 0
8. Vш=4/3.π.R3
Vц=Sосн.h = πr2.2R=2πR3=60 ⇒ πR3=30
Vш=4/3.π.R3=4/3.30 = 40
9.
10.
11. 12.0,75=9
12.
Ответ: 2
Част 2
13.
Ответ:
б)
Ответ:
14.
Ответы и решение – Тренировочный вариант № 199 Alexlarin.net
Данный вариант взят с сайта alexlarin.net
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 546 | 20 | 3 | 0,441 | -1,5 | 4 | 0 | 40 | 1,5 | 18 | 3 | 2 |
1. 37292-37142=150
120.3,5=420
30.4,2=126
420+126=546
2. 31-11=20
3.
4. P=3.0,7.0,7.(1-0,7)=0,441
5.
6. 16=12+x ⇒ x=4
7. 0
8. Vш=4/3.π.R3
Vц=Sосн.h = πr2.2R=2πR3=60 ⇒ πR3=30
Vш=4/3.π.R3=4/3.30 = 40
9.
10.
11. 12.0,75=9
12.
Ответ: 2
Част 2
13.
Ответ:
б)
Ответ:
14.
Contents
- 1 Задание №1. Решение варианта №199 ОГЭ по математике Ларин
- 1.1 Решение
- 2 Задание №2. Решение варианта №199 ОГЭ по математике Ларин
- 2.1 Решение
- 3 Задание №3. Решение варианта №199 ОГЭ по математике. Ларин
- 3.1 Решение
- 4 Задание №4. Решение варианта №199 ОГЭ по математике Ларин
- 4.1 Решение
- 5 Задание №5. Решение варианта №199 ОГЭ по математике. Ларин
- 5.1 Решение
- 6 Задание №6
- 6.1 Решение
- 7 Задание №7. Решение варианта №199 ОГЭ по математике Ларин
- 7.1 Решение
- 8 Задание №8
- 8.1 Решение
- 9 Задание №9. Решение варианта №199 ОГЭ по математике Ларин
- 9.1 Решение
- 10 Задание №10
- 10.1 Решение
- 11 Задание №11
- 11.1 Решение
- 12 Задание №12. Решение варианта №199 ОГЭ по математике. Ларин
- 12.1 Решение
- 13 Задание №13
- 14 Решение
- 15 Задание №14
- 15.1 Решение
- 16 Задание №15
- 16.1 Решение
- 17 Задание №16
- 17.1 Решение
- 18 Задание №17. Решение варианта №199 ОГЭ по математике Ларин
- 18.1 Решение
- 19 Задание №18
- 19.1 Решение
- 20 Задание №19
- 20.1 Решение
- 21 Задание №20. Решение варианта №199 ОГЭ по математике Ларин
- 21.1 Решение
- 22 Задание №21
- 22.1 Решение
- 23 Задание №22. Решение варианта №199 ОГЭ по математике Ларин
- 23.1 Решение
- 24 Задание №23
- 24.1 Решение
- 25 Задание №24
- 25.1 Решение
- 26 Задание №25
- 26.1 Решение
- 27 Задание №26. Решение варианта №199 ОГЭ по математике Ларин
- 27.1 Решение
- 28 Видео: Разбор Варианта ОГЭ Ларина №199 (№1-20)
- 29 Видео: Разбор Варианта ОГЭ Ларина №199 (№21-26)
Найдите значение выражения:
(8,9 — 10,1)/(5,3 — 4,7).
Решение
(8,9 — 10,1)/(5,3 — 4,7) = -1,2/0,6 = -2.
Ответ: -2.
Задание №2. Решение варианта №199 ОГЭ по математике Ларин
| Отправление от ст. Нара | Прибытие на Киевский вокзал |
| 06:35 | 07:59 |
| 07:05 | 08:15 |
| 07:28 | 08:30 |
| 07:34 | 08:57 |
Студент Кузнецов выезжает из Наро-Фоминска в Москву на занятия в университет. Занятия начинаются в 9:00. В таблице приведено расписание утренних электропоездов от станции Нара до Киевского вокзала в Москве.
Путь от вокзала до университета занимает 40 минут. Укажите время отправления от станции Нара самого позднего из электропоездов, которые подходят студенту.
- 1) 06:35.
- 2) 07:05.
- 3) 07:28.
- 4) 07:34.
Решение
Чтобы успеть на занятия, Студент Кузнецов должен прибыть на Киевский вокзал он должен не позднее 08:20, чему соответствует 2 вариант.
Ответ: 2.
Задание №3. Решение варианта №199 ОГЭ по математике. Ларин
На координатной прямой:
отмечены числа a , b и c.
Какое из следующих утверждений об этих числах верно?
Варианты ответа
Решение
По условию:
.
Допустим a = -2; b = 1; c = 3.
- <4 < 1 -неверно.
- 3/-2 > 0 — неверно.
- a+b<c -2+1 < 3 -верно.
- 1/1 <-1-неверно.
Ответ: 3.
Задание №4. Решение варианта №199 ОГЭ по математике Ларин
Найдите значение выражения: √(8*30)*√60.
Решение
√(8*30)*√60 = √(42*30*2*30) = 4*30 = 120.
Ответ: 120.
Задание №5. Решение варианта №199 ОГЭ по математике. Ларин
На рисунке изображен график движения автомобиля из пункта A в пункт B и автобуса из пункта B в пункт A.

Решение
Автобус проехал 240 км за 5 часов. Таким образом, его скорость равна 48 км/ч. Автомобиль проехал это же расстояние за 3 часа со скоростью 80 км/ч. Таким образом, скорость автомобиля больше скорости автобуса на 32 км/ч.
Ответ: 32.
Задание №6
Решите уравнение:
(9x+6)/7 + 3 = 7x/6.
Решение
Ответ: -32,4.
Задание №7. Решение варианта №199 ОГЭ по математике Ларин
Площадь земель крестьянского хозяйства, отведённая под посадку сельскохозяйственных культур, составляет 63 га и распределена между зерновыми культурами и картофелем в отношении 4:5. Сколько гектаров занимают зерновые культуры?
Решение
Пусть:
- 4x — зерновые,
- 5x — картофель.
Тогда .
Следовательно, зерновые занимают: 4*7=28.
Ответ: 28.
Задание №8
В городе из учебных заведений имеются школы, колледжи, училища и институты. Всего в городе 45 учебных заведений. Данные представлены на круговой диаграмме. Какое из утверждений относительно количества учебных заведений разных видов верно?
- 1) В городе более 30 школ.
- 2) В городе более трети всех учебных заведений – институты.
- 3) В городе школ, колледжей и училищ более 15 16 всех учебных заведений.
- 4) В городе примерно четверть всех учебных заведений – училища.
Решение
- неверно, так как сегмент школ не меньше чем 2/3 окружности.
- неверно, сегмент институтов меньше 1/3.
- неверно.
- верно.
Ответ: 4.
Задание №9. Решение варианта №199 ОГЭ по математике Ларин
Игральную кость бросают дважды. Найдите вероятность того, что наибольшее из двух выпавших чисел равно 5.
Решение
Общее количество исходов:
Исходы, где наибольшее 5 (первое число — первая кость, второе число — вторая кость):
15;25;35;45;55;54;53;52;51 — 9 исходов =n.
Вероятность:
Ответ: 0,25.
Задание №10
На рисунке изображены графики функций вида y=ax2+c.
Установите соответствие между графиками и знаками коэффициентов a и c.
- a>0, c>0.
- a>0, c<0.
- a<0, c<0.
- a<0, c>0.
Решение
При a>0 — ветви параболы вверх,
a<0 — вниз,
c>0 — ордината точки пересечения оси Oy над Ox, c<0 — под Ox.
⇒ A-2; Б-3; B-1; Г-4.
Ответ: 2314.
Задание №11
Дана арифметическая прогрессия (an), для которой a6 = — 30, a16= 150.
Найдите разность прогрессии.
Решение
Ответ: 18.
Задание №12. Решение варианта №199 ОГЭ по математике. Ларин
Найдите значение выражения:
при x = -0,25 и
Решение
Ответ: -8.
Задание №13
Закон Менделеева–Клапейрона можно записать в виде PV = vRT, где P — давление (в паскалях), V — объём (в м³ ), v — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К моль).
Пользуясь этой формулой, найдите количество вещества v (в молях), если T=700 К, P=20941,2 Па, V=9,5 м³.
Решение
Ответ: 34,2.
Задание №14
Укажите неравенство, решение которого изображено на рисунке:
- x² — 36 < 0.
- x² — 6x > 0.
- x² — 6x < 0.
- x² — 36 > 0.
Решение
Ответ: 3.
Задание №15
Лестницу длиной 2 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?
Решение
Задача сводится к нахождению катета прямоугольного треугольника, по теореме Пифагора:
√(2² — 1,2²) = √(4 — 1,44) = 1,6 м.
Ответ: 1,6.
Задание №16
В треугольнике АВС углы А и С равны 32° и 68° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
Решение
- (DB — биссектриса).
- ( — прямоугольный).
Ответ: 18.
Задание №17. Решение варианта №199 ОГЭ по математике Ларин
Периметр треугольника равен 56, одна из сторон равна 19, а радиус вписанной в него окружности равен 5.
Найдите площадь этого треугольника.
Решение
По формуле площади треугольника через его полу периметр и радиус вписанной окружности:
r = 2S/a+b+c, где a, b, c -стороны треугольника, а S — его площадь.
r = 5см, а P = a+b+c = 56см.
По формуле:
2S/56 = 5.
2S = 280.
S = 140 см².
Ответ: 140.
Задание №18
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 10.
Решение
- (свойство радиуса, проведенного в точку касания).
- (по гипотенузе и катету)
Ответ: 5.
Задание №19
В треугольнике ABC угол C равен 90°, AC=12, tg A=0,75. Найдите BC.
Решение
CB = AC*tgA = 12*0,75 =
Ответ: 9.
Задание №20. Решение варианта №199 ОГЭ по математике Ларин
Какие из следующих утверждений верны?
- Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон.
- Площадь круга меньше квадрата длины его диаметра.
- Существует квадрат, который не является ромбом.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
Решение
- Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон — верно (теорема Пифагора для полученных треугольников).
- Площадь круга меньше квадрата длины его диаметра — верно.
- Неверно.
Ответ: 12.
Задание №21
Решите уравнение:
Решение
Найдем ОДЗ:
Ответ: -5.
Задание №22. Решение варианта №199 ОГЭ по математике Ларин
. Поезд, двигаясь равномерно со скоростью 141 км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям со скоростью 6 км/ч, за 8 секунд. Найдите длину поезда в метрах.
Решение
- Пусть пешеход стоит, тогда скорость поезда относительно него:
кмч.
- Переведем секунды в часы:
6 c = 8/3600 = 1/ часа.
- Найдем длину по формуле расстояния:
км = 300 метров.
Ответ: 300.
Задание №23
Постройте график функции:
и определите, при каких значениях а прямая y=а будет пересекать построенный график в трех точках.
Решение
Рассмотрим . Найдем координаты вершины параболы:
; .
Построим график функции с учетом ограничения по х:
Рассмотрим — это гипербола, расположенная в первой и третьей координатных четвертях. С учетом ограничениях по х:
Объединим полученные кусочные функции:
Прямая — прямая, параллельная оси Ох. Три точки пересечения будет при a
Ответ:
Задание №24
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 12.
Решение
Рассмотрим : PK-диаметр описанной окружности
Ответ: 12.
Задание №25
Основания BC и AD трапеции ABCD равны соответственно 4 и 64, BD = 16. Докажите, что треугольники CBD и BDA подобны.
Решение
(накрест лежащие).
. С учетом п.1 ⇒
Ответ: треугольники CBD и BDA подобны.
Задание №26. Решение варианта №199 ОГЭ по математике Ларин
В трапеции ABCD с боковыми сторонами АВ = 9 и CD = 5 биссектриса угла D пересекает биссектрисы углов А и С в точках М и Nсоответственно, а биссектриса угла В пересекает те же две биссектрисы в точках L и K, причём точка K лежит на основании AD.
Найдите отношение МN : KL, если LM : KN = 3 : 7
Решение
1) (BL-биссектриса ), (накрест лежащие) ; AL-биссектриса , медиана и высота равнобедренного : и
2) : CD = DK = 5; ; . С учетом (1) — LN-средняя линия и AD = 14.
Ответ: 5/21.






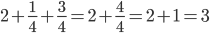

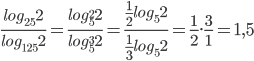
^2%7D%7B2g%7D.png)
^2%7D%7B2.10%7D=-frac%7B-frac%7B1%7D%7B4%7D.V^2%7D%7B20%7D.png)
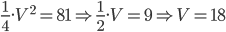
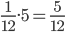
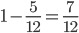
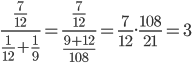
=x^2-3,75x-ln(x+2).png)
=2x-3,75--frac%7B1%7D%7Bx+2%7D.png)
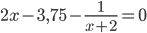
-3,75(x+2)-1%7D%7Bx+2%7D=0.png)
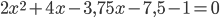
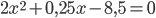
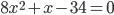
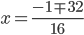
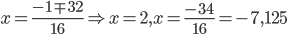
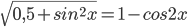
^2.png)
)^2.png)
^2.png)