Третье задание егэ математика профиль



СДАМ ГИА:

РЕШУ ЕГЭ

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

Математика профильного уровня

≡ Математика

Базовый уровень

Профильный уровень

Информатика

Русский язык

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Эксперту

Справочник

Карточки

Теория

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

10 марта

Как подготовиться к ЕГЭ и ОГЭ за 45 дней

6 марта

Изменения ВПР 2023

3 марта

Разместили утвержденное расписание ЕГЭ

27 января

Вариант экзамена блокадного Ленинграда

23 января

ДДОС-атака на Решу ЕГЭ. Шантаж.

6 января

Открываем новый сервис: «папки в избранном»

22 декабря

От­кры­ли но­вый пор­тал Ре­шу Олимп. Для под­го­тов­ки к пе­реч­не­вым олим­пи­а­дам!

4 ноября

Материалы для подготовки к итоговому сочинению 2022–2023

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

21 марта

Новый сервис: рисование

31 января

Внедрили тёмную тему!

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Каталог заданий.
Треугольники общего вида


Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

1

Тип 1 № 27591

Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30°.

Аналоги к заданию № 27591: 55255 55257 55303 530817 530892 55259 55261 55263 55265 55267 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора

Решение

·

·

Курс Д. Д. Гущина

·

Сообщить об ошибке · Помощь

2

Тип 1 № 27592

Площадь треугольника ABC равна 4, DE   — средняя линия, параллельная стороне AB. Найдите площадь треугольника CDE.

Аналоги к заданию № 27592: 55305 55353 549312 55307 55309 55311 55313 55315 55317 55319 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора

Решение

·

·

Курс Д. Д. Гущина

·

Сообщить об ошибке · Помощь

3

Тип 1 № 27623

У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?

Аналоги к заданию № 27623: 56755 56801 56805 513617 56757 56759 56761 56763 56765 56767 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора

Решение

·

·

Курс Д. Д. Гущина

·

Сообщить об ошибке · Помощь

4

Тип 1 № 27743

В треугольнике ABC угол A равен 40 градусов, внешний угол при вершине B равен 102 градусов. Найдите угол C. Ответ дайте в градусах.

Аналоги к заданию № 27743: 46035 46089 505144 505165 46037 46039 46041 46043 46045 46047 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.1 Величина угла, градусная мера угла

Решение

·

·

Курс Д. Д. Гущина

·

Сообщить об ошибке · Помощь

5

Тип 1 № 27752

Углы треугольника относятся как 2 : 3 : 4. Найдите меньший из них. Ответ дайте в градусах.

Аналоги к заданию № 27752: 46705 46707 46709 46711 46713 46715 46717 46719 46721 46723 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.1 Величина угла, градусная мера угла

Решение

·

·

Курс Д. Д. Гущина

·

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

О проекте · Редакция · Правовая информация · О рекламе

© Гущин Д. Д., 2011—2023

Источник

ЕГЭ по математике Профиль. Задание 3: Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».

ЕГЭ Профиль. Задание № 3

АЛГОРИТМ ВЫПОЛНЕНИЯ

Задание № 3 рассчитано на умение использовать геометрические понятия и теоремы для решения практических задач, связанных с нахождением геометрических величин (длин, углов, площадей).

Задание состоит из текстовой задачи и рисунка. Необходимо внимательно прочитать текст, решить задачу и записать результат в поле ответа в тексте работы и бланк ответов. Если в итоге получилась обыкновенная дробь, её нужно перевести в десятичную.

Чтобы успешно справиться с данным заданием, нужно повторить определения и свойства плоских фигур:

  • треугольники:
  • четырёхугольники, в частности параллелограмм, прямоугольник, ромб, квадрат, трапеция;
  • многоугольники, в частности правильные многоугольники;
  • окружность и круг, описанные и вписанные в многоугольник окружности;
  • площади треугольника, параллелограмма, трапеции, круга, сектора.

План выполнения:

  1. Внимательно прочитайте задачу.
  2. При необходимости выполните на чертеже дополнительные построения.
  3. Выполните арифметические вычисления.
  4. Запишите полученное число в поле ответа КИМ и бланк ответов № 1.

Задачи на Прямоугольные треугольники

При подготовке следует повторить значение синуса, косинуса и тангенса основных углов; отношения между сторонами прямоугольника; теорему Пифагора.

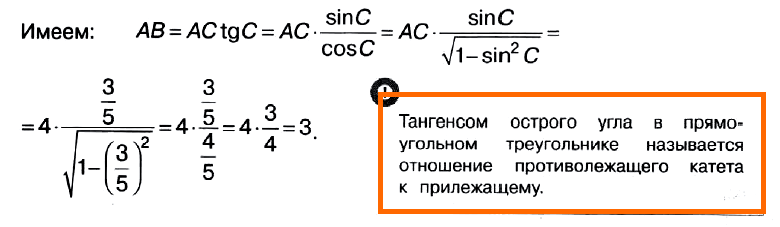
ЕГЭ по математике Профиль. Задание 3

Задача № 3 (1). В треугольнике АВС угол А равен 90°, АС = 4, sin C = 3/5. Найдите АВ.

Решение:
ЕГЭ по математике Профиль. Задание 3

Ответ: 3.

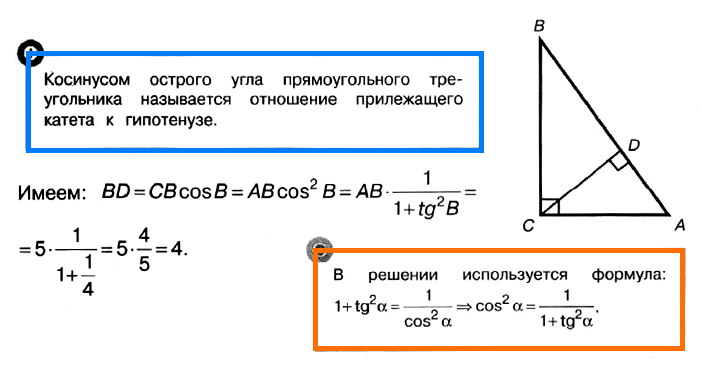
Задача № 3 (2). В треугольнике АВС угол С равен 90°, CD – высота, АВ = 5, tg B = 1/2. Найдите BD.

Решение:
ЕГЭ по математике Профиль. Задание 3

Ответ: 4.

Задачи на Равнобедренные треугольники

ЕГЭ по математике Профиль. Задание 3

Задача № 3 (3). В треугольнике АВС АС = ВС = 10, sin А = 3/5. Найдите АВ.

Решение:
ЕГЭ по математике Профиль. Задание 3

Ответ: 16.

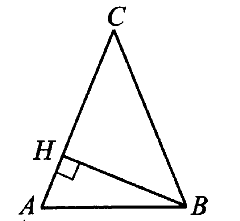
Задача № 3 (4). В треугольнике АВС АС = ВС = 25, sin BAC = 3/5. Найдите высоту АН.

Решение:
ЕГЭ по математике Профиль. Задание 3

Ответ: 24.

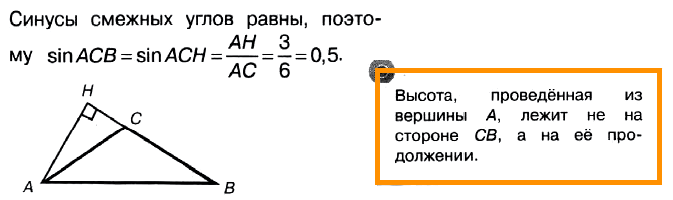
Задача № 3 (5). В тупоугольном треугольнике АВС АС = ВС = 6, высота АН = 3. Найдите sin АСВ.

Решение:
ЕГЭ по математике Профиль. Задание 3

Ответ: 0,5.

Задачи на Разносторонние треугольники

Задача № 3 (6). Площадь треугольника АВС равна 8. DE — средняя линия CDE.

Решение:
ЕГЭ по математике Профиль. Задание 3

Ответ: 2.

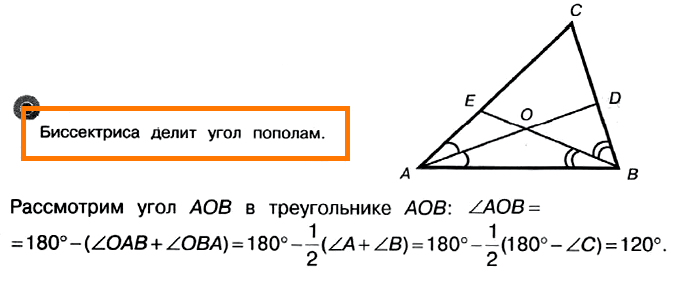
Задача № 3 (7). В треугольнике АВС угол С равен 60°, AD и BE — биссектрисы, пересекающиеся в точке О. Найдите угол АОВ. Ответ дайте в градусах.

Решение:
ЕГЭ по математике Профиль. Задание 3

Ответ: 120.

Задачи на Параллелограммы

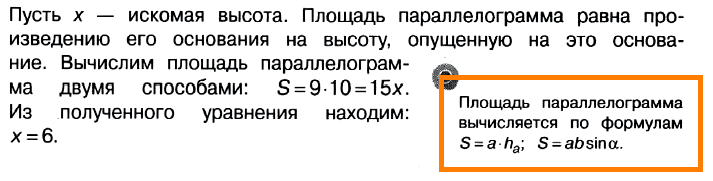
ЕГЭ по математике Профиль. Задание 3

Задача № 3 (8). Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.

Решение:
ЕГЭ по математике Профиль. Задание 3

Ответ: 6.

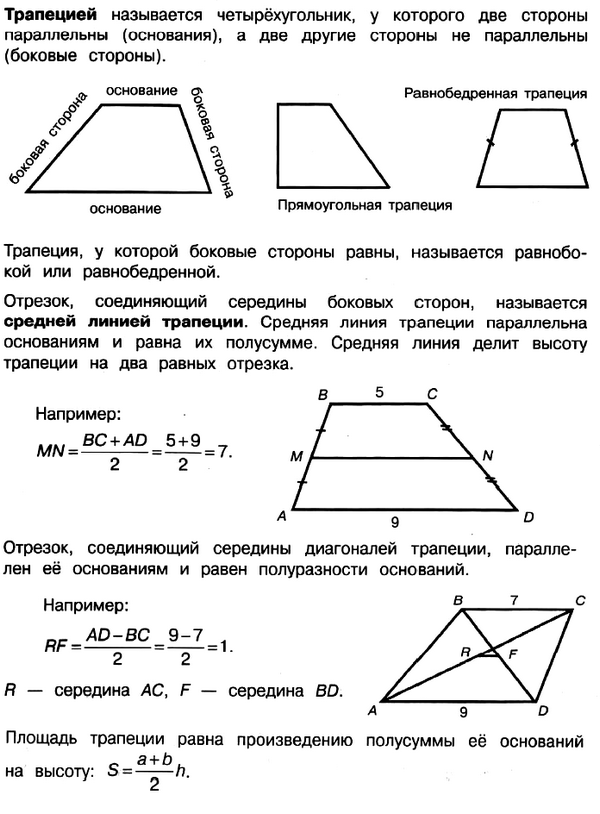
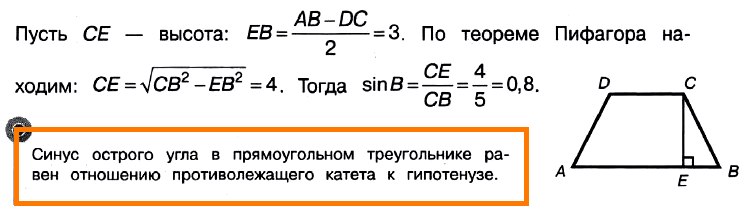
Задачи на Трапецию

ЕГЭ по математике Профиль. Задание 3

Задача № 3 (9). 

Решение:
ЕГЭ по математике Профиль. Задание 3

Ответ: 0,8.

Задачи на Центральные и вписанные углы

При подготовке нужно повторить свойства центральных и вписанных углов, понятия хорды, касательной и секущей к окружности; знать правила нахождения величин центральных и вписанных углов, дуг окружностей.

ЕГЭ по математике Профиль. Задание 3

Задача № 3 (10). Найдите угол АСВ, если вписанные углы ADB и DAE опираются на дуги окружности, градусные величины которых равны соответственно 158° и 38°. Ответ дайте в градусах.

Решение:
ЕГЭ по математике Профиль. Задание 3

Ответ: 60.

Задачи на Вписанные и описанные окружности

ЕГЭ по математике Профиль. Задание 3

Задача № 3 (11). В четырёхугольник ABCD вписана окружность, АВ = 4, CD = 6. Найдите периметр четырёхугольника ABCD.

Решение:
ЕГЭ по математике Профиль. Задание 3

Ответ: 20.

Задача № 3 (12). 

Решение:
ЕГЭ по математике Профиль. Задание 3

Ответ: 1.

Тренировочные задания с самопроверкой

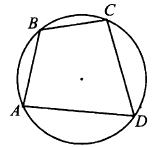
№ 3.1. Стороны АВ, ВС, CD и AD четырёхугольника ABCD стягивают дуги описанной окружности, градусные величины которых равны соответственно 75°, 63°, 93°, 129° (см. рис.). Найдите угол BCD. Ответ дайте в градусах.
ЕГЭ по математике Профиль. Задание 3

Открыть ОТВЕТ

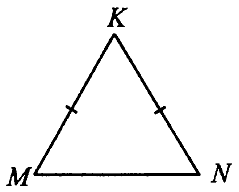
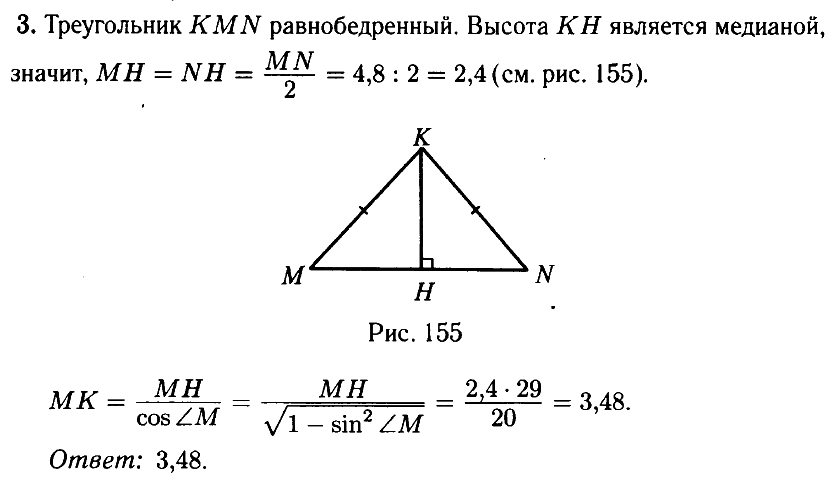
ЕГЭ по математике Профиль. Задание 3

№ 3.2. В треугольнике MNK известно, что МК = NK, MN = 4,8, sin М = 21/29 (см. рис.). Найдите МК.
ЕГЭ по математике Профиль. Задание 3

Открыть ОТВЕТ

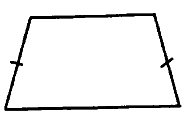
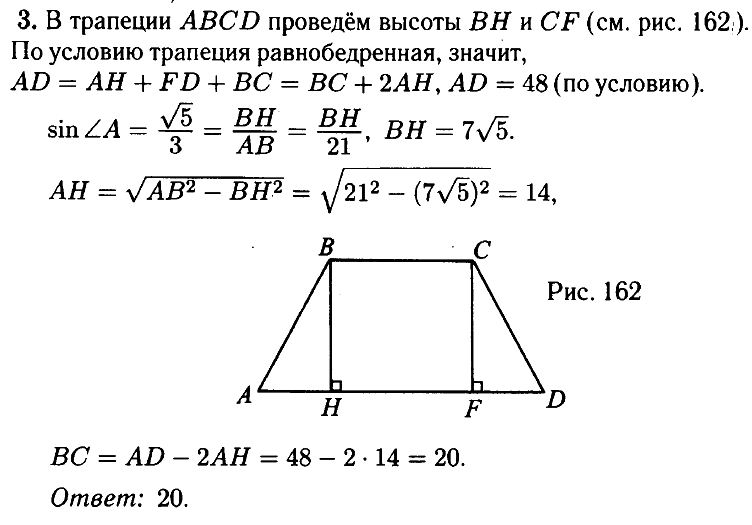
ЕГЭ по математике Профиль. Задание 3

№ 3.3. Большее основание равнобедренной трапеции равно 48. Боковая сторона равна 21. Синус острого угла равен √5/3 (см. рис.). Найдите меньшее основание.
ЕГЭ по математике Профиль. Задание 3

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 3

№ 3.4. В треугольнике АВС известно, что АС = ВС, высота ВН равна 9, АВ = 3√13 (см. рис.). Найдите tg АВС.
ЕГЭ по математике Профиль. Задание 3

Открыть ОТВЕТ

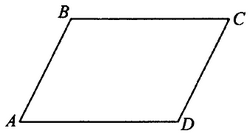
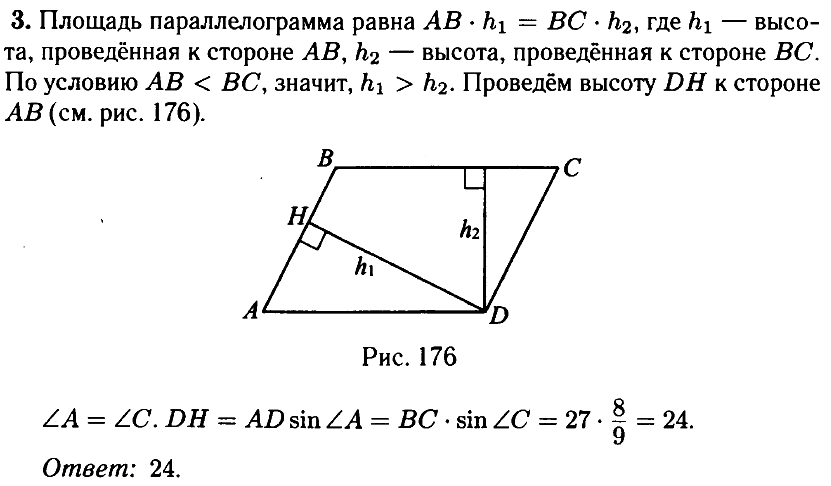
ЕГЭ по математике Профиль. Задание 3

№ 3.5. В параллелограмме ABCD известно, что АВ = 18, ВС = 27, sin ∠C = 8/9 (см. рис.). Найдите большую высоту параллелограмма.
ЕГЭ по математике Профиль. Задание 3

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 3

Вы смотрели: ЕГЭ по математике Профиль. Задание 3: Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».


Просмотров:
18 617

Источник

За это задание ты можешь получить 1 балл. На решение дается около 3 минут. Уровень сложности: базовый.
Средний процент выполнения: 95%
Ответом к заданию 3 по математике (профильной) может быть целое число или конечная десятичная дробь.

Разбор сложных заданий в тг-канале

Задачи для практики

Задача 1

Перед началом первого тура чемпионата по спортивным нардам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует $56$ игроков, среди которых $12$ спортсменов из России, в том числе Евгений Победкин. Найдите вероятность того, что в первом туре Евгений Победкин будет играть с каким-либо игроком из России.

Решение

Будем считать случайным экспериментом выбор соперника Евгения Победкина. Этот эксперимент имеет $56-1 = 55$ равновозможных исходов (сам с собой он играть не может!). При этом $12 — 1 = 11$ исходов благо приятствуют событию «Евгений Победкин будет играть со спортсменом из России» (так как есть $11$ спортсменов из России, не считая самого Евгения Победкина). По определению искомая вероятность равна ${11}/{55} = 0.2$.

Ответ: 0.2

Задача 2

Перед началом первого тура чемпионата по настольному теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует $76$ спортсменов, среди которых $46$ спортсменов из России, в том числе Григорий Соколенко. Найдите вероятность того, что в первом туре Григорий Соколенко будет играть с каким-либо теннисистом из России.

Решение

Будем считать случайным экспериментом выбор соперника Григория Соколенко. Этот эксперимент имеет $76-1=75$ равновозможных исходов (сам с собой он играть не может!). При этом $46-1=45$ исходов благоприятствуют событию «Григорий Соколенко будет играть со спортсменом из России» (так как есть $45$ спортсменов из России, не считая самого Григория Соколенко). По определению, искомая вероятность равна ${45} / {75}=0{,}6$.

Ответ: 0.6

Задача 3

Вероятность того, что новая электрическая кофемашина прослужит больше года, равна $0{,}92$. Вероятность того, что она прослужит больше двух лет, равна $0{,}85$. Найдите вероятность того, что она прослужит меньше двух лет, но больше года.

Решение

Заметим, что из событий «кофемашина прослужит меньше года», «кофемашина прослужит от 1 до 2 лет» и «кофемашина прослужит больше двух лет» произойдёт обязательно ровно одно, то есть, говоря математическим языком, они попарно несовместны, а их объединение — достоверное событие. Следовательно, сумма вероятностей этих событий равна 1.

При этом события «кофемашина прослужит меньше года» и «кофемашина прослужит больше года» противоположны, поэтому вероятность события «кофемашина прослужит меньше года» равна 1 — 0.92 = 0.08. Заполним таблицу.

Событие Прослужит меньше года Прослужит от 1 до 2 лет Прослужит больше двух лет
Вероятность 0.08 ? 0.85

Отсюда искомая вероятность равна 1 — 0.08 — 0.85 = 0.07.

Ответ: 0.07

Задача 4

В некотором городе из $5000$ появившихся на свет младенцев $2075$ мальчиков. Найдите частоту рождения девочек в этом городе. Результат округлите до сотых.

Решение

Из каждых $5000$ появившихся на свет младенцев девочек $5000 — 2075 = 2925$. По определению искомая частота равна ${2925}/{5000} = 0.585 ≈ 0.59$.

Ответ: 0.59

Задача 5

На экзамене по физике студент отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Элект-
ричество», равна $0{,}3$. Вероятность того, что это вопрос по теме «Механика», равна $0{,}42$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене студенту достанется вопрос по одной из этих двух тем.

Решение

Из условия следует, что события A = «достанется вопрос по теме Электричество» и B = «достанется вопрос по теме Механика» несовместны. Действительно, нет билетов, относящихся к обоим этим темам одновременно. Событие «достанется вопрос по одной из этих двух тем» — это объединение событий A и B (A $∪$ B). По формуле вероятности объединения несовместных событий получим, что искомая вероятность равна P(A $∪$ B) = P(A) + P(B) = 0.3 + 0.42 = 0.72.

Ответ: 0.72

Задача 6

При производстве в среднем на каждые $468$ исправных телефонов приходится $32$ неисправных. Найдите вероятность того, что случайно выбранный телефон окажется неисправным.

Решение

Из условия следует, что в среднем из каждых $468 + 32 = 500$ телефонов $32$ неисправных. По определению искомая вероятность равна ${32}/{500} = 0.064$.

Ответ: 0.064

Задача 7

Завод выпускает съёмные жёсткие диски. В среднем $15$ дисков из $300$ имеют скрытые дефекты. Найдите вероятность того, что купленный диск окажется без дефектов.

Решение

По определению вероятность покупки диска с дефектом равна ${15}/{300} = 0.05$. Тогда по формуле вероятности противоположного события вероятность купить диск без дефекта равна $1 — 0.05 = 0.95$.

Ответ: 0.95

Задача 8

Фабрика выпускает туфли. В среднем $12$ пар туфель из $200$ пар имеют скрытые дефекты. Найдите вероятность того, что купленная пара туфель окажется без дефектов.

Решение

Из условия следует, что в среднем из каждых $200$ пар $200 — 12 = 188$ не имеют дефектов. Тогда искомая вероятность равна ${188}/{200} = 0.94$.

Ответ: 0.94

Задача 9

В чемпионате мира участвуют $16$ команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: $1$, $1$, $1$, $1$, $2$, $2$, $2$, $2$, $3$, $3$, $3$, $3$, $4$, $4$, $4$, $4$. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда «Плутон», участвующая в чемпионате, окажется во второй группе?

Решение

Будем считать, что случайный эксперимент заключается в том, что капитан команды «Плутон» тянет карточку с номером группы. У этого эксперимента $16$ равновозможных исходов (по числу карточек). Событию «Команда „ Плутон“ окажется во второй группе» благоприятствуют $4$ исхода (количество карточек с номером $2$). По определению вероятности искомая вероятность равна ${4} / {16}=0{,}25$.

Ответ: 0.25

Задача 10

На конференцию приехали $7$ учёных из Китая, $5$ — из России и $8$ — из Египта. Каждый из них делает на конференции один доклад. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад учёного из России.

Решение

Будем считать, что случайный эксперимент заключается в том, что выбирается учёный, который будет выступать восьмым. Всего существует $20$ равновозможных исходов ($7+5+8=20$ учёных, все имеют равные шансы выступить восьмыми). Событию «Восьмым будет выступать учёный из России» благоприятствуют $5$ исходов. По определению искомая вероятность равна ${5}/{20} = {1}/{4} = 0.25$.

Ответ: 0.25

Задача 11

В чемпионате по спортивной гимнастике участвуют $40$ спортсменов: $16$ — из России, $9$ — из Франции, остальные — из Беларуси. Порядок, в котором выступают гимнасты, определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, окажется из Беларуси.

Решение

Из Беларуси $40-16-9 = 15$ спортсменов. Будем считать, что случайный эксперимент заключается в том, что выбирается спортсмен, который будет выступать первым. Всего существует $40$ равновозможных исходов ($40$ спортсменов, все имеют равные шансы выступить первыми). Событию Первым будет выступать спортсмен из Беларуси благоприятствуют $15$ исходов. По определению искомая вероятность равна ${15}/{40} = {3}/{8} = 0.375$.

Ответ: 0.375

Задача 12

В кармане у Валерия было пять конфет — «Птичье молоко», «Ромашка», «Черноморочка», «Мишка косолапый» и «Ласточка», а также ключи от квартиры. Вынимая ключи, Валерий случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Ромашка».

Решение

Валерий мог с одинаковой вероятностью выронить каждую из пяти конфет, значит, искомая вероятность равна ${1}/{5} = 0.2$.

Ответ: 0.2

Задача 13

Света, Марина, Оля и Ксюша бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должна будет Света.

Решение

Жребий имеет $4$ равновозможных исхода (все девочки имеют равные шансы начинать игру). Значит, вероятность события «Игру будет начинать Света» равна ${1} / {4}=0{,}25$.

Ответ: 0.25

Рекомендуемые курсы подготовки

Источник

Задание №3 ЕГЭ 2023 по математике для 11 класса профильный уровень все возможные  тренировочные задачи с ответами из банка заданий ФИПИ, новые прототипы заданий ЕГЭ 2023 для подготовки.

  • Прямоугольный треугольник задачи с ответами
  • Вписанные окружности задачи с ответами
  • Описанные окружности задачи с ответами
  • Равнобедренный треугольник задачи с ответами
  • Треугольник общего вида задачи с ответами
  • Квадрат, прямоугольник, ромб задачи с ответами
  • Трапеция задачи с ответами
  • Центральный и вписанные углы задачи с ответами
  • Окружность, касательная, хорда задачи с ответами

Прямоугольный треугольник задание №3 ЕГЭ профиль математика задачи с ответами:

Вписанные окружности задание №3 ЕГЭ профиль математика задачи с ответами:

Описанные окружности задание №3 ЕГЭ профиль математика задачи с ответами:

Равнобедренный треугольник задание №3 ЕГЭ профиль математика задачи с ответами:

Треугольник общего вида задание №3 ЕГЭ профиль математика задачи с ответами:

Квадрат, ромб, прямоугольник задание №3 ЕГЭ профиль математика задачи с ответами:

Трапеция задание №3 ЕГЭ профиль математика задачи с ответами:

Центральный и вписанные углы задание №3 ЕГЭ профиль математика задачи с ответами:

Окружность, касательная хорда задание №3 ЕГЭ профиль математика задачи с ответами:

1)Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10.

Правильный ответ: 24

2)Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.

Правильный ответ: 6

3)В треугольнике ABC угол C равен 90 , угол В равен 58 , CD медиана. Найдите угол ACD. Ответ дайте в градусах.

Правильный ответ: 32

4)Острый угол прямоугольного треугольника равен 32 . Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.

Правильный ответ: 61

5)Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.

Правильный ответ: 45

6)Один из углов прямоугольного треугольника равен 29 . Найдите угол между высотой и биссектрисой, проведёнными из вершины прямого угла. Ответ дайте в градусах.

Правильный ответ: 16

7)В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла, равен 21°. Найдите меньший угол данного треугольника. Ответ дайте в градусах.

Правильный ответ: 24

8)Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Правильный ответ: 42

9)В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 40°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.

Правильный ответ: 65

10)Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах

Правильный ответ: 21

11)Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 14°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.

Правильный ответ: 21

12)В треугольнике ABC угол C равен 90 , CH — высота, угол A равен 30°, AB 2 . Найдите AH.

Правильный ответ: 1,5

13)В треугольнике ABC угол C равен 90°, CH — высота, угол A равен 30°, AB 4 . Найдите BH.

Правильный ответ: 1

14)Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Боковая сторона треугольника равна 10. Найдите площадь этого треугольника.

Правильный ответ: 25

15)Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150°. Боковая сторона треугольника равна 20. Найдите площадь этого треугольника.

Правильный ответ: 100

16)Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника.

Правильный ответ: 12

17)Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Найдите боковую сторону треугольника, если его площадь равна 25.

Правильный ответ: 10

18)Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150°. Найдите боковую сторону треугольника, если его площадь равна 100.

Правильный ответ: 20

19)В треугольнике ABC угол A равен 38°, AC = BC. Найдите угол C. Ответ дайте в градусах.

Правильный ответ: 104

20)В треугольнике ABC угол C равен 118°, AC = BC. Найдите угол A. Ответ дайте в градусах.

Правильный ответ: 31

21)В треугольнике ABC AC = BC, угол C равен 52°. Найдите внешний угол CBD. Ответ дайте в градусах.

Правильный ответ: 116

22)В треугольнике ABC AC = BC. Внешний угол при вершине B равен 122°. Найдите угол C. Ответ дайте в градусах.

Правильный ответ: 64

23)В треугольнике ABC AB = BC. Внешний угол при вершине B равен 138°. Найдите угол C. Ответ дайте в градусах.

Правильный ответ: 69

24)Больший угол равнобедренного треугольника равен 98°. Найдите меньший угол. Ответ дайте в градусах.

Правильный ответ: 41

25)Один угол равнобедренного треугольника на 90° больше другого. Найдите меньший угол. Ответ дайте в градусах.

Правильный ответ: 30

26)В треугольнике ABC AC=BC, угол С равен 120 градусов, AB= 2√3. Найдите AC.

Правильный ответ: 2

27)Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30°.

Правильный ответ: 24

28)Площадь треугольника ABC равна 4. DE — средняя линия. Найдите площадь треугольника CDE.

Правильный ответ: 1

29)У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?

Правильный ответ: 6

30)В треугольнике ABC угол A равен 40°, внешний угол при вершине B равен 102°. Найдите угол C. Ответ дайте в градусах.

Правильный ответ: 62

31)Углы треугольника относятся как 2: 3: 4. Найдите меньший из них.

Правильный ответ: 40

32)В треугольнике ABC угол A равен 30°, CH — высота, угол BCH равен 22°. Найдите угол ACB. Ответ дайте в градусах.

Правильный ответ: 38

33)В треугольнике ABC AD — биссектриса, угол C равен 50°, угол CAD равен 28°. Найдите угол B. Ответ дайте в градусах.

Правильный ответ: 74

34)В треугольнике ABC AD — биссектриса, угол C равен 30°, угол BAD равен 22°. Найдите угол ADB. Ответ дайте в градусах.

Правильный ответ: 52

35)В треугольнике ABC угол A равен 72°, а углы B и C — острые. BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.

Правильный ответ: 108

36)Два угла треугольника равны 58° и 72°. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.

Правильный ответ: 130

37)В треугольнике ABC угол C равен 58°, AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол AOB. Ответ дайте в градусах.

Правильный ответ: 119

38)В треугольнике ABC CH — высота, AD — биссектриса, O — точка пересечения CH и AD, угол BAD равен 26°. Найдите угол AOC. Ответ дайте в градусах.

Правильный ответ: 116

39)В треугольнике ABC проведена биссектриса AD и AB = AD = CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.

Правильный ответ: 36

40)В треугольнике ABC угол A равен 44°, угол C равен 62°. На продолжении стороны AB отложен отрезок BD = BC. Найдите угол D треугольника BCD. Ответ дайте в градусах.

Правильный ответ: 37

41)В треугольнике ABC угол B равен 45°, угол C равен 85°, AD — биссектриса, E — такая точка на AB, что AE = AC. Найдите угол BDE. Ответ дайте в градусах.

Правильный ответ: 40

42)В треугольнике ABC угол A равен 30°, угол B равен 86°, CD — биссектриса внешнего угла при вершине C, причем точка D лежит на прямой AB. На продолжении стороны AC за точку C выбрана такая точка E, что CE = CB. Найдите угол BDE. Ответ дайте в градусах.

Правильный ответ: 56

43)В треугольнике ABC угол A равен 60°, угол B равен 82°. AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.

Правильный ответ: 49

44)В треугольнике ABC угол A равен 60°, угол B равен 82°. AD, BE и CF — высоты, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.

Правильный ответ: 82

45)Площадь треугольника ABC равна 12. DE – средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.

Правильный ответ: 9

46)Найдите площадь квадрата, если его диагональ равна 1

Правильный ответ: 0,5

47)Найдите диагональ квадрата, если его площадь равна 2.

Правильный ответ: 2

48)Найдите площадь прямоугольника, если его периметр равен 18, и одна сторона на 3 больше другой.

Правильный ответ: 18

49)Площадь прямоугольника равна 18. Найдите его большую сторону, если она на 3 больше меньшей стороны.

Правильный ответ: 6

50)Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1:2.

Правильный ответ: 18

51)Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1:2.

Правильный ответ: 18

52)Периметр прямоугольника равен 42, а площадь 98. Найдите большую сторону прямоугольника.

Правильный ответ: 14

53)Периметр прямоугольника равен 28, а диагональ равна 10. Найдите площадь этого прямоугольника.

Правильный ответ: 48

54)Периметр прямоугольника равен 34, а площадь равна 60. Найдите диагональ этого прямоугольника.

Правильный ответ: 13 

56)Сторона прямоугольника относится к его диагонали, как 4:5, а другая сторона равна 6. Найдите площадь прямоугольника.

Правильный ответ: 48

57)Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность?

Правильный ответ: 2

58)Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.

Правильный ответ: 30

59)Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.

Правильный ответ: 6

60)Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.

Правильный ответ: 8

61)Найдите площадь ромба, если его высота равна 2, а острый угол 30 .

Правильный ответ: 8

62)Найдите площадь ромба, если его диагонали равны 4 и 12.

Правильный ответ: 24

63)Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.

Правильный ответ: 3

64)Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.

Правильный ответ: 2

65)Сумма двух углов параллелограмма равна 100°. Найдите один из оставшихся углов. Ответ дайте в градусах.

Правильный ответ: 130

66)Один угол параллелограмма больше другого на 70°. Найдите больший угол. Ответ дайте в градусах.

Правильный ответ: 125

67)Диагональ параллелограмма образует с двумя его сторонами углы 26° и 34°. Найдите больший угол параллелограмма. Ответ дайте в градусах.

Правильный ответ: 120

68)Периметр параллелограмма равен 46. Одна сторона параллелограмма на 3 больше другой. Найдите меньшую сторону параллелограмма.

Правильный ответ: 10

69)Диагональ прямоугольника вдвое больше одной из его сторон. Найдите больший из углов, который образует диагональ со сторонами прямоугольника? Ответ выразите в градусах.

Правильный ответ: 60

70)Найдите высоту ромба, сторона которого равна √3, а острый угол равен 60°. 

Правильный ответ:

71)Найдите больший угол параллелограмма, если два его угла относятся как 3:7. Ответ дайте в градусах.

Правильный ответ: 1,5

72)Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.

Правильный ответ: 126

73)Две стороны параллелограмма относятся как 3:4, а периметр его равен 70. Найдите большую сторону параллелограмма.

Правильный ответ: 90

74)Боковая сторона равнобедренного треугольника равна 10. Из точки, взятой на основании этого треугольника, проведены две прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма.

Правильный ответ: 20

75)Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4:3, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.

Правильный ответ: 28

76)Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.

Правильный ответ: 10

77)Найдите большую диагональ ромба, сторона которого равна √3, а острый угол равен 60°.

Правильный ответ: 3

78)Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба.

Правильный ответ: 48

79)В ромбе ABCD угол ABC равен 122°. Найдите угол ACD. Ответ дайте в градусах.

Правильный ответ: 29

80)В ромбе ABCD угол ACD равен 43°. Найдите угол ABC. Ответ дайте в градусах.

Правильный ответ: 94

81)Площадь параллелограмма ABCD равна 189. Точка E — середина стороны AD. Найдите площадь трапеции AECB.

Правильный ответ: 141,75

82)Площадь параллелограмма ABCD равна 153. Найдите площадь параллелограмма A’B’C’D’, вершинами которого являются середины сторон данного параллелограмма.

Правильный ответ: 76,5

83)Площадь параллелограмма ABCD равна 176. Точка E — середина стороны CD. Найдите площадь треугольника ADE.

Правильный ответ: 44

84)Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.

Правильный ответ: 9

85)Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.

Правильный ответ: 0,96

86)Основания равнобедренной трапеции равны 43 и 73. Косинус острого угла трапеции равен 5/7 . Найдите боковую сторону.

Правильный ответ: 21

87)Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен 5/11 . Найдите высоту трапеции.

Правильный ответ: 10

88)Меньшее основание равнобедренной трапеции равно 23. Высота трапеции равна 39. Тангенс острого угла равен 13/8 . Найдите большее основание.

Правильный ответ: 71

89)Основания равнобедренной трапеции равны 17 и 87. Высота трапеции равна 14. Найдите тангенс острого угла.

Правильный ответ: 0,4

90)Основания трапеции равны 8 и 34, площадь равна 168. Найдите ее высоту.

Правильный ответ: 8

91)Основание трапеции равно 13, высота равна 5, а площадь равна 50. Найдите второе основание трапеции.

Правильный ответ: 7

92)Высота трапеции равна 10, площадь равна 150. Найдите среднюю линию трапеции.

Правильный ответ: 15

93)Средняя линия трапеции равна 12, площадь равна 96. Найдите высоту трапеции.

Правильный ответ: 8

94)Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.

Правильный ответ: 160

95)Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.

Правильный ответ: 30

96)Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 45°.

Правильный ответ: 16

97)Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в градусах.

Правильный ответ: 45

98)Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.

Правильный ответ: 160

99)Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции.

Правильный ответ: 5

99)Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150 . Найдите площадь трапеции.

Правильный ответ: 42

100)Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.

Правильный ответ: 30

101)Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 50 ? Ответ дайте в градусах.

Правильный ответ: 115

102)Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.

Правильный ответ: 38

103)Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.

Правильный ответ: 5

104)В равнобедренной трапеции большее основание равно 25, боковая сторона равна 10, угол между ними 60°. Найдите меньшее основание.

Правильный ответ: 15

105)В равнобедренной трапеции основания равны 12 и 27, острый угол равен 60°. Найдите ее периметр.

Правильный ответ: 69

106)Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.

Правильный ответ: 23

107)Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.

Правильный ответ: 10

108)Основания равнобедренной трапеции равны 15 и 9, один из углов равен 45 . Найдите высоту трапеции.

Правильный ответ: 3

109)Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.

Правильный ответ: 0,5

110)В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.

Правильный ответ: 12

111)Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону.

Правильный ответ: 5

112)Найдите величину острого вписанного угла, опирающегося на хорду, равную радиусу окружности. Ответ дайте в градусах.

Правильный ответ: 30

113)Найдите хорду, на которую опирается угол 30 , вписанный в окружность радиуса 3.

Правильный ответ: 3

114)Чему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

Правильный ответ: 150

115)Найдите хорду, на которую опирается угол 120°, вписанный в окружность радиуса √3.

Правильный ответ: 3

116)Дуга окружности AC, не содержащая точки B, имеет градусную меру 200°, а дуга окружности BC, не содержащая точки A, имеет градусную меру 80 . Найдите вписанный угол ACB. Ответ дайте в градусах.

Правильный ответ: 40

117)Хорда AB делит окружность на две дуги, градусные меры которых относятся как 5:7. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.

Правильный ответ: 105

118)Точки A, B, C расположенные на окружности, делят ее на три дуги, градусные меры которых относятся как 1:3:5. Найдите больший угол треугольника ABC. Ответ дайте в градусах.

Правильный ответ: 100

119)AC и BD — диаметры окружности с центром O. Угол ACB равен 38 . Найдите угол AOD. Ответ дайте в градусах.

Правильный ответ: 104

120)В окружности с центром O AC и BD — диаметры. Центральный угол AOD равен 110°. Найдите вписанный угол ACB. Ответ дайте в градусах.

Правильный ответ: 35

121)Найдите угол ABC. Ответ дайте в градусах.

Правильный ответ: 45

122)Найдите градусную меру дуги AC окружности, на которую опирается угол ABC. Ответ дайте в градусах.

Правильный ответ: 45

123)Хорда AB стягивает дугу окружности в 92°. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах

Правильный ответ: 46

124)Угол между хордой AB и касательной BC к окружности равен 32°. Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.

Правильный ответ: 64

125)Через концы A, B дуги окружности в 62° проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.

Правильный ответ: 118

126)Касательные CA и CB к окружности образуют угол ACB, равный 122°. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.

Правильный ответ: 58

127)Найдите угол ACO, если его сторона CA касается окружности, О- центр окружности, сторона CO пересекает окружность в точке B, а дуга AB окружности, заключенная внутри этого угла равна 64°. Ответ дайте в градусах.

Правильный ответ: 26

128)Угол ACO равен 28°, где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.

Правильный ответ: 62

129)Найдите угол ACO, если его сторона CA касается окружности, O— центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 116°. Ответ дайте в градусах.

Правильный ответ: 26

130)Угол ACO равен 24°. Его сторона CA касается окружности с центром в точке O. Найдите градусную меру дуги AD окружности, заключенной внутри этого угла. Ответ дайте в градусах.

Правильный ответ: 114

131)Найдите угол ACB, если вписанные углы ADB и DAE опираются на дуги окружности, градусные меры которых равны соответственно 118° и 38°. Ответ дайте в градусах.

Правильный ответ: 40

132)Угол ACB равен 42°. Градусная мера дуги AB окружности, не содержащей точек D и E, равна 124°. Найдите угол DAE. Ответ дайте в градусах.

Правильный ответ: 20

Задание 3 ЕГЭ математика 11 класс рабочая тетрадь И.В. Ященко

Тренировочные варианты ЕГЭ по математике 11 класс с ответами

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник
3652 В группе 16 человек, среди них — Анна и Татьяна. Группу случайным образом делят на 4 одинаковые по численности подгруппы. Найдите вероятность того, что Анна и Татьяна окажутся в одной подгруппе.
Решение		 В группе 16 человек, среди них — Анна и Татьяна ! Статград 28-02-2023 11 класс Вариант МА2210309 Задание 3 ...X
3588 Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 16 шахматистов, среди которых 4 спортсмена из России, в том числе Фёдор Волков. Найдите вероятность того, что в первом туре Фёдор Волков будет играть с каким-либо шахматистом из России
Решение		 Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия ! 36 вариантов ФИПИ Ященко 2023 Вариант 18 Задание 3 ...X
3574 На чемпионате по прыжкам в воду выступают 30 спортсменов, среди них
3 прыгуна из Польши и 4 прыгуна из Дании. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что четвёртым будет
выступать прыгун из Польши
Решение		 На чемпионате по прыжкам в воду выступают 30 спортсменов, среди них 3 прыгуна из Польши и 4 прыгуна из Дании ! Тренировочная работа по математике №2 СтатГрад 11 класс 13.12.2022 Задание 3 Вариант МА2210209 ...X
3565 Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже 36,8° С равна 0,71. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8° С или выше
Решение		 Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже 36,8° С равна 0,71 ! 36 вариантов ФИПИ Ященко 2023 Вариант 16 Задание 3 ...X
3555 Из множества натуральных чисел от 56 до 80 (включительно) на удачу выбирают одно число. Какова вероятность того, что оно делится на 4?
Решение		 Из множества натуральных чисел от 56 до 80 (включительно) на удачу выбирают одно число ! 36 вариантов ФИПИ Ященко 2023 Вариант 14 Задание 3 ...X
3546 Рассмотрим случайный телефонный номер. Какова вероятность того, что среди трёх последних цифр этого номера хотя бы две цифры одинаковы?
Решение		 Рассмотрим случайный телефонный номер. Какова вероятность того, что среди трёх последних цифр этого номера хотя бы две цифры одинаковы ! 36 вариантов ФИПИ Ященко 2023 Вариант 10 Задание 3 ...X
3541 Какова вероятность того, что последние три цифры номера случайно выбранного паспорта одинаковы?
Решение		 Какова вероятность того, что последние три цифры номера случайно выбранного паспорта одинаковы ! 36 вариантов ФИПИ Ященко 2023 Вариант 9 Задание 3 ...X
3521 Вероятность того, что новый блендер в течение года поступит в гарантийный ремонт, равна 0,06. В некотором городе из 1000 проданных блендеров в течение года в мастерские по гарантии поступило 54 штуки. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
Решение		 Вероятность того, что новый блендер в течение года поступит в гарантийный ремонт, равна 0,06 ! 36 вариантов ФИПИ Ященко 2023 Вариант 6 Задание 3 ...X
3512 Вероятность того, что новый принтер в течение года поступит в гарантийный ремонт, равна 0,097. В некотором городе из 1000 проданных принтеров в течение года в мастерские по гарантии поступила 101 штука. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
Решение		 Вероятность того, что новый принтер в течение года поступит в гарантийный ремонт, равна 0,097 ! 36 вариантов ФИПИ Ященко 2023 Вариант 5 Задание 3 ...X
3487 Вероятность того, что на тестировании по физике учащийся К. верно решит больше 9 задач, равна 0,79. Вероятность того, что К. верно решит больше 8 задач, равна 0,85. Найдите вероятность того, что К. верно решит ровно 9 задач
Решение		 Вероятность того, что на тестировании по физике учащийся К. верно решит больше 9 задач, равна 0,79 ! 36 вариантов ФИПИ Ященко 2023 Вариант 1 Задание 3 ...X
Источник

За третьим заданием негласно закрепилось название «фигура на бумаге в клетку». В задании представлена какая-либо фигура (круг, четырехугольник, треугольник или угол) на клетчатой бумаге.

Проверяется знание основ планиметрии: определений, наиболее известных теорем и формул.

Тип задания: с кратким ответом
Уровень сложности: базовый
Количество баллов: 1
Примерное время на выполнение: 2 минуты

Задание 3 егэ математика профильный уровень

В заданиях встречаются фигуры: угол, все виды треугольников, произвольный выпуклый четырехугольник, трапеция (в том числе равнобедренная и прямоугольная), параллелограмм, прямоугольник, ромб, квадрат, круг.

При решении надо учитывать, что размер клетки 1*1см. В заданиях это указано. Очень редко попадаются другие размеры клетки — надо внимательно читать задание.

По умолчанию считается, что ученик легко находит на бумаге в клетку углы в 180, 135, 90 и 45 градусов.

Вершины многоугольников и центры окружностей во всех заданиях лежат в вершинах клеток (имеют целые координаты). Однако концы искомых отрезков, например, средней линии трапеции, могут иметь произвольные координаты. Но всё очень легко вычисляется по формулам.

При подготовке полезно пользоваться прилагающимися к билету справочными материалами, даже если вам все это давно и отлично знакомо. В самый ответственный момент эта привычка может оказаться полезной. Во время решения третьего задания на экзамене большинство сдающих еще находятся в состоянии стресса от процедуры начала экзамена. Поэтому навык использования справочных материалов снижает риск ошибки и даже оказывает некоторую психологическую поддержку.

Определения, а также свойства фигур и их элементов, в справочных материалах не даются. Их надо знать. Все они изучаются в курсе геометрии за 7-8 класс. При подготовке к экзамену полезно выписать из учебника теоремы и время от времени перечитывать их.

Сложных вычислений в третьем задании нет. Бываю задания, где достаточно знать определение, а искомую величину можно отсчитать по клеточкам. Если решение получается в несколько действий – ищите способ проще.

Большинство задач можно решить несколькими способами.

Пример №1

Найдите большую диагональ ромба.

Задание 3 егэ математика 1

Решение: Собственно, все, что нужно знать – определение диагонали и понятие больше-меньше.

Задание 3 егэ математика 2

Ответ: 4 см.

Удивительно, что в профильной математике встречаются такие задания. И в них тоже допускают ошибки. Видимо, от неожиданности уровня сложности.

Далее для разбора выбраны наиболее сложные задачи, встречавшиеся в третьем задании на экзаменах прошлых лет.

Пример №2

Найдите площадь треугольника.

Задание 3 егэ математика 3

Решение:

1) Достроим фигуру до прямоугольника. Его площадь равна 6*4=24

Задание 3 егэ математика 4

2) Найдем площади «лишних» прямоугольных треугольников

(4*4)/2=8 (зеленый)
(2*2)/2=2 (синий)
(6*2)/2=6 (красный)

Задание 3 егэ математика 5

3) Вычтем из площади прямоугольника лишние площади треугольников: 24-8-2-6=8

Ответ: 8.

Эту же задачу можно решить другим способом.

1) Треугольник является прямоугольным, так как его катеты расположены под углом 45 градусов к вертикальной линии.

2) Катеты найдем из прямоугольных треугольников

Задание 3 егэ математика 6

Sqrt(4^2+4^2)=4sqrt2 (четыре корня из двух)
Sqrt(2^2+2^2)=2sqrt2 (два корня из двух)

3) Площадь искомого треугольника равна половине произведения катетов: (4sqrt2*2sqrt2)/2=(4*2*2)/2=8

Ответ: 8.

Пример №3

Найдите площадь многоугольника

Задание 3 егэ математика 7

Решение: Разобьем многоугольник на удобные фигуры и найдем их площади.

Задание 3 егэ математика 8

Площадь зеленого треугольника 1*3/2=1,5
Площадь синего треугольника 2*1/2=1
Площадь красного треугольника 1*2/2=1
Площадь квадрата 2*2=4
Площадь многоугольника равна их сумме: 1,5+1+1+4=7,5

Ответ: 7,5.

Эту задачу можно решить и вычитанием из площади прямоугольника.

Задание 3 егэ математика 9

Ответ: 7,5.

Пример №4

Найти площадь многоугольника.

Задание 3 егэ математика 10

Решение: Можно найти площадь вычитанием, как и в предыдущих заданиях.

Задание 3 егэ математика 11

Но быстрее можно получить результат с помощью формулы Пика. Для этого нужно сосчитать точки с целыми координатами внутри фигуры (синие) и точки с целыми координатами на контуре фигуры (красные).

Задание 3 егэ математика 12

Далее к числу точек внутри многоугольника прибавить половину точек на контуре и вычесть единицу.

7+9/2-1=10,5

Ответ: 10,5

Формула Пика не указана в кодификаторе, применять ее при решении заданий с развернутым ответом нельзя. Но в заданиях с кратким ответом она позволяет сэкономить время. Проверьте справедливость формулы на предыдущих примерах.

Пример № 5

Найдите градусную меру угла АВС.

Задание 3 егэ математика 13

Решение: Точка А имеет нецелые координаты, однако теорема о вписанном и центральном углах позволяет легко решить задачу.

Проведем радиусы в точки А и С.

Задание 3 егэ математика 14

По рисунку видно, что центральный угол АОС равен 135 градусам. Вписанный угол АВС опирается на те же точки окружности А и С. Согласно теореме, он в два раза меньше центрального.

135/2=67,5

Ответ: 67,5.

Пример №6

Найдите тангенс угла.

Задание 3 егэ математика 15

Решение: Выделим смежный острый угол.

Задание 3 егэ математика 16

Выделим прямоугольный треугольник с целочисленными координатами вершин, содержащий этот угол. Найдем тангенс острого угла как отношение противолежащего (зеленого) катета к прилежащему (синему).

Задание 3 егэ математика 17

tgA=4/1=4

Тангенс смежного тупого угла противоположен по знаку.

Ответ: -4.

В завершении хочется еще раз напомнить: листы с заданиями не проверяются. Можно все необходимые построения и вычисления делать прямо на рисунке. Это позволяет избежать ошибок по невнимательности.

Профессиональный преподаватель также сделал подробный разбор 1 и 2 задания, с которыми можно ознакомиться по ссылкам.

Источник
Skip to content

ЕГЭ Профиль №3. Прямоугольный треугольник

ЕГЭ Профиль №3. Прямоугольный треугольникadmin2022-07-27T12:25:28+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №3. Прямоугольный треугольник

Задача 1. В треугольнике ABC угол C равен ({90^ circ }), (AB = 5), (sin A = frac{7}{{25}}). Найдите АС.

Ответ

ОТВЕТ: 4,8.
Задача 2. В треугольнике ABC угол C равен ({90^ circ }), (AB = 8) , (sin A = 0,5). Найдите ВС.

Ответ

ОТВЕТ: 4.
Задача 3. В треугольнике ABC угол C равен ({90^ circ }), (AB = 8) , (cos A = 0,5). Найдите AС.

Ответ

ОТВЕТ: 4.
Задача 4. В треугольнике ABC угол C равен ({90^ circ }), (AB = 5), (cos A = frac{7}{{25}}). Найдите ВС.

Ответ

ОТВЕТ: 4,8.
Задача 5. В треугольнике ABC угол C равен ({90^ circ }), (AB = 7), ({text{tg}},A = frac{{33}}{{4sqrt {33} }}). Найдите AС.

Ответ

ОТВЕТ: 4.
Задача 6. В треугольнике ABC угол C равен ({90^ circ }), (AB = 7), ({text{tg}},A = frac{{4sqrt {33} }}{{33}}). Найдите BС.

Ответ

ОТВЕТ: 4.
Задача 7. В треугольнике ABC угол C равен ({90^ circ }), (AC = 4,8), (sin A = frac{7}{{25}}). Найдите АB.

Ответ

ОТВЕТ: 5.
Задача 8. В треугольнике ABC угол C равен ({90^ circ }), (AC = 2), (sin A = frac{{sqrt {17} }}{{17}}). Найдите BC.

Ответ

ОТВЕТ: 0,5.
Задача 9. В треугольнике ABC угол C равен ({90^ circ }), (AC = 4), (cos A = 0,5). Найдите АB.

Ответ

ОТВЕТ: 8.
Задача 10. В треугольнике ABC угол C равен ({90^ circ }), (AC = 0,5), (cos A = frac{{sqrt {17} }}{{17}}). Найдите BC.

Ответ

ОТВЕТ: 2.
Задача 11. В треугольнике ABC угол C равен ({90^ circ }), (AC = 4), (tgA = frac{{33}}{{4sqrt {33} }}). Найдите АB.

Ответ

ОТВЕТ: 7.
Задача 12. В треугольнике ABC угол C равен ({90^ circ }), (AC = 8) , ({text{tg}},A = 0,5). Найдите BC.

Ответ

ОТВЕТ: 4.
Задача 13. В треугольнике ABC угол C равен ({90^ circ }), (BC = 4), (sin A = 0,5). Найдите АB.

Ответ

ОТВЕТ: 8.
Задача 14. В треугольнике ABC угол C равен ({90^ circ }), (BC = 0,5), (sin A = frac{{sqrt {17} }}{{17}}). Найдите AC.

Ответ

ОТВЕТ: 2.
Задача 15. В треугольнике ABC угол C равен ({90^ circ }), (BC = 4,8), (cos A = frac{7}{{25}}). Найдите AB.

Ответ

ОТВЕТ: 5.
Задача 16. В треугольнике ABC угол C равен ({90^ circ }), (BC = 2), (cos A = frac{{sqrt {17} }}{{17}}). Найдите AC.

Ответ

ОТВЕТ: 0,5.
Задача 17. В треугольнике ABC угол C равен ({90^ circ }), (BC = 4), ({text{tg}},A = frac{{4sqrt {33} }}{{33}}). Найдите AB.

Ответ

ОТВЕТ: 7.
Задача 18. В треугольнике ABC угол C равен ({90^ circ }), (BC = 4), ({text{tg}},A = 0,5). Найдите AC.

Ответ

ОТВЕТ: 8.
Задача 19. В треугольнике ABC угол C равен ({90^ circ }), (AC = 24,;;BC = 7.) Найдите (sin A.)

Ответ

ОТВЕТ: 0,28.
Задача 20. В треугольнике ABC угол C равен ({90^ circ }), (AC = 7,;;BC = 24.) Найдите (cos A.)

Ответ

ОТВЕТ: 0,28.
Задача 21. В треугольнике ABC угол C равен ({90^ circ }), (AC = 8,;;BC = 4.) Найдите ({text{tg}},A.)

Ответ

ОТВЕТ: 0,5.
Задача 22. В треугольнике ABC угол C равен ({90^ circ }), (AB = 8,;;BC = 4.) Найдите (sin A.)

Ответ

ОТВЕТ: 0,5.
Задача 23. В треугольнике ABC угол C равен ({90^ circ }), (AB = 25,;;BC = 20.) Найдите (cos A.)

Ответ

ОТВЕТ: 0,6.
Задача 24. В треугольнике ABC угол C равен ({90^ circ }), (AB = 4sqrt 5 ,;;BC = 4.) Найдите ({text{tg}},A.)

Ответ

ОТВЕТ: 0,5.
Задача 25. В треугольнике ABC угол C равен ({90^ circ }), (AB = 25,;;AC = 20.) Найдите (sinA.)

Ответ

ОТВЕТ: 0,6.
Задача 26. В треугольнике ABC угол C равен ({90^ circ }), (AB = 8,;;AC = 4.) Найдите (cos A.)

Ответ

ОТВЕТ: 0,5.
Задача 27. В треугольнике ABC угол C равен ({90^ circ }), (AB = 4sqrt 5 ,;;AC = 8.) Найдите ({text{tg}},A.)

Ответ

ОТВЕТ: 0,5.
Задача 28. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AB = 27,;;sin A = frac{2}{3}.) Найдите AH.

Ответ

ОТВЕТ: 15.
Задача 29. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AB = 27,;;sin A = frac{2}{3}.) Найдите BH.

Ответ

ОТВЕТ: 12.
Задача 30. В треугольнике ABC угол C равен ({90^ circ }), (AB = 4sqrt {15} ,;;sin A = 0,25.) Найдите высоту СH.

Ответ

ОТВЕТ: 3,75.
Задача 31. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AB = 27,;;cos A = frac{2}{3}.) Найдите AH.

Ответ

ОТВЕТ: 12.
Задача 32. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AB = 27,;;cos A = frac{2}{3}.) Найдите BH.

Ответ

ОТВЕТ: 15.
Задача 33. В треугольнике ABC угол C равен ({90^ circ }), (AB = 4sqrt {15} ,;;cos A = 0,25.) Найдите высоту СH.

Ответ

ОТВЕТ: 3,75.
Задача 34. В треугольнике ABC угол C равен ({90^ circ }), CH — высота,  (AB = 13,;;{text{tg}},A = frac{1}{5}). Найдите AH.

Ответ

ОТВЕТ: 12,5.
Задача 35. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AB = 13,;;{text{tg}},A = 5). Найдите BH.

Ответ

ОТВЕТ: 12,5.
Задача 36. В треугольнике ABC угол C равен ({90^ circ }), (AB = 13,;;{text{tg}},A = frac{1}{5}). Найдите высоту CH.

Ответ

ОТВЕТ: 2,5.
Задача 37. В треугольнике ABC угол C равен ({90^ circ }), CH — высота,  (BC = 3,;;sin ,A = frac{1}{6}). Найдите AH.

Ответ

ОТВЕТ: 17,5.
Задача 38. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 8,;;sin ,A = 0,5.) Найдите BH.

Ответ

ОТВЕТ: 4.
Задача 39. В треугольнике ABC угол C равен ({90^ circ }), (BC = 5,;;sin ,A = frac{7}{{25}}.) Найдите высоту CH.

Ответ

ОТВЕТ: 4,8.
Задача 40. В треугольнике ABC угол C равен ({90^ circ }), CH — высота,      (BC = 3,;;cos ,A = frac{{sqrt {35} }}{6}.) Найдите AH.

Ответ

ОТВЕТ: 17,5.
Задача 41. В треугольнике ABC угол C равен ({90^ circ }), CH — высота,       (BC = 5,;;cos ,A = frac{7}{{25}}.) Найдите BH.

Ответ

ОТВЕТ: 4,8.
Задача 42. В треугольнике ABC угол C равен ({90^ circ }), (BC = 8,;;cos ,A = 0,5.) Найдите высоту CH.

Ответ

ОТВЕТ: 4.
Задача 43. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 7,;{text{tg}},A = frac{{4sqrt {33} }}{{33}}.) Найдите BH.

Ответ

ОТВЕТ: 4.
Задача 44. В треугольнике ABC угол C равен ({90^ circ }), (BC = 7,;{text{tg}},A = frac{{33}}{{4sqrt {33} }}.) Найдите высоту СH.

Ответ

ОТВЕТ: 4.
Задача 45. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AC = 3,;;sin ,A = frac{{sqrt {35} }}{6}.) Найдите BH.

Ответ

ОТВЕТ: 17,5.
Задача 46. В треугольнике ABC угол C равен ({90^ circ }), (AC = 8,;sin A = 0,5.) Найдите высоту СH.

Ответ

ОТВЕТ: 4.
Задача 47. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AC = 8,;;cos ,A = 0,5.) Найдите AH.

Ответ

ОТВЕТ: 4.
Задача 48. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AC = 3,;;cos ,A = frac{1}{6}.) Найдите BH.

Ответ

ОТВЕТ: 17,5.
Задача 49. В треугольнике ABC угол C равен ({90^ circ }), (AC = 5,;cos A = frac{7}{{25}}.) Найдите высоту СH.

Ответ

ОТВЕТ: 4,8.
Задача 50. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AC = 7,;{text{tg}},A = frac{{33}}{{4sqrt {33} }}.) Найдите AH.

Ответ

ОТВЕТ: 4.
Задача 51. В треугольнике ABC угол C равен ({90^ circ }), (AC = 7,;{text{tg}},A = frac{{4sqrt {33} }}{{33}}.) Найдите высоту СH.

Ответ

ОТВЕТ: 4.
Задача 52. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 8,;;BH = 4.) Найдите (sin A.)

Ответ

ОТВЕТ: 0,5.
Задача 53. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 25,;;BH = 20.) Найдите (cos A.)

Ответ

ОТВЕТ: 0,6.
Задача 54. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 4sqrt 5 ,;;BH = 4.) Найдите ({text{tg}},A.)

Ответ

ОТВЕТ: 0,5.
Задача 55. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 20, (BC = 25.) Найдите (sin A.)

Ответ

ОТВЕТ: 0,6.
Задача 56. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 4, (BC = 8.) Найдите (cos A.)

Ответ

ОТВЕТ: 0,5.
Задача 57. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 4, (BC = sqrt {17} .) Найдите ({text{tg}},A.)

Ответ

ОТВЕТ: 0,25.
Задача 58. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 24, (BH = 7.) Найдите (sin A.)

Ответ

ОТВЕТ: 0,28.
Задача 59. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 7, (BH = 24.) Найдите (cos A.)

Ответ

ОТВЕТ: 0,28.
Задача 60. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 8, (BH = 4.) Найдите ({text{tg}},A.)

Ответ

ОТВЕТ: 0,5.
Задача 61. В треугольнике ABC угол C равен ({90^ circ }), CH — высота,  (AH = 27,;;{text{tg}},A = frac{2}{3}.) Найдите BH.

Ответ

ОТВЕТ: 12.
Задача 62. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BH = 12,;;{text{tg}},A = frac{2}{3}.) Найдите AH.

Ответ

ОТВЕТ: 27.
Задача 63. В треугольнике ABC угол C равен ({90^ circ }), CH — высота,  (BH = 12,;;sin A = frac{2}{3}.) Найдите AB.

Ответ

ОТВЕТ: 27.
Задача 64. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AH = 12,;;cos A = frac{2}{3}.) Найдите AB.

Ответ

ОТВЕТ: 27.
Задача 65. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10.

Ответ

ОТВЕТ: 24.
Задача 66. Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.

Ответ

ОТВЕТ: 6.
Задача 67. В треугольнике ABC угол C равен ({90^ circ }), угол В равен ({58^ circ }), CD медиана. Найдите угол ACD. Ответ дайте в градусах.

Ответ

ОТВЕТ: 32.
Задача 68. Острый угол прямоугольного треугольника равен ({32^ circ }). Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.

Ответ

ОТВЕТ: 61.
Задача 69. Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.

Ответ

ОТВЕТ: 45.
Задача 70. Один из углов прямоугольного треугольника равен ({29^ circ }). Найдите угол между высотой и биссектрисой, проведёнными из вершины прямого угла. Ответ дайте в градусах.

Ответ

ОТВЕТ: 16.
Задача 71. В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла, равен 21°. Найдите меньший угол данного треугольника. Ответ дайте в градусах.
Задача 72. Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Задача 73. В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 40°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
Задача 74. Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Задача 75. Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 14°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
Задача 76. В треугольнике ABC угол C равен 90°, угол A равен 30°, (AB = 2sqrt 3 ). Найдите высоту CH.
Задача 77. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, угол A равен 30°, (AB = 2). Найдите AH.
Задача 78. В треугольнике ABC угол C равен 90°, CH — высота, угол A равен 30°, (AB = 4). Найдите BH.

Источник

Понравилась статья? Поделить с друзьями:
  • Тренировочный экзамен по информатике 2022
  • Третье задание егэ информатика
  • Тренировочный экзамен по географии огэ 9 класс
  • Третье задание егэ биология теория
  • Тренировочный экзамен по географии вариант 90810 ответы 9 класс