Всего: 137 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 311. (Часть C)
Решите систему уравнений
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 345.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 372.
Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону где t — время в секундах, амплитуда U0 = 2 В, частота ω =120 °/c , фаза φ = 15° . Датчик настроен так, что если напряжение в нём не ниже чем 1 В, то загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 307. (Часть C)
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 349.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 376.
Источник: Пробный экзамен по профильной математике Санкт-Петербург 05.04.2016. Вариант 2.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 299.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 320. (Часть C)
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 378.
Скорость колеблющегося на пружине груза меняется по закону (см/с), где t − время в секундах. Какую долю времени из первой секунды скорость движения была не менее 2,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
Скорость колеблющегося на пружине груза меняется по закону (см/с), где t — время в секундах. Какую долю времени из первой секунды скорость движения превышала 3 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
Решите неравенство:
Источник: А. Ларин: Тренировочный вариант № 181.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 379.
Источник: Пробный экзамен по профильной математике Санкт-Петербург 05.04.2016. Вариант 1.
Всего: 137 1–20 | 21–40 | 41–60 | 61–80 …
Каталог заданий.
Тригонометрические уравнения и неравенства
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 8 № 28008
При нормальном падении света с длиной волны нм на дифракционную решeтку с периодом d нм наблюдают серию дифракционных максимумов. При этом угол
(отсчитываемый от перпендикуляра к решeтке), под которым наблюдается максимум, и номер максимума k связаны соотношением
Под каким минимальным углом
(в градусах) можно наблюдать второй максимум на решeтке с периодом, не превосходящим 1600 нм?
Аналоги к заданию № 28008: 28633 28639 509418 560776 28635 28637 28641 43497 43499 43501 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
2
Тип 8 № 28009
Два тела массой кг каждое, движутся с одинаковой скоростью
м/с под углом
друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении определяется выражением
Под каким наименьшим углом
(в градусах) должны двигаться тела, чтобы в результате соударения выделилось не менее 50 джоулей?
Аналоги к заданию № 28009: 28643 43741 541375 541819 28645 28647 28649 28651 28653 43527 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
·
Курс Д. Д. Гущина
·
2 комментария · Сообщить об ошибке · Помощь
3
Тип 8 № 28010
Катер должен пересечь реку шириной м и со скоростью течения
м/с так, чтобы причалить точно напротив места отправления. Он может двигаться с разными скоростями, при этом время в пути, измеряемое в секундах, определяется выражением
где
− острый угол, задающий направление его движения (отсчитывается от берега). Под каким минимальным углом
(в градусах) нужно плыть, чтобы время в пути было не больше 200 с?
Аналоги к заданию № 28010: 28655 43795 28657 28659 28661 28663 43743 43745 43747 43749 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
4
Тип 8 № 28011
Скейтбордист прыгает на стоящую на рельсах платформу, со скоростью м/с под острым углом
к рельсам. От толчка платформа начинает ехать со скоростью
(м/с), где
кг — масса скейтбордиста со скейтом, а
кг — масса платформы. Под каким максимальным углом
(в градусах) нужно прыгать, чтобы разогнать платформу не менее чем до 0,25 м/с?
Аналоги к заданию № 28011: 28665 43825 28667 28669 28671 28673 43797 43799 43801 43803 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
5
Тип 8 № 28012
Груз массой 0,08 кг колеблется на пружине. Его скорость υ меняется по закону где t — время с момента начала колебаний, T = 12 с — период колебаний,
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
где m — масса груза в килограммах, υ — скорость груза в м/с. Найдите кинетическую энергию груза через 1 секунду после начала колебаний. Ответ дайте в джоулях.
Аналоги к заданию № 28012: 513877 513878 513879 513880 513881 513882 513883 513884 513885 513886 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 152 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону где t — время в секундах, амплитуда U0 = 2 В, частота ω =120 °/c , фаза φ = 15° . Датчик настроен так, что если напряжение в нём не ниже чем 1 В, то загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?
Источник: Пробный экзамен по профильной математике Санкт-Петербург 05.04.2016. Вариант 2.
Деталью некоторого прибора является квадратная рамка с намотанным на неe проводом, через который пропущен постоянный ток. Рамка помещена в однородное магнитное поле так, что она может вращаться. Момент силы Ампера, стремящейся повернуть рамку, (в Нм) определяется формулой
где
— сила тока в рамке,
Тл — значение индукции магнитного поля,
м — размер рамки,
— число витков провода в рамке,
— острый угол между перпендикуляром к рамке и вектором индукции. При каком наименьшем значении угла
(в градусах) рамка может начать вращаться, если для этого нужно, чтобы раскручивающий момент M был не меньше 0,9 Н
м?
При нормальном падении света с длиной волны нм на дифракционную решeтку с периодом d нм наблюдают серию дифракционных максимумов. При этом угол
(отсчитываемый от перпендикуляра к решeтке), под которым наблюдается максимум, и номер максимума k связаны соотношением
Под каким минимальным углом
(в градусах) можно наблюдать второй максимум на решeтке с периодом, не превосходящим 1800 нм?
Скорость колеблющегося на пружине груза меняется по закону (см/с), где t — время в секундах. Какую долю времени из первых двух секунд скорость движения превышала 3,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
Деталью некоторого прибора является квадратная рамка с намотанным на неe проводом, через который пропущен постоянный ток. Рамка помещена в однородное магнитное поле так, что она может вращаться. Момент силы Ампера, стремящейся повернуть рамку, (в Нм) определяется формулой
где
— сила тока в рамке,
Тл — значение индукции магнитного поля,
м — размер рамки,
— число витков провода в рамке,
— острый угол между перпендикуляром к рамке и вектором индукции. При каком наименьшем значении угла
(в градусах) рамка может начать вращаться, если для этого нужно, чтобы раскручивающий момент M был не меньше 0,63 Н
м?
Всего: 152 1–20 | 21–40 | 41–60 | 61–80 …
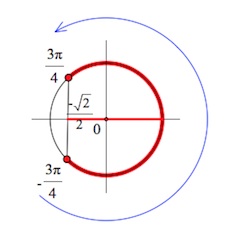
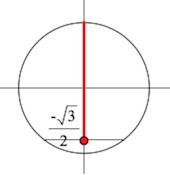
Согласно неравенству, нам нужны значения синуса больше либо равные (-frac{sqrt{2}}{2}), на рисунке показали их при помощи синей штриховки. Этим значениям соответствуют углы, лежащие на дуге (MN), включая точки (M) и (N). Дугу (MN) с нужными углами можно записать в виде промежутка ПРОТИВ часовой стрелки. То есть от точки (M) к (N). Получается такой промежуток:
$$x in [-frac{pi}{4}+2pi*n; -frac{3pi}{4}+2pi*n], quad n in Z;$$
Скобки квадратные так как знак неравенства нестрогий и не забываем про период (2pi*n). Но сам промежуток неправильный!
Внимание! Так записывать ответ нельзя, потому что промежуток всегда должен быть от меньшего числа к большему. У нас это правило не соблюдается:
$$-frac{pi}{4}>-frac{3pi}{4};$$
Чтобы ответ был в правильном виде, достаточно просто прибавить к правой границе промежутка (2pi).
$$x in [-frac{pi}{4}+2pi*n; -frac{3pi}{4}+2pi+2pi*n], quad n in Z;$$
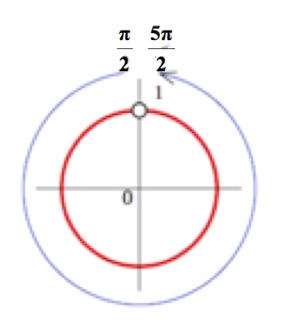
Приведем подобные слагаемые:
$$x in [-frac{pi}{4}+2pi*n; frac{5pi}{4}+2pi*n], quad n in Z;$$
Левая граница меньше правой, значит можно записывать ответ.
Ответ: (x in [-frac{pi}{4}+2pi*n; frac{5pi}{4}+2pi*n], quad n in Z).
Рассмотрим неравенство с синусом, которое наиболее часто встречается при нахождении ОДЗ.
Пример 3
$$sin(x)>0;$$
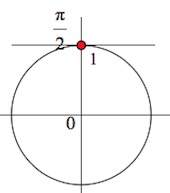
Решение аналогично предыдущим примерам. Рисуем единичную окружность, отмечаем на оси синусов значение (0), оно находится в начале координат. Углы на окружности, синус от которых будет равен (0) находятся в точках (A) и (C): это углы (0+2pi*n) и (pi+2pi*n). Все значения синуса выше (0) нас устраивают, соответствующие им углы лежат на дуге (AC), от точки (A) до (C).
-
Главная
-
Теория ЕГЭ
-
Математика — теория ЕГЭ
-
Тригонометрические неравенства: как решать
Тригонометрические неравенства: как решать
- 29.04.2017
Разбор неравенств различных типов, решения, методы решений, алгоритмы, задачи для самостоятельного решения и подготовки к ЕГЭ по математике. Тема «Тригонометрические неравенства».
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Сохранить ссылку:
Комментарии (0)
Добавить комментарий
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Имя (обязательное)
E-Mail
Подписаться на уведомления о новых комментариях
Отправить
08
Фев 2014
Категория: Справочные материалыТригонометрические выражения, уравнения и неравенства
Простейшие тригонометрические неравенства
2014-02-08
2015-04-20
Часть 1.
(Часть 2 см. здесь)
Примеры решения простейших тригонометрических неравенств
Простейшими тригонометрическими неравенствами называются неравенства вида
,
,
,
,
где – один из знаков
,
.
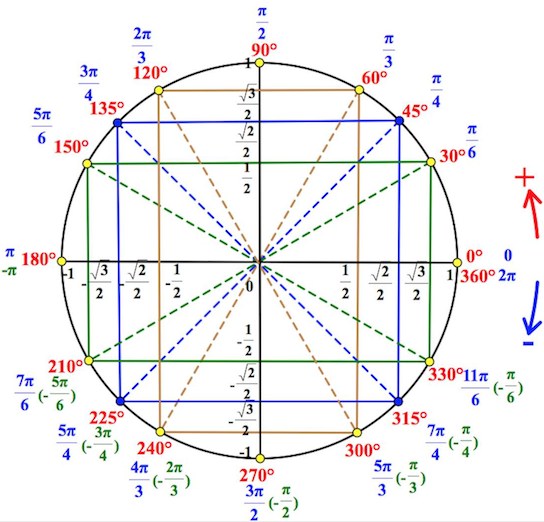
Вы должны прежде, конечно, хорошо ориентироваться в тригонометрическом круге и уметь решать простейшие тригонометрические уравнения (часть I, часть II).
Кстати, умение решать тригонометрические неравенства может пригодиться, например, в заданиях №11 ЕГЭ по математике.
Сначала мы рассмотрим простейшие тригонометрические неравенства с синусом и косинусом. Во второй части статьи – с тангенсом, котангенсом.
Пример 1.
Решить неравенство:
Решение:
Отмечаем на оси косинусов
Все значения , меньшие
– левее точки
на оси косинусов.
Отмечаем все точки (дугу, точнее – серию дуг) тригонометрического круга, косинус которых будет меньше
Полученную дугу мы проходим против часовой стрелки (!), то есть от точки до
.
Обратите внимание, многие, назвав первую точку вместо второй точки
указывают точку
, что неверно!
Становится видно, что неравенству удовлетворяют следующие значения
Следите за тем, чтобы «правая/вторая точка» была бы больше «левой/первой».
Не забываем «накидывать» счетчик
Вот так выглядит графическое решение неравенства не на тригонометрическом круге, а в прямоугольной системе координат:
Пример 2.
Решить неравенство:
Решение:
Отмечаем на оси косинусов
Все значения , большие или равные
– правее точки
, включая саму точку.
Тогда выделенные красной дугой аргументы отвечают тому условию, что
.
Пример 3.
Решить неравенство:
Решение:
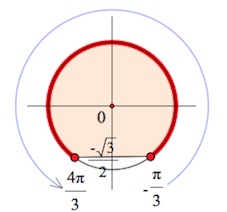
Отмечаем на оси синусов
Все значения , большие или равные
– выше точки
, включая саму точку.
«Транслируем» выделенные точки на тригонометрический круг:
Пример 4.
Решить неравенство:
Решение:
Кратко:
или все , кроме
Пример 5.
Решить неравенство:
Решение:
Неравенство равносильно уравнению
, так как область значений функции
–
Пример 6.
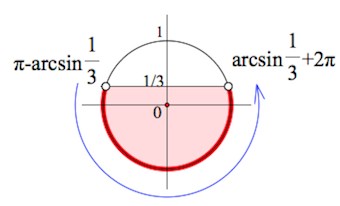
Решить неравенство:
Решение:
Действия – аналогичны применяемым в примерах выше. Но дело мы имеем не с табличным значением синуса.
Здесь, конечно, нужно знать определение арксинуса.
Если не очень понятно, загляните сюда –>+ показать
Тренируемся в решении простейших тригонометрических неравенств
Имейте ввиду, решения (ответы) к одному и тому же неравенству могут выглядеть по-разному, неся один и тот же смысл собою. Например, в задании 2 ответ можно было записать и так:
1. Решить неравенство:
Ответ: + показать
2. Решить неравенство:
Ответ: + показать
3. Решить неравенство:
Ответ: + показать
4. Решить неравенство:
Ответ: + показать
5. Решить неравенство:
Ответ: + показать
Часть 2
Если у вас есть вопросы, – пожалуйста, – спрашивайте!
Автор: egeMax |
комментариев 179
Печать страницы