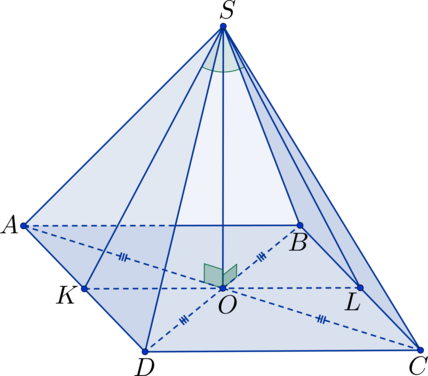
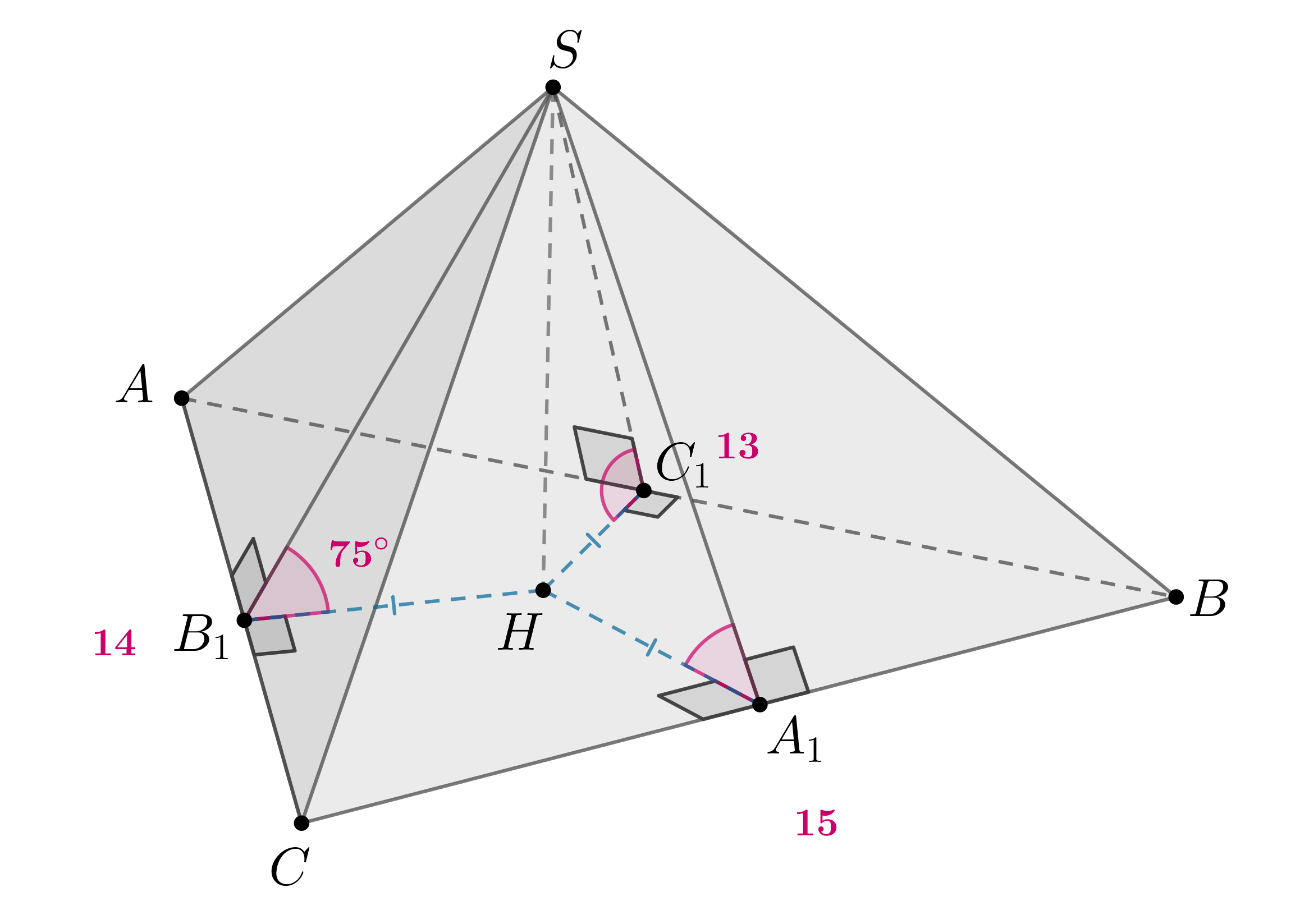
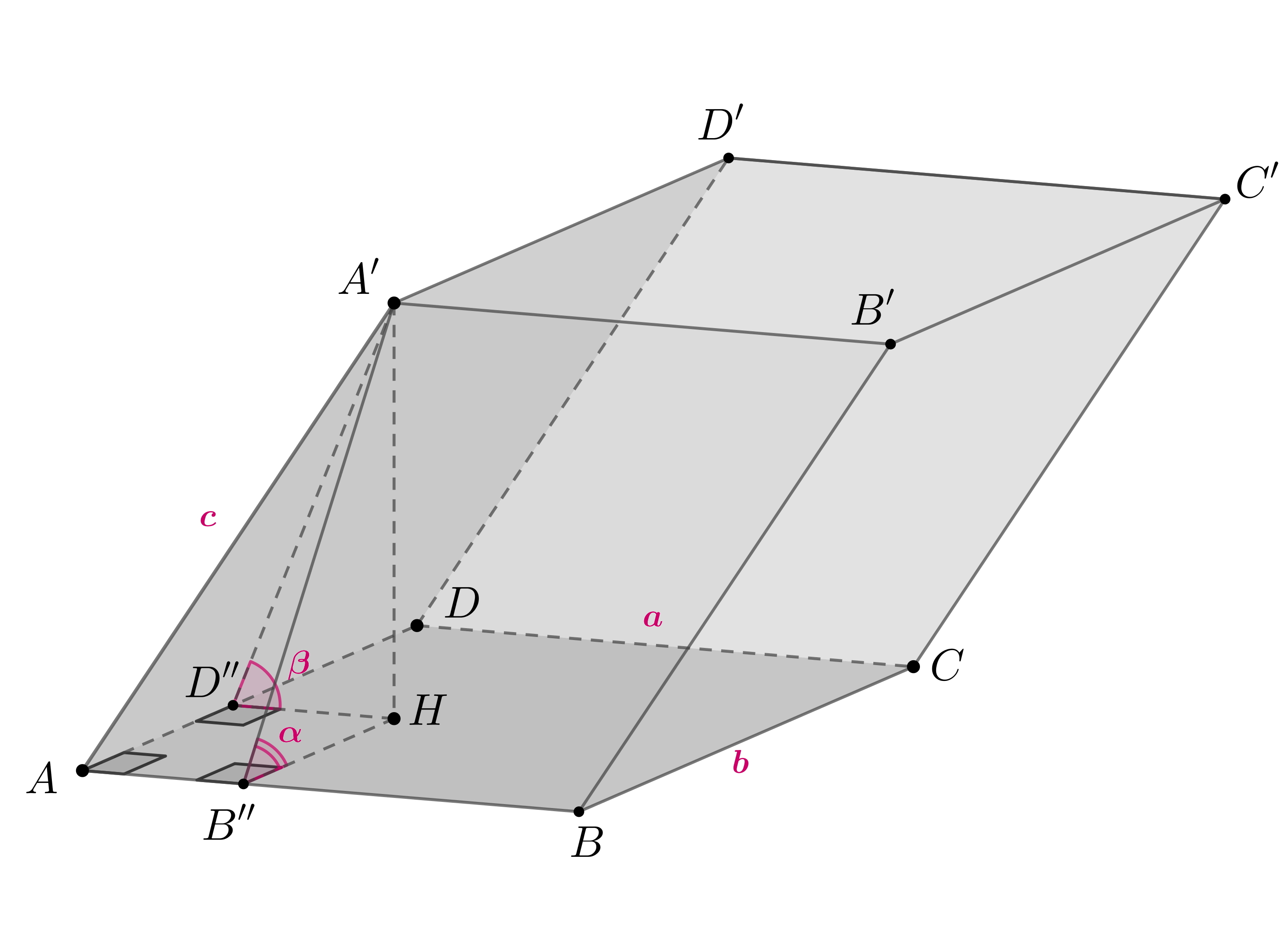
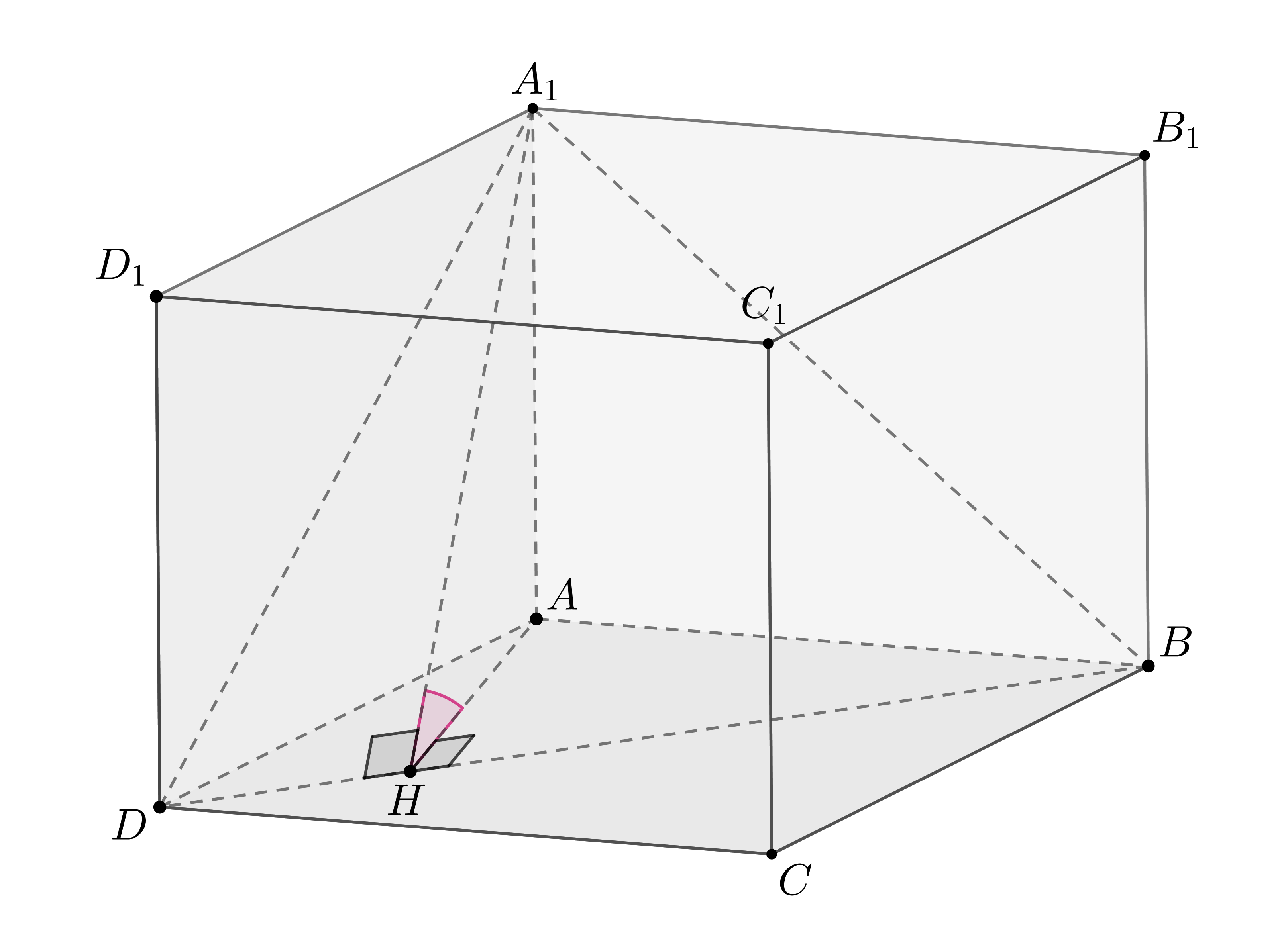
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
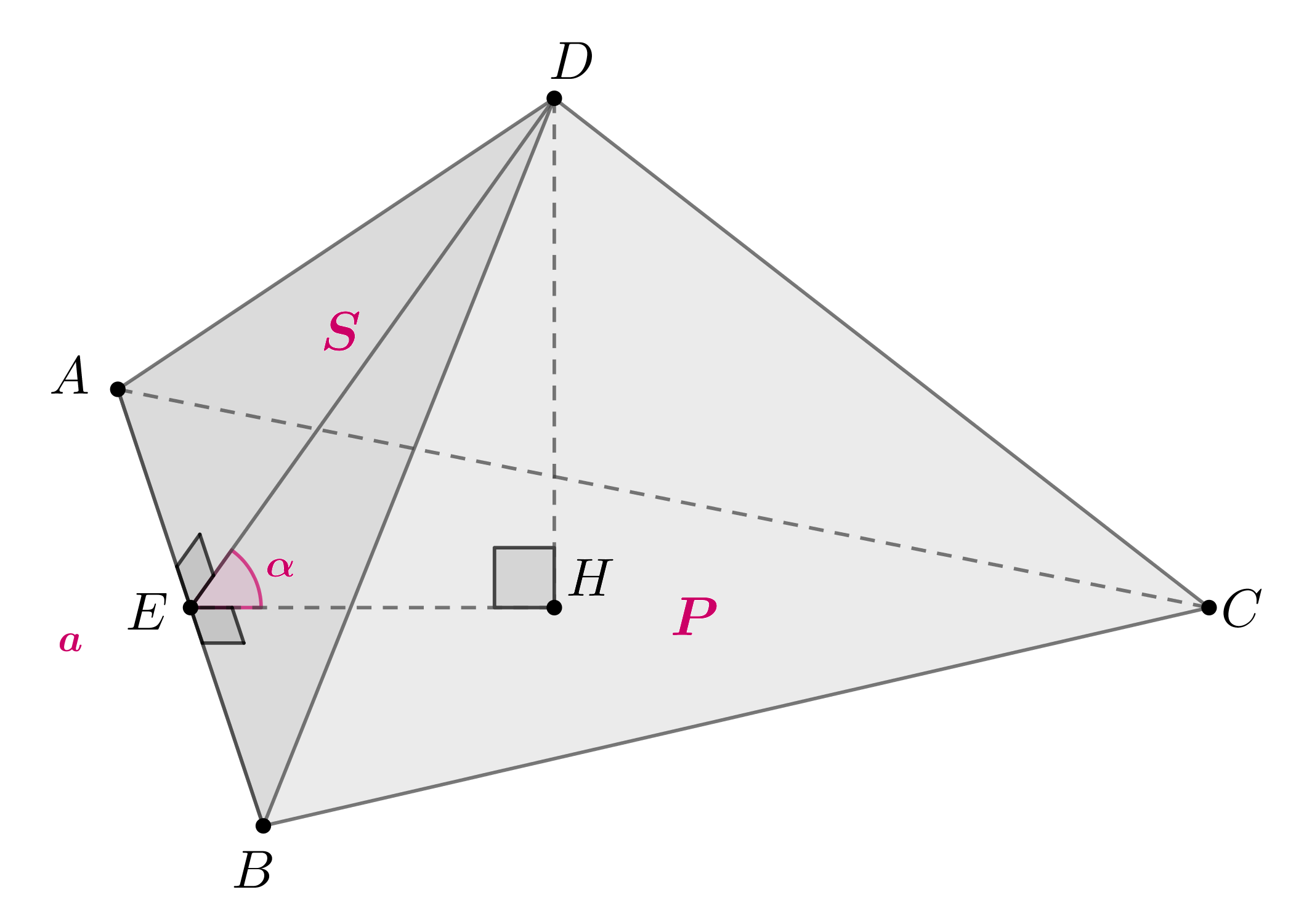
В кубе ABCDA1B1C1D1 все рёбра равны 4. На его ребре BB1 отмечена точка K так, что KB = 3. Через точки K и C1 построена плоскость α, параллельная прямой BD1.
а) Докажите, что A1P : PB1 = 2 : 1, где P — точка пересечения плоскости α с ребром A1B1.
б) Найдите угол наклона плоскости α к плоскости грани BB1C1C.
Источник: ЕГЭ по математике — 2015. Досрочная волна, Запад. , ЕГЭ по математике 26.03.2015. Досрочная волна, Восток.
2
Все рёбра правильной треугольной призмы ABCA1B1C1 имеют длину 6. Точки M и N— середины рёбер AA1 и A1C1 соответственно.
а) Докажите, что прямые BM и MN перпендикулярны.
б) Найдите угол между плоскостями BMN и ABB1.
Источник: Демонстрационная версия ЕГЭ—2016 по математике. Профильный уровень., Демонстрационная версия ЕГЭ—2018 по математике. Профильный уровень., Демонстрационная версия ЕГЭ—2020 по математике. Профильный уровень.
3
В основании прямой призмы ABCDA1B1C1D1 лежит квадрат ABCD со стороной 2, а высота призмы равна 1. Точка E лежит на диагонали BD1, причём BE = 1.
а) Постройте сечение призмы плоскостью A1C1E.
б) Найдите угол между плоскостью сечения и плоскостью ABC.
Источник: Демонстрационная версия ЕГЭ—2015 по математике. Профильный уровень.
4
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны рёбра AB = 35, AD = 12, CC1 = 21.
а) Докажите, что высоты треугольников ABD и A1BD, проведённые к стороне BD, имеют общее основание.
б) Найдите угол между плоскостями ABC и A1DB.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016
5
В правильной треугольной призме ABCA1B1C1 стороны основания равны 4, боковые рёбра равны 7, точка D — середина ребра BB1.
а) Пусть прямые C1D и BC пересекаются в точке E. Докажите, что угол EAC — прямой.
б) Найдите угол между плоскостями ABC и ADC1.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016
Пройти тестирование по этим заданиям
ЕГЭ Профиль №14. Угол между плоскостями
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Угол между плоскостями»
Открытый банк заданий по теме угол между плоскостями. Задания C2 из ЕГЭ по математике (профильный уровень)
Тригонометрические уравнения
Задание №1188
Тип задания: 14
Тема:
Угол между плоскостями
Условие
Дана правильная призма ABCDA_1B_1C_1D_1, M и N — середины ребер AB и BC соответственно, точка K — середина MN.
а) Докажите, что прямые KD_1 и MN перпендикулярны.
б) Найдите угол между плоскостями MND_1 и ABC, если AB=8, AA_1=6sqrt 2.
Показать решение
Решение
а) В triangle DCN и triangle MAD имеем: angle C=angle A=90^{circ}, CN=AM=frac12AB, CD=DA.
Отсюда triangle DCN=triangle MAD по двум катетам. Тогда MD=DN, triangle DMN равнобедренный. Значит, медиана DK — является также высотой. Следовательно, DK perp MN.
DD_1 perp MND по условию, D_1K — наклонная, KD — проекция, DK perp MN.
Отсюда по теореме о трех перпендикулярах MNperp D_1K.
б) Как было доказано в а), DK perp MN и MN perp D_1K, но MN — линия пересечения плоскостей MND_1 и ABC, значит angle DKD_1 — линейный угол двугранного угла между плоскостями MND_1 и ABC.
В triangle DAM по теореме Пифагора DM= sqrt {DA^2+AM^2}= sqrt {64+16}= 4sqrt 5, MN= sqrt {MB^2+BN^2}= sqrt {16+16}= 4sqrt 2. Следовательно, в triangle DKM по теореме Пифагора DK= sqrt {DM^2-KM^2}= sqrt {80-8}= 6sqrt 2. Тогда в triangle DKD_1, tgangle DKD_1=frac{DD_1}{DK}=frac{6sqrt 2}{6sqrt 2}=1.
Значит, angle DKD_1=45^{circ}.
Ответ
45^{circ}.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1187
Тип задания: 14
Тема:
Угол между плоскостями
Условие
В правильной четырёхугольной призме ABCDA_1B_1C_1D_1 стороны основания равны 4, боковые рёбра равны 6. Точка M — середина ребра CC_1, на ребре BB_1 отмечена точка N, такая, что BN:NB_1=1:2.
а) В каком отношении плоскость AMN делит ребро DD_1?
б) Найдите угол между плоскостями ABC и AMN.
Показать решение
Решение
а) Плоскость AMN пересекает ребро DD_1 в точке K, являющейся четвёртой вершиной сечения данной призмы этой плоскостью. Сечением является параллелограмм ANMK, потому что противоположные грани данной призмы параллельны.
BN =frac13BB_1=2. Проведём KL parallel CD, тогда треугольники ABN и KLM равны, значит ML=BN=2, LC=MC-ML=3-2=1, KD=LC=1. Тогда KD_1=6-1=5. Теперь можно найти отношение KD:KD_1=1:5.
б) F — точка пересечения прямых CD и KM. Плоскости ABC и AMN пересекаются по прямой AF. Угол angle KHD =alpha — линейный угол двугранного угла (HDperp AF, тогда по теореме, обратной теореме о трех перпендикулярах, KH perp AF), и является острым углом прямоугольного треугольника KHD, катет KD=1.
Треугольники FKD и FMC подобны (KD parallel MC), поэтому FD:FC=KD:MC, решая пропорцию FD:(FD+4)=1:3, получим FD=2. В прямоугольном треугольнике AFD (angle D=90^{circ}) с катетами 2 и 4 вычислим гипотенузу AF=sqrt {4^2+2^2}=2sqrt 5, DH= ADcdot FD:AF= frac{4cdot 2}{2sqrt 5}= frac4{sqrt 5}.
В прямоугольном треугольнике KHD найдём tg alpha =frac{KD}{DH}=frac{sqrt 5}4, значит, искомый угол alpha =arctgfrac{sqrt 5}4.
Ответ
а) 1:5;
б) arctgfrac{sqrt 5}4.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1183
Тип задания: 14
Тема:
Угол между плоскостями
Условие
Дана правильная четырёхугольная пирамида KMNPQ со стороной основания MNPQ, равной 6, и боковым ребром 3sqrt {26}.
а) Постройте сечение пирамиды плоскостью, проходящей через прямую NF параллельно диагонали MP, если точка F — середина ребра MK.
б) Найдите величину угла между плоскостью сечения и плоскостью KMP.
Показать решение
Решение
а) Пусть KO — высота пирамиды, F — середина MK; FE parallel MP (в плоскости PKM ). Так как FE — средняя линия triangle PKM, то FE=frac{MP}2.
Построим сечение пирамиды плоскостью, проходящей через NF и параллельной MP, то есть плоскостью NFE. L — точка пересечения EF и KO. Так как точки L и N принадлежат искомому сечению и лежат в плоскости KQN, то точка T, полученная как пересечение LN и KQ, является также точкой пересечения искомого сечения и ребра KQ. NETF — искомое сечение.
б) Плоскости NFE и MPK пересекаются по прямой FE. Значит, угол между этими плоскостями равен линейному углу двугранного угла OFEN, построим его: LO perp MP, MP parallel FE, следовательно, LO perp FE; triangle NFE — равнобедренный (NE=NF как соответствующие медианы равных треугольников KPN и KMN ), NL — его медиана (EL=LF, так как PO=OM, а triangle KEF sim triangle KPM ). Отсюда NL perp FE и angle NLO — искомый.
ON=frac12QN=frac12MNsqrt 2=3sqrt 2.
triangle KON — прямоугольный.
Катет KO по теореме Пифагора равен KO=sqrt {KN^2-ON^2}.
OL= frac12KO= frac12sqrt{KN^2-ON^2}= frac12sqrt {9cdot 26-9cdot 2}= frac12sqrt{9(26-2)}= frac32sqrt {24}= frac32cdot 2sqrt 6= 3sqrt 6.
tgangle NLO =frac{ON}{OL}=frac{3sqrt 2}{3sqrt 6}=frac1{sqrt 3},
angle NLO=30^{circ}.
Ответ
30
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №986
Тип задания: 14
Тема:
Угол между плоскостями
Условие
Все рёбра правильной треугольной призмы ABCA_{1}B_{1}C_{1} равны 6. Через середины рёбер AC и BB_{1} и вершину A_{1} проведена секущая плоскость.
а) Докажите, что ребро BC делится секущей плоскостью в отношении 2:1, считая от вершины C.
б) Найдите угол между плоскостью сечения и плоскостью основания.
Показать решение
Решение
а) Пусть D и E — середины ребер AC и BB_{1} соответственно.
В плоскости AA_{1}C_{1} проведем прямую A_{1}D, которая пересекает прямую CC_{1} в точке K, в плоскости BB_{1}C_{1} — прямую KE, которая пересекает ребро BC в точке F. Соединие точки A_{1} и E, лежащие в плоскости AA_{1}B_{1}, а также D и F, лежащие в плоскости ABC, получим сечение A_{1}EFD.
bigtriangleup AA_{1}D=bigtriangleup CDK по катету AD=DC и острому углу.
angle ADA_{1}=angle CDK — как вертиальные, отсюда следует, что AA_{1}=CK=6. bigtriangleup CKF и bigtriangleup BFE подобны по двум углам angle FBE=angle KCF=90^circ, angle BFE=angle CFK — как вертикальные.
frac{CK}{BE}=frac{6}{3}=2, то есть коэффициент подобия равен 2, откуда следует, что CF:FB=2:1.
б) Проведём AH perp DF. Угол между плоскостью сечения и плоскостью основания равен углу AHA_{1}. Действительно, отрезок AH perp DF (DF — линия пересечения этих плоскостей) и является проекцией отрезка A_{1}H на плоскость основания, следовательно, по теореме о трёх перпендикулярах, A_{1}H perp DF. angle AHA_{1}=arctgfrac{AA_{1}}{AH}. AA_{1}=6.
Найдём AH. angle ADH =angle FDC (как вертикальные).
По теореме косинусов в bigtriangleup DFC:
DF^2=FC^2+DC^2- 2FC cdot DC cdot cos 60^circ,
DF^2=4^2+3^2-2 cdot 4 cdot 3 cdot frac{1}{2}=13.
FC^2=DF^2+DC^2- 2DF cdot DC cdot cos angle FDC,
4^2=13+9-2sqrt{13} cdot 3 cdot cos angle FDC,
cos angle FDC=frac{6}{2sqrt{13} cdot 3}=frac{1}{sqrt{13}}.
По следствию из основного тригонометрического тождества
sin angle FDC=sqrt{1-left ( frac{1}{sqrt{13}}right )^2}=frac{2sqrt{3}}{sqrt{13}}. Из bigtriangleup ADH найдём AH:
AH=AD cdot sin angle ADH, (angle FDC=angle ADH). AH=3 cdot frac{2sqrt{3}}{sqrt{13}}=frac{6sqrt{13}}{sqrt{13}}.
angle AHA_{1}= arctgfrac{AA_{1}}{AH}= arctgfrac{6 cdot sqrt{13}}{6sqrt{3}}= arctgfrac{sqrt{39}}{3}.
Ответ
arctgfrac{sqrt{39}}{3}.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №983
Тип задания: 14
Тема:
Угол между плоскостями
Условие
Основанием прямой призмы ABCDA_{1}B_{1}C_{1}D_{1} является ромб с тупым углом B, равным 120^circ. Все ребра этой призмы равны 10. Точки P и K — середины ребер CC_{1} и CD соответственно.
а) Докажите, что прямые PK и PB_{1} перпендикулярны.
б) Найдите угол между плоскостями PKB_{1} и C_{1}B_{1}B.
Показать решение
Решение
а) Будем использовать метод координат. Найдём скалярное произведение векторов vec{PK} и vec{PB_{1}}, а затем косинус угла между этими векторами. Направим ось Oy вдоль CD, ось Oz вдоль CC_{1}, и ось Ox perp CD. C — начало координат.
Тогда C (0;0;0); C_{1}(0;0;10); P(0;0;5); K(0;5;0); B(BC cos 30^circ; BCsin 30^circ; 0), то есть B(5sqrt{3}; 5;0), B_{1}(5sqrt{3}; 5;10).
Найдём координаты векторов: vec{PK}={0;5;-5}; vec{PB_{1}}={5sqrt{3}; 5;5}.
Пусть угол между vec{PK} и vec{PB_{1}} равен alpha.
Получаем cos alpha=frac{vec{PK} cdot vec{PB_{1}}}{|vec{PK}| cdot |vec{PB_{1}}|}= frac{0 cdot 5sqrt{3} + 5 cdot 5-5 cdot 5}{|vec{PK}| cdot |vec{PB_{1}}|}=0.
cos alpha =0, значит, vec{PK} perp vec{PB_{1}} и прямые PK и PB_{1} перпендикулярны.
б) Угол между плоскостями равен углу между ненулевыми векторами, перпендикулярными этим плоскостям (или, если угол тупой, смежному с ним углу). Такие векторы называют нормалями к плоскостям. Найдём их.
Пусть vec{n_{1}}={x; y; z} перпендикулярен плоскости PKB_{1}. Найдем его, решив систему begin{cases} vec{n_{1}} perp vec{PK}, \ vec{n_{1}} perp vec{PB_{1}}. end{cases}
begin{cases} vec{n_{1}} cdot vec{PK}=0, \ vec{n_{1}} cdot vec{PB_{1}}=0; end{cases}
begin{cases} 0x+5y-5z=0, \ 5sqrt{3}x+5y+5z=0; end{cases}
begin{cases}y=z, \ x=frac{-y-z}{sqrt{3}}. end{cases}
Возьмем y=1; z=1; x=frac{-2}{sqrt{3}}, vec{n_{1}}=left { frac{-2}{sqrt{3}}; 1;1 right }.
Пусть vec{n_{2}}={x; y; z} перпендикулярен плоскости C_{1}B_{1}B. Найдем его, решив систему begin{cases} vec{n_{2}} perp vec{CC_{1}}, \ vec{n_{2}} perp vec{CB}. end{cases}
vec{CC_{1}}={0;0;10}, vec{CB}={5sqrt{3}; 5; 0}.
begin{cases} vec{n_{2}} cdot vec{CC_{1}}=0, \ vec{n_{2}} cdot vec{CB}=0; end{cases}
begin{cases} 0x+0y+10z=0, \ 5sqrt{3}x+5y+0z=0; end{cases}
begin{cases}z=0, \ y=-sqrt{3}x. end{cases}
Возьмем x=1; y=-sqrt{3}; z=0, vec{n_{2}}={1; -sqrt{3};0}.
Найдем косинус искомого угла beta (он равен модулю косинуса угла между vec{n_{1}} и vec{n_{2}}).
cos beta= frac{|vec{n_{1}} cdot vec{n_{2}}|}{|vec{n_{1}}| cdot |vec{n_{2}}|}= frac{left |-dfrac{2}{sqrt{3}}cdot 1+1 cdot (-sqrt{3})+1 cdot 0 right |}{sqrt{dfrac{4}{3}+1+1} cdot sqrt{1+3+0}}= frac{dfrac{5}{sqrt{3}}}{2sqrt{dfrac{10}{3}}}= frac{sqrt{10}}{4}.
cos beta =frac{sqrt{10}}{4}, beta=arccosfrac{sqrt{10}}{4}.
Ответ
arccosfrac{sqrt{10}}{4}
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №981
Тип задания: 14
Тема:
Угол между плоскостями
Условие
В правильной четырёхугольной призме ABCDA_{1}B_{1}C_{1}D_{1} на ребре AA_{1} взята точка M так, что AM:MA_{1}=2:3.
а) Постройте сечение призмы плоскостью, проходящей через точки D и M параллельно диагонали основания AC.
б) Найдите угол между плоскостью сечения и плоскостью основания, если AA_{1}=5sqrt{6}, AB=4.
Показать решение
Решение
а) По условию ABCDA_{1}B_{1}C_{1}D_{1} — правильная призма, это означает, что основание ABCD — квадрат и боковые грани — равные прямоугольники.
Так как плоскость сечения проходит через точки M и D параллельно диагонали AC, то для её построения в плоскости A_{1}AC через точку M проведём отрезок MN параллельный AC. Получим AC parallel (MDN) по признаку параллельности прямой и плоскости.
Плоскость MDN пересекает параллельные плоскости A_{1}AD и B_{1}BC, тогда, по свойству параллельных плоскостей, линии пересечения граней A_{1}ADD_{1} и B_{1}BCC_{1} плоскостью MDN параллельны.
Проведём отрезок NE параллельно отрезку MD.
Четырехугольник DMEN — искомое сечение.
б) Найдём угол между плоскостью сечения и плоскостью основания. Пусть плоскость сечения пересекает плоскость основания по некоторой прямой p, проходящей через точку D. AC parallel MN, следовательно, AC parallel p (если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна этой прямой). BD perp AC как диагонали квадрата, значит, BD perp p. BD — проекция ED на плоскость ABC, тогда по теореме о трех перпендикулярах ED perp p, следовательно, angle EDB — линейный угол двугранного угла между плоскостью сечения и плоскостью основания.
Установим вид четырехугольника DMEN. MD parallel EN, аналогично ME parallel DN, значит, DMEN — параллелограмм, а так как MD=DN (прямоугольные треугольники MAD и NCD равны по двум катетам: AD=DC как стороны квадрата, AM=CN как расстояния между параллельными прямыми AC и MN), следовательно, DMEN — ромб. Отсюда, F — середина MN.
По условию AM:MA_{1}=2:3, тогда AM=frac{2}{5}AA_{1}=frac{2}{5} cdot 5sqrt{6}=2sqrt{6}.
AMNC — прямоугольник, F — середина MN, O — середина AC. Значит, FOparallel MA, FO perp AC, FO=MA=2sqrt{6}.
Зная, что диагональ квадрата равна asqrt{2}, где a — сторона квадрата, получим BD=4sqrt{2}. OD=frac{1}{2}BD=frac{1}{2} cdot 4sqrt{2}=2sqrt{2}.
В прямоугольном треугольнике FODenspace tg angle FDO=frac{FO}{OD}=frac{2sqrt{6}}{2sqrt{2}}=sqrt{3}. Следовательно, angle FDO=60^circ.
Ответ
60^circ
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
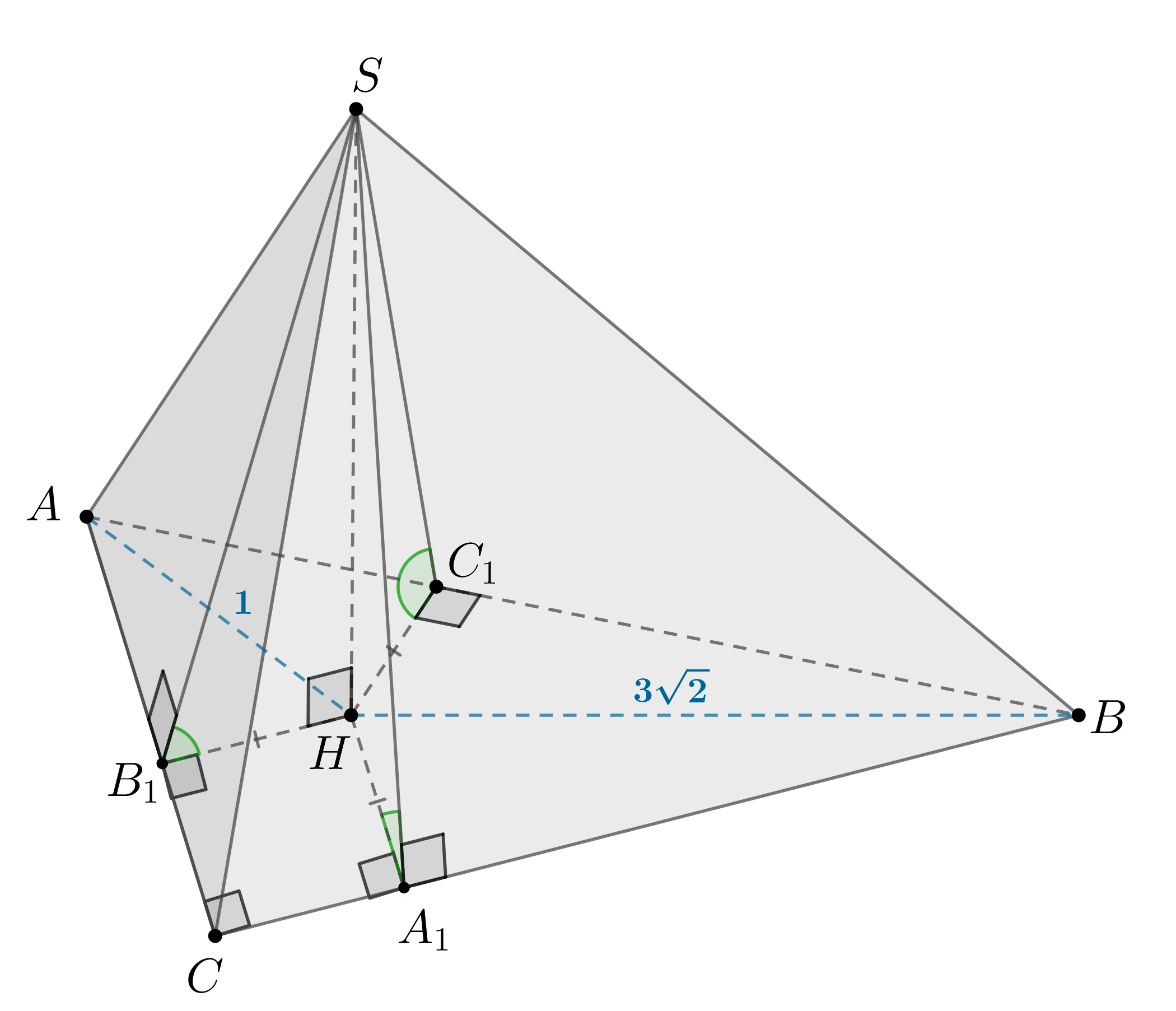
Задание №234
Тип задания: 14
Тема:
Угол между плоскостями
Условие
ABCDEFA_1B_1C_1D_1E_1F_1 — правильная шестиугольная призма с ребрами длиной 1.
а) Докажите, что угол между прямыми ED_1 и BE_1 прямой.
б) Найдите угол между плоскостями BB_1E и ABD_1.
Показать решение
Решение
а) Рассмотрим рисунок.

Заметим, что параллелепипед ABB_{1}A_{1}EDD_{1}E_{1} является правильной призмой (ABB_{1}A_{1} — квадрат). BD perp EDD_{1}, тогда BD perp ED_{1}, ED_{1} perp ED как диагонали квадрата, значит, ED_{1} perp A_{1}BD, следовательно, ED_{1} perp BE_{1}, и угол между ними прямой.
б) Рассмотрим двугранный угол EE_{1}BD_{1} и его линейный угол EOD_{1}. С помощью теоремы косинусов можно найти высоту AE=sqrt{3} параллелепипеда. Диагональ боковой грани BE=sqrt{BA^{2}+AE^{2}}=2 и диагональ BE_{1}=sqrt{BE^{2}+EE_{1}^{2}}=sqrt{5} параллелепипеда.
В прямоугольном треугольнике с известными катетами BE=2, EE_{1}=1 и гипотенузой BE_{1}=sqrt{5} найдем высоту EO=frac{BE cdot EE_{1}}{BE_{1}}=frac{2}{sqrt{5}}.
Из равенства треугольников BEE_{1} и E_{1}BD_{1} следует, что треугольник EOD_{1}является равнобедренным OE=OD_{1}=frac{2}{sqrt{5}} с основанием ED_{1}=sqrt{ED^{2}+DD_{1}^{2}}=sqrt{2}.
Применяя теорему косинусов ED_{1}^{2}= EO^{2}+OD^{2}-2EOD_{1} cos angle EOD_{1}, найдем cos EOD_{1}=-frac{1}{4}, значит, угол между плоскостями ABD_{1} и BB_{1}E равен arccosfrac{1}{4}.
Ответ
arccosfrac14
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №199
Тип задания: 14
Тема:
Угол между плоскостями
Условие
В кубе ABCDA_1B_1C_1D_1, ребро которого равно 4, точка M является серединой отрезка BC_1.
а) Постройте сечение куба плоскостью, проходящей через прямую AM, параллельно прямой A_1B.
б) Найдите расстояние между прямыми A_1B и AM.
Показать решение
Решение
а) В плоскости грани AA_1B_1B через точку A проведем прямую, параллельную A_1B. Q и K — точки пересечения этой прямой соответственно с прямыми A_1B_1 и BB_1.
Прямая KM пересекает ребро BC в точке N, а ребро B_1C_1 — в точке S. Отрезок SQ пересекает ребро A_1D_1 в точке T.
Четырехугольник ATSN образует искомое сечение, так как все его вершины лежат в плоскости QSK, которая проходит через AM и прямую AK, параллельную A_1B, и, следовательно (QSK)parallel A_1B.
б) 1) В плоскости грани AA_1B_1B построим отрезок AK parallel A_1B. A_1Bparallel (AMK), AK=A_1B.
2) В плоскости BCC_1 проведем BRperp MK, тогда по теореме, обратной теореме о трех перпендикулярах, AR perp MK как наклонная к плоскости BCC_1, проекция которой BRperp MK по построению.
3) Плоскость ABR perp MK, следовательно, любая прямая плоскости ABR перпендикулярна прямой MK.
4) Проведем отрезок BHperp AR. Длина этого отрезка — искомое расстояние.
Действительно, отрезок BH перпендикулярен двум пересекающимся прямым (AR и MK) плоскости AMK, параллельной A_1B.
5) Из bigtriangleup MBK найдем высоту BR:
MB=2sqrt{2}, BK=4, angle MBK = 135^{circ}. По теореме косинусов MK= sqrt{MB^2+KB^2-2MBcdot KBcdot cos 135^{circ}}= sqrt{8+16-2cdot 2sqrt{2}cdot 4cdot left(-frac{sqrt{2}}{2}right)}= 2sqrt{10}.
S_{MBK}= frac{1}{2}MBcdot BKcdot sin 135^{circ}= frac{1}{2}cdot 2sqrt{2}cdot 4cdot frac{sqrt{2}}{2}= 4,
S_{MBK}= frac{1}{2}MKcdot BR= frac{1}{2}cdot 2sqrt{10}cdot BR = BRcdot sqrt{10}.
sqrt{10}cdot BR=4, откуда BR=frac{2sqrt{10}}{5}.
Из прямоугольного bigtriangleup ABR высоту BH найдем из условия ABcdot BR=ARcdot BH.
По теореме Пифагора из bigtriangleup ABR; AR=sqrt{AB^2+BR^2}=sqrt{frac{88}{5}}, тогда 4cdot frac{2sqrt{10}}{5}=sqrt{frac{88}{5}}cdot BH, BH=frac{4sqrt{11}}{11}.
Ответ
frac{4sqrt{11}}{11}
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №159
Тип задания: 14
Тема:
Угол между плоскостями
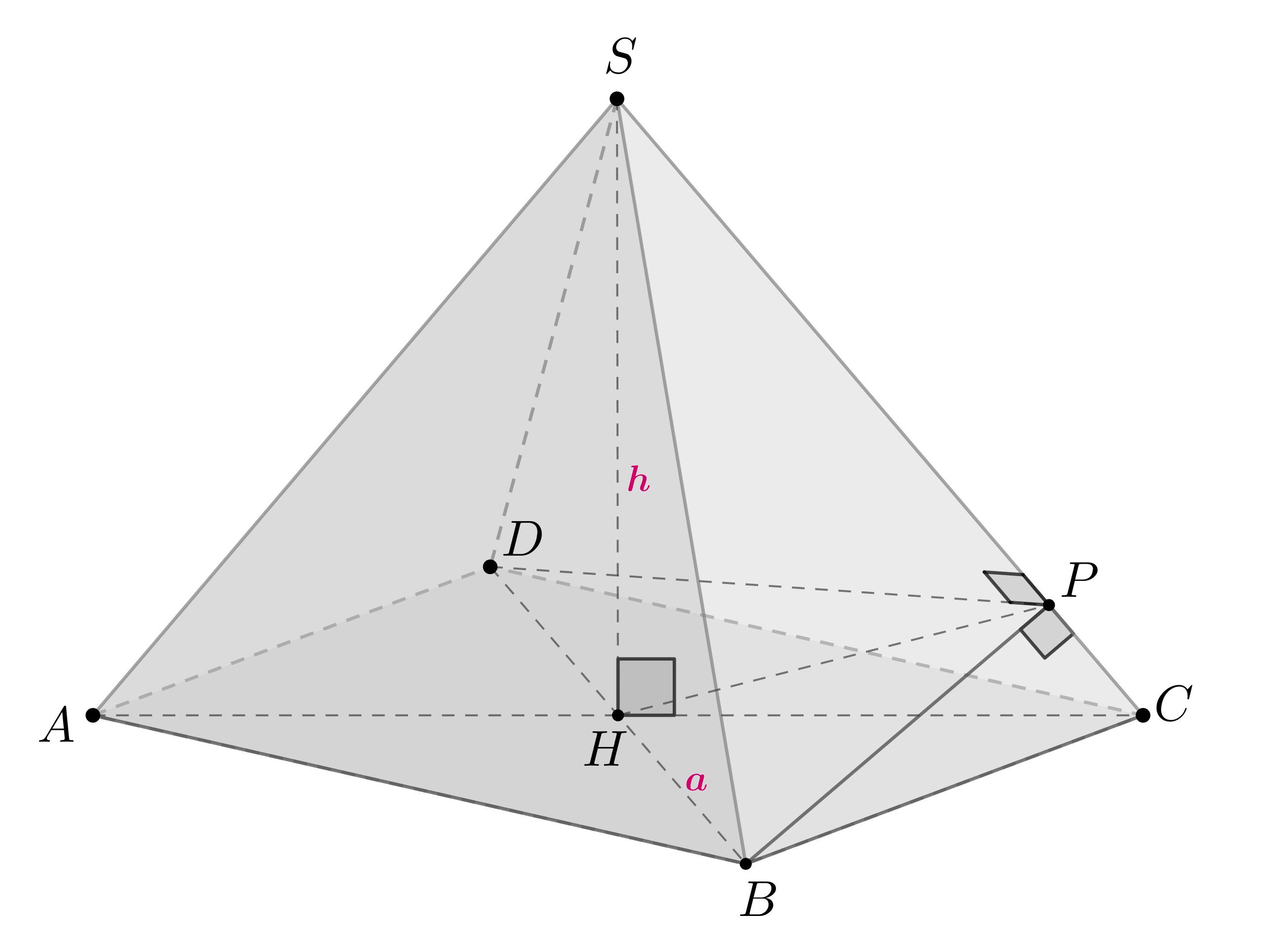
Условие
Площадь полной поверхности правильной четырехугольной пирамиды SABCD с основанием ABCD равна 144, а площадь боковой поверхности равна 108.
а) Докажите, что угол между плоскостью SAC и плоскостью, которая проходит через вершину S данной пирамиды, середину стороны AB и центр основания, равен 45^{circ}.
б) Найдите чему равна площадь сечения пирамиды плоскостью SAC.
Показать решение
Решение
Найдем площадь основания пирамиды 144 − 108 = 36, исходя из этого AB = 6.
Определим площадь боковой грани frac{108}{4}=27.
Примем SM за высоту SAB. Получим S_{SAB}=frac{SMcdot AB}{2}=SMcdot 3=27, поэтому SM = 9.
а) Пусть SH – высота пирамиды, H – середина основания. Исходя из этого SH – прямая, по которой пересекаются данные плоскости, так же она перпендикулярна прямым AH и MH и другим прямым, лежащим в плоскости основания пирамиды. От сюда следует, что угол между плоскостью SAC и плоскостью SMH – это угол AHM, который равен 45^{circ}.
б) SH=sqrt{SM^{2}-MH^{2}}=sqrt{72}=6sqrt{2}.
Получаем S_{SAC}=frac{SHcdot AC}{2}=6sqrt{2}cdot 3sqrt{2}=36.
Ответ
а) 45^{circ}; б) 36
Источник: «Математика ЕГЭ 2016. Типовые тестовые задания». Под ред. И. В. Ященко.
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Нахождение угла между плоскостями (двугранный угол)
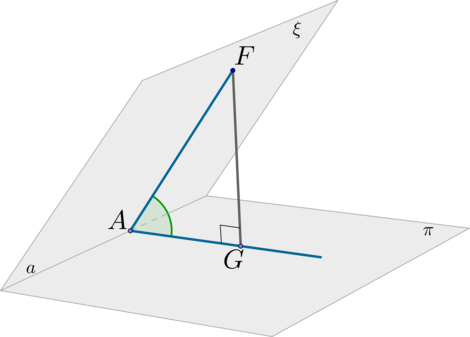
(blacktriangleright) Двугранный угол – угол, образованный двумя полуплоскостями и прямой (a), которая является их общей границей.
(blacktriangleright) Чтобы найти угол между плоскостями (xi) и (pi), нужно найти линейный угол (причем острый или прямой) двугранного угла, образованного плоскостями (xi) и (pi):
Шаг 1: пусть (xicappi=a) (линия пересечения плоскостей). В плоскости (xi) отметим произвольную точку (F) и проведем (FAperp
a);
Шаг 2: проведем (FGperp pi);
Шаг 3: по ТТП ((FG) – перпендикуляр, (FA) –наклонная, (AG) – проекция) имеем: (AGperp a);
Шаг 4: угол (angle FAG) называется линейным углом двугранного угла, образованного плоскостями (xi) и (pi).
Заметим, что треугольник (AG) – прямоугольный.
Заметим также, что плоскость (AFG), построенная таким образом, перпендикулярна обеим плоскостям (xi) и (pi). Следовательно, можно сказать по-другому: угол между плоскостями (xi) и (pi) — это угол между двумя пересекающимися прямыми (cin xi) и (binpi), образующими плоскость, перпендикулярную и (xi), и (pi).
Задание
1
#2875
Уровень задания: Сложнее ЕГЭ
Дана четырехугольная пирамида, все ребра которой равны, причем основание является квадратом. Найдите (6cos alpha), где (alpha) – угол между ее смежными боковыми гранями.
Пусть (SABCD) – данная пирамида ((S) – вершина), ребра которой равны (a). Следовательно, все боковые грани представляют собой равные равносторонние треугольники. Найдем угол между гранями (SAD) и (SCD).
Проведем (CHperp SD). Так как (triangle SAD=triangle SCD), то (AH) также будет высотой в (triangle SAD). Следовательно, по определению (angle AHC=alpha) – линейный угол двугранного угла между гранями (SAD) и (SCD).
Так как в основании лежит квадрат, то (AC=asqrt2). Заметим также, что (CH=AH) – высота равностороннего треугольника со стороной (a), следовательно, (CH=AH=frac{sqrt3}2a).
Тогда по теореме косинусов из (triangle AHC): [cos alpha=dfrac{CH^2+AH^2-AC^2}{2CHcdot AH}=-dfrac13 quadRightarrowquad
6cosalpha=-2.]
Ответ: -2
Задание
2
#2876
Уровень задания: Сложнее ЕГЭ
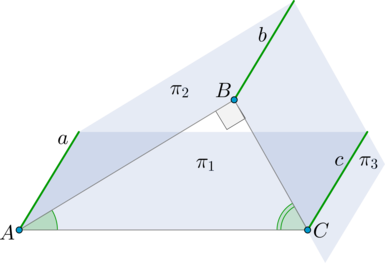
Плоскости (pi_1) и (pi_2) пересекаются под углом, косинус которого равен (0,2). Плоскости (pi_2) и (pi_3) пересекаются под прямым углом, причем линия пересечения плоскостей (pi_1) и (pi_2) параллельна линии пересечения плоскостей (pi_2) и (pi_3). Найдите синус угла между плоскостями (pi_1) и (pi_3).
Пусть линия пересечения (pi_1) и (pi_2) – прямая (a), линия пересечения (pi_2) и (pi_3) – прямая (b), а линия пересечения (pi_3) и (pi_1) – прямая (c). Так как (aparallel b), то (cparallel aparallel b) (по теореме из раздела теоретической справки “Геометрия в пространстве” (rightarrow) “Введение в стереометрию, параллельность”).
Отметим точки (Ain a, Bin b) так, чтобы (ABperp a, ABperp b) (это возможно, так как (aparallel b)). Отметим (Cin c) так, чтобы (BCperp c), следовательно, (BCperp b). Тогда (ACperp c) и (ACperp a).
Действительно, так как (ABperp b, BCperp b), то (b) перпендикулярна плоскости (ABC). Так как (cparallel aparallel b), то прямые (a) и (c) тоже перпендикулярны плоскости (ABC), а значит и любой прямой из этой плоскости, в частности, прямой (AC).
Отсюда следует, что (angle BAC=angle (pi_1, pi_2)), (angle
ABC=angle (pi_2, pi_3)=90^circ), (angle BCA=angle (pi_3,
pi_1)). Получается, что (triangle ABC) прямоугольный, а значит [sin angle BCA=cos angle BAC=0,2.]
Ответ: 0,2
Задание
3
#2877
Уровень задания: Сложнее ЕГЭ
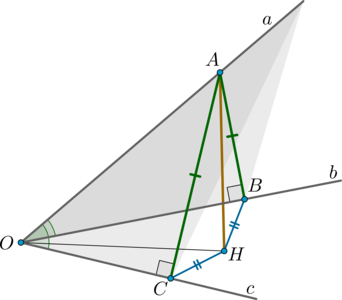
Даны прямые (a, b, c), пересекающиеся в одной точке, причем угол между любыми двумя из них равен (60^circ). Найдите (cos^{-1}alpha), где (alpha) – угол между плоскостью, образованной прямыми (a) и (c), и плоскостью, образованной прямыми (b) и (c). Ответ дайте в градусах.
Пусть прямые пересекаются в точке (O). Так как угол между любыми двумя их них равен (60^circ), то все три прямые не могут лежать в одной плоскости. Отметим на прямой (a) точку (A) и проведем (ABperp
b) и (ACperp c). Тогда (triangle AOB=triangle AOC) как прямоугольные по гипотенузе и острому углу. Следовательно, (OB=OC) и (AB=AC).
Проведем (AHperp (BOC)). Тогда по теореме о трех перпендикулярах (HCperp c), (HBperp b). Так как (AB=AC), то (triangle
AHB=triangle AHC) как прямоугольные по гипотенузе и катету. Следовательно, (HB=HC). Значит, (OH) – биссектриса угла (BOC) (так как точка (H) равноудалена от сторон угла).
Заметим, что таким образом мы к тому же построили линейный угол двугранного угла, образованного плоскостью, образованной прямыми (a) и (c), и плоскостью, образованной прямыми (b) и (c). Это угол (ACH).
Найдем этот угол. Так как точку (A) мы выбирали произвольно, то пусть мы выбрали ее так, что (OA=2). Тогда в прямоугольном (triangle AOC): [sin 60^circ=dfrac{AC}{OA}
quadRightarrowquad AC=sqrt3 quadRightarrowquad
OC=sqrt{OA^2-AC^2}=1.] Так как (OH) – биссектриса, то (angle
HOC=30^circ), следовательно, в прямоугольном (triangle HOC): [mathrm{tg},30^circ=dfrac{HC}{OC}quadRightarrowquad HC=dfrac1{sqrt3}.] Тогда из прямоугольного (triangle ACH): [cosangle alpha=cosangle ACH=dfrac{HC}{AC}=dfrac13 quadRightarrowquad
cos^{-1}alpha=3.]
Ответ: 3
Задание
4
#2910
Уровень задания: Сложнее ЕГЭ
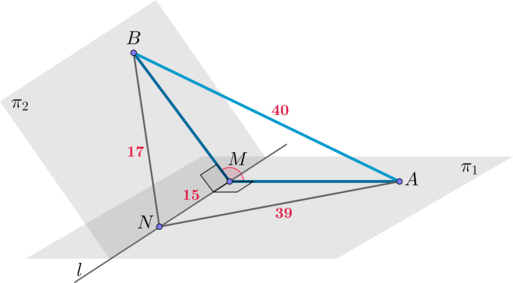
Плоскости (pi_1) и (pi_2) пересекаются по прямой (l), на которой лежат точки (M) и (N). Отрезки (MA) и (MB) перпендикулярны прямой (l) и лежат в плоскостях (pi_1) и (pi_2) соответственно, причем (MN = 15), (AN = 39), (BN = 17), (AB = 40). Найдите (3cosalpha), где (alpha) – угол между плоскостями (pi_1) и (pi_2).
Треугольник (AMN) прямоугольный, (AN^2 = AM^2 + MN^2), откуда [AM^2 = 39^2 — 15^2 = 36^2.] Треугольник (BMN) прямоугольный, (BN^2 = BM^2 + MN^2), откуда [BM^2 = 17^2 — 15^2 = 8^2.] Запишем для треугольника (AMB) теорему косинусов: [AB^2 = AM^2 + MB^2 — 2cdot AMcdot MBcdotcosangle AMB.] Тогда [40^2 = 36^2 + 8^2 — 2cdot 36cdot 8cdotcosangle AMBqquadLeftrightarrowqquad cosangle AMB = -dfrac{5}{12}] Так как угол (alpha) между плоскостями – это острый угол, а (angle AMB) получился тупым, то (cosalpha=dfrac5{12}). Тогда [3cosalpha = dfrac54=1,25.]
Ответ: 1,25
Задание
5
#2911
Уровень задания: Сложнее ЕГЭ
(ABCDA_1B_1C_1D_1) – параллелепипед, (ABCD) – квадрат со стороной (a), точка (M) – основание перпендикуляра, опущенного из точки (A_1) на плоскость ((ABCD)), кроме того (M) – точка пересечения диагоналей квадрата (ABCD). Известно, что (A_1M = dfrac{sqrt{3}}{2}a). Найдите угол между плоскостями ((ABCD)) и ((AA_1B_1B)). Ответ дайте в градусах.
Построим (MN) перпендикулярно (AB) как показано на рисунке.
Так как (ABCD) – квадрат со стороной (a) и (MNperp AB) и (BCperp AB), то (MNparallel BC). Так как (M) – точка пересечения диагоналей квадрата, то (M) – середина (AC), следовательно, (MN) – средняя линия и (MN =frac12BC= frac{1}{2}a).
(MN) – проекция (A_1N) на плоскость ((ABCD)), причем (MN) перпендикулярен (AB), тогда по теореме о трех перпендикулярах (A_1N) перпендикулярен (AB) и угол между плоскостями ((ABCD)) и ((AA_1B_1B)) есть (angle A_1NM).
[mathrm{tg}, angle A_1NM = dfrac{A_1M}{NM} = dfrac{frac{sqrt{3}}{2}a}{frac{1}{2}a} = sqrt{3}qquadRightarrowqquadangle A_1NM = 60^{circ}]
Ответ: 60
Задание
6
#1854
Уровень задания: Сложнее ЕГЭ
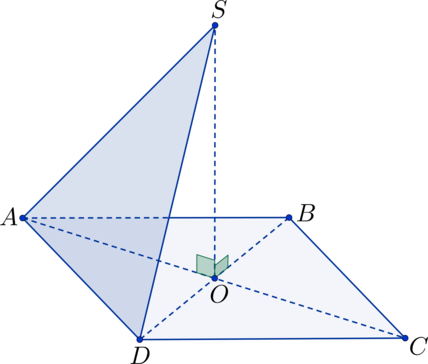
В квадрате (ABCD): (O) – точка пересечения диагоналей; (S) – не лежит в плоскости квадрата, (SO perp ABC). Найдите угол между плоскостями (ASD) и (ABC), если (SO = 5), а (AB = 10).
Прямоугольные треугольники (triangle SAO) и (triangle SDO) равны по двум сторонам и углу между ними ((SO perp ABC) (Rightarrow) (angle SOA = angle SOD = 90^circ); (AO = DO), т.к. (O) – точка пересечения диагоналей квадрата, (SO) – общая сторона) (Rightarrow) (AS = SD) (Rightarrow) (triangle ASD) – равнобедренный. Точка (K) – середина (AD), тогда (SK) – высота в треугольнике (triangle ASD), а (OK) – высота в треугольнике (AOD) (Rightarrow) плоскость (SOK) перпендикулярна плоскостям (ASD) и (ABC) (Rightarrow) (angle SKO) – линейный угол, равный искомому двугранному углу.
В (triangle SKO): (OK = frac{1}{2}cdot AB = frac{1}{2}cdot 10 = 5 = SO) (Rightarrow) (triangle SOK) – равнобедренный прямоугольный треугольник (Rightarrow) (angle SKO = 45^circ).
Ответ: 45
Задание
7
#1855
Уровень задания: Сложнее ЕГЭ
В квадрате (ABCD): (O) – точка пересечения диагоналей; (S) – не лежит в плоскости квадрата, (SO perp ABC). Найдите угол между плоскостями (ASD) и (BSC), если (SO = 5), а (AB = 10).
Прямоугольные треугольники (triangle SAO), (triangle SDO), (triangle SOB) и (triangle SOC) равны по двум сторонам и углу между ними ((SO perp ABC) (Rightarrow) (angle SOA = angle SOD = angle SOB = angle SOC = 90^circ); (AO = OD = OB = OC), т.к. (O) – точка пересечения диагоналей квадрата, (SO) – общая сторона) (Rightarrow) (AS = DS = BS = CS) (Rightarrow) (triangle ASD) и (triangle BSC) – равнобедренные. Точка (K) – середина (AD), тогда (SK) – высота в треугольнике (triangle ASD), а (OK) – высота в треугольнике (AOD) (Rightarrow) плоскость (SOK) перпендикулярна плоскости (ASD). Точка (L) – середина (BC), тогда (SL) – высота в треугольнике (triangle BSC), а (OL) – высота в треугольнике (BOC) (Rightarrow) плоскость (SOL) (она же плоскость (SOK)) перпендикулярна плоскости (BSC). Таким образом получаем, что (angle KSL) – линейный угол, равный искомому двугранному углу.
(KL = KO + OL = 2cdot OL = AB = 10) (Rightarrow) (OL = 5); (SK = SL) – высоты в равных равнобедренных треугольниках, которые можно найти по теореме Пифагора: (SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50). Можно заметить, что (SK^2 + SL^2 = 50 + 50 = 100 = KL^2) (Rightarrow) для треугольника (triangle KSL) выполняется обратная теорема Пифагора (Rightarrow) (triangle KSL) – прямоугольный треугольник (Rightarrow) (angle KSL = 90^circ).
Ответ: 90
Подготовка учащихся к сдаче ЕГЭ по математике, как правило, начинается с повторения основных формул, в том числе и тех, которые позволяют определить угол между плоскостями. Несмотря на то, что этот раздел геометрии достаточно подробно освещается в рамках школьной программы, многие выпускники нуждаются в повторении базового материала. Понимая, как найти угол между плоскостями, старшеклассники смогут оперативно вычислить правильный ответ в ходе решения задачи и рассчитывать на получение достойных баллов по итогам сдачи единого государственного экзамена.
Основные нюансы
-
Чтобы вопрос, как найти двугранный угол, не вызывал затруднений, рекомендуем следовать алгоритму решения, который поможет справиться с заданиями ЕГЭ.
-
Вначале необходимо определить прямую, по которой пересекаются плоскости.
-
Затем на этой прямой нужно выбрать точку и провести к ней два перпендикуляра.
-
Следующий шаг — нахождение тригонометрической функции двугранного угла, который образован перпендикулярами. Делать это удобнее всего при помощи получившегося треугольника, частью которого является угол.
-
Ответом будет значение угла или его тригонометрической функции.
Подготовка к экзаменационному испытанию вместе со «Школково» — залог вашего успеха
В процессе занятий накануне сдачи ЕГЭ многие школьники сталкиваются с проблемой поиска определений и формул, которые позволяют вычислить угол между 2 плоскостями. Школьный учебник не всегда есть под рукой именно тогда, когда это необходимо. А чтобы найти нужные формулы и примеры их правильного применения, в том числе и для нахождения угла между плоскостями в Интернете в режиме онлайн, порой требуется потратить немало времени.
Математический портал «Школково» предлагает новый подход к подготовке к госэкзамену. Занятия на нашем сайте помогут ученикам определить наиболее сложные для себя разделы и восполнить пробелы в знаниях.
Мы подготовили и понятно изложили весь необходимый материал. Базовые определения и формулы представлены в разделе «Теоретическая справка».
Для того чтобы лучше усвоить материал, предлагаем также попрактиковаться в выполнении соответствующих упражнений. Большая подборка задач различной степени сложности, например, на нахождение угла между прямой и плоскостью, представлена в разделе «Каталог». Все задания содержат подробный алгоритм нахождения правильного ответа. Перечень упражнений на сайте постоянно дополняется и обновляется.
Практикуясь в решении задач, в которых требуется найти угол между двумя плоскостями, учащиеся имеют возможность в онлайн-режиме сохранить любое задание в «Избранное». Благодаря этому они смогут вернуться к нему необходимое количество раз и обсудить ход его решения со школьным учителем или репетитором.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Тема 13.
Задачи по стереометрии
13
.
16
Угол между плоскостями
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
задачи по стереометрии
13.01Задачи из ЕГЭ прошлых лет
13.02Задачи из сборника И.В. Ященко ЕГЭ 2023
13.03Задачи формата ЕГЭ на многогранники. Пирамида, призма
13.04Задачи формата ЕГЭ на тела вращения. Шар, цилиндр, конус
13.05Аксиомы. Доказательство базовых фактов
13.06Параллельность. Доказательство базовых фактов
13.07Перпендикулярность. Доказательство базовых фактов
13.08Тела вращения. Доказательство базовых фактов
13.09Задачи на построение
13.10Упрощенные задачи
13.11Построение сечений
13.12Нахождение площади сечения
13.13Расстояние от точки до прямой
13.14Расстояние от точки до плоскости
13.15Угол между прямой и плоскостью
13.16Угол между плоскостями
13.17Нахождение объема или площади поверхности
13.18Угол между скрещивающимися прямыми
13.19Расстояние между скрещивающимися прямыми
13.20Метод объемов
Решаем задачи
Основание пирамиды — равнобедренный прямоугольный треугольник. Каждый из
двугранных углов при основании равен Высота пирамиды равна
. Найдите
площадь основания.
Показать ответ и решение
Ответ:
Основание пирамиды — треугольник со сторонами 13, 14 и 15. Все двугранные
углы при сторонах основания равны Найдите высоту пирамиды.
Показать ответ и решение
Если боковые грани пирамиды наклонены к плоскости основания под одинаковыми
углами, то основание высоты пирамиды — центр вписанной в основание пирамиды
окружности. Докажем это.
Опустим высоту пирамиды
к основанию
Опустим
перпендикуляры
на стороны
По теореме о трех
перпендикулярах отрезки
перпендикулярны сторонам
треугольника
Тогда по определению — линейные углы
двугранных углов, образуемых боковыми гранями пирамиды и ее основанием.
Следовательно, по общему катету и острому углу
Следовательно, Таким образом, точка
— центр
вписанной в окружности радиуса
Будем искать по формуле
Площадь равна
Тогда
Так как то найдем
Следовательно,
Ответ:
Основанием пирамиды служит треугольник со сторонами 10, 10 и 12. Все боковые
грани пирамиды наклонены к плоскости основания под углом Найдите
высоту пирамиды.
Показать ответ и решение
Ответ:
Показать ответ и решение
Пусть Проведем
Тогда по ТТП
Следовательно, по определению
— линейные углы двугранных углов между боковыми гранями и
основанием.
Пусть
— четырехугольник, три угла которого прямые,
следовательно, это прямоугольник. Таким образом,
Так как , то
Следовательно,
Ответ:
Показать ответ и решение
Ответ:
Показать ответ и решение
Проведем Тогда по теореме о трех перпендикулярах наклонная
Следовательно,
По теореме Пифагора в треугольнике имеем:
Так как то
Тогда
Ответ:
Докажите, что плоскость, делящая пополам двугранный угол при ребре тетраэдра,
делит противоположное ребро на части, пропорциональные площадям граней,
заключающих этот угол.
Показать ответ и решение
— высота тетраэдра, проведенная к грани площадью
,
,
, тогда по ТТП наклонная
, следовательно,
. Так
как , то
. Из прямоугольного
имеем
, следовательно,
Мы рассмотрели случай, когда . В случай, если
, точка
находится вне грани и работать мы будем с тем же треугольником
,
но с его углом , синус которого равен синусу угла
. Следовательно,
формула останется прежней.
Показать ответ и решение
— линия пересечения плоскостей
и
. Следовательно, так как
,
— линейный угол двугранного угла
между этими плоскостями. Если он острый или прямой, то он равен углу между
этими плоскостями, если он тупой, то смежный с ним угол равен углу между этими
плоскостями, следовательно, угол между и
равен
, если
, и
, если
.
Показать ответ и решение
— перпендикуляр к плоскости, содержащей точку
. Проведем
,
тогда по ТТП наклонная . Следовательно,
— линейный
угол двугранного угла между двумя плоскостями, то есть .
Тогда
Ответ:
Показать ответ и решение
Ответ:
Показать ответ и решение
Ответ:
Показать ответ и решение
Проведем через точку прямые параллельно прямым
и
и
переобозначим точки. Пусть эти прямые пересекают ребра и
в точках
и
соответственно, как показано на рисунке. Тогда
Построим линейный угол двугранного угла, образуемого плоскостями
и Для этого нужно найти линию пересечения этих плоскостей.
Пусть тогда
— линия пересечения плоскостей
и
Проведем
Тогда по ТТП
Следовательно,
— искомый линейный угол.
Пусть Тогда
следовательно,
Так как то
, следовательно,
правильный,
то есть
Из подобия имеем:
Тогда
По теореме косинусов для
По теореме синусов для этого же треугольника:
Из имеем:
Следовательно, из
Ответ:
Показать ответ и решение
— правильная четырехугольная пирамида, следовательно, в
основании лежит квадрат, боковые ребра равны между собой, а основание
высоты пирамиды — точка
— точка пересечения диагоналей
Проведем . Так как боковые грани — равные равнобендренные
треугольники, то . Следовательно,
— двугранный угол при
боковом ребре пирамиды.
Если прямая перпендикулярна двум пересекающимся прямым плоскости, то
она перпендикулярна этой плоскости, следовательно, любой прямой из этой
плоскости. Следовательно,
, то есть
—
высота прямоугольного треугольника , проведенная к гипотенузе. Введем
. Так как
.
— проекция
на плоскость
. Так как
по
ТТП
Так как
— медиана
прямоугольного треугольника, проведенная к гипотенузе, то
Ответ:
Найдите объем правильной четырехугольной пирамиды с высотой и
двугранным углом при боковом ребре.
Показать ответ и решение
— правильная четырехугольная пирамида, следовательно, в
основании лежит квадрат, боковые ребра равны между собой, а основание
высоты пирамиды — точка
— точка пересечения диагоналей
Проведем . Так как боковые грани — равные равнобендренные
треугольники, то . Следовательно,
— двугранный угол при
боковом ребре пирамиды. Введем .
Если прямая перпендикулярна двум пересекающимся прямым плоскости, то
она перпендикулярна этой плоскости, следовательно, любой прямой из этой
плоскости. Следовательно,
, то есть
—
высота прямоугольного треугольника , проведенная к гипотенузе. Так как
.
Так как , то
, следовательно,
Ответ:
Показать ответ и решение
Если боковые грани пирамиды наклонены к плоскости основания под одинаковыми
углами (двугранные углы при ребрах основания равны), то основание высоты
пирамиды — центр вписанной в основание окружности. Докажем это.
Проведем ,
,
. Тогда по ТТП
,
,
. Следовательно,
—
двугранные углы при ребрах основания пирамиды. Следовательно,
как прямоугольные по катету и острому углу.
Отсюда , то есть
— центр вписанной в
окружности радиуса
,
— отрезки биссектрис
и
.
Так как в прямоугольном треугольнике синус одного острого угла равен
косинусу другого острого угла, то получаем равенство
Проверим, выполняется ли теорема Пифагора для при найденных
значениях
Заметим, что
,
как отрезки
касательных, проведенных к вписанной окружности из точек
соответственно.
Если , то
,
,
— верно.
Если , то
,
,
— неверно.
Следовательно, . Так как
то
. Так как из
выше приведенного равенства треугольников , то площадь
боковой поверхности пирамиды равна
Ответ:
Найдите двугранный угол при ребре основания правильной треугольной пирамиды,
если угол между ее боковыми ребрами равен
Показать ответ и решение
Ответ:
Докажите теорему косинусов для трехгранного угла:
Косинус плоского угла трехгранного угла равен произведению косинусов
двух других плоских углов и
трехгранного угла, сложенному с
произведением синусов этих углов на косинус двугранного угла при
противолежащем ему ребре:
Показать ответ и решение
а) Высота пирамиды проходит через центр окружности, описанной около основания, значит, боковые рёбра пирамиды равны.
Обозначим Тогда по теореме Пифагора для треугольников
и
Из прямоугольных треугольников и
Следовательно, то есть
— середина
б) В равнобедренном треугольнике через точку
лежащую на боковой стороне
, проведём прямую,
параллельную высоте Пусть
— точка её пересечения со стороной
По теореме о пропорциональных отрезках
— середина Значит, если
то имеем:
Из прямоугольного треугольника
Из прямоугольного треугольника
Так как и
то
— линейный угол двугранного угла, образованного гранями
и
По теореме косинусов для
Следовательно, угол между гранями и
равен
Ответ:
б)
Критерии оценки
|
Содержание критерия |
Балл |
|
Имеется верное доказательство |
3 |
|
Обоснованно получен верный ответ в |
2 |
|
ИЛИ |
|
|
имеется верное |
|
|
Имеется верное доказательство |
1 |
|
ИЛИ |
|
|
при обоснованном решении пункта |
|
|
ИЛИ |
|
|
обоснованно получен верный ответ в |
|
|
Решение не соответствует ни одному |
0 |
|
Максимальный балл |
3 |


.png)