Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Длина ребра правильного тетраэдра ABCD равна 1. M — середина ребра BC, L — середина ребра AB.
а) Докажите, что плоскость, параллельная прямой CL и содержащая прямую DM, делит ребро AB в отношении 3 : 1, считая от вершины A.
б) Найдите угол между прямыми DM и CL.
2
Сторона основания правильной треугольной призмы ABCA1B1C1 равна 8. Высота этой призмы равна 6.
а) Докажите, что плоскость, содержащая прямую AB1 и параллельная прямой CA1 проходит через середину ребра BC.
б) Найти угол между прямыми CA1 и AB1.
3
В основании прямой призмы ABCA1B1C1 лежит равнобедренный прямоугольный треугольник ABC с гипотенузой AB, равной Высота призмы равна 6.
а) Докажите, что плоскость, содержащая прямую AC1 и параллельная прямой CB1 проходит через середину ребра A1B1.
б) Найдите угол между прямыми AC1 и CB1.
4
В пирамиде DABC прямые, содержащие ребра DC и AB, перпендикулярны.
а) Постройте сечение плоскостью, проходящей через точку E — середину ребра DB, и параллельно DC и AB. Докажите, что получившееся сечение является прямоугольником.
б) Найдите угол между диагоналями этого прямоугольника, если DC = 24, AB = 10.
Источник: Пробный экзамен по математике Кировского района Санкт-Петербурга, 2015. Вариант 1.
5
Точка E — середина ребра CC1 куба ABCDA1B1C1D1.
а) Докажите, что угол между прямыми BE и AD равен углу CBE.
б) Найдите угол между прямыми BE и AD.
Пройти тестирование по этим заданиям
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Нахождение угла между прямыми
(blacktriangleright) Угол между прямыми – это такой угол (alpha), что (0leqslant alphaleqslant 90^circ).
(blacktriangleright) В пространстве существует 4 типа взаимного расположения прямых: совпадают, пересекаются, параллельны, скрещиваются.
(blacktriangleright) Скрещивающиеся прямые – это прямые, через которые нельзя провести одну плоскость.
Признак скрещивающихся прямых: если первая прямая пересекает плоскость, в которой лежит вторая прямая, в точке, не лежащей на второй прямой, то такие прямые скрещиваются.
(blacktriangleright) Порядок нахождения угла между скрещивающимися прямыми:
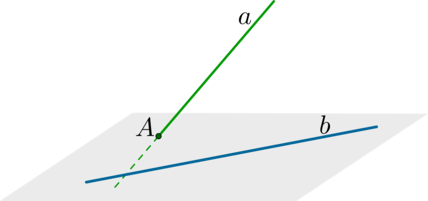
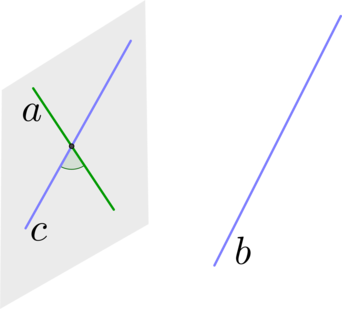
Шаг 1: через одну из двух прямых (a) провести плоскость, параллельную второй прямой (b) (напомним признак: прямая параллельна плоскости, если она параллельна какой-нибудь прямой из этой плоскости);
Шаг 2: в этой плоскости найти прямую (c), параллельную прямой (b);
Шаг 3: тогда угол между прямыми (a) и (b) будет равен углу между прямыми (a) и (c).
Задание
1
#934
Уровень задания: Равен ЕГЭ
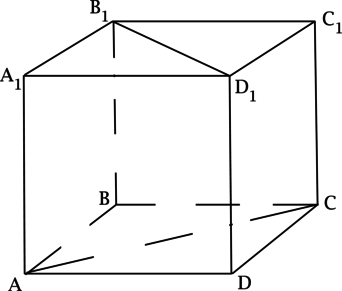
(ABCDA_1B_1C_1D_1) – куб. Найдите угол между прямыми, содержащими отрезки (AC) и (B_1D_1). Ответ дайте в градусах.
Прямая (BD) параллельна прямой (B_1D_1), тогда угол между (AC) и (B_1D_1) равен углу между (AC) и (BD), но (AC) и (BD) – диагонали квадрата, тогда они пересекаются под прямым углом, следовательно ответ (90^{circ}).
Ответ: 90
Задание
2
#2847
Уровень задания: Равен ЕГЭ
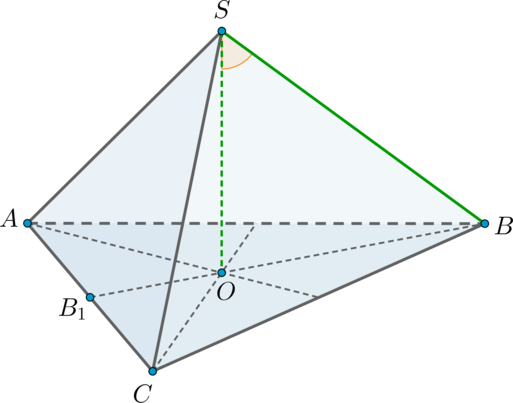
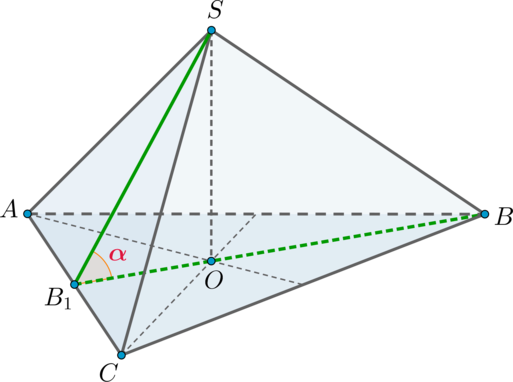
Дана правильная треугольная пирамида (SABC) с вершиной (S). Найдите угол между высотой пирамиды и ребром (SB), если высота пирамиды равна (2sqrt3), а сторона основания пирамиды равна (6). Ответ дайте в градусах.
Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, высота (SO) падает в точку пересечения медиан основания.
Пусть (BB_1) – медиана, а значит, и высота. По теореме Пифагора [BB_1=sqrt{BC^2-B_1C^2}=3sqrt3 quadRightarrowquad BO=dfrac23BB_1=2sqrt3,] так как медианы точкой пересечения делятся в отношении (2:1), считая от вершины.
Следовательно, прямоугольный (triangle SOB) является равнобедренным ((SO=BO=2sqrt3)), значит, острые углы равны по (45^circ).
Ответ: 45
Задание
3
#933
Уровень задания: Равен ЕГЭ
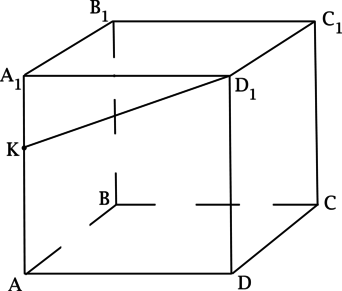
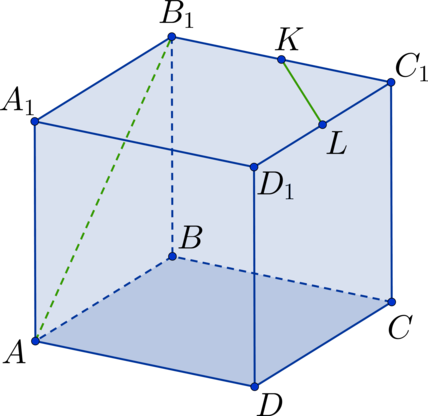
(ABCDA_1B_1C_1D_1) – куб. Точка (K) лежит на ребре (AA_1). Найдите угол между прямыми, содержащими отрезки (D_1K) и (AB). Ответ дайте в градусах.
Так как (ABCDA_1B_1C_1D_1) – куб, то (AB) перпендикулярен плоскости ((ADD_1)), тогда (AB) перпендикулярен любой прямой, лежащей в плоскости ((ADD_1)), следовательно, угол между прямыми, содержащими отрезки (D_1K) и (AB) равен (90^{circ}).
Ответ: 90
Задание
4
#2845
Уровень задания: Равен ЕГЭ
Дан правильный тетраэдр (SABC). Найдите квадрат тангенса угла между высотой грани (SAC), опущенной из вершины (S), и высотой грани (ABC), опущенной из вершины (B).
Пусть (SB_1) – высота грани (SAC). Так как тетраэдр правильный, то все его грани – равные правильные треугольники, то есть (SB_1) также является и медианой, значит, (AB_1=B_1C). Также у правильного тетраэдра высота из каждой вершины падает в точку пересечения медиан (биссектрис, высот) противоположной грани. Следовательно, если (SO) – высота, то (O) – точка пересечения медиан треугольника (ABC), а значит и высот, так как (triangle ABC) правильный. Следовательно, (BB_1) — медиана и высота.
Таким образом, необходимо найти (mathrm{tg}^2angle (SB_1,
BB_1)).
Пусть (a) – ребро тетраэдра. Тогда (BC=a, B_1C=0,5a), следовательно, по теореме Пифагора [BB_1=sqrt{BC^2-B_1C^2}=dfrac{sqrt3}2a] Так как (O) – точка пересечения медиан, а медианы точкой пересечения делятся в отношении (2:1), считая от вершины, то (OB_1=frac13BB_1=frac{sqrt3}6a).
Так как (triangle ABC=triangle SAC), то (SB_1=BB_1). Следовательно, из прямоугольного (triangle SB_1O): [cos
alpha=dfrac{OB_1}{SB_1}=dfrac13 quadRightarrowquad sin alpha
=sqrt{1-cos^2alpha}=dfrac{2sqrt2}3 quadRightarrowquad
mathrm{tg}^2alpha=(2sqrt2)^2=8.]
Ответ: 8
Задание
5
#1846
Уровень задания: Равен ЕГЭ
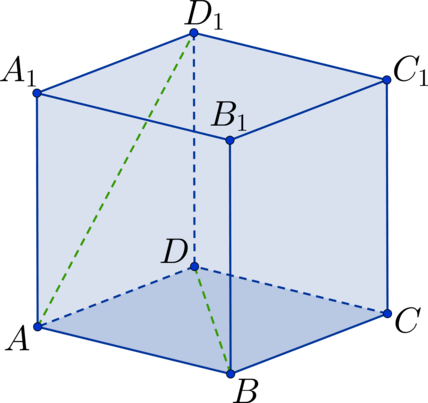
Дан куб (ABCDA_1B_1C_1D_1). Найдите угол между прямыми (AD_1) и (BD). Ответ дайте в градусах.
Заметим, что (BC_1 || AD_1), тогда рассмотрим треугольник (triangle BDC_1), в котором необходимо определить (angle DBC_1). Он состоит из диагоналей соответствующих квадратов. Так как квадраты между собой равны, то равны и диагонали (Rightarrow) (triangle BDC_1) – равносторонний треугольник (Rightarrow) (angle DBC_1 = 60^circ).
Ответ: 60
Задание
6
#1847
Уровень задания: Равен ЕГЭ
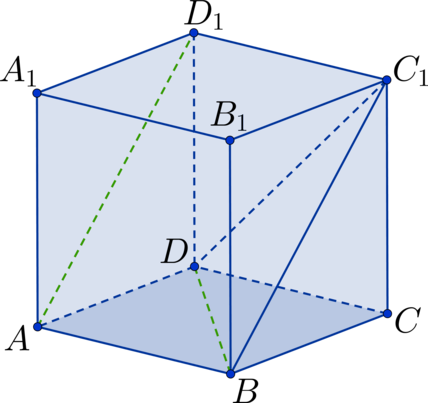
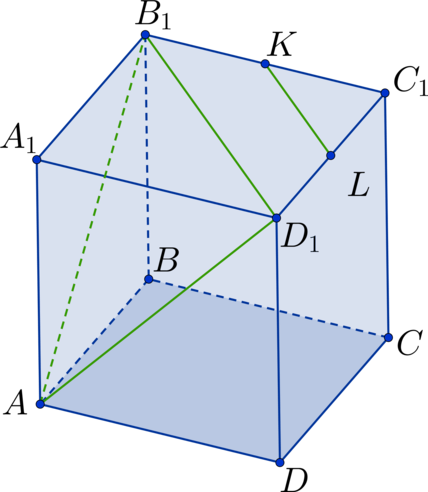
Дан куб (ABCDA_1B_1C_1D_1). Точка (K) – середина стороны (B_1C_1), а точка (L) – середина стороны (C_1D_1). Найдите угол между прямыми (AB_1) и (KL). Ответ дайте в градусах.
Проведем диагональ (B_1D_1) в квадрате (A_1B_1C_1D_1). Тогда (KL) – средняя линия в (triangle B_1C_1D_1) (Rightarrow) (KL || B_1D_1) (Rightarrow) (angle AB_1D_1) – искомый угол. Рассмотрим (triangle AB_1D_1). Он состоит из диагоналей соответствующих квадратов (Rightarrow) треугольник является равносторонним (Rightarrow) (angle AB_1D_1 = 60^circ).
Ответ: 60
Задание
7
#2846
Уровень задания: Сложнее ЕГЭ
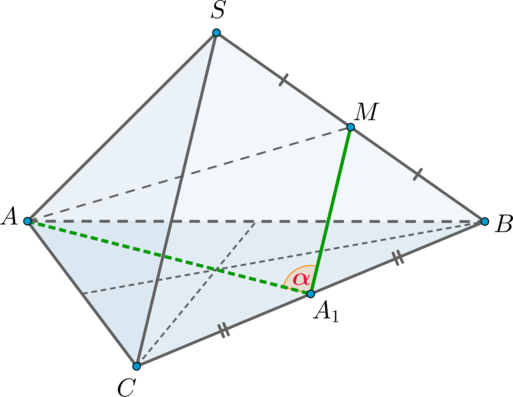
Дана правильная треугольная пирамида (SABC) с вершиной (S). Найдите косинус угла между высотой основания (AA_1) и ребром (SC), если сторона основания равна (sqrt3), а боковое ребро равно (2).
Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, (AA_1) также является и медианой.
Заметим, что прямые (AA_1) и (SC) скрещиваются. Проведем (A_1Mparallel SC), следовательно, (angle (AA_1, SC)=angle (AA_1,
A_1M)).
Так как (A_1Mparallel SC) и (A_1) – середина (BC), то (M) – середина (SB). Следовательно, (A_1M) – средняя линия и [A_1M=frac12SC=1.] По теореме Пифагора из (triangle ABA_1): [AA_1=sqrt{AB^2-A_1B^2}=dfrac32.] Медиану (AM) из (triangle SAB) можно найти по формуле медианы: [AM^2=dfrac{2AS^2+2AB^2-SB^2}4=dfrac52.] Следовательно, по теореме косинусов из (triangle AA_1M): [cos alpha=dfrac{AA_1^2+A_1M^2-AM^2}{2AA_1cdot A_1M}=dfrac14=0,25.]
Ответ: 0,25
Каждому школьнику, который готовится к ЕГЭ по математике, будет полезно повторить тему «Нахождение угла между прямыми». Как показывает статистика, при сдаче аттестационного испытания задачи по данному разделу стереометрии вызывают трудности у большого количества учащихся. При этом задания, требующие найти угол между прямыми, встречаются в ЕГЭ как базового, так и профильного уровня. Это значит, что уметь их решать должны все.
Основные моменты
В пространстве существует 4 типа взаимного расположения прямых. Они могут совпадать, пересекаться, быть параллельными или скрещивающимися. Угол между ними может быть острым или прямым.
Для нахождения угла между прямыми в ЕГЭ или, например, в решении задач по теореме о трех перпендикулярах, школьники Москвы и других городов могут использовать несколько способов решения задач по данному разделу стереометрии. Выполнить задание можно путем классических построений. Для этого стоит выучить основные аксиомы и теоремы стереометрии. Школьнику нужно уметь логически выстраивать рассуждение и создавать чертежи, для того чтобы привести задание к планиметрической задаче.
Также можно использовать векторно-координатный метод, применяя простые формулы, правила и алгоритмы. Главное в этом случае — правильно выполнить все вычисления. Отточить свои навыки решения задач по стереометрии и другим разделам школьного курса вам поможет образовательный проект «Школково».

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Дана правильная треугольная пирамида DABC с вершиной D. Сторона основания пирамиды равна 𝟔 , высота равна 𝟑𝟎 . Найдите расстояние от середины бокового ребра BD до прямой МТ, где точки М и Т — середины ребер АС и AВ соответственно.
Пусть Q — середина ребра CD, P — середина ребра ВD. По теореме о средней линии треугольника
следовательно, точки М, Т, Р, Q лежат в одной плоскости.
следовательно, точки М, Т, Р, Q являются вершинами параллелограмма. Кроме того,
теореме о трёх перпендикулярах , поэтому этот параллелограмм — прямоугольник. Значит, искомое расстояние есть длина отрезка РТ. Отрезок АО равен
По теореме Пифагора
Электронные дидактические материалы «Нахождение угла между скрещивающимися прямыми» для учащихся 10-11 классов
Пояснительная записка к электронным дидактическим материалам
«Нахождение угла между скрещивающимися прямыми» для учащихся 10-11 классов
Источник:1.материалы краевых диагностических работ ККИДППО Краснодарского края,
2.В.А.Смирнов «геометрия. Пособие для подготовки к ЕГЭ, Москва 2009г
3.Корянов А.Г., Проскурин А.А. « Математика. ЕГЭ 2014 (Типовые задания С2)
Уровень сложности: повышенный
Дидактические материалы «Нахождениеугла между скрещивающимися прямыми» для учащихся 10-11 классов состоят из 33 задач уровня С2 материалов ЕГЭ по математике.
Учитель, в зависимости от дидактических целей, может использовать самостоятельные работы в том виде, как они представлены, может, по своему усмотрению, составить самостоятельную работу из необходимого числа уравнений.. Электронная версия дидактических материалов позволит учителю быстро создать новый документ и использовать его и на бумажном носителе, и в цифровом формате, например, для работы на интерактивной доске. Наличие ответов упрощает процедуру проверки.
Электронный математический дидактический материал возможно использовать при дистанционной поддержке образовательного процесса ( поместить на странице учителя на школьном сайте или разослать ученикам по электронной почте для дальнейшей работы).
Представленные дидактические материалы могут быть использованы на этапе изучения нового материала, на этапе контроля, повторения.
. Получив дидактический материал в электронном виде, учащийся сам составляет себе карточки на перспективу по данной теме, включая задания, которые он уже умеет решать, и те, которые нужно освоить. Ученик включает себя в рефлексию своей деятельности, он отвечает на вопросы «Что я умею», «Чему хочу научиться », учится анализировать, распределять и группировать. Снимается фактор психологической напряжённости, тревожности не соответствовать предъявляемым требованиям, ведь задания ученик запланировал себе сам, повышаются мотивация и ответственность за выполнение заданий. Это, несомненно, способствует формированию учебно-познавательной компетенции.Представленные электронные дидактические материалыдополнят арсенал учителя при подготовке учащихся к ЕГЭ.
|
Ответ |
||
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
. В кубе A…D1 найдите косинус угла между прямыми AA1 и BD1. |
|
|
12 |
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите угол между прямыми: ABи A1C. |
|
|
13 |
. В правильной шестиугольной призме A… F1, все ребра которой равны 1, найдите угол между прямыми AB1 и BE1. |
90о. |
|
14 |
В правильной шестиугольной призме A… F1, все ребра которой равны 1, найдите косинус угла между прямыми AB1 и BD1. |
|
|
флэшкарта декабрь 2010егэ2012-2013геометрияПодготовка к ЕГЭНахождение углов,презентация№3 |
||
|
15 |
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите угол между прямыми: AA1 и BC1. |
45o |
|
16 |
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите угол между прямыми: ABи A1C. |
|
|
17 |
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите угол между прямыми: AB1 и BC1. |
|
|
18 |
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AA1 и BD1. |
|
|
19 |
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AA1 и CE1. |
: 60о. |
|
20 |
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AA1 и BE1. |
|
|
21 |
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AB1 и BC1. |
|
|
22 |
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AB1 и BD1. |
|
|
23 |
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AB1 и BE1. |
90o |
|
24 |
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AB1 и BF1. |
|
|
25 |
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AB1 и CD1. |
|
|
26 |
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AB1 и CE1. |
|
|
27 |
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AB1 и CF1. |
|
|
28 |
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AB1 и CA1. |
|
|
29 |
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AB1 и DF1 |
|
|
30 |
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AB1 и DA1 |
90o. |
|
31 |
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AB1 и DC1. |
|
|
32 |
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AC1 и BD1. |
|
|
33 |
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AC1 и BE1. |
|