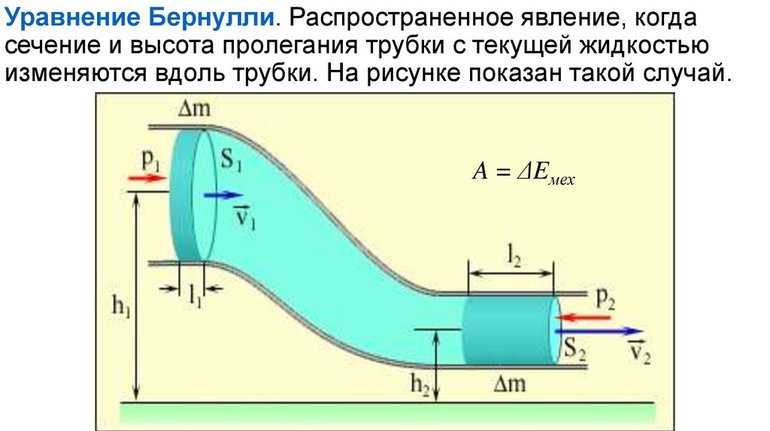
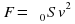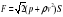В задачах сегодняшней статьи снова «не школьные» темы: закон Бернулли и формула Эйлера (закон неразрывности струи).
Задача 1.
По каналу с радиусом закругления м и шириной
м течёт вода. Два манометра, находящиеся в одной горизонтальной плоскости у наружной и внутренней стенок канала, дают показания, отличающиеся на
Па. Чему равна скорость воды в канале? Плотность воды
кг/м
Ответ дать в м/с, округлить до целых.
Решение.
Для трубки тока, расположенной горизонтально (), уравнение Бернулли имеет вид:
. По условию задачи
Скорость воды в канале на повороте должна подчиняться условию
где — скорость течения воды в канале на середине реки,
и
— скорости у берегов, соответственно.
Таким образом, и
Подставляя скорости в уравнение для , получим
откуда
Ответ: 2 м/с.
Задача 2.
На некоторых реках недалеко от устья во время прилива наблюдается бор — волна, представляющая собой резкое повышение уровня воды. Определите скорость движения бора, считая, что его форма не меняется со временем. Высота бора м, глубина реки
м, скорость течения
м/с. Ответ дать в м/с, округлить до десятых.
К задаче 2
Решение.
Пусть скорость бора равна . Перейдём в сопутствующую систему отсчета, движущуюся со скоростью бора. Тогда вода набегает со скоростью
, а после бора движется с некоторой скоростью
Из закона Бернулли
и из уравнения неразрывности
получаем
, окончательно
Ответ: 6,3 м/с.
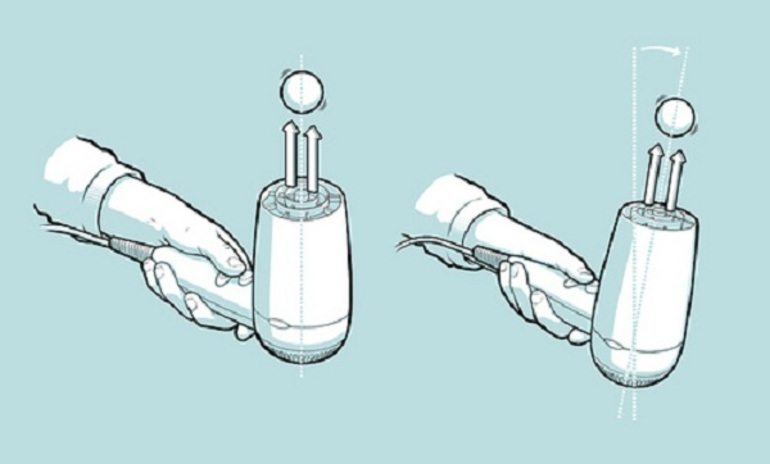
Задача 3.
Что произойдёт, если продувать струю воздуха между двумя шариками от пинг-понга, подвешенными на нитях?
К задаче 3
- Останутся неподвижными
- Будут двигаться вместе вправо или влево
- Отклонятся друг от друга
- Приблизятся друг к другу
Решение.
В системе отсчёта шариков воздух между ними имеет скорость, а воздух снаружи неподвижен. В соответствии с законом Бернулли давление в движущейся среде меньше, чем в неподвижной. Поэтому шарики начнут сближаться.
Ответ: 4.
Задача 4.
На поршень горизонтально расположенного шприца площадью поперечного сечения см
действует постоянная горизонтальная сила
Н. С какой скоростью вытекает струя из отверстия площадью
см
, если плотность жидкости
кг/м
и поршень движется равномерно? Ответ дать в м/с. Округлить до целых.
К задаче 4
Решение.
Пусть скорость движения поршня , а скорость струи на выходе из шприца
. Тогда по уравнению Бернулли
Но, из уравнения неразрывности
. Обобщая всё написанное выше, получаем, что
м/с. Малой площадью выходного отверстия в последней формуле можно пренебречь.
Ответ: 7 м/с.
Задача 5.
Вода течёт по горизонтальной трубе переменного сечения. Скорость течения в широкой части трубы 20 см/с. Определите скорость течения воды в узкой части трубы, диаметр которой в 2 раза меньше диаметра широкой части. Ответ дать в см/с, округлив до целых.
Решение.
Применим уравнение неразрывности струи , где
см/с,
— диаметр узкой трубы. Откуда
см/с.
Ответ: 80 см/с.
4 комментария
Николай Синев aka biglebowsky
✉️
29.05.2019 11:05:09
Уважаемая Анна
Гидродинамика — это не Ваша область знаний.
Задача 1.
На поворотах течение реки будет приблизительно безвихревым: V(R)~1/R
Ваше решение ошибочно.
Задача 3.
Ваше объяснение ошибочно полностью, от начала и до конца. Абсолютное непонимание теоремы Бернулли.
Вместо шариков повесьте 2 треуголные призмы, «остриями» к направлению продувки. Например вот так (вид сверху): ^^ . Направление продувки на картинке — сверху вниз. Призмы не притянутся, а разойдутся.
Задача 4.
Истекающая струя в Вашей задачке отнюдь не будет иметь площадь S2. Надо учесть так называемый коэффициент сжатия струи. Для Вашей геометрии — приблизительно 0,7
Анна Валерьевна
✨
29.05.2019 11:16:35
1. Там это и написано. Решение верно.
3. Воздух продувают горизонтально. Решение верно.
4. Мы с Вами в рамках школьной физики. Решение верно.
Николай Синев aka biglebowsky
✨
29.05.2019 15:22:25
1) Нет. Ваше решение предполагает, что угловая_скорость=const(R) Это верно для вращения твердого тела, но отнюдь не всегда верно для вращения жидкости.
3) Вместо шариков повесьте на ниточках 2 призмы и продуйте воздух между ними. Вас ожидает сюрприз.
4) Формула v_1*S_1=v_2*S_2 в геометрии данной задачки ошибочна.
Правильная формула v_1*S_1=v_2*0,7*S_2
Другое дело, что в приближении S_2<<S_1 площадь S2 вообще не входит в ответ, так что на правильность ответа «скорость истечения = 7м/с» ошибка в решении не повлияла. Вот если бы Вы решали другую задачку: «каков будет расход воды через отверстие?», то Ваша ошибка в промежуточной формуле немедленно бы проявилась в ответе.
Анна Валерьевна
✨
29.05.2019 16:00:07
Не буду спорить. Но это задачи для школьников. Здесь лучшее — враг хорошего. Для них все упрощено. Так что оставим. А с призмами сделаю, интересно, хоть в задачах и не призмы, а именно шары.
Выберите два верных утверждения, которые соответствуют содержанию текста. Запишите в ответ их номера.
1. Жидкость течёт по горизонтальной трубе переменного сечения, полностью заполняя её. При увеличении скорости потока жидкости давление в ней увеличивается.
2. Жидкость течёт по горизонтальной трубе переменного сечения, полностью заполняя её. При увеличении скорости потока жидкости давление в ней уменьшается.
3. Жидкость течёт по горизонтальной трубе переменного сечения, полностью заполняя её. При увеличении скорости потока жидкости давление в ней не изменяется.
4. Между двумя параллельными листами бумаги, свободно подвешенными вертикально, продувают поток воздуха. Листы будут «притягиваться» друг к другу.
5. Между двумя параллельными листами бумаги, свободно подвешенными вертикально, продувают поток воздуха. Давление между листами будет больше, чем снаружи от них.
Задачи гидродинамика. Уравнение Бернулли
http://k—a—t.ru/gidravlika/zadachi_2/index.shtml
1) Направленная горизонтальная струя воды бьет в вертикальную стенку. С какой силой струя давит на стенку, если скорость истечения воды v = 10 м/с и вода поступает через трубку, имеющую сечение s = 4 см2? Считать, что после удара вода стекает вдоль стенки.
Дано 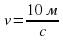
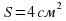
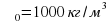
Реш 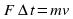
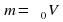
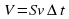
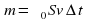
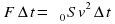
3). В сосуд, в дне которого узкое отверстие закрыт пробкой, налита вода до высоты h = 1 м. На поверхн воды находится поршень массой m = 1 кг и пло S = 100 см2. Между поршнем и стенками сосуда вода не просачивается. Найдите скорость истечения воды из отверстия в дне сосуда сразу после того, как из отверстия будет вынута пробка. Трение не учитывать.
Реш. Воспользуемся уравнением Бернулли. Давл в струе воды p0. Давл под порш на высоте h от отв p0 + mg/S. Скорость течения жидкости под поршнем м пренебречь, так как она мала по сравнению со скоростью истечения из отверстия , потому что площадь отверстия значительно меньше площади поршня. Согласно уравнению Бернулли
p0 + ρυ2/2= p0 + ρgh + mg/S. Отсюда υ = 2gh + 2mg/ρS 4,9 м/с
4) Брусок массы m удерживается в воздухе струями воды, бьющими вертикально вверх из отверстия, сечения S . Скорость воды на выходе из отверстия v. Достигнув бруска, вода разлетается от него в горизонтальной плоскости. На какой высоте над отверстием удерживается брусок? Плотность воды
Реш Сила давления на брусок одной струи тогда
=
т к из условия неразрывности струи следует, что
из уравнения Бернулли имеем
Решая совместно эти уравнения, получим
1) Насос представляет расположенный горизонтально цилиндр с поршнем площади S и выходящим отверстием площади s, расположенном на оси цилиндра. Определить скорость истечения струи из насоса, если поршень под действ силы F перемещается с постоянной скоростью. Плотность жидкости 
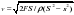
2) По наклонной плоскости стекает широкий поток воды. На расстоянии l по течению глубина потока уменьш вдвое. На каком расстоянии глубина потока уменьшится в 4 раза? [x = 5l]
6)по горизонт распол и изогнутой под прямым углом трубе сеч S течет жидкость плотности 
Реш изменение импульса в единицу времени
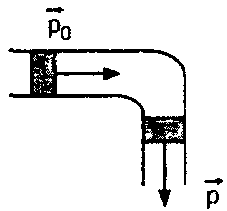
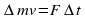
откуда

и высотой h. С какой скоростью вода начнет вытекать из сосуда, если на дне его обр отверстие? Понижением уровня воды в баке пренебречь. Плотность воды
10)В подводной лодке находящейся на глубине Н образовалась пробоина сечением S
.Какое количество воды нальется в лодку за время
Реш. Давление на одной глубине одинаково (по зну Паскаля), следовательно, снаружи давление жидкости p = ρgh. Чтобы удержать заплату, закрыв отверстие с внутренней стороны судна потребуется создать давление равное наружному p = F/S, Тогда, приравняв давления
F/S = ρgh и F = ρghS. Приняв плотность воды . имеем
F = 1,0 × 103 × 10 × 3 × 5,0 × 10−4 = 15 Н.
7) Из крана выливается вода. Начиная с некоторого места, диаметр струи уменьшается на протяжении h от а до b Сколько воды вытечет из крана за время t? a=3см b=2см h=3см t=1 мин
Реш: Воспользуемся условием стационарности течения несжимаемой жидкости
. (1)
Для идеальной жидкости уравнение Бернулли:.
Поскольку жид своб падает, то давл в обоих сеч одинак, и ур Бернулли прин вид: . За время t через любое сеч протекает один и тот же объем воды, поэтому
.
.Подставив полученное значение v1 получим :
.
При a=3см b=2см h=3см t=60c
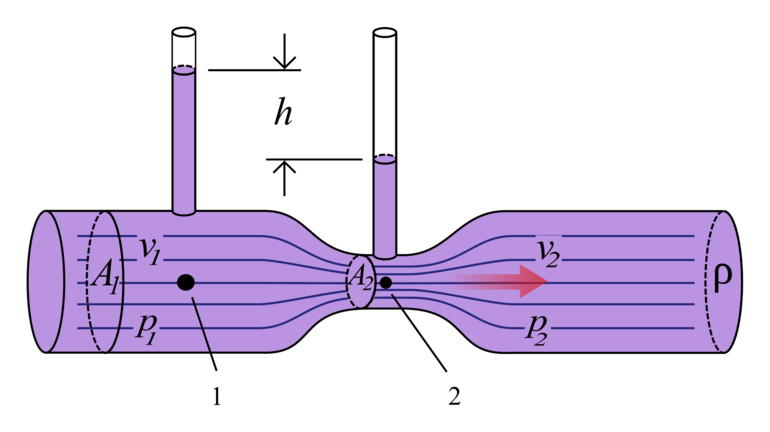
2)На рис 3 2 манометра различной формы Найти разницу давлений показываемых этими манометрами если они поочередно измеряют давление в одной и той же трубе в которой течет вода со скоростью v
3)По гибкому шлангу сеч S течет жидкость плотн ρ со скор v. Найти натяж нити AB, соед концы A и B шланга, если изв, что она явл диам полуокружн, кот обр шланг (рис.).
4) Если полн открыт кран хол воды, а кран гор воды закрыт (рис.), то ванна наполн за t1= 8 мин; если при этом на вых отв насад шланг с душем на конце, то время наполн увел до t2 = 14 мин. Когда кран хол воды закрыт, а кран гор открыт полн, время наполн t3 = 12 мин; при тех же усл, но с душем на конце − t4 = 18 мин. За какое время наполн ванна, если полн отк оба крана? А если при этом насажен шланг с душем?
Зад 3 зад 4
5) В дне бака высотой H=4см проделано отв пл 
РЕШ расход при истечении из малого отв скорость струи по ф-ле Торичелли
тогда
6)какую мощность должен иметь электродвигатель привода водяного насоса если насос при подаче создает напор H=40м а его полный кпд
плотность воды
решение: Полезная мощн любого насоса м б опр по фле: NП = ρgQH, .
Потребл мощ, т. е. мощн, кот на работу насоса затрач электродв (NЭД),= полезной мощн с учетом КПД: NЭД = NП/η = ρgQH/η = 1000×9,81×0,05×40/0,6 = 32700 Вт = 32,7 кВт
7) Привод водян насоса обеспечивает частоту вращения его вала n1 = 15 с-1, при этом подача насоса Q1 = 0,01 м3/с, а напор H1 = 20 м. какова должна быть частотта вращения вала насоса, если потребуется увеличить его напор до 80 м. Как изменится при этом подача насоса?
реш: Зависимость работы парового насоса от частоты вращения вала
n1/n2 =Q1/Q2; n12/n22 = H1/H2,
т. е. для увеличения напора в 4 раза, частота вращения вала насоса должна возрасти в 2 раза: n2 = √(n12H2/H1) = n1√4 = 2n1.
при увеличении частоты вращения вала насоса в 2 раза его подача тоже возрастет в 2 раза, и составит Q2 = 0,02 м3/с.
Гидростатика.
Для несжимаемой жидкости ее плотность
не зависит от давления. При поперечном
сечении S
столба жидкости плотностью r
и
высотой
h
давление жидкости р
на нижнее основание:
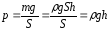
Давление

гидростатическим давлением.
Гидродинамика.
Графически движение жидкостей изображается
с помощью линий
тока,
которые проводятся так, что касательные
к ним совпадают по направлению с вектором
скорости жидкости в соответствующих
точках пространства (рис. 9). Линии тока
проводятся таким образом, чтобы их
густота характеризовала величину
скорости: густота больше там, где больше
скорость течения жидкости, и меньше
там, где жидкость течет медленнее.
Часть
жидкости, ограниченную линиями тока,
называют трубкой
тока
(рис.
10).
Течение жидкости называется установившимся
(или стационарным),
если форма и расположение линий тока,
а также значения скоростей в каждой ее
точке со временем не изменяются.
Рис.
9 Рис. 10
Уравнение
неразрывности струи для несжимаемой
жидкости. Рассмотрим
какую-либо трубку тока. Выберем два ее
сечения S1
и S2
,
перпендикулярные направлению скорости
(рис. 10).
За
время Dt
через сечение S1
проходит объем жидкости
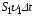
где

сеченияS1
,
а через сечение S2
за
тоже время
Dt
пройдет объем жидкости

где
сеченияS2
.
Если жидкость несжимаемая, то через
сечение S2
пройдет такой же объем жидкости, как и
через сечение S1
,
т. е.
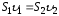
Так
как положения сечений S1
и
S2
выбраны произвольно, то отсюда следует,
что вдоль
данной трубки тока

Это соотношение называется
уравнением неразрывности
струи для несжимаемой жидкости.
Уравнение
Бернулли.
Бернулли рассмотрел изменения
гидродинамических параметров вдоль
произвольно выбранной трубки тока
стационарно текущей жидкости плотностью
r
(рис. 11).
Рис.
11
В
месте сечения трубки тока S1
скорость течения жидкости

давлениеp1
и высота, на которой это сечение
расположено относительно выбранного
уровня отсчета, h1.
Аналогично, в месте сечения трубки тока
S2
скорость течения жидкости

и высота расположения этого сечения
над тем же уровнем отсчета h2
.
Бернулли
установил, что для любых двух сечений
одной трубки тока несжимаемой жидкости
выполняется равенство:

Так
как положения сечений было выбрано
произвольно, то для любой трубки тока
несжимаемой жидкости гидродинамические
параметры жидкости подчиняются следующему
уравнению (уравнению
Бернулли):
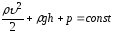
Для
горизонтальной трубки тока (h
=
const)
уравнение Бернулли принимает вид:

где
величина

полным давлением,
величина
р
называется
статическим давлением,
величина
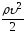
динамическим давлением.
Из
уравнения Бернулли для горизонтальной
трубки тока и уравнения неразрывности
струи следует, что при течении жидкости
по горизонтальной трубе, имеющей
различные сечения, скорость жидкости
больше в местах сужения, а статическое
давление, наоборот, в местах сужения
меньше.
Формула
Торричелли. Формула
Торричелли позволяет находить скорость
истечения жидкости через малое отверстие
в стенке или дне сосуда (рис. 12). Формула
Торричелли следует из уравнения Бернулли.
Если
применить это уравнение для двух сечений
S1
и S2
(S1
на уровне h1
cвободной
поверхности
жидкости в сосуде и S2
на
уровне отверстия h2),
то получим равенство:
Рис.12
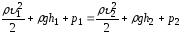
Так
как давления р1
и р2
жидкости на уровнях первого и второго
сечений равны атмосферному, то р1=р2
,
а полученное соотношение примет вид:

Из
уравнения неразрывности струи следует,
что

где
S1
и S2
–
площади поперечных сечений сосуда и
отверстия.
Так
как S1>>S2
,
то
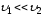

Тогда
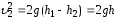
откуда
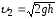
Это
выражение получило название формулы
Торричелли,
где h
–
высота свободной поверхности жидкости
в сосуде над уровнем отверстия.
Формула
Торричелли справедлива только для
идеальной
жидкости,
то есть для жидкости, в которой отсутствует
вязкость
или внутреннее
трение.
Только в этом случае скорость истечения
жидкости из малого отверстия такая же
по величине, как и скорость тела, свободно
падающего с высоты h.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Исследования учёного
Даниил Бернулли родился в Голландии в 1700 году. В 1725 году он начал работать на кафедре физиологии, где увлёкся основами теоретической физики. Через 25 лет он возглавил кафедру экспериментальной физики, которой и руководил до конца своих дней. Основным его трудом считается создание теории гидродинамической зависимости, известной как Закон Бернулли. Открытие учёного предвосхитило зарождение молекулярно-кинетического учения поведения газов.
Причиной открытия принципа стало изучение действия закона сохранения энергии в различных ситуациях. Бернулли установил, что давление жидкости в замкнутом пространстве зависит от сечения объекта, в котором она находится. Чем меньше сечение трубы, тем ниже будет созданное давление в пропускаемом через неё жидком веществе.
Этот факт был доказан экспериментально и описан математически.
Правило в математической формулировке имеет вид (pv2/ 2) + p * g * h + ρ = const, где:
- p — количество жидкости на единицу объёма;
- v — скорость движения потока;
- h — уровень, на который поднят элемент жидкости;
- ρ — сила, действующая на единицу площади;
- g — ускорение, придаваемое жидкости под действием притяжения Земли.
Чтобы понять физический смысл уравнения Бернулли, нужно рассмотреть трубу переменного сечения, в которой существует точка А и Б. Первая располагается в широкой части, а вторая — в узкой. В соответствии с уравнением непрерывности скорость V1 в части трубы, имеющей большее сечение, будет меньше, чем скорость жидкости V2 в узком сечении. Если в жидкость поместить прибор для измерения давления, он покажет какое-то значение P1 в точке A и P2 в точке Б. При этом там, где скорость движения жидкости медленнее, давление будет больше.
Объясняется это следующим образом: если V1 больше V2, значит, при движении происходит изменение скорости течения. Представив, что в жидкости находится точка, можно утверждать о её движении с ускорением. Это означает, что на неё действуют силы.
Одна из них совпадает с направлением течения, тем самым ускоряя движение. Обусловлена эта сила разностью давления.
Так как движение происходит от точки А к Б, то и давление возле А будет больше, чем около Б. Эта разность давлений и приводит к ускорению.
Условия действия
Закон применим для условия, при котором соблюдается неразрывность струи воздуха или жидкости. В тех участках потока, где скорость течения больше, давление будет меньше и наоборот. Это утверждение и называется теоремой Бернулли. По сути, закон позволяет установить связь между давлением, скоростью, высотой.
Пусть имеется труба переменного сечения с изменяющейся высотой. Внизу она широкая, а затем сужается. По ней течёт жидкость. Площадь сечения можно обозначить как S1 и S2, а давление участков и скорость движения на них P1, P2, V1, V2. Высота внизу будет равняться S1, а вверху S2.
Выделив участок в трубе с жидкостью, можно сказать, что она движется слева направо и через некоторое время полностью сдвинется в область S2. Изменение положения слева будет равно расстоянию дельта L1, а справа — дельта L2.
Течение является:
- ламинарным — находящаяся в трубке жидкость перемешивается слоями без хаотических изменений давления и скорости, турбулентность отсутствует;
- стационарным — распределение скоростей не изменяется с течением времени;
- скоростным — в движении принимает участие такой параметр, как ускорение;
- идеальным с несжимаемой жидкостью.
Последнее обозначает, что нет вязкости. Поэтому на жидкость действует только сила упругости и тяжести, а силы трения нет. Система не является замкнутой, а значит закон сохранения энергии применительно к рассматриваемому участку использовать нельзя. Зато вполне можно применить теорему о кинетической энергии.
Для газов уравнение можно использовать лишь в том случае, если их плотность изменяется незначительно. Но касаемо аэродинамики учитывается и то, что изменение давления воздуха гораздо меньше атмосферного. Поэтому уравнение можно применять в аэродинамических расчётах.
Согласно ему, сумма действующих всех сил на тело (рассматриваемый кусок жидкости) равняется изменению кинетической энергии объекта: ΣAi = ΔEk. На нижний участок действует сила давления, выполняющая положительную работу, а на верхний — отрицательную. Кроме этого, действует и сила тяжести. Так как жидкость поднимается, она имеет тоже отрицательный знак. Сила бокового давления перпендикулярна любой точке в системе, поэтому никакого влияния она не оказывает.
Количественная сторона
Исходя из сил, действующих на тело, изменение кинетической энергии можно описать выражением: ΔEk = Ap1 +Ap2 +Ag. Чтобы найти работу, необходимо силу умножить на пройденное расстояние. Поэтому работа силы давления равна произведению самой силы F на модуль перемещения ΔL и косинусу угла между ними: Ap1 = F1* ΔL *1.
Чтобы найти силу, нужно давление умножить на площадь. Значит: Ap1 = p 1 * S1 * ΔL1 = p1V1. Таким же образом находится работа для второго состояния: Ap2 = F1* ΔL2 *(-1) = — p2 * S2 * ΔL2 = -p2 * V2. Жидкость несжимаемая, следовательно: V1=V2=V.
Работу силы тяжести можно вычислить исходя из того, что рассматриваемый кусок жидкости является относительным, то есть он, хотя и не статический, в любом месте будет подвергаться воздействию одинаковой силы тяжести. Верным будет выражение: Ag = — ΔEp = — (m2 * g * h2 — m1 * g * h1) = m1 * g * h1 — m2 * g * h2. Так как жидкость несжимаемая, её плотность не изменится. Отсюда можно утверждать: Ag = ρ * V * g * h1 — ρ * V * g * h2.
Зная количественные показатели всех трёх работ, можно найти изменение кинетической энергии. Из физики известно, что оно равно разнице конечной и начальной энергии. Течение стационарное, значит, скорость с течением времени не изменится. Следовательно, кинетическая энергия будет определяться разницей появившейся энергии в верхней части и ушедшей из нижней области: ΔEk = (m2 * v22)/2 — (m1 * v12) / 2.
Воспользовавшись тем, что масса равняется произведению плотности на объём, формулу можно привести к виду: ΔEk = (ρ * V * v22)/2 — (ρ * V * v12) / 2. Теперь найденные выражения для работ нужно подставить в теорему о кинетической энергии. Получится следующее равенство: p1V — p2V + ρ * V * g * h1 — ρ * V * g * h2 = (ρ * V * v22) / 2 — (ρ * V * v12) / 2. Разделив левую и правую часть на объём, выражение можно упростить до вида: p1 — p2 + ρ * g * h1 — ρ * g * h2 = (ρ * v22)/2 — (ρ * v12) / 2 .
То место, где давление p1, некая точка внутри трубки, пусть будет обозначено цифрой один, а там, где p2, — цифрой два. Всё что относится к единице можно записать в левой части, а к двойке — в правой: ρ1 * g * h1 + (ρ * v12) / 2 = ρ * g * h2 + (ρ * v22) / 2. Полученная формула показывает, что при переходе в пределе одной линии скорость, давление и высота изменяются. Поэтому в любой точке будет справедливым выражение: ρ1+ ρ * g * h + (ρ * v1) / 2 = const. Это и есть количественное описание уравнения Бернулли для идеальной жидкости.
Применение в гидравлике
Наиболее типичным примером использования уравнения является решение заданий по нахождению скорости вытекания жидкости из отверстия в широком сосуде. Такой ёмкостью называют систему, в которой диаметр сосуда значительно больше размера отверстия. Необходимо найти скорость вытекающей жидкости U1. Известно, что высота столба жидкости, на который действует сила тяжести g, равна h.
Пусть в жидкости, находящейся сверху, имеется точка один. Через некоторое время она окажется внизу в положении два. На верх жидкости давит атмосферное давление, поэтому p1=pатм. Высота в точке один равна h. Скорость U1 считают равной нулю. Давление p2 в точке два будет также равно атмосферному. Так как жидкость опустится на дно, то высота h2 станет нулевой.
Все эти величины следует подставить в уравнение Бернулли. Получится выражение: pатм + ρ * g * h + 0 = pатм + (ρ * U2) / 2 + 0. Атмосферное давление взаимно уничтожается: ρ * g * h = (ρ * U2) / 2. В левой и правой части стоит плотность, на которую можно сократить. Отсюда получается, что вид жидкости значения не имеет. Это может быть: вода, ртуть, расплавленный металл. Эффект от этого не поменяется. Из формулы можно выразить искомое U2. Оно будет равно: U2 = (2 * g * h)½.
Интересным фактом является то, что полученный ответ при решении задачи называется формулой Торричелли. Она показывает, что скорость, с которой вытекает жидкость из широкого сосуда, равна скорости тела при свободном падении с той же высоты.
Используя уравнение, можно легко рассчитать давление жидкости на дно и стенки сосуда. В этом случае закон Бернулли является обобщением для формулы гидростатического давления. Пусть имеется сосуд с жидкостью высотой h. Точка, находящаяся наверху, характеризуется давлением p1 = pатм., высотой h1 равной h и скоростью U1. Для точки на дне параметры будут следующие: p2 = p, h2 = 0, U2 = 0. Скорости принимаются равными нулевому значению, так как рассматриваемая жидкость находится в состоянии покоя.
Данные следует подставить в уравнение. В итоге получится равенство: pатм + ρ * g * h + 0 = p + 0 + 0. Из него несложно найти неизвестное: p = pатм + ρ * g * h. Полученный ответ является формулой гидростатического давления и подтверждает закон Паскаля.
Аналогично уравнение Бернулли для потока реальной жидкости используется при расчёте расхода в карбюраторе, пульверизаторе, учёте статического и динамического давления.
Подъёмная сила
Самолёт летает благодаря тому, что набегающий на крыло напор воздуха создаёт подъёмную силу. Её можно рассчитать и оценить с помощью уравнения. Геометрически крыло можно представить в виде плоскости с углом a (угол атаки). На него действует поток воздуха со скоростью U. Частица воздуха ударяет в твёрдую поверхность и отражается от неё. Угол отражения равен углу атаки, а её скорость равняется U’. Нужно рассчитать подъёмную силу. Для этого необходимо выполнить три шага:
- рассмотреть изменение скорости воздуха;
- узнать импульс частиц;
- используя закон Ньютона, определить силу.
В результате получится, что на крыло действует сила, состоящая из двух компонентов: подъёмной силы Fy и аэродинамического сопротивления Fx. Fy = Cy * p * U2 * S, а Fx = Cx * p * U2 * S. В формулах С является коэффициентом, а S — площадью крыла.
Для расчёта используется уравнение Бернулли. Выглядеть оно будет следующим образом: Pп. к + (ρ * Uп. к) * 2 / 2 + ρ * g * hп. к = Pн. к + (ρ * Uн. к) * 2 / 2 + ρ * g * hн. к, где: п. к — под крылом, а н. к — над крылом. Это уравнение можно упростить, приняв, что давления над и под крылом примерно одинаковые, поэтому плотность будет также одинаковая. Кроме того, высота крыла довольно маленькая. Исходя из этого, формулу можно упростить, и она примет вид: pп. к-pн.к = (ρ * (Uн.к + Uп. к) * (Uн.к — Uп. к)) / 2 = 2 * U1 * U2. Теперь можно найти подъёмную силу. Для этого разность давлений нужно умножить на площадь крыла: Fy = (pп.к-pн. к) * S.
Таким образом, используя метод, можно рассчитать подъёмную силу, обусловленную эффектом Бернулли. Например, пусть дано, что площадь крыла равна 50 м². Скорость потока воздуха над крылом и под ним соответственно равны: U1 = 320 м/с, U2 = 290 м/с. Найти грузоподъёмность. Для решения задания нужно знать дифференциальную плотность воздуха. Это справочная величина, равная 1,29 кг/м3.
Используя уравнение Бернулли, можно записать: pп. к-pн.к = ρ * (U2н.к — U2п. к). Подъёмная сила равна площади крыла, умноженной на разность давления. Подставив одно выражение в другое, получим рабочую формулу: Fy = ρ * (U2н.к — U2п. к) * S / 2. После выполнения расчёта получится ответ 590 кН. То есть грузоподъёмность самолёта составит порядка 59 тонн.
Реальные вычисления для таких задач довольно сложные, поэтому часто используют онлайн-калькуляторы.