09
Янв 2022
Категория: 10 Графики функций
2022-01-09
2022-09-11
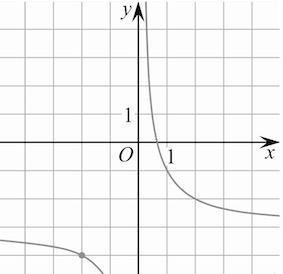
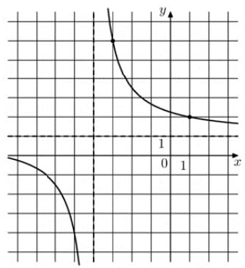
Задача 1. На рисунке изображён график функции Найдите
Решение: + показать
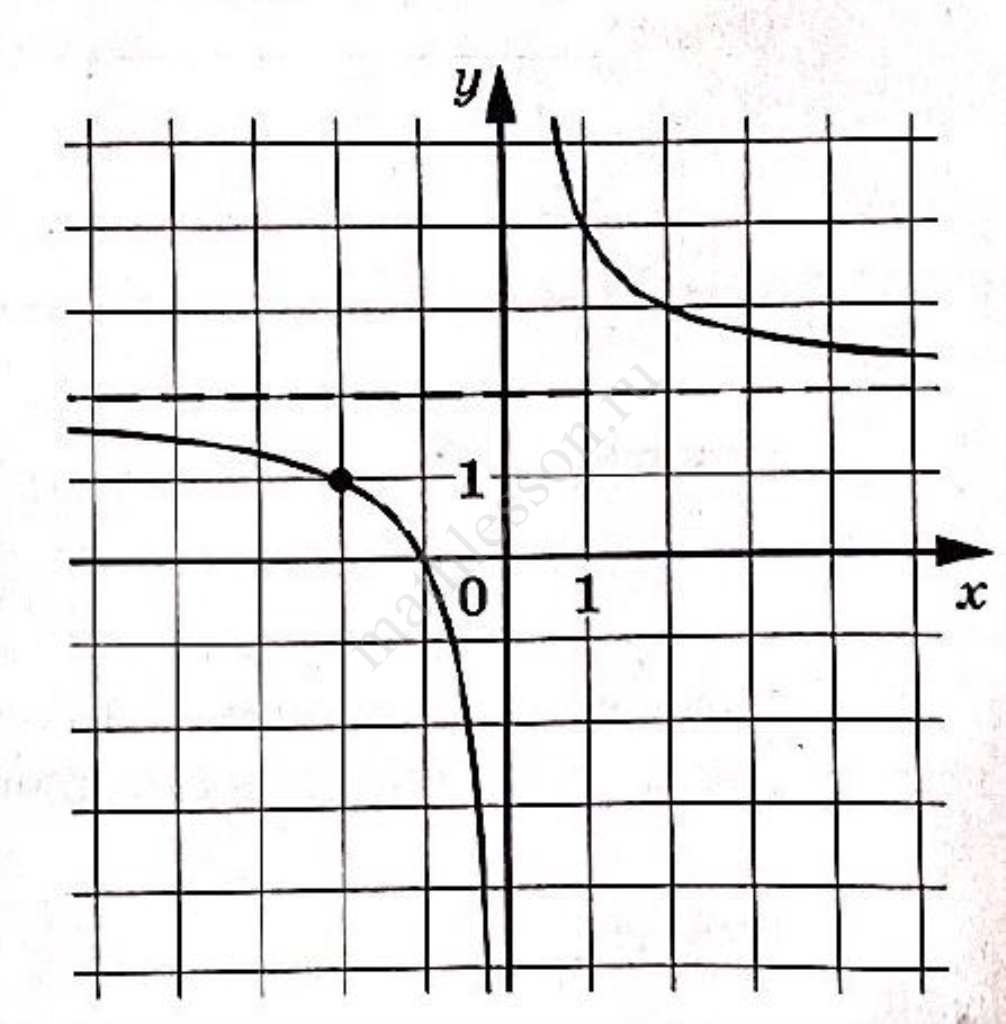
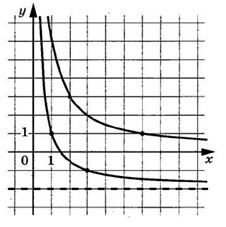
Задача 2. На рисунке изображён график функции вида где числа
и
— целые. Найдите значение
, при котором
Решение: + показать
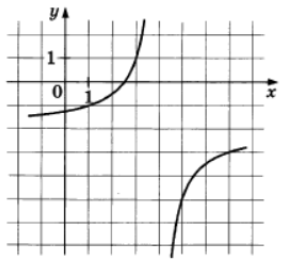
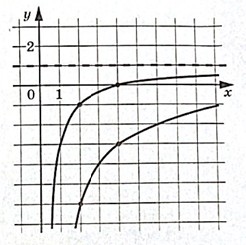
Задача 3. На рисунке изображён график функции вида где
– целые числа. Найдите
Решение: + показать
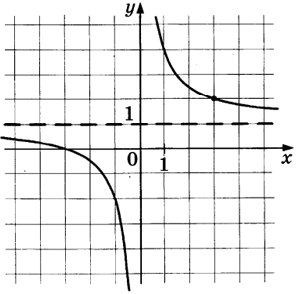
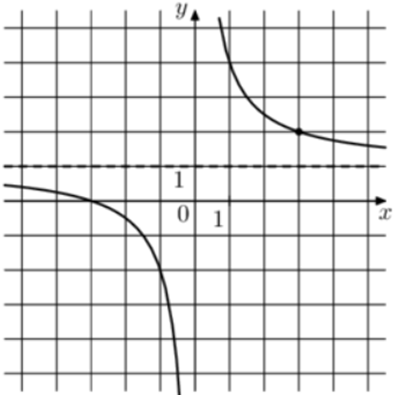
Задача 4. На рисунке изображён график функции Найдите
Решение: + показать
Задача 5. На рисунке изображены графики функций и
и которые пересекаются в точках
и
. Найдите ординату точки
Решение: + показать
Вы можете пройти тест “Гиперболы”
Автор: egeMax |
Нет комментариев
Каталог заданий.
Гиперболы
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 10 № 508951
На рисунке изображён график функции
Найдите
Аналоги к заданию № 508951: 508971 508952 508953 508954 508955 508956 508957 508958 508959 508960 … Все
Источник: А. Ларин: Тренировочный вариант № 110.
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график
Решение
·
·
Сообщить об ошибке · Помощь
2
Тип 10 № 508961
На рисунке изображён график функции
Найдите, при каком значении x значение функции равно 0,8.
Аналоги к заданию № 508961: 508983 508962 508963 508964 508965 508966 508967 508968 508969 508970 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график
Решение
·
·
Сообщить об ошибке · Помощь
3
Тип 10 № 564197
На рисунке изображён график функции вида
где числа a, b и c — целые. Найдите
Аналоги к заданию № 564197: 564198 564199 564200 564201 564202 564203 564204 564205 564206 564207 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график
Решение
·
·
Сообщить об ошибке · Помощь
4
Тип 10 № 564198
На рисунке изображён график функции вида
где числа a, b и c — целые. Найдите
Аналоги к заданию № 564197: 564198 564199 564200 564201 564202 564203 564204 564205 564206 564207 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график
Решение
·
·
Сообщить об ошибке · Помощь
5
Тип 10 № 564199
На рисунке изображён график функции вида
где числа a, b и c — целые. Найдите
Аналоги к заданию № 564197: 564198 564199 564200 564201 564202 564203 564204 564205 564206 564207 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график
Решение
·
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
ЕГЭ Профиль №10. Гипербола
Скачать файл в формате pdf.
ЕГЭ Профиль №10. Гипербола
| Задача 1. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите (fleft( { — 12} right).)
Ответ
ОТВЕТ: 0,75. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1;4} right)) и (left( {3;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{4 = frac{k}{1} + a}\{2 = frac{k}{3} + a}end{array}} right.) Вычтем из первого уравнения второе: (2 = k — frac{k}{3},,,,,,,, Leftrightarrow ,,,,,,,k = 3.) Тогда: (4 = 3 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{3}{x} + 1) и (fleft( { — 12} right) = frac{3}{{ — 12}} + 1 = 0,75.) Ответ: 0,75. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = 1). Следовательно, (a = 1). График проходит через точку (left( {1;4} right)), поэтому: (4 = frac{k}{1} + 1,,,,,,,, Leftrightarrow ,,,,,,,k = 3.) Таким образом, (fleft( x right) = frac{3}{x} + 1) и (fleft( { — 12} right) = frac{3}{{ — 12}} + 1 = 0,75.) Ответ: 0,75. |
|
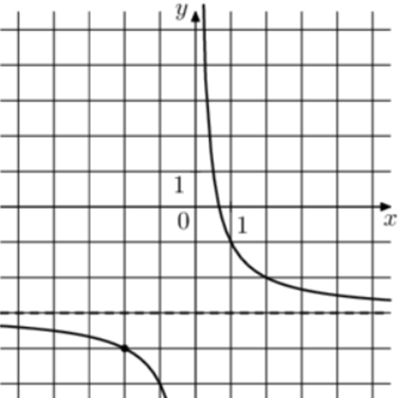
| Задача 2. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите (fleft( {50} right).)
Ответ
ОТВЕТ: — 2,96. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1; — 1} right)) и (left( {2; — 2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = frac{k}{1} + a}\{ — 2 = frac{k}{2} + a}end{array}} right.) Вычтем из первого уравнения второе: (1 = k — frac{k}{2},,,,,,,, Leftrightarrow ,,,,,,,k = 2.) Тогда: ( — 1 = 2 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 3.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{2}{x} — 3) и (fleft( {50} right) = frac{2}{{50}} — 3 = — 2,96.) Ответ: – 2,96. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = — 3). Следовательно, (a = — 3). График проходит через точку (left( {1; — 1} right)), поэтому: ( — 1 = frac{k}{1} — 3,,,,,,,, Leftrightarrow ,,,,,,,k = 2.) Таким образом, (fleft( x right) = frac{2}{x} — 3) и (fleft( {50} right) = frac{2}{{50}} — 3 = — 2,96.) Ответ: – 2,96. |
|
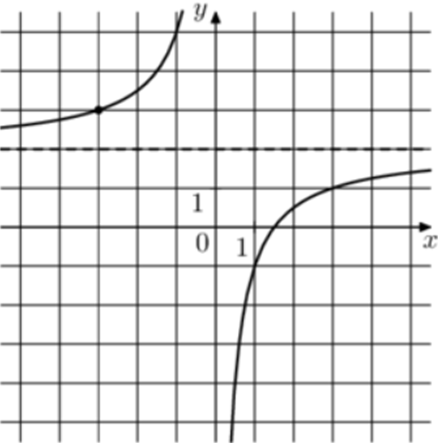
| Задача 3. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите (fleft( {7,5} right).)
Ответ
ОТВЕТ: 1,6. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1; — 1} right)) и (left( {3;1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = frac{k}{1} + a}\{1 = frac{k}{3} + a}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = k — frac{k}{3},,,,,,,, Leftrightarrow ,,,,,,,k = — 3.) Тогда: ( — 1 = — 3 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 2.) Следовательно, уравнение гиперболы: (fleft( x right) = — frac{3}{x} + 2) и (fleft( {7,5} right) = — frac{3}{{7,5}} + 2 = 1,6.) Ответ: 1,6. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = 2). Следовательно, (a = 2). График проходит через точку (left( {1; — 1} right)), поэтому: ( — 1 = frac{k}{1} + 2,,,,,,,, Leftrightarrow ,,,,,,,k = — 3.) Таким образом, (fleft( x right) = — frac{3}{x} + 2) и (fleft( {7,5} right) = — frac{3}{{7,5}} + 2 = 1,6.) Ответ: 1,6. |
|
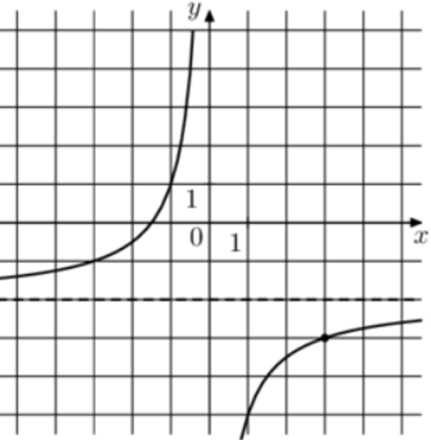
| Задача 4. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите (fleft( {0,25} right).)
Ответ
ОТВЕТ: — 14. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1; — 5} right)) и (left( {3; — 3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 5 = frac{k}{1} + a}\{ — 3 = frac{k}{3} + a}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = k — frac{k}{3},,,,,,,, Leftrightarrow ,,,,,,,k = — 3.) Тогда: ( — 5 = — 3 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 2.) Следовательно, уравнение гиперболы: (fleft( x right) = — frac{3}{x} — 2) и (fleft( {0,25} right) = — frac{3}{{0,25}} — 2 = — 14.) Ответ: – 14. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = — 2). Следовательно, (a = — 2). График проходит через точку (left( {1; — 5} right)), поэтому: ( — 5 = frac{k}{1} — 2,,,,,,,, Leftrightarrow ,,,,,,,k = — 3.) Таким образом, (fleft( x right) = — frac{3}{x} — 2) и (fleft( {0,25} right) = — frac{3}{{0,25}} — 2 = — 14.) Ответ: – 14. |
|
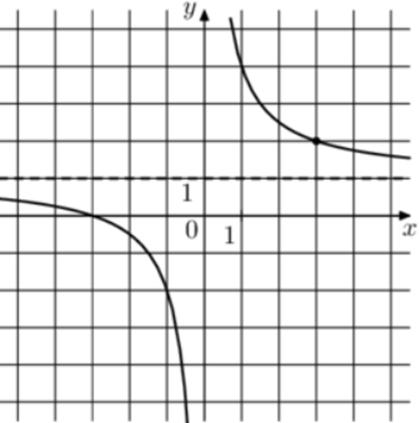
| Задача 5. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите, при каком значении x значение функции равно 0,8.
Ответ
ОТВЕТ: — 15. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1;4} right)) и (left( {3;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{4 = frac{k}{1} + a}\{2 = frac{k}{3} + a}end{array}} right.) Вычтем из первого уравнения второе: (2 = k — frac{k}{3},,,,,,,, Leftrightarrow ,,,,,,,k = 3.) Тогда: (4 = 3 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{3}{x} + 1) и (frac{3}{x} + 1 = 0,8,,,,,,, Leftrightarrow ,,,,,,,,frac{3}{x} = — frac{1}{5},,,,,,,,, Leftrightarrow ,,,,,,,,,x = — 15.) Ответ: – 15. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = 1). Следовательно, (a = 1). График проходит через точку (left( {1;4} right)), поэтому: (4 = frac{k}{1} + 1,,,,,,,, Leftrightarrow ,,,,,,,k = 3.) Таким образом, (fleft( x right) = frac{3}{x} + 1) и (frac{3}{x} + 1 = 0,8,,,,,,,, Leftrightarrow ,,,,,,,,frac{3}{x} = — frac{1}{5},,,,,,,,, Leftrightarrow ,,,,,,,,,,x = — 15.) Ответ: – 15. |
|
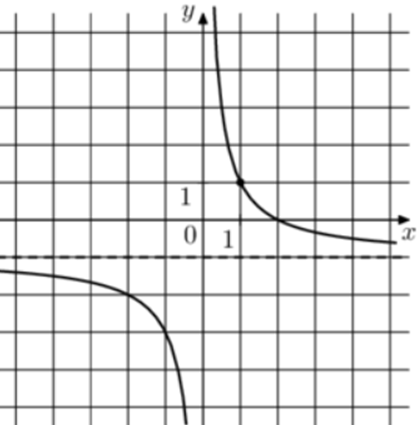
| Задача 6. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите, при каком значении x значение функции равно 19.
Ответ
ОТВЕТ: 0,1. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1;1} right)) и (left( {2;0} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = frac{k}{1} + a}\{0 = frac{k}{2} + a}end{array}} right.) Вычтем из первого уравнения второе: (1 = k — frac{k}{2},,,,,,,, Leftrightarrow ,,,,,,,k = 2.) Тогда: (1 = 2 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 1.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{2}{x} — 1) и (frac{2}{x} — 1 = 19,,,,,,,, Leftrightarrow ,,,,,,,,,frac{2}{x} = 20,,,,,,,,, Leftrightarrow ,,,,,,,,,x = 0,1.) Ответ: 0,1. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = — 1). Следовательно, (a = — 1). График проходит через точку (left( {1;1} right)), поэтому: (1 = frac{k}{1} — 1,,,,,,,, Leftrightarrow ,,,,,,,k = 2.) Таким образом, (fleft( x right) = frac{2}{x} — 1) и (frac{2}{x} — 1 = 19,,,,,,, Leftrightarrow ,,,,,,,,,frac{2}{x} = 20,,,,,,,, Leftrightarrow ,,,,,,,,x = 0,1.) Ответ: 0,1. |
|
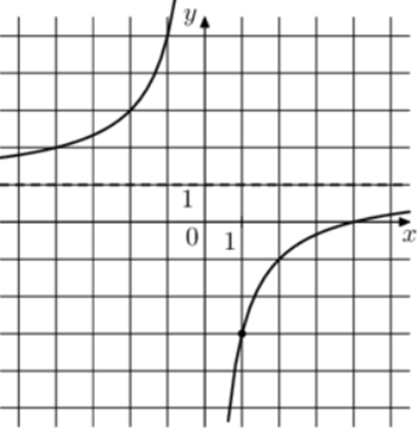
| Задача 7. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите, при каком значении x значение функции равно 0,75.
Ответ
ОТВЕТ: 16. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1; — 3} right)) и (left( {2; — 1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 3 = frac{k}{1} + a}\{ — 1 = frac{k}{2} + a}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = k — frac{k}{2},,,,,,,, Leftrightarrow ,,,,,,,k = — 4.) Тогда: ( — 3 = — 4 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1.) Следовательно, уравнение гиперболы: (fleft( x right) = — frac{4}{x} + 1) и ( — frac{4}{x} + 1 = 0,75,,,,,,, Leftrightarrow ,,,,,,, — frac{4}{x} = — frac{1}{4},,,,,,,, Leftrightarrow ,,,,,,,,x = 16.) Ответ: 16. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = 1). Следовательно, (a = 1). График проходит через точку (left( {1; — 3} right)), поэтому: ( — 3 = frac{k}{1} + 1,,,,,,,, Leftrightarrow ,,,,,,,k = — 4.) Таким образом, (fleft( x right) = — frac{4}{x} + 1) и ( — frac{4}{x} + 1 = 0,75,,,,,,, Leftrightarrow ,,,,,, — frac{4}{x} = — frac{1}{4},,,,,,, Leftrightarrow ,,,,,,x = 16.) Ответ: 16. |
|
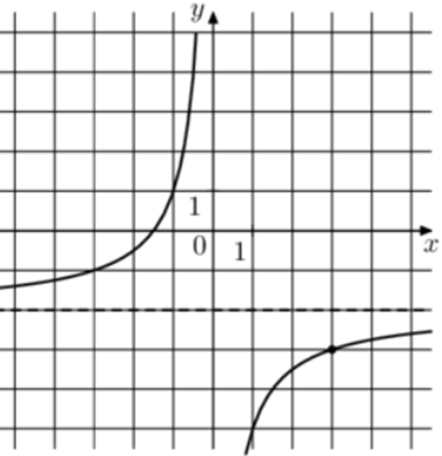
| Задача 8. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите, при каком значении x значение функции равно ( — 9,5.)
Ответ
ОТВЕТ: 0,4. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1; — 5} right)) и (left( {3; — 3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 5 = frac{k}{1} + a}\{ — 3 = frac{k}{3} + a}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = k — frac{k}{3},,,,,,,, Leftrightarrow ,,,,,,,k = — 3.) Тогда: ( — 5 = — 3 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 2.) Следовательно, уравнение гиперболы: (fleft( x right) = — frac{3}{x} — 2) и ( — frac{3}{x} — 2 = — 9,5,,,,,,,, Leftrightarrow ,,,,,,,, — frac{3}{x} = — frac{{15}}{2},,,,,,,, Leftrightarrow ,,,,,,,,x = 0,4.) Ответ: 0,4. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = — 2). Следовательно, (a = — 2). График проходит через точку (left( {1; — 5} right)), поэтому: ( — 5 = frac{k}{1} — 2,,,,,,,, Leftrightarrow ,,,,,,,k = — 3.) Таким образом, (fleft( x right) = — frac{3}{x} — 2) и ( — frac{3}{x} — 2 = — 9,5,,,,,,, Leftrightarrow ,,,,,,, — frac{3}{x} = — frac{{15}}{2},,,,,, Leftrightarrow ,,,,,,x = 0,4.) Ответ: 0,4. |
|
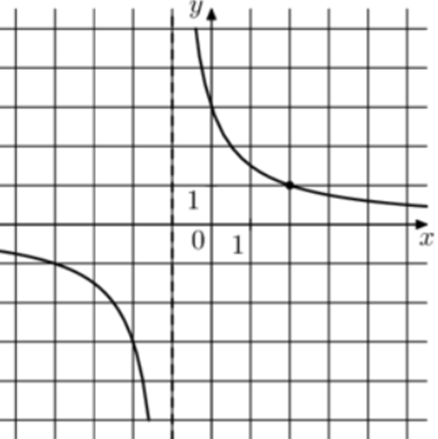
| Задача 9. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите (fleft( {19} right).)
Ответ
ОТВЕТ: 0,15. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( {0;3} right)) и (left( {2;1} right)). (left{ {begin{array}{*{20}{c}}{3 = frac{k}{{0 + a}}}\{1 = frac{k}{{2 + a}}}end{array}} right.,,,,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{k = 3a,,,,,}\{k = 2 + a}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,,3a = 2 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1,,,,k = 3.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{3}{{x + 1}}) и (fleft( {19} right) = frac{3}{{19 + 1}} = 0,15.) Ответ: 0,15. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = — 1). Следовательно, (a = 1). График проходит через точку (left( {0;3} right)), поэтому: (3 = frac{k}{{0 + 1}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = 3.) Таким образом, (fleft( x right) = frac{3}{{x + 1}}) и (fleft( {19} right) = frac{3}{{19 + 1}} = 0,15). Ответ: 0,15. |
|
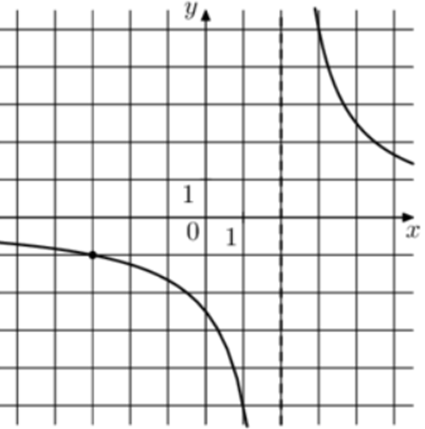
| Задача 10. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите (fleft( { — 4frac{2}{3}} right).)
Ответ
ОТВЕТ: — 0,75. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( { — 3; — 1} right)) и (left( {1; — 5} right)). (left{ {begin{array}{*{20}{c}}{ — 1 = frac{k}{{ — 3 + a}}}\{ — 5 = frac{k}{{1 + a}}}end{array}} right.,,,,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{k = 3 — a,,,,,}\{k = — 5 — 5a}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,,3 — a = — 5 — 5a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 2,,,,k = 5.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{5}{{x — 2}}) и (fleft( { — 4frac{2}{3}} right) = frac{5}{{ — 4frac{2}{3} — 2}} = frac{5}{{ — frac{{20}}{3}}} = — 0,75.) Ответ: – 0,75. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = 2). Следовательно, (a = — 2). График проходит через точку (left( { — 3; — 1} right)), поэтому: ( — 1 = frac{k}{{ — 2 — 1}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = 3.) Таким образом, (fleft( x right) = frac{3}{{x — 2}}) и (fleft( { — 4frac{2}{3}} right) = frac{3}{{ — 4frac{2}{3} — 2}} = frac{5}{{ — frac{{20}}{3}}} = — 0,75.) Ответ: – 0,75. |
|
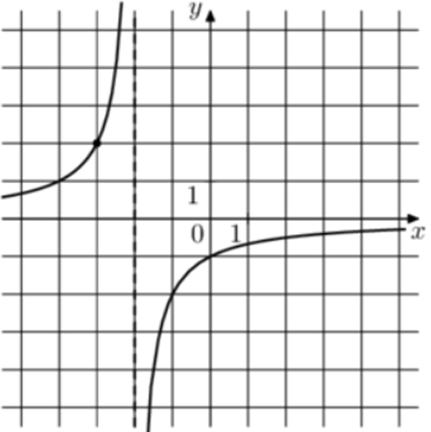
| Задача 11. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите (fleft( {18} right).)
Ответ
ОТВЕТ: — 0,1. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( { — 1; — 2} right)) и (left( { — 3;2} right)). (left{ {begin{array}{*{20}{c}}{ — 2 = frac{k}{{ — 1 + a}}}\{2 = frac{k}{{ — 3 + a}}}end{array}} right.,,,,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{k = 2 — 2a,,,,,}\{k = 2a — 6,,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,,2a — 6 = 2 — 2a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 2,,,,k = — 2.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{{ — 2}}{{x + 2}}) и (fleft( {18} right) = frac{{ — 2}}{{18 + 2}} = — 0,1.) Ответ: – 0,1. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = — 2). Следовательно, (a = 2). График проходит через точку (left( { — 1; — 2} right)), поэтому: ( — 2 = frac{k}{{ — 1 + 2}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 2.) Таким образом, (fleft( x right) = frac{{ — 2}}{{x + 2}}) и (fleft( {18} right) = frac{{ — 2}}{{18 + 2}} = — 0,1.) Ответ: – 0,1. |
|
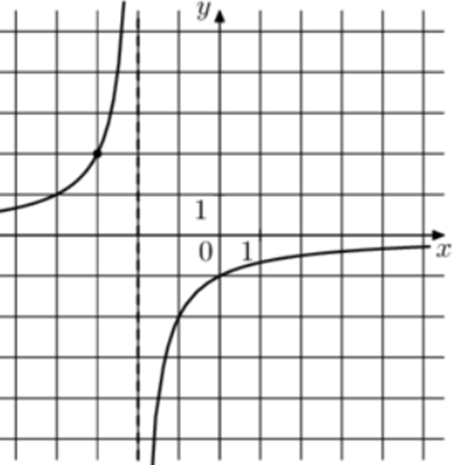
| Задача 12. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите (fleft( {6frac{1}{3}} right).)
Ответ
ОТВЕТ: — 0,24. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( { — 1; — 2} right)) и (left( { — 3;2} right)). (left{ {begin{array}{*{20}{c}}{ — 2 = frac{k}{{ — 1 + a}}}\{2 = frac{k}{{ — 3 + a}}}end{array}} right.,,,,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{k = 2 — 2a,,,,,}\{k = 2a — 6,,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,,2a — 6 = 2 — 2a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 2,,,,k = — 2.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{{ — 2}}{{x + 2}}) и (fleft( {6frac{1}{3}} right) = frac{{ — 2}}{{6frac{1}{3} + 2}} = frac{{ — 2}}{{frac{{25}}{3}}} = — 0,24.) Ответ: – 0,24. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = — 2). Следовательно, (a = 2). График проходит через точку (left( { — 1; — 2} right)), поэтому: ( — 2 = frac{k}{{ — 1 + 2}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 2.) Таким образом, (fleft( x right) = frac{{ — 2}}{{x + 2}}) и (fleft( {6frac{1}{3}} right) = frac{{ — 2}}{{6frac{1}{3} + 2}} = frac{{ — 2}}{{frac{{25}}{3}}} = — 0,24.) Ответ: – 0,24. |
|
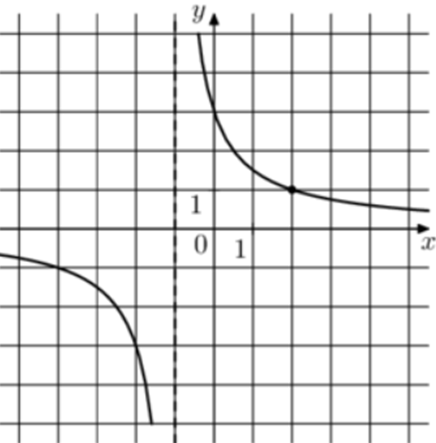
| Задача 13. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите значение x, при котором (fleft( x right) = 0,2.)
Ответ
ОТВЕТ: 14. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( {0;3} right)) и (left( {2;1} right)). (left{ {begin{array}{*{20}{c}}{3 = frac{k}{a},,,,,,}\{1 = frac{k}{{2 + a}}}end{array}} right.,,,,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{k = 3a,,,,,,,,,,,}\{k = 2 + a,,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,,3a = 2 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1,,,,k = 3.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{3}{{x + 1}}) и (frac{3}{{x + 1}} = 0,2,,,,,,,, Leftrightarrow ,,,,,,,x + 1 = 15,,,,,,, Leftrightarrow ,,,,,,,x = 14.) Ответ: 14. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = — 1). Следовательно, (a = 1). График проходит через точку (left( {0;3} right)), поэтому: (3 = frac{k}{{0 + 1}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = 3.) Таким образом, (fleft( x right) = frac{3}{{x + 1}}) и (frac{3}{{x + 1}} = 0,2,,,,,,,, Leftrightarrow ,,,,,,,x + 1 = 15,,,,,,, Leftrightarrow ,,,,,,,x = 14.) Ответ: 14. |
|
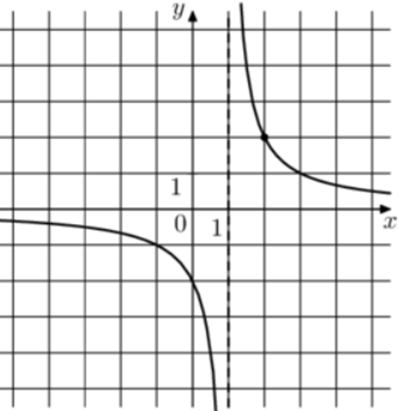
| Задача 14. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите значение x, при котором (fleft( x right) = — 0,08.)
Ответ
ОТВЕТ: — 24. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( {2;2} right)) и (left( {3;1} right)). (left{ {begin{array}{*{20}{c}}{2 = frac{k}{{2 + a}},,,,,,}\{1 = frac{k}{{3 + a}},,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{k = 4 + 2a,,,,,,,,,,,}\{k = 3 + a,,,,,,,,,,,,,,}end{array}} right., Leftrightarrow ,,,,,,,4 + ,2a = 3 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 1,,,,k = 2.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{2}{{x — 1}}) и (frac{2}{{x — 1}} = — 0,08,,,,,,,, Leftrightarrow ,,,,,,,x — 1 = — 25,,,,,,, Leftrightarrow ,,,,,,,x = — 24.) Ответ: – 24. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = 1). Следовательно, (a = — 1). График проходит через точку (left( {2;2} right)), поэтому: (2 = frac{k}{{2 — 1}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = 2.) Таким образом, (fleft( x right) = frac{2}{{x — 1}}) и (frac{2}{{x — 1}} = — 0,08,,,,,,,, Leftrightarrow ,,,,,,,x — 1 = — 25,,,,,,, Leftrightarrow ,,,,,,,x = — 24.) Ответ: – 24. |
|
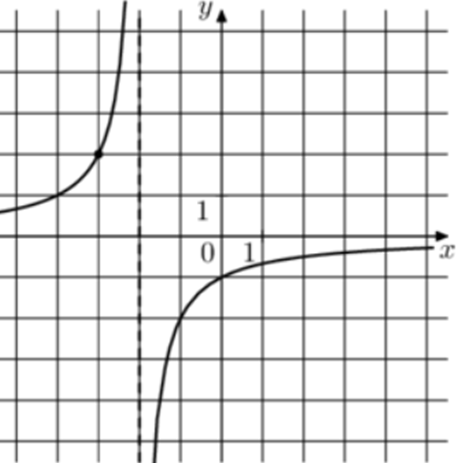
| Задача 15. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите значение x, при котором (fleft( x right) = — 0,04.)
Ответ
ОТВЕТ: 48. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( { — 1; — 2} right)) и (left( { — 3;2} right)). (left{ {begin{array}{*{20}{c}}{ — 2 = frac{k}{{ — 1 + a}},,,,,,}\{2 = frac{k}{{ — 3 + a}},,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{k = 2 — 2a}\{k = 2a — 6}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,2a — 6 = 2 — 2a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 2,,,,k = — 2.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{{ — 2}}{{x + 2}}) и (frac{{ — 2}}{{x + 2}} = — 0,04,,,,,,,, Leftrightarrow ,,,,,,,x + 2 = 50,,,,,,, Leftrightarrow ,,,,,,,x = 48.) Ответ: 48. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = — 2). Следовательно, (a = 2). График проходит через точку (left( { — 1; — 2} right)), поэтому: ( — 2 = frac{k}{{ — 1 + 2}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 2.) Таким образом, (fleft( x right) = frac{{ — 2}}{{x + 2}}) и (frac{{ — 2}}{{x + 2}} = — 0,04,,,,,,,, Leftrightarrow ,,,,,,,x + 2 = 50,,,,,,, Leftrightarrow ,,,,,,,x = 48.) Ответ: 48. |
|
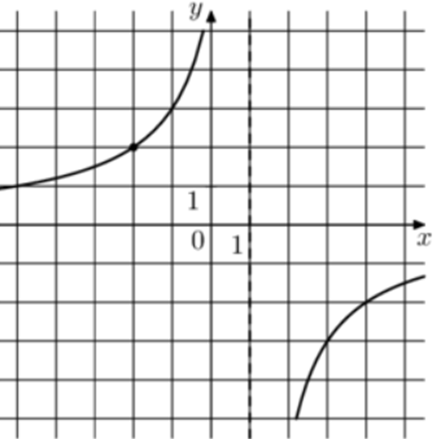
| Задача 16. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите значение x, при котором (fleft( x right) = 0,2.)
Ответ
ОТВЕТ: — 29. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( {3; — 3} right)) и (left( { — 1;3} right)). (left{ {begin{array}{*{20}{c}}{ — 3 = frac{k}{{3 + a}},,,,,,}\{3 = frac{k}{{ — 1 + a}},,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{k = — 9 — 3a,,,,,,,,,,,}\{k = 3a — 3,,,,,,,,,,,,,,}end{array}} right., Leftrightarrow ,,,,,,,3a — 3 = — 9 — 3a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 1,,,,k = — 6.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{{ — 6}}{{x — 1}}) и (frac{{ — 6}}{{x — 1}} = 0,2,,,,,,,, Leftrightarrow ,,,,,,,x — 1 = — 30,,,,,,, Leftrightarrow ,,,,,,,x = — 29.) Ответ: – 29. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = 1). Следовательно, (a = — 1). График проходит через точку (left( {3; — 3} right)), поэтому: ( — 3 = frac{k}{{3 — 1}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 6.) Таким образом, (fleft( x right) = frac{{ — 6}}{{x — 1}}) и (frac{{ — 6}}{{x — 1}} = 0,2,,,,,,,, Leftrightarrow ,,,,,,,x — 1 = — 30,,,,,,, Leftrightarrow ,,,,,,,x = — 29.) Ответ: – 29. |
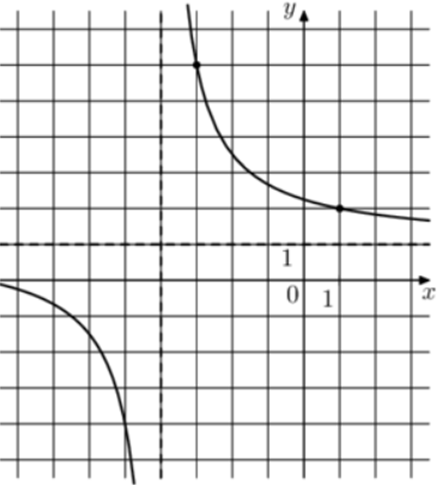
| Задача 17. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите k.
Ответ
ОТВЕТ: 1. |
 |
|
Решение
Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = 1), то (k = 1). Ответ: 1. |
|
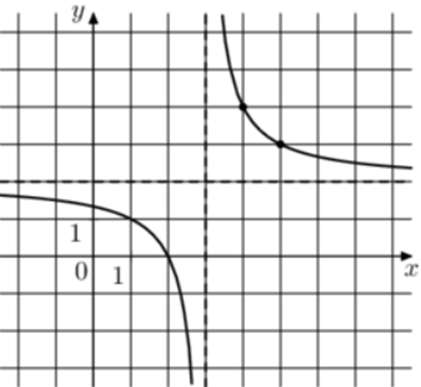
| Задача 18. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите k.
Ответ
ОТВЕТ: 2. |
 |
|
Решение
Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = 2), то (k = 2). Ответ: 2. |
|
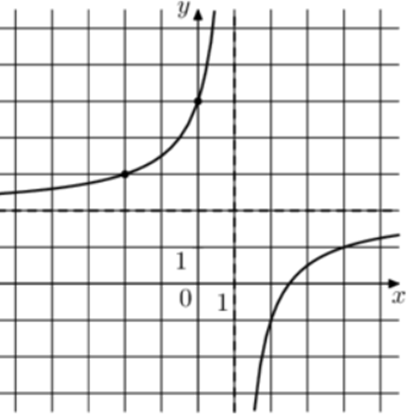
| Задача 19. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите k.
Ответ
ОТВЕТ: 2. |
 |
|
Решение
Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = 2), то (k = 2). Ответ: 2. |
|
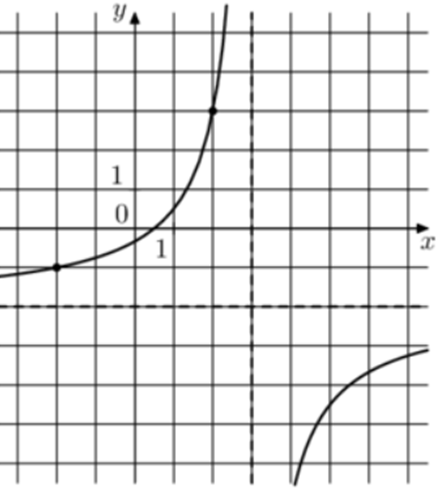
| Задача 20. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите k.
Ответ
ОТВЕТ: — 2. |
 |
|
Решение
Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = -2), то (k = -2). Ответ: -2. |
|
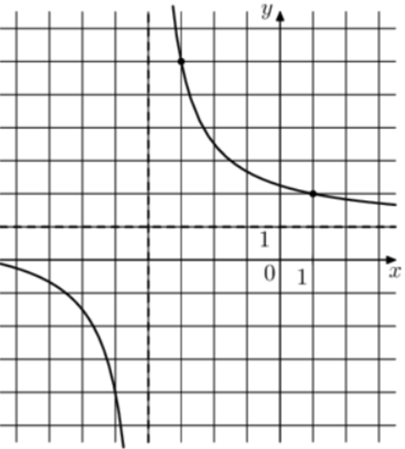
| Задача 21. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите a.
Ответ
ОТВЕТ: 9. |
 |
|
Решение
Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = 1), то (k = 1). Так как график функции имеет вертикальную асимптоту (x = — 4), то (b = 4). Следовательно: (fleft( x right) = 1 + frac{{a — 4}}{{x + 4}}.) Воспользуемся тем, что график функции проходит через точку (left( { — 3;6} right)). Тогда: (6 = 1 + frac{{a — 4}}{{ — 3 + 4}},,,,,,,, Leftrightarrow ,,,,,,,,frac{{a — 4}}{1} = 5,,,,,,,,, Leftrightarrow ,,,,,,,,a = 9.,,,) Ответ: 9. |
|
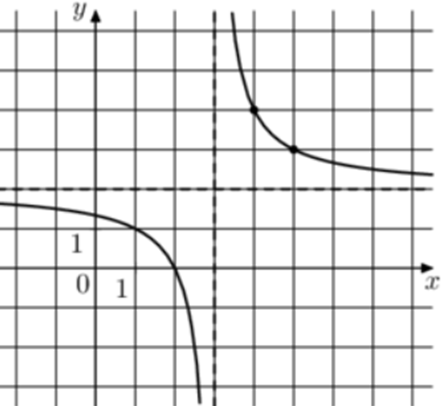
| Задача 22. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите a.
Ответ
ОТВЕТ: — 4. |
 |
|
Решение
Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = 2), то (k = 2). Так как график функции имеет вертикальную асимптоту (x = 3), то (b = — 3). Следовательно: (fleft( x right) = 2 + frac{{a + 6}}{{x — 3}}.) Воспользуемся тем, что график функции проходит через точку (left( {5;3} right)). Тогда: (3 = 2 + frac{{a + 6}}{{5 — 3}},,,,,,,, Leftrightarrow ,,,,,,,,frac{{a + 6}}{2} = 1,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 4.,,,) Ответ: – 4. |
|
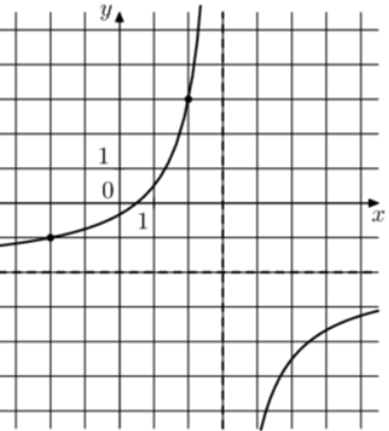
| Задача 23. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите a.
Ответ
ОТВЕТ: 1. |
 |
|
Решение
Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = — 2), то (k = — 2). Так как график функции имеет вертикальную асимптоту (x = 3), то (b = — 3). Следовательно: (fleft( x right) = — 2 + frac{{a — 6}}{{x — 3}}.) Воспользуемся тем, что график функции проходит через точку (left( {2;3} right)). Тогда: (3 = — 2 + frac{{a — 6}}{{2 — 3}},,,,,,,, Leftrightarrow ,,,,,,,,frac{{a — 6}}{{ — 1}} = 5,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1.,,,) Ответ: 1. |
|
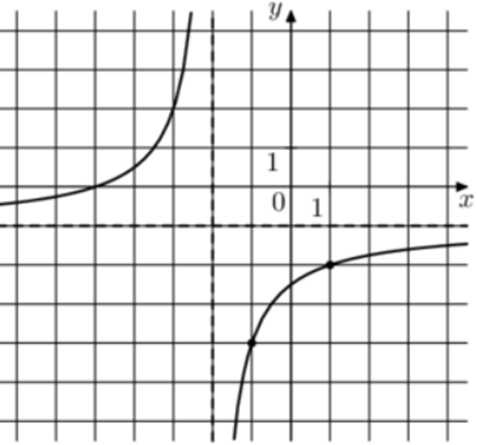
| Задача 24. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите a.
Ответ
ОТВЕТ: — 5. |
 |
|
Решение
Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = — 1), то (k = — 1). Так как график функции имеет вертикальную асимптоту (x = — 2), то (b = 2). Следовательно: (fleft( x right) = — 1 + frac{{a + 2}}{{x + 2}}.) Воспользуемся тем, что график функции проходит через точку (left( { — 1; — 4} right)). Тогда: ( — 4 = — 1 + frac{{a + 2}}{{ — 1 + 2}},,,,,,,, Leftrightarrow ,,,,,,,,a + 2 = — 3,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 5.,,,) Ответ: – 5. |
|
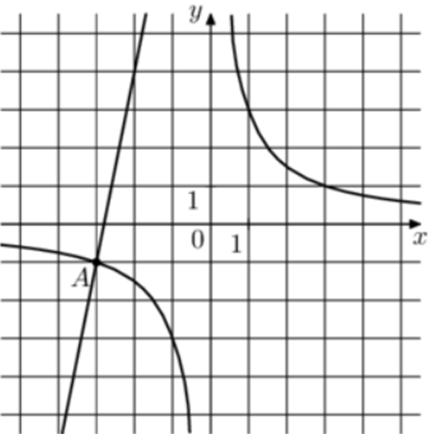
| Задача 25. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: 0,2. |
 |
|
Решение
График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( {1;3} right)). Следовательно: (3 = frac{k}{1},,,,,,,,, Leftrightarrow ,,,,,,,,,k = 3.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = frac{3}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( { — 3; — 1} right)) и (left( { — 2;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = — 3a + b}\{4 = — 2a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 5 = — a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = 5.) Тогда: ( — 1 = — 3 cdot 5 + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = 14.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = 5x + 14.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = 5x + 14}\{y = frac{3}{x},,,,,,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,5x + 14 = frac{3}{x},,,,,,,,, Leftrightarrow ,,,,,,,5{x^2} + 14x — 3 = 0,,,,,,, Leftrightarrow ,,,,,,,,{x_1} = 0,2,,,,{x_2} = — 3.) Значение (x = — 3) является абсциссой точки А. Следовательно, абсцисса точки В равна 0,2. Ответ: 0,2. |
|
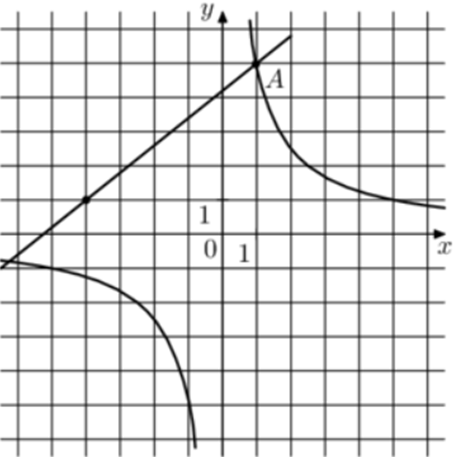
| Задача 26. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: — 6,25. |
 |
|
Решение
График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( {1;5} right)). Следовательно: (5 = frac{k}{1},,,,,,,,, Leftrightarrow ,,,,,,,,,k = 5.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = frac{5}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( { — 4;1} right)) и (left( {1;5} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = — 4a + b}\{5 = a + b,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 4 = — 5a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = frac{4}{5}.) Тогда: (1 = — 4 cdot frac{4}{5} + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = frac{{21}}{5}.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = frac{4}{5}x + frac{{21}}{5}.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = frac{4}{5}x + frac{{21}}{5}}\{y = frac{5}{x},,,,,,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,frac{4}{5}x + frac{{21}}{5} = frac{5}{x},,,,,,,,, Leftrightarrow ,,,,,,,4{x^2} + 21x — 25 = 0,,,,,,, Leftrightarrow ,,,,,,,,{x_1} = 1,,,,{x_2} = — 6,25.) Значение (x = 1) является абсциссой точки А. Следовательно, абсцисса точки В равна – 6,25. Ответ: – 6,25. |
|
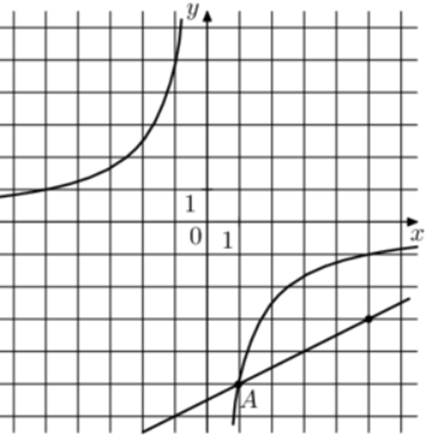
| Задача 27. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: 10. |
 |
|
Решение
График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( {1; — 5} right)). Следовательно: ( — 5 = frac{k}{1},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 5.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = — frac{5}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( {1; — 5} right)) и (left( {5; — 3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 5 = a + b,,,}\{ — 3 = 5a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = — 4a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = frac{1}{2}.) Тогда: ( — 5 = frac{1}{2} + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = — frac{{11}}{2}.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = frac{1}{2}x — frac{{11}}{2}.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = frac{1}{2}x — frac{{11}}{2}}\{y = — frac{5}{x},,,,,,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,frac{1}{2}x — frac{{11}}{2} = — frac{5}{x},,,,,,,,, Leftrightarrow ,,,,,,,{x^2} — 11x + 10 = 0,,,,,,, Leftrightarrow ,,,,,,,,{x_1} = 1,,,,{x_2} = 10.) Значение (x = 1) является абсциссой точки А. Следовательно, абсцисса точки В равна 10. Ответ: 10. |
|
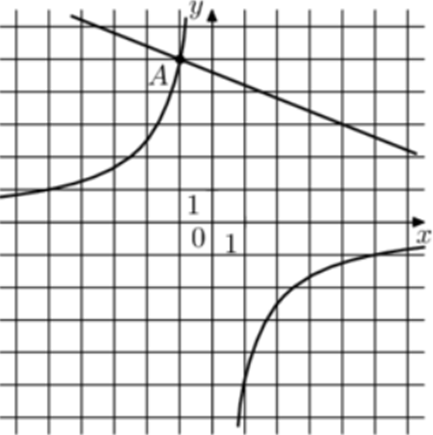
| Задача 28. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: 12,5. |
 |
|
Решение
График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( { — 1;5} right)). Следовательно: (5 = frac{k}{{ — 1}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 5.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = — frac{5}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( { — 1;5} right)) и (left( {4;3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{5 = — a + b}\{3 = 4a + b}end{array}} right.) Вычтем из первого уравнения второе: (2 = — 5a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = — frac{2}{5}.) Тогда: (5 = frac{2}{5} + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = frac{{23}}{5}.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = — frac{2}{5}x + frac{{23}}{5}.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — frac{2}{5}x + frac{{23}}{5}}\{y = — frac{5}{x},,,,,,,,,,,,,,,,}end{array}} right.,,,,,, Leftrightarrow ,,,,,,, — frac{2}{5}x + frac{{23}}{5} = — frac{5}{x},,,,,,, Leftrightarrow ,,,,,,2{x^2} — 23x — 25 = 0,,,,,, Leftrightarrow ,,,,,,{x_1} = — 1,,,,{x_2} = 12,5.) Значение (x = — 1) является абсциссой точки А. Следовательно, абсцисса точки В равна 12,5. Ответ: 12,5. |
|
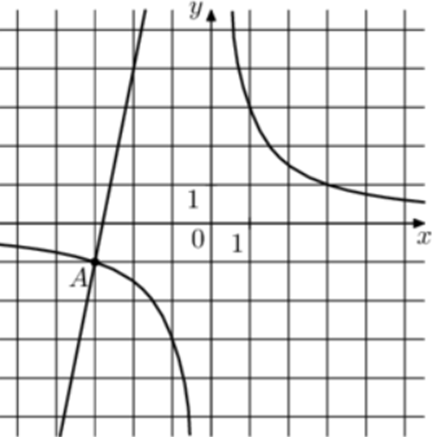
| Задача 29. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: 15. |
 |
|
Решение
График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( { — 3; — 1} right)). Следовательно: ( — 1 = frac{k}{{ — 3}},,,,,, Leftrightarrow ,,,,,,,k = 3.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = frac{3}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( { — 3; — 1} right)) и (left( { — 2;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = — 3a + b}\{4 = — 2a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 5 = — a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = 5.) Тогда: ( — 1 = — 15 + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = 14.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = 5x + 14.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = 5x + 14}\{y = frac{3}{x},,,,,,,,,,,,,}end{array}} right.,,,,,, Leftrightarrow ,,,,,,5x + 14 = frac{3}{x},,,,,, Leftrightarrow ,,,,,5{x^2} + 14x — 3 = 0,,,,,, Leftrightarrow ) ( Leftrightarrow ,,,,,{x_1} = — 3,,,,{x_2} = frac{1}{5},,,,{y_1} = — 1,,,,,{y_2} = 15.) Следовательно, (Aleft( { — 3; — 1} right)) и (Bleft( {frac{1}{5};15} right)). Таким образом, ордината точки В равна 15. Ответ: 15. |
|
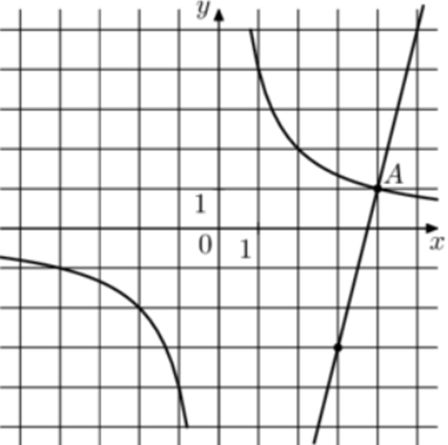
| Задача 30. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: — 16. |
 |
|
Решение
График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( {4;1} right)). Следовательно: (1 = frac{k}{4},,,,,,,,, Leftrightarrow ,,,,,,,,,k = 4.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = frac{4}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( {4;1} right)) и (left( {3; — 3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = 4a + b,,}\{ — 3 = 3a + b}end{array}} right.) Вычтем из первого уравнения второе: (4 = a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = 4.) Тогда: (1 = 16 + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = — 15.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = 4x — 15.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = 4x — 15}\{y = frac{4}{x},,,,,,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,4x — 15 = frac{4}{x},,,,,,,,, Leftrightarrow ,,,,,,,4{x^2} — 15x — 4 = 0,,,,,,, Leftrightarrow )( Leftrightarrow ,,,,,{x_1} = 4,,,,{x_2} = — frac{1}{4},,,,{y_1} = 1,,,,,{y_2} = — 16.) Следовательно, (Aleft( {4;1} right)) и (Bleft( { — frac{1}{4}; — 16} right)). Таким образом, ордината точки В равна – 16. Ответ: – 16. |
|
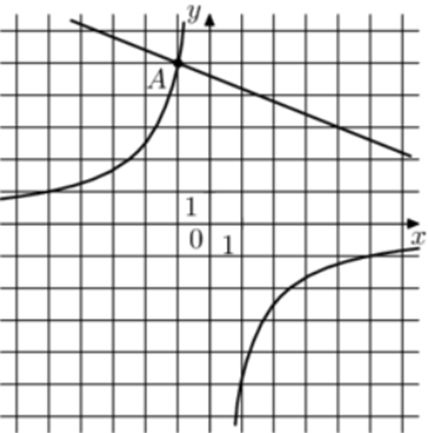
| Задача 31. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: — 0,4. |
 |
|
Решение
График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( { — 1;5} right)). Следовательно: (5 = frac{k}{{ — 1}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 5.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = — frac{5}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( { — 1;5} right)) и (left( {4;3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{5 = — a + b,,}\{3 = 4a + b,,}end{array}} right.) Вычтем из первого уравнения второе: (2 = — 5a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = — frac{2}{5}.) Тогда: (5 = frac{2}{5} + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = frac{{23}}{5}.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = — frac{2}{5}x + frac{{23}}{5}.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — frac{2}{5}x + frac{{23}}{5}}\{y = — frac{5}{x},,,,,,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,, — frac{2}{5}x + frac{{23}}{5} = — frac{5}{x},,,,,,,,, Leftrightarrow ,,,,,,,2{x^2} — 23x — 25 = 0,,,,,,, Leftrightarrow ,,,,,,,,,,,) ( Leftrightarrow ,,,,,,{x_1} = — 1,,,,{x_2} = frac{{25}}{2},,,,,,,,,,{y_1} = 5,,,,{y_2} = — 0,4.) Следовательно, (Aleft( { — 1;5} right)) и (Bleft( {frac{{25}}{2}; — 0,4} right)). Таким образом, ордината точки В равна – 0,4. Ответ: – 0,4. |
|
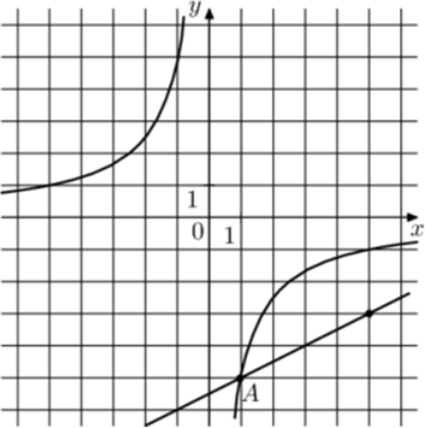
| Задача 32. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: — 0,5. |
 |
|
Решение
График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( {1; — 5} right)). Следовательно: ( — 5 = frac{k}{1},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 5.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = — frac{5}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( {1; — 5} right)) и (left( {5; — 3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 5 = a + b,,,}\{ — 3 = 5a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = — 4a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = frac{1}{2}.) Тогда: ( — 5 = frac{1}{2} + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = — frac{{11}}{2}.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = frac{1}{2}x — frac{{11}}{2}.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = frac{1}{2}x — frac{{11}}{2}}\{y = — frac{5}{x},,,,,,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,frac{1}{2}x — frac{{11}}{2} = — frac{5}{x},,,,,,,,, Leftrightarrow ,,,,,,,{x^2} — 11x + 10 = 0,,,,,,, Leftrightarrow ,,,,,,,,) ( Leftrightarrow ,,,,,,,,{x_1} = 1,,,,{x_2} = 10,,,,,,,,,,,{y_1} = — 5,,,,{y_2} = — 0,5.) Следовательно, (Aleft( {1; — 5} right)) и (Bleft( {10; — 0,5} right)). Таким образом, ордината точки В равна – 0,5. Ответ: – 0,5. |
-
Решение
-
Видеорешение
Чтобы найти точку, в которой (displaystyle f(x)) равно (displaystyle 2{small,})
- найдем неизвестные коэффициенты (displaystyle k) и (displaystyle b) в уравнении гиперболы,
- решим уравнение (displaystyle f(x)=2{small.})
Найдем (displaystyle k) и (displaystyle b{small.})
Для этого составим и решим систему уравнений относительно (displaystyle k) и (displaystyle b{small.})
Заметим, что гипербола (displaystyle y=frac{k}{x+b}) проходит через точки (displaystyle (-2;, -4)) и (displaystyle (2;, 1){small.})
Значит,
- если в уравнение гиперболы (displaystyle y=frac{k}{x+b}) подставить (displaystyle color{blue}{x=-2}) и (displaystyle color{blue}{y=-4},) то получится первое верное равенство (первое уравнение на (displaystyle k) и (displaystyle b)),
- если в уравнение гиперболы (displaystyle y=frac{k}{x+b}) подставить (displaystyle color{green}{x=2}) и (displaystyle color{green}{y=1},) то получится второе верное равенство (второе уравнение на (displaystyle k) и (displaystyle b)).
Получаем систему уравнений:
(displaystyleleft{begin{aligned}color{blue}{-4}&=frac{k}{color{blue}{-2}+b}{small,}\color{green}{1}&=frac{k}{color{green}{2}+b}{small.}end{aligned}right.)
Решение данной системы уравнений (displaystyle k=3{,}2) и (displaystyle b=1{,}2{small.})
Тогда уравнение гиперболы имеет вид:
(displaystyle f(x)=frac{3{,}2}{x+1{,}2}{small.})
Найдём те значения (displaystyle x{small,}) при которых значение (displaystyle f(x)) равно (displaystyle 2{small.})
Все такие (displaystyle x) удовлетворяют уравнению
(displaystyle 2=frac{3{,}2}{x+1{,}2}{small.})
Решим его.
Для (displaystyle x{ small ,}) не равных (displaystyle -1{,}2{ small ,}) можно домножить обе части уравнения на (displaystyle x+1{,}2{small.})
Тогда:
(displaystyle 2cdot(x+1{,}2)=3{,}2{small,})
(displaystyle x=frac{3{,}2}{2}-1{,}2{small,})
(displaystyle x=0{,}4{small.})
Полученное значение (displaystyle x) отлично от (displaystyle -1{,}2{ small .})
Значит, (displaystyle f(0{,}4)=2{small.})
Ответ: (displaystyle f(0{,}4)=2{small.})
Задание
№9 «Графики функции»
ЕГЭ
математика профиль
1) Гиперболы
2) Кусочно-линейная функция
3)Параболы
4) Синусоиды
1) Гиперболы
1. 
где числа a, b и c — целые.
Найдите
Решение.
1. 
изображён график функции вида где
числа a, b и c — целые. Найдите
Решение.
График функции имеет горизонтальную асимптоту значит,
График функции имеет вертикальную асимптоту значит,
По графику тогда
Таким образом, Найдём
Асимпто́та, или аси́мптота[1] (от др.-греч. ἀσύμπτωτος — несовпадающая, не касающаяся кривой с бесконечной ветвью) — прямая, обладающая тем свойством, что расстояние от
точки кривой до этой прямой стремится к нулю при удалении точки вдоль
ветви в бесконечность[2]. Термин впервые появился у Аполлония
Пергского, хотя
асимптоты гиперболы исследовал ещё Архимед[3].
2. 
где числа a, b и c — целые.
Найдите
2. 
изображён график функции вида где
числа a, b и c — целые. Найдите
Решение.
График функции имеет горизонтальную асимптоту значит,
График функции имеет вертикальную асимптоту значит,
По графику тогда
Таким образом, Найдём
Ответ: −0,75.
3. 
где числа a, b и c — целые.
Найдите
3. 
изображён график функции вида где
числа a, b и c — целые. Найдите
Решение.
График функции имеет горизонтальную асимптоту значит,
График функции имеет вертикальную асимптоту значит,
По графику тогда
Таким образом, Найдём
Ответ: 2,875.
2) Кусочно-линейная функция
1. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите корень уравнения
1. 
изображён график функции вида где числа a, b, c и d —
целые. Найдите корень уравнения
Решение.

случаев раскрытия модуля получаем линейную функцию где угловой коэффициент
или
а
свободный член или
Очевидно, что
значит, большему значению
углового коэффициента соответствует а
меньшему — Аналогично большему
значению свободного члена соответствует а
меньшему —
По рисунку определяем, что
Значит,
Решим уравнение
Ответ: 1.
2.
На
рисунке изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
2. 
изображён график функции вида где числа a, b, c и d — целые.
Найдите корень уравнения
Решение.
Заметим, что в точке излома, т.е.
при Значит, корнем уравнения
является число 2.
3. 
где числа a, b, c и d — целые.
Найдите корень уравнения
4. 
где числа a, b, c и d — целые.
Найдите корень уравнения
4. 
изображён график функции вида где числа a, b, c и d — целые.
Найдите корень уравнения
Решение.
Заметим, что в точке излома, т.е.
при Значит, корнем уравнения
является число 3.
3)Параболы

где числа a, b и c —
целые. Найдите значение .
Решение.1 способ
По рисунку определяем, что значит,
Тогда
Решение.2 способ
Выбрать три точки . Например (0;-1),
(6,8), (2;4). Подставив координаты первой точки, мы найдем с=-1. Далее
подставив две другие координаты и с, решаем систему уравнений и находим а и в.
4) Синусоиды

изображён график функции вида где числа a, b, c и d — целые.
Найдите
Решение.
По графику
тогда
и
По графику тогда, если
то
— не
имеет целочисленных решений,
если то
Значит, и
Найдём наименьший положительный период функции
Наименьший положительный период функции равен
а по графику наименьший
положительный период равен 2, тогда
Таким образом, Найдём
Ответ: −2.
Задание 13539
На рисунке изображён график функции $$y=frac{k}{x}+a$$. Найдите $$f(-8)$$.
Ответ: -0,5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 13557
На рисунке изображён график функции $$f(x)=frac{k}{x}+a$$. Найдите, при каком значении х значение функции равно 7.
Ответ: 0,4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 14432
На рисунке изображён график функции $$f(x)=frac{k}{x+a}$$.Найдите $$f(-7)$$.
Ответ: -0,4
Скрыть
Точка $$A(-4;1)$$ и $$B(-1;2)$$ принадлежат графику функции. Тогда:
$$left{begin{matrix} -1=frac{k}{-4a}\ 2=frac{k}{-1+a} end{matrix}right.Leftrightarrow left{begin{matrix} 4-a=k\ 2a-2=k end{matrix}right.Leftrightarrow left{begin{matrix} 4-a=2a-2\ k=4-a end{matrix}right.Leftrightarrow left{begin{matrix} a=2\ k=2 end{matrix}right.$$
Получим: $$f(-7)=frac{2}{-7+2}=frac{2}{-5}=-0,4$$
Задание 14449
На рисунке изображён график функции $$f(x)=frac{k}{x+a}.$$ Найдите значение х, при котором $$f(x)=-0,2.$$
Ответ: -13
Скрыть
Вертикальная асимптота графика гиперболы проходит через точку $$x=2,$$ следовательно, параметр $$a=-2.$$
Второй параметр k вычислим из координаты точки $$(-1; -1)$$ на графике:
$$-1=frac{k}{-1-2}Rightarrow k=3$$
Получаем график гиперболы:
$$f(x)=frac{3}{x-2}$$
Найдем точку x, при которой $$f(x)=-0,2:$$
$$-frac{1}{5}=frac{3}{x-2}Rightarrow x=-3cdot5+2=-13$$
Задание 14591
На рисунке изображён график функции $$f(x)=frac{kx+a}{x+b}.$$ Найдите $$k.$$
Ответ: -2
Скрыть
Точки $$(-4;-1)$$ и $$(-2;1)$$ принадлежат графику функции $$f(x).$$ Тогда:
$$left{begin{matrix} -1=frac{a-4k}{b-4}\ 1=frac{a-2k}{b-2} end{matrix}right.Leftrightarrowleft{begin{matrix} a-4k=4-b\ a-2k=-2+b end{matrix}right.Leftrightarrowleft{begin{matrix} 2a-6k=2\ 2k=-6-2b end{matrix}right.Leftrightarrowleft{begin{matrix} a=3k+1\ k=-3-b end{matrix}right.Rightarrow b=-k-3$$
Точка $$(0;5)$$ принадлежит графику функции $$f(x).$$ Тогда:
$$frac{a}{b}=5$$
$$a=5b$$
$$left{begin{matrix} 3k+1=5b\ b=-k-3 end{matrix}right.$$
$$3k+1=5(-k-3)$$
$$8k=-16$$
$$k=-2$$
Задание 14596
На рисунке изображён график функции $$f(x)=frac{kx+a}{x+b}.$$ Найдите $$а.$$
Ответ: 6
Скрыть
$$f(x)=frac{kx+a}{x+b}=k+frac{a-kb}{x+b}$$
При этом $$b=-2,$$ так как вертикальная асимптота сдвинута на 2 единицы вправо.
Получим: $$f(x)=k+frac{a+2k}{x-3}.$$
При этом $$k=-1,$$ так как горизонтальная асимптота сдвинута на 1 единицу вниз.
Получим: $$f(x)=-1+frac{a-2}{x-3}.$$
График проходит через $$(-2;-2).$$
Получим: $$-2=-1+frac{a-2}{-2-2}Leftrightarrow -1=frac{a-2}{-4}Rightarrow a=6.$$
Задание 14621
На рисунке изображен график функции $$y=frac{1}{x+a}+c,$$ где $$a,c$$ ‐ целые числа. Найдите $$c.$$
Ответ: -2
Скрыть
График проходит через $$(4;-1)$$ и $$(2;-3)$$
Получим: $$left{begin{matrix} -1=frac{1}{4+a}+c\ -3=frac{1}{2+a}+c end{matrix}right.Leftrightarrowleft{begin{matrix} -c-1=frac{1}{4+a}\ -c-3=frac{1}{2+a} end{matrix}right.$$
Вычтем из второго уравнения первое:
$$-2=frac{1}{2+a}-frac{1}{4+a}Leftrightarrow -2=frac{4+a-2-a}{(4+a)(2+a)}$$
$$-2(8+6a+a^2)=2Leftrightarrow a^2+6a+8=-1Leftrightarrow a^2+6a+9=0$$
$$Rightarrow a=-3Rightarrow -c-1=frac{1}{4-3}Rightarrow -c=1+1Rightarrow c=-2$$
Задание 14875
На рисунке изображён график функции $$f(x)=frac{k}{x+a}.$$ Найдите $$f(19).$$
Ответ: 0,15
Скрыть
Точки $$(2;1)$$ и $$(-4;-1)$$ принадлежат графику функции. Тогда:
$$left{begin{matrix} frac{k}{2+a}=1\ frac{k}{-4+a}=-1 end{matrix}right.Leftrightarrowleft{begin{matrix} k=2+a\ k=4-a end{matrix}right.$$
$$2+a=4-a$$
$$2a=2$$
$$a=1$$
$$k=4-1=3$$
$$f(x)=frac{3}{x+1}$$
$$f(19)=frac{3}{19+1}=frac{3}{20}=0,15$$
Задание 14894
На рисунке изображен график функции $$f(x)=frac{ax+b}{x+c},$$ где числа $$a, b, c$$ — целые. Найдите значение $$f(29).$$
Ответ: -2,12
Скрыть
График проходит через $$(1;-1); (3;1); (5;-5).$$ Получим:
$$left{begin{matrix} -1=frac{acdot1+b}{1+c}\ 1=frac{3a+b}{3+c}\ -5=frac{5a+b}{5+c} end{matrix}right.Leftrightarrowleft{begin{matrix} -1-c=a+b\ 3+c=3a+b\ -25-5c=5a+b end{matrix}right.Leftrightarrowleft{begin{matrix} 4+2c=2a\ 28+6c=-2a\ 3+c=3a+b end{matrix}right.Leftrightarrowleft{begin{matrix} 32+8c=0\ a=2+c\ b=c+3-3a end{matrix}right.Leftrightarrow$$
$$Leftrightarrowleft{begin{matrix} c=-4\ a=-2\ b=5 end{matrix}right.$$
Получим: $$y=frac{-2x+5}{x-4}.$$ Тогда $$f(29)=frac{-2cdot29+5}{29-4}=frac{-53}{25}=-2,12$$
Задание 15049
На рисунке изображены графики функций $$f(x)=frac{k}{x}$$ и $$g(x)=ax+b,$$ которые пересекаются в точках $$А(-2;3)$$ и $$В(x_0;y_0).$$ Найдите $$x_0.$$
Ответ: 0,75
Скрыть
Прямая проходит через $$(-2;-3)$$ и $$(0;5).$$ Получим:
$$left{begin{matrix} -3=-2k+b\ 5=0k+b end{matrix}right.Leftrightarrowleft{begin{matrix} -2k=-8\ b=5 end{matrix}right.Leftrightarrowleft{begin{matrix} k=4\ b=5 end{matrix}right.$$
Гипербола проходит через $$(-2;-3).$$ Тогда:
$$-3=frac{k}{-2}Rightarrow k=6.$$ Получим $$y=frac{6}{x}.$$
$$frac{6}{x}=4x+5Leftrightarrow 4x^2+5x-6=0$$
$$D=25+96=121$$
$$x_1=frac{-5+11}{2cdot4}=frac{1,5}{2}=0,75$$
$$x_2=frac{-5-11}{2cdot4}=-2$$
Задание 15068
На рисунке изображен график функции $$f(x)=frac{ax+b}{x+c},$$ где a, b и с — целые. Найдите значение f(17).
Ответ: -1,9
Скрыть
График проходит через $$(-1;-1); (-2;0)$$ и $$(-4;-4).$$
Получим:
$$left{begin{matrix} -1=frac{acdot(-1)+b}{-1+c}\ 0=frac{acdot(-2)+b}{-2+c}\ -4=frac{acdot(-4)+b}{-4+c} end{matrix}right.Leftrightarrowleft{begin{matrix} -1=frac{b-a}{c-1}\ 0=frac{b-2a}{c-2}\ -4=frac{b-4a}{c-4} end{matrix}right.Leftrightarrowleft{begin{matrix} 1-c=b-a\ b-2a=0\ 16-4c=b-4a end{matrix}right.Leftrightarrowleft{begin{matrix} 1-c=2a-a\ b=2a\ 16-4c-b=-4a end{matrix}right.Leftrightarrow$$
$$Leftrightarrowleft{begin{matrix} c=1-a\ b=2a\ 16-4+4a-2a=-4a end{matrix}right.Leftrightarrowleft{begin{matrix} a=-2\ b=-4\ c=3 end{matrix}right.$$
Получим:
$$y=frac{-2x-4}{x+3}.$$
$$y(17)=frac{-34-4}{17+3}=frac{-38}{20}=-1,9$$
Задание 15125
На рисунке изображен график функции $$f(x)=frac{k}{x}+a.$$ Найдите $$f(-12).$$
Ответ: 0,75
Скрыть
$$2=frac{k}{3}+a$$
$$−2=frac{k}{-1}+a$$
Решая систему, получаем:
$$f(x)=frac{3}{x}+1$$
$$f(-12)=0,75$$
Задание 15302
На рисунке изображен график функции $$f(x)=frac{kx+a}{x+b}.$$ Найдите $$a.$$
Ответ: 9
Скрыть
График проходит через $$(1;2), (-3;6), (-5;-4).$$ Получим:
$$left{begin{matrix} 2=frac{k+a}{1+b}\ 6=frac{-3k+a}{-3+b}\ -4=frac{-5k+a}{-5+b} end{matrix}right.Leftrightarrowleft{begin{matrix} 2+2b=k+a\ -18+6b=-3k+a\ 20-4b=-5k+a end{matrix}right.$$
Вычтем второе из первого и третьего:
$$left{begin{matrix} 20-4b=4k\ 38-10b=-2k end{matrix}right.Leftrightarrowleft{begin{matrix} 5-b=k\ -19+5b=k end{matrix}right.Leftrightarrowleft{begin{matrix} 24-6b=0\ 5-b=k end{matrix}right.Leftrightarrowleft{begin{matrix} b=4\ k=1 end{matrix}right.$$
Тогда:
$$2+2cdot4=1+aRightarrow a=9$$
Задание 15533
На рисунке изображены части графиков функций $$f(x)=frac{k}{x}$$ и $$g(x)=frac{c}{x}+d$$. Найдите ординату точки пересечения графиков этих функций.
Ответ: -4
Скрыть
Задание 15689
На рисунке изображены части графиков функций $$f(x)=frac{k}{x}$$ и $$g(x)=frac{c}{x}+d$$. Найдите абсциссу точки пересечения графиков этих функций.
Ответ:
Скрыть
В 2022 задание 9 по математике профильного уровня изменилось — появился новый формат, проверяющий знание свойств параболы. Номер вызывает вопросы у учеников, но на деле решается просто. В статье разберем правила выполнения задания 9 ЕГЭ по математике.
Способы решения номера
9 задание по математике профильного уровня 2022 получится решить четырьмя методами.
Первый вариант
Начнем с простого способа, не требующего глубокого понимания темы. Условие выглядит следующим образом:
Присмотревшись к картинке задания 9 по профильной математике, видим: график содержит целочисленные точки. Отметим их на изображении (экзамен разрешает использовать текст КИМа). Решение требует минимум три точки:
Видим: в точке «-4» ордината равна «-3». Запишем уравнение, подставив значения значения абсциссы и ординаты:
16a — 4b + c = -3
Аналогичным образом записываем выражение, используя две остальные точки:
9a — 3b + c = -2
4a — 2b + c = 1
Получаем систему трех уравнений с тремя неизвестными. Решить достаточно легко. Простейший вариант: вычесть последнюю строчку из первых двух, избавившись от коэффициента “c”. После первое уравнение сокращаем на «2», вычитаем из него второе. Находим: a = 1. Подставляем далее, получаем:
b = 8;
c = 13.
Имея коэффициенты, переписываем уравнение, подставляем значение абсциссы:
f(x) = x2 + 8x + 13
f(-12) = 144 — 96 + 13 = 61
Второй вариант
Мы решили 9 задание по математике профилю наиболее простым способом. Однако вычисления получится сократить. Построим локальную систему координат около вершины параболы:
Видим особенность параболы: в точке «1» ордината равна 1, в точке «2» — 4. Представленный график отражает классическое выражение: y = x2, сдвинутое в системе координат. Известно: преобразования не меняют старший коэффициент. Делаем вывод, “a” равно “1”. Теперь найдем “b”. Используем выражение вершины параболы: x0 = -b / 2a. По рисунку видно: x0 = -4. Поставляя это число, найденное значение “a”, находим: b = 8. Дальнейшее решение требует одного уравнения из первого способа. Теперь выполнить номер проще.
Третий вариант
9 задание по математике профильного уровня реально упростить еще сильнее. Изучим способ образования данной параболы. Она получилась путем смещения исходной на “4” налево и на “3” вниз. Запишем уравнения. Изначальный пример:
y = x2
Сдвиг влево записывается:
y = (x + 4)2
Сдвиг вниз:
y = (x + 4)2 — 3
Получаем готовое уравнение, достаточно подставить “-12”. Ответ аналогичный: 61.
Четвертый вариант
Рассмотрим последний способ выполнения задания 9 по профильной математике 2022, требующий логического мышления. Снова изучим локальную систему координат:
Сравнивая с изначальной, получим: абсцисса «-12» из условия представляет собой значение «-8» локальной системы. Это связано со сдвигом. Ордината соответственно равна “64”. Не забываем: парабола сдвинута также на три пункта вниз. Получается, итоговое значение будет на 3 меньше найденного. Ответ снова 61!
В статье мы разобрали способы решения нового 9 задания из ЕГЭ по математике. Хотите изучить принципы выполнения остальных номеров? Записывайтесь на курсы «Уникум» Российского университета дружбы народов. Обучение проходит под руководством опытных преподавателей, форматы — очный, дистанционный. Для закрепления материала существует учебный портал Unikum.
Содержание данной статьи носит ознакомительный характер. При подготовке к сдаче ЕГЭ пользуйтесь дополнительными источниками информации!