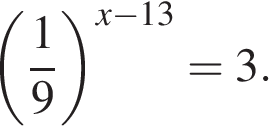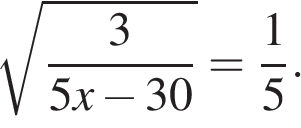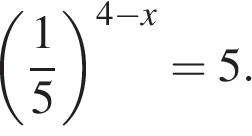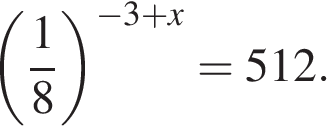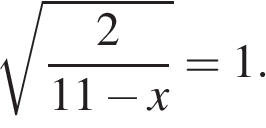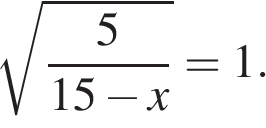Уравнения для подготовки к егэ по математике - Помощь в подготовке к экзаменам и поступлению

В задании №5 варианта ЕГЭ вам встретятся всевозможные уравнения: квадратные и сводящиеся к квадратным, дробно-рациональные, иррациональные, степенные, показательные и логарифмические и даже тригонометрические. Видите, как много нужно знать, чтобы справиться с заданием! И еще ловушки и «подводные камни», которые ждут вас в самом неожиданном месте.

Вот список тем, которые стоит повторить:

Квадратные уравнения

Арифметический квадратный корень

Корни и степени

Показательная функция

Показательные уравнения

Логарифмическая функция

Логарифмические уравнения

Тригонометрический круг

Формулы приведения

Формулы тригонометрии

Простейшие тригонометрические уравнения 1

Уравнения, сводящиеся к квадратным

1. Решите уравнение $frac{6}{13}x^2=19frac{1}{2}$ . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Кажется, что уравнение очень простое. Но иногда здесь ошибаются даже отличники. А вот шестиклассник бы не ошибся.

С левой частью уравнения все понятно. Дробь $frac{6}{13}$ умножается на x^2. А в правой части — смешанное число $19frac{1}{2}.$ Его целая часть равна 19, а дробная часть равна $frac{1}{2}.$ Запишем это число в виде неправильной дроби:

$19frac{1}{2}= frac{19cdot 2+1}{2} = frac{39}{2}.$

Получим:

$frac{6}{13}x^2=frac{39}{2};$

$x^2=frac{39cdot 13}{2cdot 6}=frac{13cdot 3cdot 13}{2cdot 6}=frac{{13}^2}{4};$

$x=pm frac{13}{2};$

или

Выбираем меньший корень.

Ответ: -6,5.

2. Решите уравнение

Возведем в квадрат левую часть уравнения. Получим:

Ответ: -6.

Дробно-рациональные уравнения

3. Найдите корень уравнения

Перенесем единицу в левую часть уравнения. Представим 1 как $frac{4x-5}{4x-5}$ и приведем дроби к общему знаменателю:

$frac{5x-3}{4x-5}-frac{4x-5}{4x-5}=0;$

$frac{x+2}{4x-5}=0;$

x= - 2.

Ответ: -2.

Это довольно простой тип уравнений. Главное — внимательность.

Иррациональные уравнения

Так называются уравнения, содержащие знак корня — квадратного, кубического или n-ной степени.

4. Решите уравнение:

$sqrt{frac{6}{4{x}-54} } =frac{1}{7}.$

Выражение под корнем должно быть неотрицательно, а знаменатель дроби не равен нулю.

Значит, .

Возведём обе части уравнения в квадрат:

$frac{6}{4{x}-{ 54}} =frac{1}{49}.$

Решим пропорцию:

Условие при этом выполняется.

Ответ: 87.

5. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

А в этом уравнении есть ловушка. Решите его самостоятельно и после этого читайте дальше.

Выражение под корнем должно быть неотрицательно. И сам корень — величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:

$left{begin{matrix} 72-x=x^2\72-xgeq 0 hfill \xgeq 0 hfill end{matrix}right.$ .

Решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов:

$sqrt{72-x}=x Leftrightarrow left{begin{matrix} 72-x=x^2\72-x geq 0 \x geq 0 end{matrix}right. Leftrightarrow$

Мы получили, что x=8 . Это единственный корень уравнения.

Типичная ошибка в решении этого уравнения такая. Учащиеся честно пишут ОДЗ, помня, что выражение под корнем должно быть неотрицательно:

Возводят обе части уравнения в квадрат. Получают квадратное уравнение: Находят его корни: x=8 или x=-9. Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.

Теперь вы знаете, в чем дело. Конечно же, число -9 корнем этого уравнения быть не может.

Ответ: 8.

6. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Запишем решение как цепочку равносильных переходов:

Ответ: 9.

Показательные уравнения

При решении показательных уравнений мы пользуемся свойством монотонности показательной функции.

7. Решите уравнение $5^{x-7}=frac{1}{125}.$

Вспомним, что $125 = 5{}^{3}.$ Уравнение приобретает вид: $5{}^{x}{}^{-}{}^{7 }= 5{}^{-}{}^{3}.$ Функция y = 5^x монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

откуда x = 4.

Ответ: 4.

8. Решите уравнение ${left(frac{1}{49}right)}^{x-8}=7.$

Представим ${left(frac{1}{49}right)}^{ }$ как $7^{-2};$

${left(7^{-2}right)}^{x-8}=7;$

$7^{-2x+16}=7.$

Функция y = 7^x монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

x=7,5.

Ответ: 7,5.

9. Решите уравнение $left(frac{1}{9} right)^{{ x}-13} =3.$

Представим ${textstylefrac{1}{9}}$ в виде степени с основанием 3 и воспользуемся тем, что $left({ a}^{{ m}} right)^{{ n}} ={ a}^{{ mn}}.$

$left(3^{-2} right)^{{ x}-{ 13}} =3;$
$3^{-2{ x}+{ 26}} =3^{1} ;$

Ответ: 12,5.

Логарифмические уравнения

Решая логарифмические уравнения, мы также пользуемся монотонностью логарифмической функции: каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, значит, равны и сами числа.

И конечно, помним про область допустимых значений логарифма:

Логарифмы определены только для положительных чисел.

Основание логарифма должно быть положительно и не равно единице.

10. Решите уравнение:

${{log}_5 left(4+xright)=2 }.$

Область допустимых значений: . Значит,

Представим 2 в правой части уравнения как ${{log}_5 25 }$ , чтобы слева и справа в уравнении были логарифмы по основанию 5.

${{log}_5 left(4+xright)={{log}_5 25 } }.$

Функция $y = {{log}_5 x }$ монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом

4+x=25;
x=21.

Ответ: 21.

11. Решите уравнение: ${{log}_8 left(x^2+xright)={{log}_8 left(x^2-4right) } }.$

Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:

Ответ: -4.

12. Решите уравнение: $2^{{{log}_4 left(4x+5right) }}=9.$

Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:

${{log}_4 b }=frac{{{log}_2 b }}{{{log}_2 4 }}=frac{{{log}_2 b }}{2}.$

Записываем решение как цепочку равносильных переходов.

Ответ: 19.

13. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

${{log}_{x-5} 49=2 }.$

В этом уравнении тоже есть ловушка. Мы помним, что основание логарифма должно быть положительно и не равно единице.

Получим систему:

$small left{begin{matrix} left ( x-5 right )^2=49\x-50 \x-5 neq 1 end{matrix}right..$

Первое уравнение мы получили просто из определения логарифма.

Квадратное уравнение имеет два корня: x=12 и x=-2.

Очевидно, корень x=-2 является посторонним, поскольку основание логарифма должно быть положительным. Значит, единственный корень уравнения: x=12.

Ответ: 12.

Тригонометрические уравнения (Часть 1 ЕГЭ по математике)

Тригонометрические уравнения? В первой части вариантов ЕГЭ? — Да. Причем это задание не проще, чем задача 13 из второй части варианта Профильного ЕГЭ.

14. Найдите корень уравнения: $cos frac{pi (x+1)}{4}=frac{sqrt{2}}{2}.$ В ответе запишите наибольший отрицательный корень.

Типичная ошибка — решать это уравнение в уме. Мы не будем так делать! Несмотря на то, что это задание включено в первую части варианта ЕГЭ, оно является полноценным тригонометрическим уравнением, причем с отбором решений.

Сделаем замену $frac{pi left(x+1right)}{4}=t.$ Получим: $cos t=frac{sqrt{2}}{2}.$

Получаем решения: $t=pm frac{pi }{4}+2pi n, nin Z.$ Вернемся к переменной x.

$frac{pi (x+1)}{4}=pm frac{pi }{4}+2pi n, nin Z.$ Поделим обе части уравнения на и умножим на 4.

$left[ begin{array}{c}x=8n, nin Z \x=-2+8n end{array}right..$

Первой серии принадлежат решения

Вторая серия включает решения

Наибольший отрицательный корень — тот из отрицательных, который ближе всех к нулю. Это x = -2.

Ответ: -2.

15. Решите уравнение: $tg frac{pi left( x+1right)}{4}= -1.$ В ответе напишите наименьший положительный корень.

Решение:

Сделаем замену $frac{pi left(x+1right)}{4}=t.$ Получим: tgt=-1. Решения этого уравнения:

$t=-frac{pi }{4}+pi n, nin Z.$ Вернемся к переменной х:

$frac{pi left(x+1right)}{4}=-frac{pi }{4}+pi n, n in Z.$ Умножим обе части уравнения на 4 и разделим на .

Выпишем несколько решений уравнения и выберем наименьший положительный корень:

Наименьший положительный корень x = 2.

Ответ: 2.

Мы разобрали основные типы уравнений, встречающихся в задании №5 Профильного ЕГЭ по математике. Конечно, это не все, и видов уравнений в этой задаче существует намного больше. Именно поэтому мы рекомендуем начинать подготовку к ЕГЭ по математике не с задания 1, а с текстовых задач на проценты, движение и работу и основ теории вероятностей.
Успеха вам в подготовке к ЕГЭ!

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание №5. Простейшие уравнения. Профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Каталог заданий.
Линейные, квадратные, кубические уравнения

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 5 № 26662

Найдите корень уравнения:

Аналоги к заданию № 26662: 10149 9653 9659 9667 9669 9673 9677 9679 9691 9693 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.2 Рациональные уравнения

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 5 № 26663

Найдите корень уравнения:

Аналоги к заданию № 26663: 9655 10135 9657 9661 9663 9665 9671 9675 9681 9683 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.2 Рациональные уравнения

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 5 № 77368

Решите уравнение

Аналоги к заданию № 77368: 100259 100757 509597 509988 510118 513336 513357 100261 100263 100265 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 1.4.2 Преобразования выражений, включающих операцию возведения в степень, 2.1.2 Рациональные уравнения

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 5 № 77369

Решите уравнение

Аналоги к заданию № 77369: 100759 100787 100761 100763 100765 100767 100769 100771 100773 100775 … Все

Решение

Курс Д. Д. Гущина

2 комментария · Сообщить об ошибке · Помощь

Тип 5 № 77371

Найдите корень уравнения Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Аналоги к заданию № 77371: 100881 101379 524042 624069 624103 100883 100885 100887 100889 100891 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.1 Квадратные уравнения, 2.1.2 Рациональные уравнения

Решение

Курс Д. Д. Гущина

3 комментария · Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Источник

Уравнения, часть $С$

Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением. Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа, — правой частью уравнения.

Схема решения сложных уравнений:

Перед решением уравнения надо для него записать область допустимых значений (ОДЗ).
Решить уравнение.
Выбрать из полученных корней уравнения то, которые удовлетворяют ОДЗ.

ОДЗ различных выражений (под выражением будем понимать буквенно — числовую запись):

1. Выражение, стоящее в знаменателе, не должно равняться нулю.

${f(x)}/{g(x)}; g(x)≠0$

2. Подкоренное выражение, должно быть не отрицательным.

$√{g(x)}; g(x) ≥ 0$.

3. Подкоренное выражение, стоящее в знаменателе, должно быть положительным.

${f(x)}/{√{g(x)}}; g(x) > 0$

4. У логарифма: подлогарифмическое выражение должно быть положительным; основание должно быть положительным; основание не может равняться единице.

$log_{f(x)}g(x)table{ g(x) > 0; f(x) > 0; f(x)≠1;$

Логарифмические уравнения

Логарифмическими уравнениями называют уравнения вида $log_{a}f(x)=log_{a}g(x)$, где $а$ – положительное число, отличное от $1$, и уравнения, сводящиеся к этому виду.

Для решения логарифмических уравнений необходимо знать свойства логарифмов: все свойства логарифмов мы будем рассматривать для $a > 0, a≠ 1, b> 0, c> 0, m$ – любое действительное число.

1. Для любых действительных чисел $m$ и $n$ справедливы равенства:

$log_{а}b^m=mlog_{a}b;$

$log_{a^m}b={1}/{m}log_{a}b.$

$log_{a^n}b^m={m}/{n}log_{a}b$

Пример:

$log_{3}3^{10}=10log_{3}3=10;$

$log_{5^3}7={1}/{3}log_{5}7;$

$log_{3^7}4^5={5}/{7}log_{3}4;$

2. Логарифм произведения равен сумме логарифмов по тому же основанию от каждого множителя.

$log_a(bc)=log_{a}b+log_{a}c$

3. Логарифм частного равен разности логарифмов от числителя и знаменателя по тему же основанию

$log_{a}{b}/{c}=log_{a}b-log_{a}c$

4. При умножении двух логарифмов можно поменять местами их основания

$log_{a}b∙log_{c}d=log_{c}b∙log_{a}d$, если $a, b, c$ и $d > 0, a≠1, b≠1.$

5. $c^(log_{a}b)=b^{log_{a}b}$, где $а, b, c > 0, a≠1$

6. Формула перехода к новому основанию

$log_{a}b={log_{c}b}/{log_{c}a}$

7. В частности, если необходимо поменять местами основание и подлогарифмическое выражение

$log_{a}b={1}/{log_{b}a}$

Можно выделить несколько основных видов логарифмических уравнений:

— Простейшие логарифмические уравнения: $log_{a}x=b$. Решение данного вида уравнений следует из определения логарифма, т.е. $x=a^b$ и $х > 0$

Пример:

$log_{2}x=3$

Представим обе части уравнения в виде логарифма по основанию $2$

$log_{2}x=log_{2}2^3$

Если логарифмы по одинаковому основанию равны, то подлогарифмические выражения тоже равны.

$x = 8$

Ответ: $х = 8$

— Уравнения вида: $log_{a}f(x)=log_{a}g(x)$. Т.к. основания одинаковые, то приравниваем подлогарифмические выражения и учитываем ОДЗ:

$table{ f(x)=g(x); f(x)>0; g(x) > 0, а > 0, а≠1;$

Пример:

$log_{3}(x^2-3x-5)=log_{3}(7-2x)$

Т.к. основания одинаковые, то приравниваем подлогарифмические выражения

$x^2-3x-5=7-2x$

Перенесем все слагаемые в левую часть уравнения и приводим подобные слагаемые

$x^2-x-12=0$

$x_1=4,x_2= -3$

Проверим найденные корни по условиям $table{ x^2-3x-5>0; 7-2x>0;$

При подстановке во второе неравенство корень $х=4$ не удовлетворяет условию, следовательно, он посторонний корень

Ответ: $х=-3$

Метод замены переменной.

В данном методе надо:

Записать ОДЗ уравнения.
По свойствам логарифмов добиться того, чтобы в уравнении получились одинаковые логарифмы.
Заменить $log_{a}f(x)$ на любую переменную.
Решить уравнение относительно новой переменной.
Вернутся в п.3, подставить вместо переменной значение и получить простейшее уравнение вида: $log_{a}x=b$
Решить простейшее уравнение.
После нахождения корней логарифмического уравнения необходимо поставить их в п.1 и проверить условие ОДЗ.

Пример:

Решите уравнение $log_{2}√x+2log_{√x}2-3=0$

Решение:

1. Запишем ОДЗ уравнения:

$table{ х>0,text»так как стоит под знаком корня и логарифма»; √х≠1→х≠1;$

2. Сделаем логарифмы по основанию $2$, для этого воспользуемся во втором слагаемом правилом перехода к новому основанию:

$log_{2}√x+{2}/{log_{2}√x}-3=0$

3. Далее сделаем замену переменной $log_{2}√x=t$

4. Получим дробно — рациональное уравнение относительно переменной t

$t+{2}/{t}-3=0$

Приведем все слагаемые к общему знаменателю $t$.

${t^2+2-3t}/{t}=0$

Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.

$t^2+2-3t=0$, $t≠0$

5. Решим полученное квадратное уравнение по теореме Виета:

$t^2-3t+2=0$

$t_1=1; t_2=2$

6. Вернемся в п.3, сделаем обратную замену и получим два простых логарифмических уравнения:

$log_{2}√x=1$, $log_{2}√x=2$

Прологарифмируем правые части уравнений

$log_{2}√x=log_{2}2$, $log_{2}√x=log_{2}4$

Приравняем подлогарифмические выражения

$√x=2$, $√x=4$

Чтобы избавиться от корня, возведем обе части уравнения в квадрат

$х_1=4$, $х_2= 16$

7. Подставим корни логарифмического уравнения в п.1 и проверим условие ОДЗ.

${table 4 >0; 4≠1;$

Первый корень удовлетворяет ОДЗ.

${table 16 >0; 16≠1;$ Второй корень тоже удовлетворяет ОДЗ.

Ответ: $4; 16$

Уравнения вида $log_{a^2}x+log_{a}x+c=0$. Такие уравнения решаются способом введения новой переменной и переходом к обычному квадратному уравнению. После того, как корни уравнения будут найдены, надо отобрать их с учетом ОДЗ.

Дробно рациональные уравнения

Если дробь равна нулю, то числитель равен нулю, а знаменатель не равен нулю.
Если хотя бы в одной части рационального уравнения содержится дробь, то уравнение называется дробно-рациональным.

Чтобы решить дробно рациональное уравнение, необходимо:

Найти значения переменной, при которых уравнение не имеет смысл (ОДЗ)
Найти общий знаменатель дробей, входящих в уравнение;
Умножить обе части уравнения на общий знаменатель;
Решить получившееся целое уравнение;
Исключить из его корней те, которые не удовлетворяют условию ОДЗ.

Если в уравнении участвуют две дроби и числители их равные выражения, то знаменатели можно приравнять друг к другу и решить полученное уравнение, не обращая внимание на числители. НО учитывая ОДЗ всего первоначального уравнения.

Показательные уравнения

Показательными называют такие уравнения, в которых неизвестное содержится в показателе степени.

$a^x=b$

При решении показательных уравнений используются свойства степеней, вспомним некоторые из них:

1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.

$a^n·a^m=a^{n+m}$

2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются

$a^n:a^m=a^{n-m}$

3. При возведении степени в степень основание остается прежним, а показатели перемножаются

$(a^n)^m=a^{n∙m}$

4. При возведении в степень произведения в эту степень возводится каждый множитель

$(a·b)^n=a^n·b^n$

5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель

$({a}/{b})^n={a^n}/{b^n}$

6. При возведении любого основания в нулевой показатель степени результат равен единице

$a^0=1$

7. Основание в любом отрицательном показателе степени можно представить в виде основания в таком же положительном показателе степени, изменив положение основания относительно черты дроби

$a^{-n}={1}/{a^n}$

${a^{-n}}/{b^{-k}}={b^k}/{a^n}$

8. Радикал (корень) можно представить в виде степени с дробным показателем

$√^n{a^k}=a^{{k}/{n}}$

Виды показательных уравнений:

1. Простые показательные уравнения:

а) Вида $a^{f(x)}=a^{g(x)}$, где $а >0, a≠1, x$ — неизвестное. Для решения таких уравнений воспользуемся свойством степеней: степени с одинаковым основанием ($а >0, a≠1$) равны только тогда, когда равны их показатели.

$f(x)=g(x)$

b) Уравнение вида $a^{f(x)}=b, b>0$

Для решения таких уравнений надо обе части прологарифмировать по основанию $a$, получается

$log_{a}a^{f(x)}=log_{a}b$

$f(x)=log_{a}b$

2. Метод уравнивания оснований.

3. Метод разложения на множители и замены переменной.

Для данного метода во всем уравнении по свойству степеней надо преобразовать степени к одному виду $a^{f(x)}$.
Сделать замену переменной $a^{f(x)}=t, t > 0$.
Получаем рациональное уравнение, которое необходимо решить путем разложения на множители выражения.
Делаем обратные замену с учетом того, что $t > 0$. Получаем простейшее показательное уравнение $a^{f(x)}=t$, решаем его и результат записываем в ответ.

Пример:

Решите уравнение $2^{3x}-7·2^{2x-1}+7·2^{x-1}-1=0$

Решение:

По свойству степеней преобразуем выражение так, чтобы получилась степень 2^x.

$(2^x)^3-{7·(2^x)^2}/{2}+{7·2^x}/{2-1}=0$

Сделаем замену переменной $2^x=t; t>0$

Получаем кубическое уравнение вида

$t^3-{7·t^2}/{2}+{7·t}/{2}-1=0$

Умножим все уравнение на $2$, чтобы избавиться от знаменателей

$2t^3-7·t^2+7·t-2=0$

Разложим левую часть уравнения методом группировки

$(2t^3-2)-(7·t^2-7·t)=0$

Вынесем из первой скобки общий множитель $2$, из второй $7t$

$2(t^3-1)-7t(t-1)=0$

Дополнительно в первой скобке видим формулу разность кубов

$2(t-1)(t^2+t+1)-7t(t-1)=0$

Далее скобку $(t-1)$ как общий множитель вынесем вперед

$(t-1)(2t^2+2t+2-7t)=0$

Произведение равно нулю, когда хотя бы один из множителей равен нулю

1) $(t-1)=0;$ 2) $2t^2+2t+2-7t=0$

Решим первое уравнение

$t_1=1$

Решим второе уравнение через дискриминант

$2t^2-5t+2=0$

$D=25-4·2·2=9=3^2$

$t_2={5-3}/{4}={1}/{2}$

$t_3={5+3}/{4}=2$

Получили три корня, далее делаем обратную замену и получаем три простых показательных уравнения

$2^x=1; 2^x={1}/{2}; 2^x=2$

$2^x=2^0; 2^x=2^{-1}; 2^x=2^1$

$х_1=0; х_2=-1; х_3=1$

Ответ: $-1; 0; 1$

4. Метод преобразования в квадратное уравнение

Имеем уравнение вида $А·a^{2f(x)}+В·a^{f(x)}+С=0$, где $А, В$ и $С$ — коэффициенты.
Делаем замену $a^{f(x)}=t, t > 0$.
Получается квадратное уравнение вида $A·t^2+B·t+С=0$. Решаем полученное уравнение.
Делаем обратную замену с учетом того, что $t > 0$. Получаем простейшее показательное уравнение $a^{f(x)}=t$, решаем его и результат записываем в ответ.

Способы разложения на множители:

Вынесение общего множителя за скобки.

Чтобы разложить многочлен на множители путем вынесения за скобки общего множителя надо:

Определить общий множитель.
Разделить на него данный многочлен.
Записать произведение общего множителя и полученного частного (заключив это частное в скобки).

Пример:

Разложить на множители многочлен: $10a^{3}b-8a^{2}b^2+2a$.

Общий множитель у данного многочлена $2а$, так как на $2$ и на «а» делятся все члены. Далее найдем частное от деления исходного многочлена на «2а», получаем:

$10a^{3}b-8a^{2}b^2+2а=2a({10a^{3}b}/{2a}-{8a^{2}b^2}/{2a}+{2a}/{2a})=2a(5a^{2}b-4ab^2+1)$

Это и есть конечный результат разложения на множители.

Применение формул сокращенного умножения

1. Квадрат суммы раскладывается на квадрат первого числа плюс удвоенное произведение первого числа на второе число и плюс квадрат второго числа.

$(a+b)^2=a^2+2ab+b^2$

2. Квадрат разности раскладывается на квадрат первого числа минус удвоенное произведение первого числа на второе и плюс квадрат второго числа.

$(a-b)^2=a^2-2ab+b^2$

3. Разность квадратов раскладывается на произведение разности чисел и их сумму.

$a^2-b^2=(a+b)(a-b)$

4. Куб суммы равен кубу первого числа плюс утроенное произведение квадрата первого на второе число плюс утроенное произведение первого на квадрат второго числа плюс куб второго числа.

$(a+b)^3=a^3+3a^2b+3ab^2+b^3$

5. Куб разности равен кубу первого числа минус утроенное произведение квадрата первого на второе число плюс утроенное произведение первого на квадрат второго числа и минус куб второго числа.

$(a-b)^3=a^3-3a^2b+3ab^2-b^3$

6. Сумма кубов равна произведению суммы чисел на неполный квадрат разности.

$a^3+b^3=(a+b)(a^2-ab+b^2)$

7. Разность кубов равна произведению разности чисел на неполный квадрат суммы.

$a^3-b^3=(a-b)(a^2+ab+b^2)$

Метод группировки

Методом группировки удобно пользоваться, когда на множители необходимо разложить многочлен с четным количеством слагаемых. В данном способе необходимо собрать слагаемые по группам и вынести из каждой группы общий множитель за скобку. У нескольких групп после вынесения в скобках должны получиться одинаковые выражения, далее эту скобку как общий множитель выносим вперед и умножаем на скобку полученного частного.

Пример:

Разложить многочлен на множители $2a^3-a^2+4a-2$

Решение:

Для разложения данного многочлена применим метод группировки слагаемых, для этого сгруппируем первые два и последние два слагаемых, при этом важно правильно поставить знак перед второй группировкой, мы поставим знак + и поэтому в скобках запишем слагаемые со своими знаками.

$2a^3-a^2+4a-2=(2a^3-a^2)+(4a-2)$

Далее из каждой группы вынесем общий множитель

$(2a^3-a^2)+(4a-2)=a^2(2a-1)+2(2a-1)$

После вынесения общих множителей получили пару одинаковых скобок. Теперь данную скобку выносим как общий множитель.

$a^2(2a-1)+2(2a-1)=(2a-1)(a^2+2)$

Произведение данных скобок — это конечный результат разложения на множители.

С помощью формулы квадратного трехчлена.

Если имеется квадратный трехчлен вида $ax^2+bx+c$, то его можно разложить по формуле

$ax^2+bx+c=a(x-x_1)(x-x_2)$, где $x_1$ и $x_2$ — корни квадратного трехчлена

Источник

Самостоятельная работа. Уравнения. База и профиль. 4 варианта

Скачать:

Предварительный просмотр:

Самостоятельная работа. Уравнения. База и профиль. 1 вариант	Самостоятельная работа. Уравнения. База и профиль. 2 вариант
Найдите корень уравнения: . Найдите корень уравнения Найдите корень уравнения: . Если уравнение имеет более одного корня, в ответе укажите больший из них. Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе запишите больший из корней. Найдите корень уравнения: Найдите корень уравнения . Решите уравнение: Решите уравнение . Найдите корень уравнения . Найдите корень уравнения . Решите уравнение . В ответе напишите наибольший отрицательный корень. Скейтбордист прыгает на стоящую на рельсах платформу, со скоростью м/с под острым углом к рельсам. От толчка платформа начинает ехать со скоростью (м/с), где кг – масса скейтбордиста со скейтом, а кг – масса платформы. Под каким максимальным углом (в градусах) нужно прыгать, чтобы разогнать платформу не менее чем до 0,25 м/с?	Найдите корень уравнения: . Решите уравнение . Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней. Найдите корень уравнения . Найдите корень уравнения: Если уравнение имеет более одного корня, укажите меньший из них. Найдите корень уравнения . Найдите корень уравнения Найдите корень уравнения . Решите уравнение . Найдите корень уравнения: В ответе запишите наибольший отрицательный корень. Груз массой 0,08 кг колеблется на пружине. Его скорость v меняется по закону где t — время с момента начала колебаний, T = 12 с — период колебаний, м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 1 секунду после начала колебаний. Ответ дайте в джоулях.
Самостоятельная работа. Уравнения. База и профиль. 3 вариант	Самостоятельная работа. Уравнения. База и профиль. 4 вариант
Решите уравнение . Найдите корень уравнения . Найдите корень уравнения: Найдите корень уравнения: Найдите корень уравнения . Решите уравнение Если уравнение имеет более одного корня, в ответе запишите меньший из корней. Найдите корень уравнения Найдите корень уравнения Решите уравнение . Решите уравнение . Если уравнение имеет более одного корня, в ответе укажите меньший из них. Найдите корни уравнения: В ответ запишите наибольший отрицательный корень. Груз массой 0,08 кг колеблется на пружине. Его скорость v меняюется по закону где — время с момента начала колебаний, T = 2 с — период колебаний, м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 1 секунду после начала колебаний. Ответ дайте в джоулях.	Решите уравнение . Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе запишите меньший из корней. Найдите корень уравнения Найдите корень уравнения Решите уравнение . Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней. Найдите корень уравнения Найдите корень уравнения Найдите корень уравнения Найдите корень уравнения Решите уравнение . В ответе напишите наибольший отрицательный корень. Плоский замкнутый контур площадью м находится в магнитном поле, индукция которого равномерно возрастает. При этом согласно закону электромагнитной индукции Фарадея в контуре появляется ЭДС индукции, значение которой, выраженное в вольтах, определяется формулой, где – острый угол между направлением магнитного поля и перпендикуляром к контуру, Тл/с – постоянная, – площадь замкнутого контура, находящегося в магнитном поле (в м). При каком минимальном угле (в градусах) ЭДС индукции не будет превышать В?

По теме: методические разработки, презентации и конспекты

Мне нравится

Источник

1.
Найдите ко рень урав не ния

2.
Найдите корень уравнения

3.
Решите урав не ние Если урав не ние имеет более од но го корня, в
от вет е ука жи те боль ший из них.

4.
Решите уравнение Если уравнение имеет более одного корня, в ответе
укажите больший из них.

5.
Найдите корень уравнения

6.
Найдите корень уравнения

7.
Найдите ко рень урав не ния .

8.
Найдите корень уравнения

9.
Решите урав не ние

Если урав не ние имеет более од но го корня, в от ве те ука
жи те больш ий из них.

10.
Решите урав не ние

Если урав не ние имеет более од но го корня, в от ве те ука
жи те больш ий из них.

11.
Решите
уравнение Если уравнение имеет более одного корня, в ответе укажите меньший из
них.

12.
Найдите корень уравнения

13.
Найдите корень уравнения

14.
Найдите корень уравнения

15.
Найдите корень уравнения

Если уравнение имеет более одного корня, в ответе укажите
меньший из них.

16.
Решите урав не ние Если урав не ние имеет более од но го корня, в
от ве те ука жи те боль ший из них.

17.
Решите урав не ние Если урав не ние имеет более од но го корня, в
от ве те ука жит е мень ший из них.

18.

Найдите корень уравнения: Если уравнение имеет более
одного корня, укажите меньший из них.

19.
Найдите ко рень урав не ния

20. Найдите корень уравнения

21.

Решите уравнение .

22.

Решите уравнение .

23.

Решите уравнение .

24.

Решите уравнение .

25.
Решите урав не ние Если урав не ние имеет более од но го корня, в от
ве те ука жи те мень‐ ший из них.

26.
Решите урав не ние Если урав не ние имеет более од но го корня, в
от ве те ука жи те мень‐ ший из них.

27.
Найдите корень уравнения

28.
Найдите корень уравнения

29.
Найдите ко рень урав не ния

30.
Найдите ко рень урав не ния

31.

Найдите корень уравнения

32.

Найдите корень уравнения

33.
Найдите корень уравнения

34.
Найдите корень уравнения

35.
Найдите корень уравнения

36.
Найдите корень уравнения

37.
Найдите корень уравнения

38.
Найдите ко рень урав не ния

39.
Найдите ко рень урав не ния

40.
Найдите ко рень урав не ния

41. Найдите ко рень урав не
ния 42. Найдите корень уравнения

43.
Найдите ко рень уравнения:

44.
Найдите ко рень урав не ния

45.
Найдите ко рень урав не ния 3^x^{− 5} = 81.

46.

Найдите корень уравнения:

47. Найдите корень
уравнения 48.

Найдите корень уравнения:

49.
Найдите корень уравнения

50.
Найдите корень уравнения

51.
Найдите корень уравнения

52. Найдите корень уравнения

53. Найдите ко рень урав не
ния

54. Найдите корень уравнения

55. Найдите корень уравнения

56.

Найдите корень уравнения

57.

Найдите корень уравнения

58.

Найдите корень уравнения

59.

Найдите корень уравнения .

60.

Найдите корень уравнения .

61.

Найдите корень уравнения

62.

Найдите корень уравнения

63.

Решите уравнение .

64.

Решите уравнение

65. Найдите корень
уравнения

66. Найдите корень уравнения

67.

Решите уравнение

68. Решите уравнение .

69.

Найдите корень уравнения

70.

Найдите корень уравнения

Источник

Вариант 1 5. Простейшие уравнения

1. Найдите корень уравнения

2. Найдите корень уравнения: Если уравнение имеет более одного корня, укажите меньший из них.

3. Найдите корень уравнения

4. Найдите корень уравнения:

5. Найдите корень уравнения:

6. Найдите корень уравнения

7. Решите уравнение В ответе напишите наибольший отрицательный корень.

8. Найдите корень уравнения

9. Найдите корень уравнения

10. Решите уравнение

Вариант 2 5. Простейшие уравнения

1. Найдите корень уравнения

2. Найдите корень уравнения:

3. Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.

4. Решите уравнение

5. Найдите корень уравнения

6. Решите уравнение

7. Решите уравнение

8. Найдите корень уравнения

9. Найдите корень уравнения

10. Решите уравнение

Вариант 3 5. Простейшие уравнения

1. Найдите корень уравнения Если уравнение имеет более одного корня, в ответе запишите больший из корней.

2. Найдите корень уравнения:

3. Решите уравнение В ответе напишите наибольший отрицательный корень.

4. Найдите корень уравнения

5. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите больший из корней.

6. Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.

7. Найдите корень уравнения:

8. Найдите корень уравнения

9. Найдите корень уравнения

10. Найдите корень уравнения:

Вариант 4 5. Простейшие уравнения

1. Найдите корень уравнения:

2. Найдите корень уравнения

3. Найдите корень уравнения

4. Найдите корень уравнения

5. Решите уравнение

6. Найдите корень уравнения 5^{2 +}^x = 125^x.

7. Решите уравнение В ответе напишите наименьший положительный корень.

8. Найдите корень уравнения:

9. Найдите корень уравнения

10. Найдите корень уравнения

Вариант 5 5. Простейшие уравнения

1. Найдите корень уравнения

2. Найдите корень уравнения

3. Найдите корень уравнения

4. Найдите корень уравнения

5. Найдите корни уравнения: В ответ запишите наибольший отрицательный корень.

6. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите больший из корней.

7. Найдите корень уравнения

8. Найдите корень уравнения

9. Найдите корень уравнения

10. Найдите корень уравнения

Вариант 6 5. Простейшие уравнения

1. Решите уравнение В ответе напишите наибольший отрицательный корень.

2. Решите уравнение

3. Найдите корень уравнения:

4. Решите уравнение (Повторяется с №77369)

5. Найдите корень уравнения

6. Найдите корень уравнения

7. Найдите корень уравнения

8. Найдите корень уравнения

9. Найдите корень уравнения:

10. Найдите корень уравнения:

Вариант 7 5. Простейшие уравнения

1. Найдите корень уравнения

2. Найдите корень уравнения

3. Найдите корень уравнения:

4. Найдите корень уравнения

5. Решите уравнение В ответе напишите наименьший положительный корень.

6. Найдите корень уравнения

7. Найдите корень уравнения: Если уравнение имеет более одного корня, в ответе укажите меньший из них.

8. Найдите корень уравнения

9. Найдите корень уравнения

10. Решите уравнение

Вариант 8 5. Простейшие уравнения

1. Найдите корень уравнения: Если уравнение имеет более одного корня, в ответе укажите меньший из них.

2. Найдите корень уравнения

3. Найдите корень уравнения:

4. Найдите корень уравнения

5. Решите уравнение

6. Решите уравнение В ответе напишите наибольший отрицательный корень.

7. Найдите корень уравнения

8. Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.

9. Найдите решение уравнения:

10. Найдите корень уравнения:

Вариант 9 5. Простейшие уравнения

1. Найдите корень уравнения

2. Найдите корень уравнения:

3. Решите уравнение В ответе напишите наибольший отрицательный корень.

4. Найдите корень уравнения

5. Найдите корень уравнения

6. Найдите корень уравнения

7. Найдите корень уравнения

8. Найдите корень уравнения

9. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите больший из корней.

10. Найдите корень уравнения

Вариант 10 5. Простейшие уравнения

1. Решите уравнение В ответе напишите наибольший отрицательный корень.

2. Найдите корень уравнения

3. Найдите корень уравнения:

4. Найдите корень уравнения

5. Найдите корень уравнения

6. Решите уравнение

7. Найдите корень уравнения

8. Найдите корень уравнения Если уравнение имеет более одного корня, в ответе запишите больший из корней.

9. Найдите корень уравнения

10. Найдите корень уравнения

5. Простейшие уравнения

Вариант 1

12,5
-9
21
-5
5
5
-1
-36
-36
1,4

Вариант 2

-0,2
0
-4
9
93
12
0
-12
3
10

Вариант 3

2
21
-2
-124
1
-0,25
-5
21
-12
0

Вариант 4

5
3
-4
-94
3
1
1
0,3
-4
5

Вариант 5

55
-0,5
2
8,75
-4
4,5
-124
-0,4
3
1

Вариант 6

-2
2
-1,25
-6
4
-4
122
-4
-5
-5

Вариант 7

1
6
0
35
1
-11
-3
5
8,75
1,5

Вариант 8

-3
8,75
13
5
10
-3
226
-0,5
0,5
-6

Вариант 9

3
3
-1
-4
21
-1
-4
-36
24
2

Вариант 10

-1
-0,4
14
6
3
-1
-4
2
-11
10

Источник