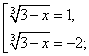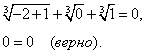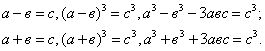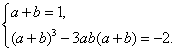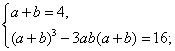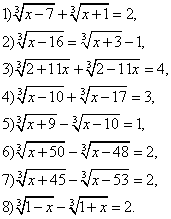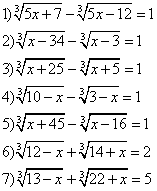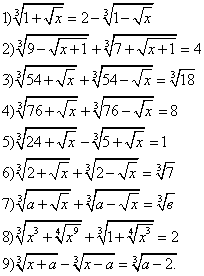Иррациональные уравнения с кубическими радикалами
Разделы: Математика
Тема: «Иррациональные уравнения вида 

(Методическая разработка.)
Основные понятия
Иррациональными уравнениями называются уравнения, в которых переменная содержится под знаком корня (радикала) или знаком возведения в дробную степень.
Уравнение вида f(x)=g(x), где хотя бы одно из выражений f(x) или g(x) иррационально является иррациональным уравнением.
Основные свойства радикалов:
- Все радикалы четной степени являются арифметическими, т.е. если подкоренное выражение отрицательно, то радикал не имеет смысла (не существует); если подкоренное выражение равно нулю, то радикал тоже равен нулю; если подкоренное выражение положительно, то значение радикала существует и положительно.
- Все радикалы нечетной степени определены при любом значении подкоренного выражения. При этом радикал отрицателен, если подкоренное выражение отрицательно; равен нулю, если подкоренное выражение равно нулю; положителен, если покоренное выражение положительно.
Методы решения иррациональных уравнений
Решить иррациональное уравнение – значит найти все действительные значения переменной, при подстановке которых в исходное уравнение оно обращается в верное числовое равенство, либо доказать, что таких значений не существует. Иррациональные уравнения решаются на множестве действительных чисел R.
Областью допустимых значений уравнения состоит из тех значений переменной, при которых неотрицательны все выражения, стоящие под знаком радикалов четной степени.
Основными методами решения иррациональных уравнений являются:
а) метод возведения обеих частей уравнения в одну и ту же степень;
б) метод введения новых переменных (метод замен);
в) искусственные приемы решения иррациональных уравнений.
В данной статье остановимся на рассмотрении уравнений определённого выше вида и приведём 6 методов решения таких уравнений.
1 метод. Возведение в куб.
Этот способ требует применения формул сокращённого умножения и не содержит «подводных» камней, т.е. не приводит к появлению посторонних корней.
Пример 1. Решить уравнение
Перепишем уравнение в виде 



Пример 2. Решить уравнение 
Перепишем уравнение в виде 



и рассмотрим полученное уравнение как квадратное относительно одного из корней


следовательно, дискриминант равен 0,а уравнение может иметь решение х=-2.
Проверка:
Замечание: Проверка может быть опущена, в том случае, если дорешивается квадратное уравнение.
2 метод. Возведение в куб по формуле.
По-прежнему будем возводить уравнение в куб, но при этом пользоваться модифицированными формулами сокращенного умножения.

(незначительная модификация известной формулы), тогда
Пример3. Решить уравнение 
Возведём уравнение в куб с использованием формул, приведённых выше.

Но выражение 


Теперь при возведении в куб получаем обычное квадратное уравнение:


Оба значения, как показывает проверка, правильные.
Но все ли преобразования здесь равносильны? Прежде чем ответить на этот вопрос, решим ещё одно уравнение.
Пример4. Решить уравнение 
Возводя, как и ранее, обе части в третью степень, имеем:

Откуда (учитывая, что выражение в скобках равно 




Ответ: 
Ответим на вопрос: «Почему возникли посторонние корни?»
Равенство 



Нетрудно проверить тождество

Итак, если 




Заменяя с на –с, получаем: если 

Поэтому при использовании этого метода решения обязательно нужно сделать проверку и убедиться что посторонних корней нет.
3 метод. Метод системы.
Пример 5. Решить уравнение 
Введём замену, составим и решим систему уравнений.
Пусть 


Второе уравнение системы получается таким образом, чтобы линейная комбинация подкоренных выражений не зависела от исходной переменной.

Ответ: Корней нет.
Пример 6. Решить уравнение 
Введём замену, составим и решим систему уравнений.
Пусть 


Возвращаясь к исходной переменной имеем:

4 метод. Использование монотонности функций.
Прежде чем использовать данный метод обратимся к теории.
Нам понадобятся следующие свойства:
- Если функции y=f(x) и y=g(x) возрастают (убывают) на некотором множестве, то функция y=f(x)+g(x) также возрастает (убывает ) на этом множестве.
- Если функции y=f(x) и y=g(x) возрастают (убывают) на некотором множестве, при чем обе они принимают неотрицательные значения при всех допустимых х, то функция y=f(x)g(x) возрастает (убывает) на данном множестве.
- Если функция y=f(x) монотонная, то уравнение f(x)=a имеет не более одного решения.
- Если функции y=f(x) и y=g(x) имеют разный характер монотонности, то уравнение f(x)=g(x) имеет не более одного решения.
- Функция вида
возрастает при к>0 и убывает при к 30.05.2009
Решение кубических уравнений
Кубическое уравнение, содержащее коэффициенты с действительным корнем, остальные два считаются комплексно-сопряженной парой. Будут рассмотрены уравнения с двучленами и возвратные, а также с поиском рациональных корней. Вся информация будет подкреплена примерами.
Решение двучленного кубического уравнения вида A x 3 + B = 0
Кубическое уравнение, содержащее двучлен, имеет вид A x 3 + B = 0 . Его необходимо приводить к x 3 + B A = 0 с помощью деления на А , отличного от нуля. После чего можно применять формулу сокращенного умножения суммы кубов. Получаем, что
x 3 + B A = 0 x + B A 3 x 2 — B A 3 x + B A 2 3 = 0
Результат первой скобки примет вид x = — B A 3 , а квадратный трехчлен — x 2 — B A 3 x + B A 2 3 , причем только с комплексными корнями.
Найти корни кубического уравнения 2 x 3 — 3 = 0 .
Решение
Необходимо найти х из уравнения. Запишем:
2 x 3 — 3 = 0 x 3 — 3 2 = 0
Необходимо применить формулу сокращенного умножения. Тогда получим, что
x 3 — 3 2 = 0 x — 3 3 2 6 x 2 + 3 3 2 6 x + 9 2 3 = 0
Раскроем первую скобку и получим x = 3 3 2 6 . Вторая скобка не имеет действительных корней, потому как дискриминант меньше нуля.
Ответ: x = 3 3 2 6 .
Решение возвратного кубического уравнения вида A x 3 + B x 2 + B x + A = 0
Вид квадратного уравнения — A x 3 + B x 2 + B x + A = 0 , где значения А и В являются коэффициентами. Необходимо произвести группировку. Получим, что
A x 3 + B x 2 + B x + A = A x 3 + 1 + B x 2 + x = = A x + 1 x 2 — x + 1 + B x x + 1 = x + 1 A x 2 + x B — A + A
Корень уравнения равен х = — 1 , тогда для получения корней квадратного трехчлена A x 2 + x B — A + A необходимо задействовать через нахождение дискриминанта.
Решить уравнение вида 5 x 3 — 8 x 2 — 8 x + 5 = 0 .
Решение
Уравнение является возвратным. Необходимо произвести группировку. Получим, что
5 x 3 — 8 x 2 — 8 x + 5 = 5 x 3 + 1 — 8 x 2 + x = = 5 x + 1 x 2 — x + 1 — 8 x x + 1 = x + 1 5 x 2 — 5 x + 5 — 8 x = = x + 1 5 x 2 — 13 x + 5 = 0
Если х = — 1 является корнем уравнения, тогда необходимо найти корни заданного трехчлена 5 x 2 — 13 x + 5 :
5 x 2 — 13 x + 5 = 0 D = ( — 13 ) 2 — 4 · 5 · 5 = 69 x 1 = 13 + 69 2 · 5 = 13 10 + 69 10 x 2 = 13 — 69 2 · 5 = 13 10 — 69 10
Ответ:
x 1 = 13 10 + 69 10 x 2 = 13 10 — 69 10 x 3 = — 1
Решение кубических уравнений с рациональными корнями
Если х = 0 , то он является корнем уравнения вида A x 3 + B x 2 + C x + D = 0 . При свободном члене D = 0 уравнение принимает вид A x 3 + B x 2 + C x = 0 . При вынесении х за скобки получим, что уравнение изменится. При решении через дискриминант или Виета оно примет вид x A x 2 + B x + C = 0 .
Найти корни заданного уравнения 3 x 3 + 4 x 2 + 2 x = 0 .
Решение
3 x 3 + 4 x 2 + 2 x = 0 x 3 x 2 + 4 x + 2 = 0
Х = 0 – это корень уравнения. Следует найти корни квадратного трехчлена вида 3 x 2 + 4 x + 2 . Для этого необходимо приравнять к нулю и продолжить решение при помощи дискриминанта. Получим, что
D = 4 2 — 4 · 3 · 2 = — 8 . Так как его значение отрицательное, то корней трехчлена нет.
Ответ: х = 0 .
Когда коэффициенты уравнения A x 3 + B x 2 + C x + D = 0 целые, то в ответе можно получить иррациональные корни. Если A ≠ 1 , тогда при умножении на A 2 обеих частей уравнения проводится замена переменных, то есть у = А х :
A x 3 + B x 2 + C x + D = 0 A 3 · x 3 + B · A 2 · x 2 + C · A · A · x + D · A 2 = 0 y = A · x ⇒ y 3 + B · y 2 + C · A · y + D · A 2
Приходим к виду кубического уравнения. Корни могут быть целыми или рациональными. Чтобы получить тождественное равенство, необходимо произвести подстановку делителей в полученное уравнение. Тогда полученный y 1 будет являться корнем. Значит и корнем исходного уравнения вида x 1 = y 1 A . Необходимо произвести деление многочлена A x 3 + B x 2 + C x + D на x — x 1 . Тогда сможем найти корни квадратного трехчлена.
Найти корни заданного уравнения 2 x 3 — 11 x 2 + 12 x + 9 = 0 .
Решение
Необходимо произвести преобразование с помощью умножения на 2 2 обеих частей, причем с заменой переменной типа у = 2 х . Получаем, что
2 x 3 — 11 x 2 + 12 x + 9 = 0 2 3 x 3 — 11 · 2 2 x 2 + 24 · 2 x + 36 = 0 y = 2 x ⇒ y 3 — 11 y 2 + 24 y + 36 = 0
Свободный член равняется 36 , тогда необходимо зафиксировать все его делители:
± 1 , ± 2 , ± 3 , ± 4 , ± 6 , ± 9 , ± 12 , ± 36
Необходимо произвести подстановку y 3 — 11 y 2 + 24 y + 36 = 0 , чтобы получить тождество вида
1 3 — 11 · 1 2 + 24 · 1 + 36 = 50 ≠ 0 ( — 1 ) 3 — 11 · ( — 1 ) 2 + 24 · ( — 1 ) + 36 = 0
Отсюда видим, что у = — 1 – это корень. Значит, x = y 2 = — 1 2 .
Далее следует деление 2 x 3 — 11 x 2 + 12 x + 9 на x + 1 2 при помощи схемы Горнера:
| x i | Коэффициенты многочлена | |||
|---|---|---|---|---|
| 2 | — 11 | 12 | 9 | |
| — 0 . 5 | 2 | — 11 + 2 · ( — 0 . 5 ) = — 12 | 12 — 12 · ( — 0 . 5 ) = 18 | 9 + 18 · ( — 0 . 5 ) = 0 |
2 x 3 — 11 x 2 + 12 x + 9 = x + 1 2 2 x 2 — 12 x + 18 = = 2 x + 1 2 x 2 — 6 x + 9
После чего необходимо найти корни квадратного уравнения вида x 2 — 6 x + 9 . Имеем, что уравнение следует привести к виду x 2 — 6 x + 9 = x — 3 2 , где х = 3 будет его корнем.
Ответ: x 1 = — 1 2 , x 2 , 3 = 3 .
Алгоритм можно применять для возвратных уравнений. Видно, что — 1 – это его корень, значит, левая часть может быть поделена на х + 1 . Только тогда можно будет найти корни квадратного трехчлена. При отсутствии рациональных корней применяются другие способы решения для разложения многочлена на множители.
Решение кубических уравнений по формуле Кардано
Нахождение кубических корней возможно при помощи формулы Кардано. При A 0 x 3 + A 1 x 2 + A 2 x + A 3 = 0 необходимо найти B 1 = A 1 A 0 , B 2 = A 2 A 0 , B 3 = A 3 A 0 .
После чего p = — B 1 2 3 + B 2 и q = 2 B 1 3 27 — B 1 B 2 3 + B 3 .
Полученные p и q в формулу Кардано. Получим, что
y = — q 2 + q 2 4 + p 3 27 3 + — q 2 — q 2 4 + p 3 27 3
Подбор кубических корней должен удовлетворять на выходе значению — p 3 . Тогда корни исходного уравнения x = y — B 1 3 . Рассмотрим решение предыдущего примера, используя формулу Кардано.
Найти корни заданного уравнения 2 x 3 — 11 x 2 + 12 x + 9 = 0 .
Решение
Видно, что A 0 = 2 , A 1 = — 11 , A 2 = 12 , A 3 = 9 .
Необходимо найти B 1 = A 1 A 0 = — 11 2 , B 2 = A 2 A 0 = 12 2 = 6 , B 3 = A 3 A 0 = 9 2 .
Отсюда следует, что
p = — B 1 2 3 + B 2 = — — 11 2 2 3 + 6 = — 121 12 + 6 = — 49 12 q = 2 B 1 3 27 — B 1 B 2 3 + B 3 = 2 · — 11 2 3 27 — — 11 2 · 6 3 + 9 2 = 343 108
Производим подстановку в формулу Кордано и получим
y = — q 2 + q 2 4 + p 3 27 3 + — q 2 — — q 2 4 + p 3 27 3 = = — 343 216 + 343 2 4 · 108 2 — 49 3 27 · 12 3 3 + — 343 216 — 343 2 4 · 108 2 — 49 3 27 · 12 3 3 = = — 343 216 3 + — 343 216 3
— 343 216 3 имеет три значения. Рассмотрим их ниже.
— 343 216 3 = 7 6 cos π + 2 π · k 3 + i · sin π + 2 π · k 3 , k = 0 , 1 , 2
Если k = 0 , тогда — 343 216 3 = 7 6 cos π 3 + i · sin π 3 = 7 6 1 2 + i · 3 2
Если k = 1 , тогда — 343 216 3 = 7 6 cosπ + i · sinπ = — 7 6
Если k = 2 , тогда — 343 216 3 = 7 6 cos 5 π 3 + i · sin 5 π 3 = 7 6 1 2 — i · 3 2
Необходимо произвести разбиение по парам, тогда получим — p 3 = 49 36 .
Тогда получим пары: 7 6 1 2 + i · 3 2 и 7 6 1 2 — i · 3 2 , — 7 6 и — 7 6 , 7 6 1 2 — i · 3 2 и 7 6 1 2 + i · 3 2 .
Преобразуем при помощи формулы Кордано:
y 1 = — 343 216 3 + — 343 216 3 = = 7 6 1 2 + i · 3 2 + 7 6 1 2 — i · 3 2 = 7 6 1 4 + 3 4 = 7 6 y 2 = — 343 216 3 + — 343 216 3 = — 7 6 + — 7 6 = — 14 6 y 3 = — 343 216 3 + — 343 216 3 = = 7 6 1 2 — i · 3 2 + 7 6 1 2 + i · 3 2 = 7 6 1 4 + 3 4 = 7 6
x 1 = y 1 — B 1 3 = 7 6 + 11 6 = 3 x 2 = y 2 — B 1 3 = — 14 6 + 11 6 = — 1 2 x 3 = y 3 — B 1 3 = 7 6 + 11 6 = 3
Ответ: x 1 = — 1 2 , x 2 , 3 = 3
При решении кубических уравнений можно встретить сведение к решению уравнений 4 степени методом Феррари.
Линейные, квадратные, кубические уравнения
Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением. Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа, — правой частью уравнения.
Линейные уравнения
Линейным называется такое уравнение, в котором неизвестное $x$ находится в числителе уравнения и без показателей. Например: $2х – 5 = 3$
Линейные уравнения сводятся к виду $ax = b$, которое получается при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей уравнения на число, отличное от нуля.
$5 (5 + 3х) — 10х = 8$
$25 + 15х — 10х = 8$
Перенесем неизвестные слагаемые в левую часть уравнения, а известные в правую. При переносе из одной части в другую, у слагаемого меняется знак на противоположный.
$15х — 10х = 8 — 25$
Приведем подобные слагаемые.
$5х = -17$ — это конечный результат преобразований.
После преобразований к виду $ax = b$, где, a=0, корень уравнения находим по формуле $х = /$
Квадратные уравнения
Квадратное уравнение — уравнение вида $ax^2 + bx + c = 0$, где $a, b, c$ — некоторые числа a$≠0$, $x$ — неизвестное. Перед тем как решать уравнение, необходимо раскрыть скобки и собрать все слагаемые в левой части уравнения.
Числа $a, b, c$ называются коэффициентами квадратного уравнения.
- $a$ — старший коэффициент;
- $b$ — средний коэффициент;
- $c$ — свободный член.
Если в квадратном уравнении коэффициенты $b$ и $c$ не равны нулю, то уравнение называется полным квадратным уравнением. Например, уравнение $2x^2 – 8x + 3 = 0$. Если один из коэффициентов $b$ или $c$ равен нулю или оба коэффициента равны нулю, то квадратное уравнение называется неполным. Например, $5x^2 – 2x = 0$.
Решение неполных квадратных уравнений
Неполное квадратное уравнение имеет вид $ax^2 + bx = 0$, если $a$≠0$; $c$=0$. В левой части этого уравнения есть общий множитель $x$.
1. Вынесем общий множитель $x$ за скобки.
Мы получим $x (ax + b) = 0$. Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому получаем $x = 0$ или $ax + b =0$. Таким образом, данное уравнение эквивалентно двум уравнениям:
2. Решаем получившиеся уравнения каждое отдельно.
Вынесем х как общий множитель за скобки:
Приравняем каждый множитель к нулю и найдем корни уравнения.
$x = 0$ или $4х — 5 = 0$
$х_1 = 0 х_2 = 1,25$
Ответ: $х_1 = 0; х_2 = 1,25$
Неполное квадратное уравнение вида $ax^2 + c = 0, a≠0, b=0$
Для решения данного неполного квадратного уравнения выразим $x^2$.
При решении последнего уравнения возможны два случая:
2. $D = 0$. В данном случае решение даёт два двукратных корня:
Извлечем кубический корень из обеих частей
Соберем известные слагаемые в правой части
Дробно рациональные уравнения
Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называется дробным.
Чтобы решить дробное уравнение, необходимо:
- найти общий знаменатель дробей, входящих в уравнение;
- умножить обе части уравнения на общий знаменатель;
- решить получившееся целое уравнение;
- исключить из его корней те, которые обращают в ноль общий знаменатель.
1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
2. находим общий знаменатель дробей и умножаем на него обе части уравнения
$4x · x + 1 · x — <3·x>/ = 0$
3. решаем полученное уравнение
Решим вторым устным способом, т.к. $а + с = b$
Тогда $х_1 = — 1, х_2 = <3>/<4>$
4. исключаем те корни, при которых общий знаменатель равен нулю В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $х_1 = — 1, х_2 = <3>/<4>$
При решении уравнения с двумя дробями можно использовать основное свойство пропорции.
Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
Воспользуемся основным свойством пропорции
Раскроем скобки и соберем все слагаемые в левой части уравнения
Решим данное квадратное уравнение первым устным способом, т.к.
В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
источники:
http://zaochnik.com/spravochnik/matematika/systems/reshenie-kubicheskih-uravnenij/
http://examer.ru/ege_po_matematike/teoriya/kvadratnye_uravneniya
5
.
02
Кубические уравнения
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
решение уравнений
5.01Линейные и квадратные уравнения
5.02Кубические уравнения
5.03Рациональные уравнения
5.04Иррациональные уравнения (со знаком корня)
5.05Показательные уравнения (с неизвестной в показателе степени)
5.06Логарифмические уравнения
5.07Тригонометрические уравнения
5.08Уравнения с модулем
5.09Задачи повышенного уровня сложности
Решаем задачи
Найдите корень уравнения
Показать ответ и решение
Представим правую часть в виду куба и извлечем кубический корень из обеих частей уравнения:
Решите уравнение. Если оно имеет более одного корня, в ответе запишите больший из них.
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
Исходное уравнение стандартного вида, оно эквивалентно уравнению
откуда заключаем,
что – подходит по ОДЗ.
Найдите корень уравнения. Если уравнение имеет более одного корня, в ответе запишите больший из них.
Показать ответ и решение
Найдем ОДЗ: — произвольное. Решим задачу на ОДЗ.
Исходное уравнение стандартного вида, оно эквивалентно уравнению
Отсюда заключаем, что
— подходит по ОДЗ.
Найдите корень уравнения. Если уравнение имеет более одного корня, в ответе запишите больший из них.
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
Исходное уравнение стандартного вида, оно эквивалентно уравнению
откуда
заключаем, что – подходит по ОДЗ.
Найдите корень уравнения. Если уравнение имеет более одного корня, в ответе запишите больший из них.
Показать ответ и решение
Найдем ОДЗ: — произвольное. Решим уравнение на ОДЗ.
Исходное уравнение стандартного вида, оно эквивалентно уравнению
Отсюда заключаем, что — подходит по ОДЗ.
Найдите корень уравнения. Если уравнение имеет более одного корня, в ответе запишите больший из них.
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
Исходное уравнение стандартного вида, оно эквивалентно уравнению
откуда
заключаем, что – подходит по ОДЗ.
Решите уравнение. В ответ запишите наибольший по модулю корень.
Показать ответ и решение
Разложим на множители левую часть:
Наибольший по модулю корень – это
Найдите корни уравнения. Если уравнение имеет несколько корней, в ответ запишите сумму тех из них, которые больше
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
Выражение в левой части можно разложить на множители:
Произведение нескольких выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и
все они не теряют смысл. Отсюда находим корни уравнения:
и
– подходят по ОДЗ. Все они
больше, чем Их сумма равна 1.
Найдите корни уравнения. Если уравнение имеет несколько корней, в ответ запишите больший из них.
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
Выражение в левой части можно разложить на множители:
Произведение нескольких выражений равно нулю в том и только том случае, когда хотя бы одно из
них равно нулю и все они не теряют смысл. Отсюда находим корень уравнения: – подходит по
ОДЗ.
Дискриминант уравнения отрицательный:
следовательно, других корней
нет.
Найдите корни уравнения. Если уравнение имеет несколько корней, в ответ запишите больший из них.
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
Выражение в левой части можно разложить на множители:
Произведение нескольких выражений равно нулю в том и только том случае, когда хотя бы одно из
них равно нулю и все они не теряют смысл. Отсюда находим корень уравнения: – подходит по
ОДЗ.
Дискриминант уравнения отрицательный:
следовательно, других корней
нет.
Решите уравнение. Если оно имеет несколько корней, в ответ запишите сумму тех из них, которые больше
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
Выражение в левой части можно разложить на множители:
Произведение нескольких выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и
все они не теряют смысл.
Отсюда находим корни уравнения:
и
– подходят по ОДЗ. Все они больше, чем
Их
сумма равна
Решите уравнение. Если уравнение имеет несколько корней, в ответ запишите больший из них.
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
Выражение в левой части можно разложить на множители:
Произведение нескольких выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и
все они не теряют смысл.
Отсюда находим корни уравнения:
и
– подходят по ОДЗ. Больший корень
Найдите целый корень уравнения
Показать ответ и решение
Перепишем уравнение в виде
и заметим, что сумма коэффициентов равна нулю: следовательно,
является корнем
уравнения. Значит, при разложении на множители левой части один из множителей должен быть Преобразуем
левую часть:
Следовательно, корнями уравнения будут и
Тогда целый корень – это
Решите уравнение. Если оно имеет несколько корней, в ответ запишите наибольший из них.
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
Можно угадать один из корней Знание этого корня позволяет вынести за скобку выражение
при
помощи деления столбиком:
Значит,
Произведение нескольких выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и
все они не теряют смысл. Отсюда находим корни исходного уравнения: и
– подходят по ОДЗ.
Наибольший из них
Решите уравнение. Если оно имеет несколько корней, в ответ запишите меньший из них.
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
Можно угадать один из корней Знание этого корня позволяет вынести за скобку выражение
при
помощи деления столбиком:
Значит,
Произведение нескольких выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и
все они не теряют смысл. Отсюда находим корни уравнения: и
– подходят по ОДЗ. Меньший из них
Найдите корни уравнения. Если уравнение имеет несколько корней, в ответ запишите произведение тех из них, которые
меньше 0.
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
Можно угадать один из корней Знание этого корня позволяет вынести за скобку выражение
при
помощи деления столбиком:
Тогда
Выражение можно разложить на множители, найдя корни уравнения
Корни
и
тогда окончательно
Произведение нескольких выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и
все они не теряют смысл. Отсюда находим корни исходного уравнения:
– подходят по ОДЗ. Произведение отрицательных корней равно
Найдите корни уравнения. Если уравнение имеет несколько корней, в ответ запишите сумму тех из них, которые больше
0.
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
Можно угадать один из корней Знание этого корня позволяет вынести за скобку выражение
при
помощи деления столбиком:
Значит,
Выражение можно разложить на множители, найдя корни уравнения
Корни
тогда окончательно
Произведение нескольких выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и
все они не теряют смысл. Отсюда находим корни исходного уравнения:
и
– подходят по ОДЗ.
Сумма больших 0 равна
Найдите корни уравнения. Если уравнение имеет несколько корней, в ответ запишите меньший из них.
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
Можно угадать один из корней Знание этого корня позволяет вынести за скобку выражение
при
помощи деления столбиком:
Значит,
Выражение можно разложить на множители, найдя корни уравнения
Корни
тогда окончательно
Произведение нескольких выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и
все они не теряют смысл. Отсюда находим корни исходного уравнения: и
– подходят по ОДЗ. Меньший
из них
Найдите корни уравнения. Если уравнение имеет несколько корней, в ответ запишите больший из них.
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
Можно угадать один из корней Знание этого корня позволяет вынести за скобку выражение
при помощи деления столбиком:
Значит,
Рассмотрим отдельно уравнение
Его дискриминант значит у рассматриваемого уравнения нет корней. Произведение
нескольких выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все
они не теряют смысл. Отсюда находим единственный корень исходного уравнения: – подходит по
ОДЗ.
Найдите корни уравнения. Если уравнение имеет несколько корней, в ответ запишите больший из них.
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
Можно угадать один из корней Знание этого корня позволяет вынести за скобку выражение
при
помощи деления столбиком:
Значит,
Второй множитель также можно разложить в произведение линейных. Для этого находим корни уравнения
Его корни
и
Теперь разложение принимает окончательный вид:
Произведение нескольких выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и
все они не теряют смысл. Отсюда находим корни исходного уравнения:
и
– подходят по ОДЗ.
Больший из них
Кубическое уравнение – уравнение вида [{large{ax^3+bx^2+cx+d=0}},]
где (ane 0, b, c, d) – некоторые числа.
Кубическое уравнение всегда имеет как минимум один корень (x_1).
Значит, всегда выполнено: (ax^3+bx^2+cx+d=a(x-x_1)(x^2+mx+n)), где (m, n) – некоторые числа.
({color{red}{I.}}) Кубические уравнения вида [x^3=a]
для любого числа (a) имеют единственный корень
[x=sqrt[3]a]
Пример.
Решением уравнения (x^3=-8) является (x=sqrt[3]{-8}=-2).
({color{red}{II.}}) Кубические уравнения вида (ax^3+bx^2+cx+d=0) в некоторых случаях можно решить, разложив на множители левую часть.
Пример.
Решить уравнение (5x^3-x^2-20x+4=0).
Сгруппируем слагаемые в левой части и разложим ее на множители: [(5x^3-20x)-(x^2-4)=0 quad Leftrightarrow quad 5x(x^2-4)-(x^2-4)=0 quad
Leftrightarrow quad (x^2-4)(5x-1)=0]
Тогда корнями данного уравнения являются (x_1=-2, x_2=2,
x_3=frac15).
В некоторых задачах полезными могут оказаться формулы сокращенного умножения:
[begin{aligned}
&(xpm y)^3=x^3pm3x^2y+3xy^2pm y^3\
&x^3pm y^3=(xpm y)(x^2mp xy+y^2) end{aligned}]
({color{red}{III.}}) Кубические уравнения вида (ax^3+bx^2+cx+d=0), в которых не удается разложить левую часть на множители, можно решить другим способом: подобрать рациональный корень, если таковой имеется.
Для этого можно использовать следующие утверждения:
(blacktriangleright) Если сумма (a+b+c+d=0), то корнем уравнения является число (1).
(blacktriangleright) Если (b+d=a+c), то корнем уравнения является число (-1).
(blacktriangleright) Пусть (a,b,c,d) – ({color{blue}{text{целые}}}) числа. Тогда если уравнение имеет рациональный корень (large{dfrac{p}{q}}), то для него будет выполнено:
(d) делится нацело на (p); (a) делится нацело на (q).
Пример.
1. У уравнения (7x^3+3x^2-x-9=0) сумма коэффициентов равна (7+3-1-9=0), значит, (x=1) является корнем (не обязательно единственным) этого уравнения.
2. У уравнения (4,5x^3-3x^2-0,5x+7=0) выполнено: (4,5-0,5=-3+7), значит, (x=-1) является корнем этого уравнения.
3. У уравнения (2x^3+5x^2+3x-3=0) коэффициенты — целые числа, поэтому можно подбирать корень: делители свободного члена (-3) : (pm 1, pm 3); делители старшего коэффициента (2): (pm1, pm2). Значит, возможные комбинации рациональных корней: [pm 1, pmdfrac12, pm 3, pm dfrac32]
Подставляя по очереди каждое число в уравнение, убеждаемся, что (x=frac12) является корнем (т.к. после подстановки этого числа в уравнение оно превращается в верное равенство):
[2cdot left(frac12right)^3+5cdot left(frac12right)^2+3cdot
frac12-3=0 quad Leftrightarrow quad 0=0]
Заметим, что если у уравнения коэффициенты — рациональные числа, то домножением уравнения на их общих знаменатель можно получить равносильное ему уравнение с целыми коэффициентами. Например, уравнение (frac12x^3+frac16x+2=0) после умножения на (6) сводится к уравнению с целыми коэффициентами: (3x^3+x+12=0).
Тема: «Иррациональные уравнения вида ,
.»
(Методическая разработка.)
Основные понятия
Иррациональными уравнениями называются уравнения, в которых переменная содержится под знаком корня (радикала) или знаком возведения в дробную степень.
Уравнение вида f(x)=g(x), где хотя бы одно из выражений f(x) или g(x) иррационально является иррациональным уравнением.
Основные свойства радикалов:
- Все радикалы четной степени являются арифметическими, т.е. если подкоренное выражение отрицательно, то радикал не имеет смысла (не существует); если подкоренное выражение равно нулю, то радикал тоже равен нулю; если подкоренное выражение положительно, то значение радикала существует и положительно.
- Все радикалы нечетной степени определены при любом значении подкоренного выражения. При этом радикал отрицателен, если подкоренное выражение отрицательно; равен нулю, если подкоренное выражение равно нулю; положителен, если покоренное выражение положительно.
Методы решения иррациональных уравнений
Решить иррациональное уравнение – значит найти все действительные значения переменной, при подстановке которых в исходное уравнение оно обращается в верное числовое равенство, либо доказать, что таких значений не существует. Иррациональные уравнения решаются на множестве действительных чисел R.
Областью допустимых значений уравнения состоит из тех значений переменной, при которых неотрицательны все выражения, стоящие под знаком радикалов четной степени.
Основными методами решения иррациональных уравнений являются:
а) метод возведения обеих частей уравнения в одну и ту же степень;
б) метод введения новых переменных (метод замен);
в) искусственные приемы решения иррациональных уравнений.
В данной статье остановимся на рассмотрении уравнений определённого выше вида и приведём 6 методов решения таких уравнений.
1 метод. Возведение в куб.
Этот способ требует применения формул сокращённого умножения и не содержит «подводных» камней, т.е. не приводит к появлению посторонних корней.
Пример 1. Решить уравнение
Решение:
Перепишем уравнение в виде и возведём в куб обе его части. Получим уравнение равносильное данному уравнению
,
,
,
Ответ: х=2, х=11.
Пример 2. Решить уравнение .
Решение:
Перепишем уравнение в виде и возведём в куб обе его части. Получим уравнение равносильное данному уравнению
,
,
,
и рассмотрим полученное уравнение как квадратное относительно одного из корней
,
,
следовательно, дискриминант равен 0,а уравнение может иметь решение х=-2.
Проверка:
Ответ: х=-2.
Замечание: Проверка может быть опущена, в том случае, если дорешивается квадратное уравнение.
2 метод. Возведение в куб по формуле.
По-прежнему будем возводить уравнение в куб, но при этом пользоваться модифицированными формулами сокращенного умножения.
Воспользуемся формулами:
,
(незначительная модификация известной формулы), тогда
Пример3. Решить уравнение .
Решение:
Возведём уравнение в куб с использованием формул, приведённых выше.
,
Но выражение должно быть равно правой части. Поэтому имеем:
, откуда
.
Теперь при возведении в куб получаем обычное квадратное уравнение:
, и два его корня
,
Оба значения, как показывает проверка, правильные.
Ответ: х=2,х=-33.
Но все ли преобразования здесь равносильны? Прежде чем ответить на этот вопрос, решим ещё одно уравнение.
Пример4. Решить уравнение .
Решение:
Возводя, как и ранее, обе части в третью степень, имеем:
.
Откуда (учитывая, что выражение в скобках равно ), получаем:
, значит
. Получаем
,
.Сделаем проверку и убедимся х=0 –посторонний корень.
Ответ: .
Ответим на вопрос: «Почему возникли посторонние корни?»
Равенство влечёт равенство
. Заменим с на –с, получим:
и
.
Нетрудно проверить тождество
,
Итак, если , то либо
, либо
. Уравнение можно представить в виде
,
.
Заменяя с на –с, получаем: если , то либо
, либо
Поэтому при использовании этого метода решения обязательно нужно сделать проверку и убедиться что посторонних корней нет.
3 метод. Метод системы.
Пример 5. Решить уравнение .
Решение:
Введём замену, составим и решим систему уравнений.
Пусть ,
. Тогда:
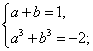
Второе уравнение системы получается таким образом, чтобы линейная комбинация подкоренных выражений не зависела от исходной переменной.
Легко убедиться , что система не имеет решения, следовательно и исходное уравнение не имеет решения.
Ответ: Корней нет.
Пример 6. Решить уравнение .
Решение:
Введём замену, составим и решим систему уравнений.
Пусть ,
. Тогда
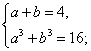
или
Возвращаясь к исходной переменной имеем:
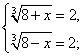
Ответ: х=0.
4 метод. Использование монотонности функций.
Прежде чем использовать данный метод обратимся к теории.
Нам понадобятся следующие свойства:
- Если функции y=f(x) и y=g(x) возрастают (убывают) на некотором множестве, то функция y=f(x)+g(x) также возрастает (убывает ) на этом множестве.
- Если функции y=f(x) и y=g(x) возрастают (убывают) на некотором множестве, при чем обе они принимают неотрицательные значения при всех допустимых х, то функция y=f(x)g(x) возрастает (убывает) на данном множестве.
- Если функция y=f(x) монотонная, то уравнение f(x)=a имеет не более одного решения.
- Если функции y=f(x) и y=g(x) имеют разный характер монотонности, то уравнение f(x)=g(x) имеет не более одного решения.
- Функция вида
возрастает при к>0 и убывает при к<0.
Пример 7. Решить уравнение .
Решение:
Левая часть уравнения возрастающая функция, а правая – число, т.е. константа, следовательно, уравнение имеет не более одного корня, который подберём: х=9. Проверкой убедимся, что корень подходит.
Ответ: х=9.
Пример 8. Решить уравнение .
Решение:
Левая часть уравнения возрастающая функция, а правая – число, т.е. константа, следовательно, уравнение имеет не более одного корня, который подберём: х=-2. Проверкой убедимся, что корень подходит.
Ответ: х=-2.
Последнее уравнение можно представить ином виде , тогда правая часть уравнения убывает, а левая возрастает, следовательно уравнение имеет не более одного корня , и приходим к х=-2.
5 метод. Графический метод решения уравнений.
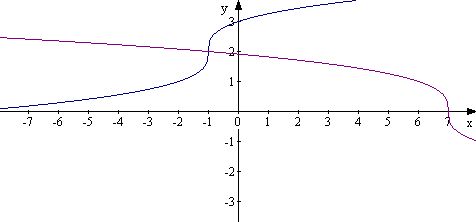
Пример 9. Решить уравнение
Решение:
Перепишем уравнение в виде: Построим графики левой и правой частей.
Рисунок 1
Графики пересекаются в точке (-1;2), х=-1.
Проверка:
2=2 (верно).
х=-1 – является корнем исходного уравнения.
Ответ: х=-1.
6 метод. Метод замены
Пример. Решить уравнение:
Решение:
Введём замену. Пусть тогда уравнение принимает вид
t=0 или — нет решений.
t=0, тогда возвращаясь к исходной переменной имеем: х=-8.
Ответ: х=-8.
Задания для самостоятельного решения.
|
№1. Решить уравнение |
№2. Каждое уравнение решите двумя способами. |
|
|
|
|
№3. Решите уравнение.
Литература:
- Глазков Ю.А. , Корешкова Т.А., Мирошин В.В. Шевелева Н.В. Математика. ЕГЭ.: методическое пособие для подготовки. – М.: Издательство «Экзамен», 2007.
- Моденов П.С. Пособие по математике, Ч.1, М:, 1977.
- Башмаков М.И. Беккер Б.М., Гольховой В.М. Сборник задач по алгебре и анализу, Библиотечка «Квант», М., 1983.
- Ципкин А.Г., Пинский А.И. Справочное пособие по методам решения задач по математике для средней школы. М., Наука, 1983.
Кубическим называют уравнение, в котором только одна переменная представлена в третьей степени. Такие выражения в любом случае имеют от одного до трех корней. Значения, которые получаются при решении таких уравнений, могут быть равными друг другу или комплексными, если их не более двух.
Решение кубических уравнений – это решение уравнений, имеющих вид: [boldsymbol{a y^{3}+b y^{2}+c y+d=0}].
В уравнении такого типа a не равно 0, вместо b,c,d могут быть любые однозначные числа.
Данный вид уравнения имеет как минимум один корень – y1.
Решение таких равнений может осуществляться разными способами. Оно может преобразовываться в стандартное квадратное уравнение. В таком случае предстоит выбрать один из трех вариантов решения квадратного уравнения:
- разложение на множители;
- применение формул для квадратных уравнений;
- метод дополнения.
Решение кубических уравнений может осуществляться посредством формулы Кардано, а также теоремы Виета. Теорема Виета применяется для решения последней, четвертой степени.
Решение кубических уравнений с двумя членами
Уравнение будет иметь вид: [boldsymbol{a y^{3}+b=0}]
Для решения необходимо преобразовать его: [y^{3}=b / a=0]
Деление на a предполагает вместо нее любую цифру, кроме 0. После преобразования можно применить формулы для решения кубических уравнений, например, сокращенного умножения суммы кубов:
y3=b/a=0
(y+3√b/a)(y2—3√b/a*y+3√(b/a)2)=0
В результате из первой скобки выводим:
y=-3√b/a
во второй скобке получаем выражение – трехчлен:
y2-3√b/a*y+3√(b/a)2
Методы решения кубических уравнений возвратного вида
Алгоритм решения кубического уравнения возвратного вида отличается от предыдущего, так как оно выглядит следующим образом:
[boldsymbol{a y^{3}+b y^{2}+b y+a=0}]
В этом уравнении переменные a и b – это коэффициенты.
Первым делом при решении таких уравнений в математике выполняется группировка:
ay3+by2+by+a=a(y3+1)+b(y2+y)=a(y+1)(y2-y+1)+by(y+1)=(y+1)(ay2+y(b-a)+a)
В полученном выражении корень равен y=-1. Исходя из этого, чтобы получить корень квадратного трехчлена ay2+y(b-a)+a, потребуется найти дискриминант.
Определение
Дискриминант – произведение квадратов разностей корней в различных вариаций.
Решение кубических уравнений в составе которых рациональные корни
Предположим, что y=0. В этом случае он будет корнем уравнения, которое выглядит следующим образом:
ay3+by2+cy+d=0
При условии, что в уравнении свободные члены, d=0. Преобразуем уравнение и получим:
ay3+by2+cy=0
Решение кубических уравнений такого вида предполагает вынесение y за скобку. В итоге получается уравнение вида:
y(ay2+by+c)=0
Рассмотрим на конкретном примере, как решить кубическое уравнение с подробным решением:
5y3+2y2+4y=0
Решение:
Первым делом стоит упростить уравнение.
5y3+2y2+4y=0
Получим уравнение вида:
y(5y2+2y+4)=0
y=0, так как является корнем выражения.
Следующий шаг – поиск корней квадратного трехчлена 5y2+2y+4, который мы получили после упрощения. Для поиска приравняем к нулю и будем использовать дискриминант.
В ходе решения кубического уравнения с дискриминантом получим:
D=22-2*5*4=-38
Так как в ответе мы получили отрицательное значение, корней у данного трехчлена нет, значит x=0.
Если в уравнениях вида ay3+by2+cy+d=0 коэффициентами являются целые числовые значения, то при решении таких уравнений и нахождении его значения мы может получить иррациональные корни.
В случае, когда a не равно 0, при умножении на a2 каждой составляющей уравнения происходит замещение переменных, и получается: x=ay
ay3+by2+cy+d=0
Каждую составляющую выражения умножаем на a2:
a3*y3+b*a2*y2+c*a*a*y+d*a2=0
Учитывая, что решение кубических уравнений с подробным решением предполагает замещение переменных x=ay, то:
x2+b*x2+c*a*x+d*a2
Полученное уравнение является кубическим. В таких уравнениях корни могут быть разными – и целыми, и рациональными. Чтобы привести такое уравнение к тождественному равенству, потребуется подставить делители в полученное равенство. В этом случае полученный x1 будет корнем, и в то же время корнем начального уравнения:
x1=y1/a
Чтобы найти значение корней квадратного трехчлена, потребуется многочлен ay3+by2+cy+d разделить на y-y1.
Рассмотрим решение кубических уравнений такого вида на примере.
Пример:
Решить уравнение [x 3-3 x 2-13 x+15=0].
Решение:
Ищем первый корень перебором чисел: [0, pm1, pm2, pm3, pm5, pm15] и подстановкой в уравнение. В результате находим, что 1 является корнем. Тогда делим левую часть этого уравнения на двухчлен x-1 и получаем:
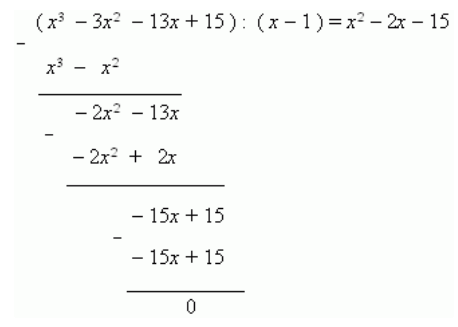
Теперь, решая квадратное уравнение: [x 2-2 x-15=0], находим оставшиеся два корня: x1=-3 и x2=5.
Ответ: 1; -3; 5.
Такой способ решения кубических уравнений используется для преобразования и решения возвратных уравнений. Из приведенного примера видно, что корнем является -1, значит, левую часть можно разделить на x+1. После того, как эти действия выполнены, можно находить корни квадратного трехчлена. Если рациональные корни отсутствуют, необходимо находить иные методы решения и разложения многочлена на множители.
Решение кубического уравнения с помощью формулы Кардано
Есть еще один способ — формула Кардано для решения кубических уравнений.
Если взять уравнение вида B0y3+B1y2+B2y+B3=0, то A1=B1/B0, A2=B2/B0, A3=B3/B0.
Z=-A21/3+A2
P=2A31/27-A1A2/3+A3.
Выведенные значение Z и P подставим в формулу Кардано.
X=3√-P/2+√P2/4+Z3/27+3√-P/2-+√P2/4+Z3/27
В итоге подбор кубических корней должен соответствовать значению –Z/3. В этом случае корни исходного уравнения будут выглядеть следующим образом:
y=x-A1/3
Применить формулу Кордано можно на примере для наглядности.
Пример
Решить уравнение [x^{3}+6 x^{2}+3 x-10=0]
Решение
Данное уравнение легко решается и без применения формулы Кардано. Легко подобрать корень [x=1]. Делением
[x=1] левой части уравнения по схеме Горнера получаем:
[begin{array}{r}+begin{array}{r}1&6&3&-10\0&1*1=1&7*1=7&10*1=10\end{array}
\hlinebegin{array}{r}1quadquadquad&7quadquadquad&10quadquadquadquad&0end{array}end{array}]
Следовательно, [x^{2}+7 x+10=0]. Решая это квадратное уравнение, получаем
[x=frac{-7 pm sqrt{7^{2}-4 * 1 * 10}}{2} Leftrightarrow x_{1}=-2, quad x_{2}=-5]
А теперь найдем корни исходного уравнения по формуле Кардано. Для данного уравнения [a=1, b=6, c=3, d=-10].
Замена переменной [x=y-frac{b}{3 a}=y-frac{6}{3}=y-2] приводит исходное уравнение к виду [y^{3}+p
y+q=0], где:
[p=frac{3 a c-b^{2}}{3 a^{2}}=frac{3 * 1 * 3-6^{2}}{3 * 1^{2}}=-9, quad q=\frac{2 b^{3}-9 a b c+27 a^{2}
d}{27 a^{3}}=frac{2 * 6^{3}-9 * 1 * 6 * 3+27 * 1^{2} *(-10)}{27 * 1^{3}}=0]
Вычислим дискриминант этого уравнения:
[Delta=left(frac{q}{2}right)^{2}+left(frac{p}{3}right)^{3}=left(frac{0}{2}right)^{2}+left(-frac{9}{3}right)^{3}=-27]
Так [Delta] каноническое уравнение имеет 3 действительных корня. Поскольку [q=0 Rightarrow
varphi=frac{pi}{2}=>]
[y_{1}=2 sqrt{-frac{p}{3}} * cos left(frac{varphi}{3}right)=2 sqrt{-frac{-9}{3}} * cos
left(frac{frac{pi}{2}}{3}right)=2 sqrt{3} * cos left(frac{pi}{6}right)=2 sqrt{3} *
frac{sqrt{3}}{2}=3,\y_{2}=2 sqrt{-frac{p}{3}} * cos left(frac{varphi}{3}+frac{2 pi}{3}right)=2
sqrt{3} * cos left(frac{frac{pi}{2}}{3}+frac{2 pi}{3}right)=2 sqrt{3} * cos left(frac{5
pi}{6}right)=-2 sqrt{3} * frac{sqrt{3}}{2}=-3,\y_{3}=2 sqrt{-frac{p}{3}} * cos
left(frac{varphi}{3}+frac{4 pi}{3}right)=2 sqrt{3} * cos left(frac{frac{pi}{2}}{3}+frac{4
pi}{3}right)=2 sqrt{3} * cos left(frac{3 pi}{2}right)=0.]
В данном случае для корней начального уравнения мы получим:
x1=y1-2=3-2=1;
x2=y2-2=-3-2=-5;
x3=y3-2=0-2=-2.
Получаем ответы: 1, -5, -2.
Нет времени решать самому?
Наши эксперты помогут!
Общее решение кубического уравнения, если известен один из корней
За исходное уравнение возьмем следующее:
y3+ay2+by+c=0
Предположим, что a,b,c являются действительными цифровыми значениями. Известный корень пометим, как y1. В таком случае, если произвести деление начального уравнения y3+ay2+by+c=0 на y-y1 получим квадратное уравнение. При решении такого уравнения удастся найти еще два корня – y2 и y3.
Чтобы доказать это, преобразуем кубический многочлен следующим образом:
y3+ay2+by+c=(y-y1)(y-y2)(y-y3)
При решении таких уравнений часто допускаются ошибки. Их решение – это сложное, многократное преобразование, которое требует точного знания формул и математических законов. Чтобы избежать ошибок и погрешностей, потребуется применить не только практические навыки, но и теоретические знания. Для решения кубических уравнений можно использовать специальный онлайн калькулятор. Принцип его действия основан на формуле Кардано. В том случае, если один или несколько коэффициентов такого уравнения равны нулю, или между ними присутствует определенная зависимость, решение будет более простым.
Чтобы научиться решать подобные уравнения, необходимо рассматривать примеры и тренироваться на их решении разными способами.
В задании №5 варианта ЕГЭ вам встретятся всевозможные уравнения: квадратные и сводящиеся к квадратным, дробно-рациональные, иррациональные, степенные, показательные и логарифмические и даже тригонометрические. Видите, как много нужно знать, чтобы справиться с заданием! И еще ловушки и «подводные камни», которые ждут вас в самом неожиданном месте.
Вот список тем, которые стоит повторить:
Квадратные уравнения
Арифметический квадратный корень
Корни и степени
Показательная функция
Показательные уравнения
Логарифмическая функция
Логарифмические уравнения
Тригонометрический круг
Формулы приведения
Формулы тригонометрии
Простейшие тригонометрические уравнения 1
Уравнения, сводящиеся к квадратным
1. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Кажется, что уравнение очень простое. Но иногда здесь ошибаются даже отличники. А вот шестиклассник бы не ошибся.
С левой частью уравнения все понятно. Дробь умножается на
А в правой части — смешанное число
Его целая часть равна 19, а дробная часть равна
Запишем это число в виде неправильной дроби:
Получим:
или
Выбираем меньший корень.
Ответ: -6,5.
2. Решите уравнение
Возведем в квадрат левую часть уравнения. Получим:
Ответ: -6.
Дробно-рациональные уравнения
3. Найдите корень уравнения
Перенесем единицу в левую часть уравнения. Представим 1 как и приведем дроби к общему знаменателю:
Ответ: -2.
Это довольно простой тип уравнений. Главное — внимательность.
Иррациональные уравнения
Так называются уравнения, содержащие знак корня — квадратного, кубического или n-ной степени.
4. Решите уравнение:
Выражение под корнем должно быть неотрицательно, а знаменатель дроби не равен нулю.
Значит, .
Возведём обе части уравнения в квадрат:
Решим пропорцию:
Условие при этом выполняется.
Ответ: 87.
5. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
А в этом уравнении есть ловушка. Решите его самостоятельно и после этого читайте дальше.
Выражение под корнем должно быть неотрицательно. И сам корень — величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:
.
Решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов:

Мы получили, что . Это единственный корень уравнения.
Типичная ошибка в решении этого уравнения такая. Учащиеся честно пишут ОДЗ, помня, что выражение под корнем должно быть неотрицательно:
Возводят обе части уравнения в квадрат. Получают квадратное уравнение: Находят его корни:
или
Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.
Теперь вы знаете, в чем дело. Конечно же, число -9 корнем этого уравнения быть не может.
Ответ: 8.
6. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
Запишем решение как цепочку равносильных переходов:

Ответ: 9.
Показательные уравнения
При решении показательных уравнений мы пользуемся свойством монотонности показательной функции.
7. Решите уравнение
Вспомним, что Уравнение приобретает вид:
Функция
монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.
откуда
Ответ: 4.
8. Решите уравнение
Представим как
Функция монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.
Ответ: 7,5.
9. Решите уравнение
Представим в виде степени с основанием 3 и воспользуемся тем, что
Ответ: 12,5.
Логарифмические уравнения
Решая логарифмические уравнения, мы также пользуемся монотонностью логарифмической функции: каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, значит, равны и сами числа.
И конечно, помним про область допустимых значений логарифма:
Логарифмы определены только для положительных чисел.
Основание логарифма должно быть положительно и не равно единице.
10. Решите уравнение:
Область допустимых значений: . Значит,
Представим 2 в правой части уравнения как , чтобы слева и справа в уравнении были логарифмы по основанию 5.
Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом
Ответ: 21.
11. Решите уравнение:
Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:

Ответ: -4.
12. Решите уравнение:
Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:
Записываем решение как цепочку равносильных переходов.
.
Ответ: 19.
13. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
В этом уравнении тоже есть ловушка. Мы помним, что основание логарифма должно быть положительно и не равно единице.
Получим систему:
Первое уравнение мы получили просто из определения логарифма.
Квадратное уравнение имеет два корня: и
Очевидно, корень является посторонним, поскольку основание логарифма должно быть положительным. Значит, единственный корень уравнения:
Ответ: 12.
Тригонометрические уравнения (Часть 1 ЕГЭ по математике)
Тригонометрические уравнения? В первой части вариантов ЕГЭ? — Да. Причем это задание не проще, чем задача 13 из второй части варианта Профильного ЕГЭ.
14. Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.
Типичная ошибка — решать это уравнение в уме. Мы не будем так делать! Несмотря на то, что это задание включено в первую части варианта ЕГЭ, оно является полноценным тригонометрическим уравнением, причем с отбором решений.
Сделаем замену Получим:
Получаем решения: Вернемся к переменной x.
Поделим обе части уравнения на
и умножим на 4.
Первой серии принадлежат решения
Вторая серия включает решения
Наибольший отрицательный корень — тот из отрицательных, который ближе всех к нулю. Это
Ответ: -2.
15. Решите уравнение: В ответе напишите наименьший положительный корень.
Решение:
Сделаем замену Получим:
Решения этого уравнения:
Вернемся к переменной х:
Умножим обе части уравнения на 4 и разделим на
.
Выпишем несколько решений уравнения и выберем наименьший положительный корень:
Наименьший положительный корень
Ответ: 2.
Мы разобрали основные типы уравнений, встречающихся в задании №5 Профильного ЕГЭ по математике. Конечно, это не все, и видов уравнений в этой задаче существует намного больше. Именно поэтому мы рекомендуем начинать подготовку к ЕГЭ по математике не с задания 1, а с текстовых задач на проценты, движение и работу и основ теории вероятностей.
Успеха вам в подготовке к ЕГЭ!
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание №5. Простейшие уравнения. Профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
Загрузить PDF
Загрузить PDF
В кубическом уравнении наивысшим показателем степени является 3, у такого уравнения 3 корня (решения) и оно имеет вид 
-
1
-
2
-
3
Разложите на множители (на произведение двух биномов) квадратное уравнение (если возможно). Многие квадратные уравнения вида
можно разложить на множители. Такое уравнение получится, если вынести
за скобки. В нашем примере:[4]
-
4
-
5
Используйте ноль и корни квадратного уравнения в качестве решений кубического уравнения. У квадратных уравнений два корня, а у кубических — три. Два решения вы уже нашли — это корни квадратного уравнения. Если же вы вынесли «х» за скобки, третьим решением будет
.[6]
Реклама
-
1
-
2
-
3
Разделите каждый множитель
на каждый множитель
. В итоге получится множество дробей и несколько целых чисел; корнями кубического уравнения будет одно из целых чисел или отрицательное значение одного из целых чисел.[9]
- В нашем примере разделите множители
(1 и 2) на множители
(1, 2, 3 и 6). Вы получите:
,
,
,
,
и
. Теперь в этот список добавьте отрицательные значения полученных дробей и чисел:
,
,
,
,
,
,
,
,
,
,
и
. Целыми корнями кубического уравнения являются какие-то числа из этого списка.
- В нашем примере разделите множители
-
4
Подставьте целые числа в кубическое уравнение. Если при этом равенство соблюдается, подставленное число является корнем уравнения. Например, подставьте в уравнение
:[10]
-
5
Реклама
-
1
-
2
Вычислите нулевой дискриминант по специальной формуле. Чтобы решить кубическое уравнение с помощью дискриминанта, нужно произвести ряд непростых вычислений, но если правильно выполнять все действия, этот метод станет незаменимым для решения наиболее сложных кубических уравнений. Сначала вычислите
(нулевой дискриминант) — это первая необходимая нам величина; для этого подставьте соответствующие значения в формулу
.[13]
-
3
Вычислите первый дискриминант по формуле
. Первый дискриминант
— это вторая важная величина; чтобы ее вычислить, подставьте соответствующие значения в указанную формулу.[14]
-
4
-
5
-
6
Реклама
Об этой статье
Эту страницу просматривали 398 639 раз.
















 возрастает при к>0 и убывает при к 30.05.2009
возрастает при к>0 и убывает при к 30.05.2009