Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Найдите все значения параметра k, при каждом из которых уравнение имеет хотя бы одно решение на интервале
2
Найдите все значения k, при каждом из которых уравнение
имеет хотя бы одно решение на отрезке
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2017. Вариант 4. (Часть C).
3
Определите, при каких значениях параметра a уравнение
имеет ровно два решения.
Источник: РЕШУ ЕГЭ — Предэкзаменационная работа 2014 по математике.
4
Найдите все значения параметра a, при каждом из которых уравнение
имеет корни, но ни один из них не принадлежит интервалу (4; 19).
5
Найдите все значения параметра a, при каждом из которых уравнение
имеет хотя бы один корень на отрезке [5; 23].
Пройти тестирование по этим заданиям
Задачи с параметрами на ЕГЭ по математике
Анна Малкова
Задача с параметрами – одна из самых сложных в ЕГЭ по математике Профильного уровня. Это задание №17.
И знать здесь действительно нужно много.
Лучше всего начать с темы «Элементарные функции и их графики».
Повторить, что такое функция, что такое четные и нечетные функции, периодические, взаимно обратные.
Научиться строить графики всех элементарных функций (и отличать по внешнему виду логарифм от корня квадратного, а экспоненту – от параболы).
Освоить преобразования графиков функций и приемы построения графиков.
И после этого – учимся решать сами задачи №17 Профильного ЕГЭ.
Вот основные типы задач с параметрами:
Что такое параметр? Простые задачи с параметрами
Базовые элементы для решения задач с параметрами
Графический способ решения задач с параметрами
Квадратичные уравнения и неравенства с параметрами
Использование четности функций в задачах с параметрами
Условия касания в задачах с параметрами
Метод оценки в задачах с параметрами
Вот пример решения и оформления задачи с параметром
Еще одна задача с параметром – повышенного уровня сложности. Автор задачи – Анна Малкова
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 1, задача 18
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 5, задача 18
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 11, задача 18
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 26, задача 18
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 18
И несколько полезных советов тем, кто решает задачи с параметрами:
1. Есть два универсальных правила для решения задач с параметрами. Помогают всегда. Хорошо, в 99% случаев помогают. То есть почти всегда.
— Если в задаче с параметром можно сделать замену переменной – сделайте замену переменной.
— Если задачу с параметром можно решить нарисовать – рисуйте. То есть применяйте графический метод.
2. Новость для тех, кто решил заниматься только алгеброй и обойтись без геометрии (мы уже рассказывали о том, почему это невозможно). Многие задачи с параметрами быстрее и проще решаются именно геометрическим способом.
Эксперты ЕГЭ очень не любят слова «Из рисунка видно…» Ваш рисунок – только иллюстрация к решению. Вам нужно объяснить, на что смотреть, и обосновать свои выводы. Примеры оформления – здесь. Эксперты ЕГЭ также не любят слова «очевидно, что…» (когда ничего не очевидно) и «ёжику ясно…».
3. Сколько надо решить задач, чтобы освоить тему «Параметры на ЕГЭ по математике»? – Хотя бы 50, и самых разных. И в результате, посмотрев на задачу с параметром, вы уже поймете, что с ней делать.
4. Задачи с параметрами похожи на конструктор. Разобрав много таких задач, вы заметите, как решение «собирается» из знакомых элементов. Сможете разглядеть уравнение окружности или отрезка. Переформулировать условие, чтобы сделать его проще.
На нашем Онлайн-курсе теме «Параметры» посвящено не менее 12 двухчасовых занятий. Кстати, оценивается задача 17 Профильного ЕГЭ в 4 первичных балла, которые отлично пересчитываются в тестовые!
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задачи с параметрами на ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи с параметром
Задание
1
#1220
Уровень задания: Легче ЕГЭ
Решите уравнение (ax+3=0) при всех значениях параметра (a).
Уравнение можно переписать в виде (ax=-3). Рассмотрим два случая:
1) (a=0). В этом случае левая часть равна (0), а правая – нет, следовательно, уравнение не имеет корней.
2) (ane 0). Тогда (x=-dfrac{3}{a}).
Ответ:
(a=0 Rightarrow xin varnothing; \
ane 0 Rightarrow
x=-dfrac{3}{a}).
Задание
2
#1221
Уровень задания: Легче ЕГЭ
Решите уравнение (ax+a^2=0) при всех значениях параметра (a).
Уравнение можно переписать в виде (ax=-a^2). Рассмотрим два случая:
1) (a=0). В этом случае левая и правая части равны (0), следовательно, уравнение верно при любых значениях переменной (x).
2) (ane 0). Тогда (x=-a).
Ответ:
(a=0 Rightarrow xin mathbb{R}; \
ane 0 Rightarrow x=-a).
Задание
3
#1222
Уровень задания: Легче ЕГЭ
Решите неравенство (2ax+5cosdfrac{pi}{3}geqslant 0) при всех значениях параметра (a).
Неравенство можно переписать в виде (axgeqslant -dfrac{5}{4}). Рассмотрим три случая:
1) (a=0). Тогда неравенство принимает вид (0geqslant
-dfrac{5}{4}), что верно при любых значениях переменной (x).
2) (a>0). Тогда при делении на (a) обеих частей неравенства знак неравенства не изменится, следовательно, (xgeqslant
-dfrac{5}{4a}).
3) (a<0). Тогда при делении на (a) обеих частей неравенства знак неравенства изменится, следовательно, (xleqslant -dfrac{5}{4a}).
Ответ:
(a=0 Rightarrow xin mathbb{R}; \
a>0 Rightarrow xgeqslant -dfrac{5}{4a}; \
a<0 Rightarrow xleqslant -dfrac{5}{4a}).
Задание
4
#1223
Уровень задания: Легче ЕГЭ
Решите неравенство (a(x^2-6) geqslant (2-3a^2)x) при всех значениях параметра (a).
Преобразуем неравенство к виду: (ax^2+(3a^2-2)x-6a geqslant 0). Рассмотрим два случая:
1) (a=0). В этом случае неравенство становится линейным и принимает вид: (-2x geqslant 0 Rightarrow xleqslant 0).
2) (ane 0). Тогда неравенство является квадратичным. Найдем дискриминант:
(D=9a^4-12a^2+4+24a^2=(3a^2+2)^2).
Т.к. (a^2 geqslant 0 Rightarrow D>0) при любых значениях параметра.
Следовательно, уравнение (ax^2+(3a^2-2)x-6a = 0) всегда имеет два корня (x_1=-3a, x_2=dfrac{2}{a}). Таким образом, неравенство примет вид:
[(ax-2)(x+3a) geqslant 0]
Если (a>0), то (x_1<x_2) и ветви параболы (y=(ax-2)(x+3a)) направлены вверх, значит, решением являются (xin (-infty; -3a]cup
big[dfrac{2}{a}; +infty)).
Если (a<0), то (x_1>x_2) и ветви параболы (y=(ax-2)(x+3a)) направлены вниз, значит, решением являются (xin big[dfrac{2}{a};
-3a]).
Ответ:
(a=0 Rightarrow xleqslant 0; \
a>0 Rightarrow xin (-infty; -3a]cup big[dfrac{2}{a}; +infty);
\
a<0 Rightarrow xin big[dfrac{2}{a}; -3abig]).
Задание
5
#1851
Уровень задания: Легче ЕГЭ
При каких (a) множество решений неравенства ((a^2-3a+2)x
-a+2geqslant 0) содержит полуинтервал ([2;3)) ?
Преобразуем неравенство: ((a-1)(a-2)x geqslant a-2). Получили линейное неравенство. Рассмотрим случаи:
1) (a=2). Тогда неравенство примет вид (0 geqslant 0), что верно при любых значениях (x), следовательно, множество решений содержит полуинтервал ([2;3)).
2) (a=1). Тогда неравенство примет вид (0 geqslant -1), что верно при любых значениях (x), следовательно, множество решений содержит полуинтервал ([2;3)).
3) ((a-1)(a-2)>0 Leftrightarrow ain (-infty;1)cup (2;+infty)). Тогда:
(xgeqslant dfrac{1}{a-1}). Для того, чтобы множество решений содержало полуинтервал ([2;3)), необходимо, чтобы
(dfrac{1}{a-1} leqslant 2 Leftrightarrow dfrac{3-2a}{a-1}
leqslant 0
Rightarrow ain (-infty; 1)cup [1,5; +infty)).
Учитывая условие (ain (-infty;1)cup (2;+infty)), получаем (ain
(-infty;1)cup (2;+infty)).
4) ((a-1)(a-2)<0 Leftrightarrow ain (1;2)). Тогда:
(xleqslant dfrac{1}{a-1} Rightarrow dfrac{1}{a-1} geqslant 3).
Действуя аналогично случаю 3), получаем (ain (1;
dfrac{4}{3}big]).
Ответ:
(ain (-infty;dfrac{4}{3}big]cup [2;+infty)).
Задание
6
#1361
Уровень задания: Легче ЕГЭ
Определить количество корней уравнения (ax^2+(3a+1)x+2=0) при всех значениях параметра (a).
Рассмотрим два случая:
1) (a=0). Тогда уравнение является линейным: (x+2=0 Rightarrow
x=-2). То есть уравнение имеет один корень.
2) (ane 0). Тогда уравнение является квадратным. Найдем дискриминант: (D=9a^2-2a+1).
Рассмотрим уравнение (9a^2-2a+1=0): (D’=4-36<0), следовательно, уравнение (9a^2-2a+1=0) не имеет корней. Значит, выражение ((9a^2-2a+1)) принимает значения строго одного знака: либо всегда положительно, либо отрицательно. В данном случае оно положительно при любых (a) (в этом можно убедиться, подставив вместо (a) любое число).
Таким образом, (D=9a^2-2a+1>0) при всех (ane 0). Значит, уравнение (ax^2+(3a+1)x+2=0) всегда имеет два корня: (x_{1,2}=dfrac{-3a-1pm
sqrt D}{2a})
Ответ:
(a=0Rightarrow) один корень
(ane 0 Rightarrow) два корня.
Задание
7
#1363
Уровень задания: Легче ЕГЭ
Решить уравнение (sqrt{x+2a}cdot (3-ax-x)=0) при всех значениях параметра (a).
Данное уравнение равносильно системе:
[begin{cases}
xgeqslant -2a\
left[ begin{gathered} begin{aligned}
&x=-2a \
&3-(a+1)x=0 qquad (*)
end{aligned} end{gathered} right.
end{cases}]
Рассмотрим два случая:
1) (a+1=0 Rightarrow a=-1). В этом случае уравнение ((*)) равносильно (3=0), то есть не имеет решений.
Тогда вся система равносильна (
begin{cases}
xgeqslant 2\
x=2
end{cases} Leftrightarrow x=2)
2) (a+1ne 0 Rightarrow ane -1). В этом случае система равносильна: [begin{cases}
xgeqslant -2a\
left[ begin{gathered} begin{aligned}
&x_1=-2a \
&x_2=dfrac3{a+1}
end{aligned} end{gathered} right.
end{cases}]
Данная система будет иметь одно решение, если (x_2leqslant -2a), и два решения, если (x_2>-2a):
2.1) (dfrac3{a+1}leqslant -2a Rightarrow a<-1 Rightarrow ) имеем один корень (x=-2a).
2.2) (dfrac3{a+1}>-2a Rightarrow a>-1 Rightarrow ) имеем два корня (x_1=-2a, x_2=dfrac3{a+1}).
Ответ:
(ain(-infty;-1) Rightarrow x=-2a\
a=-1 Rightarrow x=2\
ain(-1;+infty) Rightarrow xin{-2a;frac3{a+1}})

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
| 3644 | При каких значениях параметра a уравнение (a^2-6a+8)x^2+. (a^2-4)x+10-3a-a^2=0. имеет более двух корней |
При каких значениях параметра a уравнение (a2-6a+8)x2 +(a2-4)x + 10-3a-a2 =0 имеет более двух корней | |
| 3591 | Найдите все значения a при каждом из которых уравнение a(a+3)x^2+(2a+6)x-3a-9=0 имеет более одного корня |
Найдите все значения a при каждом из которых уравнение a(a+3)x2 +(2a+6)x -3a -9 =0 имеет более одного корня | |
| 3585 | Найдите все значения a при каждом из которых уравнение 2sqrt(x^4+(a-3)^4)=abs(x+a-3)+abs(x-a+3) имеет единственное решение |
Найдите все значения a при каждом из которых уравнение 2sqrt(x4 +(a-3)4) = abs(x+a-3) +abs(x-a+3) имеет единственное решение ! Тренировочная работа по математике №2 СтатГрад 11 класс 13.12.2022 Задание 17 Вариант МА2210209 #Задачи — аналоги 621 104 | |
| 3544 | Найдите все значения a, при которых система уравнений {(abs(y+x^3)-abs(y+3x)=2y+x^3+3x), (abs(-y-3x+1)-abs(y+x^3-a)=), (= -3y-6x-x^3+a+2) :} имеет единственное решение |
Найдите все значения a, при которых система уравнений {|y+x^3|-|y+3x| = 2y+x^3+3x), |-y-3x+1| -|y+x^3-a| =-3y-6x-x3+a+2 имеет единственное решение ! математика 50 вариантов ЕГЭ 2022 профильный уровень Ященко Вариант 6 Задание 17 |
|
| 3434 | Найдите все значения параметра a, b при которых неравенство a^3x^4+2ax^3+b <= 2bx^2+b^3x+a выполняется для всех x из отрезка [0; 1] |
Найдите все значения параметра a, b при которых неравенство выполняется для всех x из отрезка [0; 1] ! ДВИ в МГУ 2022 — 5 поток, Вариант 225 Задание 6 # Решение Натальи Яковлевны Захаровой youtube видео разбор | |
| 3405 | Найдите все значения a, при которых система уравнений {(abs(y+1/2x^3)-abs(y+3/2x)=2y+1/2x^3+3/2x), (abs(-y-3/2x+1)-abs(y+1/2x^3-a)=), (-4 y-9/2x-1/2x^3+a+3) :}. имеет единственное решение |
Найдите все значения a, при которых система уравнений { |y+1/2×3| -|y+3/2x| = 2y + 1/2×3 +3/2x |-y-3/2x+1| — |y+1/2×3 -a| = -4y -9/2x -1/2×3 +a +3 имеет единственное решение ! математика 50 вариантов ЕГЭ 2022 профильный уровень Ященко Вариант 8 Задание 17 # Ошибка в ответе пособия у Ященко ? : color{red}{a > -1 ?} |
|
| 3404 | Найдите все значения параметра a, при которых уравнение x^2+(1-a+root(4)(abs(x)))^2=a^2/4. имеет ровно три решения |
Найдите все значения параметра a, при которых уравнение x2 + (1-a+ корень 4 степени из |x|) 2 = a 2/4 имеет ровно три решения ! ДВИ в МГУ 2022 — 1 поток, Вариант 1 Задание 6 | |
| 3391 | Найдите все значения параметра a, при каждом из которых уравнение sqrt(15x^2+6ax+9)=x^2+ax+3 имеет три различных решения |
Найдите все значения параметра a, при каждом из которых уравнение корень из 15×2 +6ax+9 =x2 +ax+3 имеет три различных решения ! ЕГЭ 2022 по математике 27.06.2022 резервный день Задание 17 | |
| 3379 | Найдите все значения параметра a, при каждом из которых уравнение x^2+a^2+2x-4a=abs(4x+2a). имеет более двух различных корней |
Найдите все значения параметра a, при каждом из которых уравнение x2 +a2 +2x -4a = |4x+2a| имеет более двух различных корней ! ЕГЭ 2022 по математике 02.06.2022 основная волна Задание 17 Санкт-Петербург | |
| 3368 | Оценки экспертов решений задания 17 ЕГЭ по математике профильного уровня. Задание № 17 — это уравнение, неравенство или их системы с параметром. Задачи с параметром допускают весьма разнообразные способы решения. Наиболее распространёнными из них являются: – чисто алгебраический способ решения; – способ решения, основанный на построении и исследовании геометрической модели данной задачи; – функциональный способ, в котором могут быть и алгебраические, и геометрические элементы, но базовым является исследование некоторой функции. Зачастую (но далеко не всегда) графический метод более ясно ведёт к цели. Кроме того, в конкретном тексте решения вполне могут встречаться элементы каждого из трёх перечисленных способов |
Критерии оценивания решений задания 17 ЕГЭ по математике профильного уровня ! Примеры оценивания реальных работ 2016-2021 гг # Приведены типы заданий с развёрнутым ответом, используемые в КИМ ЕГЭ по математике и критерии оценки выполнения заданий с развёрнутым ответом, приводятся примеры оценивания выполнения заданий и даются комментарии, объясняющие выставленную оценку | |

Показана страница 1 из 55
ЕГЭ Профиль №17. Уравнения, неравенства и системы с параметрами
23 апреля 2017
В закладки
Обсудить
Жалоба
Параметры. От простого к сложному. Практикум по решению задач
Решение задач с параметрами является одним из самых трудных разделов школьной математики и требует большого количества времени на их изучение.
Теоретическое изучение физических процессов, решение экономических задач часто приводит к различным уравнениям или неравенствам, содержащим параметры, и необходимой частью их решения является исследование характера процесса в зависимости от значений параметров. Таким образом, задачи с параметрами представляют собой небольшие исследовательские задачи.
Автор: Агашкова Надежда Анатольевна.
pr-sl-p.pdf
Тема 17.
Задачи с параметром
17
.
01
Задачи из ЕГЭ прошлых лет
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
задачи с параметром
17.01Задачи из ЕГЭ прошлых лет
17.02Задачи из сборника И.В. Ященко ЕГЭ 2023
17.03Алгебра. Исследование при всех значениях параметра
17.04Алгебра. Связь между множествами решений
17.05Алгебра. Теорема Виета
17.06Алгебра. «Гвозди» для квадратичной функции
17.07Алгебра. Исследование замены
17.08Алгебра. Метод хорошего/плохого корня
17.09Алгебра. Задачи, решающиеся аналитически
17.10Функции. Монотонность: f(x) ∨ const и f(f(x)) = x
17.11Функции. Монотонность: f(t) = f(z)
17.12Функции. Монотонность: f(x) ∨ g(x), f(x)↑, g(x)↓
17.13Функции. Метод главного модуля/слагаемого
17.14Функции. Область значений функций
17.15Функции. Четность/нечетность функций
17.16Функции. Исследование функции на возрастание/убывание
17.17Функции. Сумма взаимно обратных
17.18Функции. Метод оценки
17.19Графика. Базовые задачи
17.20Графика. Нахождение касательной к графику
17.21Графика. Окружность
17.22Графика. Функции с модулем: корыто и другие
17.23Графика. Области
17.24Графика. Отрезок, ромб, квадрат и другие нестандартные графики
17.25Метод xOa (параметр как вторая неизвестная)
17.26Четность как частный случай симметрии
17.27Симметрия
17.28Три неизвестные x,y,z
17.29Задачи с несколькими параметрами
Решаем задачи
Найдите все значения параметра при каждом из которых уравнение
имеет больше 2 различных решений.
(ЕГЭ 2022, основная волна)
Показать ответ и решение
Рассмотрим данное уравнение в системе координат Будем рассматривать параметр
как переменную. Построим в
системе координат множество
решений данного уравнения. Если некоторая точка плоскости с координатами
принадлежит этому множеству то для исходной задачи это означает, что если параметр
принимает значение
то
будет одним из решений уравнения. Нас просят найти все такие значения параметра
при каждом из которых более двух
точек вида где
принадлежит множеству решений
изображенному на плоскости
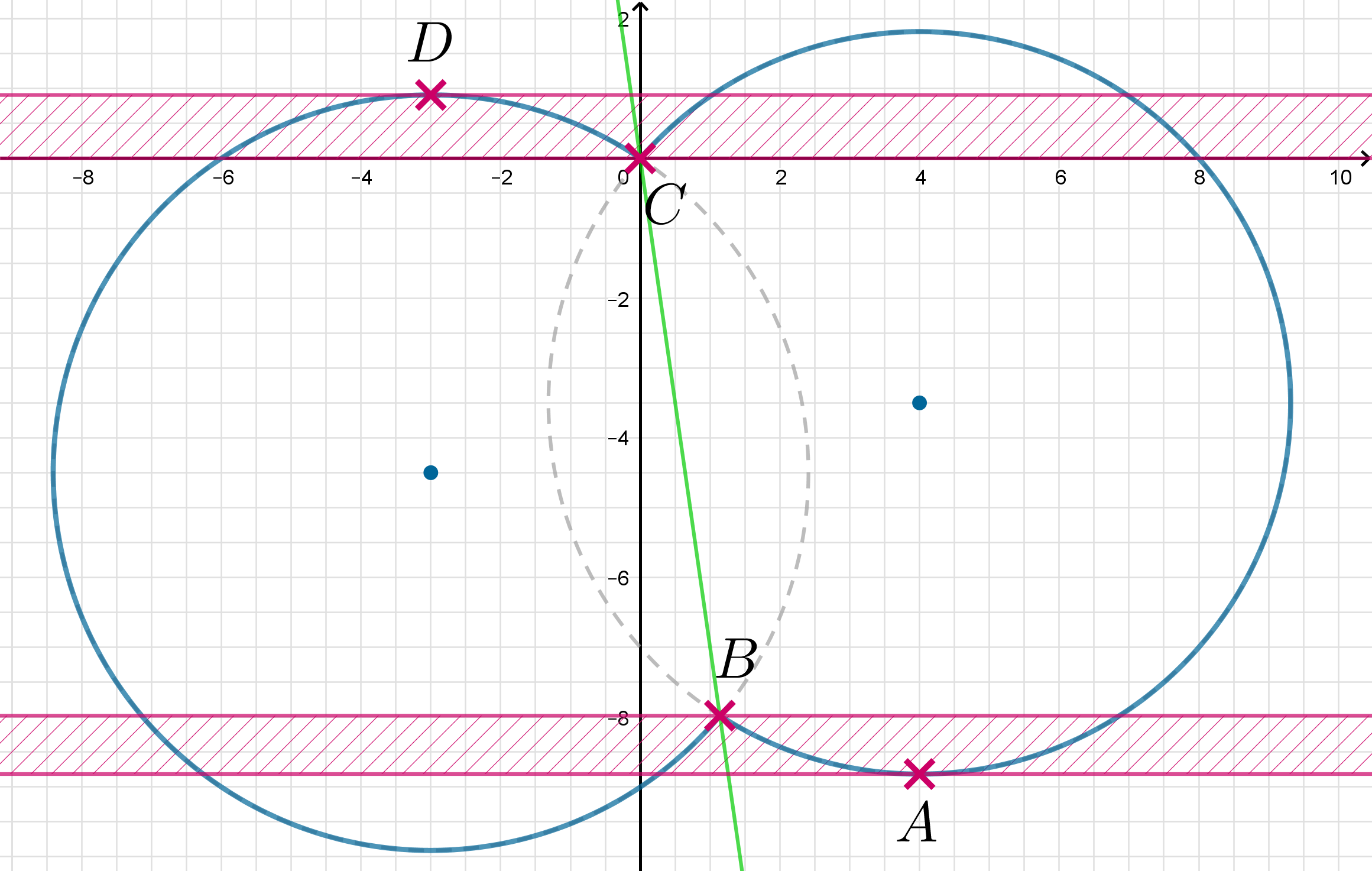
Фактически
это равносильно тому, что горизонтальная прямая имеет более двух точек пересечения с множеством
В области модуль раскроется положительно и уравнение примет вид
То есть мы получим часть окружности, находящуюся не ниже прямой
В области модуль раскроется отрицательно и мы получим
То есть мы получим часть окружности, находящуюся ниже прямой
Построим графики.
Заметим, что
- 1)
- самая высшая точка у правой окружности выше, чем у левой, так как
- 2)
- самая низшая точка у левой окружности ниже, чем у правой, так как
- 3)
- окружности пересекаются в двух точках
и
на прямой
Все горизонтальные прямые находящиеся в заштрихованной области, то есть между точками
и
и
имеют 3 или 4 точки пересечения с областью которая является объединением двух частей окружностей. Следовательно, все
эти значения параметров нам подходят.
Осталось найти ординаты точек
Ординаты точек можно найти из пересечения какой-то из окружностей с прямой
Следовательно, подходят значения параметра
Ответ:
Найдите все значения параметра при каждом из которых уравнение
имеет меньше 4 различных решений.
(ЕГЭ 2022, основная волна)
Показать ответ и решение
Данное уравнение равносильно совокупности
Полученная совокупность может иметь максимум 4 решения, следовательно, найдем те значения параметра, при которых она
имеет ровно 4 решения, тогда все другие значения параметра будут искомыми.
Чтобы совокупность имела 4 решения, каждая из систем должна иметь по два различных решения, следовательно, каждое
квадратное уравнение и
должно иметь два корня, удовлетворяющие условию
или
соответственно.
Во-первых, дискриминанты квадратных уравнений должны быть положительны:
Во-вторых, чтобы парабола пересекала ось абсцисс в двух точках
, абсцисса вершины параболы должна быть
положительна и значение функции в должно быть неотрицательно. Чтобы парабола
пересекала ось абсцисс в двух
точках меньше нуля, значение функции в должно быть положительно, а абсцисса вершины параболы должна быть
отрицательна. Таким образом, получаем:
Таким образом, 4 решения будет при . Следовательно, меньше 4 решений будет при
Ответ:
Найдите все значения параметра при каждом из которых уравнение
имеет ровно 2 различных корня.
(ЕГЭ 2022, основная волна)
Показать ответ и решение
Ответ:
Найдите все значения параметра при каждом из которых уравнение
имеет менее 4 различных решений.
(ЕГЭ 2022, основная волна)
Показать ответ и решение
Данное уравнение равносильно совокупности
Полученная совокупность может иметь максимум 4 решения, следовательно, найдем те значения параметра, при которых она
имеет 4 решения, тогда все другие значения параметра будут искомыми.
Чтобы совокупность имела 4 решения, каждая из систем должна иметь по два различных решения, следовательно, каждое
квадратное уравнение и
должно иметь два корня, удовлетворяющие условиям
или
соответственно.
Во-первых, дискриминанты квадратных уравнений должны быть положительны:
Во-вторых, чтобы парабола пересекала ось абсцисс в двух точках
абсцисса вершины параболы должна быть
положительна и значение функции в должно быть неотрицательно. Чтобы парабола
пересекала ось абсцисс в двух
точках значение функции в 0 должно быть положительно, а абсцисса вершины параболы должна быть отрицательна.
Таким образом, получаем:
Таким образом, 4 решения будет при Следовательно, меньше 4 решений будет при
Ответ:
Критерии оценки
|
Содержание критерия |
Балл |
|
Обоснованно получен верный ответ |
4 |
|
С помощью верного рассуждения |
3 |
|
С помощью верного рассуждения получен |
2 |
|
ИЛИ |
|
|
в решении верно найдены все граничные |
|
|
В случае аналитического решения: задача |
1 |
|
ИЛИ |
|
|
в случае графического решения: задача |
|
|
Решение не соответствует ни одному из |
0 |
|
Максимальный балл |
4 |
Найдите все значения параметра при каждом из которых уравнение
имеет ровно 4 различных решения.
(ЕГЭ 2022, основная волна)
Показать ответ и решение
Ответ:
Критерии оценки
|
Содержание критерия |
Балл |
|
Обоснованно получен верный ответ |
4 |
|
С помощью |
3 |
|
В решении верно найдены все |
2 |
|
ИЛИ |
|
|
получен неверный ответ |
|
|
Задача верно сведена к исследованию |
1 |
|
Решение не соответствует ни одному из |
0 |
|
Максимальный балл |
4 |
Найдите все значения параметра при каждом из которых уравнение
имеет ровно два различных решения.
(ЕГЭ 2022, основная волна)
Показать ответ и решение
Будем рассматривать параметр как переменную. Построим в системе координат
множество
решений
системы. Если некоторая точка плоскости с координатами принадлежит этому множеству
то для
исходной задачи это означает, что если параметр принимает значение
то
будет одним из решений
системы. Нас просят найти все такие значения параметра
при каждом из которых ровно две из точек вида
где
принадлежат множеству решений
изображенному на плоскости
Фактически
это равносильно тому, что горизонтальная прямая имеет ровно две точки пересечения с множеством
Построим на плоскости множество решений данного уравнения.
Раскроем знак модуля в двух случаях.
Случай 1.
В график полученного уравнения — окружность. С учетом
получаем дугу окружности не выше прямой
Найдем пересечение прямой
с окружностью с помощью подстановки:
Тогда прямая пересекает окружность
в точках
и
Случай 2.
Аналогично получаем дугу окружности не ниже прямой Подстановкой убедимся, что прямая
пересекает
вторую окружность в тех же точках.
Построим графики.
- При
прямая
не пересекает графики.
- При
прямая
касается левой окружности, так как точка
— центр левой окружности,
а— ее радиус.
- При
прямая
пересекает дугу левой окружности в двух точках. Значит, имеем 2
точки пересечения. - При
прямая
пересекает дугу левой окружности в двух точках и касается правой, то есть
имеем 3 точки пересечения. - При
прямая
пересекает дугу левой окружности в двух точках и дугу правой окружности
в двух точках, то есть имеем 4 точки пересечения. - При
прямая
пересекает дугу левой окружности в двух точках и дугу правой окружности в двух
точках, но две из этих точек совпадают, то есть имеем 3 точки пересечения. - При
прямая
пересекает дугу левой окружности в одной точке и дугу правой окружности в
одной точке, то есть имеем 2 точки пересечения. - При
прямая
пересекает дугу левой окружности в двух точках и дугу правой окружности в двух
точках, но две из этих точек совпадают, то есть имеем 3 точки пересечения. - При
прямая
пересекает дугу правой окружности в двух точках и дугу левой окружности
в двух точках, то есть имеем 4 точки пересечения. - При
прямая
пересекает дугу правой окружности в двух точках и касается левой, то есть
имеем 3 точки пересечения. - При
прямая
пересекает дугу правой окружности в двух точках. Значит, имеем 2
точки пересечения. - При
прямая
касается правой окружности, так как точка
— центр правой окружности,
а— ее радиус.
- При
прямая
не пересекает графики.
Значит, исходное уравнение имеет ровно два различных решения при
Ответ:
Критерии оценки
|
Содержание критерия |
Балл |
|
Обоснованно получен верный ответ |
4 |
|
С помощью верного рассуждения |
3 |
|
С помощью верного рассуждения получен |
2 |
|
ИЛИ |
|
|
в решении верно найдены все граничные |
|
|
В случае аналитического решения: задача |
1 |
|
ИЛИ |
|
|
в случае графического решения: задача |
|
|
Решение не соответствует ни одному из |
0 |
|
Максимальный балл |
4 |
Найдите все значения параметра , при каждом из которых система
имеет три решения.
(ЕГЭ 2022, досрочная волна)
Показать ответ и решение
Запишем систему, равносильную данной:
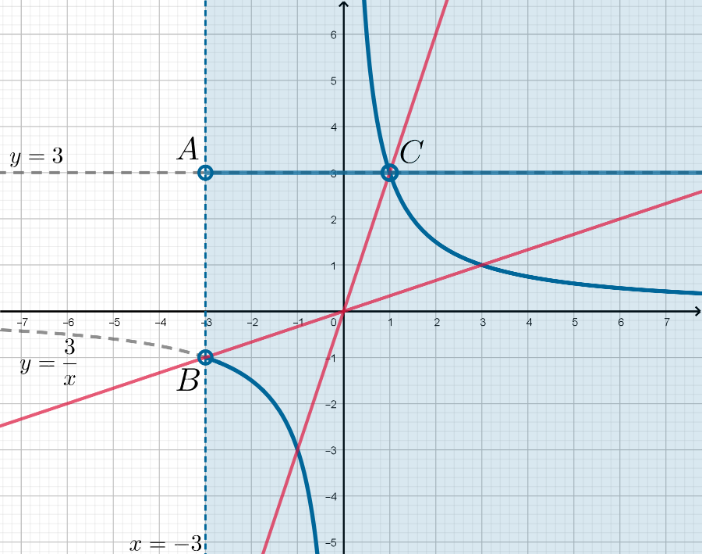
Графиком первого уравнения является объединение двух графиков: горизонтальной прямой и гиперболы
Заметим, что в уравнении можно разделить обе части на
так как
не является решением этого
уравнения.
Графиком второго уравнения при каждом фиксированном является прямая, проходящая через начало координат
При этом прямая может быть любой, кроме вертикальной, так как вертикальная прямая задается уравнением
Неравенство задает область соответствующую правой полуплоскости, образованной прямой
не включая
границу. Следовательно, нам необходимо найти такие положения прямой при которых она имеет ровно три точки
пересечения с графиком первого уравнения в области
При всех прямая
расположена во второй и четвертой четвертях, следовательно, с графиком первого уравнения
имеет не более одной точки пересечения.
При имеем:
Найдем значения параметра, при которых прямая проходит через точки
Точка — точка пересечения гиперболы с прямой
следовательно,
значит,
Точка — точка пересечения прямой
и гиперболы, следовательно,
откуда
следовательно,
Найдем соответствующие значения параметра:
Следовательно, исходная система имеет три решения при
Ответ:
Найдите все значения параметра при каждом из которых уравнение
имеет ровно 3 различных решения.
(ЕГЭ 2022, резервная волна)
Показать ответ и решение
Исходное уравнение равносильно системе
Рассмотрим уравнение последней системы:
Дискриминант выражения в скобках равен
Следовательно, нулями выражения в скобках являются
Таким образом, получаем:
Чтобы данная система имела три различных решения, необходимо:
Отсюда
Ответ:
Найдите все значения при каждом из которых уравнение
имеет ровно два различных корня.
(ЕГЭ 2021, основная волна)
Показать ответ и решение
Преобразуем условие к виду
Рассмотрим случаи раскрытия модулей, чтобы привести функцию к кусочно заданному виду:
Раскроем модули в зависимости от принадлежности к одному из трех промежутков:
- 1.
-
- 2.
-
- 3.
-
Резюмируя, получим
Найдем координаты точек излома функции
Мы получили, что на первом промежутке функция линейная убывающая, на третьем — линейная возрастающая. На втором
промежутке функция также линейная. Более того, коэффициент при
зависит от параметра
поэтому заранее мы не
знаем, убывает или возрастает наша функция на втором промежутке.
Рассмотрим три возможных случая.
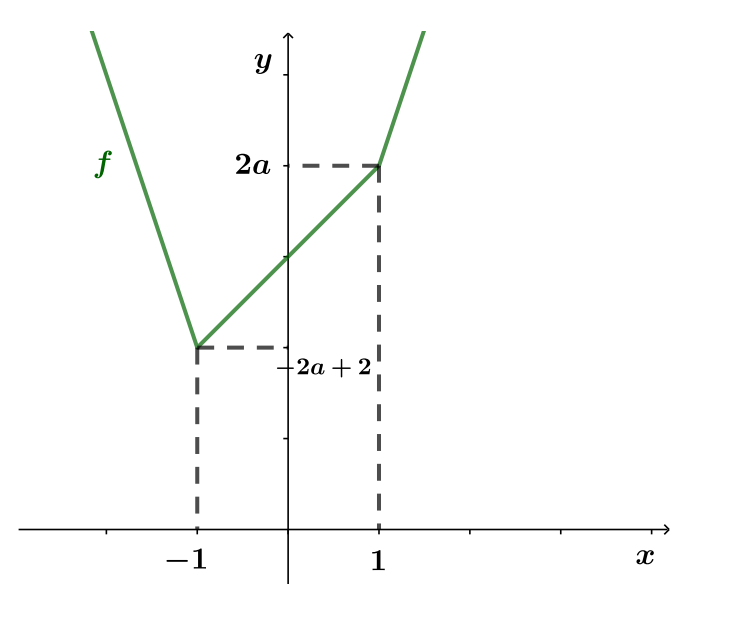
-
Функция возрастает на отрезке
то есть
В этом случае график примет следующий вид
(оси изображены для удобства, мы не знаем, как график будет располагаться относительно них и не пользуемся этим):В этом случае уравнение будет иметь ровно два различных решения, если горизонтальная прямая
проходит выше
левой точки излома графика, то естьПересекая с условием
получаем
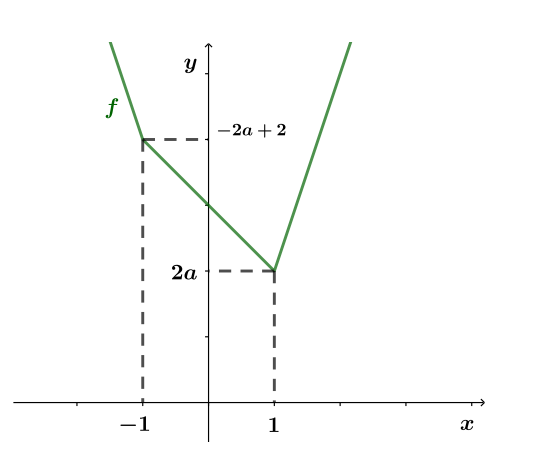
-
Функция убывает на отрезке
то есть
В этом случае график примет следующий вид (оси
изображены для удобства, мы не знаем, как график будет располагаться относительно них и не пользуемся этим):В этом случае уравнение будет иметь ровно два различных решения, если горизонтальная прямая
проходит выше
правой точки излома графика, то естьПересекая с условием
получаем
-
Коэффициент при
зануляется, то есть
Подставив это значение параметра в уравнение,
получимЛевая часть этого уравнения неотрицательна, так как является суммой двух модулей, а правая отрицательна. Значит, при
таком значенииуравнение не имеет решений, и это значение
нам не подходит.
Объединив найденные значения получим
Ответ:
Найти все значения параметра при каждом из которых уравнение
имеет ровно два решения.
(ЕГЭ 2021, основная волна)
Показать ответ и решение
Ответ:
Определите, при каких значениях параметра уравнение
имеет два различных решения.
(ЕГЭ 2021, основная волна)
Показать ответ и решение
1способ.
Перепишем уравнение в виде
Найдем дискриминант квадратного уравнения:
Рассмотрим несколько случаев.
- 1)
Тогда квадратное уравнение имеет единственный корень
Следовательно, для
того, чтобы вся совокупность, а значит и исходное уравнение, имела два решения, нужно, чтобыудовлетворял
условию(то есть
) и чтобы
(они равны при
). Оба этих условия выполняются
приследовательно, это значение параметра — первая часть ответа.
- 2)
и
(то есть
удовлетворяет условию
). Тогда квадратное уравнение
имеет два корня. Следовательно, чтобы исходное уравнение имело два корня, нужно, чтобы один из
исовпадал с
Это значит, что
— корень квадратного уравнения
то есть
Оба эти значения параметра удовлетворяют условиям
и
следовательно, они — вторая часть ответа.
- 3)
и
Тогда квадратное уравнение имеет два корня, а
не является решением
исходного уравнения, так как не удовлетворяет условиюПолучили третью часть ответа.
Следовательно, ответ:
2 способ.
Преобразуем уравнение:
Посмотрим, при каких значения параметра каждое из уравнений совокупности имеет решение.
Тогда поймем, какое количество решений имеет исходное уравнение в зависимости от значения параметра
Найдем такие значения параметра при которых какие-то два корни совпадают. Для этого рассмотрим все три пары
корней.
Все три полученных значения параметра принадлежат отрезку
— отрезку, на котором исходное уравнение имеет три
необязательно различных корня. При этих значениях параметра ровно два корня из трех совпадают, значит, при
исходное уравнение имеет ровно два различных корня.
На промежутке никакие корни не совпадают, поэтому исходное уравнение имеет два различных решения при
При исходное уравнение имеет ровно один корень.
Значит, исходное уравнение имеет ровно два различных корня при
Ответ:
Найдите все значения при каждом из которых уравнение
имеет ровно один корень.
(ЕГЭ 2021, основная волна)
Показать ответ и решение
- При
и первая, и вторая системы совокупности имеют решения, значит, весь этот промежуток нам не
подходит. - При
имеется бесконечное число решений, следовательно, такое
нам тоже не подходит.
- При
только вторая система имеет решение, причем ровно одно, такие
нам подходят.
- При
обе системы имеют по одному решению, такие
нам не подходят.
- При
только первая система имеет решение, причем ровно одно, такое
нам подходит.
Резюмируя, получаем ответ
Ответ:
Критерии оценки
|
Содержание критерия |
Балл |
|
Обоснованно получен верный ответ |
4 |
|
С |
3 |
|
С |
2 |
|
Верно получена хотя бы одна граничная |
1 |
|
Решение не соответствует ни одному из |
0 |
|
Максимальный балл |
4 |
При каких значениях параметра уравнение
имеет ровно три различных решения?
(ЕГЭ 2021, основная волна)
Показать ответ и решение
Ответ:
Критерии оценки
|
Содержание критерия |
Балл |
|
Обоснованно получен верный ответ |
4 |
|
Все значения параметра найдены верно, но |
3 |
|
Верно обосновано, когда уравнение будет |
2 |
|
ИЛИ |
|
|
рассмотрены не все ситуации, но при |
|
|
В ходе верных преобразований найдены |
1 |
|
Решение не соответствует ни одному из |
0 |
|
Максимальный балл |
4 |
Найдите все значения параметра при каждом из которых уравнение
имеет ровно два различных решения.
(ЕГЭ 2021, основная волна)
Показать ответ и решение
Перепишем уравнение в следующем виде
Введем обозначения:
Сразу ясно, что график функции — это «уголок» модуля ветвями вниз с вершиной в точке
Чтобы построить график функции сначала представим ее в кусочно-заданном виде, раскрыв модули. При
оба
модуля раскрываются с минусом, при первый раскрывается с плюсом, второй — с минусом, при
— оба с
плюсом:
Получили, что график функции — это ломаная, крайние звенья которой горизонтальны. Построим график функции
и
графики функции при различных
чтобы понять, как они себя ведут.
Заметим, что координата по правого излома ломаной совпадает с координатой по
вершины уголка — точки
Нам нужно, чтобы ломаная имела пересечения с уголком, тогда есть два ключевых для нас положения ломаной.
По полученной картинке видим следующее:
- При
ломаная не будет иметь пересечений уголком, такие
нам гарантированно не подходят.
- В положениях
и
пересечение будет ровно одно, они там тоже не подойдут.
- При
левый излом ломаной будет лежать ниже левой ветви уголка. Тогда левое звено ломаной будет иметь
ровно одно пересечение с левой ветвью уголка, среднее звено ломаной также будет иметь ровно одно пересечение
с левой ветвью уголка, правое звено ломаной не будет иметь пересечений с левой ветвью уголка. С правой ветвью
уголка ни одно из звеньев ломаной не будет иметь пересечений. Получаем, что при такихломаная и уголок
будут иметь ровно две точки пересечения, что нам подходит. - При
правый излом ломаной будет лежать ниже вершины уголка. Тогда левое звено ломаной не будет
иметь пересечений с уголком, среднее звено ломаной будет иметь ровно одно пересечение только с левой ветвью
уголка, правое звено ломаной будет иметь ровно одно пересечение только с правой ветвью уголка. Получаем, что
при такихломаная и уголок будут иметь ровно две точки пересечения, что нам подходит.
Объединяя все подходящие значения, получаем
Ответ:
Критерии оценки
|
Содержание критерия |
Балл |
|
Обоснованно получен верный ответ |
4 |
|
С |
3 |
|
С |
2 |
|
Верно получена хотя бы одна граничная |
1 |
|
Решение не соответствует ни одному из |
0 |
|
Максимальный балл |
4 |
Найдите все значения параметра при каждом из которых уравнение
имеет хотя бы два решения.
(ЕГЭ 2021, резервная волна)
Показать ответ и решение
Рассмотрим данное нам уравнение. Оно является биквадратным, если коэффициент при не равен 0, то есть когда
Пусть
тогда
Значит, при исходное уравнение будет иметь два решения. Теперь будем рассматривать
При таких
значения параметра коэффициент при
не будет равняться
следовательно, исходное уравнение будет
биквадратным.
Пусть Тогда исходное уравнение примет вид квадратного уравнения:
Заметим, что если полученное уравнение имеет хотя бы один положительный корень то исходное уравнение будет
иметь два различных корня Значит, нам нужно найти такие значения параметра
при которых полученное
квадратное уравнение имеет хотя бы один положительный корень.
Поймем, какими по знаку могут быть корни полученного квадратного уравнения. По теореме Виета произведение корней
приведенного квадратного уравнения равно свободному члену, тогда произведение корней полученного уравнения равно
Следовательно, оба корня обязаны быть одного знака, либо один из них равен 0, так как если корни имеют разные
знаки, то их произведение меньше 0.
Тогда посмотрим, чему должна равняться сумма корней для того, чтобы хотя бы один корень был положительный. Если это
так, то второй корень должен быть не меньше 0, так как произведение корней неотрицательно. Тогда сумма корней должна быть
строго положительна. По теореме Виета сумма корней приведенного квадратного уравнения равна
Тогда
сумма корней нашего уравнения равна Значит,
Теперь осталось обеспечить наличие хотя бы одного корня, то есть найти такие значения параметра при которых
дискриминант уравнения неотрицателен с учетом
Заметим, что все полученные значения параметра больше 0, поэтому при таких значениях будет хотя бы один
положительный корень Значит, у исходного уравнения будет хотя бы два различных корня. При
у исходного
уравнения тоже будет два различных корня, следовательно, окончательный ответ:
Ответ:
Найдите все значения параметра , при каждом из которых уравнение
имеет ровно два различных решения.
(ЕГЭ 2020)
Показать ответ и решение
Рассмотрим данное нам уравнение. Оно является биквадратным, если коэффициент при не равен 0, то есть когда
.
Пусть , тогда
и
Значит, при , где
исходное уравнение имеет ровно один корень. Далее будем рассматривать
. При таких значения параметра
коэффициент при
не будет равняться
, следовательно,
исходное уравнение будет биквадратным. Пусть . Тогда исходное уравнение примет вид квадратного
уравнения:
Заметим, что если полученное уравнение имеет хотя бы один положительный корень , то исходное уравнение будет
иметь два различных корня . Если же уравнение будет иметь два различных положительных корня
, то
исходное уравнение уже будет иметь хотя бы три различных корня. Значит, полученное уравнение должно иметь ровно один
положительный корень.
Тогда полученное уравнение должно иметь хотя бы один корень, то есть его дискриминант должен быть
неотрицательным:
По теореме Виета произведение корней приведенного квадратного уравнения равно свободному члену, то есть . Значит,
корни уравнения одного знака. Тогда если они положительные, то и их сумма положительна, если отрицательны, то сумма
отрицательна. Нам нужно найти такие значения параметра , при которых у этого уравнения ровно один положительный
корень, значит, оно должно иметь два равных положительных корня, то есть дискриминант равен 0, а сумма корней больше
0.
По теореме Виета сумма корней приведенного квадратного уравнения равна
. Значит, если
корни положительны, то
Тогда имеем систему:
Ответ:
Найдите все значения параметра при каждом из которых система
имеет ровно два различных решения.
(ЕГЭ 2020)
Показать ответ и решение
Преобразуем первое уравнение исходной системы так, чтобы получилось уравнение
окружности:
Мы получили уравнение окружности с центром в точке и радиусом
Преобразуем второе уравнение исходной системы так, чтобы получилось
уравнение окружности:
Мы получили уравнение окружности с центром в точке
и радиусом Тогда исходную систему можно переписать так:
В итоге мы получили систему из уравнений двух окружностей. Нам нужно
найти такие значения параметра при которых система имеет ровно два
решения. Мы знаем, что окружности могут иметь 0, 1, 2 или бесконечное
количество точек пересечения. 2 точки пересечения окружности с одинаковыми
радиусами имеют только тогда, когда расстояние между их центрами больше 0, но
меньше их удвоенного радиуса. Выразим расстояние между центрами
и
Значит, имеем неравенство:
Получается, что исходная система имеет ровно два решения при
Ответ:
При каких значениях система
имеет ровно два решения?
(ЕГЭ 2020)
Показать ответ и решение
Преобразуем первое уравнение системы:
Тогда исходная система имеет вид:
Найдем для каждой системы полученной совокупности такие значения параметра , при которых она имеет
решение. Рассмотрим первую систему:
Решим левое неравенство:
Это неравенство верно при любом значении . Решим правое неравенство:
Значит, первая система совокупности имеет решение при , причем это решение только одно. Решим вторую
систему совокупности:
Решим правое неравенство:
Это неравенство верно при любом значении . Решим левое неравенство:
Значит, вторая система совокупности имеет решение при , причем это решение только одно. Не
трудно заметить, что третья система имеет единственное решение при любом значении параметра
.
В задаче нам требуется найти такие значения параметра , при которых исходная система имеет ровно два
решения. Посмотрим сколько решений (необязательно различных) имеет система при определенных :
Посмотрим при каких значениях параметра корни совпадают:
Так как , при
исходная система имеет только одно решение. Аналогично,
так как , при
исходная система имеет только одно решение. При
исходная
система имеет не три, а только два корня. Значит, два ровно решения исходная система имеет при
Ответ:
Найдите все значения , при каждом из которых система уравнений
имеет ровно два различных решения.
(ЕГЭ 2020)
Показать ответ и решение
Преобразуем первое уравнение системы:
Тогда исходная система имеет вид:
Найдем для каждой системы полученной совокупности такие значения параметра , при которых она имеет решение.
Рассмотрим первую систему:
Решим левое неравенство:
Это неравенство верно при любом значении . Решим правое неравенство:
Значит, первая система совокупности имеет решение при , причем это решение только одно. Решим вторую систему
совокупности:
Решим правое неравенство:
Это неравенство верно при любом значении . Решим левое неравенство:
Значит, вторая система совокупности имеет решение при , причем это решение только одно. Не трудно заметить, что
третья система имеет решение при любом значении параметра
.
В задаче нам требуется найти такие значения параметра , при которых исходная система имеет ровно два решения.
Посмотрим сколько решений (необязательно различных) имеет система при определенных :
Посмотрим при каких значениях параметра корни совпадают:
Так как , то и при
исходная система имеет два решения. Тогда исходная система имеет
ровно два решения при .
Ответ:
Найдите все значения при каждом из которых уравнение
имеет ровно один корень.
(ЕГЭ 2020)
Показать ответ и решение
Преобразуем исходное уравнение:
Будем рассматривать левую и правую части по отдельности. Левая часть задает функцию
При этом значит,
Это уравнение «верхней» полуокружности с центром в точке и радиусом 1. Правая часть задает
функцию
При этом значит,
Это уравнение верхней полуокружности с центром в точке и радиусом 1. При изменении значения параметра
центр этой полуокружности перемещается по прямой Посмотрим, как могут располагаться две эти
полуокружности. Они могут не пересекаться, пересекаться ровно в одной точке или полностью совпадать при
Нарисуем на плоскости зеленым цветом полуокружность, заданную уравнением Далее будет
рассматривать полуокружности, заданные уравнением изменяя значение параметра
Заметим, что при
полуокружности не пересекаются. Тогда будем увеличивать значение
При полуокружности впервые пересекутся в одной точке. До
они будут иметь ровно одну точку пересечения.
При достижении этого значения полуокружности совпадут. Далее до включительно полуокружности снова будут иметь
одну точку пересечения.
Значит, при исходное уравнение будет иметь ровно одно решение.
Ответ: