Урок подготовки к егэ по математике в 11 классе конспект урока

МАОУ «Свердловская СОШ №2»

План- конспект открытого урока

 по математике в 11 Б классе

 «Подготовка к ЕГЭ. Решение сложных комбинированных уравнений»

Урок разработала и провела:

 Сушкова Э.А.,

учитель математики

МАОУ «Свердловская СОШ №2»

Апрель 2021 г

https://yandex.ru/efir?stream_id=vIL5MDlVhUGQ&from_block=player_context_menu_yavideo

Тип урока: семинарское занятие.

Цели урока:

Познавательные: повторить и обобщить изученный за курс средней школы материал по математике, закрепить навыки решения сложных уравнений различными методами.

Развивающие: развивать ключевые коммуникативные компетенции, речь, внимание, память, логическое мышление, умение обобщать, делать выводы, развивать навыки самоконтроля и творческие способности учащихся.

Воспитательные: совершенствовать навыки этичного межличностного общения, сознательное отношение к математике; активизировать познавательную деятельность в коллективе, формировать навыки сотрудничества в решении поисковых задач, воспитывать у учащихся морально-ценностные чувства.

Задачи урока:

1. Систематизировать теоретические знание по теме.
2. Развивать умение работать с заданиями ЕГЭ.

Совершенствовать навыки решения сложных уравнений различными методами.

Ход урока:

I Организационный момент:

а) готовность класса к уроку;

б Слово учителя: Ребята, сегодня у нас необычный урок. Мы проверим наши знания,  уровень нашей подготовки к сдаче ЕГЭ. И я хочу начать сегодняшний урок с притчи.

— Учитель, я уже целый год живу у тебя, но до сих пор выполняю только работы по хозяйству. Когда ты будешь меня учить? Разве я для этого пришёл к тебе в ученики, скажи? 
— Имей терпение, — ответил учитель, — ещё не пришло время.  Иди в нижнюю долину и посади дерево, вырасти его, а я подумаю.

     Долгий и тяжёлый путь проделал ученик, пока спустился в долину. По дороге он выкопал маленький саженец и посадил его.  С той поры, дважды в день он проходил опасный путь, между хижиной и долиной, чтобы полить деревце. Изо дня в день, он присматривал за деревом.     Так прошёл год. Усилия его не пропали даром. Дерево выросло высоким и крепким. Однажды на рассвете, он вышел из хижины и увидел своего учителя, сидящего у ручья под деревом. 
— Учитель! – обрадовался юноша. – Как я счастлив вновь увидеть тебя!  Я должен извиниться перед тобой, что не смог стать твоим учеником, обманув твоё доверие! Ты подумал, что я слаб, когда я остался жить в долине. Но я должен был заботиться о своём деревеИ теперь, ты вряд ли возьмёшь меня обратно… 
      Выслушав пылкую речь юноши, старик сказал ему: — Именно в этот год, ты вместе с деревом взращивал такие качества своего характера, которые тебе помогут постигать знания. 
Твоё дерево говорит о твоей готовности. Посмотри!

Ответственность ты имел, но только по необходимости, Был нетерпелив и эмоционален, как переплетенные побеги саженца. Чтобы обрести знания, нужна, прежде всего, дисциплина. 
Ибо корни дерева – твоя ответственность, 
ствол дерева – твоё терпение, 
ветви дерева – спокойствие, 
а листья – знания! 

      И вам я желаю такого же упорства и терпения, чтобы хорошо подготовиться к ЕГЭ и успешно его  сдать.

А теперь приступим к выполнению заданий.

Проверка дз.

 Дать определение уравнения и его корня, равносильности двух уравнений.

Ответ:

Арифметическое выражение, содержащее неизвестную переменную и знаки равенства называют уравнением. Значение переменной, превращающее уравнение в верное равенство, называют корнем уравнения. Два уравнения называют равносильными, если любой корень первого уравнения является корнем второго уравнения и любой корень второго уравнения является корнем первого уравнения.

Дать определение равносильности преобразования уравнения и перечислить основные равносильные преобразования.

Ответ:

Замену одного уравнения другим, равносильным ему уравнением называют равносильным преобразованием уравнения.

Равносильными преобразованиями уравнения являются:

• перенос члена уравнения с противоположным знаком из одной части уравнения в другую;
• умножение (деление) обеих частей уравнения на отличную от нуля число;
• возведение уравнения в нечетную степень;
• извлечение корня нечетной степени с обеих частей уравнения:
• логарифмирование показательного уравнения;
• применение тождеств, т. е равенств, справедливых для любого числа.

Рассказать, какие равносильные преобразования нужно выполнить, чтобы решить следующие уравнения

 

;

Дайте определение уравнения – следствия и перечислите преобразования, приводящие к уравнению следствия.

Ответ:

Пусть даны два уравнения. Если любой корень первого уравнения является корнем второго уравнения, то второе уравнение называют уравнением- следствием первого.

Замену уравнения другим уравнением, которое является его следствием, называют переходом к уравнению- следствию.

При переходе к уравнению- следствия возможно появление лишних корней, посторонних для исходного уравнения, поэтому проверка полученных корней является обязательной частью решения уравнения.

Преобразованиями, приводящими к уравнению- следствия является:

• возведение уравнения в четную степень;
• потенцирование логарифмического уравнения;
• освобождение уравнения от знаменателя;
• приведение подобных членов;
• применение формул (тригонометрических, логарифмических и других).

1. Расскажите, каким способом приводится следующие уравнения к уравнению – следствия.

;

;

.

Карточки имеются у  каждого ученика на парте.

Сложные уравнения можно решить, приводя их к системам. Правила перехода от уравнений к равносильным системам:

1.

2.

3.

4.

5.

6.

7.

М-область существования 

8.

9.

10.

11. 

Работа в группах.

Запишите системы, равносильные уравнениям. (Работы выполняют на листочках)..

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

Очень часто можно встретить уравнение, которое имеет дополнительное условие, например:

Как можно упростить решение такого типа уравнения?

Разбор решения на доске.

Ответ:

Учитывая, что левая часть уравнения неотрицательное число получаем  значит, множество решений данного уравнения есть. Левая часть уравнения для любого  есть отрицательное число, значит, рассматривается только одно уравнение . Решается квадратное уравнение, находим и выбираем те, которые принадлежат множеству М.

Самыми сложными считаются уравнения с параметром. Дайте определение уравнения с параметром. Давайте рассмотрим несколько таких уравнений с использованием свойств функций:

а)

 имеет ровно три корня.

Ответ:

Для каждого значения a рассмотрим функцию

Она определена на множестве R, четная, поэтому, если  — корень уравнения, то  — тоже является корнем уравнения.

Уравнение (1) имеет три корня тогда и только тогда, когда оно имеет  и еще два отличных от нуля корня, отличающихся знаками.

получаем: 

При  уравнение примет вид  у уравнения только один корень.

При  уравнение имеет вид . Это уравнение имеет три корня  Ответ:3

Видеоурок.

Максимум за выполнение данного задания(18 задание) можно получить 4 балла.

В задачах с параметром допускают весьма разнообразные способы решений. Наиболее распространенными из них являются;

Чисто алгебраический способ решения;

-способ решения,основанный на построении и исследовании геометрической модели данной задачи;

-функциональный способ, в котором могут быть и алгебраические, и геометрические моменты, но базовым является исследование некоторой функции.

Критерии оценивания:

	Обоснованно получен верный ответ	4 балла
	С помощью верного рассуждения получены оба верных значения параметра, но -или в ответ включены и одно-два неверных значения; -или решение недостаточно обосновано.	3 балла
	С помощью верного рассуждения получено хотя бы одно верное значение параметра	2 балла
	Задача сведена к исследованию: -или взаимного расположения трех окружносей; -или двух квадратных уравнений с параметром.	1 балл
	Решение не соответствует ни одному из критериев, перечисленных выше	О баллов

 Выполнения тренировочных упражнений на закрепление навыков и умений решать уравнения.

1. 
2. ;
3. 

VI Домашнее задание:

 Разбор заданий типа С с индивидуальных карточек с сайта www.ege.edu.ru Банк заданий на доске.

Карточка №1

С1.(В13) 

Карточка №2

C1.(B1) 

Карточка №3

C1.(B12) 

Карточка №4

C1.(B19) 

Карточка №5

С5. Найти все значения a, такие, что уравнение имеет единственное решение:

Карточка №6

С5. Найти все значения a, такие, что уравнение имеет единственное решение:

Карточка № 7

Найти наибольший корень уравнения:

.

Карточка № 8

Найти значение р, при которых уравнение

не имеет решений.

Карточка №9

Решить уравнение

1. Повторить теорию по темам:

•  Уравнения-следствия.
•  Равносильность уравнений системам.
•  Равносильность уравнений на множествах.

VII Подведение итогов урока.

1. 
   Оцените вашу работу на уроке.

Сколько баллов вы набрали?

К какому выводу пришли?

Лист самооценки работы  учащегося

———————————————————————————(Ф.И. учащегося)

———————————————————————————(тема урока)

Мой вклад…	Баллы
	1(плохо)	2(слабо)	3(хорошо)	4(отлично)
В поисках материала по теме
В теоретическом изучении материала
В решении примеров
В  групповой работе
В защите работ, анализе решений

Перевод баллов:

0-9 баллов-2

10-13 баллов-3

14-16 баллов-4

15-20 баллов-5

Лист самооценки работы  учащегося

———————————————————————————(Ф.И. учащегося)

———————————————————————————(тема урока)

Мой вклад…	Баллы
	1(плохо)	2(слабо)	3(хорошо)	4(отлично)
В поисках материала по теме
В теоретическом изучении материала
В решении примеров
В  групповой работе
В защите работ, анализе решений

Перевод баллов:

0-9 баллов-2

10-13 баллов-3

14-16 баллов-4

15-20 баллов-5

Урок математики в 11 классе.

Тема: «Повторение. Подготовка к ЕГЭ».

Цель урока:

1. Повторение материала, подготовка учащихся к экзаменам.

2. развитие логического мышления, навыков самостоятельной и групповой деятельности.

3. Воспитание коллективизма.

План урока:

1. Оргмомент.

2. Устная работа. Задания типа В2

3. Повторение темы « Площади». Составление кластера.

4. Повторение темы «Логарифмы», использование ЭОРов.

5. Подведение итогов урока

(Тип урока:  урок повторения и закрепления пройденного материала.

Методы обучения: словесный,  наглядный, практический (частично-поисковый,  метод самостоятельной работы).

Средства обучения:  наглядный материал  (карточки, плакаты, учебное пособие «Банк открытых заданий ЕГЭ»).

Формы работы:  групповая, индивидуальная.

Триединая цель урока:

• Образовательная:

  • систематизировать и обобщить знания учащихся по теме «Площади».

• Развивающая:

  • способствовать формированию умений применять приемы: сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию, анализировать условие задачи, составлять модель решения;

  • способствовать развитию умений и навыков применять математические знания к решению практических задач, ориентироваться в простейших геометрических конструкциях.

• Воспитательная:

  • содействовать воспитанию интереса к математике, активности, мобильности, умения общаться.

Задачи урока:

• Выявить уровень подготовки учащихся по геометрии по данной теме, систематизировать полученные знания с помощью приема «Кластер»

• Помочь в развитии и самореализации творческих способностей личности; обучить приемам организации интеллектуального труда

• Научить учащихся находить главное

• Продолжить воспитание у учащихся уважительного отношения друг к другу, чувства      товарищества, культуры общения, чувства ответственности. )

Ход урока.

1. Оргмомент.

1. Устные упражнения: Разрешите открыть урок с высказывания Декарта: «Я мыслю, следовательно, существую». Сейчас вам дается возможность проявить свою мысль при выполнении ряда заданий для подготовки к ЕГЭ.

ЕГЭ это вершина ,к которой мы медленно поднимаемся, переходя из класса в класс, изучая одну тему за другой. Задания ЕГЭ это ступени, по которым легче покорить эту вершину. Сегодня на уроке мы преодолеем вместе с вами некоторые из этих ступеней.

Итак , первая ступенька на которую мы с вами сегодня поднимемся -задания В2. Их можно решить устно. Мы сейчас рассмотрим несколько разных заданий этого типа.

Задание B2

На рисунке изображен график осадков в г.Калининграде с 4 по 10 февраля 1974 г. На оси абсцисс откладываются дни, на оси ординат — осадки в мм.

Определите по графику, сколько дней из данного периода осадков выпало между 2 и 8 мм.

Ответ: 3

Задание B2

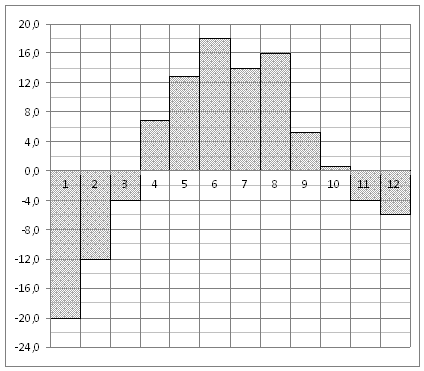
На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме разность между наибольшей и наименьшей среднемесячными температурами в 1973 году.

Ответ: 38

Задание B2

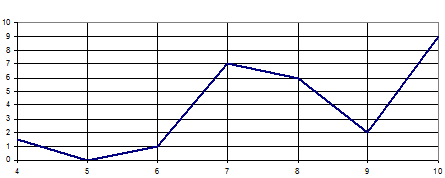
Посев семян тыквы рекомендуется проводить в мае при дневной температуре воздуха не менее  ° С. На рисунке показан прогноз дневной температуры воздуха в первой и второй декадах мая. Определите, в течение скольких дней за этот период можно производить посев тыквы.

Ответ: 7

Задание B2

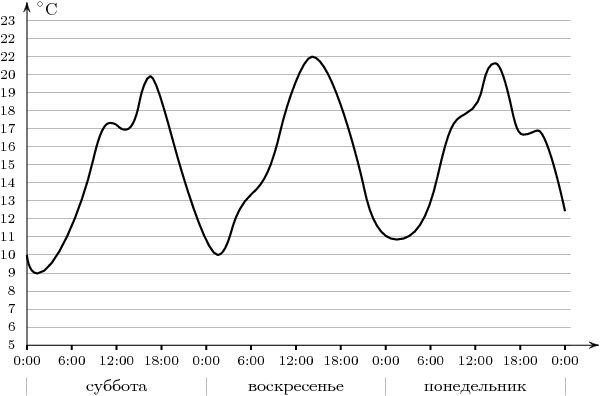
На графике показано изменение температуры воздуха в некотором населённом пункте на протяжении трех суток, начиная с 0 часов субботы. На оси абсцисс отмечается время суток в часах, на оси ординат — значение температуры в градусах Цельсия. Определите по графику наименьшую температуру воздуха в ночь с субботы на воскресенье. Ответ дайте в градусах Цельсия.

Ответ: 10

Задание B2

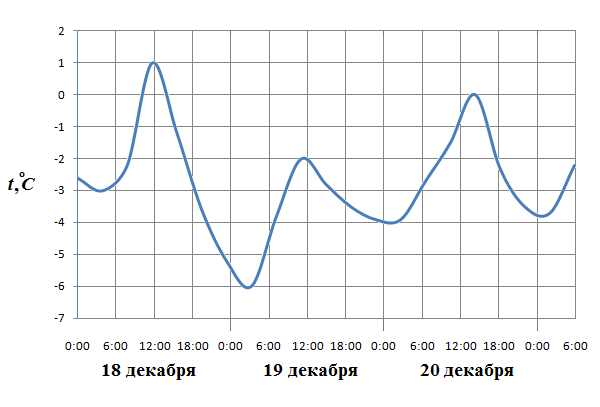
На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей температурой воздуха 19 декабря.

Ответ: 4

Задание B2 (18881)

(показов: 1885, ответов: 1026)

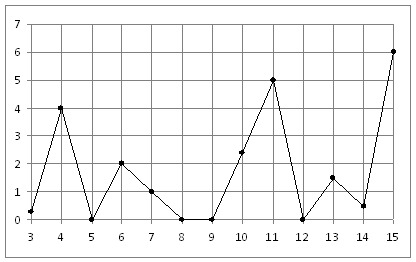
На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа выпало наибольшее количество осадков.

Ответ: 15

Задание B2

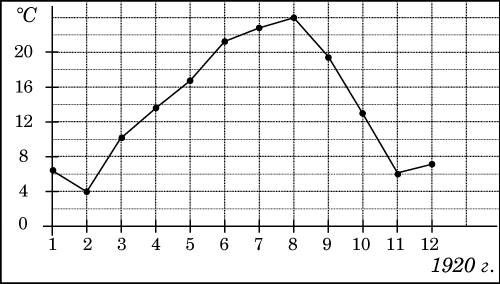
На рисунке жирными точками показана среднемесячная температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку наименьшую среднемесячную температуру в период с мая по декабрь 1920 года.

Ответ: 6

Задание B2

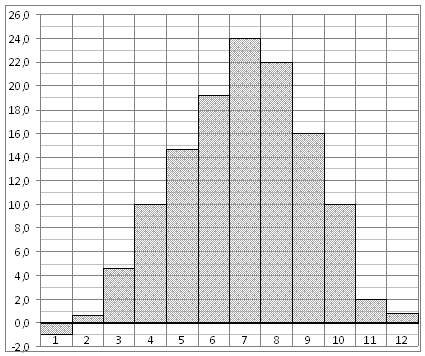
На диаграмме показана среднемесячная температура воздуха в Симферополе за каждый месяц 1988 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в 1988 году.

Ответ: 24

Задание B2

На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода выпадало более 3 миллиметров осадков.

Ответ: 3

1. Обобщение и коррекция  опорных знаний по теме «Площади плоских фигур»

Формулы для кластера

(ромб) (трапеция) (параллелепипед) S = ha S= аbsinγ S= (d1×d2×sinγ) 2 (прямоугольник) S = a*b (квадрат) (прямоугольный треугольник) (треугольник) Формула Геррона S= 1/2ab sinγ S=1/2 r×P S= abc 4R (круг) (круговой сектор) S=πR²α 360 (правильные многоугольники) n=3, S=a²√3 4 n =4, S=a² n=6, S=3√3a² 2

(пирамида) (правильная пирамида) Sбок=1/2Pоснd (апофему) (усеченная пирамида) Sбок=1/2(P1 +P2)d (апофему) (куб) S = 6a² (прямоугольный параллелепипед) S = 2(ab+bc+ac) (цилиндра) S бок= 2πRh Sпол=2πR(R + h) (призма)S= Sбок + 2Sосн (прямой призмы) Sбок= Ph (конус) Sбок=πrl Sпол=πr(l + r) (усеченный конус) Sбок=π (r + r1) l (сфера)

Учащимся предлагается составить кластер по теме «Площади». На столах у каждого находится лист (формат А4).
На листе делается посередине надпись «Площади». Затем учащимся предлагается слева записать виды плоских фигур и их площадей.
Одному обучающемуся можно предложить это задание выполнить на доске. Затем групповое обсуждение полученного кластера. Корректировка кластера.

Деятельность учащихся по самостоятельному применению знаний и умений при решении простейших геометрических задач. Работа устно.

Учащимся предлагается устно решить несколько задач из сборника «Банк открытых заданий ЕГЭ по математике». Работать предлагается в парах или индивидуально. Обязательно необходимо подчеркнуть, что при решении задач необходимо применять формулы площадей, можно пользоваться составленным кластером.
После небольшого обсуждения в парах, ответы вслух. Обсуждение.
Учитель показывает чертеж из сборника, дети говорят ответ.

Вопросы, задаваемые при обсуждении задач:

• Площадь какой фигуры находили?

• Какую формулу применяли?

• Можно ли решить данную задачу другим способом?

Предлагаемые задачи для устной работы:

(количество заданий можно увеличить или уменьшить в зависимости от времени урока)

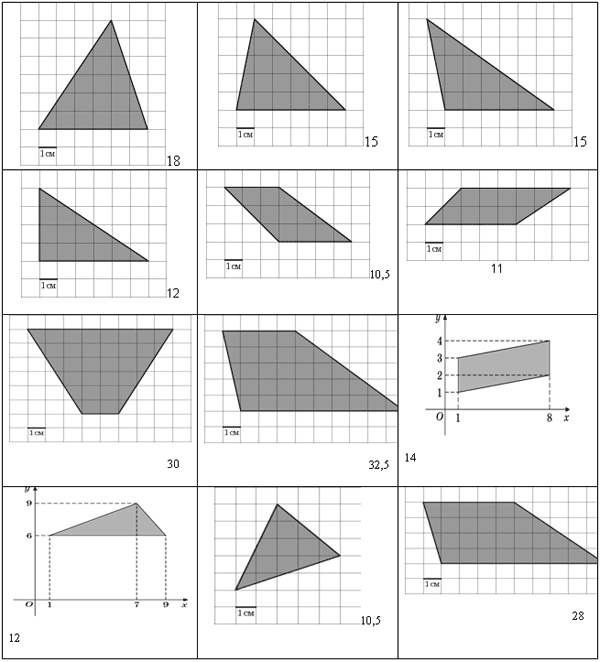
На клетчатой бумаге с клетками размером 1 см х 1 см изображена фигура.  Найдите его площадь.

1. Теперь давайте перейдем к заданиям типа В5, В7. Логарифмы. Перед вами лежат формулы, выражающие свойства логарифмов. При работе можете ими пользоваться.

ЭОРы: а) работа вместе с учителем

Б) самостоятельная работа ученика.

Одновременно класс работает с ним, корректирует знания.

1. Откройте «Репетитор по математике. Варианты ЕГЭ, 2012 год». Выполняете каждый свой вариант. Начинаем выполнять тест. Результаты тестирования отправьте на печать.

2. Подведение итогов урока

3. 1. Домашнее задание.

4. – Задачи из банка открытых задач ЕГЭ: №5061, 5067,5201, 21337.
   – Оформить кластер, ответить на вопросы, отмеченные в кластере

5. 2. Выставление оценок

6. 3. Рефлексия

7. – Что дает нам прием «Кластер»?
   – Имеет ли практическое значение данная тема?
   – Понравился ли вам урок?

9. Сегодня мы проводим урок – отчет самостоятельного решения

задачи. Вы решали одну задачу разными способами. Мы ждем от вас красивого решения, а добиться этого можно лишь в результате кропотливой работы над задачей.

Красивое решение приходит тогда, когда придумано несколько вариантов решения задачи. Метода, который гарантировал бы решение любой задачи – нет. Но все же существуют весьма общие приемы, которые при умелом применении заметно облегчают решение многих трудных задач. Разработка этих приемов называется — эвристика. Слово происходит от знаменитого «Эврика».

«Эврика» — нашел! – воскликнул, согласно легенде, древнегреческий ученый Архимед, выскочив из ванны, он понял как решить, возникшую перед ним задачу.

Стихотворение (читает ученица)

Преданье старинное знает весь свет,

Как, нежась горячею ванной,

Открыл свой великий закон Архимед,

Связав его с выходкой странной.

Сияющий выскочил вон Архимед,

Из ванны горячей, где мылся,

И прямо из бани, как был, неодет,

Куда-то бежать он пустился.

Картина, достойная кисти богов,

По улице, солнцем согретой,

Пунктир оставляя из мокрых следов,

Бежит Архимед неодетый.

Толпа сиракузцев несется во след,

В восторге от бешеной гонки,

И громко ликует, когда Архимед,

Выкрикнул «Эврика» звонко.

«Нашел!» Он нашел тот желанный ответ,

Который искал так упорно.

«Нашел!» В упоенье кричал Архимед,

«Нашел!» — повторяли задорно.

Подобно Архимеду, вы искали решение задачи, каждая группа предлагает свой способ. Когда вы получили задание сделать проект решения задачи, то вы думали, что это невозможно, но сейчас посмотрим, что из этого получилось

1. Заключение.

Сейчас, прослушав несколько способов решения одной задачи, мы повторили несколько тем. Вы должны выбрать тот способ решения, который вам больше понравился, и если на экзамене вам встретилась задача, которую не можете решить, то вспомните, что можно попытаться решить другим способом.

В этом году вы выпускаетесь из школы и вас ждут большие жизненные испытания. Так вы должны знать, что безвыходных ситуаций не бывает.

В любой ситуации можно найти решение.

Закончим наш урок словами Эйнштейна: «Каждый важный успех приносит новые вопросы».

Цели урока:

• обобщить знания по теме: «Применение
  производной к исследованию функций, к
  нахождению наибольшего и наименьшего значения
  функции на отрезке»;
• формирование умения применять теоретические
  знания к  работе с графиком функции,
  производной и касательной;
• развитие интереса и внимания при решении задач
  по готовым чертежам.

Задачи: отработка навыка работы с
производной при подготовке к ЕГЭ.

План урока:   

1. Организационный момент. Постановка цели урока.
   Мотивация учебно-познавательной цели
2. Устная работа на вычисление производных
3. Исследование функции и её производной.
   Сопоставление полученных графиков.
4. Нахождение наименьшего и наибольшего значения
   функции на отрезке с использованием графика
   функции.
5. Динамическая пауза
6. Вычисление значения производной в точке по
   графику функции и касательной
7. Тест типовых вариантов реальных заданий ЕГЭ (В8,
   В11)
8. Подведение итогов урока
9. Рефлексия
10. Домашнее задание

Оборудование:  Мультимедиа
установка.

ХОД УРОКА

Задания для устной работы отображаются на
слайде 2 Приложения 1.

1. Найдите производную

1. 
2. 
3. 
4. 
5. 
6. 

2.  Исследуйте функцию и постройте её график.

Исследование выполняется учеником на доске и
обсуждается с классом, график функции
отображается на слайде 3 Приложения
1. После этого учитель предлагает
исследовать и построить график самой
производной, на том же слайде 3 Приложения
1. отображается соответствующий график.
Теперь учитель предлагает сопоставить оба
графика и проследить за тем, как ведёт себя
функция по мере изменения производной. На слайде
можно проследить данный процесс за счёт
анимации. Учащиеся формулируют соответствующие
выводы.
Решение задач по готовым чертежам.

Укажите по графику производной функции
промежутки возрастания, убывания, экстремумы
самой функции (Приложение 1,
слайды 4, 5) 

3. Нахождение наименьшего и наибольшего
значения функции на отрезке с использованием
графика функции и аналитически

Учащимся предлагается сначала по графику одной
функции слайд 6 Приложения 1.
найти наименьшее и наибольшее значения функции
на различных отрезках, после обсуждения
возможных ситуаций сформулировать алгоритм
решения таких задач без построения графика (Приложение 1, слайд 7).
Решение типовой задачи  ЕГЭ на нахождение
наименьшего и наибольшего значения функции на
отрезке по алгоритму у доски: y = 14tgx – 14x+
5 – 5 (Приложение
1, слайд

4. Вычисление значения производной в точке
по графику функции и касательной

Обратимся к следующему слайду 9 Приложения 1. Чтобы иметь
возможность проверить наши рассуждения, 
рассмотрим не только график неизвестной функции
и касательной проведённой в некоторой точке (а
именно такой случай нас будет интересовать
позже), а и формулу, задающую эту функцию.

Зная и х₀
= 2, учащиеся вычисляют значение производной в
данной точке и записывают ответ.
Учащиеся формулируют, в чём заключается
геометрический смысл производной и по чертежу
 вычисляют tgA из прямоугольного
треугольника АВС. Полученные результаты
сравниваются.
Переход к следующему слайду 10 Приложения
1.
Учащиеся рассматривают случай, когда
касательная с положительным направлением оси ОХ
образует тупой угол. В ходе решения
рассматриваем смежные углы и формулу приведения.
Замечаем, что не всегда удобно вычислять тангенс
угла, и обращаемся в решении к уравнению прямой и
угловому коэффициенту.
Учащиеся формулируют способы нахождения
производной в точке касания по графику,
используя геометрический смысл производной.
Решение типовой задачи  ЕГЭ на вычисление
значения производной в точке по графику функции
и касательной. Приложение 1.
Слайд 11.

5. Проверочный минитест по вариантам

Приложение 1. Слайды
12, 13, 14

6. Подведение итогов урока

7. Рефлексия

8. Домашнее задание

19.12.2022

Оценить

127

Решение задач с физическим и практическим содержанием ЕГЭ по математике.

Учитель: Васильева Вадия Фаритовна

Тип урока: формирование новых знаний и их применение. 

Межпредметные связи: математика, физика.

Методы работы: кейс-технология.

Тип кейса: обучающий

Цели урока:

1. Подготовка к ЕГЭ. Разработка и составление рекомендаций по решению задач физического и практического содержания №10 профильного уровня ЕГЭ по математике.

2.Развитие исследовательских навыков, умения  анализировать, систематизировать, интерпретировать полученные результаты.

3.Повышение интереса учащихся к математике. Расширение кругозора через решение задач связанными с жизненными ситуациями.

Задачи урока:

Образовательные: Систематизировать знания и умения учащихся по решению задач физического и практического содержания.

Развивающие: Развивать умение работать с информацией в нестандартной ситуации; развивать логическое мышление, память, наблюдательность, умение представлять решение; развивать самостоятельную, творческую, исследовательскую деятельность; развивать способность к самооценке.
Воспитательные: Воспитывать уважительное отношение к товарищам, умение работать в команде; умение критически относиться к мнению одноклассников.

Метапредметные УУД:

1.Регулятивные:

1)определять цели, включая постановку новых целей, преобразование практической задачи в познавательную;

2)принимать решения в проблемной ситуации на основе переговоров;

2. Познавательные:

1) учиться основам реализации проектно-исследовательской деятельности;

2) осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий.

3.Коммуникативные:

1) учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве;

2)формулировать собственное мнение и позицию, аргументировать и координировать ее с позициями партнеров в сотрудничестве при выработке общего решения в совместной деятельности;

3)работать в группе — устанавливать рабочие отношения, эффективно сотрудничать и способствовать продуктивной кооперации; интегрироваться в группу сверстников и строить продуктивное взаимодействие со сверстниками и взрослыми.

Содержание кейса.

1. Текст «Трудности ЕГЭ»

2. План работы группы.

3. Правила работы с кейсом.

4. Характеристика задания.

5. Задания группам.

6. Лист достижений группы.

7. Домашнее задание.

ХОД    УРОКА.

1этап. Постановка проблемы, определение темы и цели урока. (10 мин)

Слово учителя:

-Здравствуйте ребята! Сегодня я хочу начать урок словами Д.Пойа «Если хочешь научиться плавать — смело входи в воду, а если хочешь научиться решать задачи — бери и решай».

-В последнее время вся деятельность на уроке направлена на то, чтобы качественно подготовиться к ЕГЭ. Сегодня мы будем это делать с помощью кейсов, работая в группах. Что это такое вы уже знаете, но я ещё раз напомню. Кейс — это набор документов, направленных на решение задач определённого типа. Работая вместе, вы чётко соблюдаете правила работы в группе (эти правила вы найдёте в кейсе). Чтобы определить тему урока и цель, предлагаю ознакомиться с первым документом кейса.

Один из учеников зачитывает текст из кейса вслух.

Первый документ. Текст «Трудности ЕГЭ»

Усилия практически всех выпускников 11 класса направлены на поступление в любой достаточно престижный ВУЗ. С этой целью они и выбирают сдавать профильный уровень ЕГЭ по математике. В настоящий момент выявилась одна из жестких проблем: как показал обзор источников информации по подготовке к ЕГЭ, зачастую, вместо стандартно сформулированных математических задач, на экзаменах появляются задания, отражающие «какие-то связи» с реальной жизнью. Ситуация усугубляется тем, что встреча с любыми величинами, напоминающими таковые в учебниках физики, приводит некоторых учеников в состояние стойкого оцепенения (ну не получается у них подружиться с физикой). Решая задания с кратким ответом, некоторые ребята сразу узнают своего «противника» — задание №10 с физическим и практическим содержанием. Им сложно оценить величие и различие слов «доход», «прибыль», «выручка», «рейтинг», мелькающих в этих задачах. Более того, там встречаются и худшие монстры: брошенные камни, то вертикально вниз, то вертикально вверх, перегревающиеся приборы, законы излучения звезд и другие не менее «интересные» задачи. Просмотрев учебник математики, мы понимаем, что там нет таких задач. К счастью, у нас много друзей. И почему бы не сосредоточить их интеллектуальные ресурсы во времени и пространстве на выработку каких -то подходов и тактик решения этой проблемы: как одолеть задание №10? Может, кто-то уже его победил? Может у кого-то есть верный способ, как обойти проблему? И как понять, нужно ли вообще волноваться по данному поводу?

Слово учителя:

-Итак, определяем тему урока: (Решение задачи №10 с физическим и прикладным содержанием)

-Какую цель вы сегодня поставите перед собой на уроке? (овладение приёмами решения задачи №10 профильного ЕГЭ по математике, разработка рекомендаций к решению задач этого типа)

-Как вы кратко охарактеризуете эту задачу? (Задачи  больше по физике, чем по математике, но необходимые формулы и величины даны в условии. Большинство задач сводится к решению линейного или квадратного уравнения, либо линейного или квадратного неравенства средствами математики).

-Каждой группе нужно разработать и представить на уроке сколько получится, но, желательно, не менее пяти рекомендаций  по   решению задания № 10 профильного ЕГЭ по математике. Доказать преимущества своих рекомендаций. У каждой группы будет ровно одна задача. На эту работу отводится 10 мин. Если группа справится раньше, представитель сразу выходит на презентацию и защиту решения.

2 этап. Работа над проблемой. (10 мин)

Далее учащиеся сначала самостоятельно изучают содержимое кейса, затем задают уточняющие вопросы, учитель даёт необходимые комментарии.

Второй документ. «План работы группы»

1. Определить руководителя группы, перед которым будет стоять задача координировать работу группы и оценивать работу её участников.

2. Определить секретаря, который будет фиксировать предложенные решения и представителя, который будет защищать эти решения.

3. Внимательно изучить материалы кейса

4. Проанализировать материал и обсудить изученную информацию

5. Обменяться мнениями и составить план работы над задачей

6. Зафиксировать основные и второстепенные проблемы.

7. Работать сообща над проблемой (дискуссия)

8. Выработать решение задачи с оформлением.

9. Представить решение и общие рекомендации по решению задач этого типа.

10. Доказать его оптимальность (чем выгодно это решение).

Третий документ. Правила работы с кейсом в группе.

Четвёртый документ. Характеристика задания.

Задачи с физическим содержанием

Задачи  больше по физике, чем по математике, но необходимые формулы и величины даны в условии. Большинство задач сводится к решению линейного или квадратного уравнения, либо линейного или квадратного неравенства.

Поэтому необходимо уметь решать такие  уравнения и неравенства, и определять ответ (имеются задачи, в которых нужно выбрать одно из двух решений, имеются и другие нюансы).  

Есть задачи которые сводятся к решению показательных, логарифмических, тригонометрических уравнений и неравенств.  Ответ в любом случае, должен получиться в виде целого числа или конечной десятичной дроби.

На экзамене с этим заданием успешно справляются около 40%.выпускников. Наибольшая трудность в заданиях такого типа – чтение, понимание условия, применение математических знаний. Около 15% участников экзамена просто не взялись за эту технически простую задачу.

На что необходимо обратить внимание:

1.Если в вопросе прозвучало «определить наибольшее значение», «определить наименьшее значение», то задача в большинстве случаев решается через составление неравенства.

2. Правильно определяйте знак при составлении неравенства. Например: b не менее 21 записывается как  b≥21.

3. Если в вопросе задачи прозвучало «сколько», то составляется уравнение.

4. Не забывайте про единицы измерения, если это необходимо (переводим метры в сантиметры, наоборот и пр.) Все величины подставлять в одних единицах измерения.

5. Не упускайте из виду, в каких единицах измерения требуется записать ответ (например, решив задачу, вы получили 0,5 часа, в условии сказано записать ответ в минутах, получается 30 минут; если запишите  0,5 – это ошибка и потерянный бал, хотя задача решена, верно).

Пятый документ Задачи для групп.

1 группа

№10 . Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в К) от времени работы: T(t)=T0 +b t+a t2​, где t — время (в мин.), T0 =1380 К, a=− 15 К / мин2​, b=165 К / мин. Известно, что при температуре нагревательного элемента свыше 1800 К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.

2 группа

№10. Высота над землёй подброшенного вверх мяча меняется по закону h(t)=1,6+13 t−5 t2, где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 6 метров?

3 группа

№10. Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением  a=9000 км /​ч​. Скорость v (в км/ч)  вычисляется по формуле v=√2la, где l — пройденный автомобилем путь (в км). Найдите, сколько километров проедет автомобиль к моменту, когда он разгонится до скорости 120 км/ч.

4 группа

№10. Груз массой 0,38 кг колеблется на пружине. Его скорость v (в м/с) меняется по закону  v=v0sin, где t — время с момента начала колебаний 
в секундах,  T=8 с — период колебаний, v0=2 м /​с. Кинетическая 
энергия E (в Дж) груза вычисляется по формуле E=(mv2)/2, где m — масса груза (в кг), v — скорость груза (в м/с). Найдите кинетическую энергию груза через 7 секунд после начала колебаний. Ответ дайте в джоулях.

5 группа

№10. Независимое агентство намерено ввести рейтинг  R новостных изданий на основе показателей информативности  In, оперативности Op и объективности  Tr публикаций. Каждый отдельный показатель — целое число от 0 до 3. Составители рейтинга считают, что информативность публикаций ценится втрое, а объективность — вчетверо дороже, чем оперативность, то есть R=(3In+Op+4Tr)/A. Найдите, каким должно быть число A, чтобы издание, у которого все показатели максимальны, получило рейтинг 30.

3 этап. Защита своих идей. (10 мин)

На этом этапе дети в произвольной форме проводят презентацию решений и формулирование рекомендаций. Скорее всего все группы не успеют выступить, поэтому, защита может быть перенесена на следующий урок с последующим фронтальным закреплением.

ПРОЕКТ ПРЕДЛОЖЕНИЙ, как общий вывод, записывается в тетрадь.

4 этап. Подведение итогов (рефлексия) (5 мин)

 Подведение итогов проходит в форме пресс-конференции, в ходе которой учащиеся отвечают на вопросы:

• Что общего в представленных заданиях?

• Что отличает  группу заданий  №10 от других заданий?

• Есть ли такие задачи в наших учебниках?

• Что хотят проверить составители подобных заданий?

• Хватит ли времени решить все задачи открытого банка задач?

• Стоит ли это делать?

• Являются ли задачи с практическим содержанием №10 отражением реальных жизненных ситуаций?

• Можно ли, проанализировав задачу, подготовиться к решению целого набора заданий?                                                                                                      

• Можете  ли вы сами  найти информацию для подготовки к ЕГЭ в сети Интернет, полезные ссылки на on-line тестирование? Все ли они помогут при подготовке к экзаменам?

• Попробуйте понять, для чего лично Вам может пригодиться сегодняшнее занятие?

5 этап. Домашнее задание.  (в кейсе)

Задания практического содержания №10из открытого банка задач ФИПИ на карточках с полным оформленным решением в тетради.

Приложение                                                                                                                  

I этап работы в группе ( поиск, обсуждение, нахождение решений) (от 0 до 5 баллов)

III этап (защита решений и представление рекомендаций)

Оценивание работы отметкой каждого участника группы.