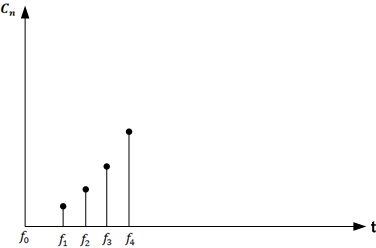
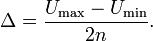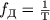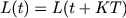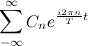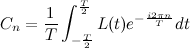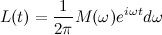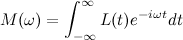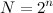Автор материалов — Лада Борисовна Есакова.
При оцифровке звука в памяти запоминаются только отдельные значения сигнала. Чем чаще записывается сигнал, тем лучше качество записи.
Частота дискретизации f – это количество раз в секунду, которое происходит преобразование аналогового звукового сигнала в цифровой. Измеряется в Герцах (Гц).
Глубина кодирования (а также, разрешение) – это количество бит, выделяемое на одно преобразование сигнала. Измеряется в битах (Бит).
Возможна запись нескольких каналов: одного (моно), двух (стерео), четырех (квадро).
Обозначим частоту дискретизации – f (Гц), глубину кодирования – B(бит), количество каналов – k, время записи – t(Сек).
Количество уровней дискретизации d можно рассчитать по формуле: d = 2B.
Тогда объем записанного файла V(бит) = f * B * k * t.
Или, если нам дано количество уровней дискретизации,
V(бит) = f * log2d * k * t.
Единицы измерения объемов информации:
1 б (байт) = 8 бит
1 Кб (килобайт) = 210 б
1 Мб (мегабайт) = 220 б
1 Гб (гигабайт) = 230 б
1 Тб (терабайт) = 240 б
1 Пб (петабайт) = 250 б
При оцифровке графического изображения качество картинки зависит от количества точек и количества цветов, в которые можно раскрасить точку.
Если X – количество точек по горизонтали,
Y – количество точек по вертикали,
I – глубина цвета (количество бит, отводимых для кодирования одной точки), то количество различных цветов в палитре N = 2I. Соответственно, I = log2N.
Тогда объем файла, содержащего изображение, V(бит) = X * Y * I
Или, если нам дано количество цветов в палитре, V(бит) = X * Y * log2N.
Скорость передачи информации по каналу связи (пропускная способность канала) вычисляется как количество информации в битах, переданное за 1 секунду (бит/с).
Объем переданной информации вычисляется по формуле V = q * t, где q – пропускная способность канала, а t – время передачи.
Кодирование звука
Пример 1.
Производится двухканальная (стерео) звукозапись с частотой дискретизации 16 кГц и глубиной кодирования 32 бит. Запись длится 12 минут, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?
1) 30 2) 45 3) 75 4) 90
Решение:
V(бит) = f(Гц)* B(бит) * k * t(Сек),
где V – размер файла, f – частота дискретизации, B – глубина кодирования, k – количество каналов, t – время.
Значит, V(Мб) = (f * B * k * t ) / 223
Переведем все величины в требуемые единицы измерения:
V(Мб) = (16*1000 * 32 * 2 * 12 * 60 ) / 223
Представим все возможные числа, как степени двойки:
V(Мб) = (24 * 23 * 125 * 25 * 2 * 22 * 3 * 15 * 22) / 223 = (5625 * 217) / 223 = 5625 / 26 =
5625 / 64 ≈ 90.
Ответ: 4
!!! Без представления чисел через степени двойки вычисления становятся намного сложнее.
!!! Частота – это физическая величина, а потому 16 кГц = 16 * 1000 Гц, а не 16 * 210. Иногда этой разницей можно пренебречь, но на последних диагностических работах она влияла на правильность ответа.
Пример 2.
В течение трех минут производилась четырёхканальная (квадро) звукозапись с частотой дискретизации 16 КГц и 24-битным разрешением. Сжатие данных не производилось. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?
1) 25 Мбайт
2) 35 Мбайт
3) 45 Мбайт
4) 55 Мбайт
Решение:
V(бит) = f(Гц)* B(бит) * k * t(Сек),
где V – размер файла, f – частота дискретизации, B – глубина кодирования (или разрешение), k – количество каналов, t – время.
Значит, V(Мб) = (f * B * k * t ) / 223 = (16 * 1000 * 24 * 4 * 3 * 60) / 223 = (24 * 23 * 125 * 3 * 23 * 22 * 3 * 15 * 22) / 223 = (125 * 9 * 15 * 214) / 223 = 16875 / 29 = 32, 96 ≈ 35
Ответ: 2
Пример 3.
Аналоговый звуковой сигнал был записан сначала с использованием 64 уровней дискретизации сигнала, а затем с использованием 4096 уровней дискретизации сигнала. Во сколько раз увеличился информационный объем оцифрованного звука?
1) 64
2) 8
3) 2
4) 12
Решение:
V(бит) = f * log2d * k * t, где V – размер файла, f – частота дискретизации, d – количество уровней дискретизации, k – количество каналов, t – время.
V1 = f * log264 * k * t = f * 6 * k * t
V2 = f * log24096 * k * t = f * 12 * k * t
V2 / V1 = 2
Правильный ответ указан под номером 3.
Ответ: 3
Кодирование изображения
Пример 4.
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 64×64 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
Решение:
V(бит) = X * Y * log2N, где V – объем памяти, X,Y – количество пикселей по горизонтали и вертикали, N – количество цветов.
V (Кб) = (64 * 64 * log2256) / 213 = 212 * 8 / 213 = 4
Ответ: 4
Пример 5.
Для хранения растрового изображения размером 64×32 пикселя отвели
1 килобайт памяти. Каково максимально возможное число цветов в палитре изображения?
Решение:
V(бит) = X * Y * log2N, где V – объем памяти, X,Y – количество пикселей по горизонтали и вертикали, N – количество цветов.
log2N = V /( X*Y) = 213 / (26 * 25) = 4
N = 16
Ответ:16
Сравнение двух способов передачи данных
Пример 6.
Документ объемом 5 Мбайт можно передать с одного компьютера на другой двумя способами:
А) Сжать архиватором, передать архив по каналу связи, распаковать.
Б) Передать по каналу связи без использования архиватора.
Какой способ быстрее и насколько, если
– средняя скорость передачи данных по каналу связи составляет 218 бит в секунду,
– объем сжатого архиватором документа равен 80% от исходного,
– время, требуемое на сжатие документа – 35 секунд, на распаковку – 3 секунды?
В ответе напишите букву А, если способ А быстрее или Б, если быстрее способ Б. Сразу после буквы напишите количество секунд, насколько один способ быстрее другого. Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23. Слов «секунд», «сек.», «с.» к ответу добавлять не нужно.
Решение:
Способ А. Общее время складывается из времени сжатия, распаковки и передачи. Время передачи t рассчитывается по формуле t = V / q, где V — объём информации, q — скорость передачи данных.
Объем сжатого документа: 5 * 0,8 = 4 Мб =4 * 223 бит.
Найдём общее время: t = 35 с + 3 с + 4 * 223 бит / 218 бит/с = 38 + 27 с = 166 с.
Способ Б. Общее время совпадает с временем передачи: t = 5 * 223 бит / 218 бит/с = 5 * 25 с = 160 с.
Способ Б быстрее на 166 — 160 = 6 с.
Ответ: Б6
Определение времени передачи данных
Пример 7.
Скорость передачи данных через ADSL─соединение равна 128000 бит/c. Через данное соединение передают файл размером 625 Кбайт. Определите время передачи файла в секундах.
Решение:
Время t = V / q, где V — объем файла, q — скорость передачи данных.
t = 625 * 210 байт / (2 7 * 1000) бит/c = 625 * 213 бит / (125 * 210) бит/c = 5 * 23 с = 40 с.
Ответ: 40
Пример 8.
У Васи есть доступ к Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения им информации 217 бит в секунду. У Пети нет скоростного доступа в Интернет, но есть возможность получать информацию от Васи по низкоскоростному телефонному каналу со средней скоростью 215 бит в секунду. Петя договорился с Васей, что тот будет скачивать для него данные объемом 4 Мбайта по высокоскоростному каналу и ретранслировать их Пете по низкоскоростному каналу. Компьютер Васи может начать ретрансляцию данных не раньше, чем им будут получены первые 512 Кбайт этих данных. Каков минимально возможный промежуток времени (в секундах), с момента начала скачивания Васей данных, до полного их получения Петей? В ответе укажите только число, слово «секунд» или букву «с» добавлять не нужно.
Решение:
Нужно определить, сколько времени будет передаваться файл объемом 4 Мбайта по каналу со скоростью передачи данных 215 бит/с; к этому времени нужно добавить задержку файла у Васи (пока он не получит 512 Кбайт данных по каналу со скоростью 217 бит/с).
Время скачивания данных Петей: t1= 4*223 бит / 215 бит/с = 210 c.
Время задержки: t2 = 512 кб / 217 бит/с = 2(9 + 10 + 3) — 17 c = 25 c.
Полное время: t1 + t2 = 210 c + 25 c = (1024 + 32) c = 1056 c.
Ответ: 1056
Пример 9.
Данные объемом 60 Мбайт передаются из пункта А в пункт Б по каналу связи, обеспечивающему скорость передачи данных 219 бит в секунду, а затем из пункта Б в пункт В по каналу связи, обеспечивающему скорость передачи данных 220 бит в секунду. Задержка в пункте Б (время между окончанием приема данных из пункта А и началом передачи в пункт В) составляет 25 секунд. Сколько времени (в секундах) прошло с момента начала передачи данных из пункта А до их полного получения в пункте В? В ответе укажите только число, слово «секунд» или букву «с» добавлять не нужно.
Решение:
Полное время складывается из времени передачи из пункта А в пункт Б (t1), задержки в пункте Б (t2) и времени передачи из пункта Б в пункт В (t3).
t1 = (60 * 223) / 219 =60 * 16 = 960 c
t2 = 25 c
t3 = (60 * 223) / 220 =60 * 8 = 480 c
Полное время t1 + t2 +t3 = 960 + 25 + 480 = 1465 c
Ответ: 1465
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задача №9. Кодирование звуковой и графической информации. Передача информации, Время записи звукового файла, время передачи данных, определение объема информации.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.03.2023
Уровень квантования
- Уровень квантования
-
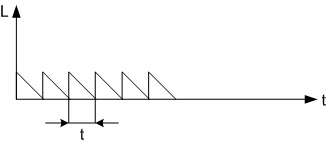
Квантованный сигнал
Неквантованный сигнал с дискретным временем
В информатике под квантованием (англ. quantization) непрерывной или дискретной величины понимают разбиение диапазона её значений на конечное число интервалов. Существует также векторное квантование — разбиение пространства возможных значений векторной величины на конечное число областей. Квантование часто используется при обработке сигналов, в том числе при сжатии звука и изображений. Простейшим видом квантования является деление целочисленного значения на натуральное число, называемое коэффициентом квантования.
Однородное (линейное) квантование — разбиение диапазона значений на отрезки равной длины. Его можно представлять как деление исходного значения на постоянную величину (шаг квантования) и взятие целой части от частного:
.
Не следует путать квантование с дискретизацией (и, соответственно, шаг квантования с частотой дискретизации). При дискретизации изменяющаяся во времени величина (сигнал) замеряется с заданной частотой (частотой дискретизации), таким образом, дискретизация разбивает сигнал по временной составляющей (на графике — по горизонтали). Квантование же приводит сигнал к заданным значениям, то есть, разбивает по уровню сигнала (на графике — по вертикали). Сигнал, к которому применены дискретизация и квантование, называется цифровым.
При оцифровке сигнала уровень квантования называют также глубиной дискретизации или битностью. Глубина дискретизации измеряется в битах и обозначает количество бит, выражающих амплитуду сигнала. Чем больше глубина дискретизации, тем точнее цифровой сигнал соответствует аналоговому. В случае однородного квантования глубину дискретизации называют также динамическим диапазоном и измеряют в децибелах (1 бит ≈ 6 дБ).
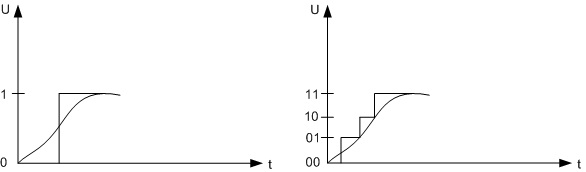
Квантование по уровню — представление величины отсчётов цифровыми сигналами. Для этого диапазон напряжения сигнала от Umin до Umax делится на 2n интервалов. Величина получившегося интервала:
Каждому интервалу присваивается n-разрядный двоичный код — номер интервала, записанный двоичным числом. Каждому отсчёту сигнала присваивается код того интервала, в который попадает значение напряжения этого отсчёта. Таким образом, аналоговый сигнал представляется последовательностью двоичных чисел, соответствующих величине сигнала в определённые моменты времени, то есть цифровым сигналом. При этом каждое двоичное число представляется последовательностью импульсов высокого (1) и низкого (0) уровня.
См. также
- Компандирование
- Дискретизация
Ссылки
Методы сжатия
Теория Информация Собственная · Взаимная · Энтропия · Условная энтропия · Сложность · Избыточность Единицы измерения Бит · Нат · Ниббл · Хартли · Формула Хартли Без потерь Энтропийное сжатие Алгоритм Хаффмана · Адаптивный алгоритм Хаффмана · Арифметическое кодирование (Алгоритм Шеннона — Фано · Интервальное) · Коды Голомба · Дельта · Универсальный код (Элиаса · Фибоначчи) Словарные методы RLE · · LZ ( · LZSS · LZW · LZWL · · · LZX · LZRW · LZJB · LZT) Прочее RLE · CTW · BWT · PPM · DMC Аудио Теория Свёртка · PCM · Алиасинг · Дискретизация · Теорема Котельникова Методы LPC (LAR · LSP) · WLPC · CELP · ACELP · A-закон · μ-закон · MDCT · Преобразование Фурье · Психоакустическая модель Прочее Dynamic range compression · Сжатие речи · Полосное кодирование Изображения Термины Цветовое пространство · Пиксел · Chroma subsampling · Артефакты сжатия Методы RLE · DPCM · Фрактальный · Wavelet · EZW · SPIHT · LP · ДКП · ПКЛ Прочее Битрейт · Test images · PSNR · Квантование Видео Термины Характеристики видео · Кадр · Типы кадров · Качество видео Методы Компенсация движения · ДКП · Квантование Прочее Видеокодек · Rate distortion theory (CBR · ABR · VBR) См. также: Программы для сжатия данных • Стандарты и форматы сжатия
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое «Уровень квантования» в других словарях:
-
уровень квантования — Дискретное значение, которое принимается в качестве величины мгновенного значения аналогового сигнала в заданный момент времени. Число уровней квантования N зависит от динамического диапазона сигнала, допустимого уровня шумов квантования и ряда… … Справочник технического переводчика
-
уровень квантования сигнала электросвязи — Значение параметра сигнала электросвязи, получаемое в результате квантования этого сигнала. [ГОСТ 22670 77] Тематики сети передачи данных Синонимы уровень квантования EN signal quantization level … Справочник технического переводчика
-
Уровень квантования сигнала электросвязи — 34. Уровень квантования сигнала электросвязи Уровень квантования Signal quantization level Значение параметра сигнала электросвязи, получаемое в результате квантования этого сигнала Источник: ГОСТ 22670 77: Сеть связи цифровая интегральная.… … Словарь-справочник терминов нормативно-технической документации
-
уровень квантования — Одно из значений функций, получаемых в результате квантования … Политехнический терминологический толковый словарь
-
Уровень квантования сигнала электросвязи — 1. Значение параметра сигнала электросвязи, получаемое в результате квантования этого сигнала Употребляется в документе: ГОСТ 22670 77 Сеть связи цифровая интегральная. Термины и определения … Телекоммуникационный словарь
-
уровень перегрузки при квантовании сигнала электросвязи — Абсолютный уровень синусоидального сигнала электросвязи, положительное и отрицательное пиковые значения которого совпадают с положительным и отрицательным виртуальными порогами квантования этого сигнала. [ГОСТ 22670 77] Тематики сети передачи… … Справочник технического переводчика
-
уровень перегрузки — 2.51 уровень перегрузки (signal overload level): Уровень, выше которого операция прекращает быть удовлетворительной в результате искажения сигнала, из за перегрева или повреждения. Источник: ГОСТ Р ИСО 12716 2009: Контроль неразрушающий.… … Словарь-справочник терминов нормативно-технической документации
-
Уровень перегрузки при квантовании сигнала электросвязи — 44. Уровень перегрузки при квантовании сигнала электросвязи Уровень перегрузки Load capacity Абсолютный уровень синусоидального сигнала электросвязи, положительное и отрицательное пиковые значения которого совпадают с положительным и… … Словарь-справочник терминов нормативно-технической документации
-
Уровень перегрузки при квантовании сигнала электросвязи — 1. Абсолютный уровень синусоидального сигнала электросвязи, положительное и отрицательное пиковые значения которого совпадают с положительным и отрицательным виртуальными порогами квантования этого сигнала Употребляется в документе: ГОСТ 22670 77 … Телекоммуникационный словарь
-
граница шага квантования — уровень квантования — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы уровень квантования EN quantizing level … Справочник технического переводчика
Аналого-цифровое преобразование сигнала для начинающих
Время на прочтение
3 мин
Количество просмотров 182K
Вступление
Темы аналого-цифрового и цифро-аналогового преобразований являются достаточно важными в курсе электроники, поскольку большинство устройств, взаимодействующих с компьютером, имеют аналоговый вход/выход, а компьютер умеет обрабатывать исключительно цифровые сигналы. В этой статье я хочу поделиться с вами самыми основами таких преобразований.
Типы сигналов
Прежде чем разбираться в самих преобразованиях нужно знать, какие сигналы существуют. А их 3 типа:
- Аналоговые
- Дискретные
- Цифровые
Аналоговые – это сигналы непрерывные во времени, они определены во все моменты времени.
Дискретные – это сигналы представленные последовательностью отсчётов, т.е. значениями сигналов в дискретные моменты времени.
Цифровые – это сигналы дискретные во времени (или в пространстве) и квантованные по уровню. Вычислительные процедуры в компьютере выполняются именно в цифровых сигналах.
Для того, что бы компьютер мог выполнить обработку сигнала необходимо выполнить преобразование сигнала из аналоговой формы в цифровую.
После обработки выполняется обратное преобразование, поскольку большинство бытовых устройств управляются аналоговыми сигналами.
Структурная схема цифровой обработки сигнала в общем виде выглядит следующим образом:
Аналого-цифровое преобразование сигнала
Аналого-цифровое преобразование сигнала включает в себя два этапа:
- Дискретизация сигнала (во времени или пространстве)
- Квантование по уровню
На этапе дискретизации берутся отсчёты сигнала с некоторым периодом дискретизации (Т).
Частоту дискретизации можно определить по формуле
Процесс получения отсчёта входного сигнала должен занимать очень малую часть периода дискретизации, что бы снизить динамические ошибки преобразования, обусловленные изменением сигнала за время снятия отсчёта.
Частота дискретизации выбирается из теоремы Котельникова. В ней утверждается, что для того что бы по отсчётам сигнала можно было бы сколь угодно точно восстановить непрерывный сигнал необходимо что бы частота дискретизации не менее чем в два раза превосходила верхнюю частоту спектра дискретизируемого сигнала.
Любой сигнал имеет своё спектральное представление. Любое представление сигнала – это представление в виде суммы (или интеграла) гармонических составляющих (синусоид и косинусоид), различных частот взятых с определёнными весовыми коэффициентами (имеющими определённую амплитуду)
Для периодических сигналов это сумма, для непериодический – интеграл.
Переход к спектру сигнала осуществляется с помощью прямого преобразования Фурье.
Рассмотрим переход к спектральному представлению в виде периодической функции:
Как известно периодическая функция удовлетворяющая условию Дирихле может быть представлена рядом гармонических функций.
По формуле Эйлера любое выражение можно представить в виде
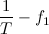
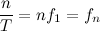
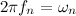
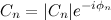
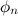
Совокупность амплитуд гармоник ряда Фурье называется амплитудным спектром, а совокупность их фаз называется фазовым спектром.
Пример спектра:
Для непериодический функции 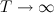
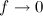
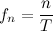
Прямое преобразование Фурье для непериодического сигнала
Таким образом спектр непериодической функции представляется суммой бесконечного количества гармонических колебаний, частоты которых расположены бесконечно близко друг к другу.
Квантование сигнала по уровню
Количество уровней квантования определяется по формуле
n — количество разрядов
N — уровень квантования
Выбор количества уровней квантования сигналов производится на основе компромиссного подхода, учитывающего с одной стороны необходимость достаточно точного представления сигнала, что требует большого числа уровней квантования, а с другой стороны количество уровней квантования должно быть меньше, что бы разрядность кода была минимальной.
На этом я закончу свою статью, что бы не перегружать читателя лишней информацией. Удачи в начинаниях!
Министерство образования и науки рф
ФЕДЕРАЛЬНОЕ
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ
ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«Белгородский
Государственный Технологический
Университет им. В.Г. Шухова»
(БГТУ им.
В.Г. Шухова)
ИИТУС
Кафедра:
«Техническая
кибернетика»
Лабораторная
работа №4
дисциплина:
«ИТ»
тема:
«Дискретизация
и квантование аналоговых сигналов»
Выполнил:
студент
группы УС-11
Татаринов
Алексей
Принял:
ст.
препод. кафедры ТК
Бушуев Д.А.
Белгород
2014
Содержание
1Список
индивидуальных задач 3
2Цель
работы 4
3Описание
алгоритмов процедур дискретизации и
квантования 5
3.1Виды квантования 7
4Решение
индивидуальных заданий 7
3.1.Дискретизация
сигнала на отрезке 7
3.2.Дискретизация
сигнала на отрезке тремя способами 9
3.3 Квантование
данного сигнала по уровню 11
1Построение
трехмерного графика 13
5Заключение 14
6Список
используемой литературы 15
-
Список
индивидуальных задач
-
Цель
работы
Ознакомиться
с основными алгоритмами дискретизации
аналоговых сигналов –
квантование
по
уровням
и
дискретизации
по
времени.
Используя возможности электронных
таблиц осуществить геометрическую
иллюстрацию подобных преобразований.
-
Описание
алгоритмов процедур дискретизации и
квантования
Большую
часть информации об окружающей среде
человек воспринимает через органы
зрения и слуха. Это естественные для
нас формы информации, которые мы сохраняем
в виде изображений и звуковых записей
на различных носителях.
Когда
мы зрительно наблюдаем ту или иную
область пространства и хотим сохранить
ее описание, то приходим к выводу, что
сделать это можно по-разному. Если
планируется сохранить информацию в
виде графического изображения, значит
надо как-то описать каждый элемент
области пространства. Но что это за
элементы? Пространство непрерывно, одну
и туже область можно разделить на десятки
элементов, можно на тысячи, а можно
согласиться с тем, что в нем бесчисленное
количество элементов — различных точек,
которые в свою очередь делятся на
микроточки и т.д.
Компьютерная
же память не резиновая. В ней невозможно
сохранить бесконечно много информации.
Только ограниченное количество, пусть
и большое. Поэтому предполагаемое для
описания пространство, должно быть
умозрительно разделено на ограниченное
количество элементов. И именно описание
этих элементов будет сохранено в
компьютерной памяти.
Дискретизация
–
это
и
есть
разделение
пространства
или
времени
на
фиксированные
по
размеру
области
(точки,
которые
точками,
по
сути,
не
являются)
или
отрезки.
Так
описываемое
двумерное
изображение
разбивается
на
маленькие
плоскости. В
пределах каждой такой плоскости
характеристики изображения считаются
одинаковыми.
Понятно, что при этом часть информации
теряется. Мы не получаем точную копию
реального объекта, мы лишь описываем
его существенные характеристики.
Итак,
мы условно разбили реальность на области
и планируем хранить информацию только
о них. Но какую информацию? Если это
изображение, то наверно это должны быть
какие-то характеристики изображения.
Чем характеризуется изображение? Как
минимум цветом и яркостью. А ведь эти
характеристики также не дискретны, а
могут иметь множество непрерывных
значений и подзначений. Так степень
яркости можно измерять очень точно, а
можно приблизительно. Если обозначить
полное отсутствие освещенности нулем,
а ее максимальное значение –
99 и
хранить
только
целые
значения,
то
их
окажется
всего
100. Для
возможности
хранения
100 различных
значений
достаточно
27
= 128 бит. Но ведь можно измерять и сохранять
степень яркости очень точно до тысячных
долей единицы и тогда для хранения
потребуется намного больше памяти
(чтобы было можно записать туда все
возможные значения).
Разделение
непрерывного ряда значений какой-либо
характеристики на ограниченное количество
диапазонов называют квантованием.
В компьютере сохраняется лишь номер
диапазона, в который попало конкретное
значение свойства.
Если
при дискретизации разделяется время
или пространство, то при квантовании
этому подвергаются возможные значения
свойств.
Понятно,
что чем более дискретна и квантована
естественная информация, тем более
точно она сохранена в памяти компьютера.
Однако этой памяти потребуется больше.
Человеческие
органы чувств имеют свои ограничения.
Поэтому различие в цвете двух точек мы
можем не уловить, хотя их физические
характеристики длин волн могут
различаться. Поэтому в определенных
значениях потеря информации может быть
незаметна для человека.
Квантова́ние
(англ. quantization) —
в
информатике —
разбиение
диапазона
значений
непрерывной
или
дискретной
величины
на конечное число интервалов.
Существует также векторное
квантование —
разбиение
пространства
возможных значений векторной величины
на конечное число областей. Простейшим
видом квантования является деление
целочисленного значения на натуральное
число,
называемое коэффициентом квантования.
Не
следует путать квантование с дискретизацией
(и, соответственно, шаг квантования с
частотой
дискретизации).
При дискретизации изменяющаяся во
времени величина (сигнал) замеряется с
заданной частотой (частотой дискретизации),
таким образом, дискретизация разбивает
сигнал по временной составляющей (на
графике —
по
горизонтали).
Квантование
же
приводит
сигнал
к
заданным
значениям,
то
есть,
разбивает
по
уровню
сигнала
(на
графике —
по
вертикали).
Сигнал,
к которому применены дискретизация и
квантование, называется цифровым.
Квантование
часто используется при обработке
сигналов,
в том числе при сжатии
звука
и изображений.
При
оцифровке
сигнала количество уровней квантования
называют также глубиной
дискретизации
или разрядностью.
Глубина дискретизации измеряется в
битах
и обозначает количество бит в двоичном
слове, выражающих амплитуду сигнала.
Чем больше глубина дискретизации и чем
больше частота дискретизации, тем точнее
цифровой сигнал соответствует аналоговому.
В случае однородного квантования глубину
дискретизации называют также динамическим
диапазоном
и измеряют в децибелах
(1 бит ≈
6 дБ).
Соседние файлы в предмете Алгоритмические языки и основы программирования
- #
- #
- #
- #
16.01.201661.73 Кб28лаба 3.xlsx
- #
16.01.201674.12 Кб41лаба 4 защита.xlsx
- #
- #
- #
- #
- #
- #
Кодирование звуковой информации
Введение
Не до конца понимаете, как происходит кодирование звуковой информации? Запутались в аналогово-цифровых и цифро-аналоговых преобразователях? Записывайтесь ко мне на индивидуальный урок по информатике и ИКТ. Кроме рассмотрения теоретических сведений мы с вами прорешаем колоссальное количество тематических примеров.
Общие сведения о звуковой информации
В течение дня обычный человек слышит большое количество различных звуков. Давайте попытаемся кратко понять, что же такое звук. Звук – колебания воздуха, которые были созданы неким источником.
Под источником звука можно понимать любой предмет, объект, который способен генерировать звуковые волны:
-
Человек, который что-то произнес.
-
Проезжающий поезд, от которого исходит шум.
-
Музыкальные инструменты, на которых играет музыкант.
В самом широком физическом смысле под звуком следует понимать простую волну. Если говорить о графической интерпретации звука, то звуковые волны следует представлять, как множество синусоидальных графиков функций, каждый из которых имеет ряд обязательных параметров.
Звук обладает множеством характеристик, но ключевыми являются лишь две:
-
Амплитуда звуковой волны.
-
Частота звуковой волны.
Об этих свойствах будет детально рассказано в следующем разделе данной статьи.
Сейчас я вам покажу график функций идеальной звуковой волны, которой в природе физически не существует.
Графическое представление идеальной звуковой волны
Также хочу продемонстрировать график функций неидеальной звуковой волны, которая является речью обыкновенного человека.
Графическое представление неидеальной звуковой волны, которая является речью человека
Посмотрев на оба выше представленных графика функций, у вас должны возникнуть следующие мысли и закономерный вопрос: если перед нами изображен график функций, то где координатная ось, координатная сетка, градуированные шкалы осей ОХ и оси ОY, а также нужно понять, на основании каких закономерностей построены данные графики функций? То есть, какие параметры выступают значением по оси абсцисс и по оси ординат. О данных характеристиках, параметрах будет рассказано ниже.
Характеристики звуковой информации
Как было сказано выше, что звук обладает двумя ключевыми характеристиками: амплитудой и частотой.
Амплитуда – по сути, громкость или сила звука, измеряемая в децибелах. В физике принято сокращение единицы децибел до дБ. Человек в дневное время суток способен воспринимать звуки громкостью от 10-15 дБ. Уровень громкости звука является относительной величиной. Болевой порог для человека составляет уровень громкости звука в 120-130 дБ.
Частота – отношение количества колебаний звуковой волны в единицу времени. Иногда вместо термина «частота звука» используется термин «высота звука». Единицей измерения частоты в мировой системе СИ является герц. Обозначается единица герц как Гц. Человек воспринимает звуковые волны в диапазоне от 20 Гц до 20000 Гц. Звуковые волны, имеющие частотность меньше, чем 20 Гц, называют инфразвуком. Звуковые волны, имеющие частотность выше, чем 20000 Гц, называют ультразвуком.
Влияние частоты на тип звука
Давайте вернемся к графикам функций идеальной и неидеальной звуковой волны.
Наша задача – разобраться, какая величина откладывается на оси абсцисс, а какая – на оси ординат.
Очевидно, что одной из осей является популярнейшая характеристика большинства физических графиков функций – время. Мы не сможем исследовать поведение звуковой волны, если не будем рассматривать ее в различные отрезки времени. Следовательно, осью абсцисс является параметр время. Единицей измерения является, например, секунда или миллисекунда.
Осью ординат выступает амплитуда или громкость рассматриваемой звуковой волны. Чем больше громкость или выше амплитуда, тем выше проходит график функций, соответствующий анализируемой звуковой волне.
Представим те же самые графики функций звуковых волн, но уже с обозначениями осей координат и их градуировкой.
Частота дискретизации звука
Необходимо знать, что процессор персонального компьютера взаимодействует с любыми данными на уровне двоичного кода. Двоичный или бинарный код – цепочки битов, которые принимают только одно из двух предопределенных значений, – 0 или 1.
Под кодированием звуковой информации следует понимать преобразование аналогового звукового сигнала в формат, понятный процессору персонального компьютера, то есть в двоичный код. Аналоговый или непрерывный звуковой сигнал у нас представлен в виде графика функций, как зависимость амплитуды от времени.
Чтобы оцифровать аналоговый звуковой сигнал разобьем ось, выражающую время, на некоторое количество равных отрезков и произведем замеры амплитуды/громкости в каждом отрезке. Предлагаю произвести разбивку с шагом 0.1 секунды.
Дискретизация – процесс преобразования непрерывного сигнала в дискретный, то есть прерывный сигнал. Под частотой дискретизации следует понимать частоту взятия отсчетов непрерывного во времени сигнала при его дискретизации. В нашем случае дискретизация – операция, связанная с разбивкой оси абсцисс, отвечающей за время, на отдельные одинаковые участки. А частотой дискретизации является значение, равное 10 Гц. То есть мы производим 10 замеров амплитуды звуковой волны за 1 секунду.
Дискретизация неидеальной звуковой волны
Таблица значений громкости звуковой волны при частоте дискретизации 10 Гц:
|
Время, сек |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
|
Громкость, дБ |
90 |
20 |
80 |
30 |
90 |
10 |
40 |
20 |
90 |
20 |
60 |
Разрядность звука при кодировании звуковой информации
В теории кодирования звуковой информации понятие разрядности взаимосвязано с понятием квантования. В грубом приближении под квантованием можно понимать операцию, которая преобразует значения громкости или амплитуды звукового сигнала в двоичный код.
Обратимся еще раз к графику функций, который выражает аналоговый неидеальный звуковой сигнал. Значения громкости находятся в диапазоне от 0 до 100 децибел. Следовательно, у нас должна быть возможность запоминания 101 различного состояния, значения. Давайте рассчитаем минимальное количество бит информации, необходимой для кодирования 101 различного значения. Для этого решим простейшее показательное неравенство: 2x ≥ 101. Очевидно, что x = 7, так как 27 = 128 ≥ 100. Следовательно, для кодирования звуковой информации нам будет достаточности разрядности в 7 бит.
Сейчас мы произведем операцию квантования по отношению к замеренной громкости звуковой волны:
|
Время, сек |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
|
Громкость, дБ |
90 |
20 |
80 |
30 |
90 |
10 |
40 |
20 |
90 |
20 |
60 |
|
Двоичный код |
1011010 |
0010100 |
1010000 |
0011110 |
1011010 |
0001010 |
0101000 |
0010100 |
1011010 |
0010100 |
0111100 |
На этом этап кодирования звуковой информации можно считать законченным. В оперативной памяти персонального компьютера входной аналоговый звуковой сигнал будет представлен в следующем виде:
101101000101001010000001111010110100001010 01010000010100101101000101000111100
Хочу обратить ваше внимание, что в приведенном примере мы использовали ничтожно малую частоту дискретизации, равную 10 Гц. В современных условиях кодирование звуковой информации осуществляют при частоте дискретизации 44100 Гц. То есть мы провели 10 замеров в течение 1 секунды, а на практике обеспечивают 44100 замеров за 1 секунду. Чем чаще производятся замеры исследуемой величины, тем точнее кодируется звуковая информация.
Для ради эксперимента давайте рассчитаем информационный объем, которые требуется для хранения звуковой волны в нашем примере, при частоте дискретизации 10 Гц и разрядности 7 бит.
V = [Частота дискретизации] ∙ [Разрядность] ∙ [Промежуток времени] = 10 ∙ 7 ∙ 1 = 70 [бит].
Данная формула справедлива для монозвука. Информационный объем для стереозвука рассчитывается по аналогичной формуле, но в начале стоит коэффициент 2. Это связано с тем, что при кодировании стерео звуковой информации используется две дорожки.
Уровни громкости звука
|
Громкость, дБ |
Характеристика |
Источник звука |
|
0 |
Абсолютная тишина |
|
|
5 |
Почти идеальная тишина |
|
|
10 |
Почти идеальная тишина |
Шорох листьев |
|
15 |
Едва слышно |
Качание веток деревьев |
|
20 |
Едва слышно |
Шепот человека |
|
25 |
Очень тихо |
Шепот человека |
|
30 |
Тихо |
Тиканье часов на стене |
|
35 |
Ниже среднего |
Речь человека на расстоянии 10 метров |
|
40 |
Ниже среднего |
Обыкновенная речь человека |
|
45 |
Ниже среднего |
Обыкновенная речь человека |
|
50 |
Средне |
Печатная машинка |
|
55 |
Выше среднего |
Офисное помещение |
|
60 |
Шумно |
Отдел продаж |
|
65-75 |
Шумно |
Громкий разговор, крики, смех |
|
80 |
Очень громко |
Крик человека |
|
85 |
Очень громко |
Громкий крик человека |
|
90 |
Очень шумно |
Движение поезда на расстоянии в 1 метр |
|
95 |
Очень шумно |
Движение метро снаружи |
|
100 |
Крайне шумно |
Оркестр |
|
120 |
Невыносимо громко |
Отбойный молоток |
|
130 |
Болевой порог |
Самолет при взлете |
|
150 |
Контузия |
Старт ракеты |
|
160 |
Шок, тяжелые травмы слухового аппарата |
Ударная волна при взрыве ядерной бомбы |
|
200 |
Смерть |
Шумовое оружие |
Громкость звука необходимо учитывать при кодировании звуковой информации, так как ее величина влияет на разрядность кодирования звуковых волн, а следовательно, и на информационный вес закодированного в двоичном коде звукового файла.
Краткие логические выводы
Подытожим алгоритм кодирования звуковой информации:
-
Анализ входного аналогового сигнала. Как правило данный сигнал выражается графиком функций в системе координат время-громкость.
-
Проведение операции дискретизации, то есть разбивка входного сигнала на конечное и одинаковые по размерам фрагменты. Чем больше значение частоты дискретизации, тем выше точность преобразования при кодировании звуковой информации.
-
Проведение операции квантования, то есть перевод значений в двоичный формат.
-
Запись двоичного кода в звуковой файл, находящегося на жестком диске персонального компьютера.
Если у вас остались какие-либо вопросы по теме «Кодирование звуковой информации», то записывайтесь ко мне на индивидуальный урок по информатике и ИКТ. Кроме теоретических сведений из области кодирования звуковой информации мы будем делать упор и на решение тематических заданий.
Анастасия Николаевна Королева
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Определение 1
Кодирование, квантование — это преобразование информационных данных в удобный для их передачи по различным каналам формат.
Передача информации
Замечание 1
Под передачей информации понимается физический процесс, при помощи которого выполняется перемещение информационных данных в пространстве.
Этот процесс может быть охарактеризован присутствием таких составляющих, как информационный источник, информационный приёмник, информационный носитель и среда, в которой выполняется передача. Передача информации, как правило, состоит в трансляции информационных данных, перемещение которых выполняется в форме сигналов при помощи электросвязи. Информационная передача может осуществляться в аналоговом или цифровом формате, а также может использоваться аналоговая модуляция или цифровое кодирование. Качественные показатели информационной передачи тем выше, чем меньше фиксируется на принимающей стороне информационных искажений и потерь. С ростом скорости информационного обмена необходимо придерживаться специальных мер, которые препятствуют информационным потерям и понижению качества трансляции информации.

Стажировки для студентов
Начни получать реальный опыт работы по специальности и полезные навыки для дальнейшей карьеры
Найти стажировку
Информационные данные транслируются в форме сообщений от определённого информационного источника к приёмнику информации через канал связи, соединяющий их. Источник отправляет пересылаемое сообщение, которое подвергается кодированию в передаваемый сигнал. Далее сигнал отправляется по каналу связи. В итоге в приёмнике формируется принимаемый сигнал, который подвергается декодированию и превращается в принимаемое сообщение. Информационный обмен по каналам связи практически всегда подвергается воздействию различных помех, которые могут вызывать искажение и даже потерю информационных данных.
Кодирование и квантование при передаче информации по разным каналам
Обмен сообщениями выполняется при помощи сигналов, являющихся информационными носителями. Главным типом сигналов считаются электрические сигналы. Сообщением является самый маленький языковый компонент, обладающий смыслом и пригодный для общения. Жизненный цикл сообщений может быть представлен в таком виде:
- Отправителем выполняется кодирование сущности сообщения.
- Отправитель пересылает закодированное сообщение через канал связи получателю.
- На стороне получателя сообщение принимается и декодируется.
«Кодирование, квантование при передаче информации по разным каналам» 👇
Средством связи является комплект оборудования, которое обеспечивает процесс преобразования исходного сообщения от информационного источника в сигналы необходимой физической природы, их трансляцию, приём и обратное преобразование в формат, необходимый потребителям. Сигналом является изменение физической величины, которое передаёт информацию, закодированную конкретным методом. Сигналом в информационной системе считается комплект отправленных и принятых информационных данных, содержащих информацию, закодированную некоторым методом.
Линией связи является набор средств связи и канала связи, при помощи которых выполняется трансляция данных от источника к приёмнику. Основным параметром всех линий связи считается допустимая скорость информационного обмена, а также уровень искажения сообщений при их трансляции.
Источником информации является объект или субъект, который порождает информацию и отображающий её в формате сообщения, то есть последовательного набора сигналов. С точки зрения математики, под источником информации понимается массив вероятных сообщений с определённой на этом массиве вероятностной мерой. Можно выделить дискретные информационные источники и непрерывные. Отличаются они тем, что дискретные элементы представляют собой счётное множество, а непрерывные элементы являются несчётным множеством.
Дискретный источник считается определённым, если возможно перечислить все его допустимые сообщения и можно указать их вероятность.
Кодирующим является устройство, которое предназначено для формирования из исходного сообщения источника удобный для передачи формат. Декодирующим является устройство, выполняющее преобразование закодированного сообщения в исходный формат.
Схема информационного канала представлена на рисунке ниже:
Рисунок 1. Схема информационного канала. Автор24 — интернет-биржа студенческих работ
Передаваемые сигналы делятся на следующие типы:
- Аналоговые сигналы.
- Дискретные сигналы.
- Квантованные сигналы.
- Цифровые сигналы.
Аналоговые и цифровые сигналы кардинально различаются между собой. Условно выражаясь, можно сказать, что они расположены на разных окончаниях единого спектра. Для их взаимного преобразования используются аналого-цифровые и цифро-аналоговые преобразователи. Большинство сигналов являются аналоговыми, то есть могут изменяться непрерывно с течением времени. Аналоговые сигналы присутствуют в телефонной связи, теле- и радио — вещании. Осуществить ввод такого сигнала в компьютер и выполнить его обработку невозможно, поскольку во всех временных интервалах он обладает бесконечным множеством значений. То есть требуется преобразовать его в последовательность чисел определённой разрядности.
Выполнение дискретизации аналоговых сигналов заключается в том, что сигнал отображается в формате последовательности значений, берущихся в дискретные временные моменты. Такие значения именуются отсчётами, а величина At представляет собой интервал дискретизации.
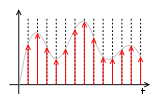
При выполнении квантования весь диапазон величин сигнала делится на уровни, число которых представляется в числах определённой разрядности. Расстояние между такими уровнями считается шагом квантования. Количество таких уровней равняется N и обозначается значениями от нуля до N – 1. Каждый уровень кодируется некоторым числом. Величина сигнала подлежит сравнению с уровнями квантования и сигналом в данный момент времени будет число, которое соответствует определённому уровню квантования. Все уровни квантования могут кодироваться двоичным n-разрядным числом. Количество уровней квантования N и количество разрядов n двоичного числа, которое кодирует данные уровни, определяются соотношением n≥log2(N). На рисунке ниже представлен образец квантованного сигнала:
Рисунок 2. Образец квантованного сигнала. Автор24 — интернет-биржа студенческих работ
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме



![y_q=left[frac{y-y_0}{h}right]](https://dic.academic.ru/pictures/wiki/files/56/856cc21ae38c22d80f3b09e6d2577c32.png) .
.