Уровни прозрачности информатика егэ - Помощь в подготовке к экзаменам и поступлению

5443. (А. Кабанов) При кодировании растрового изображения для каждого пикселя используется палитра из 224 цветов и 256 уровней прозрачности. Коды пикселей записываются в файл один за другим без промежутков. Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 1024 на 768 пикселей?

Задание КИМ № 7: Кодирование графической и звуковой информации
Раздел № 38: Информационный объём изображений

(А. Кабанов) При кодировании растрового изображения для каждого пикселя используется палитра из 2²⁴ цветов и 256 уровней прозрачности. Коды пикселей записываются в файл один за другим без промежутков. Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 1024 на 768 пикселей?

Ответ:

3072

Посмотрите видео решение:

Источник

Тема 7.

Передача данных. Размеры файлов.

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

передача данных. размеры файлов.

7.01Изображение

7.02Звукозапись

7.03Видеофайлы

7.04Текстовые файлы

7.05Передача по каналу связи

7.06Сравнение двух способов передачи данных

7.07Смешанное

7.08Измерение информации

Решаем задачу:

Показать ответ и решение

210 Кбайт — это объем, включающий в себя информацию о самом изображении и о его прозрачности.

Сначала найдем, сколько памяти занимает информация о прозрачности:

= 860160 бит, т.е. 860160-= 105
8⋅1024 Кбайт.

Значит, информация об изображении занимает Кбайт.

Найдем глубину цвета: 13
1100524⋅2⋅120 = 7 бит.

Значит, максимальное количество цветов .

Источник

Урок посвящен разбору задания 7 ЕГЭ по информатике

Содержание:

Объяснение заданий 7 ЕГЭ по информатике
- Кодирование текстовой информации
- Кодирование графической информации
- Кодирование звуковой информации
- Определение скорости передачи информации
Решение заданий 7 ЕГЭ по информатике
- Тема: Кодирование изображений
- Тема: Кодирование звука
- Тема: Кодирование видео
- Тема: Скорость передачи данных

7-е задание: «Кодирование графической и звуковой информации, объем и передача информации»

Уровень сложности

— базовый,

Требуется использование специализированного программного обеспечения

— нет,

Максимальный балл

— 1,

Примерное время выполнения

— 5 минут.

Проверяемые элементы содержания: Умение определять объём памяти, необходимый для хранения графической и звуковой информации

До ЕГЭ 2021 года — это было задание № 9 ЕГЭ

Типичные ошибки и рекомендации по их предотвращению:

«Если вычисления получаются слишком громоздкими, значит, Вы неправильно решаете задачу. Удобно выделить во всех множителях степени двойки, тогда умножение сведётся к сложению
показателей степеней, а деление – к вычитанию»

ФГБНУ «Федеральный институт педагогических измерений»

Кодирование текстовой информации

I = n * i

где:

n — количество символов

i — количество бит на 1 символ (кодировка)

Кодирование графической информации

Рассмотрим некоторые понятия и формулы, необходимые для решения ЕГЭ по информатике данной темы.

Пиксель – это наименьший элемент растрового изображения, который имеет определенный цвет.
Разрешение – это количество пикселей на дюйм размера изображения.
Глубина цвета — это количество битов, необходимое для кодирования цвета пикселя.
Если глубина кодирования составляет i битов на пиксель, код каждого пикселя выбирается из 2ⁱ возможных вариантов, поэтому можно использовать не более 2ⁱ различных цветов.

Формула для нахождения количества цветов в используемой палитре:

i = log₂N

N — количество цветов
i — глубина цвета
В цветовой модели RGB (красный (R), зеленый (G), синий (B)): R (0..255) G (0..255) B (0..255) -> получаем 2⁸ вариантов на каждый из трех цветов.
R G B: 24 бита = 3 байта — режим True Color (истинный цвет)

Найдем формулу объема памяти для хранения растрового изображения:

I = M * N * i

где:

I — объем памяти, требуемый для хранения изображения
M — ширина изображения в пикселях
N — высота изображения в пикселях
i — глубина кодирования цвета или разрешение

Или можно формулу записать так:

I = N * i битов

где N – количество пикселей (M * N) и i – глубина кодирования цвета (разрядность кодирования)

* для указания объема выделенной памяти встречаются разные обозначения (V или I).

Следует также помнить формулы преобразования:

1 Мбайт = 2²⁰ байт = 2²³ бит,
1 Кбайт = 2¹⁰ байт = 2¹³ бит

Кодирование звуковой информации

Познакомимся с понятиями и формулами, необходимыми для решения заданий 7 ЕГЭ по информатике.

Оцифровка или дискретизация – это преобразование аналогового сигнала в цифровой код.

Дискретизация, объяснение задания 7 ЕГЭ

T – интервал дискретизации (измеряется в с)
ƒ — частота дискретизации (измеряется в Гц, кГц)

* Изображение взято из презентации К. Полякова

Частота дискретизации определяет количество отсчетов, т.е. отдельных значений сигнала, запоминаемых за 1 секунду. Измеряется в герцах, 1 Гц (один герц) – это один отсчет в секунду, а, например, 7 кГц – это 7000 отсчетов в секунду.
Разрядность кодирования (глубина, разрешение) — это число битов, используемое для хранения одного отсчёта.

Разрядность кодирования

* Изображение взято из презентации К. Полякова

Получим формулу объема звукового файла:

Для хранения информации о звуке длительностью t секунд, закодированном с частотой дискретизации ƒ Гц и глубиной кодирования β бит требуется бит памяти:

I = β * ƒ * t * S

I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S — количество каналов

S для моно = 1, для стерео = 2, для квадро = 4

Пример: при ƒ=8 кГц, глубине кодирования 16 бит на отсчёт и длительности звука 128 с. потребуется:

✍ Решение:

I = 8000*16*128 = 16384000 бит
I = 8000*16*128/8 = 2³ * 1000 * 2⁴ * 2⁷ / 2³ = 2¹⁴ / 2³ =2¹¹ =
= 2048000 байт

Определение скорости передачи информации

Канал связи всегда имеет ограниченную пропускную способность (скорость передачи информации), которая зависит от свойств аппаратуры и самой линии связи(кабеля)

Объем переданной информации I вычисляется по формуле:

I = V * t

I — объем информации
v — пропускная способность канала связи (измеряется в битах в секунду или подобных единицах)
t — время передачи

* Вместо обозначения скорости V иногда используется q
* Вместо обозначения объема сообщения I иногда используется Q

Скорость передачи данных определяется по формуле:

V = I/t

и измеряется в бит/с

Егифка ©:

Решение заданий 7 ЕГЭ по информатике

Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ

Тема: Кодирование изображений

7_1:

Какой минимальный объем памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 160 х 160 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.

Типовые задания для тренировки

✍ Решение:

Используем формулу нахождения объема:
Подсчитаем каждый сомножитель в формуле, стараясь привести числа к степеням двойки:
M x N:

160 * 160 = 20 * 2³ *  20 * 2³ = 400 * 2⁶ = 
= 25 * 2⁴ * 2⁶

Нахождение глубины кодирования i:

256 = 2⁸ 
т.е. 8 бит на пиксель  (из формулы кол-во цветов = 2ⁱ)

Находим объем:

I = 25 * 2⁴ * 2⁶ * 2³ = 25 * 2¹³ - всего бит на всё изображение

Переводим в Кбайты:

(25 * 2¹³) / 2¹³ = 25 Кбайт

Результат: 25

Детальный разбор задания 7 ЕГЭ по информатике предлагаем посмотреть в видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование изображений:

ЕГЭ по информатике задание 7.2:

Рисунок размером 128 на 256 пикселей занимает в памяти 24 Кбайт (без учёта сжатия). Найдите максимально возможное количество цветов в палитре изображения.

Типовые задания для тренировки

✍ Решение:

По формуле объема файла изображения имеем:
где M * N — общее количество пикселей. Найдем это значение, используя для удобства степени двойки:

128 * 256 = 2⁷ * 2⁸ = 2¹⁵

В вышеуказанной формуле i — это глубина цвета, от которой зависит количество цветов в палитре:
Найдем i из той же формулы:

i = I / (M*N)

Учтем, что 24 Кбайт необходимо перевести в биты. Получим:

2³ * 3 * 2¹⁰ * 2³:
i = (2³ * 3 * 2¹⁰ * 2³) / 2¹⁵ = 
= 3 * 2¹⁶ / 2¹⁵ = 6 бит

Теперь найдем количество цветов в палитре:

2⁶ = 64 вариантов цветов в цветовой палитре

Результат: 64

Смотрите видеоразбор задания:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование изображений:

ЕГЭ по информатике задание 7.3:

После преобразования растрового 256-цветного графического файла в 4-цветный формат его размер уменьшился на 18 Кбайт. Каков был размер исходного файла в Кбайтах?

Типовые задания для тренировки

✍ Решение:

По формуле объема файла изображения имеем:

где N — общее количество пикселей,
а i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель)

i можно найти, зная количество цветов в палитре:

до преобразования: i = 8 (2⁸ = 256)
после преобразования: i = 2 (2² = 4)

Составим систему уравнений на основе имеющихся сведений, примем за x количество пикселей (разрешение):

I = x * 8
I - 18 = x * 2

Выразим x в первом уравнении:

x = I / 8

Подставим во второе уравнение и найдем I (объем файла):

I - 18 = I / 4
4I - I = 72
3I = 72
I = 24

Результат: 24

Подробный разбор 7 задания ЕГЭ смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование изображений:

ЕГЭ по информатике задание 7.4:

Цветное изображение было оцифровано и сохранено в виде файла без использования сжатия данных. Размер полученного файла – 42 Мбайт. Затем то же изображение было оцифровано повторно с разрешением в 2 раза меньше и глубиной кодирования цвета увеличили в 4 раза больше по сравнению с первоначальными параметрами. Сжатие данных не производилось. Укажите размер файла в Мбайт, полученного при повторной оцифровке.

Типовые задания для тренировки

✍ Решение:

По формуле объема файла изображения имеем:

где N — общее количество пикселей или разрешение,
а i — глубина цвета (количество бит, выделенное на 1 пиксель)

В такого рода задачах необходимо учесть, что уменьшение разрешения в 2 раза, подразумевает уменьшение в 2 раза пикселей отдельно по ширине и по высоте. Т.е. в целом N уменьшается в 4 раза!
Составим систему уравнений на основе имеющихся сведений, в которой первое уравнение будет соответствовать данным до преобразования файла, а второе уравнение — после:

42 = N * i
I = N / 4 * 4i

Выразим i в первом уравнении:

i = 42 / N

Подставим во второе уравнение и найдем I (объем файла):

[ I= frac {N}{4} * 4* frac {42}{N} ]

После сокращений получим:

I = 42

Результат: 42

Тема: Кодирование изображений:

ЕГЭ по информатике задание 7.5:

Изображение было оцифровано и сохранено в виде растрового файла. Получившийся файл был передан в город А по каналу связи за 72 секунды. Затем то же изображение было оцифровано повторно с разрешением в 2 раза больше и глубиной кодирования цвета в 3 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б, пропускная способность канала связи с городом Б в 3 раза выше, чем канала связи с городом А.
Сколько секунд длилась передача файла в город Б?

Типовые задания для тренировки

✍ Решение:

По формуле скорости передачи файла имеем:

где I — объем файла, а t — время

По формуле объема файла изображения имеем:

где N — общее количество пикселей или разрешение,
а i — глубина цвета (количество бит, выделенное на 1 пиксель)

Для данной задачи, необходимо уточнить, что разрешение на самом деле имеет два сомножителя (пикселей по ширине * пикселей по высоте). Поэтому при увеличении разрешения в два раза, увеличатся оба числа, т.е. N увеличится в 4 раза вместо двух.
Изменим формулу получения объема файла для города Б:

[ I= frac {2*N * i}{3} ]

Для города А и Б заменим значения объема в формуле для получения скорости:

Город А:

[ V= frac {N*i}{72} ]

Город Б:

[ 3*V= frac{frac {4*N*i}{3}}{t} ]

или:

[ t*3*V= frac {4*N*i}{3} ]

Подставим значение скорости из формулы для города А в формулу для города Б:

[ frac {t*3*N*i}{72}= frac {4*N*i}{3} ]

Выразим t:

t = 4 * 72 / (3 * 3) = 32 секунды

Результат: 32

Другой способ решения смотрите в видеоуроке:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование изображений:

ЕГЭ по информатике задание 7.6:

Камера делает фотоснимки размером 1024 х 768 пикселей. На хранение одного кадра отводится 900 Кбайт.
Найдите максимально возможное количество цветов в палитре изображения.

Типовые задания для терировки

✍ Решение:

Количество цветов зависит от глубины кодирования цвета, которая измеряется в битах. Для хранения кадра, т.е. общего количества пикселей выделено 900 Кбайт. Переведем в биты:

900 Кбайт = 2² * 225 * 2¹⁰ * 2³ = 225 * 2¹⁵

Посчитаем общее количество пикселей (из заданного размера):

1024 * 768 = 2¹⁰ * 3 * 2⁸

Определим объем памяти, необходимый для хранения не общего количества пикселей, а одного пикселя ([память для кадра]/[кол-во пикселей]):

[ frac {225 * 2^{15}}{3 * 2^{18}} = frac {75}{8} approx 9 ]

9 бит на 1 пиксель

9 бит — это i — глубина кодирования цвета. Количество цветов = 2ⁱ:

2⁹ = 512

Результат: 512

Смотрите подробное решение на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование изображений:

7_8: Демоверсия ЕГЭ 2018 информатика:

Автоматическая фотокамера производит растровые изображения размером 640×480 пикселей. При этом объём файла с изображением не может превышать 320 Кбайт, упаковка данных не производится.
Какое максимальное количество цветов можно использовать в палитре?

✍ Решение:

По формуле объема файла изображения имеем:

I = N * i

где N — общее количество пикселей или разрешение, а i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель)

Посмотрим, что из формулы нам уже дано:

I = 320 Кбайт, 
N = 640 * 420 = 307200 = 75 * 2¹² всего пикселей, 
i - ?

Количество цветов в изображении зависит от параметра i, который неизвестен. Вспомним формулу:

количество цветов = 2ⁱ

Поскольку глубина цвета измеряется в битах, то необходимо объем перевести из Килобайт в биты:

320 Кбайт = 320 * 2¹⁰ * 2³ бит  = 320 * 2¹³ бит

Найдем i:

[ i = frac {I}{N} = frac {320 * 2^{13}}{75 * 2^{12}} approx 8,5 бит ]

Найдем количество цветов:

2ⁱ = 2⁸ = 256

Результат: 256

Подробное решение данного 7 (9) задания из демоверсии ЕГЭ 2018 года смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

7_21: : ЕГЭ по информатике задание 7.21:

Для хранения в информационной системе документы сканируются с разрешением 300 ppi. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 5 Мбайт. В целях экономии было решено перейти на разрешение 150 ppi и цветовую систему, содержащую 16 цветов. Средний размер документа, отсканированного с изменёнными параметрами, составляет 512 Кбайт.

Определите количество цветов в палитре до оптимизации.

Типовые задания для тренировки

✍ Решение:

По формуле объема файла изображения имеем:

I = N * i

где N — общее количество пикселей или разрешение, а i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель).

Так как по заданию имеем разрешение, выраженное в пикселях на дюйм, то фактически это означает:

I = значение ppi² * N * i

Формула количества цветов:

количество цветов = 2ⁱ

Посмотрим, что из формулы нам уже дано до экономного варианта и при экономном варианте:

Неэкономный вариант:
I = 5 Мбайт = 5 * 2²³ бит, 
N - ?, 
i - ?
300 ppi

Экономный вариант:
I = 512 Кбайт = 2⁹ * 2¹³ бит = 2²² бит, 
N - ?, 
i = 4 бит (2⁴ = 16)
150 ppi

Так как в экономном режиме нам известны все составляющие формулы, кроме разрешения (N), то найдем разрешение:

N = I / (i * 150*150 ppi)
N = 2²² / (4 * 22500)

Подставим все известные значения, включая найденное N, в формулу для неэкономного режима:

I = N * 300*300 ppi * i
5 * 2²³ = (2²² * 300 * 300 * i) / (22500 * 4);

Выразим i и вычислим его значение:

i = (5 * 2²³ * 22500 * 4) / (2²² * 300 * 300) = 9000 / 900 = 10 бит

По формуле нахождения количества цветов в палитре имеем:

2¹⁰ = 1024

Результат: 1024

Тема: Кодирование звука

7_7:

На студии при четырехканальной (квадро) звукозаписи с 32-битным разрешением за 30 секунд был записан звуковой файл. Сжатие данных не производилось. Известно, что размер файла оказался 7500 Кбайт.

С какой частотой дискретизации (в кГц) велась запись? В качестве ответа укажите только число, единицы измерения указывать не нужно.

Типовые задания для тренировки

✍ Решение:

По формуле объема звукового файла получим:

I = β * t * ƒ * S

Из задания имеем:

I= 7500 Кбайт
β= 32 бита
t= 30 секунд
S= 4 канала

ƒ — частота дискретизации — неизвестна, выразим ее из формулы:

[ ƒ = frac {I}{S*B*t} = frac {7500 * 2^{10} * 2^3 бит}{2^7 * 30}Гц = frac { 750 * 2^6}{1000}КГц = 2^4 = 16 ]

2⁴ = 16 КГц

Результат: 16

Для более детального разбора предлагаем посмотреть видео решения данного 7 задания ЕГЭ по информатике:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звука:

ЕГЭ по информатике задание 7_9:

Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 2 раза выше и частотой дискретизации в 3 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 15 секунд; пропускная способность канала связи с городом Б в 4 раза выше, чем канала связи с городом А.

Сколько секунд длилась передача файла в город A? В ответе запишите только целое число, единицу измерения писать не нужно.

Типовые задания для тренировки

✍ Решение:

Для решения понадобится формула нахождения скорости передачи данных формулы:

V = I/t

Вспомним также формулу объема звукового файла:

I = β * ƒ * t * s

где:
I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S — кол-во каналов (если не указывается, то моно)

Выпишем отдельно, все данные, касающиеся города Б (про А практически ничего не известно):

город Б: 
β - в 2 раза выше
ƒ - в 3 раза меньше
t - 15 секунд, 
пропускная способность (скорость V) - в 4 раза выше

Исходя из предыдущего пункта, для города А получаем обратные значения:

город А: 
β_Б / 2
ƒ_Б * 3
I_Б / 2
V_Б / 4
t_Б / 2, t_Б * 3, t_Б * 4  -  ?

Дадим объяснения полученным данным:
так как глубина кодирования (β) для города Б выше в 2 раза, то для города А она будет ниже в 2 раза, соответственно, и t уменьшится в 2 раза:

t = t/2

так как частота дискретизации (ƒ) для города Б меньше в 3 раза, то для города А она будет выше в 3 раза; I и t изменяются пропорционально, значит, при увеличении частоты дискретизации увеличится не только объем, но и время:

t = t * 3

скорость (V)(пропускная способность) для города Б выше в 4 раза, значит, для города А она будет ниже в 4 раза; раз скорость ниже, то время выше в 4 раза (t и V — обратно пропорциональная зависимость из формулы V = I/t):

t = t * 4

Таким образом, с учетом всех показателей, время для города А меняется так:

[ t_А = frac {15}{2} * 3 * 4 ]

90 секунд

Результат: 90

Подробное решение смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звука:

ЕГЭ по информатике задание 7.10:

Музыкальный фрагмент был записан в формате стерео (двухканальная запись), оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 30 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате моно и оцифрован с разрешением в 2 раза выше и частотой дискретизации в 1,5 раза меньше, чем в первый раз. Сжатие данных не производилось.

Укажите размер файла в Мбайт, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно.

Типовые задания для тренировки

✍ Решение:

Вспомним формулу объема звукового файла:

I = β * ƒ * t * S

I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S -количество каналов

Выпишем отдельно, все данные, касающиеся первого состояния файла, затем второго состояния — после преобразования:

1 состояние:
S = 2 канала
I = 30 Мбайт

2 состояние:
S = 1 канал
β = в 2 раза выше
ƒ = в 1,5 раза ниже
I = ?

Так как изначально было 2 канала связи (S), а стал использоваться один канал связи, то файл уменьшился в 2 раза:

I = I / 2

Глубина кодирования (β) увеличилась в 2 раза, то и объем (I) увеличится в 2 раза (пропорциональная зависимость):

I = I * 2

Частота дискретизации (ƒ) уменьшилась в 1,5 раза, значит, объем (I) тоже уменьшится в 1,5 раза:

I = I / 1,5

Рассмотрим все изменения объема преобразованного файла:

I = 30 Мбайт / 2 * 2 / 1,5 = 20 Мбайт

Результат: 20

Смотрите видеоразбор данной задачи:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звуковых файлов:

ЕГЭ по информатике задание 7_11:

Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 100 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 3 раза выше и частотой дискретизации в 4 раз меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 15 секунд.

✍ Решение:

Вспомним формулу объема звукового файла:

I = β * ƒ * t * S

I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время

Выпишем отдельно, все данные, касающиеся файла, переданного в город А, затем преобразованного файла, переданного в город Б:

А:
t = 100 c.

Б:
β = в 3 раза выше
ƒ = в 4 раза ниже
t = 15 c.

✎ 1 способ решения:

Скорость передачи данных (пропускная способность) зависит от времени передачи файла: чем больше время, тем ниже скорость. Т.е. во сколько раз увеличится время передачи, во столько раз уменьшится скорость и наоборот.
Из предыдущего пункта видим, что если мы вычислим, во сколько раз уменьшится или увеличится время передачи файла в город Б (по сравнению с городом А), то мы поймем, во сколько раз увеличится или уменьшится скорость передачи данных в город Б (обратная зависимость).
Соответственно, представим, что преобразованный файл передается в город А. Объем файла изменился в 3/4 раза (глубина кодирования (β) в 3 раза выше, частота дискретизации (ƒ) в 4 раза ниже). Объем и время изменяются пропорционально. Значит и время изменится в 3/4 раза:

 t_{A для преобразов.} = 100 секунд * 3 / 4 = 75 секунд

Т.е. преобразованный файл передавался бы в город А 75 секунд, а в город Б 15 секунд. Вычислим, во сколько раз снизилось время передачи:

75 / 15 = 5

Раз время передачи в город Б снизилось в 5 раз, соответственно, скорость увеличилась в 5 раз.

Ответ: 5

✎ 2 способ решения:

Выпишем отдельно все данные, касающиеся файла, переданного в город А:
```
А:
t_А = 100 c.
V_А = I / 100
```
Поскольку увеличение или уменьшение во сколько-то раз разрешения и частоты дискретизации приводит к соответствующему увеличению или уменьшению объема файла (пропорциональная зависимость), то запишем известные данные для преобразованного файла, переданного в город Б:

Б:
β = в 3 раза выше
ƒ = в 4 раза ниже
t = 15 c.
I_Б = (3 / 4) * I
V_Б = ((3 / 4) * I) / 15

Теперь найдем соотношение V_Б к V_А:

[ frac {V_Б}{V_А} = frac {3/_4 * I}{15} * frac {100}{I} = frac {3/_4 * 100}{15} = frac {15}{3} = 5 ]

(((3/4) * I) / 15) * (100 / I)= (3/4 * 100) / 15 = 15/3 = 5

Результат: 5

Подробный видеоразбор задания:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звука:

ЕГЭ по информатике задание 7_12:

Производится четырёхканальная (квадро) звукозапись с частотой дискретизации 32 кГц и 32-битным разрешением. Запись длится 2 минуты, её результаты записываются в файл, сжатие данных не производится.

Определите приблизительно размер полученного файла (в Мбайт). В качестве ответа укажите ближайшее к размеру файла целое число, кратное 10.

✍ Решение:

Вспомним формулу объема звукового файла:

I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S — количество каналов

Для простоты расчетов пока не будем брать во внимание количество каналов. Рассмотрим, какие данные у нас есть, и какие из них необходимо перевести в другие единицы измерения:

β = 32 бита
ƒ = 32кГц = 32000Гц
t = 2 мин = 120 с

Подставим данные в формулу; учтем, что результат необходимо получить в Мбайтах, соответственно, произведение будем делить на 2²³ (2³ (байт) * 2¹⁰ (Кбайт) * 2¹⁰(Мбайт)):

(32 * 32000 * 120) / 2²³ = 
=( 2⁵ * 2⁷ * 250 * 120) / 2²³ = 
= (250*120) / 2¹¹ = 
= 30000 / 2¹¹ = 
= (2⁴ * 1875) / 2¹¹ =
= 1875 / 128 ~ 14,6

Полученный результат значения объема умножим на 4 с учетом количества каналов связи:

 14,6 * 4 = 58,5

Ближайшее число, кратное 10 — это 60.

Результат: 60

Смотрите подробное решение:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звука:

7_19: Государственный выпускной экзамен ГВЭ 2018 (информатика ГВЭ ФИПИ, задание 7):

Производится двухканальная (стерео) цифровая звукозапись. Значение сигнала фиксируется 48 000 раз в секунду, для записи каждого значения используется 32 бит. Запись длится 5 минут, её результаты записываются в файл, сжатие данных не производится.

Какая из приведённых ниже величин наиболее близка к размеру полученного файла?

1) 14 Мбайт
2) 28 Мбайт
3) 55 Мбайт
4) 110 Мбайт

✍ Решение:

По формуле объема звукового файла имеем:

I — объем
β — глубина кодирования = 32 бита
ƒ — частота дискретизации = 48000 Гц
t — время = 5 мин = 300 с
S — количество каналов = 2

Подставим в формулу имеющиеся значения:

I = 48000 * 32 * 300 * 2

Поскольку значения большие, необходимо числа 48000 и 300 выразить в степенях двойки:

48000 | 2
24000 | 2
12000 | 2
 6000 | 2     = 375 * 2⁷
 3000 | 2
 1500 | 2
  750 | 2 
  375 | 2 - уже не делится
 187,5

300 | 2     = 75 * 2²
150 | 2
 75 | 2 - уже не делится 
37,5

Получим:

I = 375 * 75 * 2¹⁵

В предложенных вариантах ответа видим, что результат везде в Мбайт. Значит, необходимо разделить полученный нами результат на 2²³ (2³ * 2¹⁰ * 2¹⁰):

I = 375 * 75 * 2¹⁵ / 2²³ = 28125 / 2⁸

Найдем приближенное к числу 28125 значение в степени двойки:

Получаем:

2¹⁰ * 2⁵ = 2¹⁵ = 32768
2¹⁰ * 2⁴ = 2¹⁴ = 16384

Число 28125 лежит между этими значениями, значит берем их:

2¹⁵ / 2⁸ = 2⁷ = 128
2¹⁴ / 2⁸ = 2⁶ = 64

Выбираем ответ, значение в котором находится между двумя этими числами: вариант 4 (110 Мбайт)

Результат: 4

Подробное решение ГВЭ задания 7 2018 года смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звука:

7_20:

Производится двухканальная (стерео) звукозапись с частотой дискретизации 4 кГц и 64-битным разрешением. Запись длится 1 минуту, ее результаты записываются в файл, сжатие данных не производится.

Определите приблизительно размер получившегося файла (в Мбайтах). В качестве ответа укажите ближайшее к размеру файла целое число, кратное 2.

✍ Решение:

По формуле объема звукового файла имеем:

I — объем
β — глубина кодирования = 32 бита
ƒ — частота дискретизации = 48000 Гц
t — время = 5 мин = 300 с
S — количество каналов = 2

Подставим в формулу имеющиеся значения. Для удобства будем использовать степени двойки:

ƒ = 4 кГЦ = 4 * 1000 Гц ~ 2² * 2¹⁰
B = 64 бит = 2⁶ / 2²³ Мбайт
t = 1 мин = 60 c = 15 * 2² c
S = 2

Подставим значения в формулу объема звукового файла:

I = 2⁶ * 2² * 2¹⁰ * 15 * 2² * 2¹ / 2²³ = 15/4 ~ 3,75

Ближайшее целое, кратное двум — это число 4

Результат: 4

Видеоразбор задания:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование видео

7_22:

Камера снимает видео без звука с частотой 120 кадров в секунду, при этом изображения используют палитру, содержащую 2²⁴ = 16 777 216 цветов. При записи файла на сервер полученное видео преобразуют так, что частота кадров уменьшается до 20, а изображения преобразуют в формат, использующий палитру из 256 цветов. Другие преобразования и иные методы сжатия не используются. 10 секунд преобразованного видео в среднем занимают 512 Кбайт.

Сколько Мбайт в среднем занимает 1 минута исходного видео?

Типовые задания для тренировки

✍ Решение:

Посмотрим, как изменялись параметры файла до преобразования и после:

ДО:
ƒ = 120, 
i = 24 бит

ПОСЛЕ:
ƒ = 20, 
i = 8 бит (2⁸ = 256)
t = 10 секунд
I = 512 Кбайт = 2⁹ Кбайт

Поскольку после преобразования количество кадров в секунду уменьшилось в 6 раз (120 / 20 = 6), а количество бит на пиксель уменьшилось в 3 раза (24 / 8 = 3), то и объем уменьшился в целом в 18 раз (6 * 3 = 18).
Вычислим объем файла, передаваемого за 10 секунд, до его преобразования:

за 10 секунд: I * 18 = 2⁹ * 18 Кбайт = (2⁹ * 18) . 2¹⁰ Мбайт = 9 Мбайт

Чтобы получить объем, переданный за 1 минуту, необходимо полученное значение умножить на 6:

за 1 мин: 9 * 6 = 54 Мбайт

Результат: 54

Тема: Скорость передачи данных

ЕГЭ по информатике задание 7_13:

Скорость передачи данных через ADSL-соединение равна 128000 бит/с. Передача текстового файла через это соединение заняла 1 минуту.

Определите, сколько символов содержал переданный текст, если известно, что он был представлен в 16-битной кодировке Unicode.

Типовые задания для тренировки

✍ Решение:

Вспомним формулу скорости передачи данных:

* Вместо Q можно использовать обозначение I (для объема файла)

V - скорость
Q - объем
t - время

Что нам известно из формулы (для удобства решения будем использовать степени двойки):

V = 128000 бит/с = 2¹⁰ * 125 бит/с
t = 1 мин = 60 с = 2² * 15 с
1 символ кодируется 16-ю битами
всего символов - ?

Если мы найдем, сколько бит необходимо для всего текста, тогда, зная что на 1 символ приходится 16 бит, мы сможем найти сколько всего символов в тексте. Таким образом, найдем объем:

Q = 2¹⁰ * 125 * 2² * 15 = 
= 2¹² * 1875 бит на все символы

Когда мы знаем, что на 1 символ необходимо 16 бит, а на все символы 2¹² * 1875 бит, то можем найти общее количество символов:

кол-во символов = 2¹² * 1875 / 16 = 2¹² * 1875 / 2⁴ = 
= 2⁸ * 1875 = 480000

Результат: 480000

Разбор 7 задания:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Скорость передачи информации:

ЕГЭ по информатике задание 7_14:

У Васи есть доступ к Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения им информации 2¹⁷ бит в секунду. У Пети нет скоростного доступа в Интернет, но есть возможность получать информацию от Васи по низкоскоростному телефонному каналу со средней скоростью 2¹⁶ бит в секунду. Петя договорился с Васей, что тот будет скачивать для него данные объемом 8 Мбайт по высокоскоростному каналу и ретранслировать их Пете по низкоскоростному каналу. Компьютер Васи может начать ретрансляцию данных не раньше, чем им будут получены первые 1024 Кбайт этих данных.

Каков минимально возможный промежуток времени (в секундах), с момента начала скачивания Васей данных, до полного их получения Петей?

Типовые задания для тренировки

✍ Решение:

Вспомним формулу скорости передачи данных:

* Вместо Q можно использовать обозначение I (для объема файла)

V - скорость
Q - объем
t - время

Определим, что нам известно:

Вася: V = 2¹⁷ бит/с
Петя: V = 2¹⁶ бит/с
Общий объем Q = 8 Мбайт

Для начала переведем объем в биты:

Q = 8Мбайт = 8 * 2²³ бит = 2³ * 2²³ = 2²⁶ бит

Также известно, что сначала 1024 Кбайта будут передаваться по скоростному каналу Васи со скоростью 2¹⁷ бит/с (примем за t1), а затем все 8 Мбайт будут передаваться по низкоскоростному каналу (примем за t2). Найдем время по двум промежуткам:

t1 = 1024 Кбайт / 2¹⁷ = 2¹⁰ * 2¹³ бит / 2¹⁷ = 
= 2¹⁰ / 2⁴ = 64 с

t2 = 2²⁶ / 2¹⁶ = 2¹⁰ = 1024 c

Найдем общее время:

t = t1 + t2 = 64 + 1024 = 1088

Результат: 1088

Подробный разбор смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Скорость передачи информации:

ЕГЭ по информатике задание 7_15:

Сколько секунд потребуется модему, передающему сообщения со скоростью 32000 бит/с, чтобы передать 16-цветное растровое изображение размером 800 x 600 пикселей, при условии, что в каждом байте закодировано максимально возможное число пикселей?

Типовые задания для тренировки

✍ Решение:

Вспомним формулу скорости передачи данных:

* Вместо Q можно использовать обозначение I (для объема файла)

V - скорость
Q - объем
t - время

Отсюда получаем формулу для времени:
Для нахождения времени вычислим объем сообщения по формуле:

N — общее количество пикселей или разрешение, 
i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель)

Q = 4 * 480000

Теперь найдем время:

t = 4 * 480000 / 32000 = 60 секунд

Результат: 60

Тема: Скорость передачи информации:

ЕГЭ по информатике задание 7_16:

Каково время (в минутах) передачи полного объема данных по каналу связи, если известно, что передано 9000 Мбайт данных, причем треть времени передача шла со скоростью 60 Мбит в секунду, а остальное время – со скоростью 90 Мбит в секунду?

✍ Решение:

Формула скорости передачи данных:

* Вместо Q можно использовать обозначение I (для объема файла)

V - скорость
Q - объем
t - время

При 1/3 t скорость (V) равна 60 Мбит/c
При 2/3 t скорость(V) равна 90 Мбит/c
Объем переданных данных выразим в Мбитах:

1 Мбайт = 8 Мбит

 Q = 9000 Мбайт * 8 = 72000 Мбит

Из формулы выразим объем:
Так как общий объем данных у нас известен, получим уравнение:

(60 * 1/3t)  + (90 * 2/3t) = 72000
вынесем t за скобки, получим уравнение:
t * (20 + 60) = 72000
выразим t:
t = 72000 / 80 = 900 с = 15 мин

Результат: 15

Решение задания можно посмотреть и на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Скорость передачи информации:

ЕГЭ по информатике задание 7.17:

Документ объемом 5 Мбайт можно передать с одного компьютера на другой двумя способами:
А) Сжать архиватором, передать архив по каналу связи, распаковать
Б) Передать по каналу связи без использования архиватора.

Какой способ быстрее и насколько, если

средняя скорость передачи данных по каналу связи составляет 2¹⁸ бит в секунду,
объем сжатого архиватором документа равен 20% от исходного,
время, требуемое на сжатие документа – 7 секунд, на распаковку – 1 секунда?

В ответе напишите букву А, если способ А быстрее или Б, если быстрее способ Б. Сразу после буквы напишите количество секунд, насколько один способ быстрее другого.

Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23.

Типовые задания для тренировки

✍ Решение:

Рассмотрим способ А:

Сначала найдем объем документа, зная, что он составляет 20% от исходного:

Q (объем) = 5 Мбайт * 0.2 = 1 Мбайт = 1 * 2²³ бит

Формула времени передачи данных:

V - скорость
Q - объем
t - время

Получим t с учетом времени на сжатие и распаковку:

t = Q / V + 7 + 1 = 8 + 2²³ / 2¹⁸ = 8 + 2⁵ = 40 c

Рассмотрим способ Б:

Для этого способа можно сразу найти время (по формуле):

t = Q / V = 5 * 2²³ / 2¹⁸ = 5 * 2⁵ = 5 * 32 = 160 c

Получаем, что способ А быстрее; вычислим насколько быстрее:

160 с - 40 с = 120 с

Результат: А120

Решение также можно посмотреть в видеоуроке:

📹 YouTube здесьздесь

Тема: Скорость передачи информации:

ЕГЭ по информатике задание 7_18:

Документ объёмом 20 Мбайт можно передать с одного компьютера на другой двумя способами:
А) сжать архиватором-1, передать архив по каналу связи, распаковать;
Б) сжать архиватором-2, передать архив по каналу связи, распаковать;

Какой способ быстрее и насколько, если

средняя скорость передачи данных по каналу связи составляет 2²⁰ бит в секунду,
объём документа, сжатого архиватором-1, равен 20% от исходного,
на сжатие документа архиватором-1 требуется 15 секунд, на распаковку — 2 секунды,
объём документа, сжатого архиватором-2, равен 10% от исходного,
на сжатие документа архиватором-2 требуется 20 секунд, на распаковку — 4 секунды?

В ответе напишите букву А, если способ А быстрее или Б, если быстрее способ Б. Сразу после буквы напишите количество секунд, насколько один способ быстрее другого.

Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23.

✍ Решение:

Рассмотрим способ А:

Сначала найдем объем документа, зная, что он составляет 20% от исходного:

Q (объем) = 20 Мбайт * 0.2  = 4 Мбайт = 2² * 2²³ бит  = 2²⁵ бит

Формула времени передачи данных:

V - скорость
Q - объем
t - время

Найдем время для способа А с учетом времени на сжатие и распаковку:

t_A = 2²⁵ / 2²⁰ + 17 с = 2⁵ + 17 = 49 с

Рассмотрим способ Б:

Сначала найдем объем документа, зная, что он составляет 10% от исходного:

Q (объем) = 20 Мбайт * 0.1  = 2 Мбайт = 2¹ * 2²³ бит  = 2²⁴ бит

Найдем общее время с учетом потраченного времени на сжатие и распаковку:

t_Б = 2²⁴ / 2²⁰ + 24 с = 2⁴ + 24 = 40 с

Получили, что второй способ (Б) быстрее. Выясним насколько быстрее:

49 - 40 = 9 с

Результат: Б9

Тема: Скорость передачи информации:

Решение 7 ЕГЭ по информатике, задание 7_19:

Документ (без упаковки) можно передать по каналу связи с одного компьютера на другой за 1 минуту и 40 секунд. Если предварительно упаковать документ архиватором, передать упакованный документ, а потом распаковать на компьютере получателя, то общее время передачи (включая упаковку и распаковку) составит 30 секунд. При этом на упаковку и распаковку данных всего ушло 10 секунд. Размер исходного документа 45 Мбайт.

Чему равен размер упакованного документа (в Мбайт)?

✍ Решение:

Выпишем исходные данные для двух состояний документа, используя неизвестное x для искомого параметра — объема:

неупакованный:

I₁ = 45 Мбайт
t₁ = 100 секунд (60 секунд + 40 секунд = 100)

упакованный:

I₂ = x Мбайт
t₂ = 20 секунд (30 секунд - 10 секунд = 20)

Получим систему уравнений:

45 = 100
х = 20

Выразим x, т.е. объем упакованного документа:

х = (45 * 20) / 100 = 9 Мбайт

Результат: 9

Источник

Урок посвящён 11 заданию из ЕГЭ по информатике нового формата 2022. Проанализируем основные примеры и научимся решать это задание!

В 11 задании из ЕГЭ по информатике часто даются задачи на умение работать с количеством информации.

Приступим к делу! Раньше это задание было под номером тринадцать.

Задача (Демонстрационный вариант ЕГЭ по информатике, 2018)

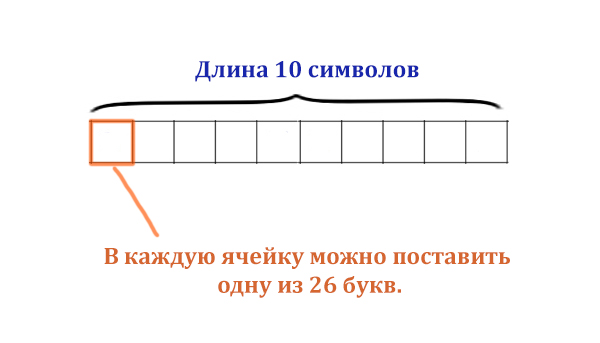
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 10 символов. В качестве символов используют прописные буквы латинского алфавита, т.е. 26 различных символов. В базе данных для хранения каждого пароля отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Определите объём памяти (в байтах), необходимый для хранения данных о 50 пользователях. В ответе запишите только целое число – количество байт.

Решение:

У каждого пользователя есть пароль, состоящий из 10 символов. Это значит, длина пароля 10 символов!

И в каждую ячейку мы может выбрать символ из 26 букв!

Здесь важно различать длину пароля и количество символов из которых пользователь выбирает для каждой ячейки пароля.

Теперь нужно определить: сколько бит занимает одна ячейка (1 символ пароля!).

Когда речь идёт о количестве бит, применяем формулу, которую мы использовали в 7 задании из ЕГЭ по информатике. Там мы кодировали цвета для одного пикселя, а здесь нужно закодировать 26 букв для одного поля пароля.

Применяем:

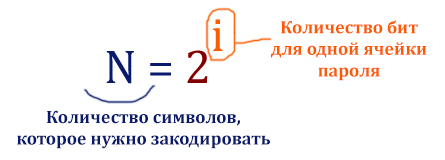
N = 2ⁱ = 26

Целого числа нету для i (количества бит), чтобы равенство было верным. Значит берём столько количество бит, сколько точно будет достаточно, чтобы закодировать 26 букв (символов).

N = 2⁵ > 26

Получаем одна ячейка (одно поле) пароля занимаем 5 бит! А в пароле их 10! Значит, весь пароль будет занимать:

V_пароля = 5 бит * 10 символов = 50 бит (в одном пароле!)

В условии сказано: для хранения каждого пароля отведено одинаковое и минимально возможное целое число байт. Это означает, что мы не может выделять память по одному биту. Память выделяется блоками по 8 бит (по одному байту).

Если взять 7 блоков по 8 бит (1 байту), то нам хватит этого на один пароль.

7 блоков (байт) * 8 бит = 56 бит > 50 бит

Таким образом, на 1 пароль потребуется 7 байт!

Тогда на 50 пользователей потребуется:

50 пользователей * 7 байт = 350 байт (для 50 пользователей).

Ответ: 350

Разберём задачу, которая была на реальном экзамене в Москве

Задача (ЕГЭ по информатике, 2020, Москва)

При регистрации в компьютерной системе каждому пользователю выдаётся
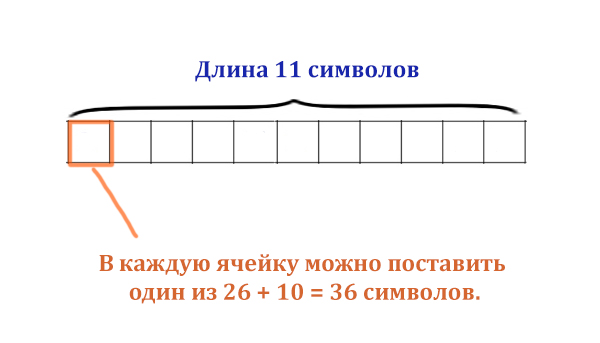
пароль, состоящий из 11 символов. В качестве символов используют 26
прописных букв из латинского алфавита и десять цифр. В базе
данных для хранения каждого пароля отведено одинаковое и минимально
возможное целое число байт. При этом используют посимвольное
кодирование паролей, все символы кодируют одинаковым
и минимально возможным количеством бит.
Кроме собственно пароля для каждого пользователя в системе хранятся дополнительные сведения.
Для кодирования данных о 30 сотрудниках было выделено 750 байт. Сколько памяти(в байтах) выделено для хранения дополнительных сведений об одном пользователе. В ответ запишите только целое число — количество байт.

Решение:

Здесь длина пароля составляет 11 символов!

Найдём сколько бит занимает одна ячейка пароля.

N = 2ⁱ = 36

N = 2⁶ = 64 > 36

Значит, 6 бит — минимальное количество бит, которое нужно, чтобы была возможность разместить любой из 36 символов в одной ячейке пароля.

Найдём сколько бит нужно на весь пароль.

V_пароля = 6 бит * 11 символов = 66 бит (в одном пароле!)

Теперь найдём, а сколько байт нужно на 1 пароль:

9 * 8 бит = 72 бит > 66 бит

Следовательно, 9 байт достаточно, чтобы покрыть 66 бит на 1 пароль.

Сказано, что для 30 сотрудников выделено 750 байт. Подсчитаем, сколько байт будет выделено на одного сотрудника.

V_{пользователя} = 750 байт / 30 = 25 байт (приходится на одного пользователя)

Мы выяснили, что на пароль из этих 25 байт потребуется 9 байт. Тогда на дополнительную информацию о каждом пользователе потребуется:

V_{доп. о 1 пол.} = 25 байт — 9 байт = 16 байт

Это и будет ответ.

Ответ: 16

Ещё один важный пример из запасов тренировочных задач ЕГЭ по информатике.

Задача (Номера спортсменов)

В велокроссе участвуют 48 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена. Какой объём памяти будет использован устройством, когда все спортсмены прошли промежуточный финиш? (Ответ дайте в байтах.)

Решение:

Узнаем сколько бит потребуется выделить на каждого спортсмена, чтобы была возможность записать любой номер от 1 до 48.

В этой задаче сказано: записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена . Это означает что у нас есть 48 различных позиций (номеров), которые нужно закодировать с помощью определённого количества бит. В предыдущей задаче, у нас было 62 различные позиции (символа), которые нужно было закодировать с помощью определённого количества бит. Мы там использовали формулу N = 2ⁱ.

Поэтому будем опять применять формулу N = 2ⁱ.

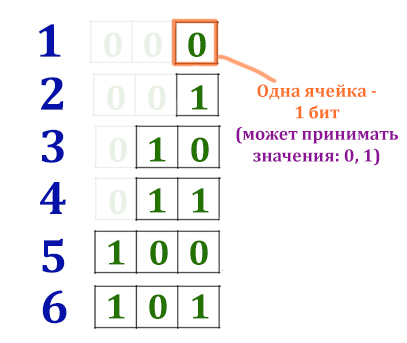
На рисунке показано, как может происходить кодирование чисел. Например, для двух номеров потребуется 1 бит (2¹ = 2), для четырёх номеров потребуется два бита (2² = 4). Нам нужно закодировать 48 чисел! Причём для каждого участника отведено одинаковое количество бит!

Можно сказать, что здесь работает формула, которую рассматривали в 8 задании. Всего нужно составить 48 различных комбинаций (закодировать 48 номеров). В каждой ячейке можно писать либо 0, либо 1 (Свойство бита информации). Какова должна быть длина «слова» (количество бит) ?

N = 2ⁱ = 2^{6 бит} = 64 > 48

Получается 6 бит потребуется для того, чтобы была возможность записать любой номер от 1 до 48 для каждого спортсмена. Если взять пять бит, то мы будем иметь возможность записать номера только от 1 до 2⁵ = 32 для каждого спортсмена (этого не хватает).

Т.к. все участники пересекли финиш, а на каждого участника выделено по 6 бит, то получается:

6 бит * 48 = 288 бит = 36 байт

Ответ: 36

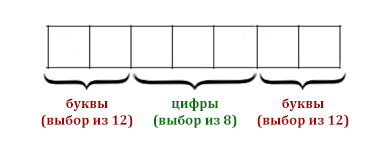
Задача (Автомобильный номер)

В некоторой стране автомобильный номер состоит из 7 символов: сначала 2 буквы, затем 3 цифры, затем ещё 2 буквы. При этом буквы могут быть выбраны только из 12 строчных букв местного алфавита. Среди цифр не используются цифры 6 и 9. Автоматизированная система хранит номера автомобилей следующим образом. Используется посимвольное кодирование. В памяти системы для кодирования каждого символа используется минимально возможное и одинаковое целое количество бит (для букв и цифр отдельно). А для номера используется минимально возможное целое количество байт. Какое количество информации (в байтах) требуется для хранения номеров 160 автомобилей ?

Решение:

Найдём сколько бит потребуется для кодирования 4-х букв.

N = 2ⁱ = 2^{4 бита} = 16 > 12

4 бита хватит для кодирования 12 букв. Всего таких ячейки 4! Поэтому в одном номере на все буквы уйдёт 4 * 4 бита = 16 бит.

Найдём сколько бит потребуется на кодирование 3 ячеек, где находятся цифры.

N = 2ⁱ = 2^{3 бита} = 8

Для кодирования одной ячейки, где находится цифра, потребуется 3 бита.

Все цифры в одном номере будут закодированы 3 бита * 3 = 9 битами.

Всего на один номер уйдёт 16 бит + 9 бит = 25 бит.

Найдём сколько байт потребуется для кодирования одного номера.

4 * 8 бит (1 байт) = 32 бита > 25 бит

4-х байт достаточно, чтобы закодировать 25 бит. Если взять 3 байта, то 3 * 8 бит (1 байт) = 24 бита. Этого будет не достаточно.

Найдём количество байт, которое нужно для кодирования 160 автомобилей

160 автомобилей * 4 байта = 640 байт

Это и будет ответ.

Ответ: 640

Задача (Закрепление формулы)

Метеорологическая станция ведет наблюдение за влажностью воздуха. Результатом одного наблюдения является целое число от 0 до 100%, записываемое при помощи минимально возможного количества бит. Станция сделала 800 измерений. Определите информационный объем результатов наблюдений. (Ответ дайте в байтах.)

Решение:

Здесь, нужно закодировать сто одно число (от 0 до 100). Ситуация похоже на ту, где мы кодировали номера спортсменов.

N = 2ⁱ = 2^{7 бит} = 128 > 101

Получается, что 7 бит потребуется, чтобы полностью закодировать 101 число.

Всего было сделано 800 таких измерений

800 * 7 бит = 5600 бит = 700 байт

Ответ: 700

На этом всё! Удачи при решении 11 задания на ЕГЭ по информатике!

Источник

С этим файлом связано 45 файл(ов). Среди них: Должностные инструкции.docx, входной контроль.docx, Нарыйа.pptx, лысенко.pdf, КЗ_Бухгалтерский учет_РЧ_2021_(1) (1).docx, МЕТОД РЕКОМЕНДАЦИИ ПП ПМ 01 2022.docx, metodicheskie_rekomendacii_po_proizvod.praktike_pm.docx, МУ к ПР по ПМ.01.doc, Документ Microsoft Word.docx, Документ Microsoft Word.docx, Справка о проведенной неделе Олонхо.docx, ЛОГОГ.docx, +РП ИЗО 5 класс ФГОС 2022-2023 г. Солодухин В.В..docx, jg.docx, Материалы и изделия для соединения и оконцевания кабеля.docx, ДОКЛАД мой.pptx, общество.docx, Введение.docx, доклад Характер и его воспитание.docx, 7 кл алгебра и 6 ВУД.doc, Практическая работа 1.docx, Задание к Лекции 4..docx, Практическая работа №1Дьяконов.docx, КТП технол. 6 Точка роста.docx, КТП техн. 5 Точка роста.docx, 5класс 8вид.odt, Истоки 8 класс.docx, 9 кл 8 вид.doc, Разработка контекстных заданий по физике.docx, ТР программы.doc, Про улицы эссе.docx, Эссе Моя улица.docx, Эссе.docx, Улица.docx, сочинение.docx, Творческое эссе Улица.docx, Творческое эссе.docx, Сочинение Моя улица.doc, ПОРОХОМ ПРОПАХШИЕ ФРОНТОВЫЕ ПИСЬМА УЧИТЕЛЕЙ – ВОИНОВ..docx, Барахов..docx, Эссе известные личности.doc, Урок мужества к 23 февраля.docx, Практическая работа по теме Потапова К.В..odt, Статья о 50- летии школы.docx, Информация…docx и ещё 35 файл(а).
Показать все связанные файлы

Подборка по базе: пиджак велюровый мужской синий 2 тыс изображений найдено в Яндек, Операции над фрагментами изображений. Использование операций коп, испаритель на норд 50 1 тыс изображений найдено в Яндекс Картинк, угарные валентинки на 14 февраля 2 тыс изображений найдено в Янд, Создание векторных изображений.docx, углы равны если синусы раныы свйоство 1 тыс изображений найдено , виски корги 1 тыс изображений найдено в Яндекс Картинках.pdf, ПЗ №2 Кодирование товаров.docx, голубянка-икар бабочка строение 1 тыс изображений найдено в Янде, статуэтка главной медсестры 1 тыс изображений найдено в Яндекс К

7 (базовый уровень, время – 5 мин)

Тема: Кодирование растровых изображений.

Что проверяется:

Умение определять объём памяти, необходимый для хранения графической и звуковой информации.

3.3.1. Форматы графических и звуковых объектов.

1.3.2. Оценивать скорость передачи и обработки информации.

Что нужно знать:

для хранения растрового изображения нужно выделить в памяти I = N · i битов, где N – количество пикселей и i – глубина цвета (разрядность кодирования)
количество пикселей изображения N вычисляется как произведение ширины рисунка на высоту (в пикселях)
глубина кодирования – это количество бит, которые выделяются на хранение цвета одного пикселя
при глубине кодирования i битов на пиксель код каждого пикселя выбирается из 2ⁱ возможных вариантов, поэтому можно использовать не более 2ⁱ различных цветов
нужно помнить, что

1 Мбайт = 2²⁰ байт = 2²³ бит,

1 Кбайт = 2¹⁰ байт = 2¹³ бит

Пример задания:

Р-03 (А.С. Гусев, г. Москва). Для хранения в информационной системе документы сканируются с разрешением 200 dpi и цветовой системой, содержащей 130 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 10 Мбайт. Для повышения качества представления информации было решено перейти на разрешение 300 dpi и цветовую систему, содержащую 2¹⁶ = 65 536 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?

Решение:

Разрешение изображения изменилось с 200 dpi на 300 dpi. Это означает, что размер изображения изменился в (300 · 300) / (200 · 200) = 9/4 раз.
Для хранения цветовой системы, состоящей из 130 цветов, необходимо 8 бит (необходимо подобрать минимально возможный i, так, чтобы N  2ⁱ; 130  2⁸ ).
Глубина кодирования изображения изменилась с 8 бит до 16 бит. Это означает, что размер изображения изменился в 16/8 = 2 раза.
Средний размер документа, отсканированного с изменёнными параметрами равно 10 · 9/4 · 2 = 45 Мб.
Ответ: 45.

Ещё пример задания:

Р-02 (демо-2021). Для хранения произвольного растрового изображения размером 128×320 пикселей отведено 20 Кбайт памяти без учёта размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать

в изображении?

Решение:

находим количество пикселей, используя для вычисления степени числа 2:

N = 128 · 320 = 2⁷· 2⁵ · 10 = 2¹³ · 5

объём файла переводим из Кбайт в биты 20 Кбайт = 20· 2¹³ бит
глубина кодирования (количество битов, выделяемых на 1 пиксель):

20· 2¹³: (5 · 2¹³) = 4 бита на пиксель

максимальное возможное количество цветов 2⁴ = 16
Ответ: 16.

Ещё пример задания:

Р-01. Рисунок размером 512 на 256 пикселей занимает в памяти 64 Кбайт (без учёта сжатия). Найдите максимально возможное количество цветов в палитре изображения.

Решение:

находим количество пикселей, используя для вычисления степени числа 2:

N = 512 · 256 = 2⁹· 2⁸ = 2¹⁷

объём файла в Кбайтах 64 = 2⁶
объём файла в битах 2⁶· 2¹³ = 2¹⁹
глубина кодирования (количество битов, выделяемых на 1 пиксель):

2¹⁹: 2¹⁷ = 2²= 4 бита на пиксель

максимальное возможное количество цветов 2⁴ = 16
Ответ: 16.

Ещё пример задания:

Р-00. Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 64 на 64 пикселов при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.

Решение:

находим количество пикселей, используя для вычисления степени числа 2:

N = 64 · 64 = 2⁶· 2⁶ = 2¹²

256 = 2⁸, поэтому для кодирования одного из 256 вариантов цвета нужно выделить в памяти 8 = 2³ бит на пиксель
объём файла в битах 2¹²· 2³ = 2¹⁵
объём файла в Кбайтах 2¹⁵: 2¹³ = 2²= 4
Ответ: 4.

Возможные ловушки и проблемы:

если умножить количество пикселей не на 8, а на 256, то получим неверный ответ 128 Кбайт

Задачи для тренировки^¹:

Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 128 на 256 пикселов при условии, что в изображении могут использоваться 64 различных цвета? В ответе запишите только целое число, единицу измерения писать не нужно.
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 128 на 128 пикселов при условии, что в изображении могут использоваться 32 различных цвета? В ответе запишите только целое число, единицу измерения писать не нужно.
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 64 на 128 пикселов при условии, что в изображении могут использоваться 128 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 64 на 256 пикселов при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 32 на 1024 пикселов при условии, что в изображении могут использоваться 128 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 1024 на 512 пикселов при условии, что в изображении могут использоваться 64 различных цвета? В ответе запишите только целое число, единицу измерения писать не нужно.
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 512 на 256 пикселов при условии, что в изображении могут использоваться 32 различных цвета? В ответе запишите только целое число, единицу измерения писать не нужно.
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 512 на 128 пикселов при условии, что в изображении могут использоваться 16 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 256 на 128 пикселов при условии, что в изображении могут использоваться 8 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 128 на 128 пикселов при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
Рисунок размером 128 на 256 пикселей занимает в памяти 24 Кбайт (без учёта сжатия). Найдите максимально возможное количество цветов в палитре изображения.
Рисунок размером 128 на 128 пикселей занимает в памяти 10 Кбайт (без учёта сжатия). Найдите максимально возможное количество цветов в палитре изображения.
Рисунок размером 64 на 128 пикселей занимает в памяти 7 Кбайт (без учёта сжатия). Найдите максимально возможное количество цветов в палитре изображения.
Рисунок размером 64 на 256 пикселей занимает в памяти 16 Кбайт (без учёта сжатия). Найдите максимально возможное количество цветов в палитре изображения.
Рисунок размером 32 на 1024 пикселей занимает в памяти 28 Кбайт (без учёта сжатия). Найдите максимально возможное количество цветов в палитре изображения.
Рисунок размером 1024 на 512 пикселей занимает в памяти 384 Кбайт (без учёта сжатия). Найдите максимально возможное количество цветов в палитре изображения.
Рисунок размером 512 на 256 пикселей занимает в памяти 80 Кбайт (без учёта сжатия). Найдите максимально возможное количество цветов в палитре изображения.
Рисунок размером 512 на 128 пикселей занимает в памяти 32 Кбайт (без учёта сжатия). Найдите максимально возможное количество цветов в палитре изображения.
Рисунок размером 256 на 128 пикселей занимает в памяти 12 Кбайт (без учёта сжатия). Найдите максимально возможное количество цветов в палитре изображения.
Рисунок размером 128 на 128 пикселей занимает в памяти 16 Кбайт (без учёта сжатия). Найдите максимально возможное количество цветов в палитре изображения.
После преобразования растрового 256-цветного графического файла в черно-белый формат (2 цвета) его размер уменьшился на 7 Кбайт. Каков был размер исходного файла в Кбайтах?
После преобразования растрового 16-цветного графического файла в черно-белый формат (2 цвета) его размер уменьшился на 21 Кбайт. Каков был размер исходного файла в Кбайтах?
После преобразования растрового 256-цветного графического файла в 16-цветный формат его размер уменьшился на 15 Кбайт. Каков был размер исходного файла в Кбайтах?
После преобразования растрового 256-цветного графического файла в 4-цветный формат его размер уменьшился на 18 Кбайт. Каков был размер исходного файла в Кбайтах?
После преобразования растрового графического файла его объем уменьшился в 1,5 раза. Сколько цветов было в палитре первоначально, если после преобразования было получено растровое изображение того же разрешения в 16-цветной палитре?
После преобразования растрового графического файла его объем уменьшился в 2 раза. Сколько цветов было в палитре первоначально, если после преобразования было получено растровое изображение того же разрешения в 16-цветной палитре?
(С. Логинова) Цветное изображение было оцифровано и сохранено в виде файла без использования сжатия данных. Размер полученного файла – 54 Мбайт. Затем то же изображение было оцифровано повторно с разрешением в 2 раза больше и глубиной кодирования цвета в 3 раза меньше по сравнению с первоначальными параметрами. Сжатие данных не производилось. Укажите размер файла в Мбайт, полученного при повторной оцифровке.
(С. Логинова) Цветное изображение было оцифровано и сохранено в виде файла без использования сжатия данных. Размер полученного файла – 42 Мбайт. Затем то же изображение было оцифровано повторно с разрешением в 2 раза меньше и глубиной кодирования цвета в 4 раза больше по сравнению с первоначальными параметрами. Сжатие данных не производилось. Укажите размер файла в Мбайт, полученного при повторной оцифровке.
(С. Логинова) Изображение было оцифровано и сохранено в виде растрового файла. Получившейся файл был передан в город А по каналу связи за 30 секунд. Затем то же изображение было оцифровано повторно с разрешением в 3 раза больше и глубиной кодирования цвета в 2 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б, пропускная способность канала связи с городом Б в 1.5 раза выше, чем канала связи с городом А. Сколько секунд длилась передача файла в город Б?
(С. Логинова) Изображение было оцифровано и сохранено в виде растрового файла. Получившейся файл был передан в город А по каналу связи за 72 секунды. Затем то же изображение было оцифровано повторно с разрешением в 2 раза больше и глубиной кодирования цвета в 3 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б, пропускная способность канала связи с городом Б в 3 раза выше, чем канала связи с городом А. Сколько секунд длилась передача файла в город Б?
(С. Логинова) Изображение было оцифровано и записано в виде файла без использования сжатия данных. Получившейся файл был передан в город А по каналу связи за 90 секунд. Затем то же изображение было оцифровано повторно с разрешением в 2 раза больше и глубиной кодирования цвета в 1,5 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 10 секунд. Во сколько раз скорость пропускная способность канала в город Б больше пропускной способности канала в город А?
(С. Логинова) Изображение было оцифровано и записано в виде файла без использования сжатия данных. Получившейся файл был передан в город А по каналу связи за 75 секунд. Затем то же изображение было оцифровано повторно с разрешением в 2 раза больше и глубиной кодирования цвета в 4 раза больше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 60 секунд. Во сколько раз скорость пропускная способность канала в город Б больше пропускной способности канала в город А?
Камера делает фотоснимки размером 1024768 пикселей. На хранение одного кадра отводится 900 Кбайт. Найдите максимально возможное количество цветов в палитре изображения.
Камера делает фотоснимки размером 16001200 пикселей. На хранение одного кадра отводится 3800 Кбайт. Определите максимальную глубину цвета (в битах на пиксель), которую можно использовать при фотосъёмке.
Камера делает фотоснимки размером 1280960 пикселей. На хранение одного кадра отводится 160 Кбайт. Найдите максимально возможное количество цветов в палитре изображения.
Камера делает фотоснимки размером 32001800 пикселей. На хранение одного кадра отводится 3 Мбайт. Найдите максимально возможное количество цветов в палитре изображения.
Камера делает фотоснимки размером 640480 пикселей. На хранение одного кадра отводится 250 Кбайт. Найдите максимально возможное количество цветов в палитре изображения.
Камера делает фотоснимки размером 16001200 пикселей. На хранение одного кадра отводится 1 Мбайт. Найдите максимально возможное количество цветов в палитре изображения.
Камера делает фотоснимки 768 на 600 пикселей. При этом объём файла с изображением не может превышать 420 Кбайт, упаковка данных не производится. Какое максимальное количество цветов можно использовать в палитре изображения?
Камера делает фотоснимки 1024 на 768 пикселей. При этом объём файла с изображением не может превышать 220 Кбайт, упаковка данных не производится. Какое максимальное количество цветов можно использовать в палитре изображения?
Камера делает фотоснимки 1024 на 768 пикселей. При этом объём файла с изображением не может превышать 600 Кбайт, упаковка данных не производится. Какое максимальное количество цветов можно использовать в палитре изображения?
Камера делает фотоснимки 800 на 600 пикселей. При этом объём файла с изображением не может превышать 100 Кбайт, упаковка данных не производится. Какое максимальное количество цветов можно использовать в палитре изображения?
Автоматическая фотокамера делает фотографии высокого разрешения с палитрой, содержащей 2²⁴ = 16 777 216 цветов. Средний размер фотографии составляет 15 Мбайт. Для хранения в базе данных фотографии преобразуют в формат с палитрой, содержащей 256 цветов. Другие преобразования и дополнительные методы сжатия не используются. Сколько Мбайт составляет средний размер преобразованной фотографии?
Автоматическая фотокамера делает фотографии высокого разрешения с палитрой, содержащей 2²⁴ = 16 777 216 цветов. Средний размер фотографии составляет 12 Мбайт. Для хранения в базе данных фотографии преобразуют в формат с палитрой, содержащей 2¹⁶ = 65536 цветов. Другие преобразования и дополнительные методы сжатия не используются. Сколько Мбайт составляет средний размер преобразованной фотографии?
Автоматическая фотокамера делает фотографии высокого разрешения с палитрой, содержащей 2²⁴ = 16 777 216 цветов. Средний размер фотографии составляет 6 Мбайт. Для хранения в базе данных фотографии преобразуют в формат с палитрой, содержащей 16 цветов. Другие преобразования и дополнительные методы сжатия не используются. Сколько Мбайт составляет средний размер преобразованной фотографии?
(А.М. Кабанов, г. Тольятти) Камера снимает видео без звука с частотой 60 кадров в секунду, при этом изображения используют палитру, содержащую 2¹⁶ = 65536 цветов. 1 минута видео в среднем занимает 12 Мегабайт. При записи файла на сервер полученное видео преобразуют так, что его частота кадров уменьшается до 20 кадров в секунду, а изображения преобразуют в формат, содержащий палитру из 256 цветов. Другие преобразования и иные методы сжатия не используются. Сколько Мбайт в среднем занимает 5 минут преобразованной видеозаписи?
(А.М. Кабанов, г. Тольятти) Камера снимает видео без звука с частотой 120 кадров в секунду, при этом изображения используют палитру, содержащую 2²⁴ = 16 777 216 цветов. При записи файла на сервер полученное видео преобразуют так, что частота кадров уменьшается до 20, а изображения преобразуют в формат, использующий палитру из 256 цветов. Другие преобразования и иные методы сжатия не используются. 10 секунд преобразованного видео в среднем занимают 512 Кбайт. Сколько Мбайт в среднем занимает 1 минута исходного видео?
(А.М. Кабанов, г. Тольятти) Камера снимает видео без звука с частотой 48 кадров в секунду, при этом изображения используют палитру, содержащую 4096 цвета. 1 минута видео в среднем занимает 18 Мегабайт. При записи файла на сервер полученное видео преобразуют так, что его частота кадров уменьшается до 24 кадров в секунду, а изображения преобразуют в формат, содержащий палитру из 16 цветов. Другие преобразования и иные методы сжатия не используются. Сколько минут преобразованного видео в среднем можно записать при ограничении размера видеозаписи в 48 Мегабайт?
(А.М. Кабанов, г. Тольятти) Камера снимает видео без звука с частотой 24 кадра в секунду, при этом изображения используют палитру, содержащую 2²⁴ = 16 777 216 цветов. Параллельно производится запись стереозвука. 1 минута видеоряда в среднем занимает 36 Мбайт, 1 минута звуковой дорожки занимает в среднем 6 Мбайт. Для хранения видео преобразуют так, что для изображений используется палитра в 256 цветов, а звук перезаписывается в формате моно, при этом частота дискретизации уменьшается в 2 раза, а глубина кодирования уменьшается в 1,5 раза. Другие преобразования и иные методы сжатия не используются. Сколько Мбайт в среднем занимает 1 минута преобразованного видео со звуком?
(А.М. Кабанов, г. Тольятти) Для мультипликационного фильма видеоряд с частотой 60 кадров в cекунду и звуковая восьмиканальная дорожка записываются отдельно. Для хранения на сервере видео преобразуют так, что частота уменьшается до 30 кадров в секунду, а количество пикселей уменьшается в 4 раза. Звук перезаписывается в формате стерео с уменьшением частоты дискретизации и глубины кодирования в 2 раза. Другие преобразования и иные методы сжатия не используются. После преобразования 1 минута видеоряда в среднем занимает 1,5 Мегабайта, а 1 минута звуковой дорожки – 512 Килобайт. Сколько Мбайт в среднем занимают 10 минут исходного видеоряда и звуковой дорожки вместе?
Для хранения в информационной системе документы сканируются с разрешением 600 ppi и цветовой системой, содержащей 2²⁴ = 16 777 216 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 18 Мбайт. В целях экономии было решено перейти на разрешение 300 ppi и цветовую систему, содержащую 2¹⁶ = 65 536 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?
Для хранения в информационной системе документы сканируются с разрешением 600 ppi и цветовой системой, содержащей 2²⁴ = 16 777 216 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 16 Мбайт. В целях экономии было решено перейти на разрешение 300 ppi и цветовую систему, содержащую 64 цвета. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?
Для хранения в информационной системе документы сканируются с разрешением 600 ppi и цветовой системой, содержащей 2²⁴ = 16 777 216 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 12 Мбайт. В целях экономии было решено перейти на разрешение 300 ppi и цветовую систему, содержащую 256 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?
Для хранения в информационной системе документы сканируются с разрешением 600 ppi и цветовой системой, содержащей 2²⁴ = 16 777 216 цветов. Методы сжатия изображений не используются. В целях экономии было решено перейти на разрешение 150 ppi и цветовую систему, содержащую 2¹⁶ = 65 536 цветов. Средний размер документа, отсканированного с изменёнными параметрами, составляет 256 Кбайт. Сколько Мбайт составлял средний размер документа до оптимизации?
Для хранения в информационной системе документы сканируются с разрешением 600 ppi и цветовой системой, содержащей 2²⁴ = 16 777 216 цветов. Методы сжатия изображений не используются. В целях экономии было решено перейти на разрешение 300 ppi и цветовую систему, содержащую 16 цветов. Средний размер документа, отсканированного с изменёнными параметрами, составляет 128 Кбайт. Сколько Мбайт составлял средний размер документа до оптимизации?
Для хранения в информационной системе документы сканируются с разрешением 400 ppi и цветовой системой, содержащей 2²⁴ = 16 777 216 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 6 Мбайт. В целях экономии было решено перейти на разрешение 100 ppi и цветовую систему с уменьшенным количеством цветов. Средний размер документа, отсканированного с изменёнными параметрами, составляет 64 Кбайт. Определите количество цветов в палитре после оптимизации.
Для хранения в информационной системе документы сканируются с разрешением 300 ppi и цветовой системой, содержащей 2²⁴ = 16 777 216 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 3 Мбайт. В целях экономии было решено перейти на разрешение 100 ppi и цветовую систему с уменьшенным количеством цветов. Средний размер документа, отсканированного с изменёнными параметрами, составляет 128 Кбайт. Определите количество цветов в палитре после оптимизации.
Для хранения в информационной системе документы сканируются с разрешением 300 ppi. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 5 Мбайт. В целях экономии было решено перейти на разрешение 150 ppi и цветовую систему, содержащую 16 цветов. Средний размер документа, отсканированного с изменёнными параметрами, составляет 512 Кбайт. Определите количество цветов в палитре до оптимизации.
Для хранения в информационной системе документы сканируются с разрешением 400 ppi. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 2 Мбайт. В целях экономии было решено перейти на разрешение 100 ppi и цветовую систему, содержащую 64 цвета. Средний размер документа, отсканированного с изменёнными параметрами, составляет 96 Кбайт. Определите количество цветов в палитре до оптимизации.
Автоматическая фотокамера каждые 10 с создаёт черно-белое растровое изображение, содержащее 256 оттенков. Размер изображения – 512 x 192 пикселей. Все полученные изображения и коды пикселей внутри одного изображения записываются подряд, никакая дополнительная информация не сохраняется, данные не сжимаются. Сколько Мбайтов нужно выделить для хранения всех изображений, полученных за сутки?
Автоматическая фотокамера каждые 5 с создаёт черно-белое растровое изображение, содержащее 256 оттенков. Размер изображения – 256 x 512 пикселей. Все полученные изображения и коды пикселей внутри одного изображения записываются подряд, никакая дополнительная информация не сохраняется, данные не сжимаются. Сколько Мбайтов нужно выделить для хранения всех изображений, полученных за сутки?
Автоматическая фотокамера каждые 3 с создаёт черно-белое растровое изображение, содержащее 256 оттенков. Размер изображения – 128 x 192 пикселей. Все полученные изображения и коды пикселей внутри одного изображения записываются подряд, никакая дополнительная информация не сохраняется, данные не сжимаются. Сколько Мбайтов нужно выделить для хранения всех изображений, полученных за сутки?
Автоматическая фотокамера каждые 6 с создаёт черно-белое растровое изображение, содержащее 256 оттенков. Размер изображения – 128 x 256 пикселей. Все полученные изображения и коды пикселей внутри одного изображения записываются подряд, никакая дополнительная информация не сохраняется, данные не сжимаются. Сколько Мбайтов нужно выделить для хранения всех изображений, полученных за сутки?
(А. Кабанов) Автоматическая фотокамера каждую секунду создаёт растровое изображение, содержащее 2¹⁶=65536 цветов. Размер изображения – 640 x 480 пикселей. Все полученные изображения и коды пикселей внутри одного изображения записываются подряд, никакая дополнительная информация не сохраняется, данные не сжимаются. Сколько Мбайт нужно выделить для хранения всех изображений, полученных за 128 секунд? В ответе укажите только целое число – количество Мбайт, единицу измерения указывать не надо.
(А. Кабанов) Автоматическая фотокамера каждые 15 секунд создаёт растровое изображение, содержащее 256 цветов. Размер изображения – 240 x 320 пикселей. Все полученные изображения и коды пикселей внутри одного изображения записываются подряд, никакая дополнительная информация не сохраняется, данные не сжимаются. Сколько Кбайт нужно выделить для хранения всех изображений, полученных за 1 минуту? В ответе укажите только целое число – количество Кбайт, единицу измерения указывать не надо.
(А. Кабанов) Автоматическая фотокамера каждые 10 секунд создаёт растровое изображение. Размер изображения – 1536 x 1024 пикселей. Все полученные изображения и коды пикселей внутри одного изображения записываются подряд, никакая дополнительная информация не сохраняется, данные не сжимаются. Все изображения, полученные за 1 минуту, занимают 9 Мбайт. Найдите максимально возможное количество цветов в палитре изображения.
(А. Минак) Автоматическая камера производит растровые изображения размером 800×600 пикселей. Для кодирования цвета каждого пикселя используется одинаковое количество байт, коды пикселей записываются в файл один за другим без промежутков. Объём файла с изображением не может превышать 700 Кбайт без учёта размера заголовка файла. Какое максимальное количество цветов можно использовать в палитре?
Для хранения в информационной системе документы сканируются с разрешением 300 dpi и цветовой системой, содержащей 2¹⁶ = 65 536 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 18 Мбайт. В целях экономии было решено перейти на разрешение 200 dpi и цветовую систему, содержащую 256 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?
Для хранения в информационной системе документы сканируются с разрешением 300 dpi и цветовой системой, содержащей 2²⁴ = 16 777 216 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 6 Мбайт. В целях экономии было решено перейти на разрешение 150 dpi и цветовую систему, содержащую 2¹⁶ = 65 536 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?
Для хранения в информационной системе документы сканируются с разрешением 300 dpi и цветовой системой, содержащей 2¹⁶ = 65 536 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 9 Мбайт. В целях экономии было решено перейти на разрешение 200 dpi и цветовую систему, содержащую 2¹² = 4096 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?
Для хранения в информационной системе документы сканируются с разрешением 200 dpi и цветовой системой, содержащей 2¹² = 4096 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 2 Мбайт. Для повышения качества представления информации было решено перейти на разрешение 300 dpi и цветовую систему, содержащую 2²⁴ = 16 777 216 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?
Для хранения в информационной системе документы сканируются с разрешением 150 dpi и цветовой системой, содержащей 256 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 3 Мбайт. Для повышения качества представления информации было решено перейти на разрешение 300 dpi и цветовую систему, содержащую 2²⁴ = 16 777 216 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?
Для хранения в информационной системе документы сканируются с разрешением 200 dpi и цветовой системой, содержащей 256 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 6 Мбайт. Для повышения качества представления информации было решено перейти на разрешение 300 dpi и цветовую систему, содержащую 2¹⁶ = 65 536 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?
Для хранения в информационной системе документы сканируются с разрешением 150 dpi и цветовой системой, содержащей 16 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 0,5 Мбайт. Для повышения качества представления информации было решено перейти на разрешение 300 dpi и цветовую систему, содержащую 2¹⁶ = 65 536 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?
(Е. Джобс) 20 изображений разрешением 1600х1200 пикселей отправили по каналу связи со средней пропускной способностью 2²³ бит/секунду. Все изображения были приняты приемником не более чем 10 секунд. Известно, что изображение кодируется, как набор пикселей, каждый из которых закодирован с помощью одинакового и минимально возможного количества бит. Изображения в целях ускорения передачи записаны в памяти подряд, без разделителей и заголовков. Какое максимальное число цветов может быть в палитре изображений?
(Е. Джобс) Автоматическая камера производит растровые изображения размером 1280х1920 пикселей. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Объем файла с одним изображением не может превышать 1500 Кбайт без учета размера заголовка файла. Какое максимальное количество цветов можно использовать в палитре?
(Е. Джобс) Автоматическая камера производит растровые изображения размером 640х1280 пикселей. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Объем файла с одним изображением не может превышать 500 Кбайт без учета размера заголовка файла. Какое максимальное количество цветов можно использовать в палитре?
(Е. Джобс) Изображение размером 12 Мбайт сжимают для экономии памяти. Известно, что разрешение уменьшили вдвое, а цветовую палитру с 2¹⁵ = 32768 цветов сократили до 1024 цветов. Сколько Мбайт займет сжатый файл?
В информационной системе хранятся изображения размером 2048 × 1600 пикселей. При кодировании используется алгоритм сжатия изображений, позволяющий уменьшить размер памяти для хранения одного изображения в среднем в 8 раз по сравнению с независимым кодированием каждого пикселя. Каждое изображение дополняется служебной информацией, которая занимает 64 Кбайт. Для хранения 32 изображений выделено 12 Мбайт памяти. Какое максимальное количество цветов можно использовать в палитре каждого изображения?
В информационной системе хранятся изображения размером 1600 × 1200 пикселей. При кодировании используется алгоритм сжатия изображений, позволяющий уменьшить размер памяти для хранения одного изображения в среднем в 5 раз по сравнению с независимым кодированием каждого пикселя. Каждое изображение дополняется служебной информацией, которая занимает 100 Кбайт. Для хранения 32 изображений выделено 10 Мбайт памяти. Какое максимальное количество цветов можно использовать в палитре каждого изображения?
В информационной системе хранятся изображения размером 1024 × 768 пикселей. При кодировании используется алгоритм сжатия изображений, позволяющий уменьшить размер памяти для хранения одного изображения в среднем в 6 раз по сравнению с независимым кодированием каждого пикселя. Каждое изображение дополняется служебной информацией, которая занимает 54 Кбайт. Для хранения 32 изображений выделено 6 Мбайт памяти. Какое максимальное количество цветов можно использовать в палитре каждого изображения?
(А. Богданов) Давным-давно, когда 640 Кбайт хватало «на всё», лучшие компьютеры поддерживали максимальное разрешение 640х480 пикселей. Известно, что каждый пиксель мог быть окрашен в один из 16 цветов. Определите объем памяти видеобуфера (памяти необходимой для хранения одной картинки) в Кбайтах (1 Кбайт = 1024 байта).
(Е. Джобс) Геннадий создает мультипликационный ролик, где каждый кадр – отдельно отрисованная картинка. Известно, что каждая картинка имеет разрешение 640х480 пикселей и цветовую палитру в 2¹⁶ = 65536 цветов. Каждый пиксель кодируется с помощью минимально возможного и одинакового для всех пикселей количества бит. Картинки записываются одна за другой без разделителей и заголовков файла. Частота смены кадров в конечном ролике – 24 кадра/сек. В качестве звукового сопровождения выбран формат стерео с глубиной кодирования 10 бит и частотой дискретизации 40 кГц. Найдите размер мультфильма в МБайтах, если известно, что его длительность 5 минут. В качестве ответа укажите число – минимальное целое количество Мбайт достаточное для хранения такого файла.
Для хранения рисунка размером 3840 x 2160 пикселей выделено 7 Мбайт памяти. Определите максимально возможное количество цветом в палитре изображения.
Для хранения рисунка размером 4096×3072 пикселя выделено 9 Мбайт памяти. Определите максимально возможное количество цветом в палитре изображения.
(И. Женецкий) Какой минимальный объём памяти (целое число Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 567×512 пикселей при условии, что в изображении могут использоваться 32 различных цвета? В ответе запишите только целое число, единицу измерения писать не нужно.
(И. Женецкий) Какой минимальный объём памяти (целое число Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 1104×542 пикселей при условии, что в изображении могут использоваться 128 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
(И. Женецкий) Какой минимальный объём памяти (целое число Мбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 1024×4096 пикселей при условии, что в изображении могут использоваться 1024 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
(И. Женецкий) Какой минимальный объём памяти (целое число Мбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 4096×2048 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
(И. Женецкий) Каким может быть максимальное количество цветов в палитре, чтобы растровое изображение размером 512х415 пикселей можно было сохранить, используя 256 Кбайт памяти? В ответе запишите только целое число, единицу измерения писать не нужно.
(И. Женецкий) Каким может быть максимальное количество цветов в палитре, чтобы растровое изображение размером 5524х8595 пикселей можно было сохранить, используя 52 Мбайт памяти? В ответе запишите только целое число, единицу измерения писать не нужно.
(И. Женецкий) Найдите битовую глубину кодирования растрового изображения размером 1024×512 пикселей, которое занимает 64 Кбайт. В ответе запишите только целое число, единицу измерения писать не нужно.
(И. Женецкий) Найдите битовую глубину кодирования растрового изображения размером 2048×8 пикселей, которое занимает 22 Кбайт? В ответе запишите только целое число, единицу измерения писать не нужно.
(И. Женецкий) Найдите битовую глубину кодирования растрового изображения размером 2048×32 пикселей, которое занимает 192 Кбайт. В ответе запишите только целое число, единицу измерения писать не нужно.
(И. Женецкий) Найдите битовую глубину кодирования растрового изображения размером 512×300 пикселей, которое занимает 600 Кбайт. В ответе запишите только целое число, единицу измерения писать не нужно.
(А. Богданов) Изображение размером 265х2084 пикселей сохраняется в памяти компьютера. Для его хранения выделяется не более 400Кбайт без учёта заголовка файла. Все пиксели кодируются одинаковым количеством бит и записываются в файл один за другим. Какое максимальное количество цветов может использоваться для хранения такого изображения?
Изображение размером 3х4 дюйма отсканировано с разрешением 300 ppi и использованием 2¹⁶ цветов. Заголовок файла занимает 4 Кбайта. Определите, сколько Кбайт памяти необходимо выделить для хранения файла. В ответе введите целое число.
Изображение размером 4х5 дюйма отсканировано с разрешением 600 ppi и использованием 2²⁴ цветов. Заголовок файла занимает 8 Кбайт. Определите, сколько Кбайт памяти необходимо выделить для хранения файла. В ответе введите целое число.
Изображение размером 4х7 дюйма отсканировано с разрешением 300 ppi и использованием 2²⁴ цветов. Заголовок файла занимает 6 Кбайт. Определите, сколько Кбайт памяти необходимо выделить для хранения файла. В ответе введите целое число.
Изображения размером 3х4 дюйма сканируются с разрешением 300 ppi и использованием 2¹⁶ цветов. Заголовок файла занимает 4 Кбайта. Для хранения таких изображений выделено 55 Мбайт памяти. Сколько изображений удастся сохранить? В ответе введите целое число.
Изображения размером 4х5 дюйма сканируются с разрешением 600 ppi и использованием 2²⁴ цветов. Заголовок файла занимает 8 Кбайт. Для хранения таких изображений выделено 760 Мбайт памяти. Сколько изображений удастся сохранить? В ответе введите целое число.
Изображения размером 4х7 дюйма сканируются с разрешением 300 ppi и использованием 2²⁴ цветов. Заголовок файла занимает 6 Кбайт. Для хранения таких изображений выделено 640 Мбайт памяти. Сколько изображений удастся сохранить? В ответе введите целое число.
(Досрочный ЕГЭ-2022) Для хранения произвольного растрового изображения размером 486×720 пикселей отведено 80 Кбайт памяти без учёта размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. При сохранении данные сжимаются, размер итогового файла после сжатия становится на 15% меньше исходного. Какое максимальное количество цветов можно использовать в изображении?
Для хранения произвольного растрового изображения размером 640×480 пикселей отведено 230 Кбайт памяти без учёта размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. При сохранении данные сжимаются, размер итогового файла после сжатия становится на 25% меньше исходного. Какое максимальное количество цветов можно использовать в изображении?
Для хранения произвольного растрового изображения размером 800×630 пикселей отведено 270 Кбайт памяти без учёта размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. При сохранении данные сжимаются, размер итогового файла после сжатия становится на 35% меньше исходного. Какое максимальное количество цветов можно использовать в изображении?
Для хранения произвольного растрового изображения размером 800×1024 пикселей отведено 300 Кбайт памяти без учёта размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. При сохранении данные сжимаются, размер итогового файла после сжатия становится на 40% меньше исходного. Какое максимальное количество цветов можно использовать в изображении?
Для хранения произвольного растрового изображения размером 1200×1600 пикселей отведено 1850 Кбайт памяти без учёта размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. При сохранении данные сжимаются, размер итогового файла после сжатия становится на 20% меньше исходного. Какое максимальное количество цветов можно использовать в изображении?
Для хранения произвольного растрового изображения размером 1366×1280 пикселей отведено 2000 Кбайт памяти без учёта размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. При сохранении данные сжимаются, размер итогового файла после сжатия становится на 25% меньше исходного. Какое максимальное количество цветов можно использовать в изображении?
(Е. Джобс) Для хранения растрового изображения размером 1200х1800 пикселей отведено 1 Мбайт памяти. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. После сохранения информации о пикселях изображение сжимается. После сжатия изображение имеет размер, равный 75% от исходного. К сжатому изображению дописывается заголовок файла размером 40 Кбайт. Какое максимальное количество цветов можно использовать в изображении?
(ЕГЭ-2022) Для хранения произвольного растрового изображения размером 1024 на 120 пикселей отведено 210 Кбайт памяти без учёта размера заголовка файла. При кодировании каждого пикселя используется 7 бит для определения степени прозрачности и одинаковое количество бит для указания его цвета. Коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов (без учета степени прозрачности) можно использовать в изображении?
(ЕГЭ-2022) Для хранения сжатого произвольного растрового изображения размером 640 на 256 пикселей отведено 170 Кбайт памяти без учёта размера заголовка файла. Исходный файл изображения больше, чем сжатый, на 35% (считая размер сжатого файла за 100%). Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении?
Компьютер поддерживает максимальное разрешение 2400х1600 пикселей, каждый пиксель может быть окрашен в один из 4096 цветов. Определите объем памяти видеобуфера (памяти необходимой для хранения одной картинки) в килобайтах.
(Е. Джобс) Изображение размером 1200х1600 пикселей кодируется с использованием палитры из 2000 цветов. После кодирования пикселей изображение сжимается. Сжатый размер закодированного фрагмента меньше исходного на 21%. К сжатому фрагменту дописывается информация о заголовке и дополнительная информация, которая суммарно занимает 20 Кбайт. Какое минимальное количество Мбайт памяти зарезервировать для хранения полученного файла?
(А. Кабанов) Для хранения произвольного растрового изображения размером 1024 на 120 пикселей отведено 210 Кбайт памяти без учёта размера заголовка файла. При кодировании каждого пикселя используется 7 бит для определения степени прозрачности и одинаковое количество бит для указания его цвета. Коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов (без учета степени прозрачности) можно использовать в изображении?
(А. Кабанов) Для хранения произвольного растрового изображения размером 640 на 480 пикселей отведено 600 Кбайт памяти без учёта размера заголовка файла. При кодировании каждого пикселя используется 64 уровня прозрачности, а также одинаковое количество бит для указания его цвета. Коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов (без учета степени прозрачности) можно использовать в изображении?
(А. Кабанов) При кодировании растрового изображения для каждого пикселя используется палитра из 2²⁴ цветов и 256 уровней прозрачности. Коды пикселей записываются в файл один за другим без промежутков. Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 1024 на 768 пикселей?
(А. Кабанов) Для хранения произвольного растрового изображения размером 480 на 768 пикселей отведено 405 Кбайт памяти без учёта размера заголовка файла. При кодировании цвета каждого пикселя используется одинаковое количество бит, при этом для каждых двух бит цвета дописывается дополнительный бит контроля чётности. Коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении?
(Е. Джобс) Растровое изображение размером 192 на 960 пикселей сохраняют в памяти компьютера. Каждый пиксель в изображении может иметь один из 2048 цветов. Все цвета представлены с помощью битовых последовательностей одинаковой длины, при этом длина этих последовательностей минимальна. На сколько процентов необходимо уменьшить полученный файл, чтобы сжатое изображение можно было сохранить в отведенные для хранения 180 Кбайт памяти? В качестве ответа приведите минимальное целое подходящее число.

1 Источники заданий:

Демонстрационные варианты КИМ ЕГЭ.
Тренировочные работы МИОО.
Крылов С.С., Ушаков Д.М. ЕГЭ 2015. Информатика. Тематические тестовые задания. — М.: Экзамен, 2015.
Ушаков Д.М. ЕГЭ-2015. Информатика. 20 типовых вариантов экзаменационных работ для подготовки к ЕГЭ. — М.: Астрель, 2014.

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 128×128 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.

Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 128×128 пикселей при условии, что в изображении могут использоваться 128 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.

Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 512×512 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.

Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 1024×1024 пикселей при условии, что в изображении могут использоваться 16 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.

Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 320×640 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.

Источник: ЕГЭ по информатике 23.03.2016. Досрочная волна

Пройти тестирование по этим заданиям

Источник

9 тема характеризуется, как задания базового уровня сложности, время выполнения – примерно 5 минут. Приведена краткая теория и задачи с решениями.

Кодирование графической информации

Рассмотрим некоторые понятия и формулы, необходимые для решения ЕГЭ по информатике.

- Пиксель – это наименьший элемент растрового изображения, который имеет определенный цвет.
- Разрешение – это количество пикселей на дюйм размера изображения.
- Глубина цвета — это количество битов, необходимое для кодирования цвета пикселя.
- Если глубина кодирования составляет i битов на пиксель, код каждого пикселя выбирается из 2ⁱ возможных вариантов, поэтому можно использовать не более 2ⁱ различных цветов.
- В цветовой модели RGB (красный (R), зеленый (G), синий (B)): R (0..255) G (0..255) B (0..255) -> 2⁸ вариантов на каждый из трех цветов.
- R G B: 24 бита = 3 байта — режим True Color (истинный цвет)
- Получим формулу объема памяти для хранения растрового изображения

Или можно формулу записать так:

I = N * i битов

- где N – количество пикселей и i – глубина цвета (разрядность кодирования)

* для указания объема выделенной памяти встречаются разные обозначения (V или I).

- Следует также помнить формулы преобразования:

1 Мбайт = 2²⁰ байт = 2²³ бит,
1 Кбайт = 2¹⁰ байт = 2¹³ бит

Кодирование звуковой информации

Познакомимся с понятиями и формулами, необходимыми для решения заданий 9 ЕГЭ по информатике.

- Оцифровка или дискретизация – это преобразование аналогового сигнала в цифровой код.

- T – интервал дискретизации (измеряется в с)
- ƒ — частота дискретизации (измеряется в Гц, кГц)
- Частота дискретизации определяет количество отсчетов, т.е. отдельных значений сигнала, запоминаемых за 1 секунду. Измеряется в герцах, 1 Гц (один герц) – это один отсчет в секунду, а, например, 7 кГц – это 7000 отсчетов в секунду.
- Разрядность кодирования (глубина, разрешение) — это число битов, используемое для хранения одного отсчёта.

- Получим формулу объема звукового файла:

Для хранения информации о звуке длительностью t секунд, закодированном с частотой дискретизации ƒ Гц и глубиной кодирования B бит требуется бит памяти:

I = B * ƒ * t * S

- I — объем
- B — глубина кодирования
- ƒ — частота дискретизации
- t — время
- S — количество каналов

S для моно = 1, для стерео = 2, для квадро = 4

Пример: при ƒ=8 кГц, глубине кодирования 16 бит на отсчёт и длительности звука 128 с. потребуется

Решение:

I = 8000*16*128 = 16384000 бит
I = 8000*16*128/8 = 2048000 байт

Определение скорости передачи информации

- Канал связи всегда имеет ограниченную пропускную способность (скорость передачи информации), которая зависит от свойств аппаратуры и самой линии (кабеля)
- Объем переданной информации Q вычисляется по формуле:

Q = q * t

Q — объем информации
q — пропускная способность канала (в битах в секунду или подобных единицах)
t — время передачи

Скорость передачи данных определяется по формуле:

V = Q/t

и измеряется в бит/с

Тема: Кодирование изображений:

ЕГЭ по информатике 2017 задание 9 ФИПИ вариант 1 (Крылов С.С., Чуркина Т.Е.):
Какой минимальный объем памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 160 х 160 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.

Решение:

- Используем формулу:

V= M x N *I

- Подсчитаем каждую составляющую формулы:
  - M x N: 20*2³ x 20*2³ = 400 * 2⁶ = 25 * 2⁴*2⁶
  - 256 = 2⁸ -> 8 бит на пиксель (из формулы Q=M^N)
- V = 25 * 2⁴*2⁶*2³ — всего бит на всё изображение
- Переводим в Кбайты: (25 * 2⁴*2⁶*2³) / 2¹³ = 25 Кбайт

Результат: 25

ЕГЭ по информатике задание 9.2 (источник: 9.1 вариант 11, К. Поляков):Рисунок размером 128 на 256 пикселей занимает в памяти 24 Кбайт (без учёта сжатия). Найдите максимально возможное количество цветов в палитре изображения.

Решение:

- По формуле объема файла изображения имеем: V = M*N*i, где M*N — общее количество пикселей. Найдем это значение, используя для удобства степени двойки:

128*256 = 2⁷ * 2⁸ = 2¹⁵

- В вышеуказанной формуле i — это глубина цвета, от которой зависит количество цветов в палитре. Количество цветов = 2ⁱ. Найдем i из той же формулы: i=V/(M*N). Учтем, что 64 Кбайт необходимо перевести в биты. Получим:

i = (2³*3*2¹⁰*2³) / 2¹⁵ = 3*2¹⁶ /2¹⁵ = 6 бит

- Теперь найдем количество цветов в палитре:

2⁶ = 64 вариантов цветов в цветовой палитре

Результат: 64

ЕГЭ по информатике задание 9.3 (источник: 9.1 вариант 24, К. Поляков):После преобразования растрового 256-цветного графического файла в 4-цветный формат его размер уменьшился на 18 Кбайт. Каков был размер исходного файла в Кбайтах?

Решение:

- По формуле объема файла изображения имеем: V = N*i, где N — общее количество пикселей, а i — глубина цвета (количество бит, выделенное на 1 пиксель)
- i можно найти, зная количество цветов палитры: кол-во цветов = 2ⁱ:

до преобразования: i = 8 (2⁸=256)
после преобразования: i = 2 (2²=4)

- Составим систему уравнений на основе имеющихся сведений, примем за x количество пикселей:

V = x*8
V-18 = x*2

- Выразим x в первом уравнении:

x=V/8

- Подставим во второе уравнение и найдем V (объем файла):

V-18 = V/4
4V-V = 72
3V = 72
V = 24

Результат: 24

ЕГЭ по информатике задание 9.4 (источник: 9.1 вариант 28, К. Поляков, С. Логинова):Цветное изображение было оцифровано и сохранено в виде файла без использования сжатия данных. Размер полученного файла – 42 Мбайт. Затем то же изображение было оцифровано повторно с разрешением в 2 раза меньше и глубиной кодирования цвета увеличили в 4 раза больше по сравнению с первоначальными параметрами. Сжатие данных не производилось. Укажите размер файла в Мбайт, полученного при повторной оцифровке.

Решение:

- По формуле объема файла изображения имеем: V = N*i, где N — общее количество пикселей или разрешение, а i — глубина цвета (количество бит, выделенное на 1 пиксель)
- Но для данной задачи, необходимо уточнить, что разрешение на самом деле имеет два сомножителя (пикселей по ширине * пикселей по высоте). Поэтому при уменьшении разрешения в два раза, уменьшатся оба числа, т.е. N уменьшится в 4 раза вместо двух.
- Составим систему уравнений на основе имеющихся сведений, в которой первое уравнение будет соответствовать данным до преобразования файла, а второе уравнение — после:

42 = N*i
V = N/4 * 4i

или

42 = N*i
V = N * i

- Выразим N в первом уравнении:

N = 42/i

- Подставим во второе уравнение и найдем V (объем файла):

V = (42/i) * i
V = 42

Результат: 42

ЕГЭ по информатике задание 9.5 (источник: 9.1 вариант 30, К. Поляков, С. Логинова):Изображение было оцифровано и сохранено в виде растрового файла. Получившийся файл был передан в город А по каналу связи за 72 секунды. Затем то же изображение было оцифровано повторно с разрешением в 2 раза больше и глубиной кодирования цвета в 3 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б, пропускная способность канала связи с городом Б в 3 раза выше, чем канала связи с городом А. Сколько секунд длилась передача файла в город Б?

Решение:

- По формуле объема файла изображения имеем: V = N*i, где N — общее количество пикселей или разрешение, а i — глубина цвета (количество бит, выделенное на 1 пиксель)
- Но для данной задачи, необходимо уточнить, что разрешение на самом деле имеет два сомножителя (пикселей по ширине * пикселей по высоте). Поэтому при увеличении разрешения в два раза, увеличатся оба числа, т.е. N увеличится в 4 раза вместо двух.
- Если разрешение увеличили в 4 раза, а глубину кодирования цвета уменьшили в три раза, значит объем файла был сначала увеличен в 4 раза и затем уменьшен в 3 раза.
- По формуле скорости передачи файла имеем: S = V/t, где V — объем файла, а t — время
- Из формулы видно, что время передачи изменяется пропорционально объему файла, то есть, к примеру, увеличив объем в два раза, время передачи будет увеличено также в два раза.
- В город А файл был передан за 72 секунды. Определим время передачи в тот же город А преобразованного файла.

72 * 4 / 3 = 96 секунд

- То есть передача преобразованного файла в город А происходила 96 секунд.
- Пропускная способность для канала в город Б увеличилась в 3 раза, значит файл в город Б был передан за:

96 / 3 = 32 секунды

Результат: 32

ЕГЭ по информатике 2017 задание 9 ФИПИ вариант 15 (Крылов С.С., Чуркина Т.Е.):
На студии при четырехканальной (квадро) звукозаписи с 32-битным разрешением за 30 секунд был записан звуковой файл. Сжатие данных не производилось. Известно, что размер файла оказался 7500 Кбайт. С какой частотой дискретизации (в кГц) велась запись? В качестве ответа укажите только число, единицы измерения указывать не нужно.

Решение:

- По формуле объема звукового файла получим:

V = M*t*I*S

- Из задания имеем:

V= 7500 Кбайт
I= 32 бита
t= 30 секунд
S= 4 канала

- М — не известно, выразим его из формулы:

М=V/(S*I*t)=7500*2¹⁰*2² бит /(2⁷*30)=750*2⁶ / 1000 Гц=2⁴ =16

Результат: 16

9 задание. Демоверсия ЕГЭ 2018 информатика:
Автоматическая фотокамера производит растровые изображения размером 640×480 пикселей. При этом объём файла с изображением не может превышать 320 Кбайт, упаковка данных не производится. Какое максимальное количество цветов можно использовать в палитре?

Решение:

- По формуле объема файла изображения имеем: V = N*i, где N — общее количество пикселей или разрешение, а i — глубина цвета (количество бит, выделенное на 1 пиксель)
- Посмотрим, что из формулы нам уже дано: V = 320 Кбайт, N = 640*420 = 307200 всего пикселей, i — ?
- Количество цветов в изображении зависит от параметра i, который неизвестен: количество цветов = 2ⁱ
- Поскольку глубина цвета измеряется в битах, то необходимо объем перевести из Килобайт в биты:

320 Кбайт = 320 * 2¹⁰ * 2³  = 320 * 2¹³

- Найдем i:

i = V/N = (320 * 2¹³)/307200 = (320 * 2¹³)/(75*2¹²) ~ 8,5 бит

- Найдем количество цветов:

2ⁱ = 2⁸ = 256

Результат: 256

Тема: Кодирование звука:

ЕГЭ по информатике задание 9.9 (источник: 9.2 вариант 36, К. Поляков):Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 2 раза выше и частотой дискретизации в 3 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 15 секунд; пропускная способность канала связи с городом Б в 4 раза выше, чем канала связи с городом А. Сколько секунд длилась передача файла в город A? В ответе запишите только целое число, единицу измерения писать не нужно.

Решение:

- Вспомним формулу объема звукового файла:

I = B * ƒ * t

I — объем
B — глубина кодирования
ƒ — частота дискретизации
t — время

- Выпишем отдельно, все данные, касающиеся города Б (про А практически ничего не известно):

город Б: 
B - в 2 раза выше
ƒ - в 3 раза меньше
t - 15 секунд, 
пропускная способность (скорость V) - в 4 раза выше

- Исходя из предыдущего пункта, для города А получаем обратные значения:

город А: 
B_Б/2
ƒ_Б*3
I_Б/2
V_Б/4
t_Б/2, t_Б*3, t_Б*4  -  ?

Дадим объяснения полученным данным:

- так как глубина кодирования (B) для города Б выше в 2 раза, то для города А она будет ниже в 2 раза, соответственно и t уменьшится в 2 раза: t = t/2;
- так как частота дискретизации (ƒ) для города Б меньше в 3 раза, то для города А она будет выше в 3 раза; I и t изменяются пропорционально, значит при увеличении частоты дискретизации увеличится не только объем, но и время: t = t * 3;
- скорость (V)(пропускная способность) для города Б выше в 4 раза, значит для города А она будет ниже в 4 раза; раз скорость ниже, то время выше в 4 раза (t и V — обратно-пропорциональная зависимость из формулы V = I/t): t = t * 4
- Таким образом, с учетом всех показателей, время для города А меняется так:

t_А = 15 / 2 * 3 * 4 = 90 секунд

Результат: 90

ЕГЭ по информатике задание 9.11 (источник: 9.2 вариант 72, К. Поляков):Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 100 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 3 раза выше и частотой дискретизации в 4 раз меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 15 секунд.
Во сколько раз скорость (пропускная способность канала) в город Б больше пропускной способности канала в город А?

Решение:

- Вспомним формулу объема звукового файла:

I = B * ƒ * t * S

I — объем
B — глубина кодирования
ƒ — частота дискретизации
t — время

- Выпишем отдельно, все данные, касающиеся файла, переданного в город А, затем преобразованного файла, переданного в город Б:

А:
t = 100 c.

Б:
B = в 3 раза выше
ƒ = в 4 раза ниже
t = 15 c.

1 способ:

- Скорость передачи данных (пропускная способность) зависит от времени передачи файла: чем больше время, тем ниже скорость. Т.е. во сколько раз увеличится время передачи, во столько раз уменьшится скорость и наоборот
- Из предыдущего пункта видим, что если мы вычислим во сколько раз уменьшится или увеличится время передачи файла в город Б (по сравнению с городом А), то мы поймем, во сколько раз увеличится или уменьшится скорость передачи данных в город Б (обратная зависимость).
- Соответственно представим, что преобразованный файл передается в город А. Объем файла изменился в 3/4 раза (глубина кодирования (B) в 3 раза выше, частота дискретизации (ƒ) в 4 раза ниже). Объем и время изменяются пропорционально. Значит и время изменится в 3/4 раза:

100 секунд * 3 / 4 = 75 секунд

- Т.е. файл передавался в город А 75 секунд, а в город Б 15 секунд. Вычислим во сколько раз снизилось время передачи:

75 / 15 = 5

- Раз время передачи в город Б снизилось в 5 раз, соответственно, скорость увеличилась в 5 раз.

2 способ:

- Выпишем отдельно, все данные, касающиеся файла, переданного в город А
```
А:
t_А = 100 c.
V_А = I/100
```
- Поскольку увеличение или уменьшение в какое-то количество раз разрешения и частоты дискретизации приводит к соответствующему увеличению или уменьшению объема файла, то запишем известные данные для преобразованного файла, переданного в город Б:

Б:
B = в 3 раза выше
ƒ = в 4 раза ниже
t = 15 c.
I_Б = (3/4) * I
V_Б = ((3/4) * I) / 15

- Теперь найдем соотношение V_Б к V_А:

(((3/4) * I) / 15) * (100 / I)= (3/4 * 100) / 15 = 15/3 = 5

Результат: 5

Тема: Скорость передачи данных:

ЕГЭ по информатике задание 9.13 (источник: 9.V вариант 5, К. Поляков):Скорость передачи данных через ADSL-соединение равна 128000 бит/с. Передача текстового файла через это соединение заняла 1 минуту. Определите, сколько символов содержал переданный текст, если известно, что он был представлен в 16-битной кодировке Unicode.

Решение:

- Вспомним формулу скорости передачи данных:

V = Q/t

V - скорость
Q - объем
t - время

- Что нам известно из формулы:

V = 128000 бит/с
t = 1 мин = 60 с
1 символ кодируется 16-ю битами
всего символов - ?

- Если мы найдем сколько бит необходимо для всего текста, тогда, зная что на 1 символ приходится 16 бит, мы сможем найти сколько всего символов в тексте. Таким образом, найдем объем:

Q = V*t

Q = 128000*60 = 2¹⁰*125*2²*15 = 
= 2¹²*1875 бит на все символы

- Когда мы знаем, что на 1 символ необходимо 16 бит, а на все символы 2¹²*1875 бит, то можем найти сколько символов всего:

символов = 2¹²*1875 / 16 = 2¹²*1875 / 2⁴ = 
= 2⁸*1875 = 480000

Результат: 480000

ЕГЭ по информатике задание 9.14 (источник: 9.V вариант 23, К. Поляков):У Васи есть доступ к Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения им информации 2¹⁷ бит в секунду. У Пети нет скоростного доступа в Интернет, но есть возможность получать информацию от Васи по низкоскоростному телефонному каналу со средней скоростью 2¹⁶ бит в секунду. Петя договорился с Васей, что тот будет скачивать для него данные объемом 8 Мбайт по высокоскоростному каналу и ретранслировать их Пете по низкоскоростному каналу. Компьютер Васи может начать ретрансляцию данных не раньше, чем им будут получены первые 1024 Кбайт этих данных. Каков минимально возможный промежуток времени (в секундах), с момента начала скачивания Васей данных, до полного их получения Петей?

Решение:

- Вспомним формулу скорости передачи данных:

V = Q/t

V - скорость
Q - объем
t - время

- Определим, что нам известно:

Вася: V = 2¹⁷ бит/с
Петя: V = 2¹⁶ бит/с
Общий объем Q = 8Мбайт

- Для начала переведем объем в биты:

Q = 8Мбайт = 8*2²³ бит = 2³*2²³ = 2²⁶ бит

- Также известно, что сначала 1024 Кбайта будут передаваться по скоростному каналу Васи со скоростью 2¹⁷ бит/с (примем за t1), а затем все 8Мбайт будут передаваться по низкоскоростному каналу (примем за t2). Найдем время по двум промежуткам:

t = Q/V

t1 = 1024 Кбайт / 2¹⁷ = 2¹⁰ * 2¹³ бит / 2¹⁷ = 
= 2¹⁰/2⁴ = 64 с

t2 = 2²⁶/2¹⁶ = 2¹⁰ = 1024 c

- Найдем общее время:

t = t1 + t2 = 64 + 1024 = 1088

Результат: 1088

Источник

Ответ:

Кодирование текстовой информации

Кодирование графической информации

Кодирование звуковой информации

Определение скорости передачи информации

Решение заданий 7 ЕГЭ по информатике

Тема: Кодирование изображений

Тема: Кодирование звука

Тема: Кодирование видео

Тема: Скорость передачи данных

7 (базовый уровень, время – 5 мин)

Пример задания:

Ещё пример задания:

Ещё пример задания:

Ещё пример задания:

Задачи для тренировки1:

Кодирование графической информации

Кодирование звуковой информации

Определение скорости передачи информации

Задачи для тренировки^¹: